Решить уравнение онлайн с дробями 8 класс: Уравнения с дробями 8 класса онлайн

Решение рациональных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями

 

Урок: Решение рациональных уравнений

 

1. Пример решения рационального уравнения, являющегося математической моделью текстовой задачи

 

 

Как вы уже успели заметить на предыдущем уроке, основа решения рациональных уравнений – техника преобразования рациональных выражений. Рассмотрим пример решения рационального уравнения.

 

Пример 1

Решить уравнение: .

Решение:

В первую очередь обратим внимание на то, что в числителях обеих дробей, а также в правой части уравнения стоят чётные числа. То есть, можно упростить уравнение, поделив обе его части на . Этот шаг не является обязательным, но, чем проще уравнение, тем легче его решать, а чем меньше числа, фигурирующие в уравнении, тем легче арифметические вычисления при его решении.

В результате сокращения получаем:

Теперь перенесём все члены уравнения в левую часть, чтобы получить справа , а затем приведём полученные в левой части дроби к общему знаменателю:

Напомним, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Поэтому наше уравнение превращается в следующую систему:

 

Теперь вспомним ещё один важный факт: произведение равно  тогда и только тогда, когда хотя бы один из его множителей равен , а остальные множители при этом существуют. И наша система превращается в следующую:

.

Оба полученных корня являются решениями данного уравнения, так как при них знаменатель определён.

Ответ: .

 

2. Пример текстовой задачи и решения её с помощью математического моделирования

 

 

Рассмотренное нами уравнение является моделью для такой задачи:

 

Задача 1

Лодка прошла  по течению реки и  против течения реки, затратив на весь путь . Чему равна собственная скорость лодки, если скорость течения реки равна ?

Решение:

Решение данной задачи осуществим с помощью метода математического моделирования и выделим 3 этапа данного метода.

Этап 1. Составление математической модели

Обозначим через  собственную скорость лодки (это стандартный приём при решении текстовых задач – обозначить с помощью неизвестной ту величину, которая спрашивается в условии задачи). Тогда:

 – скорость движения лодки по течению реки;

 – скорость движения лодки против течения реки.

В этом случае, воспользовавшись формулой: , получаем, что время движения лодки по течению реки выражается как , а время движения лодки против течения реки – . Тогда общее время движения лодки равно , откуда получаем уравнение:

 – это и есть математическая модель данной задачи.

Этап 2. Работа с математической моделью

В данном случае работа с математической моделью сводится к решению данного рационального уравнения, что мы уже сделали в примере 1. При этом получили корни уравнения: .

Этап 3. Ответ на вопрос задачи

Дело в том, что математическая модель потому и является математической, что абстрагирована от реальной жизни. Если брать конкретно данную задачу, то математическая модель – это уравнение, которое может иметь любые корни. Однако неизвестная величина обозначает скорость лодки, поэтому не может быть, к примеру, отрицательной. Или: не может быть меньше скорости течения реки, иначе бы лодка не смогла бы плыть против течения. И такие ограничения могут быть в самых разных задачах. Поэтому, прежде чем записать ответ, необходимо оценить, является ли он правдоподобным.

В данном случае очевидно, что  не подходит, так как лодка не смогла бы с такой скоростью плыть против течения. Поэтому в ответ пойдёт только одна величина: .

Ответ:

 

3. Различные примеры решения рациональных уравнений

 

 

Рассмотрим несколько примеров на решение непосредственно рациональных уравнений.

 

Пример 2

Решить уравнение: .

Решение:

Перенесём все слагаемые в левую часть, а затем приведём дроби к общему знаменателю.

Снова воспользуемся тем фактом, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

Ответ:.

Пример 3

Решить уравнение: .

Решение:

В данном уравнении в правой части уже стоит , поэтому ничего переносить левую часть не нужно. Сразу приведём дроби в левой части к общему знаменателю:

.

Снова воспользуемся тем фактом, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

. Подставив данное значение в знаменатель, убеждаемся, что он не равен . Значит, это значение переменной является ответом.

Ответ:.

Пример 4

Решить уравнение: .

Решение:

Схема решения данного уравнения абсолютно такая же, как и у предыдущих:

Ответ:.

 

4. Решение задачи, сводящейся к рациональному уравнению

 

 

К решению рациональных уравнений часто сводятся различные задачи. Рассмотрим один из таких примеров.

 

Задача 2

Существует ли такое значение , при котором разность дробей  и  равна ?

Решение:

Запишем уравнение, соответствующее условию данной задачи: .

Решим данное рациональное уравнение точно так же, как и в предыдущих примерах.

Приведём подобные слагаемые в числителе (они отмечены одинаковым цветом):

То есть, такое значение  существует.

Ответ: существует:.

Итак, мы рассмотрели примеры решения рациональных уравнений, а также их использование при решении различных задач. На следующих уроках мы перейдём к изучению новой темы, посвящённой различным функциям.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей «Открытый урок» (Источник).

2. Портал для всей семьи (Источник).

3. Обучающие курсы (Источник).

 

Домашнее задание

1. №№165, 178. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

2. Решить уравнения: а), б) .

3. Выполнить действия: а) , б) .

4. Два экскаватора могут выкопать котлован за . Первый экскаватор может выкопать котлован в 4 раза быстрее, чем второй. За сколько часов может выкопать такой же котлован каждый экскаватор, работая отдельно?

 

Алгебраические дроби (урок повторения и обобщения). 8 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

АЛГЕБРАИЧЕСКИЕ ДРОБИ
(урок повторения и обобщения)

2. Цель урока

• Обобщить и повторить учебный
материал данной темы
• Развивать вычислительные
навыки
• Воспитывать добросовестное
отношение к учению

3. Оборудование

• Компьютер
• Мультимедийный проектор
• Экран или интерактивная доска

4. Ход урока

Организационный
момент
Постановка цели урока
Обобщение

5. Повторение всех основных правил

1. Что такое алгебраическая дробь?
2. Что такое многочлен?
3. Какова алгоритм сложения ( вычитания)
алгебраических дробей?
4. Сформулировать правило произведения
алгебраических дробей
5. Сформулировать правило деления алгебраических
дробей
6. Правило возведения дроби в степень
7. Что значит доказать тождество?
8. Что такое О.Д.З уравнения?
9. Что такое рациональное уравнение?
10. Этапы решения текстовых задач
11. Формула квадрата суммы и квадрата разности
12. Формула разности квадратов

6. • Отработка практических умений

a) Найти значение алгебраической дроби
а²-в² / а²-2ав+в² при: а=3, в=2.
b) Привести дробь
3х / 2х-3у к знаменателю 3у-2х.
c) Сократить дробь
а²+2ав / а²-4в²
d) Сложим дроби 3а-3в / 16а²в и 5а+3в / 16а²в
e) Вычтем из дроби 3а² / а+2в дробь 12в² / а+2в.
f) Перемножим дробь х+2у / х+у и многочлен
х²-у².
g) Возведем дробь 3а² / 4в в четвертую
степень.
h) Разделим дробь 15х / 4у на дробь 5х² / 2у.

7. • Творческое задание

Лодка прошла 10 км по течению
реки и 6 км против течения,
затратив на весь путь 2 ч. Чему
равна собственная скорость
лодки, если скорость течения
реки равна 2 км/ч?

8. Решение. Первый этап. Составление математической модели. Пусть х км/ч – собственная скорость лодки, тогда (х+2) км/ч — скорость

лодки по течению реки
(х-2) км/ч. – скорость лодки против течения
По течению реки, т. е. со скоростью (х+2) км/ч, лодка прошла путь
S=10 км. Значит, время (t), затраченное на этот путь, выражается
формулой 10 / х+2 (ч).
Против течения реки, т.е. со скоростью (х-2) км/ч, лодка прошла
путь S=6 км. Следовательно, время, затраченное на этот путь,
выражается формулой 6 / х-2 (ч).
По условию задачи на весь путь (т.е. на 10 км по течению и 6 км
против течения) суммарно затрачено 2 ч.
Итак, получаем уравнение 10/х+2 + 6/х-2=2.

9. Второй этап. Работа с составленной моделью. х = 0 или х = 8. Третий этап. Ответ на вопрос задачи. Мы получили, что либо х = 0,

либо х = 8.
Первое значение нас явно не устраивает: собственная
скорость лодки не может быть равной 0 км/ч.
Второе значение нас устраивает.
Ответ: собственная скорость лодки равна 8 км/ч.

10. • Домашнее задание

Домашняя контрольная работа №1.
Вариант 1. ( №1 — №10, стр. 57-58 )
А.Г.Мордкович Алгебра, 8кл.: Задачник для
общеобразовательных учреждений. — 2-е
изд. – М.: Мнемозина, 2000.- 247с.
Изучение дополнительной литературы:
Математика. Решебник. Подготовка к ЕГЭ2011: учебно-методическое пособие / Под
редакцией Ф.Ф.Лысенко. – Ростов-на-Дону :
Легион-М, 2010.-192с.
• Подведение итогов урока.

English     Русский Правила

8. Уравнения с дробями

В этом разделе мы можем легко найти решение, умножая все на наименьший общий знаменатель (LCD) . Это упростит наше уравнение и облегчит его решение.

Нужно не забыть умножить все члены в уравнении (обе стороны от знака равенства) на LCD, иначе окончательный ответ будет неверным.

Мы начнем с некоторых алгебраических примеров, затем продолжим с задачами на дроби.

а. Алгебраические типы

Пример 1

Решить для x :

`х/5+3/10 = 1/2`

Ответить

Сначала рассмотрим знаменателей дробей и найдем наименьший общий знаменатель. В этом случае это будет «10».

Мы умножаем на «10», и результат:

`10xx(x/5+3/10) = 10xx(1/2)`

`2x+3=5`

Затем мы просто решаем найденное нами более простое уравнение.

Вычесть «3» с обеих сторон:

`2x=2`

Разделите обе стороны на «2», чтобы получить окончательный ответ:

`х=1`

Пример 2

Решить для x :

`(2x)/3+2/5 = 8+x/2`

Ответить

Еще раз смотрим на знаменателей дробей и определяем наименьший общий знаменатель. В этом случае это будет «30».

Мы умножаем на «30» и получаем:

`30xx((2x)/3+2/5) = 30xx(8+x/2)`

`20x+12=240+15x`

Вычитание «12» с обеих сторон:

`20x=228+15x`

Вычесть «15x» с обеих сторон:

`5x=228`

Разделите обе части на «5», чтобы получить окончательный ответ:

`х=228/5=45,6`

Пример 3

Этот следующий имеет переменную в знаменатель .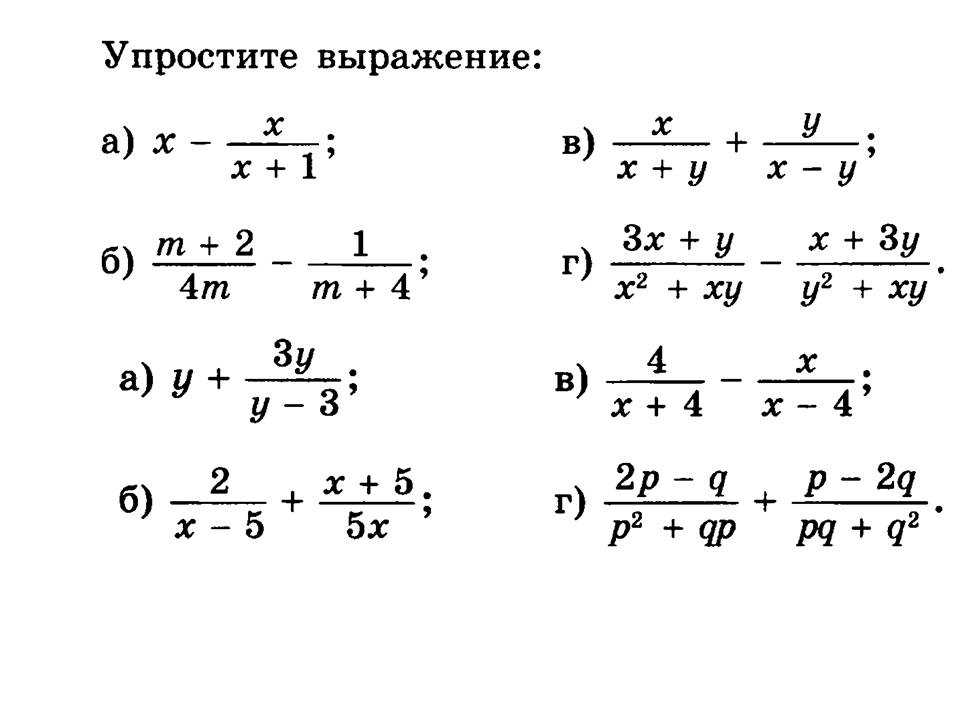 Нам все равно нужно будет найти ЖК-дисплей, как и раньше.

Решить для x :

`4/x+1/3 = 7/(5x)`

Ответить

В этом случае наименьший общий знаменатель равен «15x».

Мы умножаем на «15x» и получаем результат:

`15x xx(4/x+1/3) = 15x xx(7/(5x))`

`60+5x=21`

Вычитание «60» с обеих сторон:

`5x=-39`

Разделите обе части на «5», чтобы получить окончательный ответ:

`х=-39/5=-7,8`

б. Проблемы со словами

Пример 4

Аквариум можно наполнить одним шлангом за 7 минут, а вторым более тонким шлангом за 10 минут.

Сколько времени потребуется для заполнения бака, если оба шланга работают вместе?

Ответить

Так как время наполнения каждого шланга составляет меньше , мы имеем чтобы сложить обратные величины вместе и взять обратную величину результата.

Нам нужно использовать:

`1/T=1/T_1+1/T_2`

Итак, мы имеем:

`1/T=1/7+1/10`

`1/T=(10+7)/70=17/70`

Так

`Т=70/17=4,1176`

Таким образом, наполнение бака при одновременной работе обоих шлангов займет 4,1 минуты.

Пример 5

Связанные страницы

Вам могут пригодиться:

• Раздел алгебраических выражений
• Решение уравнений
• Формулы и буквенные уравнения
• Прикладные вербальные задачи

Для 2 резисторов с сопротивлениями Р ₁ и R ₂ параллельно, общее сопротивление R определяется как:

`1/R=1/R_1+1/R_2`

Для конкретной цепи комбинированное сопротивление R оказалось 4 Ом (Ом), а R ₁ = 10 Ом. Найти R

2 .

Ответить

У нас есть:

`1/4=1/10+1/R_2`

Нам нужно умножить на наименьший общий знаменатель: 20 R ₂

`1/4=1/10+1/R_2`

`(20R_2)/4=(20R_2)/10+(20R_2)/(R_2)`

`5R_2=2R_2+20`

`3R_2=20`

`R_2=20/3=6 2/3Омега`

«Омега» — это символ «Ом», единицы сопротивления.

Пример 6

Средняя скорость автомобиля от дома до работы составляла 30 км/ч, а обратно – 40 км/ч. Если общее время двух поездок составляет 50 минут, какое расстояние от дома до работы?

Ответить

Пусть длина пути от дома до работы равна х км.

Напомним, что

`текст(скорость) = текст(расстояние)/текст(время)`

Так

`текст(время) = текст(расстояние)/текст(скорость)`

Мы должны использовать одни и те же единицы измерения времени. Мы будем использовать часы.

Сейчас

`50\текст(минуты)=50/60=5/6текст(часы)`

Время в пути было `х/30` часов.

Для обратного пути время было `x/40` часов.

Общее время было `x/30+x/40=5/6\ text(hours)`

Итак `(4x+3x)/120=(7x)/120=5/6`

Это дает нам `7x=(5xx120)/6=100`

То есть `x=100/7=14,286`

Таким образом, расстояние от дома до работы составляет 14,3 км.

Equation rearranger online

• Expression
• Equation
• Inequality
• Contact us

• Simplify
• Factor
• Expand
• GCF
• LCM

• Solve
• Graph
• System

• Решить
• График
• Система

• Математический решатель на вашем сайте

Наших пользователей:

Математика не может быть проще с Algebrator. Спасибо!
DE, Кентукки

Мне никогда не было легко понять математику, но эта программа облегчает ее понимание. Спасибо!
Хелен Диллануэва, Вирджиния

Я очень рада, что нашла эту программу!
Мигель Сан-Мигель-Гонсалес, Ларедо, инт. Университет

Мой сын использовал Алгебратор в старшей школе, и, похоже, он будет использовать его и в колледже (кстати, спасибо за бесплатное обновление). Мне очень нравится тот факт, что я могу рассчитывать на то, что ваша компания будет постоянно улучшать программное обеспечение, а не просто делать продажи и забывать о клиентах.
Марджи Тейт, Вирджиния

Как учитель я хвалю алгебра, потому что ученики любят его и находят его наиболее стимулирующим и интересным. То, что они видят, это то, что они узнают, и, кроме того, это имеет отношение к учебной программе.

Риз Понтон, Миссури

---

Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт.

Сможете ли вы найти среди них свою?

Поисковые фразы, использованные 16.06.2012:

• алгебра; уравнения
• расписание по математике до 12 рабочих листов ks2 (в квадрате)
• математический решатель
• макдугал Литтел алгебра две задачи ответы
• TI 92 решить линейную систему
• решать комплексные числа
• решение математических задач художник и галлоны
• калькулятор excel по правилу Крамера
• поиск бесплатного теста iq для начального уровня с ответами
• начало теста по алгебре
• обратная десятичная таблица
• полиномы плана урока
• сокращающие дроби с квадратными корнями
• Калькулятор записи дробей
• примечания к редакции гидромеханики
• онлайн-факторинг
• Результаты экзамена по математике KS3 онлайн
• отношения+алгебра+развлечения+деятельность+рабочие листы
• ответов на интегрированную зеленую книгу по алгебре
• факторинговые калькуляторы трехчленов
• обратный журнал ti84 как найти
• математическая формула кс2
• ти89 факториал
• упростить каждое подкоренное выражение
• glencoe ответы ключи к биологии глава 4 концептуальное картирование
• онлайн ks2 практические научные тесты
• java найти минимальное «квадратное уравнение»
• gcse + алгебраическое доказательство
• фото параболы
• Калькулятор наименьших множителей
• Образец экзамена для начинающих по химии
• факторинг в кубе
• Экзамен по математике за 8 класс Онтарио
• упорядоченных пар + алгебра
• нелинейные уравнения Matlab
• уравнения балансировки онлайн
• прентис холл математика алгебра 1
• математических радикалов ответы на один шаг
• алгебра 1 тесты по математике для учеников
• образцов квадратных уравнений
• бесплатные практические занятия по науке ks2 uk
• листы с заданиями по алгебре
• уравнения факторинга онлайн
• практиковать экзамен по английскому языку онлайн
• учет затрат 12 глава 16 решение ответ
• как ввести кубический корень в калькулятор
• gcse Окружность и площадь кругов рабочий лист
• листы линейных измерений
• Бесплатный ключ к алгебре Переменные, термины и выражения № 2 рабочая тетрадь
• Каковы основные правила построения графика уравнения или неравенства?
• Масштабный коэффициент калькулятора геометрии
• ОНЛАЙН-КАЛЬКУЛЯТОР ДЛЯ ДЕЛЕНИЯ Дробей И СМЕШАННЫХ ЧИСЕЛ
• все ответы для prentice hall pre алгебра
• Расчет стандартного масштабного коэффициента
• бесплатных математических игр с десятичными дробями
• Matlab решает числовое число
Онлайн калькулятор кубического корня
• алгебра формула треугольник
• зачем придумали алгебру?
• смешанные числа в десятичный калькулятор
• шагов метода подстановки
• РЕШЕНИЕ МАТЕМАТИЧЕСКИХ ЗАДАЧ
• Калькулятор трехчленов
• практические задачи по электрической цепи гр. 10
• десятичная строка для дроби ti-84
• калькулятор наименьшего общего знаменателя
• Алгебра 2: рабочий лист с вариантами
• упростить алгебраические уравнения
• г. 7 тестов по математике
• простые электронные книги по математическим расчетам
• Решатель квадратных уравнений
• Макдугал Литтел Текст глава 9алгебра 2
• бесплатные вычисления по алгебре
• простые правила алгебры средние классы
• программа квадратное уравнение в ТИ-84
• Glencoe Algebra 1 рабочая тетрадь
• бесплатный рабочий лист для словесных задач по алгебре с длиной, шириной, периметром
• Решатель 3 одновременных уравнений
• Engineering Fluid Mechanics Student Solutions Manual 7th Edition
• ти-86 решает нелинейные программы
• бесплатный онлайн-решатель рациональных выражений
• как решать биномы бесплатно
• упрощение алгебры с использованием отрицательных показателей
• бесплатное решение математических задач
• вопросы по алгебре и математике для 7-х классов
• онлайн-решатель уравнений с шагами
• Математика для 10 класса: решение линейных уравнений с использованием сравнения
• бесплатных упражнений по алгебре
• алгебраические суммы
• математическая индукция для чайников
• Калькулятор коэффициентов умножения
• Математические перестановки
• помогите с домашним заданием по алгебре
• графический калькулятор онлайн таблица
• Решатель уравнений балансирующей химии
• математика для пятого класса PowerPoint
• решить уравнение с помощью ЖК-дисплея
• г.

  No related posts.