Геометрия. Урок 2. Углы — ЁП
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Углы
Понятие угла
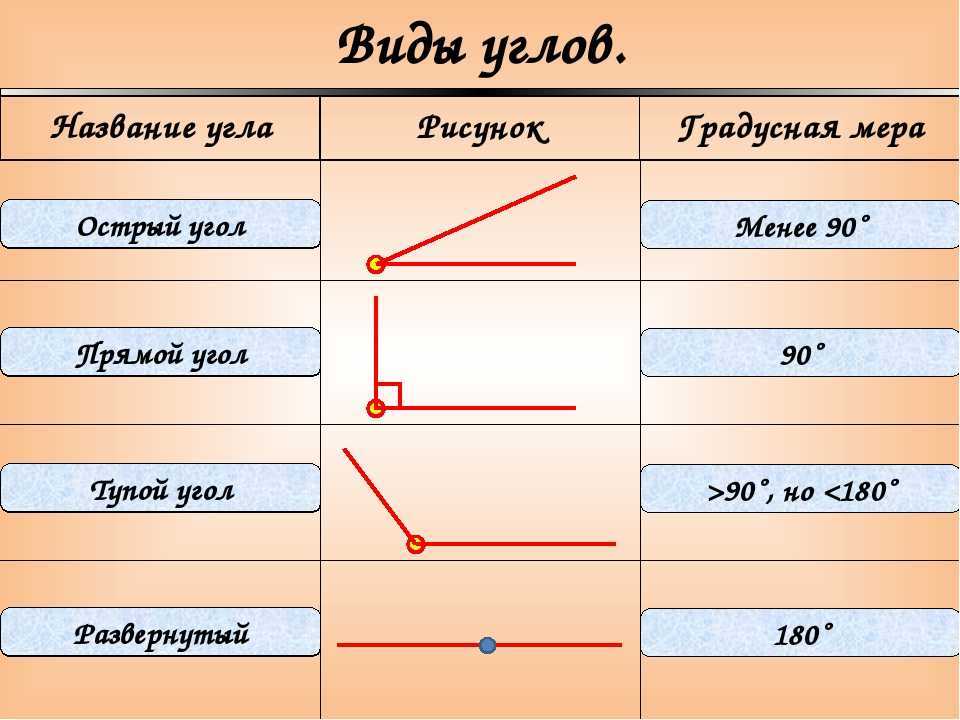
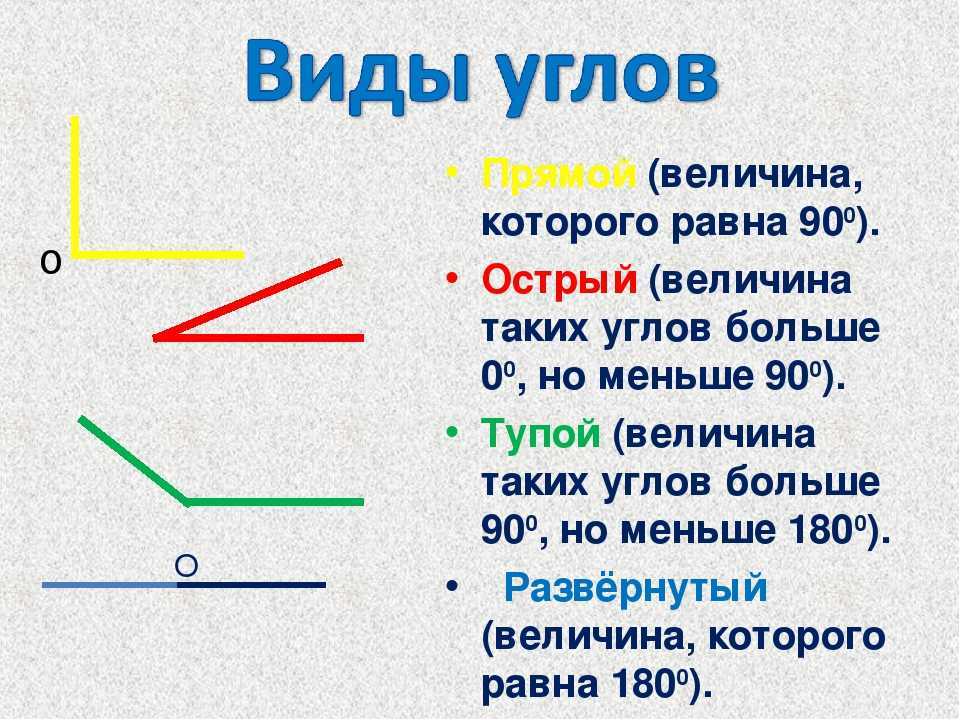
Виды углов
Биссектриса угла
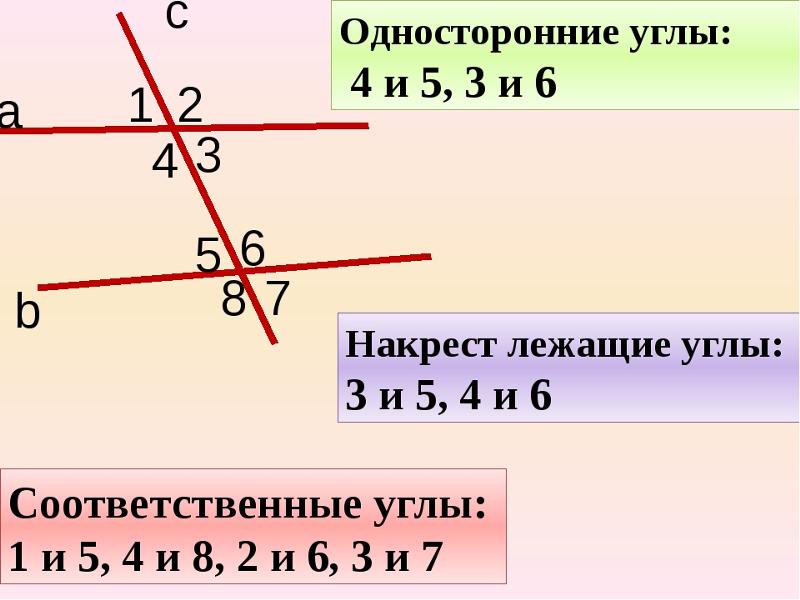
Углы, образованные при пересечении двух прямых
Углы, образованные при пересечени двух прямых секущей
Углы, образованные при пересечении двух параллельных прямых секущей
- Сумма углов многоугольника
Правильный многоугольник
- Примеры решений заданий из ОГЭ
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB или ∠BOA, но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.
Величину угла измеряют в градусах. ∠AOB=24°.
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Или
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.
∠AOD=∠BOD=∠AOB2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.
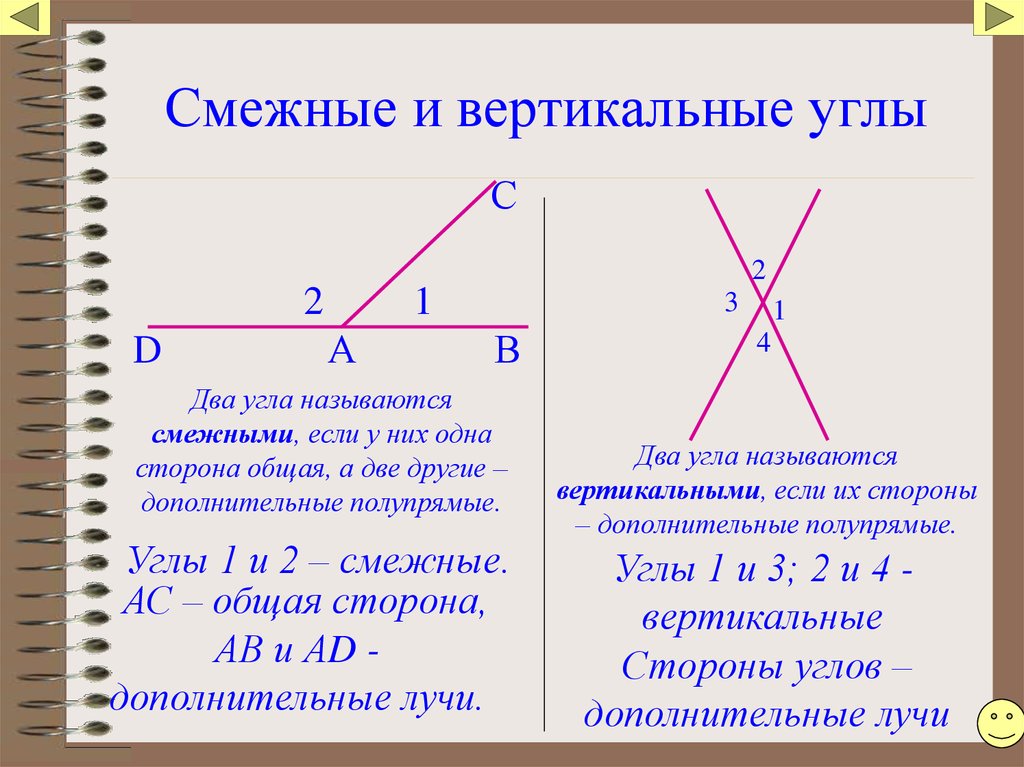
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180°.
Пример:
Пары углов
(1) и (3)
(2) и (4)
называются вертикальными.
По свойству вертикальных углов:
∠COD=∠AOB
∠BOD=∠AOC
Пары углов
(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)
называются смежными.
По свойству смежных углов:
∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°
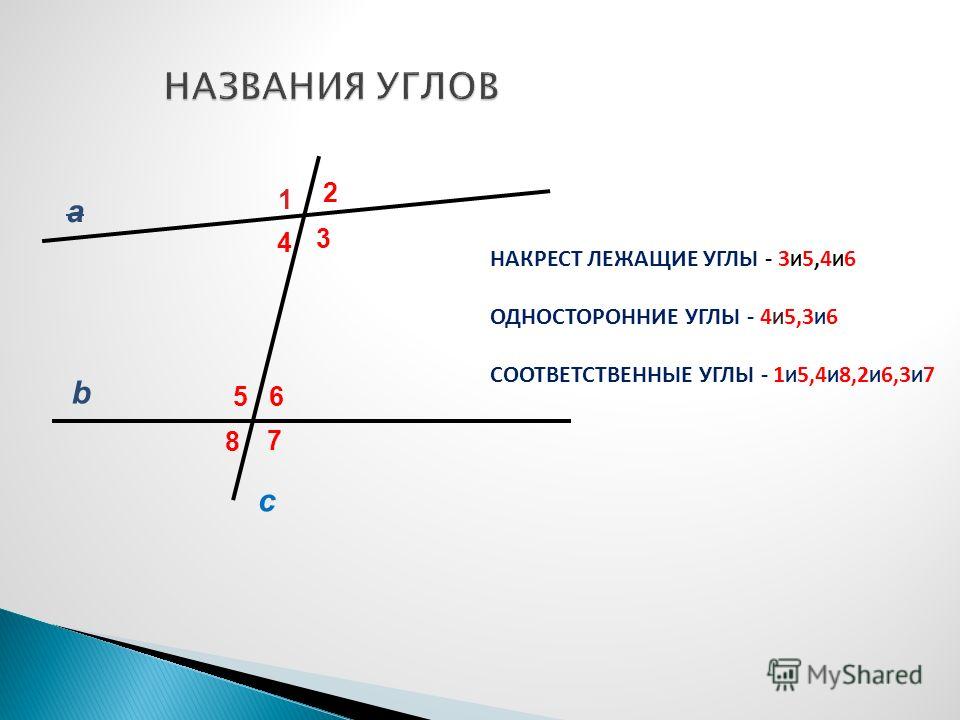
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
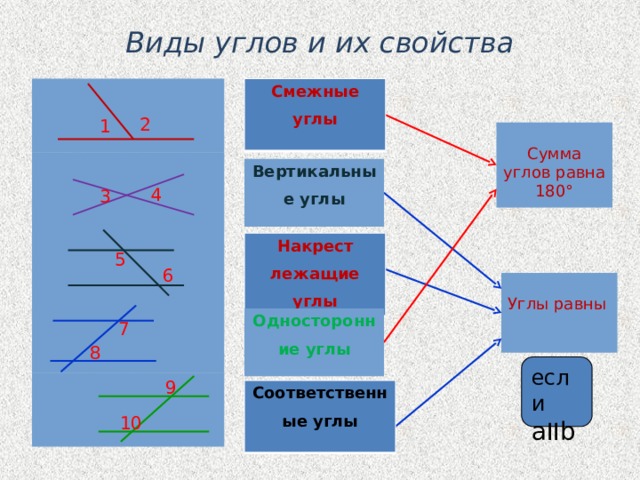
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
Пары углов:
(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)
называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
Пары углов:
(3) и (5)
(4) и (6)
называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
Пары углов:
(1) и (7)
(2) и (8)
называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
Пары углов:
(3) и (6)
(4) и (5)
называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
Пары углов:
(1) и (8)
(2) и (7)
называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180°.
- Сумма внешних односторонних углов равна 180°.
Сумма углов произвольного n-угольника вычисляется по формуле:
Sn=180°⋅(n−2)
где n – это количество углов в n-угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.
Сумма углов треугольника: S3=180°⋅(3−2)=180°
Сумма углов четырехугольника: S4=180°⋅(4−2)=360°
Сумма углов пятиугольника: S5=180°⋅(5−2)=540°
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.
αn=180°⋅(n−2)n
Модуль геометрия: задания, связанные с углами
Скачать домашнее задание к уроку 2.
Виды углов между прямыми, основные примеры
4.
2
Средняя оценка: 4.2
Всего получено оценок: 235.
4.2
Средняя оценка: 4.2
Всего получено оценок: 235.
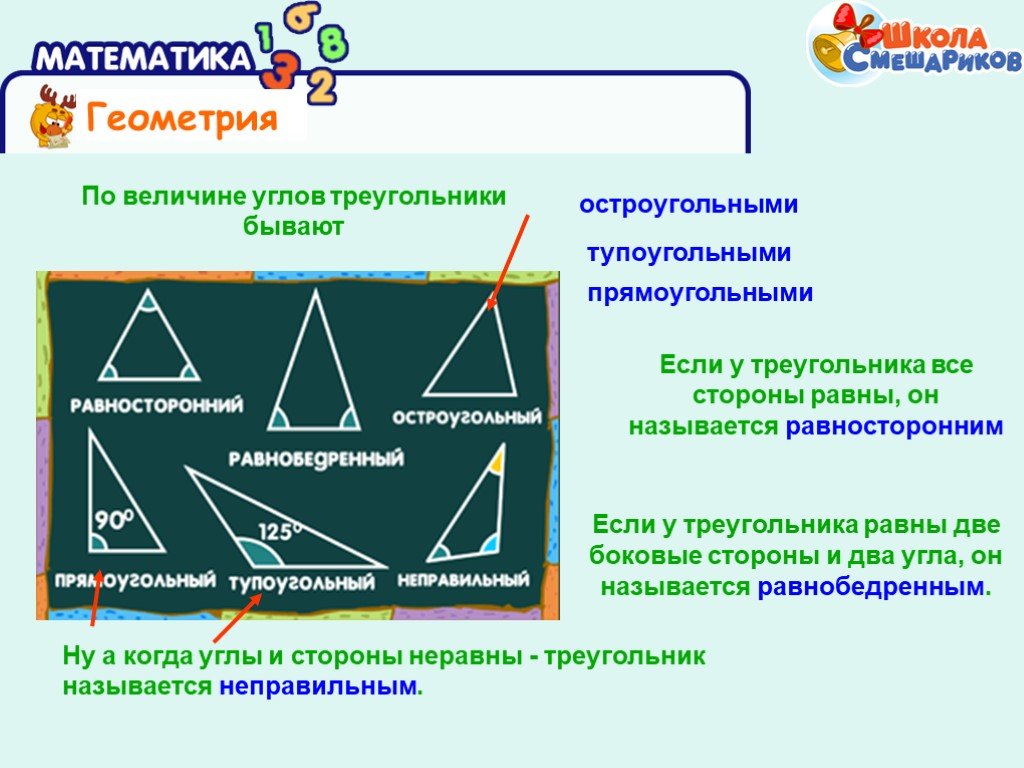
Углы – это такая же характеристика фигуры, как стороны, периметр или площадь. С помощью углов можно понять, какая фигуры перед нами и какой именно ее вид. Если это треугольник, то по углу визуально можно определить, прямоугольный ли это треугольник, тупоугольный или произвольный, а по общему углу можно доказать равенство или подобие фигур.
Определение
Что такое угол? Существует три определения угла. Рассмотрим каждое из них, выберем наиболее простое и понятное.
Угол – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. То есть это просто два луча. Это определение дается практически в каждом учебнике геометрии. Оно правильное, но прочитав его, не совсем понятно, откуда берется значение угла.
Это и есть угол. Так проще представить фигуру, но опять не ясно, откуда берется значение угла. Это можно понять только из 3 определения.Угол – это мера поворота луча, вокруг своего начала. Это сложно понять, но легко представить. Представьте часы. Вот на часах 12 часов дня, минутная и часовая стрелка находятся на одном уровне, тут минутная стрелка начинает двигаться. И каждый раз, время, а значит положение стрелок можно определить именно углом между часовой и минутной стрелкой. Углы могут быть разными, но если выделять угол в каждый момент времени дугой, то можно заметить, что дуга в конце концов превратится в круг.
Именно круг и является началом отчета для градуса. Дуга $$1\over360$$ части круга это градус. А по количеству градусов в угле можно выделить основные виды углов между прямыми: острые, прямые, тупые и полные углы.
Виды углов: острый, прямой, тупой, полный
Острый угол
Острый угол это угол, значение которого меньше 90 градусов. В произвольном параллелограмме всегда есть два острых и два тупых угла, тогда как в произвольном треугольнике все углы прямые.
Если хоть один из углов треугольника прямой или тупой, то фигуру уже нельзя считать произвольной.
Прямой угол
Прямой угол очень много значит в геометрии. Прямой угол в параллелограмме, означает, что перед вами квадрат или прямоугольник. Произвольный треугольник, если доказать, что в нем есть прямой угол, сразу же превращается в прямоугольный треугольник, для которого действует больший набор теорем и правил, нежели для произвольного.
Рис. 2. Прямой угол.Тупой угол
Тупой угол, это угол больше 90 градусов. Это значение очень широко используется в задачах по тригонометрии. Но и в геометрии очень часто можно встретить задачи на тупоугольный треугольник. Считается, что тупоугольный треугольник сложнее воспринимается чисто визуально, но на деле, стоит только привыкнуть и задачи эти уже не будут казаться такими страшными.
Полный угол
Полный угол это угол в 360 градусов. То есть тот самый момент, когда минутная и часовая стрелка совпадает.
Тогда с одной стороны будет полный угол, а с другой угол в 0 градусов. Чисто теоретически и нулевой угол тоже существует, он означает, что стрелки или лучи друг от друга не отклонялись.
Что мы узнали?
Мы узнали, что такое угол, определили виды углов, поговорили о том, какую роль каждый из видов играет в геометрии и привели примеры каждого из них.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Елена Никитина
10/10
Бетти Нуар
10/10
Ольга Журавлева
10/10
Валерия Качанова
10/10
Артём Мещеряков
9/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 235.
А какая ваша оценка?
Типы углов. Примеры
Когда два луча или линии встречаются в одной точке, образуется угол, и каждый угол отличается по своей величине.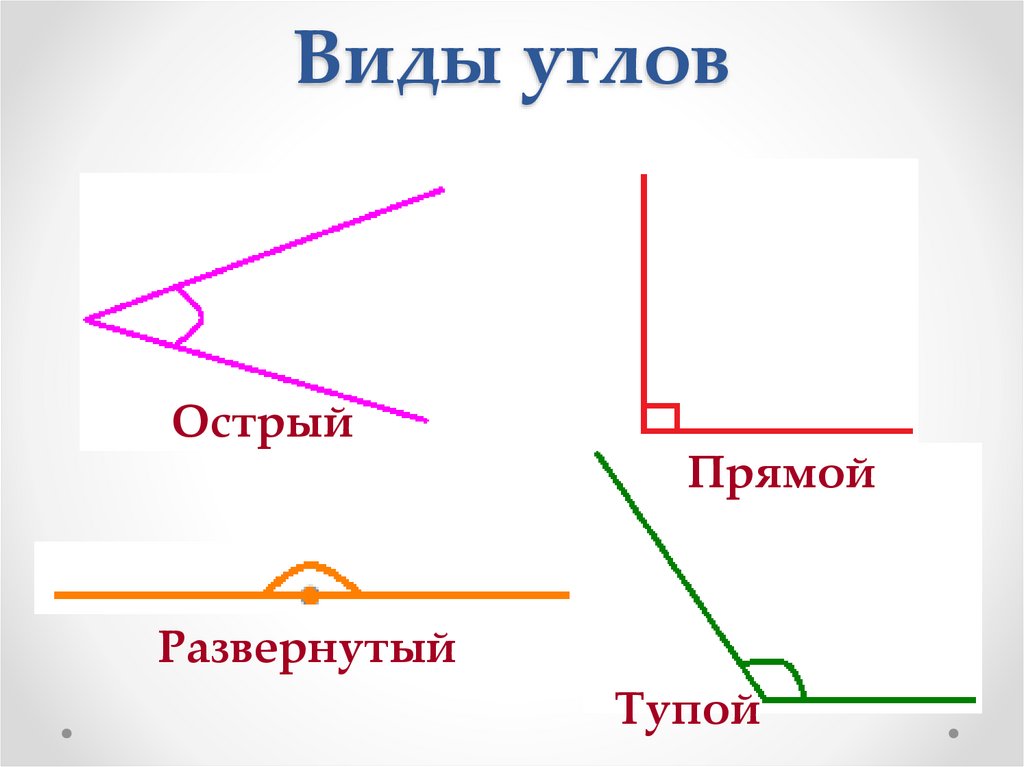
Существуют различные типы углов в геометрии, такие как острый угол, тупой угол, прямой угол, рефлекторный угол и прямой угол. Например, острый угол — это угол, который меньше 90°, а тупой угол — это угол, который больше 90°. Существуют также некоторые специальные типы пар углов. Давайте узнаем о различных типах углов в деталях.
| 1. | Типы углов на основе измерения |
| 2. | Типы углов на основе вращения |
| 3. | Типы угловых пар |
| 4. | Решенные примеры типов углов |
| 5. | Практические вопросы по типам углов |
| 6. | Часто задаваемые вопросы о типах углов |
Типы углов на основе измерения
Пространство, образованное при встрече двух лучей в одной точке, называется углом. Углы можно классифицировать как по их измерению, так и по способу их вращения.
В зависимости от размера углы классифицируют следующим образом. На следующем рисунке показаны различные виды углов, описанные ниже.
Острый угол
Любой угол меньше 90° является острым. Если два луча пересекаются в вершине, образуя угол, меньший 90°, то образуется острый угол. Некоторые примеры острого угла: 20°, 30°, 45°, 60°. Обратите внимание на рисунок, на котором показано, что угол ∠XYZ острый.
Прямой угол
Если угол между двумя лучами равен 90°, то он называется прямым углом или углом 90°. Обратите внимание на рисунок, который показывает, что ∠AOB является прямым углом или углом 90°.
Тупоугольный угол
Любой угол, который больше 90°, но меньше 180°, является тупым углом. Угол, образованный лучами PQ и QR на рисунке, является тупым углом. Некоторые примеры тупых углов: 110°, 130°, 145°, 165°.
Прямой угол
Как следует из названия, прямой угол представляет собой прямую линию, а угол между двумя лучами точно равен 180°.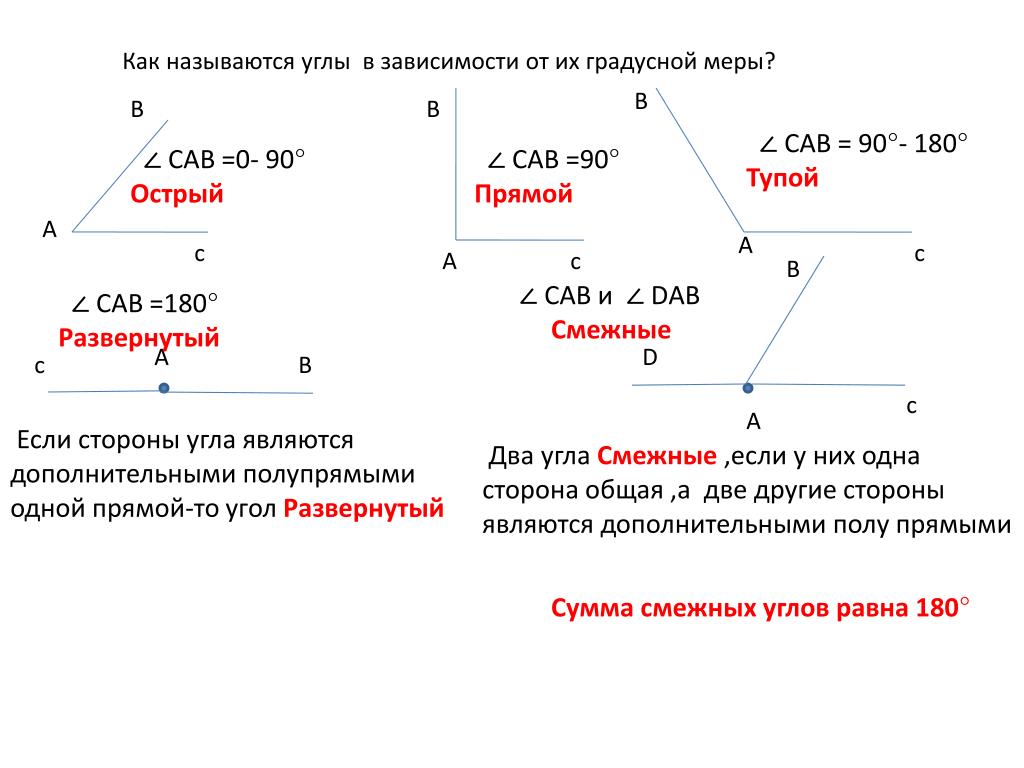
Под прямым углом два луча противоположны друг другу. Прямой угол может быть образован путем соединения двух смежных прямых углов или, другими словами, два прямых угла составляют прямой угол. На рисунке ∠SRT представляет собой угол 180° или прямой угол.
Угол рефлекса
Угол больше 180° и меньше 360° называется углом рефлекса. На рисунке ∠ABC — угол рефлекса. Примеры углов рефлекса: 210°, 250°, 310°.
Полный угол поворота
Полный угол поворота образуется, когда одно из плеч угла совершает полный оборот или делает 360°. На рисунке ∠MNR = 360° и называется полным углом поворота.
Типы углов на основе вращения
Следующий тип углов основан на направлении вращения одного плеча угла. Когда две прямые пересекаются и встречаются в одной точке, образуется угол. Давайте обсудим типы углов на основе вращения.
Положительные углы
Положительные углы — это углы, в которых углы поворачиваются от основания против часовой стрелки или против часовой стрелки.
На рисунке ниже при повороте стороны 1(AB) против часовой стрелки на угол θ образуется положительный угол.
Отрицательные углы
Отрицательные углы — это углы, в которых углы поворачиваются от основания по часовой стрелке. На рисунке ниже при повороте стороны 1 (DE) по часовой стрелке на угол θ образуется отрицательный угол.
Типы угловых пар
Пара углов обозначает два угла. Давайте прочитаем о различных парах углов в геометрии.
Смежные углы
Чтобы два угла были смежными, должны выполняться следующие условия.
- Два угла имеют общую вершину.
- Два угла имеют общее плечо.
- Есть два оружия, которые не являются обычными.
Дополнительные уголки
Когда сумма двух углов равна 90°, они называются дополнительными углами. Два угла могут быть любой величины, чтобы в сумме они составляли 90°. Например, два угла могут быть равны 30° и 60°. Здесь один угол является дополнением другого угла.
Дополнительные углы
Когда сумма двух углов равна 180°, они называются дополнительными углами. Два угла при сложении составляют 180°. Например, 110° и 70° составляют 180°. Поэтому эти два угла называются дополнительными. Здесь один угол является дополнением другого угла. Например, дополнение к 60° равно (180° — 60°), что составляет 120°.
Альтернативные внутренние углы
Когда прямая или секущая проходит через две параллельные линии, углы, образованные на противоположных сторонах линии или секущей, называются альтернативными внутренними углами, которые равны.
Альтернативные внешние углы
Когда прямая или секущая проходит через две параллельные линии, углы, образованные на внешней стороне линии или секущей, называются альтернативными внешними углами, которые равны.
Соответствующие углы
Когда прямая или секущая проходит через две параллельные прямые, углы, образованные в одном и том же месте или по одну сторону от секущей, являются соответствующими углами, и эти углы конгруэнтны.
Вертикальные углы
Когда две линии пересекаются друг с другом, углы, противоположные друг другу, равны и называются вертикальными углами или вертикально противоположными углами.
Обратите внимание на следующий рисунок, чтобы соотнести углы, указанные выше.
Темы, относящиеся к типам углов
Ознакомьтесь с некоторыми интересными статьями, связанными с углами.
- Уголки
- Острый угол
- Вертикальные углы
- Последовательные углы
- Геометрия
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о типах углов
Как классифицируются типы углов?
Угол образуется при пересечении двух лучей или прямых в одной точке. Типы углов классифицируются на основе различных факторов, таких как их размеры или способ их вращения. Учитывая эти факты, типы углов, основанные на измерениях, – это острый угол, тупой угол, прямой угол, прямой угол, угол полного поворота, угол отражения.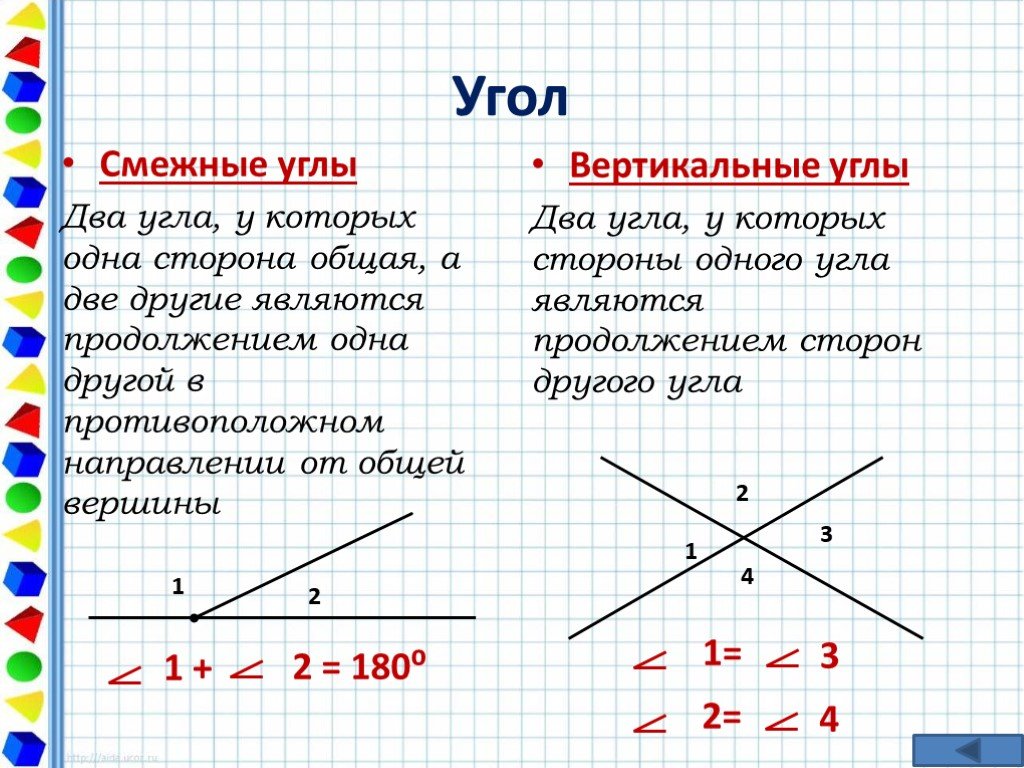
В зависимости от поворота углы делятся на положительные и отрицательные.
Какие существуют типы пар углов?
Типы угловых пар следующие.
- Смежные углы: имеют общую вершину и одно плечо. Два других плеча не пересекаются.
- Дополнительные углы: когда сумма двух углов равна 90°, такие углы называются дополнительными углами. Каждый угол называется дополнением другого угла.
- Дополнительные углы: Два угла считаются дополнительными, если их сумма составляет 180°. Каждый угол называется дополнением другого угла.
- Альтернативные внутренние углы: Углы, образованные, когда секущая проходит через две параллельные линии на внутренних сторонах секущей, называются альтернативными внутренними углами, и они конгруэнтны.
- Альтернативные внешние углы: Углы, образованные при прохождении секущей через две параллельные прямые на внешних сторонах секущей, называются альтернативными внешними углами, и они конгруэнтны.
- Соответствующие углы: Углы, образованные с одной и той же стороны, когда секущая проходит через две параллельные прямые, называются соответственными углами, которые равны.
- Вертикальные углы: Углы, образованные при пересечении двух прямых, являются вертикальными углами. Противоположные углы, образованные этим пересечением, равны по размеру и также известны как вертикально противоположные углы.
Какие типы углов меньше 180°?
Острые и тупые углы — это типы углов, размер которых меньше 180°. Острые углы всегда меньше 90°, а тупые углы больше 90°, но всегда меньше 180°. Примеры острых углов: 60°, 70°, тупые углы: 110°, 125°.
Какие виды углов образуются при прохождении секущей через две параллельные прямые?
Когда секущая проходит через две параллельные прямые, образуется множество пар углов, таких как чередующиеся внутренние углы, чередующиеся внешние углы и соответствующие углы. Все эти пары углов равны по размеру.
Какой тип угла больше 180°, но меньше 360°?
Угол рефлекса — это угол, размер которого больше 180°, но меньше 360°. Например, угол измерения 270° является углом отражения.
Как называются типы углов, сумма которых составляет 90° и 180°?
Когда два угла в сумме составляют 90°, они называются дополнительными углами. Два угла могут быть любой величины, чтобы в сумме они составляли 90°. Например, 20° и 70° являются дополнительными углами, потому что в сумме они дают 90°. Когда сумма двух углов равна 180°, они называются дополнительными углами. Два угла всегда в сумме дают 180°. Например, 105° и 75° являются дополнительными, поскольку в сумме дают 180°.
углов — Значение | Определение | Примеры
Углы образуются при пересечении двух прямых в одной точке. Мера «расстояния» между этими двумя лучами называется «углом». Обозначается символом ∠. Углы обычно измеряются в градусах и радианах, что является мерой округлости или вращения. Углы являются частью нашей повседневной жизни. Инженеры и архитекторы используют углы для проектирования дорог, зданий и спортивных сооружений. Давайте узнаем больше о определение углов в математике , значение углов, различные свойства углов, а также некоторые примеры углов.
| 1. | Что такое углы? |
| 2. | Типы углов и их свойства |
| 3. | Углы на основе поворота |
| 4. | Как измерить угол? |
| 5. | Как построить углы? |
| 6. | Часто задаваемые вопросы об углах |
Что такое углы?
В геометрии угол образуется при соединении двух лучей в их концах. Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.
Части угла
С углом связаны две основные части — стороны и вершина.
Плечи угла
Два луча, которые соединяются в одной точке, образуя угол, называются плечами угла . Обратите внимание на приведенный ниже рисунок, на котором показано, что ОА и ОВ являются сторонами угла АОВ.
Вершина угла
Вершина является общей конечной точкой, общей для двух лучей.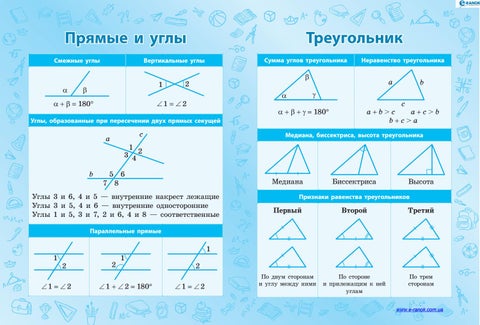
Мера угла
Угол измеряется в градусах. Один полный оборот вокруг точки образует полный угол в 360°.
Углы лучше всего измерять с помощью транспортира. Транспортир представляет собой измерительный инструмент, имеющий форму полукруга. Это полупрозрачный инструмент, который помогает нам измерять углы в градусах. Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.
Типы углов и их свойства
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла. Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
Острый угол
Острый угол — это угол, который больше 0° и меньше 90°.
Прямой угол
Когда угол равен 90°, он называется прямым углом.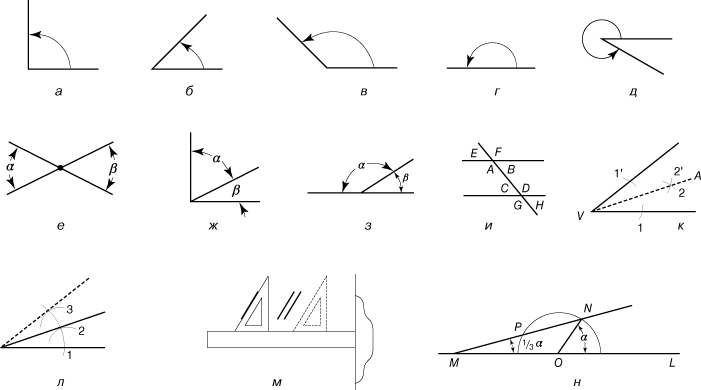
Прямой угол легко заметить, так как он образует форму буквы L.
Тупой угол
Если угол больше 90°, но меньше 180°, это тупой угол.
Прямой угол
Угол, образованный прямой линией, называется прямым углом. Другими словами, прямой угол — это прямая линия, а угол, образованный между двумя лучами, равен 180°. Под прямым углом два луча противоположны друг другу. Два прямых угла составляют прямой угол. Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.
Угол рефлекса
Угол рефлекса — это угол, величина которого больше 180°, но меньше 360°.
Полный угол
Когда измерение угла равно 360°, это полный угол.
Угол на основе поворота
В зависимости от направления измерения или направления вращения углы могут быть двух типов:
- Положительные углы
- Отрицательные углы
Положительные углы
Угол, измеренный в направлении против часовой стрелки (против часовой стрелки), является положительным углом.
Другими словами, положительные углы — это те углы, которые повернуты от основания в направлении против часовой стрелки.
Отрицательные углы
Отрицательные углы — это углы, которые измеряются по часовой стрелке от основания. Другими словами, отрицательные углы — это те углы, которые представляют собой углы, повернутые от основания по часовой стрелке.
Как измерить угол?
Мы используем транспортиры для измерения углов. Обратите внимание на приведенный ниже рисунок, на котором показано ∠AOB. Давайте попробуем и посмотрим, сможем ли мы выяснить, к какому типу относится угол ∠AOB. Разве это не похоже на острый угол? Это означает, что его мера больше 0° и меньше 90°. Давайте научимся измерять этот угол с помощью транспортира.
Как измерить острый угол?
Попробуем измерить заданную ∠AOB.
- Шаг 1: Совместите транспортир с лучом OB, как показано ниже. Начните читать внутреннюю шкалу с отметки 0 ° в правом нижнем углу транспортира.
- Шаг 2: Число на транспортире, которое совпадает со вторым лучом , является мерой угла. Измерьте угол, используя внутреннюю шкалу транспортира. Таким образом, ∠AOB = 37°
Как измерить тупой угол?
Теперь попробуем измерить заданный ∠AOC.
- Шаг 1: Измерьте угол по внешней шкале транспортира от отметки 0° в левом нижнем углу .
- Шаг 2: Число на внешней шкале транспортира, совпадающее с OA, является мерой ∠AOC. Таким образом, ∠AOC = 143°
Как построить углы?
Мы можем строить углы, используя такие инструменты, как транспортир или циркуль. Здесь воспользуемся транспортиром для построения углов. Начертим угол 50°.
- Шаг 1: Сначала нарисуйте луч OB и совместите транспортир с OB , как показано.
- Шаг 2: Используя внутреннюю шкалу транспортира, отметьте точку A над отметкой на транспортире, которая соответствует 50°.
- Шаг 3: Снимите транспортир и проведите луч, начинающийся в точке O и проходящий через эту точку A. Таким образом, ∠AOB — искомый угол, то есть ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева.
На приведенном ниже рисунке показано, как нарисовать угол 50°, когда луч направлен в другую сторону.
После размещения транспортира на ВО мы используем внешнюю шкалу и отмечаем 50°, как показано. Затем мы отмечаем эту точку как A и соединяем ее с точкой O. Это образует угол AOB = 50°
Важные замечания по углам
- 0°< Острый угол < 90°
- 90°< Тупой угол < 180°
- 180° < угол отражения < 360°
- Прямой угол равен 90°
- Прямой угол равен 180°.
☛ Связанные статьи
- Пары уголков
- Секущие и связанные углы
- Внутренние уголки
Примеры углов
Пример 1: Обратите внимание на величину углов и определите тип углов для каждой фигуры.
Решение:
а) Данный угол равен 40°. Это острый угол, потому что его градусная мера меньше 90°.
б) Данный угол равен 117°. Это тупой угол, потому что его градусная мера больше 90°, но меньше 180°.
в) Данный угол равен 121°. Это тупой угол, потому что его градусная мера больше 90°, но менее 180°.
г) данный угол равен 185°. Это рефлекторный угол, потому что его величина больше 180°, но меньше 360°.
Пример 2:
Классифицируйте следующие углы на острые, тупые, прямые и рефлекторные.
а) 24°
б) 150°
в) 90°
г) 270°
Решение:
(а) 24° лежит между 0° и
0°, значит угол острый.
(b) 154° лежит между 90° и 180°, поэтому это тупой угол.
(c) 90° известен как прямой угол.
(d) 270° находится между 180° и 360°, поэтому это рефлекторный угол.
Пример 3: Напишите верно или неверно следующие утверждения:
a.) 180° < угол отражения < 360°
b.) 0°< тупой угол < 90°
c.) Два луча, которые соединяющиеся в одной точке и образующие угол, называются сторонами угла.
Решение:
а.) Верно, 180° < угол отражения < 360°
б.) Неверно, 0°< острый угол < 90° общие точки, образующие угол, называются плечами угла.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об углах
Что такое угол в математике?
Углы образуются при пересечении двух лучей в одной точке.
«Отверстие» между этими двумя лучами называется «углом», который обозначается символом ∠. Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.
Каковы 6 типов углов?
6 типов углов: прямые углы, острые углы, тупые углы, прямые углы, отраженные углы и полные углы.
Как вы описываете углы?
Угол можно описать как фигуру, образованную двумя лучами, встречающимися в общей конечной точке, называемой вершиной угла.
☛ Также проверьте:
- Рабочие листы углов
- Углы в четырехугольнике Рабочие листы
- Геометрические углы Рабочие листы
Какие существуют типы углов, основанные на вращении?
В зависимости от направления измерения или направления вращения углы можно разделить на два типа:
- Положительные углы: Положительные углы — это углы, которые измеряются и поворачиваются от основания в направлении против часовой стрелки.
- Отрицательные углы: отрицательные углы — это те углы, которые измеряются и поворачиваются от основания по часовой стрелке.
В чем разница между прямым углом и рефлекторным углом?
Прямой угол – это прямая линия, а угол между двумя лучами равен 180°. Его можно образовать путем совмещения двух смежных прямых углов. Другими словами, два прямых угла составляют прямой угол. Принимая во внимание, что угол рефлекса больше 180°, но меньше 360°.
Какие виды углов образуются при прохождении секущей через параллельные прямые?
Когда секущая проходит через параллельные прямые, образуется много пар углов, таких как соответствующие углы, вертикально противоположные углы, чередующиеся внутренние углы и чередующиеся внешние углы.
Какие типы углов меньше 180°?
Существует два типа углов, мера которых меньше 180°, т. е. острые и тупые углы. Мера острых углов всегда меньше 90°, а тупых углов больше 90°, но всегда меньше 180°. Примеры острых углов: 50°, 60°, тупые углы: 170°, 165°.
Какова сумма всех трех углов треугольника?
Сумма трех углов треугольника равна 180°.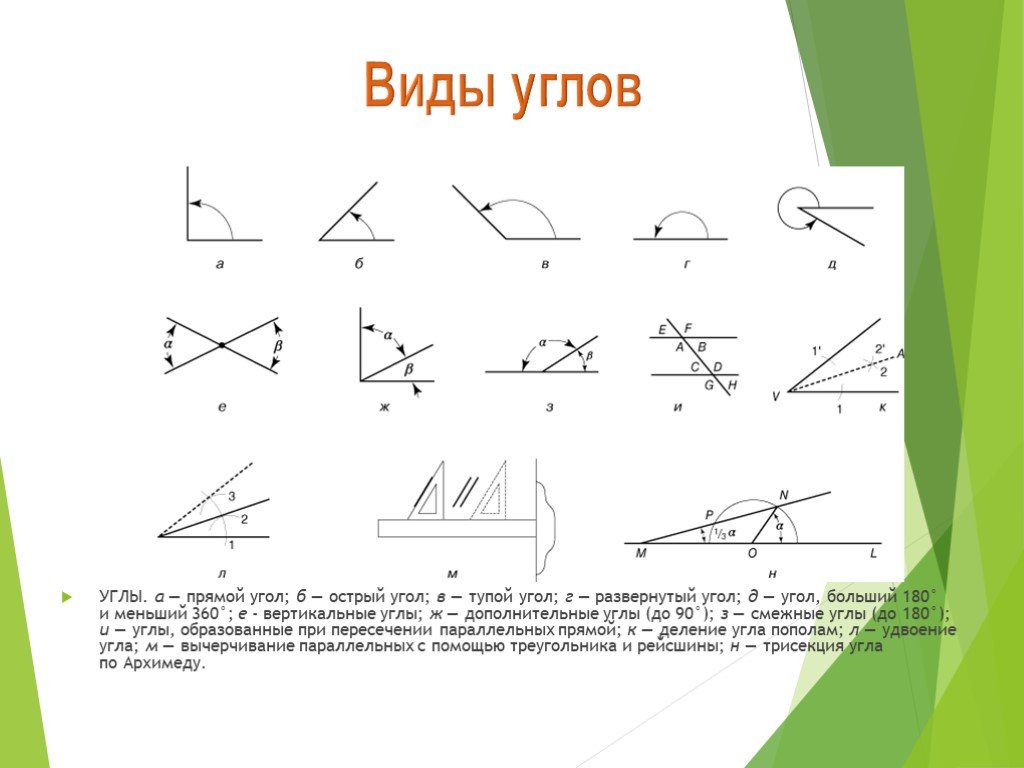
☛ Проверить сейчас:
- Углы треугольника Рабочие листы
- Калькулятор углов треугольника
Сколько углов по 90 градусов в прямом угле?
В 180-градусном или прямом угле есть два угла 90°. Так как 90° + 90° = 180°, то в прямом углу два угла по 90°.
Перечислите типы парных углов.
Типы уголков попарно перечислены ниже:
- Смежные углы
- Дополнительные уголки
- Дополнительные уголки
- Альтернативные внутренние углы
- Альтернативные внешние углы
- Соответствующие углы
- Вертикальные уголки
- Последовательные внутренние углы
Что такое полный угол?
Когда угол завершает полный оборот, начиная с 0° и заканчивая 360°, он называется полным углом. Другими словами, полный угол равен 360°.
Как вы измеряете углы?
Углы можно легко измерить с помощью простого измерительного инструмента, известного как транспортир.