Решить уравнение с косинусом: Решение тригонометрических уравнений — 39 примеров!

Задача на решение тригонометрического уравнения — «Шпаргалка ЕГЭ»

а) Решите уравнение:  .

б) Найдите все корни этого уравнения, принадлежащие отрезку . 

Решение задачи

Данный урок показывает, как правильно решать тригонометрическое уравнение, если оно представляет из себя алгебраическую дробь, т.е. имеет тригонометрическую функцию и в числителе и в знаменателе. Как и любое решение уравнения, представленного в виде дроби, начинаем с области определения функции. В данном случае это будет тригонометрическое уравнение с тангенсом. Числитель дроби представлен в виде тригонометрической функции с косинусом, а значит, решение данного уравнения будет содержать функцию арккосинус. Сами решения уравнения не представляют определенных сложностей, а вот определить, все ли корни являются решениями уравнения, оказывается не таким простым делом. Учитывая, что при определенных значениях косинуса и синуса (значение синуса можно получить по основной тригонометрической формуле: формула  – для решения необходимо выбрать только подходящие решения и определить для них конкретные условия – в данном случае приходится отбросить все корни со знаком минус.

Тем самым мы получили ответ на пункт а) данного задания. Для решения пункта б) необходимо использовать решение пункта а) и получить возможные значения корней уравнения, входящие в заданный промежуток, при различных значениях неизвестной n, которая принимает всевозможные целые значения. Используя формулы приведения ответом на пункт б) был получен только один корень.

Решение данной задачи рекомендовано для учащихся 10-х классов при изучении тем «Тригонометрические функции» («Синус и косинус», «Тангенс и котангенс», «Формулы приведения»), «Тригонометрические уравнения» («Арккосинус», «Арккосинус и решение уравнения cost=a», «Арктангенс и решение уравнения tgx=a»). При подготовке к ЕГЭ урок рекомендован при повторении тем «Тригонометрические функции», «Тригонометрические уравнения».

Рекомендуем

Отзывы учеников

• Светлана Иванова
  К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.

  Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.

• Влад Долгорукий

  Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.

• Александр Шпик

  Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.

Простейшие тригонометрические уравнения – формулы и примеры к теме

4. 6

Средняя оценка: 4.6

Всего получено оценок: 288.

4.6

Средняя оценка: 4.6

Всего получено оценок: 288.

Простейшие тригонометрические уравнения – это первый шаг к решению тригонометрических уравнений. Тема подобных уравнений крайне сложна, а поэтому требует особой внимательности на каждом этапе изучения. Разберемся подробнее в простейших уравнения, а также разрешим все вопросы с числом пи.

Что такое число $\pi$?

Необходимо понимать значение числа $\pi$, для того, чтобы разбираться в правильной записи корней уравнения. Число $\pi$ в общем случае это отношение длины окружности к ее диаметру.

Для чего нужно число $\pi$ в тригонометрии? Дело в том, что $\pi$ радиан соответствует 180 градусам, а ответ в тригонометрических уравнениях принято записывать именно в радианах.

Базовые значения тригонометрических функций предусмотрены для следующих градусных делений: это 30 градусов, 45, 90 и 180.

Промежуточные значения можно найти по аналогии.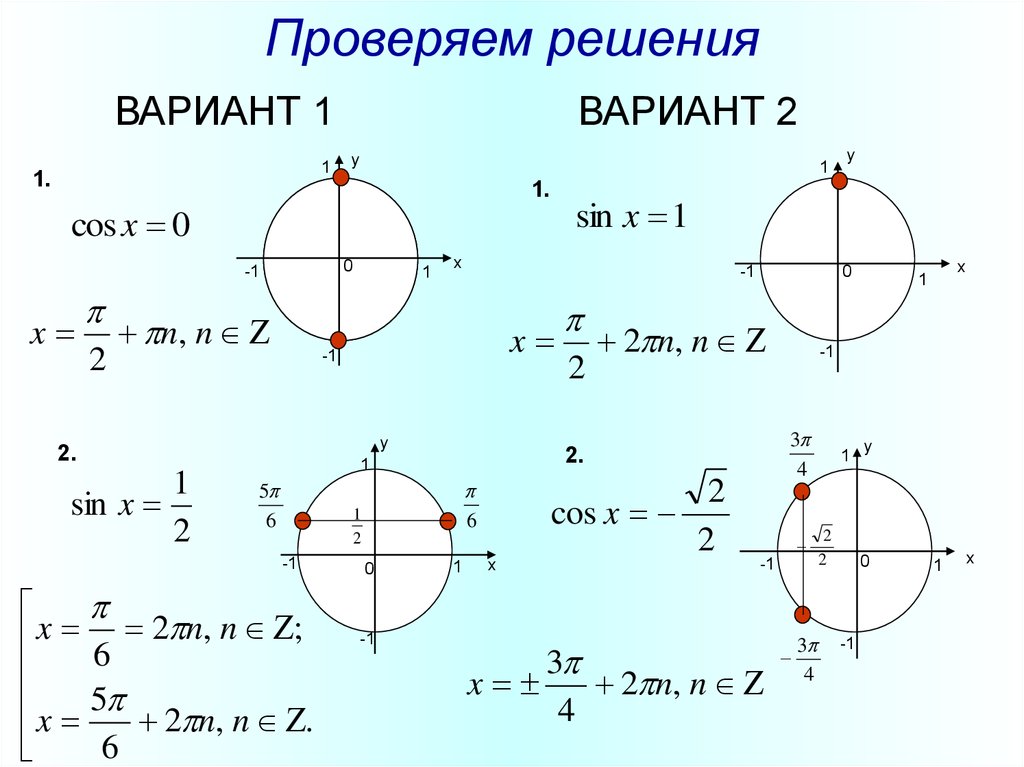 Например, 270=180+90 и так далее.

Для каждого из этих делений значение числа $\pi$ лучше запомнить, чтобы ускорить решение уравнений. Итак, число $\pi$ соответствует 180 градусам, значит, $\pi\over2$ это 90 градусов, $\pi\over4$ – 45 градусов, а $\pi\over6$-30 градусов.

Разберемся, как записывать промежуточный результат:

$$270=180+90={{\pi}+{{\pi}\over{2}}}={3\pi\over2}$$

По аналогии выполняются все промежуточные вычислении.

Простейшие тригонометрические уравнения

Простейшие тригонометрические уравнения – это уравнения, не требующие никаких преобразований. Перед вами будет тригонометрическая функция с неизвестным в качестве аргумента. Достаточно просто записать значение аргумента функции, которое соответствует значению угла в правой части тождества.

Разберем формулу простейшего тригонометрического уравнения на примере для функций синуса и косинуса.

$cos(x)=1$

Когда косинус х равен 1? Когда угол равен 0. Как это можно быстро запомнить? Окружность делиться на 4 координатные части. Окружность имеет центр в точке 0 и диаметр 1. Если луч 0-1 это одна сторона угла, а второй луч провести так, чтобы угол соответствовал искомому, то получится точка на окружности. Координата у точки соответствует синус, а координата х косинусу.

Для нашего случая достаточно отложить 1 на оси х и мы увидим, что такое значение возможно только при х=0, но это значение будет повторяться 1 раз в круг. Это нужно учесть, поэтому запишем решение в следующем виде:

$$Х=0+2*\pi=2\pi$$

Аналогично для синуса:

sin(x)=0,5

$$x={\pi\over2+2\pi}$$

Функция тангенса и котангенса в тригонометрических уравнениях рассматривается, как отношение синуса к косинусу или косинуса к синусу соответственно. Подбирается значение угла, для которого отношение будет равняться заданному в уравнении.

Что мы узнали?

Мы узнали, что такое простейшие тригонометрические уравнения, разобрались с понятием числа пи и правильной записью ответов при решении тригонометрических уравнений.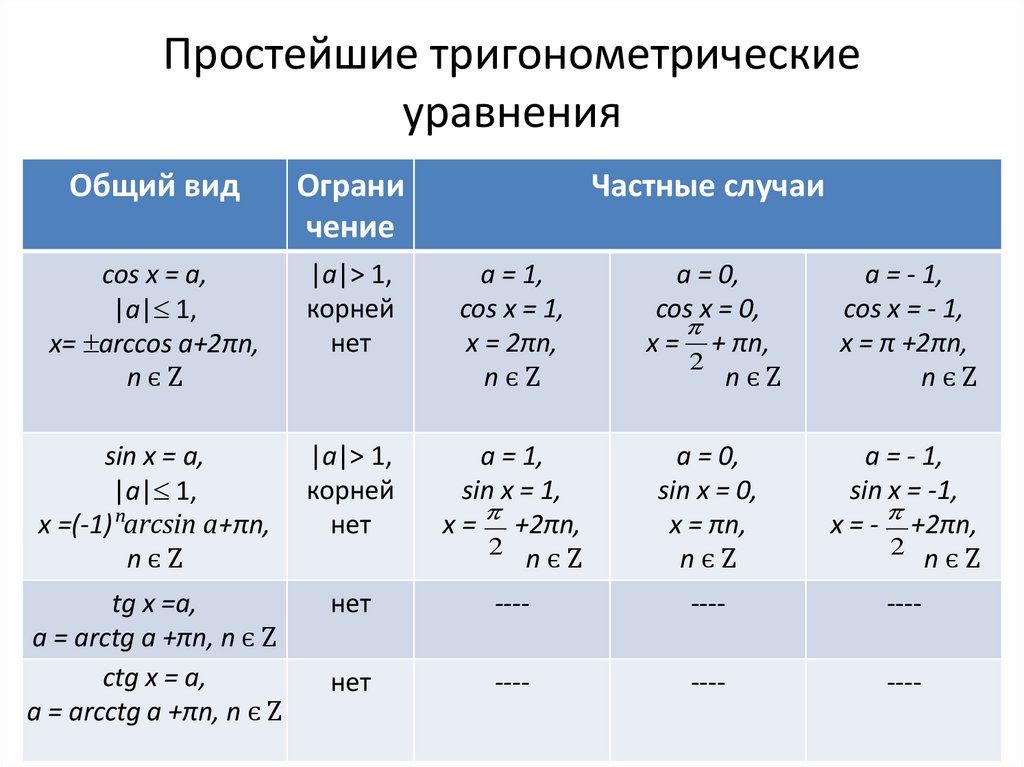 Поговорили о единичной окружности и методах ее использования. Отдельно поговорили о методах решения тригонометрических уравнений и разобрали их на примере основных функций тригонометрии: синуса и косинуса.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Ольга Титова

  3/5

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 288.

---

А какая ваша оценка?

тригонометрия. Есть ли способ решить уравнение с синусом и косинусом?

спросил 5 лет, 9 месяцев назад

Изменено 5 лет, 9 месяцев назад

Просмотрено 3к раз

$\begingroup$

Я пытаюсь решить систему уравнений. Я получаю синус и косинус в одном уравнении и параметр обоих как последний неизвестный. Вот так:

 число1 = число2 * sin(начало) + число3 * cos(начало)
 

num1 , num2

, num3 — известные скаляры, а start — неизвестные скаляры. Так есть ли простой способ решить это уравнение?

---

Исходная система уравнений :

 ось + с * Ьх = сх
ау + с * по = су
cx + rx * грех (начало) = px
cy + ry * cos (начало) = py
 

ax, ay, bx, by, px, py, rx, ry известны. s, start, cx и cy неизвестны. Я подумал, что 4 уравнения и 4 неизвестных должны как-то работать, верно?
В итоге получаю:

 px * by - ax * by + ay * bx - py * bx = ry * bx * cos(start) + rx * by * sin(start)
 

(Я программист. Извините за отсутствие математических формул.)

• тригонометрия
• системы уравнений

$\endgroup$

1

$\begingroup$

Чтобы решить $a \cos(\theta) + b \sin(\theta) = c$, запишите это как $r \cos(\theta — \phi) = c$, где $r = \sqrt{a^2 + b^2}$, $\cos(\phi) = a/r$ и $\sin(\phi ) = б/р$.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Тригонометрические уравнения | Brilliant Math & Science Wiki

Содержание

• Конкретные решения — основные
• Конкретные решения — средний уровень
• Общие решения — основные
• Общие решения — средний уровень
• Факторинг — Базовый
• Факторинг — Промежуточный уровень
• Решение проблем — базовое
• Решение проблем — средний уровень

Каковы решения уравнения

sin⁡2x=32 \sin 2x = \frac{\sqrt{3}}{2} sin2x=23​​

в интервале xxx [0,2π]? [0, 2\пи] ?[0,2π]?

---

Так как 0≤2x≤4π, 0 \leq 2x \leq 4\pi ,0≤2x≤4π, мы имеем

2x=π3,23π,73π,83π⇒x=π6,π3,76π,43π. □\begin{выровнено} 2x&= \ frac {\ pi} {3}, \ frac {2} {3} \ pi, \ frac {7} {3} \ pi, \ frac {8} {3} \ pi \\\\ \Rightarrow x&= \frac{\pi}{6}, \frac{\pi}{3}, \frac{7}{6} \pi, \frac{4}{3} \pi. \ _\площадь \end{выровнено} 2x⇒x​=3π​,32​π, 37​π, 38​π=6π​,3π​,67​π, 34​π. □​​

Каковы решения

sin⁡(x−π3)=−12 \sin\left(x-\frac{\pi}{3} \right) = -\frac{1}{2} sin(x−3π​)=−21​

в интервале xxx [0,2π]? [0, 2\пи] ?[0,2π]?

---

Так как −π3≤x−π3≤53π, -\frac{\pi}{3} \leq x-\frac{\pi}{3} \leq \frac{5}{3} \pi ,−3π ​≤x−3π​≤35​π, имеем

х−π3=−π6,76π⇒x=π6,32π. □\begin{выровнено} x-\frac{\pi}{3} &=-\frac{\pi}{6}, \frac{7}{6} \pi\\\\ \Rightarrow x &= \frac{\pi}{6}, \frac{3}{2} \pi. \ _\площадь \end{align}x−3π​⇒x​=−6π​,67​π=6π​,23​π. □​​

Каково общее решение

?

тангенс⁡х=1? \загар x = 1 ?tanx=1?

---

В первом периоде 0≤x<π, 0 \leq x < \pi,0≤x<π, решением этого уравнения является x=π4. x= \frac{\pi}{4}.x= 4π​. Поскольку период tan⁡x\tan xtanx равен π,\pi,π, общее решение данного уравнения равно

х=nπ+π4. □ Икс знак равно п \ пи + \ гидроразрыва {\ пи} {4} . \ _\squarex=nπ+4π​. □​

Каково общее решение

?

cos⁡2x+3cos⁡x−1=0? \cos 2x +3\cos x -1=0 ?cos2x+3cosx−1=0? 92 х -1 + 3\cos х -1 &= 0 \\ (2\cos x -1)(\cos x +2) &= 0\\ \cos x &= \frac{1}{2}. \qquad (\text{начиная с}\lvert \cos x \rvert \leq 1) \end{выровнено} 2cos2x−1+3cosx−1(2cosx−1)(cosx+2)cosx​=0=0=21​.(так как ∣cosx∣≤1)​

Поскольку период cos⁡x \cos x cosx равен 2π, 2\pi,2π, общее решение данного уравнения равно

х=2nπ±π3. □ x = 2n \pi \pm \frac{\pi}{3}. \ _\квадрат х=2nπ±3π​. □​

Каково общее решение

?

тангенс⁡2x−3tan⁡x=0? \tan 2x — 3\tan x = 0 ?tan2x−3tanx=0? 92 х -1\справа) &= 0 \\ \Rightarrow \tan x &= 0, \pm \frac{1}{\sqrt{3}}. \end{выровнено} tan2x−3tanx1−tan2x2tanx​−3tanx2tanx−3tanx(1−tan2x)tanx(3tan2x−1)⇒tanx​=0=0=0=0=0,±3​1​. ​

Поскольку период tan⁡x \tan xtanx равен π,\pi,π, общее решение данного уравнения равно

x=nπ или x=nπ±π6. □ x= n \pi, \text{ или } x=n \pi \pm \frac{\pi}{6}. \ _\squarex=nπ или x=nπ±6π​. □​

Каковы решения следующего уравнения для 0≤x≤2π:0 \leq x \leq 2\pi:0≤x≤2π: 92 х)-\sin х -1 &= 0 \\ \влево(2\sin x — 1\вправо)(\sin x + 1) &=0 \\ \sin x &= \frac{1}{2}, -1. \end{выровнено} 2cos2x-sinx-1⇒2(1-sin2x)-sinx-1(2sinx-1)(sinx+1)sinx​=0=0=0=21​, −1.​

Так как 0≤x≤2π,0 \leq x \leq 2\pi,0≤x≤2π, для sin⁡x=12 \sin x = \frac{1}{2}sinx=21​ мы имеем

x=π6,56π.(1) x = \frac{\pi}{6}, \frac{5}{6} \pi. \qquad (1) x=6π​,65​π.(1)

Для sin⁡x=-1, \sin x = -1,sinx=-1 имеем

x=32π.(2) x = \frac{3}{2} \pi. \qquad (2) x=23​π.(2) 92 х &= \фракция{3}{4} \\ \sin x &= \pm \frac{\sqrt{3}}{2}. \end{выровнено} sin4x+sin2x-1sin4x-cos4x+sin2x-cos2x-1(sin2x+cos2x)(sin2x-cos2x)+sin2x-cos2x-12sin2x-2cos2x-12sin2x-2(1-sin2x)-1⇒sin2xsinx =cos4x+cos2x=0=0=0=0=43​=±23​​. ​

Поскольку 0≤x≤2π,0 \leq x \leq 2\pi,0≤x≤2π, для sin⁡x=32 \sin x = \frac{\sqrt{3}}{2}sinx=23​ у нас

x=π3,23π.(1) x = \frac{\pi}{3}, \frac{2}{3} \pi . \qquad (1) x=3π​,32​π.(1)

Для sin⁡x=-32, \sin x = -\frac{\sqrt{3}}{2} ,sinx=-23​​, мы имеем 92 х)&=0\ \Rightarrow \cos x &= 0, ~\sin x = \frac{1}{2}, — \frac{1}{2}. \end{выровнено} cos2x−sin22xcos2x−4sin2xcos2xcos2x(1−4sin2x)⇒cosx=0=0(так как sin2x=2sinxcosx)=0=0, sinx=21,−21.​

Поскольку 0≤x≤2π,0 \leq x \leq 2\pi,0≤x≤2π, для cos⁡x=0 \cos x =0cosx=0 имеем

x=π2,32π.(1) x = \frac{\pi}{2}, \frac{3}{2} \pi. \qquad (1) x=2π​,23​π.(1)

Для sin⁡x=12, \sin x = \frac{1}{2},sinx=21​ мы имеем

x=π6,56π.(2) x = \frac{\pi}{6}, \frac{5}{6} \pi. \qquad (2) x=6π​,65​π.(2)

Для sin⁡x=−12, \sin x = -\frac{1}{2},sinx=−21​ мы имеем

x=76π,116π.(3) x= \frac{7}{6} \pi, \frac{11}{6} \pi. \qquad (3) x=67​π, 611​π.(3)

Таким образом, из (1), (2) (1), (2) (1), (2) и (3)(3)(3) решения

х=π2,32π,π6,56π,76π,116π.

No related posts.