Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
04.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .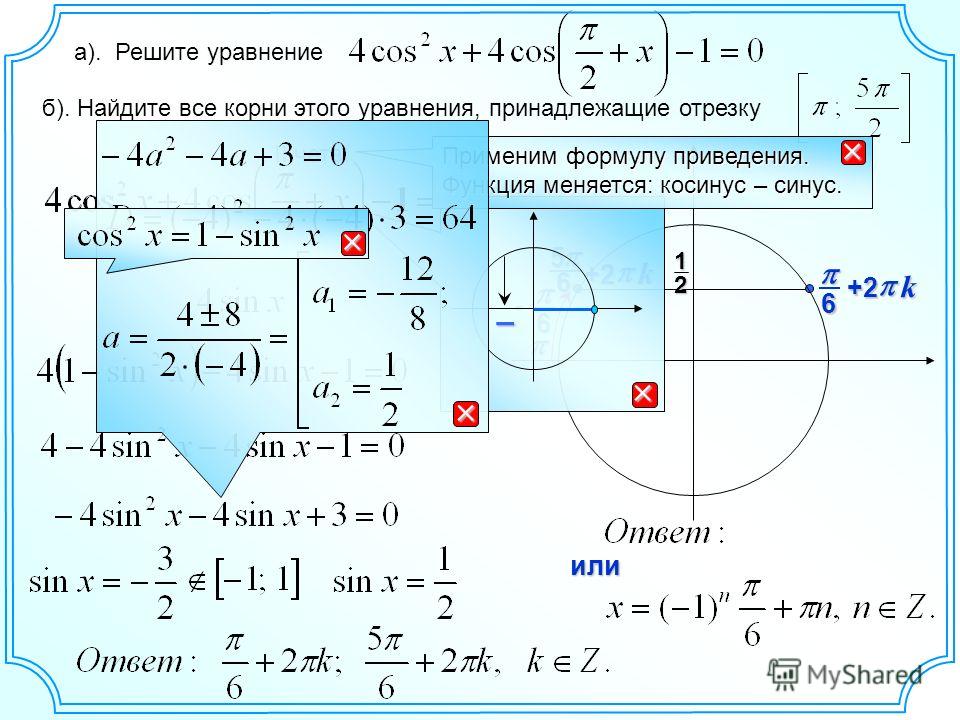
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Высота правильной треугольной пирамиды равно…
Периметр прямоугольника 150 дм. Длина его больше ширины на 150 см. Вычислить длины сторон прямоугольника.
Решено
1)В остроугольном треугольникеMNP биссектриса угла M пересекает высоту NK в точке О, причем ОК =9см. Найдите расстояние от точки О до прямой МN.
Пользуйтесь нашим приложением
6.4: Решение тригонометрических уравнений — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13867
- Дэвид Липпман и Мелони Расмуссен
- Магазин OpenTextBookStore
В разделе 6.
1 мы определили, что рост всадника на колесе обозрения London Eye можно определить по уравнению
\[h(t)=-65\cos\left(\dfrac{\pi }{15} t\right)+70. \номер\]
Если бы мы хотели узнать продолжительность времени, в течение которого всадник находится на высоте более 100 метров над землей, нам нужно было бы решить уравнения, включающие триггерные функции.
Решение с использованием известных значений
В предыдущей главе мы узнали значения синуса и косинуса для часто встречающихся углов. Мы можем использовать их для решения уравнений синуса и косинуса, включающих эти общие углы.
Пример \(\PageIndex{1}\)
Решить \(\sin \left(t\right)=\dfrac{1}{2}\) для всех возможных значений \(t\).
Решение
Обратите внимание, что нас просят идентифицировать все углы \(t\), которые имеют синусоидальное значение \(\dfrac{1}{2}\). В то время как оценка функции всегда дает один результат, решение входных данных может дать несколько решений.
Из предыдущей главы сразу же приходят на ум два решения: \(t=\dfrac{\pi }{6}\) и \(t=\dfrac{5\pi }{6}\), потому что они являются общими углами на единичной окружности с грехом \(\dfrac{1}{2}\).
Глядя на график, можно убедиться, что этих двух решений больше. Хотя на этом графике видно восемь, существует бесконечное количество решений!
Помните, что любой котерминальный угол также будет иметь одно и то же значение синуса, поэтому любой котерминальный угол с этими нашими первыми двумя решениями также является решением. Котерминальные углы можно найти, добавив полные обороты 2\(\pi \), поэтому мы можем записать полный набор решений:
\(t=\dfrac{\pi }{6} +2\pi k\) где k — целое число, и \(t=\dfrac{5\pi }{6} +2\pi k\), где \(k\) — целое число.
Пример \(\PageIndex{2}\)
Окружность радиусом \(5\sqrt{2}\) пересекает прямую \(x = -5\) в двух точках. Найдите углы \(\theta\) на отрезке \(0 \le \theta <2\pi\), где пересекаются окружность и прямая.
Решение
Координата \(x\) точки на окружности может быть найдена как \(x=r\cos \left(\theta \right)\), поэтому координата \(x\) точек на этом круге будет \(x=5\sqrt{2} \cos\left(\theta\right)\).
Чтобы найти, где линия \(x = -5\) пересекает окружность, мы можем решить, где значение \(x\) на окружности будет равно -5.
\[-5=5\sqrt{2} \cos \left(\theta \right)\nonumber\]Выделение косинуса
\[\dfrac{-1}{\sqrt{2} } =\cos \left(\theta \right)\nonumber\] Напомним, что \(\dfrac{-1}{\sqrt{2} } =\dfrac{-\sqrt{2} }{2}\), поэтому мы решаем
\[\cos \left(\theta \right)=\dfrac{-\sqrt{2} }{2}\nonumber\]
Мы можем распознать это как одно из наших специальных значений косинуса из нашего единичного круга, и соответствует углам \[\theta =\dfrac{3\pi }{4}\text{ и }\theta =\dfrac{5\pi }{4}\nonumber\]
Упражнение \(\PageIndex{1}\)
Решите \(\tan \left(t\right)=1\) для всех возможных значений \(t\).
- Ответить
С наших специальных углов мы знаем, что один ответ равен \(t=\dfrac{\pi }{4}\). Касательные уравнения имеют только одно уникальное решение за цикл или период, поэтому дополнительные решения можно найти, добавляя кратные полному периоду \(\pi \).
\[t=\dfrac{\pi} }{4} +\pi k\nonumber\]
\[t=\dfrac{\pi} }{4} +\pi k\nonumber\]Пример \(\PageIndex{3}\)
Глубина воды в доке увеличивается и уменьшается с приливом в соответствии с уравнением \(f(t)=4\sin\left(\dfrac{\pi }{12} t\right)+7\), где t измеряется в часах после полуночи. Лодке требуется глубина 9 футов, чтобы пришвартоваться в доке. Между какими промежутками времени глубина будет 9 футов?
Решение
Чтобы найти глубину 9 футов, нужно решить \(f(t) = 9\).
\[4\sin \left(\dfrac{\pi }{12} t\right)+7=9\nonumber\]Выделение синуса
\[4\sin \left(\dfrac{\pi }{ 12} t\right)=2\nonnumber\]Деление на \(4\)
\[\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\nonumber\]Мы знаем \(\sin \left(\theta \right)=\ dfrac{1}{2}\) when \(\theta =\dfrac{\pi }{6} \quad or\quad \theta =\dfrac{5\pi }{6}\)
Хотя мы знаем, что углы имеют синусоидальное значение \(\dfrac{1}{2}\), из-за горизонтального растяжения/сжатия менее ясно, как действовать дальше.
Чтобы справиться с этим, мы можем сделать замену, определив новую временную переменную \(u\) как \(u=\dfrac{\pi }{12} t\), так что наше уравнение \(\sin \ влево (\ dfrac {\ pi} {12} t \ right) = \ dfrac {1} {2} \) становится
\[\sin \left(u\right)=\dfrac{1}{2}\nonumber\]
Ранее мы видели, что решениями этого уравнения являются
\[u=\dfrac{\pi }{6} +2\pi k\nonumber\], где \(k\) — целое число, и
\[u=\dfrac{5\pi }{6} +2\pi k\nonumber\], где k является целым числом
Чтобы отменить нашу замену, мы заменяем \(u\) в решениях на \(u=\dfrac{\pi }{12} t\) и находим \(t\).
\(\dfrac{\pi }{12} t=\dfrac{\pi }{6} +2\pi k\), где \(k\) — целое число, а \(\dfrac{\pi } {12} t=\dfrac{5\pi }{6} +2\pi k\), где \(k\) — целое число.
Разделив на \(\pi \)/12, получим решения
\(t=2+24k\), где \(k\) — целое число, и \(t=10+24k\), где \( к\) является целым числом.
Глубина составит 9 футов, и лодка сможет подойти к причалу между 2 и 10 часами утра.
Обратите внимание, что в обоих сценариях 24k показывает, как каждые 24 часа цикл будет повторяться.
В предыдущем примере, оглядываясь назад на исходное упрощенное уравнение \(\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\), мы можем использовать отношение «нормального периода» к коэффициенту растяжения, чтобы найти период: \(\dfrac{2\pi }{\left(\dfrac{\pi }{12} \right)} =2\pi \left(\ dfrac{12}{\pi } \right)=24\). Обратите внимание, что синусоидальная функция имеет период 24, что отражено в решениях: на одном полном цикле синусоидальной функции было два уникальных решения, а дополнительные решения были найдены путем сложения кратных полному периоду.
Упражнение \(\PageIndex{2}\)
Решите \(4\sin (5t)-1=1\) для всех возможных значений \(t\).
- Ответить
\[4\sin (5t)-1=1\номер\]
\[\sin (5t)=\dfrac{1}{2}\nonumber\] Пусть \(u=5t\), чтобы это стало \(\sin (u)=\dfrac{1}{2}\) , который имеет решения
\[u=\dfrac{\pi }{6} +2\pi k,\dfrac{5\pi }{6} +2\pi k\nonumber\] Решение \[5t=u=\dfrac{\ pi }{6} +2\pi k,\dfrac{5\pi }{6} +2\pi k\nonumber\] дает решения
\[t=\dfrac{\pi }{30} +\dfrac{2\pi }{5} k\qquad t=\dfrac{\pi }{6} +\dfrac{2\pi }{5} к\номер\]
Решение с использованием обратных триггерных функций
Не все уравнения включают «особые» значения триггерных функций, о которых мы узнали.
Чтобы найти решения этих уравнений, нам нужно использовать обратные триггерные функции.
Пример \(\PageIndex{4}\)
Используйте функцию обратного синуса, чтобы найти одно решение для \(\sin \left(\theta \right)=0,8\). 9\круг\).
Если вы работаете с составной триггерной функцией и не вычисляете угол, убедитесь, что вы работаете в радианах. В исчислении мы почти всегда хотим работать с радианами, поскольку они безразмерны.
Обратите внимание, что обратные триггерные функции делают именно то, что вы ожидаете от любой функции — для каждого входа они дают ровно один выход. Хотя это необходимо для того, чтобы они были функцией, это означает, что для нахождения всех решений уравнения типа \(\sin\left(\theta\right)=0,8\) нам нужно сделать больше, чем просто вычислить обратная функция.
Чтобы найти дополнительные решения, полезно помнить четыре вещи:
- Синус — это \(y\)-значение точки на единичной окружности
- Косинус — это значение \(x\) точки на единичной окружности
- Тангенс — это наклон линии под заданным углом
- Другие углы с тем же самым \(\sin\)/\(\cos\)/\(\tan\) будут иметь тот же исходный угол
Пример \(\PageIndex{5}\)
Найти все решения \(\sin \left(\theta \right)=0,8\).
{-1} (0,8)\), или примерно \(\theta \приблизительно \pi -0,9{-1} \влево(3\вправо) \примерно 1,249\). В отличие от синуса и косинуса, функция тангенса достигает любого выходного значения только один раз за цикл, поэтому нет второго решения ни в одном цикле.
Добавляя \(\pi \), полный период функции тангенса, мы можем найти второй угол с таким же значением тангенса. Обратите внимание, что это дает другой угол, где линия имеет тот же наклон.
Если желательны дополнительные решения, мы могли бы продолжать добавлять кратные \(\pi \), чтобы все решения принимали форму \(x=1,249{-1} \left(-\dfrac{2}{3} \right)\приблизительно 2.301\nonumber\]
Мы ищем два угла, где \(x\)-координата на единичной окружности составляет -2/3. Второй угол с таким же косинусом будет находиться в третьем квадранте. Обратите внимание, что положение этого угла может быть представлено как \(t=-2,301\). Чтобы представить это как положительный угол, мы могли бы найти котерминальный угол, добавив полный цикл.
\[t=-2,301+2\pi = 3,982\не число\]
У уравнения есть два решения между 0 и 2\(\pi \), при \(t = 2,301\) и \(t = 3,9{-1} \left(0.2\right)\приблизительно 1.369\nonumber\]
Второе решение в одном цикле будет располагаться в четвертом квадранте с тем же опорным углом.
\[u=2\pi -1.369=4.914\nonnumber\]
В этом случае нам нужны все решения на двух циклах, поэтому нам нужно найти решения на втором цикле. Мы можем сделать это, добавив полный оборот к двум предыдущим решениям.
\[\begin{array}{l} {u=1,369+2\pi =7,653} \\ {u=4,914+2\pi =11,197} \end{array}\nonumber\]
Отменив подстановку, мы получим наши четыре решения:
\[3t = 1,369\текст{, поэтому }t = 0,456\нечисло\]
\[3t = 4,914\текст{, так }t = 1,638\нечисло\ ]
\[3t = 7,653\текст{, поэтому }t = 2,551\нечисло\]
\[3t = 11,197\текст{, поэтому }t = 3,732\нечисло\]
Пример \(\PageIndex{10}\ )
Решите \(3\sin\left(\pi \, t\right)=-2\) для всех решений.
Решение
\[3\sin \left(\pi \, t\right)=-2\nonnumber\]Выделение синуса 9{-1} \left(-\dfrac{2}{3} \right)\приблизительно -0,730\nonnumber\]
Этот угол находится в четвертом квадранте. Второй угол с тем же синусом находился бы в третьем квадранте с опорным углом 0,730:
\[u=\pi +0,730=3,871\нечисло\]
Мы можем записать все решения уравнения \(\sin \left(u\right)=-\dfrac{2}{3}\) as
\[u=-0,730+2\pi {\kern 1pt} k\text{или}u=3,871+2\pi {\kern 1pt} k\nonumber\], где \(k\) — целое число.
Отменив нашу замену, мы можем заменить u в наших решениях на \(u=\pi \, t\) и найти \(t\)
\[\pi t=-0,730+2\pi k\text{ или }\pi t=3,871+2\pi k\нечисло\]
Разделить на \(\pi \)
\[ t=- 0,232+2 k\text{ или } t=1,232+2 k\nonumber\]
Упражнение \(\PageIndex{4}\)
Решить \(5\sin \left(\dfrac{\pi }{2 } t\right)+3=0\) для всех решений на одном цикле, \(0 \le t < 4\).
- Ответить
\[\sin \left(\dfrac{\pi }{2} t\right)=-\dfrac{3}{5}\nonumber\] Пусть \(u=\dfrac{\pi }{2} t \), так что это становится \[\sin \left(u\right)=-\dfrac{3}{5}\nonumber\] 9{-1} \left(-\dfrac{3}{5} \right)\приблизительно -0,6435\).
Поскольку нам нужны положительные решения, мы можем найти котерминальное решение, добавив полный цикл: \(u=-0,6435+2\pi =5,6397\). Другой угол с таким же грехом будет в третьем квадранте с опорным углом 0,6435. \(и=\пи +0,6435=3,7851\).Решение для \(t\), \[u=\dfrac{\pi }{2} t=5,6397\nonumber\], поэтому \[t=5,6397\left(\dfrac{2}{\pi} \right )=3,5903\нечисло\]
и \[u=\dfrac{\pi }{2} t=3,7851\нечисло\], поэтому \[t=3,7851\left(\dfrac{2}{\pi} \right )=2,4097\номер\]
\[t = 2,4097\текст{ или }t = 3,5903\неномер\]
Поскольку нам нужны положительные решения, мы можем найти котерминальное решение, добавив полный цикл: \(u=-0,6435+2\pi =5,6397\). Другой угол с таким же грехом будет в третьем квадранте с опорным углом 0,6435. \(и=\пи +0,6435=3,7851\).РЕШЕНИЕ ТРИГ-УРАВНЕНИЙ ТРИГОНОМЕТРИЯ: СИНУСОИДАЛЬНЫЕ ФУНКЦИИ
- Выделение триггерной функции в одной части уравнения
- Замена внутренней части синуса, косинуса или тангенса (или другой триггерной функции)
- Используйте обратные триггерные функции, чтобы найти одно решение
- Использовать симметрии для поиска второго решения в одном цикле (когда существует второй)
- При необходимости найдите дополнительные решения, добавив полные точки
- Отменить замену
Теперь мы можем вернуться к вопросу, с которого мы начали этот раздел.
Пример \(\PageIndex{11}\)
Рост всадника на колесе обозрения London Eye можно определить по уравнению \(h(t)=-65\cos \left(\dfrac{\pi {15} т\справа)+70\). Как долго всадник находится на высоте более 100 метров над землей?
Решение
Чтобы найти, как долго всадник находится выше 100 метров, мы сначала найдем время, в которое всадник находится на высоте 100 метров, решив h(t) = 100,9.{-1} \left(\dfrac{30}{-65} \right)\приблизительно 2,051\nonnumber\]
Этот угол находится во втором квадранте. Второй угол с таким же косинусом будет симметричен в третьем квадранте. Этот угол можно представить как u = -2,051, но нам нужен котерминальный положительный угол, поэтому мы добавляем 2\(\pi \):
\[u=2\pi -2,051\приблизительно 4,230\нечисло\]
Теперь мы можем отменить подстановку, чтобы найти \(t\)
\(\dfrac{\pi }{15} t=2,051\), поэтому \(t = 9,793\) минут после начала поездки
\(\dfrac{\pi }{15} t=4,230\) поэтому \(t = 20,197\) минут после начала заезда
Гонщик будет на высоте 100 метров через 9,793 минуты и снова через 20,197 минут .
По поведению графика роста мы знаем, что в промежутке между этими моментами гонщик будет выше 100 метров. Гонщик будет находиться выше 100 метров в течение 20,197 — 9,793 = 10,404 минут езды.
Важные темы этого раздела
- Решение триггерных уравнений с использованием известных значений
- Использование подстановки для решения уравнений
- Поиск ответов за один цикл или период по сравнению с поиском всех возможных решений
- Метод решения тригонометрических уравнений
Эта страница под названием 6.4: Решение тригонометрических уравнений распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Дэвидом Липпманом и Мелони Расмуссен (The OpenTextBookStore) посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Липпман и Мелони Расмуссен
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@http://www. opentextbookstore.com/details.php?id=30
- источник@http://www.
opentextbookstore.com/details.php?id=30| 1 | Найти точное значение | грех(30) | ||
| 2 | Найти точное значение | грех(45) | ||
| 3 | Найти точное значение | грех(30 градусов) | ||
| 4 | Найти точное значение | грех(60 градусов) | ||
| 5 | Найти точное значение | загар (30 градусов) | ||
| 6 | Найти точное значение | угловой синус(-1) | ||
| 7 | Найти точное значение | грех(пи/6) | ||
| 8 | Найти точное значение | соз(пи/4) | ||
| 9 | Найти точное значение | грех(45 градусов) | ||
| 10 | Найти точное значение | грех(пи/3) | ||
| 11 | Найти точное значение | арктический(-1) | ||
| 12 | Найти точное значение | cos(45 градусов) | ||
| 13 | Найти точное значение | cos(30 градусов) | ||
| 14 | Найти точное значение | желтовато-коричневый(60) | ||
| 15 | Найти точное значение | csc(45 градусов) | ||
| 16 | Найти точное значение | загар (60 градусов) | ||
| 17 | Найдите точное значение | сек(30 градусов) | ||
| 18 | Найти точное значение | cos(60 градусов) | ||
| 19 | Найти точное значение | соз(150) | ||
| 20 | Найти точное значение | грех(60) | ||
| 21 | Найти точное значение | cos(pi/2) | ||
| 22 | Найти точное значение | загар (45 градусов) | ||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | ||
| 24 | Найти точное значение | csc(60 градусов) | ||
| 25 | Найти точное значение | сек(45 градусов) | ||
| 26 | Найти точное значение | csc(30 градусов) | ||
| 27 | Найти точное значение | грех(0) | ||
| 28 | Найти точное значение | грех(120) | ||
| 29 | Найти точное значение | соз(90) | ||
| 30 | Преобразовать из радианов в градусы | пи/3 | ||
| 31 | Найти точное значение | желтовато-коричневый(30) | ||
| 32 | Преобразование градусов в радианы | 45 | 92 | |
| 35 | Преобразовать из радианов в градусы | пи/6 | ||
| 36 | Найти точное значение | детская кроватка(30 градусов) | ||
| 37 | Найти точное значение | арккос(-1) | ||
| 38 | Найти точное значение | арктический(0) | ||
| 39 | Найти точное значение | детская кроватка(60 градусов) | ||
| 40 | Преобразование градусов в радианы | 30 | ||
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | ||
| 42 | Найти точное значение | sin((5pi)/3) | ||
| 43 | Найти точное значение | sin((3pi)/4) | ||
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | ||
| 45 | Найти точное значение | грех(300) | ||
| 46 | Найти точное значение | соз(30) | ||
| 47 | Найдите точное значение | соз(60) | ||
| 48 | Найти точное значение | соз(0) | ||
| 49 | Найти точное значение | соз(135) | ||
| 50 | Найти точное значение | cos((5pi)/3) | ||
| 51 | Найти точное значение | соз(210) | ||
| 52 | Найти точное значение | сек(60 градусов) | ||
| 53 | Найти точное значение | грех(300 градусов) | ||
| 54 | Преобразование градусов в радианы | 135 | ||
| 55 | Преобразование градусов в радианы | 150 | ||
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | ||
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | ||
| 58 | Преобразование градусов в радианы | 89 градусов | ||
| 59 | Преобразование градусов в радианы | 60 | ||
| 60 | Найти точное значение | грех(135 градусов) | ||
| 61 | Найти точное значение | грех(150) | ||
| 62 | Найти точное значение | грех(240 градусов) | ||
| 63 | Найти точное значение | детская кроватка(45 градусов) | ||
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | ||
| 65 | Найти точное значение | грех(225) | ||
| 66 | Найти точное значение | грех(240) | ||
| 67 | Найти точное значение | cos(150 градусов) | ||
| 68 | Найти точное значение | желтовато-коричневый(45) | ||
| 69 | Оценка | грех(30 градусов) | ||
| 70 | Найти точное значение | сек(0) | ||
| 71 | Найти точное значение | cos((5pi)/6) | ||
| 72 | Найти точное значение | КСК(30) | ||
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | ||
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | ||
| 76 | Оценить | грех(60 градусов) | ||
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | ||
| 78 | Преобразовать из радианов в градусы | (3 шт. |