решите уравнение x 2 x 12
Вы искали решите уравнение x 2 x 12? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решите уравнение x 2 x 12 0, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «решите уравнение x 2 x 12».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как решите уравнение x 2 x 12,решите уравнение x 2 x 12 0,решите уравнение x2 x 12 0,решить уравнение x 2 x 12.
Где можно решить любую задачу по математике, а так же решите уравнение x 2 x 12 Онлайн?
Решить задачу решите уравнение x 2 x 12 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решатель примеров онлайн
Введите в форму ниже уравнение, функцию или неравенство и подобное и нажмите Enter
Синтаксис программы:
Графики
Чтобы построить график функции, необходимо использовать оператор plot, например plot x^3-6x^2+4x+12 или plot sin x + cos (sqrt(3)x)
График функции с заданной областью определения plot e^x from x=0 to 10
График функции двух переменных с заданной областью определения plot x^2 y^3, x=-1. 3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
Оператор expand раскроет скобки и разложит выражение, например expand (x – 1)(x2+x+1) приведёт выражение к x3 -2x +1.
Оператор partial fractions разложит отношение многочленов в сумму простейших дробей.
minimize минимизирует функцию, а maximize максимизирует
Число «Пи» записывается, как pi
Тригонометрические функции: sin, cos, tan, ctan, arcsin, arccos, arctan, arcctan
Команда series раскладывает функцию в ряд, например: taylor series sinx at x=0 даст нам разложение функции sin(x) в ряд Тейлора в точке x=0
Производные и интегралы
Чтобы найти предел, необходимо в начале функции подставить lim, а после записать саму функцию, в конце указать к чему стремится предел: as-> далее число (бесконечность записывается infinity). 8
8
Оператор factor раскладывает число на множители
! выводит факториал, например 123!
Оператор gcd выводит наибольший общий делитель, например gcd 164, 88 выводит наибольший общий делитель чисел 164 и 88
Как найти Дискриминант? 🤔 Формулы, Примеры решений.
Понятие квадратного уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.
Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.
Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Есть три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы ваш ребенок легко справиться с будущими экзаменами, запишите его на курс подготовки к ОГЭ или ЕГЭ по математике в Skysmart. На занятиях с личным преподавателем он потренируется решать пробные варианты экзамена на время, увидит свои сильные и слабые стороны, разберется в каждой сложной теме и выработает тактику поведения на экзамене, чтобы добиться отличных результатов без стресса.
Записывайтесь на бесплатный пробный урок математики: познакомим с платформой, наметим программу обучения и вдохновим ребенка.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Чаще всего для поиска дискриминанта используют формулу:
В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:
Эта формула подходит даже для неполных квадратных уравнений.
Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.
Как решать квадратные уравнения через дискриминант
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- как найти дискрининант: D = b2 − 4ac;
- если дискриминант отрицательный — зафиксировать, что действительных корней нет;
- если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b
- если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней
А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!
Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x2 — 4x + 2 = 0.
Как решаем:
- Определим коэффициенты: a = 3, b = -4, c = 2.

- Найдем дискриминант: D = b2 — 4ac = (-4)2 — 4 * 3 * 2 = 16 — 24 = -8.
Ответ: D < 0, корней нет.
Пример 2. Решить уравнение: x2 — 6x + 9 = 0.
Как решаем:
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b2 — 4ac = (-6)2 — 4 * 1 * 9 = 36 — 36 = 0.
- D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x2 — 4x — 5 = 0.
Как решаем:
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b2 — 4ac = (-4)2 — 4 * 1 * (-5) = 16 + 20 = 36.
- D > 0, значит уравнение имеет два корня:
x1 = (4 + 6) : 2 = 5,
x2 = (4 — 6) : 2 = -1.
Ответ: два корня x1 = 5, x2 = -1.
Не желаешь повторить формулы сокращенного умножения?
12. Уравнения, содержащие модуль. Рациональные уравнения
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Уравнения, содержащие модуль
Пример 1
Решить уравнение |3x-6|=x+2.
Решение:
Рассмотрим первый случай: 3х-6≥0, тогда 3х-6=х+2, 2х=8, х=4.
Рассмотрим второй случай: 3х-6<0, тогда 3х-6=-(х+2), 4х=4, х=1.
Ответ: 1; 4.
Пример 2
Решить уравнение |x-2| — 3|x-1| + 4|x-3| = 5.
Отметим на координатной прямой точки:
х-2=0 х-1=0 х-3=0х=2 х=1 х=3
Рассмотрим решения уравнения на промежутках (-∞; 1]; (1; 2]; (2; 3] и (3; +∞).
При х≤1: -(х-2) + 3(х-1) -4(х-3)=5, -х+2+3х-3-4х+12=5, -2х=-6, х=3. Ответ не принадлежит промежутку, следовательно нет решений.
Ответ не принадлежит промежутку, следовательно нет решений.При 1<х≤2: -(х-2) — 3(х-1) -4(х-3)=5, -х+2-3х+3-4х+12=5, -8х=-12, х=1,5. Ответ принадлежит промежутку.
При 2<х≤3: х-2 — 3(х-1) -4(х-3)=5, х-2-3х+3-4х+12=5, -6х=-8, х=4/3. Ответ не принадлежит промежутку, следовательно нет решений.
При х>3: х-2 — 3(х-1) +4(х-3)=5, х-2-3х+3+4х-12=5, 2х=16, х=8. Ответ принадлежит промежутку.
Ответ: 1,5; 8.
Рациональные уравнения Рациональным уравнением называется уравнение вида
где P(x), Q(x) — многочлены.
Решение уравнения сводится к решению системы:Пример
Решить уравнение
Решение:
x2-4=0, х-2≠0,x2=4, х≠ 2.
х=-2 или х=2.
Число 2 не может быть корнем.
Ответ: -2.
 Из данных уравнений выберите те, которые не имеют корней:
Из данных уравнений выберите те, которые не имеют корней:а) |x|+4=1; |x-5|=2; |x+3|=-6. б) |1+x|=3; |1-x|=-4; 8+|x|=2.
Решение:
а) |x|+4=1 не имеет корней, т.к. |x|=-3 и модуль не может быть отрицательным числом; |x-5|=2 имеет корни; |x+3|=-6 не имеет корней, т.к. модуль не может быть отрицательным числом.
Ответ: |x|+4=1; |x+3|=-6.
2. Решите уравнение:
а) |5x|=15; б) |2x|=16.
Решение:
а) |5x|=15;
|5||x|=15;
5|x|=15;
|x|=3;
x=3 или x=-3.
3. Решите уравнение:
а) |5x+1|=5; б) |2x-1|=10.
Решение:а) |5x+1|=5;
Ответ: -1,2; 0,8.
4. Решите уравнение:
а) |5x2+3x-1|=-x2-36; б) |3x2-5x-4|=-4x2-23.
Решение:
а) |5x2+3x-1|=-x2-36. Рассмотрим выражение -x2-36, оно принимает отрицательные значения при любых значениях х, следовательно уравнение |5x2+3x-1|=-x2-36 не имеет корней.
Ответ: нет корней
5. Решите уравнение: Решение:
Ответ: -1/3.
6. Решите уравнение:
Решение:
14х2-5x-1=0,
7. Решите уравнение:
Решение:
8. Решите уравнение: Решение:
х ≠3.
Ответ: -4; 1.
9. Найдите, при каком значении переменной значение выражения
равно: а) -6; б) 6.
 Решение:
Решение:10. Решите уравнение:
Решение:
а) Разложим знаменатели на множители:
х2-36=(x-6)(x+6).
108-24x+х2=(x-6)(x-18).
2x-36=2(x-18).
11. Решите уравнение:
а) х2-6|x|=0; б) х2+4|x|=0.
Решение:а) х2-6|x|=0;
х≥0: х2-6x=0; х(х-6)=0, x1=0, x2=6.
x<0: х2+6x=0; х(х+6)=0, x1=0, x2=-6.
Ответ: -6; 0; 6.
12.Решите уравнение:
а) х2-3|x|+2=0; б) х2-2|x|+1=0.
Решение:а) х2-3|x|+2=0.
х≥0: х2-3x+2=0; D=9-8=1, x1=2, x2=1.
x<0: х2+3x+2=0; D=9-8=1, x1=-2, x2=-1.

Ответ: -2; -1; 1; 2.
13. Решите уравнение:
а) |x-2|+|x-4|=5; б) |x-1|-|x-4|=6.
Решение:а) |x-2|+|x-4|=5.
x≤2: -(x-2)-(x-4)=5, -x+2-x+4=5, x=0,5.
2<x≤4: x+2-(x-4)=5, x-2-x+4=5, 2=5 — нет решений.
x>4: x-2+x-4=5, 2x=11, x=5,5.
Ответ: 0,5; 5,5.
14.Решите уравнение:
а) |3- |4- |x|||=5; б) 8-|2 -|x|||=3.
Решение:а) |3- |4- |x|||=5;
3- |4- |x||=5 или 3- |4- |x||=-5;
|4-|x||=-2 — нет решений |4-|x||=8
4-|x|=8 или 4-|x|=-8
|x|=-4 — нет решений |x|=12
х=12 или х=-12.

Ответ: -12; 12.
15. Решите уравнение:
Решение:
а)
3x-7≥0: х2-3x+10=0; D=9-40=-31<0 — нет корней.
3x-7<0: х2-3x-10=0; D=9+40=49, x1=5, x2=-2.
3x-7≠0, x≠7/3.
Ответ: -2; 5.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Какие из чисел -4; -1; 2; 1,5; 2,5 являются корнями уравнения:
а) |3x-1|=5; б) |4-2x|=1?
2. Решите уравнение:
а) |3x|=21; б) |2x|=-12.
3. Решите уравнение:
а) |2x-5|=1; б) |3x+6|=18.
4. Решите уравнение:
5. Решите уравнение:
6. Решите уравнение:
7. Решите уравнение:
8. Решите уравнение:
9. Решите уравнение:
а) 3(x-1) = |2x-1|; б) |5-2x|=|x+4|.
10. Решите уравнение:
а) |х2+x|=12; б) |х2-3x|=10.
Проверь себя
Равносильные уравнения. Преобразование уравнений | Математика
Два или более уравнений называются равносильными, если они имеют одни и те же корни. Например, уравнения:
x2 + 2 = 3x
и
x2 — 3x + 2 = 0
равносильные, потому что имеют одни и те же корни (2 и 1 — это можно проверить подстановкой).
Уравнения, не имеющие корней, также считаются равносильными.
Преобразование уравнений
Если одно уравнение заменяется другим уравнением, равносильным данному, то такая замена называется преобразованием уравнения. Например, уравнение
x2 + 5 = 9
можно преобразовать в такое:
5 + x2 = 9.
Если одно уравнение заменяется другим, равносильным данному и при этом более простым, то такое преобразование называется упрощением уравнения. Например, упростим следующее уравнение:
Например, упростим следующее уравнение:
2x + 3x = 15,
заменив его равносильным уравнением
5x = 15.
Все преобразования уравнений основаны на двух свойствах равенств, и следствиях, которые вытекают из данных свойств.
Если к обеим частям уравнения прибавить или отнять одно и то же число или алгебраическое выражение, то получится уравнение, равносильное данному.
Рассмотрим уравнение x — 5 = 7. Прибавив к обеим частям уравнения число 5
x — 5 + 5 = 7 + 5,
получим уравнение x = 12. Если в уравнение x — 5 = 7 вместо x подставить число 12, то можно удостовериться, что, прибавив к обеим частям уравнения число 5, мы не только получили равносильное уравнение, но и нашли его корень.
Из данного свойства можно вывести три следствия:
- Если в обеих частях уравнения есть одинаковые члены с одинаковыми знаками, то эти члены можно опустить (сократить).

Возьмём уравнение x + 13 = 10 + 13. Отняв от обеих частей по 13, получим
x = 10.
- Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Рассмотрим уравнение 5x — 4 = 12 + x. Прибавим к обеим частям уравнения по 4:
5x — 4 + 4 = 12 + x + 4.
Получим:
5x = 12 + x + 4,
то есть член 4 перешёл в другую часть с обратным знаком. Теперь вычтем из обеих частей уравнения 5x — 4 = 12 + x по x:
5x — 4 — x = 12 + x — x.
Получим:
5x — 4 — x = 12,
то есть член x перешёл в другую часть с обратным знаком.
- Знаки всех членов уравнения можно заменить на противоположные.
Перенесём все члены левой части уравнения 5x — 4 = 12 + x в правую, а все члены правой в левую:
-12 — x = -5x + 4.

И, учитывая, что части любого равенства ( в том числе и любого уравнения) можно менять местами, то, поменяв левую часть с правой, получим:
-5x + 4 = -12 — x,
то есть получилось, что мы просто заменили знаки всех членов уравнения на противоположные.
Данное преобразование можно также рассматривать как умножение обеих частей уравнения на -1.
Если обе части уравнения умножить или разделить на одно и то же число или алгебраическое выражение, то получится уравнение, равносильное данному.
Рассмотрим уравнение 3x = 12. Разделив обе части уравнения на число 3:
3x : 3 = 12 : 3,
получим уравнение x = 4. Если в уравнение 3x = 12 вместо x подставить число 4, то можно удостовериться, что, разделив обе части уравнения на 3, мы не только получили равносильное уравнение, но и нашли его корень.
Из данного свойства можно вывести два следствия:
- Если все члены уравнения имеют общий множитель, то можно разделить на него все члены уравнения, таким образом, упростив его.

Возьмём уравнение 16x + 8 = 40. Разделив все члены на общий множитель 8, получим:
2x + 1 = 5.
- Если в уравнении есть дробные члены, то от них можно освободить уравнение, приведя все члены к одному знаменателю и затем отбросить его.
Возьмём уравнение:
x + 12 — x = 26 — x . 4 2 После приведения всех членов к общему знаменателю получим:
4x + 12 — x = 2(26 — x) . 4 4 4 Теперь, умножив все члены уравнения на 4, или, что то же самое, просто отбросив знаменатель, получим:
4x + 12 — x = 2(26 — x).
Решение квадратных уравнений
youtube.com/embed/LlQXp2EtkyQ» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0.
Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравненияКогда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Например, первую:
\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Решение неполного квадратного уравненияПоскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Правила комбинаторики в задаче B6
- Как представить обычную дробь в виде десятичной
- Задача B15: частный случай при работе с квадратичной функцией
Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике
В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Квадратные уравнения
Арифметический квадратный корень
Корни и степени
Показательная функция
Показательные уравнения
Логарифмическая функция
Логарифмические уравнения
Тригонометрический круг
Формулы приведения
Формулы тригонометрии
Простейшие тригонометрические уравнения 1
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:
Получим:
или
Выбираем меньший корень.
Ответ: — 6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Ответ: — 6
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Это довольно простой тип уравнений. Главное — внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит, .
Возведём обе части уравнения в квадрат:
Решим пропорцию:
Условие при этом выполняется.
Ответ: 87.
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:
Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов.
Ответ: 9.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
откуда
8. Решите уравнение
Представим как
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
Ответ: 7,5.
9. Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел;
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: . Значит,
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
«Отбросим» логарифмы! Конечно, при этом
Ответ: 21.
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
Ответ: -4.
12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
Ответ: 19.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Получим систему:
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Значит, единственный корень уравнения:
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:
Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
Ответ: -2.
15. Решите уравнение В ответе напишите наименьший положительный корень.
Решение:
Сделаем замену Получим: Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
Наименьший положительный корень
Ответ: 2
Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Успеха вам в подготовке к ЕГЭ!
2-x- (12) = 0Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1.1 Факторинг x 2 -x-12
Первый член: x 2 его коэффициент равен 1.
Средний член, -x, его коэффициент -1.
Последний член, «константа», равен -12
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -12 = -12
Шаг-2: Найдите два множителя -12, сумма которых равен коэффициенту среднего члена, который равен -1.
| -12 | + | 1 | = | -11 | ||
| -6 | + | 2 | = | -4 | ||
| -4 | + | 3 | = | -1 | Вот и все |
Шаг 3: Перепишите полином, разделяющий средний член, используя два фактора, найденные на шаге 2 выше, -4 и 3
x 2 — 4x + 3x — 12
Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
x • (x-4)
Складываем последние 2 члена, вычитая общее факторы:
3 • (x-4)
Шаг 5: сложите четыре члена шага 4:
(x + 3) • (x-4)
Какой желаемый фактор ion
Уравнение в конце шага 1:
(x + 3) • (x - 4) = 0
Шаг 2:
Теория — Истоки продукта:
2.1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.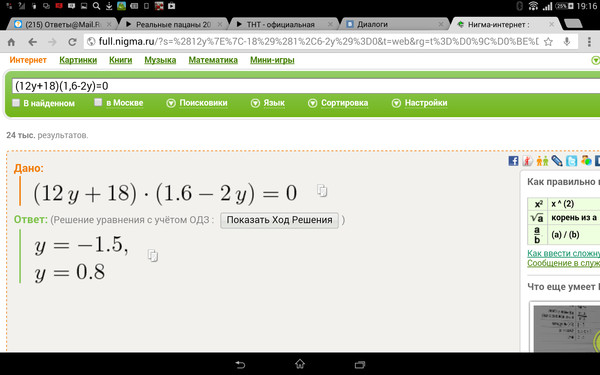
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте
Любое решение для члена = 0 также решает продукт = 0.
Решение уравнения с одной переменной:
2.2 Решите: x + 3 = 0
Вычтем 3 из обеих частей уравнения:
x = -3
Решение уравнения с одной переменной:
2.3 Решите: x-4 = 0
Добавьте 4 к обеим сторонам уравнения:
x = 4
Дополнение: Решение квадратного уравнения напрямую
Решение x 2 -x-12 = 0 напрямую
Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Парабола, найдя вершину:
3.1 Найдите вершину y = x 2 -x-12
Параболы имеют наибольшее значение или самая низкая точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 0.5000
Подставляя в формулу параболы 0,5000 для x, мы можем вычислить координату y:
y = 1,0 * 0,50 * 0,50 — 1,0 * 0,50 — 12,0
или y = -12,250
Парабола, графическая вершина и пересечение по оси X:
Корневой график для: y = x 2 -x-12
Ось симметрии (пунктирная линия) {x} = {0,50}
Вершина в точке {x, y} = {0,50, -12,25}
x -Переходы ( Roots):
Корень 1 при {x, y} = {-3. 00, 0.00}
00, 0.00}
Корень 2 при {x, y} = {4.00, 0.00}
Решите квадратное уравнение, заполнив квадрат
3.2 Решение x 2 -x-12 = 0, завершив Квадрат.
Добавьте 12 к обеим сторонам уравнения:
x 2 -x = 12
Теперь умный бит: возьмите коэффициент при x, равный 1, разделите его на два, получив 1/2, и возведите его в квадрат. давая 1/4
Добавьте 1/4 к обеим частям уравнения:
В правой части мы имеем:
12 + 1/4 или, (12/1) + (1/4)
Общий знаменатель две дроби равны 4. Сложение (48/4) + (1/4) дает 49/4
Таким образом, сложив обе стороны, мы, наконец, получаем:
x 2 -x + (1/4) = 49/4
Сложение 1/4 превратила левую часть в полный квадрат:
x 2 -x + (1/4) =
(x- (1/2)) • (x- (1/2)) =
( x- (1/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Так как
x 2 -x + (1/4) = 49/4 и
x 2 -x + (1/4) = (x- (1/2)) 2
то по закону транзитивности,
(x- (1/2)) 2 = 49/4
Мы будем называть это уравнение уравнением. # 3.2.1
# 3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x- (1/2)) 2 равен
(x- (1/2)) 2/2 =
(x- (1/2)) 1 =
x- (1/2)
Теперь, применяя принцип квадратного корня к уравнению.# 3.2.1 получаем:
x- (1/2) = √ 49/4
Добавьте 1/2 к обеим сторонам, чтобы получить:
x = 1/2 + √ 49/4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — x — 12 = 0
имеет два решения:
x = 1/2 + √ 49/4
или
x = 1/2 — √ 49/4
Обратите внимание, что √ 49/4 можно записать как
√ 49 / √ 4, что равно 7/2
Решите квадратное уравнение с помощью квадратичной формулы
3.3 Решение x 2 -x-12 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, определяется по формуле:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = -1
C = -12
Соответственно B 2 — 4AC =
1 — (-48) =
49
Применение квадратичной формулы:
1 ± √ 49
x = —————
2
Можно ли упростить √ 49?
Да! Разложение на простые множители 49 равно
7 • 7
Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i. е. второй корень).
е. второй корень).
√ 49 = √ 7 • 7 =
± 7 • √ 1 =
± 7
Итак, теперь мы смотрим на:
x = (1 ± 7) / 2
Два реальных решения:
x = ( 1 + √49) / 2 = (1 + 7) / 2 = 4.000
или:
x = (1-√49) / 2 = (1-7) / 2 = -3.000
Были найдены два решения :
- x = 4
- x = -3
решить: 2 / x = 12 | Wyzant Спросите эксперта
Здравствуйте, Татьяна (и др., Интересующиеся этим вопросом).
Вы задали вопрос (я исправил орфографию и заглавные буквы в цитате):
Решить: 2 / x = 12
Возможные ответы: 6, 24, 1/6, 1/24
Во-первых, удивительно по двум причинам, что вы задали этот вопрос, а не кричали на вас. Вот они:
1. Предлагаются четыре возможных ответа, поэтому методом проб и ошибок вы можете попробовать каждый из них и получить ответ быстрее, чем вы могли бы разместить вопрос здесь,
и,
2.Цифры довольно простые, поэтому вы можете почти угадать ответ, даже если не было предложено никаких вариантов.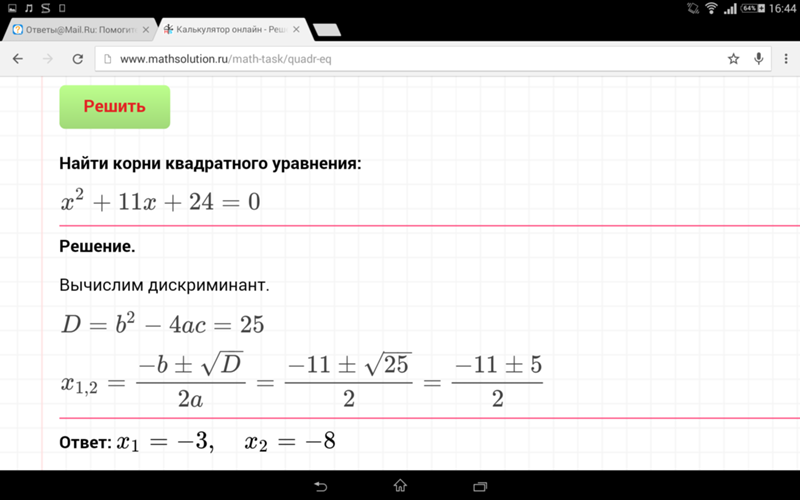
При этом позвольте мне заверить вас, что я считаю, что вы не ленитесь и что этот вопрос представляет для вас настоящую трудность. Итак, я подумал об этом и, учитывая желание WyzAnt, чтобы репетиторы,
… Помните, как их ответы могут помочь ученику в долгосрочной перспективе. Отвечать на вопросы так, чтобы учащийся понял, как прийти к ответу, предпочтительнее, чем просто дать ответ,
Я задумался о возможных причинах.
1. Возможно, вы не знаете, что означает слово «решить». Вы можете найти это в Интернете или в словаре.
2. Вам не хватило пиццы. Приобретите или приготовьте несколько круглых пицц. Разрежьте их на 2,3,4,5,6,12 клинья и оставьте 1 неразрезанный. Сколько кусочков пиццы, разрезанных на 2, уместится поверх всей пиццы? Если вы съели один кусок, какая часть от целого останется? Сколько кусочков пиццы, разрезанных на 12 частей, может поместиться в 1 кусок пиццы, разрезанный на 6? Задавайте себе аналогичные вопросы, пока не поймете дроби. Если вы устали от пиццы, съедите вишневый пирог или используйте бумажные тарелки или плотную бумагу для изображения пирогов и изучения дробей.
Если вы устали от пиццы, съедите вишневый пирог или используйте бумажные тарелки или плотную бумагу для изображения пирогов и изучения дробей.
3. Вы можете не понимать части дроби или обозначение: 2 / x = 12. Число 2 — это числитель, который указывает количество частей целого, которое у вас есть. Линия — это «vinculum», что означает «разделить на». «X» — знаменатель. Он сообщает, сколько частей находится во всем объекте.
3. Итак, посмотрим на уравнение еще раз.
Решить: 2 / x = 12
4. Изложите это словами (подсказки см. В пункте 3. выше).
Две части, которые у нас есть, , разделенное на x частей в целом, равняется двенадцати частям.5. Поместите в другой формат,
Дано 2 ÷ x = 12, найти x.
Вы можете это решить? Если нет, замените x маленькой рамкой или буквой «?» И посмотрите, сможете ли вы это сделать. Тогда это будет больше похоже на математическую задачу начальной школы.
2 ÷? = 12
Теперь вы можете использовать правила математики или алгебры, чтобы переместить двойку на другую сторону и оставить вопросительный знак или квадрат отдельно.Умножьте обе стороны на неизвестное (x, квадрат или вопросительный знак, в зависимости от используемой вами записи. Здесь мы вернемся к использованию x.
2 = 12x
Разделим обе стороны на 12: 2 = 12x
12 12
Так как 12 делится на 2 и 12, то правая часть равна 2 больше 12, а правая часть равна 1x, или 1/6 = x.
6. Попробуйте это:
2 / х = 12
2 = 12
x 1
Перекрестное умножение: 2 умножить на 1 = 12x
или, 2 = 12 x.
Разделите обе стороны на 2. Что вы получите?
снова 2/2, поэтому остается только 1/6. поэтому x = 1/6
Попробуйте это:
Если 2/12 = 1x, и, поскольку 2/2 = 1, то правая часть здесь просто x.
Уменьшить дробь 2/12.
1/6 = х
По принципу тождественности,
х = 1/6
7. Если это все еще сбивает с толку или просто для развлечения, вы можете поиграть в игры с дробями.Если вы свяжетесь со мной, я поделюсь с вами некоторыми из них.
Если это все еще сбивает с толку или просто для развлечения, вы можете поиграть в игры с дробями.Если вы свяжетесь со мной, я поделюсь с вами некоторыми из них.
8. Вернитесь сейчас и изучите тестовый навык. Попробуйте вставить каждый ответ и посмотрите, что вы получите.
Решить: 2 / x = 12
возможные ответы: 6, 24, 1/6, 1/24
Вы можете сделать для этого схему.
Если x: _ | Уравнение: ________ | __ Да, если работает, Нет, если нет ____
6 | |
24 | |
1/6 | |
1/24 | |
9.Было бы полезно выучить список общеупотребительных дробей или их эквивалентов, чтобы в будущем быстрее решать математические задачи. Точно так же вы можете изучать квадраты и кубы до 20. Это в конечном итоге поможет вам с такими тестами, как SAT, NCLEX. MCAT, помимо прочего, также поможет вам в работе и даже в покупках.
10. Если все это не поможет, вы можете пройти тестирование на трудности с обработкой информации, и они могут научить вас некоторым приемам, которые помогут вам во всех ваших исследованиях. В этом вам поможет школьный консультант или академический декан.
В этом вам поможет школьный консультант или академический декан.
Удачи. Я был бы признателен, если бы вы сообщили мне, помогло ли вам это обсуждение и была ли какая-то конкретная часть более полезной. Спасибо.
Цитаты из вопроса, который вы задали в WyzAnt. Математические символы взяты из Википедии.
(c) JSS 2013. При необходимости свяжитесь с доктором J для получения разрешений.
Решение кубических уравнений — методы и примеры
Решение полиномиальных уравнений высшего порядка — важный навык для любого, кто изучает естественные науки и математику.Однако понять, как решать такие уравнения, довольно сложно.
В этой статье будет обсуждаться, как решать кубические уравнения, используя различные методы, такие как метод деления, теорема о множителях и разложение на множители по группировке.
Но прежде чем перейти к этой теме, давайте обсудим , что такое полиномиальное и кубическое уравнение.
Многочлен — это алгебраическое выражение с одним или несколькими членами, в которых знак сложения или вычитания разделяет константу и переменную.
Общая форма многочлена: ax n + bx n-1 + cx n-2 +…. + kx + l, где каждая переменная сопровождается константой в качестве коэффициента. Различные типы полиномов включают в себя; двучлены, трехчлены и четырехчлены. Примеры полиномов: 3x + 1, x 2 + 5xy — ax — 2ay, 6x 2 + 3x + 2x + 1 и т. Д.
Кубическое уравнение — это алгебраическое уравнение третьей степени.
Общий вид кубической функции: f (x) = ax 3 + bx 2 + cx 1 + d.Кубическое уравнение имеет вид ax 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, а d — постоянная.
Как решать кубические уравнения?
Традиционный способ решения кубического уравнения — свести его к квадратному уравнению, а затем решить его либо факторизацией, либо квадратной формулой.
Подобно тому, как квадратное уравнение имеет два действительных корня , кубическое уравнение может иметь три действительных корня. Но в отличие от квадратного уравнения, которое может не иметь реального решения, кубическое уравнение имеет по крайней мере один действительный корень.
Два других корня могут быть действительными или мнимыми.
Всякий раз, когда вам задают кубическое уравнение или какое-либо уравнение, вы всегда должны сначала преобразовать его в стандартную форму.
Например, если вам дано что-то вроде этого, 3x 2 + x — 3 = 2 / x, вы перегруппируете его в стандартную форму и напишете это как, 3x 3 + x 2 — 3x — 2 = 0. Тогда вы можете решить это любым подходящим методом.
Давайте рассмотрим несколько примеров ниже для лучшего понимания:
Пример 1
Определите корни кубического уравнения 2x 3 + 3x 2 — 11x — 6 = 0
Решение
Так как d = 6, то возможными множителями являются 1, 2, 3 и 6.
Теперь примените теорему о факторах, чтобы проверить возможные значения методом проб и ошибок.
f (1) = 2 + 3 — 11 — 6 ≠ 0
f (–1) = –2 + 3 + 11 — 6 ≠ 0
f (2) = 16 + 12 — 22 — 6 = 0
Следовательно, x = 2 — первый корень.
Мы можем получить другие корни уравнения, используя метод синтетического деления.
= (x — 2) (ax 2 + bx + c)
= (x — 2) (2x 2 + bx + 3)
= (x — 2) (2x 2 + 7x + 3 )
= (x — 2) (2x + 1) (x +3)
Следовательно, решения следующие: x = 2, x = -1/2 и x = -3.
Пример 2
Найдите корни кубического уравнения x 3 — 6x 2 + 11x — 6 = 0
Решение
x 3 — 6x 2 + 11x — 6
(x — 1) — один из факторов.
Разделив x 3 — 6x 2 + 11x — 6 на (x — 1),
⟹ (x — 1) (x 2 — 5x + 6) = 0
⟹ (x — 1) (x — 2) (x — 3) = 0
Это решение кубического уравнения: x = 1, x = 2 и x = 3.
Пример 3
Решить x 3 — 2x 2 — x + 2
Решение
Факторизуйте уравнение.
x 3 — 2x 2 — x + 2 = x 2 (x — 2) — (x — 2)
= (x 2 — 1) (x — 2)
= (x + 1) (x — 1) (x — 2)
x = 1, -1 и 2.
Пример 4
Решите кубическое уравнение x 3 — 23x 2 + 142x — 120
Решение
Сначала разложите многочлен на множители.
x 3 — 23x 2 + 142x — 120 = (x — 1) (x 2 — 22x + 120)
Но x 2 — 22x + 120 = x 2 — 12x — 10x + 120
= x (x — 12) — 10 (x — 12)
= (x — 12) (x — 10)
Следовательно, x 3 — 23x 2 + 142x — 120 = ( x — 1) (x — 10) (x — 12)
Приравняйте каждый множитель к нулю.
x — 1 = 0
x = 1
x — 10 = 10
x — 12 = 0
x = 12
Корни уравнения — x = 1, 10 и 12.
Пример 5
Решите кубическое уравнение x 3 — 6 x 2 + 11x — 6 = 0.
Решение
Чтобы решить эту задачу методом деления, возьмите любой множитель постоянная 6;
let x = 2
Разделите многочлен на x-2 до
(x 2 — 4x + 3) = 0.
Теперь решите квадратное уравнение (x 2 — 4x + 3) = 0 чтобы получить x = 1 или x = 3
Следовательно, решения следующие: x = 2, x = 1 и x = 3.
Пример 6
Решите кубическое уравнение x 3 — 7x 2 + 4x + 12 = 0
Решение
Пусть f (x) = x 3 — 7x 2 + 4x + 12
Поскольку d = 12, возможные значения — 1, 2, 3, 4, 6 и 12.
Методом проб и ошибок мы находим, что f (–1) = –1 — 7 — 4 + 12 = 0
Итак, (x + 1) является множителем функции.
x 3 — 7x 2 + 4x + 12
= (x + 1) (x 2 — 8x + 12)
= (x + 1) (x — 2) (x — 6)
Следовательно, x = –1, 2, 6
Пример 7
Решите следующее кубическое уравнение:
x 3 + 3x 2 + x + 3 = 0.
Решение
x 3 + 3x 2 + x + 3
= (x 3 + 3x 2 ) + (x + 3)
= x 2 (x + 3) + 1 (x + 3)
= (x + 3) (x 2 + 1)
Следовательно, x = -1, 1-3.
Пример 8
Решить x 3 — 6x 2 + 11x — 6 = 0
Решение
Разложить на множители
x 3 — 6x 2 + 11x — 6 = 0 ⟹ (x — 1) (x — 2) (x — 3) = 0
Приравнивание каждого множителя к нулю дает;
x = 1, x = 2 и x = 3
Пример 9
Решить x 3 — 4x 2 — 9x + 36 = 0
Решение
Разложить каждый набор два срока.
x 2 (x — 4) — 9 (x — 4) = 0
Извлеките общий множитель (x — 4), чтобы получить
(x 2 — 9) (x — 4) = 0
Теперь разложите разность двух квадратов на множители
(x + 3) (x — 3) (x — 4) = 0
Приравнивая каждый множитель к нулю, мы получаем;
x = −3, 3 или 4
Пример 10
Решите уравнение 3x 3 −16x 2 + 23x — 6 = 0
Решение
Divide 3x 3 −16x 2 + 23x — 6 на x -2, чтобы получить 3x 2 — 1x — 9x + 3
= x (3x — 1) — 3 (3x — 1)
= (x — 3) ( 3x — 1)
Следовательно, 3x 3 −16x 2 + 23x — 6 = (x- 2) (x — 3) (3x — 1)
Приравняем каждый множитель к нулю, чтобы получить,
x = 2, 3 и 1/3
Пример 11
Найдите корни 3x 3 — 3x 2 — 90x = 0
Решение
множитель 3x
3x 3 — 3x 2 — 90x ⟹3x (x 2 — x — 30)
Найдите пару множителей, произведение которых равно −30, а сумма равна −1.
⟹- 6 * 5 = -30
⟹ −6 + 5 = -1
Перепишите уравнение, заменив член «bx» на выбранные множители.
⟹ 3x [(x 2 — 6x) + (5x — 30)]
Разложите уравнение на множители;
⟹ 3x [(x (x — 6) + 5 (x — 6)]
= 3x (x — 6) (x + 5)
Приравнивая каждый множитель к нулю, получаем:
x = 0, 6, -5
Решение кубических уравнений с использованием графического метода
Если вы не можете решить кубическое уравнение ни одним из вышеперечисленных методов, вы можете решить его графическим способом.Для этого вам необходимо иметь точный набросок данного кубического уравнения.
Точка (точки), где его график пересекает ось x, является решением уравнения. Количество реальных решений кубических уравнений равно количеству пересечений его графиком оси абсцисс.
Пример 12
Найдите корни x 3 + 5x 2 + 2x — 8 = 0 графически.
Решение
Просто нарисуйте график следующей функции, подставив случайные значения x:
f (x) = x 3 + 5x 2 + 2x — 8
. График отсекает ось абсцисс в 3 точках, следовательно, существует 3 реальных решения.
График отсекает ось абсцисс в 3 точках, следовательно, существует 3 реальных решения.
На графике решения следующие:
x = 1, x = -2 & x = -4.
Практические вопросыРешите следующие кубические уравнения:
- x 3 — 4x 2 — 6x + 5 = 0
- 2x 3 — 3x 2 — 4x — 35 = 0
- x 3 — 3x 2 — x + 1 = 0
- x 3 + 3x 2 — 6x — 8 = 0
- x 3 + 4x 2 + 7x + 6 = 0
- 2x 3 + 9x 2 + 3x — 4 = 0
- x 3 + 9x 2 + 26x + 24 = 0
- x 3 — 6x 2 — 6x — 7 = 0
- x 3 — 7x — 6 = 0
- x 3 — 5x 2 — 2x + 24 = 0
- 2x 3 + 3x 2 + 8x + 12 = 0
- 5x 3 — 2x 2 + 5x — 2 = 0
- 4x 3 + x 2 — 4x — 1 = 0
- 5x 3 — 2x 2 + 5x — 2 = 0
- 4x 3 900 23 — 3x 2 + 20x — 15 = 0
- 3x 3 + 2x 2 — 12x — 8 = 0
- x 3 + 8 = 0
- 2x 3 — x 2 + 2x — 1 = 0
- 3x 3 — 6x 2 + 2x — 4 = 0
- 3x 3 + 5x 2 — 3x — 5 = 0
Алгебраическое решение уравнений
Алгебраическое решение уравнений Содержание: Эта страница соответствует § 2. 4
(с. 200) текста.
4
(с. 200) текста.
Предлагаемые задачи из текста:
с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87, 88, 95, 97
Квадратные уравнения
Уравнения с участием радикалов
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения
Квадратные уравнения
Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a — не равно 0.
Факторинг
Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое. Подробнее о факторизации многочленов см. В разделе обзора P.3 (p.26) текста.
Пример 1.
2x 2 — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2, или x = 4.
Принцип квадратного корня
Если x 2 = k, то x = ± sqrt (k).
Пример 2.
x 2 — 9 = 0.
x 2 = 9.
x = 3 или x = -3.
Пример 3.
Пример 4.
x 2 + 7 = 0.
х 2 = -7.
х = ±.
Обратите внимание, что = =, так что решения
x = ±, два комплексных числа.
Завершение площади
Идея завершения квадрата заключается в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат корневой принцип.
Пример 5.
x 2 + 6x — 1 = 0.
x 2 + 6x = 1.
x 2 + 6x + 9 = 1 + 9.
9, прибавленная к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) 2 = 9. Причина выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами). Поэтому эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это истина, учитывая (x + a) 2 = x 2 + 2ax + a 2 . Чтобы получить «а» нужно всего лишь разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
(x + 3) 2 = 10.
Теперь мы можем применить принцип квадратного корня и затем решить относительно x.
x = -3 ± sqrt (10).
Пример 6.
2x 2 + 6x — 5 = 0.
2x 2 + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент (коэффициент x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив обе части уравнения на 2.
x 2 + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат, (3/2) 2 = 9/4. Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
x 2 + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(х + 3/2) 2 = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2
До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере.
Пример 7.
x 2 = 16.
x 2 — 16 = 0.
(x + 4) (x — 4) = 0.
x = -4 или x = 4.
В некоторых случаях уравнение можно решить путем факторизации, но факторизация не очевидна.
Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие: всегда одинаковы, поэтому их можно применить к общему квадратному уравнению
топор 2 + bx + c = 0.
Результатом квадрата этого общего уравнения является формула для решений уравнения называется квадратной формулой.
Квадратичная формула
Решения уравнения ax 2 + bx + c = 0 равны
Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае, где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.
Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как сделай это!
Примеры использования квадратичной формулы:
Пример 8.
2x 2 + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика функции f (x) = 2x 2 + 6x — 5.
Пример 9.
4x 2 + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует обратить внимание на два момента.
- Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
- Решение упрощено, поэтому квадратный корень не используется. Это означает, что уравнение могло быть решается факторингом.
(Все квадратные уравнения могут быть решены разложением на множители! Я имею в виду, что это могло быть решено легко факторингом.)
4x 2 + 4x + 1 = 0.
(2x + 1) 2 = 0.
х = -1/2.
Пример 10.
х 2 + х + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов. функции f (x) = x 2 + x + 1. Таким образом, решения сложны, поскольку график y = x 2 + x + 1 не имеет пересечений по x.
Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом
уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.
1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.
Примечания к проверке решений
Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример 3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения, потому что при решении уравнений очень легко допустить неосторожные ошибки.
Алгебраический метод, который состоит из обратной подстановки числа в уравнение и проверки того, что полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда решение предполагает радикальное.
Например, в нашем предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) 2 +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере, 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2. Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический проверить или использовать калькулятор для алгебраической проверки быстрее.
Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту для построения графика y = 2x 2 + 6x — 5 и проследите график, чтобы приблизительно определить, где х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения. Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно не точное решение.
Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и перешли непосредственно к графику утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя (алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень близко к найденным вами числам, то вы, наверное, правы!
Упражнение 1:
Решите следующие квадратные уравнения.
(а) 3x 2 -5x — 2 = 0. Ответ
(б) (x + 1) 2 = 3. Ответ
(в) x 2 = 3x + 2. Ответ
Вернуться к содержанию
Уравнения с участием радикалов
Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал
является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить.
Если в уравнении только один радикал, то перед возведением в степень вам следует договориться, чтобы радикальный член сам по себе на одной стороне уравнения.
Пример 11.
Теперь, когда мы изолировали радикальный член в правой части, возводим обе части в квадрат и решаем полученное уравнение для x.
Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно раствор .
Решение : x = 3.
Примечание: Решением является x-координата точки пересечения графиков y = x и у = sqrt (х + 1) +1.
Посмотрите, что бы произошло, если бы мы возвести в квадрат обе части уравнения до , выделив радикал
срок.
Это хуже того, с чего мы начали!
Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью возведение в степень один раз. Однако мы можем уменьшить число радикальных членов, возведя в степень.
Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и возвести в степень. Затем мы повторяем этот процесс.
Пример 12.
Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат снова обе стороны.
Чек:
Подставляя x = 5/4 в исходное уравнение, получаем
sqrt (9/4) + sqrt (1/4) = 2.
3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.
Примечание по проверке решений:
В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение — координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).
Упражнение 2:
Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ
Вернуться к содержанию
Полиномиальные уравнения высшей степени
Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) с одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее.Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с графической утилитой.
Нулевая постоянная
Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий x, чтобы начать задачу.
Пример 13.
Коэффициент2x 3 + 3x 2 -5x = 0.
x (2x 2 + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения.
x = 0 или 2x 2 + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом. Примечание: Если бы мы не смогли разложить квадратичный фактор во втором уравнении, мы могли бы прибегнуть к к использованию квадратичной формулы.[Убедитесь, что вы получили те же результаты, что и ниже.]
x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится из пересечений графиков f (x) = 2x 3 + 3x 2 -5x.
по группировке
Пример 14.
x 3 -2x 2 -9x +18 = 0.
Коэффициент x 2 в 2 раза больше, чем x 3 , и такое же соотношение существует между коэффициенты при третьем и четвертом членах. Группа термины один и два, а также термины третий и четвертый.
x 2 (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители.
(x — 2) (x 2 — 9) = 0.
Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.
x — 2 = 0 или x 2 — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся на пересечении графика f (x) = x 3 -2x 2 -9x +18.
Квадратичная форма
Пример 15.
x 4 — x 2 — 12 = 0.
Этот многочлен неквадратичный, у него четвертая степень. Однако его можно рассматривать как квадратичный по x 2 .
(x 2 ) 2 — (x 2 ) — 12 = 0.
Это может помочь вам фактически заменить z на x 2 .
z 2 — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на x 2 и решите полученные уравнения.
x 2 = 4.
х = 2, х = -2.
х 2 = -3.
x = i , или x = — i.
Итак, есть четыре решения, два реальных и два комплексных.
Примечание: Эти решения находятся на пересечении графика f (x) = x 4 — х 2 — 12.
График f (x) = x 4 — x 2 -12 и увеличение, показывающее его локальное экстремумы.
Упражнение 3:
Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ
Вернуться к содержанию
Уравнения, содержащие дробные выражения или абсолютные значения
Пример 16.
Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы убедитесь, что оба этих решения проверяют.
Решением является координата x точки пересечения графиков. из y = 1 и y = 2 / x-1 / (x + 2).
Пример 17.
5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что количество внутри абсолютного значения столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности, и все решения должны быть проверены.
Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (х — 1) = х + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.
Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот точка часто сбивает студентов с толку, потому что это выглядит так, как будто мы говорим, что абсолютное значение выражения отрицательно, но это не так.
Выражение (x — 1) уже отрицательное, поэтому — (x — 1) положительное.
Теперь наше уравнение принимает вид
.-5 (x — 1) = x + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по x, или вы можете найти решение как x-координаты точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).
Упражнение 4:
(а) Решите уравнение. Ответ
.(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ
Вернуться к содержанию
Решение квадратных уравнений с использованием факторинга
Чтобы решить квадратное уравнение, используя факторинг :
1
. Преобразуйте уравнение, используя стандартную форму, в которой одна сторона равна нулю.
Преобразуйте уравнение, используя стандартную форму, в которой одна сторона равна нулю.
2 . Фактор ненулевой стороны.
3 . Установите каждый коэффициент равным нулю (помните: произведение факторов равно нулю тогда и только тогда, когда один или несколько факторов равны нулю).
4 . Решите каждое полученное уравнение.
Пример 1:
Решите уравнение, Икс 2 — 3 Икс — 10 знак равно 0
Разложите на множители левую сторону: ( Икс — 5 ) ( Икс + 2 ) знак равно 0
Установите каждый коэффициент на ноль: Икс — 5 знак равно 0 или же Икс + 2 знак равно 0
Решите каждое уравнение: Икс знак равно 5 или же Икс знак равно — 2
Набор решений
{
5
,
—
2
}
.
Пример 2:
Решите уравнение, 2 Икс 2 + 5 Икс знак равно 12
Установите правую сторону на ноль: 2 Икс 2 + 5 Икс — 12 знак равно 0
Фактор левой стороны: ( 2 Икс — 3 ) ( Икс + 4 ) знак равно 0
Установите каждый коэффициент на ноль: 2 Икс — 3 знак равно 0 или же Икс + 4 знак равно 0
Решите каждое уравнение: Икс знак равно 3 2 или же Икс знак равно — 4
Набор решений
{
3
2
,
—
4
}
.
Решение квадратных уравнений с факторингом
Purplemath
Этот урок охватывает множество способов решения квадратичных вычислений, таких как извлечение квадратного корня, вычисление квадрата и использование квадратичной формулы. Но начнем с решения по факторингу.
(Прежде чем перейти к теме решения квадратных уравнений, вы уже должны знать, как разложить квадратные выражения на множители.Если нет, сначала рассмотрите, как учитывать квадратичный фактор.)
Вы уже разложили квадратные выражения на множители. Новым здесь является то, что квадратное выражение является частью уравнения, и вам предлагается найти значения переменной, которые делают уравнение истинным. Вот как это работает:
MathHelp.
 com
comРешите (
x — 3) ( x — 4) = 0 путем факторизации.
Хорошо, эта квадратичная для меня уже учтена. Но как мне использовать эту факторизацию для решения уравнения?
Чтобы решить квадратичные вычисления с помощью факторинга, мы используем то, что называется «Свойство нулевого произведения». Это свойство говорит о том, что кажется довольно очевидным, но только после того, как нам на это указали; а именно:
Свойство нулевого произведения: если мы умножаем две (или более) вещи вместе и результат равен нулю, то мы знаем, что по крайней мере одна из тех вещей, которые мы умножили, также должны быть равны нулю. Другими словами, единственный способ получить ноль при умножении двух (или более) множителей состоит в том, чтобы один из множителей был равен нулю.
Другими словами, единственный способ получить ноль при умножении двух (или более) множителей состоит в том, чтобы один из множителей был равен нулю.
Итак, если мы умножаем два (или более) множителя и получаем нулевой результат, то мы знаем, что по крайней мере один из множителей сам был равен нулю. В частности, мы можем установить каждый из факторов равным нулю и решить полученное уравнение для одного решения исходного уравнения.
Мы можем сделать полезный вывод о факторах (а именно, что один из этих факторов должен был быть равен нулю, поэтому мы можем установить факторы равными нулю), только если сам продукт равен нулю.Если произведение множителей равно на все, что ненулевое, то мы не можем сделать какое-либо утверждение о значениях факторов.
Следовательно, при решении квадратных уравнений путем факторизации мы, , должны всегда иметь уравнение в форме «(квадратное выражение) равно (нулю)», прежде чем предпринимать какие-либо попытки решить квадратное уравнение путем факторизации.
Возвращение к упражнению:
Принцип нулевого фактора говорит мне, что хотя бы один из факторов должен быть равен нулю.Поскольку хотя бы один из факторов должен быть равен нулю, я могу установить каждый из факторов равным нулю:
x — 3 = 0 или x — 4 = 0
Это дает мне простые линейные уравнения, которые легко решить:
И эти два значения — то решение, которое они ищут:
Обратите внимание, что « x = 3, 4» означает то же самое, что и « x = 3 или x = 4»; единственная разница — это форматирование.Формат « x = 3, 4» более распространен.
Решите
x 2 + 5 x + 6 = 0 и проверьте.
Это уравнение уже имеет форму «(квадратичное) равно (нулю)», но, в отличие от предыдущего примера, оно еще не учтено. Я ДОЛЖЕН сначала разложить на множители квадратичный, потому что только когда я УМНОЖИВАЮ и получаю ноль, я могу что-либо сказать о факторах и решениях.Я не могу сделать никаких выводов об отдельных членах квадратичной функции без учета фактора (например, 5 x или 6), потому что я могу добавить много всего, что в сумме равно нулю.
Итак, первое, что мне нужно сделать, это фактор:
x 2 + 5 x + 6 = ( x + 2) ( x + 3)
Теперь я могу переформулировать исходное уравнение в терминах произведения факторов, при этом произведение равно нулю:
Теперь я могу решить каждый фактор, установив каждый из них равным нулю и решив получившиеся линейные уравнения:
x + 2 = 0 или x + 3 = 0
x = –2 или x = — 3
Эти два значения являются решением исходного квадратного уравнения.Итак, мой ответ:
Я еще не закончил, потому что в исходном упражнении мне предлагалось «проверить», что означает, что мне нужно вставить свои ответы обратно в исходное уравнение и убедиться, что оно получилось правильным. В этом случае я буду вставлять выражение в левой части исходного уравнения и проверять, что я получаю правую часть; а именно с 0:
проверка x = –3:
[–3] 2 + 5 [–3] + 6
9–15 + 6
9 + 6–15
15–15
0
проверка x = –2:
[–2] 2 + 5 [–2] + 6
4–10 + 6
4 + 6 — 10
10–10
0
Когда в упражнении указано, что вы должны решить «и проверить» вышеуказанное «plug-n-chug», они ищут вас, чтобы показать, что вы включили свой ответ в исходное упражнение и получили что-то, что сработало правильно.Выше, где я показал свои чеки, все, что им нужно. Но делайте свою работу аккуратно!
Между прочим, вы можете использовать эту технику «проверки», чтобы проверить свои ответы на любое «решающее» упражнение. Так, например, если вы не уверены в своем ответе на вопрос «фактор и решение» в следующем тесте, попробуйте включить свои ответы в исходное уравнение и убедиться, что ваши решения приводят к истинным утверждениям.
Это уравнение не в форме «(квадратичное) равно (нулю)», поэтому я пока не могу его решить.Первое, что мне нужно сделать, это перебрать все термины с одной стороны, а с другой стороны — ноль. Только тогда я могу разложить на множители и решить:
x 2 — 3 = 2 x
x 2 -2 x -3 = 0
( x — 3) ( x + 1) = 0
x — 3 = 0, x + 1 = 0
x = 3, x = –1
Тогда мое решение:
Решите (
x + 2) ( x + 3) = 12.
Студенты часто видят уравнения такого типа и говорят:
«Круто! Это уже учтено! Я установлю множители равными 12 и решу, чтобы получить x = 10 и x = 9. Это было легко!»
Да, это было легко; это тоже было неправильно. Очень-очень неправильно.
Помимо того факта, что ни (10 + 2) (10 + 3), ни (9 + 2) (9 + 3) не равно 12, мы никогда не должны забывать, что мы должны иметь «(квадратичное) равно (нулю)», прежде чем мы сможем решить по факторингу.
Возвращение к упражнению:
Каким бы заманчивым это ни казалось, я не могу приравнять каждый из множителей в левой части уравнения к другой части уравнения и решить. В противном случае я бы получил совершенно неправильную путаницу.
Вместо этого мне сначала нужно умножить и упростить левую часть, затем вычесть 12 из левой и повторно разложить на множители. Только тогда я смогу решить.
( x + 2) ( x + 3) = 12
x 2 + 5 x + 6 = 12
x 2 + 5 x — 6 = 0
( x + 6) ( x — 1) = 0
x + 6 = 0, x — 1 = 0
x = –6, x = 1
Тогда мое решение:
Эту двухчленную квадратичную легче разложить на множители, чем предыдущие квадратичные: я сразу вижу, что могу разложить на множители x из обоих членов, взяв x вперед.Это дает мне:
Очень распространенная ошибка, которую делают ученики на этом этапе, — это «решить» уравнение для « x + 5 = 0» путем деления на x . Но это неверный шаг. Почему? Потому что мы не можем делить на ноль. Как это здесь играет роль?
При делении на коэффициент x подразумевается, что x не равно нулю.Для такого предположения нет абсолютно никаких оснований! И если мы сделаем это предположение, то потеряем половину нашего решения этого уравнения.
Возвращение к упражнению:
Мне нужно помнить, что фактор может содержать только переменную без добавления к другим терминам; в частности, « x » — вполне допустимый коэффициент. Мне нужно установить и коэффициентов равными нулю, а затем решить два результирующих линейных уравнения:
x ( x + 5) = 0
x = 0, x + 5 = 0
x = 0, x = –5
Тогда мое решение:
В предыдущем примере было два члена, и его было легко разложить на множители.Есть еще один случай двухчленной квадратичной системы, который мы можем разложить на множители. Это только немного сложнее:
Это уравнение имеет форму «(квадратичное) равно (нулю)», поэтому я могу решить его с помощью факторизации. Но как это учесть? Заметив, что это разница квадратов. Применим формулу разности квадратов, которую выучил:
x 2 — 4 = 0
( x -2) ( x + 2) = 0
x — 2 = 0, x + 2 = 0
x = 2, x = –2
Тогда мое решение:
Примечание. Приведенное выше решение также можно отформатировать как « x = ± 2».Это произносится как « x равно плюс-минус 2».
В последнем примере, приведенном выше, на следующей странице мы расскажем, как вычислить квадратный корень.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении квадратных уравнений путем факторизации. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Решить с учетом факторинга», чтобы сравнить свой ответ с ответом Mathway. (Или перейдите к следующей странице.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvquad.htm
Использование FOIL — Бесплатная справка по математике
Вы уже знаете, как упростить выражение типа \ (7 (4x + 3) \), верно? Просто используйте распределительное свойство умножить 7 на 4x , а затем на 7 умножить на 3 . 2 + 14x + 12 \).2-13х + 20) \).
Освоить метод FOIL несложно, если вспомнить, что он означает. Просто повторите сначала, снаружи, внутри, в последнюю очередь, и вы это запомните. Помимо этого, нужно просто умножить каждый из этих шагов и сложить все вместе. Даже если числа действительно уродливые, с дробями и отрицательными знаками, просто следуйте инструкциям, и метод будет работать.
Если у вас есть дополнительные вопросы о FOIL, как всегда, не стесняйтесь обращаться за помощью на доску справочных сообщений по математике или воспользуйтесь калькулятором FOIL ниже.



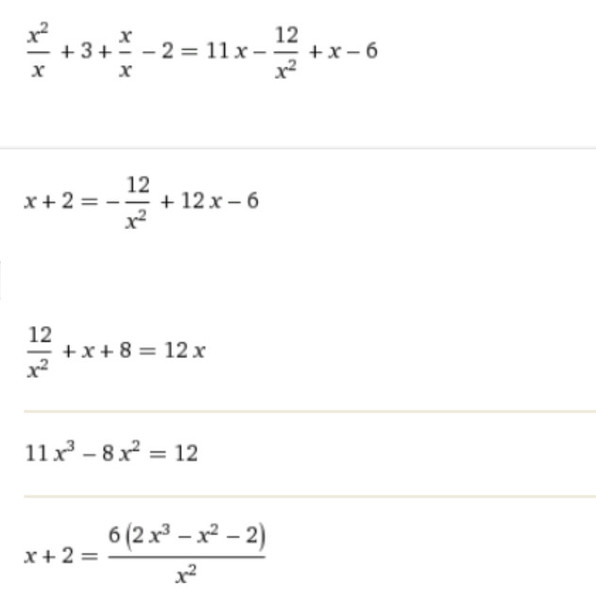

 Тогда дискриминант — это просто число D = b2 − 4ac.
Тогда дискриминант — это просто число D = b2 − 4ac.




 (Все квадратные уравнения могут быть решены разложением на множители! Я имею в виду, что это могло быть
решено легко факторингом.)
(Все квадратные уравнения могут быть решены разложением на множители! Я имею в виду, что это могло быть
решено легко факторингом.)





 Решением является координата x точки пересечения графиков.
из y = 1 и y = 2 / x-1 / (x + 2).
Решением является координата x точки пересечения графиков.
из y = 1 и y = 2 / x-1 / (x + 2). Выражение (x — 1) уже отрицательное, поэтому — (x — 1) положительное.
Выражение (x — 1) уже отрицательное, поэтому — (x — 1) положительное.