1. Решение линейной краевой задачи для обыкновенных дифференциальных уравнений высших порядков и их систем Справочная информация
Краевая задача для нормальных систем обыкновенных дифференциальных уравнений и уравнений высших порядков предполагает отыскание их частного решения, которое подчиняется граничным (краевым) условиям. Количество этих условий должно быть равно порядку системы уравнений или порядку уравнения, чье частное решение ищется. В простейшей постановке краевая задача записывается в виде дифференциального уравнения
,
область действия которого ограничено отрезком [0, l], и граничных условий, задаваемых на концах этого отрезка
при x = 0 при x = l
Здесь φi (i = 1, 2,…, s)
и ψj (j = 1, 2,…, k)
некоторые функции, аргументами которых
являются значения искомого решения и
его производных в граничных точках.
n = s + k.
В другой постановке краевая задача может быть сформулирована в виде нормальной системы дифференциальных уравнений с граничными условиями
,
при x = 0 при x = l
Краевая задача в таком виде имеет следующую матричную форму записи
,
при x = 0: , приx = l: ,
где
, .
Здесь и далее рассматривается случай, когда решение краевой задачи существует и единственно.
Одним
из эффективных методов решения
рассматриваемых краевых задач является
метод стрельбы, который иногда называют
методом пристрелки или методом прогонки.
Его идея состоит в сведении краевой
задачи к задаче Коши, для которой
существуют хорошо отработанные методы
численного решения.
На самом деле, краевая задача для нормальной системы дифференциальных уравнений может быть заменена задачей Коши
где постоянные с1,с2,…,сnподбираются так, чтобы её решение совпадало с решением исходной краевой задачи.
Это достигается следующим способом. Решение задачи Коши кроме аргумента xбудет содержать постоянныес1,с2,…,сn
а, следовательно левые части граничных условий в точках x = 0 и точке x = l тоже будут функциями этих постоянных, так как
Все
сказанное выше позволяет сформировать
алгоритм решения линейной краевой
задачи методом стрельбы.
Пусть линейная краевая задача записана в общем виде следующим образом:
,
при x = 0 при x = l
где a11(x),…,ann(x),f1(x),…,fn(x) – ограниченные на отрезке [0,l] известные функции, аp11,…,pn, q11,…,qkn,θ1,…,θsи,…,– заданные постоянные.
В матричной форме эта краевая задача имеет вид
,
при x = 0: , приx = l: ,
где
,
.
Эквивалентная ей задача Коши имеет вид
, ,
где с– вектор, составленный из постоянныхс1,с2,…,сn
,
Подстановка её решения в граничные условия краевой задачи при x= 0 иx=lдаётnалгебраических уравнений относительно постоянныхс1,с2,…,сn
↔
↔
Первая система из sуравнений является линейной, а для конкретизации второй системы из
Как известно
из теории дифференциальных уравнений
общее решение таких систем является
линейной комбинацией их линейно
независимых частных решений,
где
,,
или
,
где квадратная матрица Y0составлена из частных решений однородной системы уравнений
.
В связи с этим вторая система уравнений, получающаяся из граничных условий при x=l, тоже будет линейной – системой линейных алгебраических уравнений
:
где
.
Отсюда,
из сравнения структуры решения нормальной
системы линейных дифференциальных
уравнений и структуры системы линейных
алгебраических уравнений, получающихся
из граничных условий при x=l,
можно построить следующий алгоритм
нахождения коэффициентов матрицыGи вектораg*.
Сначала задача Коши численно решается для нулевых начальных условий. В этом случае все слагаемые с постоянными с1,с2,…,сnи в решении задачи Коши, и в граничных условиях приx=l, будут отсутствовать. Поэтому с помощью такого решения появляется возможность найти элементы вектораg*:
.
Затем задача Коши
численно решается ещё nраз с единичными начальными условиями.
Под такими начальными условиями имеются
в виду условия, у которых одна компонента
равна единице, а остальные считаются
равными нулю. По этим решениям находятся
элементы столбцов матрицы
,
,
………………………………………………………….
.
После этого системы линейных алгебраических уравнений, полученные из граничных условий при x= 0 иx=l, объединяются в одну систему изnуравнений
,
где
,
которая решается одним
из известных методов решения систем
линейных алгебраических уравнений и,
таким образом, определяются постоянных с1,с2,…,сn.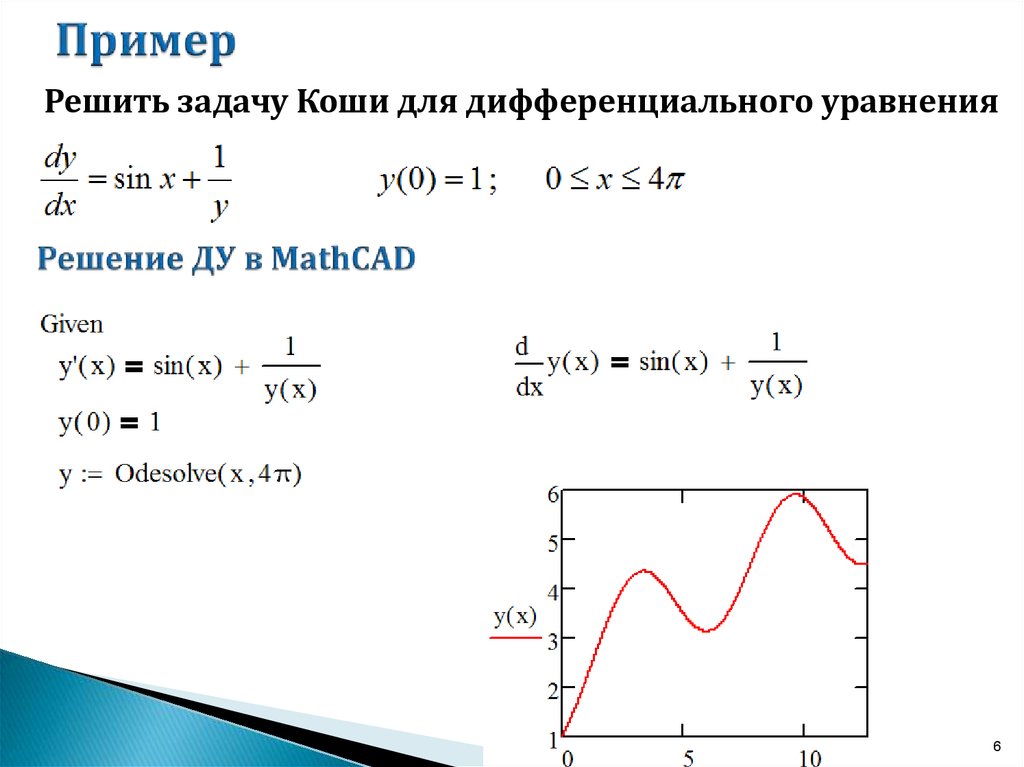
Иллюстрацией данному алгоритму может служить решение следующей краевой задачи для линейного уравнения 2-го порядка
, .
Сначала эта задача приводится к краевой задаче для нормальной системы дифференциальных уравнений
, ,
где введены обозначения ,. В матричной форме она имеет вид
,
при x = 0: , приx = l: .
Здесь
.
Затем для неё записывается эквивалентная задача Коши
,
которая решается трижды для следующих начальных условий
Её решение методом Эйлера для первой пары начальных условий даёт следующие значения y1(x) и y2(x), которые сведены в таблицу
x | 0 | 0. | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
y1 | 0.000 | 0.000 | 0.000 | 0.006 | 0.024 | 0.060 | 0.117 | 0.199 | 0.306 | 0.438 | 0.5897 |
y2 | 0. | 0.000 | 0.060 | 0.180 | 0.355 | 0.573 | 0.820 | 1.074 | 1.316 | 1.520 | 1.666 |
1
000Повторное решение этой же задачи для второй и третьей пар начальных условий даёт другие значения
x | 0 | 0.1 | 0. | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
y1 | 1.000 | 1.000 | 0.910 | 0.736 | 0.492 | 0.200 | –0.112 | –0.413 | –0.667 | –0.842 | –0.909 |
y2 | 0. | –0.900 | –1.740 | –2.439 | –2.921 | –3.124 | –3.004 | –2.543 | –1.751 | –0.671 | 0.627 |
2
000x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0. | 0.8 | 0.9 | 1.0 |
y1 | 0.000 | 0.100 | 0.200 | 0.297 | 0.388 | 0.470 | 0.542 | 0.601 | 0.647 | 0.681 | 0.7051 |
y2 | 1.000 | 1.000 | 0.970 | 0.910 | 0. | 0.714 | 0.590 | 0.463 | 0.342 | 0.240 | 0.1670 |
7
823Значит
,
,
.
Поэтому система линейных алгебраических уравнений для определения постоянных с1ис2будет иметь вид
.
Её решение легко находится
.
С полученными значениями с1 и с2 методом Эйлера строится окончательное решение задачи Коши. Оно приведено в следующей таблице.
x | 0 | 0. | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
y1 | 0.000 | –0.511 | –1.022 | –1.481 | –1.836 | –2.039 | –2.054 | –1.855 | –1.435 | –0.806 | 0.000 |
y2 | –5. | –5.109 | –4.589 | –3.549 | –2.037 | –0.145 | 1.991 | 4.199 | 6.288 | 8.059 | 9.324 |
1
109Из неё видно, что на левом (при x = 0) и на правом (при x = 1) концах отрезка поиска решения заданной краевой задачи получено равенство искомого решения нулю.
Оценка погрешности метода стрельбы
Основной вклад в ошибку приближённых решений краевых задач получаемых методом стрельбы вносят методы решения задачи Коши. На каждом шаге h по аргументу x они вносят в решение абсолютную погрешность, оцениваемую неравенством
,
где m = 2 для метода Эйлера, m = 3 для усовершенствованного метода
Эйлера и m = 5 для метода Рунге-Кутта 4-го порядка.
Абсолютная погрешность приближённого
решения на всём отрезке интегрирования
системы дифференциальных уравнений
описывается неравенством
,
Однако на практике из-за необходимости вычисления Ck и Ek такая оценка абсолютных погрешностей решения краевой задачи затруднительна. Поэтому для вычисления погрешности рассматриваемых методов на всём отрезке поиска решения используют апостериорную оценку, базирующуюся на правиле Рунге
,
где y(xk, h) и y(xk, 2h) – приближённые значения решения, вычисленные в точке xk при шагах интегрирования или разбиения отрезка поиска решения краевой задачи, отличающихся друг от друга в два раза. В качестве относительной погрешности решения краевой задачи используют её интервальную оценку
.
Такой
подход вполне оправдан до тех пор, пока
при реализации вычислений не начинают
сказываться неустранимые ошибки
округления.
Калькулятор метода Эйлера — улучшенный решатель метода Эйлера
Онлайн-калькулятор метода Эйлера поможет вам оценить решение дифференциального уравнения первого порядка с использованием метода Эйлера. Формула Эйлера Калькулятор использует начальные значения для решения дифференциального уравнения и подставляет их в таблицу. Давайте посмотрим на закон Эйлера и модифицированный метод.
Что такое Метод Эйлера?Метод Эйлера (также известный как прямой метод Эйлера) — это численный метод первого порядка, используемый для решения обыкновенных дифференциальных уравнений (ОДУ) с определенными начальными значениями. Это наиболее явный метод численного интегрирования обыкновенных дифференциальных уравнений.
Тем не менее, онлайн-калькулятор E, который позволяет вычислить значение e в степени x. Здесь «X» может быть любой степенью или числовым значением по вашему выбору, а e — показателем степени.
Формула метода Эйлера: Для аппроксимации решения дифференциальных уравнений можно использовать множество различных методов.
Итак, поймите формулу Эйлера, которая используется калькулятором метода Эйлера, и это один из самых простых и лучших способов дифференцировать уравнения. Любопытно, что этот метод и формула, первоначально изобретенные Эйлером, называются методом Эйлера.
$$A_n = A_{n-1} + hA (B_{n-1}, A_{n-1})$$
Пример:
Учитывая задачу с начальным значением
x’= x , x(0)=1,
За четыре шага метод Эйлера приближает x(4).
Используя размер шага, равный 1 (h = 1)
Уравнение метода Эйлера имеет вид \(x_{n+1} = x_n +hf(t_n,x_n)\), поэтому сначала вычислите \(f( t_{0},x_{0})\).
Тогда функция (f) определяется как f(t,x)=x:
$$f(t_{0},x_{0})=f(0,1)=1.$$
Наклон линии, касательной к кривой в точках (0,1). Таким образом, наклон представляет собой изменение x, деленное на изменение t или Δx/Δt.
умножить указанное выше значение на размер шага h:
$$f(x_0) = 1 . 1 = 1$$
Поскольку шаг представляет собой изменение t, при умножении наклона касательной и размера шага мы получаем изменение значения x.
Подставив начальное значение x в формулу метода Эйлера, чтобы найти следующее значение. Кроме того, вы можете найти эти значения с помощью калькулятора метода Эйлера.
$$x_0 + hf(x_0) = x_1 = 1 + 1 . 1 = 2$$
Повторяя вышеуказанные шаги, чтобы найти x_{2},x_{3} и x_{4}.
$$x_2 = x_1 + hf(x_1) = 2 + 1 . 2 = 4$$
$$x_3 = x_2 + hf(x_2) = 4 + 1 . 4 = 8$$
$$x_4 = x_3 + hf(x_3) = 8 + 1 . 8 = 16$$
Из-за повторяющегося характера этого метода Эйлера может быть полезно организовать все вычисления в таблице методов Эйлера.
| Шаг | Х_0 | склон | X_n |
| 1 | 1 | 1 | 2 |
| 2 | 2 | 2 | 4 |
| 3 | 4 | 4 | 8 |
| 4 | 8 | 8 | 16 |
Следовательно, расчет таков, что x_{4}=16.
{4} = 54,59.8$$
Однако онлайн-калькулятор линейной аппроксимации поможет вам вычислить линейную аппроксимацию параметрических, полярных или явных кривых в любой заданной точке.
Как работает калькулятор метода Эйлера?Онлайн-калькулятор метода Эйлера решает обыкновенные дифференциальные уравнения и подставляет полученные значения в таблицу, следуя этим простым инструкциям:
Ввод:- Введите функцию по правилу Эйлера.
- Теперь подставьте значение размера шага или количество шагов.
- Затем добавьте значение y и начальные условия.
- «Рассчитать»
- Калькулятор метода Эйлера предоставляет значение y и ваш ввод.
- Он отображает каждый расчет размера шага в таблице и дает пошаговые расчеты с использованием формулы метода Эйлера.
- Вы можете сделать эти расчеты быстро и много раз, нажав на кнопку пересчета.
Обычно метод Эйлера является основой для создания более сложных методов. Метод Эйлера основан на том, что вблизи точки смысл функции и ее тангенса почти одинаков. Измените координату x, также известную как размер шага.
Можно ли использовать метод Эйлера в обратном направлении?В численном анализе и научных расчетах обратный метод Эйлера (или неявный метод Эйлера) является одним из наиболее важных численных методов решения обыкновенных дифференциальных уравнений. Он похож на (стандартный) метод Эйлера, но разница в том, что это неявный метод.
Почему Эйлер более устойчив в обратном направлении? Прямая и обратная схемы Эйлера имеют одинаковые пределы точности. Однако обратный метод Эйлера является неявным, поэтому он очень устойчив для большинства задач. Поэтому при решении линейных уравнений (например, уравнений Фурье) обратный метод Эйлера устойчив.
Метод Эйлера делает маятник простым. Преимущества: метод Эйлера прост и понятен. Может использоваться для нелинейного IVP. Недостатки: низкая точность и нестабильное значение. Ошибка приближения Эйлера пропорциональна размеру шага h.
Почему Рунге-Кутта точнее?Методы RK высокого порядка являются многоуровневыми, поскольку они включают многоуровневые вычисления наклона между текущим значением и следующим значением дискретного времени.
Заключение:Используйте этот онлайн-калькулятор метода Эйлера для аппроксимации дифференциальных уравнений, которые отображают размер каждого шага и связанные значения в таблице с использованием закона Эйлера. Конечно, вручную решать дифференциальные уравнения по методу Эйлера затруднительно, но при использовании усовершенствованного калькулятора по методу Эйлера это будет удобно.
Ссылка: Из источника Википедии: Метод Эйлера, Неформальное геометрическое описание, Пример кода MATLAB, Пример кода R, Использование других размеров шага, Локальная ошибка усечения, Глобальная ошибка усечения, Численная устойчивость, Ошибки округления, Модификации и расширения.
Из источника Колледжа Дельта: краткое изложение метода Эйлера, предварительный пример, применение метода, общая проблема начального значения.
Из источника Brilliant: метод Эйлера, метод, влияние размера шага, последующие шаги.
Из источника «Примечаний Пола»: раздел «Интервалы достоверности», «Использование метода Эйлера», немного псевдокода, «Аппроксимационные методы».
Функциональная-линейна-функция-калькулятор-Google Suce
AllebildershoppingVideoSmapsNewsbücher
Sucoptionen
Таблица функций (2 переменные) Calculator
Keisan.casio.com ›execulation
Keisan.casio.com› execulate
Keisan.casio.com ›execulate
.casio.com. указанная функция с двумя переменными, указанными как переменная таблица данных.
Таблица функций (1 переменная) · Таблица 2-функций (2 переменные) · Стандартная оценка
Таблица функций (1 переменная) Calculator — Keisan Online Calculator
таблица указанной функции с переменной, указанной как таблица переменных данных.
Алгебра Примеры | Столы | Поиск правила функции — Mathway
www.mathway.com › примеры › алгебра › таблицы › правило поиска функции
Бесплатное средство решения математических задач отвечает на домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике… Проверьте, линейно ли правило функции.
Бесплатный калькулятор линейных функций — Mathepower
www.mathepower.com › linearfunctions
Введите уравнение, точки или наклон. Mathepower вычисляет другую информацию о вашей функции шаг за шагом.
Калькулятор таблицы значений функций — указан F(x) — онлайн-решатель
www.dcode.fr › Калькулятор значения функции
Инструмент для вычисления различных значений функции из ее уравнения f(x) и заданных значений для вычисления их изображений с помощью калькулятора функций …
Функция поиска уравнения по таблице точек — онлайн-калькулятор
www.dcode.fr › function-equation-finder
Чтобы найти уравнение по графику: Метод 1 (подгонка): анализ кривой (посмотрев на нее) в чтобы определить, к какому типу относится эта функция (скорее линейная, .
..
Ähnliche Fragen
Как определить, является ли функция линейной или нелинейной калькулятор?
Онлайн-калькулятор линейной функции — Cuemath
www.cuemath.com › калькуляторы › линейная-функц…
Калькулятор линейной функции. Линейное уравнение определяется как уравнение, которое записано с одной или двумя переменными или так далее. Это уравнение будет …
Калькулятор входной таблицы — MathCelebrity
www.mathcelebrity.com › input-table
Какая 1 формула используется для калькулятора таблицы ввода? Создайте функцию ƒ(x) = y, где каждый вход удовлетворяет ожидаемому результату. Для получения дополнительных математических формул, …
Калькулятор линейной регрессии — GraphPad
www.graphpad.com › quickcalcs › linear1
Под калькулятором мы размещаем ресурсы для получения дополнительной информации о предположениях и интерпретации линейной регрессии. 1. Введите данные. Внимание! Поле таблицы .