Общие сведения о неравенствах
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Предварительные навыкиОпределения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, <, ≥, ≤ или ≠.
Пример: 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
Если 5 > 3, то 3 < 5. То есть левую и правую часть неравенства можно поменять местами, изменив знак неравенства на противоположный. В ситуации с весами: большой арбуз можно положить на правую чашу, а маленький арбуз на левую. Тогда правая чаша перевесит левую, и экран покажет знак
Если в неравенстве 5 > 3, не трогая левую и правую часть, поменять знак на <, то получится неравенство 5 < 3. Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Рассмотрим некоторые важные свойства для неравенства 5 > 3.
В будущем эти свойства будут работать и для других неравенств.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Знак неравенства при этом не изменится.
Например, перенесём в неравенстве 5 > 3, член 5 из левой части в правую часть, изменив знак этого члена. После переноса члена 5 в правую часть, в левой части ничего не останется, поэтому запишем там 0
0 > 3 − 5
0 > −2
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь отрицательное число, скажем на число −2. Тогда получим:
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Например, чтобы ответить на вопрос является ли верным неравенство 7 > 3, нужно проверить выполняется ли условие «больше ли 7, чем 3». Мы знаем, что число 7 больше, чем число 3. То есть условие выполнено, а значит и неравенство 7 > 3 верно.
Неравенство 8 < 6 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Составим разность из членов 7 и 3. Тогда получим 7 − 3 = 4. Согласно правилу, число 7 будет больше числа 3, если разность 7 − 3 окажется положительной. У нас она равна 4, то есть разность положительна. А значит число 7 больше числа 3.
Проверим с помощью разности верно ли неравенство 3 < 4. Составим разность, получим 3 − 4 = −1. Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Проверим верно ли неравенство 5 > 8. Составим разность, получим 5 − 8 = −3. Согласно правилу, число 5 будет больше числа 8, если разность 5 − 8 окажется положительной. У нас разность равна −3, то есть она не является положительной. А значит число 5 не больше числа 8. Иными словами, неравенство 5 > 8 не является верным.
Строгие и нестрогие неравенства
Неравенства, содержащие знаки >, < называют строгими. А неравенства, содержащие знаки ≥, ≤ называют нестрогими.
Примеры строгих неравенства мы рассматривали ранее. Таковыми являются неравенства 5 > 3, 7 < 9.
Нестрогим, например, является неравенство 2 ≤ 5. Данное неравенство читают следующим образом: «2 меньше или равно 5».
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
Полная запись этого неравенства выглядит следующим образом:
Тогда становится очевидным, что неравенство 2 ≤ 5 состоит из двух условий: «два меньше пять» и «два равно пять».
Нестрогое неравенство верно в том случае, если выполняется хотя бы одно из его условий. В нашем примере верным является условие «2 меньше 5». Значит и само неравенство 2 ≤ 5 верно.
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Пример 3. Неравенство 5 ≤ 2 не является верным, поскольку не выполняется ни одно из его условий: ни 5 < 2 ни 5 = 2.
Двойное неравенство
Число 3 больше, чем число 2 и меньше, чем число 4. В виде неравенства это высказывание можно записать так: 2 < 3 < 4. Такое неравенство называют двойным.
Двойное неравенство может содержать знаки нестрогих неравенств. К примеру, если число 5 больше или равно, чем число 2, и меньше или равно, чем число 7, то можно записать, что 2 ≤ 5 ≤ 7
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Например, неравенство x > 2 содержит переменную x. Обычно такое неравенство нужно решить, то есть выяснить при каких значениях x данное неравенство становится верным.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
3 > 2
4 > 2
5 > 2
Число 2, располагающееся в правой части неравенства x > 2, будем называть границей данного неравенства. В зависимости от знака неравенства, граница может принадлежать множеству решений неравенства либо не принадлежать ему.
В нашем примере граница неравенства не принадлежит множеству решений, поскольку при подстановке числа 2 в неравенство x > 2 получается не верное неравенство 2 > 2. Число 2 не может быть больше самого себя, поскольку оно равно самому себе (2 = 2).
Неравенство x > 2 является строгим. Его можно прочитать так: «x строго больше 2″. То есть все значения, принимаемые переменной x должны быть строго больше 2. В противном случае, неравенство верным не будет.
Если бы нам было дано нестрогое неравенство x ≥ 2, то решениями данного неравенства были бы все числа, которые больше 2, в том числе и само число 2. В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
Решая уравнения мы выполняли тождественные преобразования до тех пор, пока в левой части уравнения не оставалась переменная, а в правой части значение этой переменной (например: x = 2, x = 5). Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Итак, нужно найти такие значения x, при подстановке которых в 2x > 6 получится верное неравенство.
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
В левой части осталась переменная x, а правая часть стала равна 3. Получилось равносильное неравенство x > 3. На этом решение завершается, поскольку в левой части осталась переменная, а в правой части граница неравенства.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
4 > 3
5 > 3
6 > 3
7 > 3
Отметим, что неравенство x > 3 является строгим. «Переменная x строго больше трёх».
А поскольку неравенство x > 3 равносильно исходному неравенству 2x > 6, то их решения будут совпадать. Иначе говоря, значения, которые подходят неравенству x > 3, будут подходить и неравенству 2x > 6. Покажем это.
Возьмём, например, число 5 и подставим его сначала в полученное нами равносильное неравенство x > 3, а потом в исходное 2x > 6.
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат числовому промежутку от трёх до плюс бесконечности.
Иначе говоря, все числа, начиная от трёх до плюс бесконечности являются решениями неравенства x > 3. Знак ∞ в математике означает бесконечность.
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
x ∈ [ 2 ; 8 ]
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Обратим внимание на то, что ответ записан с помощью квадратных скобок, поскольку границы неравенства 2 ≤ x ≤ 8, а именно числа 2 и 8 принадлежат множеству решений этого неравенства.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
Здесь границы числового промежутка 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8.
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
Открытыми их называют по той причине, что числовой промежуток остаётся открытым из-за того, что его границы не принадлежат этому числовому промежутку. Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой лучЧисловым лучом называют числовой промежуток, который задаётся неравенством x ≥ a, где a — граница данного неравенства, x — решение неравенства.
Пусть a = 3. Тогда неравенство x ≥ a примет вид x ≥ 3. Решениями данного неравенства являются все числа, которые больше 3, включая само число 3.
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Здесь точка 3 соответствует границе неравенства x ≥ 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≥ 3.
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
[ a ; +∞ )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
x ∈ [ 3 ; +∞ )
В этом выражении говорится, что переменная x, входящая в неравенство x ≥ 3, принимает все значения от 3 до плюс бесконечности.
Иначе говоря, все числа от 3 до плюс бесконечности, являются решениями неравенства x ≥ 3. Граница 3 принадлежит множеству решений, поскольку неравенство x ≥ 3 является нестрогим.
Закрытым числовым лучом также называют числовой промежуток, который задаётся неравенством x ≤ a. Решениями неравенства x ≤ a являются все числа, которые меньше a, включая само число a.
К примеру, если a = 2, то неравенство примет вид x ≤ 2. На координатной прямой граница 2 будет изображаться закрашенным кружком, а вся область, находящаяся слева, будет выделена штрихами. В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
Здесь точка 2 соответствует границе неравенства x ≤ 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≤ 2.
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
x ∈ ( −∞ ; 2 ]
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытым числовым лучом называют числовой промежуток, который задаётся неравенством x > a, где a — граница данного неравенства, x — решение неравенства.
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
Пусть a = 3. Тогда неравенство примет вид x > 3. Решениями данного неравенства являются все числа, которые больше 3, за исключением числа 3
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Здесь точка 3 соответствует границе неравенства x > 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x > 3. Точка 3, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x > 3 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x > a, обозначается следующим образом:
( a ; +∞ )
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
x ∈ ( 3 ; +∞ )
В этом выражении говорится, что все числа от 3 до плюс бесконечности, являются решениями неравенства x > 3. Граница 3 не принадлежит множеству решений, поскольку неравенство x > 3 является строгим.
Открытым числовым лучом также называют числовой промежуток, который задаётся неравенством x < a, где a — граница данного неравенства, x — решение неравенства. Решениями неравенства x < a являются все числа, которые меньше a, исключая число a.
К примеру, если a = 2, то неравенство примет вид x < 2. На координатной прямой граница 2 будет изображаться пустым кружком, а вся область, находящаяся слева, будет выделена штрихами:
Здесь точка 2 соответствует границе неравенства x < 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x < 2. Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x < a, обозначается следующим образом:
( −∞ ; a )
Запишем ответ к неравенству x < 2 с помощью обозначения открытого числового луча:
x ∈ ( −∞ ; 2 )
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x < 2. Граница 2 не принадлежит множеству решений, поскольку неравенство x < 2 является строгим.
ОтрезокОтрезком называют числовой промежуток, который задаётся двойным неравенством a ≤ x ≤ b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x ≤ b примет вид 2 ≤ x ≤ 8. Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8. Точки 2 и 8, являющиеся границами отрезка, изображены в виде закрашенных кружков, поскольку границы неравенства 2 ≤ x ≤ 8 принадлежат множеству его решений.
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
[ a ; b ]
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8 включительно, являются решениями неравенства 2 ≤ x ≤ 8.
Интервал
Интервалом называют числовой промежуток, который задаётся двойным неравенством a < x < b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a < x < b примет вид 2 < x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая числа 2 и 8.
Изобразим интервал на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x < 8. Точки 2 и 8, являющиеся границами интервала, изображены в виде пустых кружков, поскольку границы неравенства 2 < x < 8 не принадлежат множеству его решений.
На письме интервал, заданный неравенством a < x < b, обозначается следующим образом:
( a ; b )
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 < x < 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, исключая числа 2 и 8, являются решениями неравенства 2 < x < 8.
Полуинтервал
Полуинтервалом называют числовой промежуток, который задаётся неравенством a ≤ x < b, где a и b — границы данного неравенства, x — решение неравенства.
Полуинтервалом также называют числовой промежуток, который задаётся неравенством a < x ≤ b.
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x < b ему (полуинтервалу) принадлежит левая граница.
А в ситуации с полуинтервалом a < x ≤ b ему принадлежит правая граница.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x < b примет вид 2 ≤ x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, включая число 2, но исключая число 8.
Изобразим полуинтервал 2 ≤ x < 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x < 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x < 8 принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x < 8 не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x < b, обозначается следующим образом:
[ a ; b )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x < 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, включая число 2, но исключая число 8, являются решениями неравенства 2 ≤ x < 8.
Аналогично на координатной прямой можно изобразить полуинтервал, заданный неравенством a < x ≤ b. Пусть a = 2, b = 8. Тогда неравенство a < x ≤ b примет вид 2 < x ≤ 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая число 2, но включая число 8.
Изобразим полуинтервал 2 < x ≤ 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x ≤ 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 < x ≤ 8 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 < x ≤ 8 принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a < x ≤ b, обозначается так: ( a ; b ]. Запишем ответ к неравенству 2 < x ≤ 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8, исключая число 2, но включая число 8, являются решениями неравенства 2 < x ≤ 8.
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:
Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5 < x < 1
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
Неравенством вида a < x < b, задаётся интервал. В данном случае переменная a равна −5, а переменная b равна единице. Неравенство −5 < x < 1 строгое, поэтому границы −5 и 1 будут изображаться в виде пустых кружка. Нас интересуют все значения x, которые больше −5, но меньше единицы, поэтому вся область между точками −5 и 1 будет выделена штрихами:
Пример 5. Изобразить на координатной прямой числовые промежутки [-1; 2] и [2; 5]
Изобразить на координатной прямой числовые промежутки [-1; 2] и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка.
Квадратными скобками с обеих сторон обозначаются отрезки. Границы отрезка принадлежат ему, поэтому границы отрезков [-1; 2] и [2; 5] будут изображаться на координатной прямой в виде закрашенных кружков. Вся область между ними будет выделена штрихами.
Чтобы хорошо увидеть промежутки [−1; 2] и [2; 5], первый можно изобразить на верхней области, а второй на нижней. Так и поступим:
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax < b), будем называть линейным неравенством с одной переменной.
В линейном неравенстве ax > b, x — это переменная, значения которой нужно найти, а — коэффициент этой переменной, b — граница неравенства, которая в зависимости от знака неравенства может принадлежать множеству его решений либо не принадлежать ему.
Например, неравенство 2x > 4 является неравенством вида ax > b. В нём роль переменной a играет число 2, роль переменной b (границы неравенства) играет число 4.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Получившееся неравенство x > 2 также является неравенством вида ax > b, то есть линейным неравенством с одной переменной. В этом неравенстве роль переменной a играет единица. Ранее мы говорили, что коэффициент 1 не записывают. Роль переменной b играет число 2.
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7 < 0
Прибавим к обеим частям неравенства число 7
x − 7 + 7 < 0 + 7
В левой части останется x, а правая часть станет равна 7
x < 7
Путём элементарных преобразований мы привели неравенство x − 7 < 0 к равносильному неравенству x < 7. Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Когда неравенство приведено к виду x < a (или x > a), его можно считать уже решённым. Наше неравенство x − 7 < 0 тоже приведено к такому виду, а именно к виду x < 7. Но в большинстве школ требуют, чтобы ответ был записан с помощью числового промежутка и проиллюстрирован на координатной прямой.
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x < a и обозначается как ( −∞ ; a)
x ∈ ( −∞ ; 7 )
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Для проверки возьмём любое число из промежутка ( −∞ ; 7 ) и подставим его в неравенство x < 7 вместо переменной x. Возьмём, например, число 2
Возьмём, например, число 2
2 < 7
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
4 < 7
Получилось верное числовое неравенство. Значит решение верное.
А поскольку неравенство x < 7 равносильно исходному неравенству x − 7 < 0, то решения неравенства x < 7 будут совпадать с решениями неравенства x − 7 < 0. Подставим те же тестовые значения 2 и 4 в неравенство x − 7 < 0
2 − 7 < 0
−5 < 0 — Верное неравенство
4 − 7 < 0
−3 < 0 Верное неравенство
Пример 2. Решить неравенство −4x < −16
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Мы привели неравенство −4x < −16 к равносильному неравенству x > 4. Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
3y − 6y> 1 − 1
Приведём подобные слагаемые:
−3y > 0
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y < 0 являются все числа, меньшие нуля. Изобразим множество решений неравенства y < 0 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства являются все числа, которые меньше . Граница принадлежит множеству решений, поскольку неравенство является нестрогим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
После приведения подобных слагаемых, получим неравенство 6x > 1. Разделим обе части этого неравенства на 6. Тогда получим:
Разделим обе части этого неравенства на 6. Тогда получим:
Решениями неравенства являются все числа, которые больше . Граница не принадлежит множеству решений, поскольку неравенство является строгим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 6. Решить неравенство
Умножим обе части на 6
После приведения подобных слагаемых, получим неравенство 5x < 30. Разделим обе части этого неравенства на 5
Решениями неравенства x < 6 являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x < 6 строгим.
Изобразим множество решений неравенства x < 6 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5.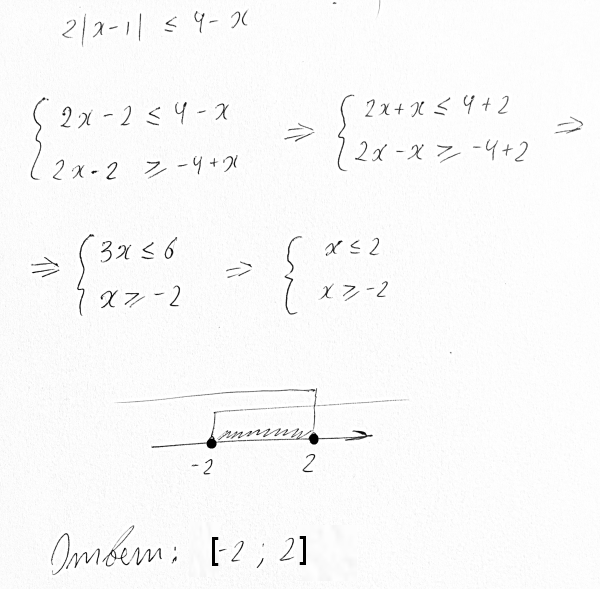 Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 8. Решить неравенство 4 < 4x < 20
Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.
Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4 < 4x < 20
Решениями неравенства 1 < x < 5 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 < x < 5 является строгим.
Изобразим множество решений неравенства 1 < x < 5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 9. Решить неравенство −1 ≤ −2x ≤ 0
Разделим все члены неравенства на −2
Получили неравенство 0,5 ≥ x ≥ 0. Двойное неравенство желательно записывать так, чтобы меньший член располагался слева, а больший справа. Поэтому перепишем наше неравенство следующим образом:
0 ≤ x ≤ 0,5
Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.
Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 10. Решить неравенство
Умножим обе неравенства на 12
Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 2
Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 11. Решить неравенство
Умножим все части неравенства на 3
Теперь из каждой части получившегося неравенства вычтем 6
Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.
Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Существуют неравенства, которые не имеют решений. Таковым, например, является неравенство 6x > 2(3x + 1). В процессе решения этого неравенства мы придём к тому, что знак неравенства > не оправдает своего местоположения. Давайте посмотрим, как это выглядит.
Таковым, например, является неравенство 6x > 2(3x + 1). В процессе решения этого неравенства мы придём к тому, что знак неравенства > не оправдает своего местоположения. Давайте посмотрим, как это выглядит.
Раскроем скобки в правой части данного неравенство, получим 6x > 6x + 2. Перенесем 6x из правой части в левую часть, изменив знак, получим 6x − 6x > 2. Приводим подобные слагаемые и получаем неравенство 0 > 2, которое не является верным.
Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:
Получили неравенство 0x > 2. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль не может быть больше, чем число 2. Значит неравенство 0x > 2 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x > 2, то не имеет решений и исходное неравенство 6x > 2(3x + 1).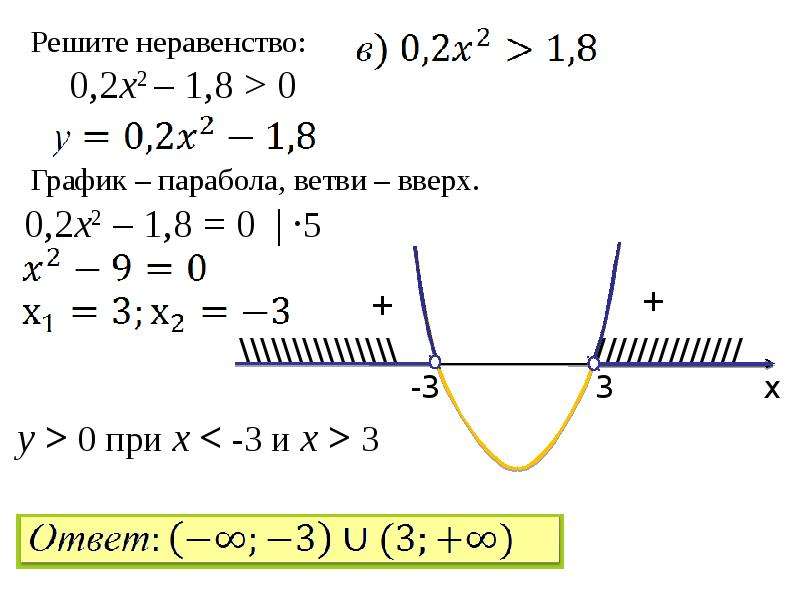
Пример 2. Решить неравенство
Умножим обе части неравенства на 3
В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:
Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x < −8 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x < −8, то не имеет решений и исходное неравенство .
Ответ: решений нет.
Когда решений бесконечно много
Существуют неравенства, имеющие бесчисленное множество решений. Такие неравенства становятся верными при любом x.
Пример 1. Решить неравенство 5(3x − 9) < 15x
Раскроем скобки в правой части неравенства:
Перенесём 15x из правой части в левую часть, изменив знак:
Приведем подобные слагаемые в левой части:
Получили неравенство 0x < 45. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль меньше, чем 45. Значит решением неравенства 0x < 45 является любое число.
В левой части располагается произведение, которое будет равно нулю при любом x. А ноль меньше, чем 45. Значит решением неравенства 0x < 45 является любое число.
А если приведённое равносильное неравенство 0x < 45 имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) < 15x имеет те же решения.
Ответ можно записать в виде числового промежутка:
x ∈ ( −∞; +∞ )
В этом выражении говорится, что решениями неравенства 5(3x − 9) < 15x являются все числа от минус бесконечности до плюс бесконечности.
Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x
Раскроем скобки в левой части неравенства:
Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Получили неравенство 0x > −31. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль больше, чем −31. Значит решением неравенства 0x < −31 является любое число.
В левой части располагается произведение, которое будет равно нулю при любом x. А ноль больше, чем −31. Значит решением неравенства 0x < −31 является любое число.
А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.
Запишем ответ в виде числового промежутка:
x ∈ ( −∞; +∞ )
Задания для самостоятельного решения
Задание 1. Решите неравенство:
Задание 2. Решите неравенство:
Задание 3. Решите неравенство:
Задание 4. Решите неравенство:
Задание 5. Решите неравенство:
Задание 6. Решите неравенство:
Задание 7. Решите неравенство:
Задание 8. Решите неравенство:
Задание 9. Решите неравенство:
Задание 10. Решите неравенство:
Задание 11. Решите неравенство:
Задание 12. Решите неравенство:
Решите неравенство:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок 1. числовые и алгебраические выражения. линейные уравнения и неравенства — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок № 1. Повторение 7-9. Числовые и алгебраические выражения. Линейные уравнения и неравенства
Перечень вопросов, рассматриваемых в теме.
- обобщение и систематизация знаний по алгебре 7-9;
- повтор арифметики алгебраических выражений;
- решение линейных уравнений и неравенств;
- решение систем линейных уравнений и неравенств.
Основная литература:
1. Колягин Ю. М., Ткачева М. В., Фёдорова Н. Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни.
Колягин Ю. М., Ткачева М. В., Фёдорова Н. Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни.
2. Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни
Дополнительная литература:
1. Шабунин М. И., Ткачева М. В., Фёдорова Н. Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень.
2. Галицкий М. Л., Гольдман А. М., Звавич Л. И. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся школ и классов с углубленным изучением математики. М.: Просвещение, 2000.
Открытые электронные ресурсы:
1. Федеральный институт педагогических измерений. http://www.fipi.ru
1.Выражения
Все выражения можно разбить на два класса на основании наличия переменных: числовые выражения и выражения с переменными.
Логическая задача на классификацию
Основание для классификации: наличие переменных | Выражения | |
Числовые выражения | Выражения с переменными | |
Для числовых выражений можно находить значение – результат всех выполненных действий. Для выражений с переменными можно также находить значение при некоторых значениях переменных, предварительно упростив его, например, с помощью свойств, правил, формул сокращенного умножения.
Пример 1.
Найдите значение выражения при a=0,01 и b=12:
1) 7a-(2a-(a-5)),
2)
3)
Решение:
1)7a-(2a-(a-5)) =7a-(2a-a+5) =7a-(a+5) =7a-a-5=6a-5;
6∙0,01-5=-4,94
2);
3)
3b-2a-3b=-2a-2a=-0,02
2.Линейное уравнение с одним неизвестным
Определение
Линейное уравнение с одним неизвестным – это уравнение вида ax=b, где a и b – заданные числа, x – неизвестное
Решить уравнение – это значит найти все его корни или установить, что корней нет
Основные свойства уравнений
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Решение уравнения ax=b,где a и b – числа, x – переменная
Если a≠0, b – любое число, то .
Если a=0, b≠0, то нет корней.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Пример 2.
Решите уравнение:
1) ,
2) |5x+7|=2.
Решение:
1),
3(3x+1)-5(2x-1)=7x+3,
9x+3-10x+5=7x+3,
-8x=-5 |:(-8),
x=0,625
Ответ: 0,625
Решим уравнение 2).
По определению модуля числа имеем 5x+7=±2.
Таким образом, либо 5x+7=2, откуда x=-1, либо 5x+7=-2, откуда x=-1,8. Получаем ответ: -1; -1,8.
Решение уравнения ax=b,где a и b – числа, x – переменная
Если a≠0, b – любое число, то .
Если a=0, b≠0, то нет корней.
Если a=0, b=0, то x – любое число.
Линейное уравнение с параметрами
Пример.
Решите уравнение (5x+7)n=x-m, где m и n – некоторые числа, x – неизвестное
Решение:
5x∙n+7n=x-m,
5xn-x=-m-7n,
x(5n-1)=-m-7n,
1)Если 5n-1≠0, то есть n≠0,2, то . Используя основное свойство дроби, получаем, что .
Используя основное свойство дроби, получаем, что .
2)Если 5n-1=0, то есть n=0,2, то уравнение примет вид 0∙x=-m-1,4;
Тогда при m=-1,4 корнем уравнения будет любое число,
при m≠-1,4 уравнение не имеет корней.
Рассмотрим задачу 1.
От пристани А до пристани В катер плывет по реке 15 минут, а обратно 20 минут. Найти скорость течения реки, если собственная скорость катера 14 км/ч.
Для ее решения необходимо:
1.Провести ориентировку в тексте задачи.
1.1.Проанализировать условие и выявить данные (известные, дополнительные, скрытые).
1.2.Проанализировать вопрос задачи и выявить искомое.
1.3.Определить связи одноуровневые и межуровневые между данными и искомым.
1.4.Построить графическую схему, например, таблицу.
1.5.Установить в ней место искомого.
2.Спланировать способ решения задачи.
2.1.Подобрать метод, например, алгебраический.
2.2.Подобрать средства.
2.3.Подобрать действия для решения составленной математической модели.
3.Исполнить намеченный план решения и найти искомое.
4.Провести самоконтроль решения задачи, проверив, что найденное искомое не противоречит условию задачи.
5.Провести самооценку решения задачи.
6.Провести самокоррекцию выполненного решения задачи, если есть в том необходимость.
1 способ: Провести повторное решение задачи от начала до конца.
2 способ: Провести дополнительную деятельность для того, чтобы ответить на вопрос задачи.
3 способ: Решить задачу другим способом.
удовлетворяет условию
Ответ: 2км/ч.
3.Системы линейных уравнений с двумя неизвестными
Определение
Система двух уравнений первой степени с двумя неизвестными – это система вида
где x и y – неизвестные,
– заданные числа,
причем и .
Определение
Решение системы двух уравнений с двумя неизвестными – это пара чисел x и y, которые при подстановке в эту систему обращают каждое ее уравнение в верное числовое равенство.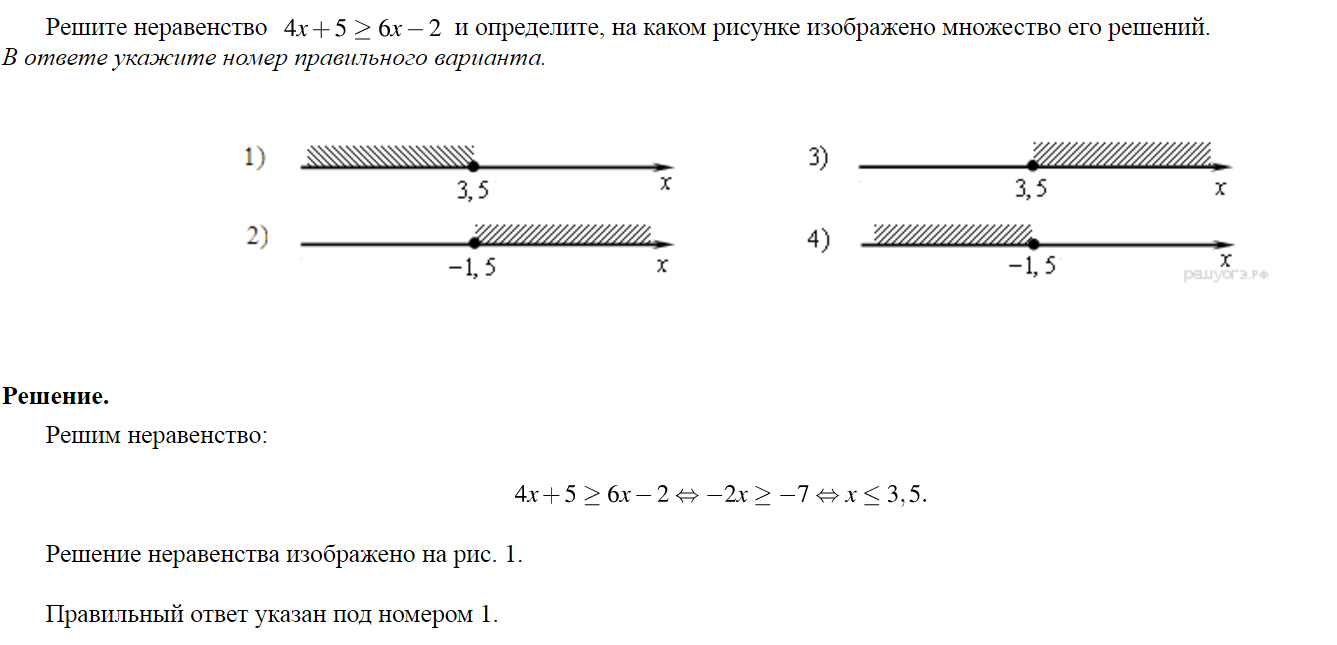
Решить систему уравнений – это значит найти все ее решения или установить, что их нет.
Способы решения систем уравнений: способ подстановки и способ сложения.
Пример 3.
Решите систему способом подстановки
Для этого необходимо:
1.Выразить одну переменную через другую из какого-либо уравнения.
2.Подставить полученное выражение вместо выраженной переменной в другое уравнение.
3.Решить полученное уравнение относительно одной переменной.
4.Найти значение другой переменной, подставив найденный корень в формулу пункта 1.
5.Записать решение системы.
y=6x-4,
3x+5(6x-4)=13,
3x+30x-20=13,
33x=33,
x=1.
y=6∙1-4=2
(1;2) – решение системы
Ответ: (1;2)
Пример 4.
Решите систему способом сложения
Для этого необходимо:
1.Домножить какое-либо уравнение системы или оба уравнения на такие числа, чтобы при почленном сложении уравнений получить уравнение относительно одной переменной.
2.Решить уравнение, полученное после почленного сложения.
3.Подставить найденный корень в какое-либо уравнение исходной системы.
4.Решить составленное уравнение.
5.Записать решение системы.
23x=69,
x=3,
2∙3+3y=3,
y=-1.
(3;-1) – решение системы
Ответ:(3;-1)
Решение системы двух линейных уравнений с двумя неизвестными
Если , то система имеет единственное решение.
Если то система не имеет решений.
Если , то система имеет бесконечно много решений.
Система линейных уравнений с параметром
Пример 5.
Решите систему уравнений с параметром a:
Решение:
Решим систему способом подстановки. Выразим y из первого уравнения системы: . Подставим выражение вместо y во второе уравнение системы:
(a-3)x+a((a+1)x-a)=-9 .
Решим полученное уравнение относительно x:
.
1. Если , то есть , то система имеет единственное решение. Найдем это решение: После сокращения получаем: . Найдем соответствующее значение y, подставив вместо x в формулу
Найдем соответствующее значение y, подставив вместо x в формулу
. Получим . Итак, если , то – решение системы.
2. Если и , то есть a=-3, то система имеет бесконечно много решений. Найдем в этом случае решения системы. Для этого подставим a=-3 в первое уравнение системы. Получим уравнение -2x-y=-3, из которого выразим y: y=3-2x. Значит, (x;3-2x), где x – любое число, — решения системы.
3. Если и , то есть a=1, то система не имеет решений.
Ответ: Если , то – решение системы;
если a=-3, то (x;3-2x), где x – любое число, — решения системы;
если a=1, то система не имеет решений.
4.Решение линейных неравенств с одним неизвестным
Определение
Неравенство первой степени с одним неизвестными – это неравенство вида ax<b / ax>b / ax≤b / ax ≥b, где a и b – заданные числа, x – неизвестное.
Определение
Решение неравенства с одним неизвестным – это то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти все его решения или установить, что их нет.
Правило решения неравенства первой степени с одним неизвестным
1.Перенести с противоположными знаками члены, содержащие неизвестное, из правой части в левую, а не содержащие неизвестное – из левой части в правую.
2.Привести подобные члены в левой и правой частях неравенства.
3.Если коэффициент при неизвестном отличен от нуля, то разделить на него обе части неравенства.
5.Системы линейных неравенств с одним неизвестным
Решение системы неравенств с одним неизвестным – это значение неизвестного, при котором все неравенства системы обращаются в верные числовые неравенства.
Пример 6.
Решить неравенство 2x-8<5,2x-1,6.
Решение:
2x-8<5,2x-1,6,
2x-5,2x<-1,6+8,
-3,2x<-9,6,
x>3.
Ответ: x>3
Решение неравенства ax<b
Если a>0, то
Если a<0, то
Если a=0, b>0, то x – любое число
Если a=0, b≤0, то решений нет
Линейное неравенство с параметром
Пример 7.
Решите неравенство с параметром a:
a(2x-1)<ax+5
Решение:
2ax-a<ax+5,
ax<5+a.
Если a>0, то
Если a<0, то
Если a=0, то 0∙x<5 верно для любого x, так как 0<5. В этом случае решением неравенства является любое число x.
Ответ: Если a>0, то ; если a<0, то ; если a=0, то x – любое число.
Решить систему неравенств – это значит найти все решения системы или установить, что их нет.
Пример 8.
Решить систему неравенств
Решим первое неравенство системы:
2x-6>0, 2x>6, x>3.
Решим второе неравенство системы:
4x-20<0, 4x<20, x<5.
Отметим найденные решения неравенств на координатной прямой.
Оба неравенства системы верны при 3<x<5.
Пример 9.
Решите неравенство |3-2x|<7.
Данное неравенство означает то же что и двойное неравенство
-7<3-2x<7.
Вычтем 3 из каждой части двойного неравенства, получим
-10<-2x<4, откуда делением на -2 каждой части неравенства найдем
-2<x<5.
Глоссарий по теме:
Линейное уравнение с одним неизвестным – это уравнение вида ax=b, где a и b – заданные числа, x – неизвестное.
Неравенство первой степени с одним неизвестными – это неравенство вида ax<b / ax>b / ax≤b / ax ≥b, где a и b – заданные числа, x – неизвестное.
Система двух уравнений первой степени с двумя неизвестными – это система вида
где x и y – неизвестные,
– заданные числа,
причем и .
2 x 4 решите неравенство
Вы искали 2 x 4 решите неравенство? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 x 2 решите неравенство, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 x 4 решите неравенство».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 2 x 4 решите неравенство,4 x 2 решите неравенство,4 x 2 решить неравенство,4 решите неравенство,x 2 4 решите неравенство,x2 3x 4 больше или равно 0,решите неравенство 2 x 4,решите неравенство 2 x 4x 0,решите неравенство 3 x 4,решите неравенство 4,решите неравенство 4 3 x,решите неравенство 4 x 2,решите неравенство x 2 4,решите неравенство x 2 4x 0,решите неравенство x 4 3,решите неравенство х 2 х 4,решите неравенство х 2 х 4 0. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 2 x 4 решите неравенство. Просто введите задачу в окошко и нажмите «решить» здесь (например, 4 x 2 решить неравенство).
Где можно решить любую задачу по математике, а так же 2 x 4 решите неравенство Онлайн?
Решить задачу 2 x 4 решите неравенство вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
правила и примеры (7 класс)
Основная функция скобок – менять порядок действий при вычислениях значений числовых выражений. Например, в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).
Однако если мы имеем дело с алгебраическим выражением, содержащим переменную — например таким: \(2(x-3)\) – то вычислить значение в скобке не получается, мешает переменная. Поэтому в таком случае скобки «раскрывают», используя для этого соответствующие правила.
Правила раскрытия скобок
Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря:
\((a-b)=a-b\)
Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.
Пример. Раскройте скобку \((1+y-7x)\).
Решение: \((1+y-7x)=1+y-7x\).
Пример. Упростите выражение: \(3+(5-2x)\).
Решение: Раскрываем скобку согласно правилу, а затем приводим подобные слагаемые:
Пример. Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).
Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).
Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:
\(-(a-b)=-a+b\)
Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.
Пример: Упростите выражение \(2x-(-7+x)\).
Решение: внутри скобки два слагаемых: \(-7\) и \(x\), а перед скобкой минус. Значит, знаки поменяются – и семерка теперь будет с плюсом, а икс – с минусом. Раскрываем скобку и приводим подобные слагаемые.
Пример. Раскройте скобку: \(-(4m+3)\).
Решение: \(-(4m+3)=-4m-3\).
Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).
Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть:
\(c(a-b)=ca-cb\)
Пример. Раскройте скобки \(5(3-x)\).
Решение: В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.
Пример. Раскройте скобки \(-2(-3x+5)\).
Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).
Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).
Осталось рассмотреть последнюю ситуацию.
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)
Пример. Раскройте скобки \((2-x)(3x-1)\).
Решение: У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.
Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:
Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…
— потом второе.
Шаг 3. Теперь перемножаем и приводим подобные слагаемые:
Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.
Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\). Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\). А если подставить минус единицу, получим правило \(-(a-b)=-a+b\). Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Скобка в скобке
Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).
Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.
Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:
|
\(7x+2(5\)\(-(3x+y)\)\()=\) |
Выполнять задание начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относиться – это сама скобка и минус перед ней (выделено зеленым). Всё остальное (не выделенное) переписываем также как было. |
|
| \(=7x+2(5\)\(-3x-y\)\()=\) |
Теперь раскрываем вторую скобку, внешнюю. |
|
| \(=7x+2·5-2·3x-2·y=\) |
Упрощаем получившееся выражение… |
|
|
\(=7x+10-6x-2y=\) |
…и приводим подобные. |
|
|
\(=x+10-2y\) |
Готово. |
Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение:
|
\(-(x+3(2x-1\)\(+(x-5)\)\())\) |
Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается. |
|
|
\(-(x+3(2x-1\)\(+x-5\)\())\) |
Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке. |
|
|
\(=-(x\)\(+3(3x-6)\)\()=\) |
Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него. |
|
|
\(=-(x\)\(+9x-18\)\()=\) |
Вновь приводим подобные. |
|
|
\(=-(10x-18)=\) |
И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные. |
|
|
\(=-10x+18\) |
Готово. |
Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.
Смотрите также:
Вынесение общего множителя за скобки
Почему сочувствие не позволит вам разбогатеть?
Как среда влияет на формирование «богатых привычек»? Что вообще такое эти «богатые привычки»? Какие зажимы объясняет понятие «выученной беспомощности»? Почему люди с отсутствующей эмпатией видятся идеальными кандидатами на богатство? И отчего бедность имеет больше влияния на человеческий мозг, чем обеспеченность? Кстати, этот самый мозг далеко не полностью изучен, так что появляется площадка для споров. Мы пришли с большим списком вопросов к психологу, психотерапевту, гештальттерапевту Владлену Писареву. Получился суровый разговор про жадность, скупость, неравный обмен, обман и антирекламу роскоши.
«Не богатство меняет мозг, а бедность»Любимый вопрос: от чего конкретно зависит богатство. С этим рождаются или этому учатся? Почему одни могут, а другие — не очень?
— Есть простой пример, который я увидел в школе, — говорит Писарев. — Берем луковицу растения, разрезаем пополам. Одну половинку сажаем на равнине, другую — в горах. Одно и то же растение, казалось бы, но с течением времени разница бросается в глаза. Выросло-то и там и там. Но в итоге одно растение значительно меньше другого.
Это про соотношение генотипа и фенотипа. Что влияет больше: среда или гены? Полностью на нас, понятно, это переносить нельзя, некорректно. И есть исследования, которые утверждают, что мозг человека из богатой семьи отличается от мозга человека, родившегося в бедной. Ученые обнаружили увеличение площади неокортекса, то есть коры больших полушарий, у детей богатых родителей по сравнению с отпрысками бедных. Это та часть мозга, которой мы думаем.
— Однозначно утверждать, что богатые рождают богатых, а бедные — бедных, мы не можем
Обнаруженную разницу легко можно объяснить питанием и образом жизни групп с разными доходами. То есть не богатство само по себе меняет мозг, а бедность, ограничение в средствах. Если мать ест плохо, мозг ее ребенка не получает необходимого количества питательных веществ для роста и развития. Причем данный процесс особенно важен на ранних этапах, когда беременность даже незаметна.
— Это о привычном питании. И речь не только про него, но и про образ жизни, употребление алкоголя, курение, физические тренировки, доступность качественной медицинской помощи и другое. Некоторые исследования все это доказывают. Но их мало. Надо проводить больше, больше, еще больше, чтобы увеличивать выборку. А также изучать проблему в различных регионах. Однозначно утверждать, что богатые рождают богатых, а бедные — бедных, мы не можем, — отмечает психолог.
«Попасть из бедности в богатство очень сложно»Теперь о среде. Ее влияние очень важно. Среда нас формирует, мы обучаемся жить в наличных условиях, вырабатываем определенный способ существования, поведение, привычки, которые после влияют на нас же.
— «Ты съешь сегодня, а я завтра» — это про известные исследования, которые проводили на детях со сладостями. Ребята из бедных семей съедают сладкое сразу, а из богатых могут откладывать их и съедать потом. Когда человек вырастает, то делает то же самое, только не со сладостями уже, а, например, с деньгами. Одним откладывать и инвестировать сложно, а другие к этому привычны с детства.
Мы можем много говорить о средовом влиянии. Но есть важный момент: люди из богатой среды имеют доступ к более качественному и дорогостоящему образованию. Замкнутый круг. Люди, которые получили хорошее образование в дорогих, престижных учебных заведениях, сразу имеют хороший старт в жизни, что после позволяет им дать такое же образование собственным детям. Отпрыски бедных родителей доступом к подобной роскоши не обеспечены, — говорит Писарев.
— Мы долго-долго меняемся, и если посмотрим на результат этого обмена, то увидим, что у кого-то на руках 200 миллиардов долларов, а у кого-то ипотека
Истории вроде той, которую рассказывает фильм «Миллионер из трущоб», скорее исключение. Понятно, такие случаи бывают, но это не норма, не закон, не правило. Удача в большей степени. Жизнь показывает, что попасть из бедности в богатство очень сложно.
— О том, как работают социальные лифты, хорошо рассказывает фильм «Хороший, плохой, злой». Один из героев, который рос в бедности, сказал что-то вроде «выбора не так-то и много». Раз — ты живешь в нищете, с трудом зарабатываешь на пропитание, каторжно работая. Два — ты выбираешь, кем стать: священником или бандитом.
«Богатство одних построено на бедности других»Также стоит поговорить о «членстве в клубе». Возьмем исследование, которое проводили во Флоренции. Ученые изучили данные местных налогоплательщиков примерно за 600 лет. Результаты удивили. Среди наиболее состоятельных налогоплательщиков 15-го и 21-го веков совпадают почти 900 фамилий. Понятно, есть однофамильцы, а некоторые люди попали туда совершенно случайно, но большая часть — родственники. Получается, что по роду занятий, доходам и состоянию нынешних флорентийцев можно достаточно точно предсказать род занятий, доходы и состояние их далеких предков, и наоборот. Эти люди образуют какую-то общность, клуб, в котором связи и деньги дают людям особое положение.
— Эта ситуация не возникла в современном мире. Мы так живем, мы — такие. Речь снова про биологию поведения. Люди склонны к парохиализму, как и другие животные. Мы социальны, поэтому постоянно объединяемся в группы. Есть свои, есть чужие. Это про окситоциновый или парохиальный альтруизм. Альтруизм у людей изначально был направлен только на членов своей группы и развивался в едином комплексе с враждебностью к чужакам. При острой межгрупповой вражде помощь своим и агрессия по отношению к чужим в равной мере идут на пользу отдельно взятому сообществу.
Есть в этой теме вещи, которые во многом затрагивают моральные аспекты, поэтому говорить о них сложно, но придется, — объясняет специалист. — Можно спорить, но в основе богатства лежит неравенство. Богатство одних построено на бедности других.
Все, что создано человеком, стало возможным благодаря обмену. Наша цивилизация построена на нем. Разделение труда — один делает табуретку, другой стулья, потом мы меняемся. Без взаимодействия, в одиночку человек не может создать что-то, что мы сейчас можем оценивать в миллиарды, элементарно своим трудом. Мы долго-долго меняемся, и если посмотрим на результат этого обмена, то увидим, что у кого-то на руках 200 миллиардов долларов, а у кого-то ипотека. Как так вышло? Может, это не про обмен? Может, просто кто-то много работает, а кто-то мало? То есть существуют работяги и лентяи. И работяга просто создал что-то на миллиарды, а лентяи закономерно бедные. Вы в это верите?
— Бедные не любят богатых. Но и богатые не любят бедных. Я не могу сказать, хорошо это или плохо
Логично задать вопрос: как стать богаче в ходе обмена? Для этого нужно в процессе обмена получить больше, чем другой. Это про выгодный обмен, неравный обмен.
— Получается, в процессе обмена кто-то захотел получить больше. По сути, это про обман. Обман выгоден, только если не раскрыт. Поэтому свои намерения нужно как-то правильно объяснить, обосновать, сделать законными. Если удастся создать и обосновать систему, в которой узаконивается неравный обмен, рисуется путь к обретению богатства. Сам феномен богатства возможен только при таких условиях.
«Неравный обмен привел к расслоению общества»— Все то — результат далеко не последних 50 или 100 лет, — рассуждает психолог. — Система складывалась постепенно в ходе развития человечества. Это давно так. Европейцы пришли в Америку и выменивали землю у индейцев на алкоголь и одеяла. Во времена первобытного коммунизма не было никакого неравенства. Благополучие племени в целом и каждого отдельного его участника связывались напрямую. Если кому-то достанется больше, остальные ослабнут — группа умрет. Это время более-менее равного распределения ресурсов. Потеря любого члена группы составляло риск для группы.
Однако по мере роста производительности труда у людей появился избыток. И как только это произошло, возникла возможность для неравного обмена. Он привел к расслоению общества. Часть населения теперь могла лучше питаться и одеваться, иметь лучшие орудия труда. Соответственно, их дети росли в более благоприятных условиях. Об этом говорилось выше. Лучшие условия для детей и другая среда.
Выходит, кто-то в этой жизни хитрее. И этот процесс формирует недовольство, которое выражается в нелюбви к богатым.
— Да, это так, бедные не любят богатых. Но и богатые не любят бедных. Я не могу сказать, хорошо это или плохо. Это не люди такие плохие. Просто так повелось: мы, сапиенсы, как и другие социальные животные, склонны к парохиализму. Бедные завидуют богатым и чувствуют какой-то обман. Неравный обмен кажется несправедливым и не нравится большинству. Снизить уровень социальной напряженности можно разными способами. Например, отвлечь людей чем-то, дать им другие причины для недовольства.
— Путь к богатству — это наличие огромной жадности и достаточной скупости
— Представьте, мы нашли врагов, внутренних или внешних, начали войну, у нас случилась эпидемия, есть проблема полового неравенства и так далее. Можно убрать знание о неравенстве. Это сейчас широко практикуется, многие богатые ведут себя достаточно скромно. Люди не знают о доходах друг друга, корпоративная тайна и так далее. Но это не разрешает проблему, а скорее отодвигает ее. Решить проблему можно только устранив неравенство, убрав эту пропасть между бедными и богатыми.
Чем меньше расслоение в обществе, тем меньше уровень социального напряжения.
«Умелое сочетание жадности и скупости рождает богатство»— Исходя из всего вышесказанного, если человек хочет стать богатым, ему нужно усвоить правила неравного обмена и приобрести или развить те качества, которые позволят иметь больше. В первую очередь это про жадность. Про основную потребность, которая движет личностью. Вся психология богатства сформирована желанием иметь больше. Откуда берется жадность? Отчасти это задано генами, отчасти формируется средой. Это связано с уровнем доминирования. Доминирующая особь всегда будет хотеть больше.
Богатство можно сформулировать как умелое сочетание жадности и скупости.
— Жадность — это желание получить больше, больше и больше. Но одной жадности мало. Если человек хочет получить много, но не может этого удержать, то он похож на трубу одного диаметра. В ней ничего не задерживается. Нужна скупость. Скупость — нежелание потерять. Если у человека очень много скупости и нет жадности — это путь в бедность. Если много жадности и недостаточно скупости, сколько бы человек ни получил, все потеряет.
— Богатство — не зона сантиментов. По сути, люди с дисоциальным расстройством личности — идеальные претенденты на него
— Путь к богатству — это наличие огромной жадности и достаточной скупости. Это как широкая труба на входе и узкая на выходе. Чем больше она на входе и чем меньше на выходе, тем больше останется. Все привычки богатых, которые они формируют в среде и которые не формируются у бедных, призваны стимулировать жадность и удерживать на достаточном уровне скупость.
«Я боюсь рекламировать богатство»Если говорить о так называемой психологии бедности, которая сейчас широко обсуждается, это про низкий уровень доминирования, когда личность не имеет высоких запросов.
— Это про сочувствие и эмпатию к другим. Ведь богатство одних формируется на бедности других. И если человек проявляет сочувствие, то не может делать других беднее. Это про выученный с детства опыт, мол, что бы ты ни сделал, все равно ничего не получится. Отсюда понятие выученной беспомощности. Она легко формируется в среде, в которой растет человек. Постоянно сообщает ему об отсутствии возможности. Человек в итоге просто отказывается что-либо делать, потому что какой смысл? Позитивный опыт отсутствует.
Богатый же человек с детства научен видеть во всем возможности, он вырос в среде, где нормально иметь больше, и у него с ранних лет формируется «правильное» поведение для этого.
— Еще один важный момент. Это то, что меня пугает. Получается, что в жесткой конкуренции за богатство преимущество получают самые жадные, самые агрессивные. Те люди, для которых прибыль важнее всего. Богатство не зона сантиментов. По сути, люди с дисоциальным расстройством личности — идеальные претенденты на него. Это люди, которые не имеют сочувствия, не испытывают страха, а других воспринимают как средство достижения собственных целей. При наличии высокого интеллекта подобные персонажи имеют преимущества в этой конкуренции.
— Было бы классно, чтобы люди стремились не к обладанию богатством и не ставили целью ограничивать этот процесс исключительно собой
— Я боюсь «рекламы» богатства. Я не хочу жить в мире, в котором все хотят быть богатыми. Подумайте, что будет, если все вдруг станут суперобеспеченными? Когда к этому начнет стремиться каждый и преуспеет, богатые вовсе исчезнут. Совсем. Всем быть богатыми невозможно. Потому что настанет равенство. Не будет ни бедных, ни богатых.
Но очень важно, чтобы это равенство находилось не внизу шкалы потребления. Это не про то, чтобы у всех ничего не было. Ситуация идеального равенства невозможна. Люди изначально обладают неравными возможностями. Один хочет больше и готов много делать для достижения этого, а другой — нет. Хорошо, чтобы мы все стремились к хорошей жизни для себя и других. Мне нравится идея жить хорошо самому и давать жить хорошо другим.
Было бы классно, если бы люди стремились не к обладанию богатством и не ставили целью ограничивать этот процесс исключительно собой. Мне больше нравится история про достойную и обеспеченную комфортную жизнь для всех без переборов.
Владлен Писарев — психотерапевт, психолог, гештальттерапевт. Врач по образованию. Карьеру в медицине начинал, работая фельдшером. В 1991 году окончил медучилище. На последних курсах трудился в скорой помощи санитаром. В том же 1991-м стал студентом Гомельского мединститута.
В 2002-м прошел специализацию по психотерапии на базе БелМАПО. С конца 2002 года начал работать психотерапевтом в наркологии. Учился эриксоновскому гипнозу, НЛП (нейролингвистическому программированию) и гештальттерапии. Окончил Московский гештальтинститут.
Как гештальттерапевт работал индивидуально, вел группы, занимался семейным консультированием, руководил обучающей программой по гештальттерапии I ступени.
«Кошелек» в Telegram: только деньги и ничего лишнего. Присоединяйтесь!
Есть о чем рассказать? Пишите в наш телеграм-бот. Это анонимно и быстро
Перепечатка текста и фотографий Onliner без разрешения редакции запрещена. [email protected]
Сложные неравенства — объяснение и примеры
Сложные неравенства — это производная форма неравенств, которые очень полезны в математике при работе с диапазоном возможных значений.
Например, после решения определенного линейного неравенства вы получаете два решения, x> 3 и x <12. Вы можете прочитать это как «3 меньше x, что меньше 12. Теперь вы можете переписать его в форма 3 Давайте теперь посмотрим, что такое сложное неравенство. Есть и другие случаи, когда вы можете использовать неравенство для представления более чем одного ограничивающего значения. В таких ситуациях применяется сложное неравенство. Следовательно, мы можем определить составное неравенство как выражение, содержащее два утверждения неравенства, соединенные словами « И » или « ИЛИ. ” Конъюнкция « и » указывает, что два утверждения верны одновременно. С другой стороны, слово « или » подразумевает, что все составное утверждение истинно, пока истинно одно из утверждений. Термин «Или» используется для обозначения комбинации наборов решений для отдельных операторов. Пример 1 Решите относительно x: 3 x + 2 <14 и 2 x - 5> –11. Решение Чтобы решить это составное неравенство, мы начнем с решения каждого уравнения отдельно. А поскольку соединяющим словом является «и», то это означает, что желаемое решение является перекрытием или пересечением. 3x + 2 <14 Вычтите 2 и разделите на 3 с обеих сторон уравнения. 3x + 2–2 <14–2 3x / 3 <12/3 х <4 А; 2x - 5> -11 Добавьте 5 к обеим сторонам и разделите все на 2 2x — 5 + 5> -11 + 5 2x> -6 х> -3 Неравенство x <4 указывает все числа слева от 4, а x> –3 указывает все числа справа от –3.Следовательно, пересечение этих двух неравенств включает все числа от –3 до 4. Решение этих сложных неравенств, следовательно, x> –3 и x <4 Пример 2 Решить 2 + x <5 и -1 <2 + x Решение Решите каждое неравенство отдельно. 2 + x <5 Чтобы изолировать переменную от первого уравнения, нам нужно вычесть обе части на 2, что дает; х <3. Мы снова вычитаем 2 из обеих частей второго уравнения -1 <2 + x. -3 <х. Следовательно, решение для этого составного неравенства: x <3 и -3 Пример 3 Решить 7> 2x + 5 или 7 <5x - 3. Решение Решите каждое неравенство отдельно: Для 7> 2x + 5 мы вычитаем обе части на 5, чтобы получить; 2> 2x. Теперь разделите обе стороны на 2, чтобы получить; 1> х. Для 7 <5x - 3 сложите обе стороны на 3, чтобы получить; 10 <5x. Если разделить каждую сторону на 5, получим; 2 <х. Решение: x <1 или x> 2 Пример 4 Решите 3 (2x + 5) ≤18 и 2 (x − 7) <- 6 Решение Решите каждое неравенство отдельно 3 (2x + 5) ≤ 18 => 6x + 15 ≤ 18 6x ≤ 3 х ≤ ½ и 2 (x − 7) <- 6 => 2x −14 <−6 2x <8 х <4 Следовательно, решение x ≤ ½ и x <4 Пример 5 Решить: 5 + x> 7 или x — 3 <5 Решение Решите каждое неравенство отдельно и объедините решения. Для 5 + x> 7; Вычтем обе части на 5, чтобы получить; х> 2 Решить x — 3 <5; Добавьте 3 к обеим сторонам неравенства, чтобы получить; x <2 Объединение двух решений со словом «или» дает; X> 2 или x <2 Пример 6 Решите относительно x: –12 ≤ 2 x + 6 ≤ 8. Решение Когда составное слово написано без соединительного слова, предполагается, что оно будет «и».”Следовательно, мы можем перевести x — 12 ≤ 2 x + 6 ≤ 8 в следующее составное предложение: –12 ≤ 2 x + 6 и 2 x + 6 ≤ 8. Теперь мы можем решить каждое неравенство отдельно. Для –12 ≤ 2 x + 6; => –18 ≤ 2 x –9 ≤ x А для 2 х + 6 ≤ 8; => 2 х ≤ 2 Неравенство –9 ≤ x означает, что все числа справа от –9, включая –9, и находятся в пределах решения, а x ≤ 1 означает, что все числа слева и включая 1 находятся в пределах решения.Поэтому решение этого составного неравенства можно записать как {x | x ≥ –9 и x ≤ 1} или {x | –9 ≤ x ≤ 1} Пример 7 Решите относительно x: 3x — 2> –8 или 2 x + 1 <9. Решение Для 3x — 2> –8; => 3x — 2 + 2> –8 + 2 => 3x> — 6 => х> — 2 Для 2 x + 1 <9; Вычтем 1 из обеих частей уравнения; => 2 х <8.=> x <4. Неравенство x> –2 означает, что решение верно для всех чисел справа от –2, а x <4 означает, что решение верно для всех чисел слева от 4. Решение записывается как; {x | x <4 или x > — 2} 1.Если у нас есть неравенство <(меньше чем) или> (больше чем), мы должны использовать пустой / незаполненный круг. 2. Если у нас есть знак неравенства ≤ (меньше или равно) или ≥ (больше или равно), мы должны использовать закрашенный кружок. Пример 1: Решите следующее линейное неравенство и график. 2x — 4 ≤ 0 Решение: 2x — 4 ≤ 0 Добавить 4 с обеих сторон 2x — 4 + 4 ≤ 0 + 4 ≤ 4 Разделить на 2 с обеих сторон 2x / 2 ≤ 4/2 x ≤ 2 Таким образом, любое действительное число меньше или равно to 2 является решением данного уравнения. Набор решений данного неравенства равен (-∞, 2]. Пример 2: Решите следующее линейное неравенство и график: -3x + 12 <0 Решение: — 3x + 12 <0 Вычесть 12 с обеих сторон -3x + 12-12 <0-12 -3x <-12 Разделить на -4 с обеих сторон -3x / (- 3) <-12 / (- 3) x <4 Итак, любое действительное число меньше 4 является решением данного уравнения. Набор решений данного неравенства равен (-∞, 2]. Пример 3: Решите следующее линейное неравенство и график: 4x — 12 ≥ 0 Решение: 4x — 12 ≥ 0 Добавить 12 с обеих сторон 4x — 12 + 12 ≥ 0 + 12 4x ≥ 12 Разделить на 4 с обеих сторон 4x / 4 ≥ 12/4 x ≥ 3 Итак, любое действительное число, большее или равное 3, является решением данного уравнения. Множество решений данного неравенства [3, ∞). Пример 4: Решите следующее линейное неравенство и график. 7x + 9> 30 Решение: 7x + 9> 30 Вычесть 9 с обеих сторон 7x + 9-9> 30-9 7x> 21 Разделить на 7 с обеих сторон 7x / 7> 21/7 x> 3 Итак, любое действительное число больше 3 является решением данного уравнения. Множество решений данного неравенства — (3, ∞). Пример 5: Решите следующее линейное неравенство и график. 5x — 3 <3x + 1 Решение: 5x — 3 <3x + 1 Вычесть 3x с обеих сторон 5x — 3 — 3x <3x + 1 - 3x 9000 2x — 3 <1 Добавить 3 с обеих сторон 2x — 3 + 3 <1 + 3 Разделить на 2 с обеих сторон 2x / 2 <4/2 Итак, любое действительное число меньше 2 является решением данного уравнения. Множество решений данного неравенства — (2, ∞). Пример 6: Решите следующее линейное неравенство и график. 3x + 17 ≤ 2 (1 — x) Решение: 3x + 17 ≤ 2 (1 — x) 3x + 17 ≤ 2 — 2x Добавить 2x с обеих сторон 3x + 2x + 17 ≤ 2 — 2x + 2x 5x + 17 ≤ 2 Вычесть 17 с обеих сторон 5x + 17-17 ≤ 2-17 5x ≤ -15 Разделить на 5 с обеих сторон 5x / 5 ≤ -15/5 x ≤ -3 Итак, любое действительное число, меньшее или равное -3, является решением данного уравнения. Множество решений данного неравенства: (-∞, -3]. Пример 7: Решите следующее линейное неравенство и график: 2 (2x + 3) — 10 ≤ 6 (x — 2 ) Решение: 2 (2x + 3) — 10 ≤ 6 (x — 2) 4x + 6 — 10 ≤ 6 x — 12 4x — 4 ≤ 6 x — 12 Вычесть 6x с обеих сторон 4x — 4 — 6x ≤ 6 x — 12 — 6x -2x — 4 ≤ — 12 Добавьте 4 с обеих сторон -2x — 4 + 4 ≤ — 12 + 4 -2x ≤ — 8 Разделить на -2 с обеих сторон -2x / (-2) ≤ — 8 / (-2) x ≤ 4 Итак, любое действительное число, меньшее или равное 4, является решение данного уравнения. Множество решений данного неравенства: (-∞, 4]. Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам: Мы всегда ценим ваши отзывы. Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики. ЗАДАЧИ СО СЛОВАМИ Задачи со словами HCF и LCM Задачи со словами на простых уравнениях Задачи со словами на линейных уравнениях Задачи со словами на квадратных уравнениях Проблемы со словами в поездах Проблемы со словами по площади и периметру Проблемы со словами по прямой и обратной вариациям Проблемы со словами по цене за единицу Проблемы со словами по скорости единицы задачи по сравнению ставок Преобразование обычных единиц в текстовые задачи Преобразование в метрические единицы в словесных задачах Word задачи по простому проценту Word по сложным процентам ngles Проблемы с дополнительными и дополнительными углами в словах Проблемы со словами с двойными фактами Проблемы со словами тригонометрии Проблемы со словами в процентах Проблемы со словами для разметки и убытков 9292 Задачи со словами Задачи с десятичными словами Задачи со словами на дроби Задачи со словами на смешанные фракции Одношаговые задачи со словами с уравнениями Проблемы со словами с линейным неравенством Проблемы со временем и рабочими словами Задачи со словами на множествах и диаграммах Венна Задачи со словами на возрастах Проблемы со словами из теоремы Пифагора Процент числового слова проблемы Проблемы со словами при постоянной скорости Проблемы со словами при средней скорости Проблемы со словами на сумме углов треугольника 180 градусов ДРУГИЕ ТЕМЫ Сокращения прибыли и убытков Сокращения в процентах Сокращения в таблице времен Сокращения времени, скорости и расстояния Сокращения соотношения и пропорции Домен и диапазон рациональных функций 9292 функции с отверстиями График рациональных функций График рациональных функций с отверстиями Преобразование повторяющихся десятичных знаков в дроби Десятичное представление рациональных чисел видение Л.Метод CM для решения задач времени и работы Преобразование задач со словами в алгебраические выражения Остаток при делении 2 в степени 256 на 17 Остаток при делении степени 17 на 16 Сумма всех трехзначных чисел, делимых на 6 Сумма всех трехзначных чисел, делимых на 7 Сумма всех трехзначных чисел, делимых на 8 Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4 Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3 Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6 Обратитесь к каждому рисунку, запишите неравенство, относящееся к данной паре углов или размеров сегмента. 9. ∠ ____ ∠10. AH ____ ACHehe paanswer наман по 2. Находится ли баскетбольная площадка на одинаковом расстоянии от поликлиники и столовой? 2. находится баскетбольная площадка на одинаковом расстоянии от поликлиники и столовой Нормативные акты, кодифицирующие обязанности работодателей по предоставлению сотрудникам информации об опасностях, связанных с химическими веществами на рабочем месте, и обеспечению того, чтобы они
… Поймите, что означает эта информация Филиппинские писатели во время американской колонизации женщины филиппины А.Учитывая набор A = {1,2,3}, B = {0,1,2,3,4}, C = {1,3,5,8}, D = {5,10,15}
Находить:
1. АУБ нижний квартиль — это значение, которое находится между наименьшим значением и средним значением. б. Почему в случае квадрата или прямоугольника длина выражения обычно используется вместо основания и ширины вместо высоты. pwede po paayos ng s
… Agot need ko talaga po na ngayon eh … 2. Находится ли баскетбольная площадка на одинаковом расстоянии от поликлиники и столовой Указания: внимательно прочтите каждый пункт.Выберите букву правильного ответа среди csubscribe1. Расположение множества объектов в порядке im
… Портант называется _____? A. Комбинации B. Перестановки C. Арифметическая последовательность D. Геометрическая подписка 2. Какая из следующих ситуаций НЕ показывает перестановку? Судьи выбирают 3 победителя из 15 конкурсантов вокального конкурса. Выбор работы по дому после завтрака. Избрание председателя, заместителя председателя и секретаря из 10 членов комитета D. Размещение 3 пар пар за круглым столом с 8 стульями.3. Что из следующего иллюстрирует комбинацию? Выбор 5 из 5 конфет в миске B. Определение трех лучших победителей в школьной викторине по математике Пчелка C. Назначение трех учеников для участия в тренинге SSG по лидерству. D. Выбор лучшего актера и лучшего актера второго плана из 10 номинантов для школьной пьесы 4. Выбор набора объектов, порядок которых НЕ важен, называется __________? Комбинации B. Перестановки C. арифметическая последовательность D. геометрическая 5. Что из следующего показывает комбинацию из 5, взятых по 2 за раз?C (5,2) B. C (5,5) C. P (2,5) D. P (2,2) 6. Что такое C (8, 5)? A. 56 B. 336 C. 1400 D. 6720 7. Какими способами Ана может выбрать 3 цвета из 5? 2 B. 10 C. 8 D. 608. Какими способами Эбби может выбрать лопатку для мороженого с 3 вкусами, если есть 6 доступных вкусов? 20 B. 40 C. 120 D. 7209. Сколько возможных комбинаций можно сделать из буквы A, B, C, если повторение не допускается? A. 1 B. 2 C. 3 D. 610. Какая комбинация из 4 объектов, взятых по 2 за раз? 4 B. 6 C. 12 D. 2411. Какая из следующих ситуаций требует перестановки?Какими способами можно выбрать пять игроков для команды из семи игроков? B. Какими способами можно выбрать три картины для показа из коллекции, состоящей из 10 произведений искусства? Каким образом пять машин могут выстроиться в очередь в гонке? D. Какими способами можно выбрать три книги из 9 разных книг для чтения на досуге? 12. Команде из 13 волейболистов необходимо выбрать капитана и второго капитана. Примером проблем, связанных с? A. Перестановка B. Комбинация C. Арифметическая последовательность D. Геометрическая последовательность 13.Какие из следующих ситуаций или действий предполагают перестановку? Соответствие рубашки и брюк B. Формирование различных треугольников из 5 точек на плоскости, три из которых не лежат на одной прямой. C. Назначение телефонных номеров для подписки D. Формирование комитета из членов клуба 14. Какими способами вы можете выбрать 6 мячей из 12 мячей? 4700 Б. 720С. 924D. 66528015. Сколько комитетов по 4 человека можно выбрать из 10 человек? 5040 B. 120 C. 240 D. 21016. Г-н Себастьян хочет купить четыре разных вида напитков: апельсиновый сок (O), яблочный сок (A), кола (C), чай с лимоном (L) и молочная команда (M). ), сколько возможных комбинаций напитков, что Mr.Себастьян можно купить? A. 5 B. 12 C. 24 D. 120 17. Какими способами можно определить 3-го, 2-го, 1-го и 1-го чемпиона в математической викторине. В пчелке приняли участие 15 участников.A. 1365 B. 1360 C. 32, 765 D. 32, 760 18. Ящик содержит 6 белых и 9 синих шариков. Сколько наборов из 3 шариков можно выбрать, по крайней мере, из 2 белых? 145 B. 150 C. 155 D. 16019. Ассоциация родителей и учителей состоит из 11 членов, в которую входят 7 родителей и 4 учителя. Подкомитет из 5 членов выбран для проведения ежегодного собрания.Какими способами можно сформировать подкомитет? 462 B.55, 440 C. 120 D. 55,000 Можете ли вы помочь мне? 1) v — 6 ≥ 4 +6 +6 v ≥ 10 График: 10 ————— — → точка 10 заполнена из-за символа «равно» ****************************************************************************************************************************************************************************************************************************************************************************** ************************************************ ********************************* 2) -5x <15 разделить на минус, чтобы символ перевернулся x> — 3 График: -3 o —————— → точка в -3 НЕ заполняется, потому что она НЕ «равна» ***** ************************************************ ************************************************ 3) 3k> 5k + 12 -5k -5k -2k> 12 делится на минус, поэтому символ перевернулся k <-6 График: ← ——- —— o -6 точка -6 НЕ заполняется, потому что она НЕ «равна» ******* ************************************************* ********************************************* 5 ) 2t ≤ 4 или 7t ≥ 49 или t ≤ 2 или t ≥ 7 График: ← ——- 2 7 ——— → точки на 2 и 7 заполняются в ************************************************************************************************************************************************************************************************************************************************************ ************************************************* *********** 6) | п + 2 | = 4 n + 2 = 4 или n + 2 = -4 -2-2-2-2 n = 2 или n = -6 n = {2, -6} ** ************************************************ ************************************************ ** 7) | 2x — 7 | > 1 2x — 7> 1 или 2x — 7 <-1 +7 +7 +7 +7 2x> 8 или 2x <6 или x> 4 или x <3 График : ← ———- o 3 4 o ———— → ******************* ************************************************ ********************************** 8) A = {1, 2, 3, 4, 5, 6, 7, 8, 9} B = {2, 4, 6, 8} AUB = {1, 2, 3, 4, 5, 6, 7, 8, 9} объединение объединяет оба набора A ∩ B = {2, 4, 6, 8} пересечение включает только те, которые находятся в ОБЕИХ наборах *********************** ************************************************ ****************************** 9) P = {1, 5, 7, 9, 13} R = {1, 2, 3, 4, 5, 6, 7} Q = {1, 3, 5} P ∩ R ∩ Q = {1, 5} P ∩ R = {7} игнорировать 1 и 5, так как они уже находятся в P∩Q∩R R ∩ Q = {3} игнорировать 1 и 5, поскольку они уже находятся в P∩Q∩R P ∩ Q = {} игнорировать 1 и 5, поскольку они уже находятся в P∩Q∩R P без пересечения = {9, 13) R без пересечения = {2, 4, 6} Q без пересечения = {} Если вы не можете понять, как его нарисовать на основе предоставленной мной информации, см. Прилагаемый диаграмма.Примечание. Обычно вы указываете только P, Q, R. Я обозначил перекрестки, чтобы вы поняли, почему эти конкретные числа помещены в определенные разделы. Существует много возможностей для ошибок с абсолютным неравенством, поэтому давайте рассмотрим эту тему медленно и попутно рассмотрим несколько полезных картинок.Когда мы закончим, я надеюсь, что у вас в голове будет хорошее представление о том, что происходит, и вы не сделаете некоторые из наиболее распространенных ошибок. Как только вы поймете, как работает это неравенство, это действительно не так уж и плохо. Давайте сначала вернемся к исходному определению абсолютного значения: «| x | — это расстояние x от нуля.»Например, и –2, и & плюс; 2 — это две единицы от нуля, как вы можете видеть на изображении ниже: Это означает, что их абсолютные значения будут равны 2; то есть имеем: | –2 | = | +2 | = 2 Имея в виду это определение и картинку, давайте рассмотрим некоторые неравенства по абсолютным значениям. Это неравенство. Если решением уравнения абсолютного значения являются точки (как на приведенном выше графике), то решением неравенства абсолютного значения (или «неравенства») будут интервалы. В этом неравенстве они просят меня найти все значения x , которые находятся менее чем на три единицы от нуля в любом направлении , поэтому решением будет набор всех точек, которые меньше чем на три единицы от нуля.Сначала я нарисую числовую линию: Глядя на неравенство, я вижу, что число 1 будет работать как решение, как и –1, потому что каждое из них меньше трех единиц от нуля. Число 2 будет работать, как и –2. Но 4 не будет работать, как и –4, потому что они слишком далеки от нуля. Даже 3 и –3 не будут работать (хотя они на грани), потому что это неравенство «меньше» (но не равно). Однако число 2,99 будет работать, как и –2,99. Другими словами, все точки между –3 и 3, но фактически не включая –3 или 3, будут работать как решения этого неравенства. Итак, графически решение выглядит так: (Открытые кружки на концах синей линии указывают «до этих точек, но не включая их». В вашей книге могут использоваться круглые скобки вместо кружков.) Переводя эту картинку в алгебраические символы, я получаю следующее решение: Этот шаблон для неравенства «меньше» по абсолютной величине всегда верен: Дано неравенство в виде | x | < a , решение всегда будет иметь вид — a < x < a . Между прочим, правильная конъюнкция для неравенства «меньше» по абсолютной величине — «и». Почему? Потому что переменная содержится в одном интервале. В приведенном выше примере x было одновременно «больше –3» и «меньше +3». x находится в интервале, который одновременно удовлетворяет обоим неравенствам. Итак, «и» — правильное соединение. Даже когда упражнения станут более сложными, вышеприведенная схема все равно будет действовать. Поскольку это неравенство «меньше чем» по абсолютному значению, мой первый шаг — очистить абсолютное значение в соответствии с шаблоном «меньше». Потом решу линейное неравенство. | 2 x + 3 | <6 –6 <2 x + 3 <6 Это образец для «меньше чем».Продолжая, я вычту 3 из всех трех «сторон» неравенства: –6 — 3 <2 x + 3 — 3 <6 - 3 –9 <2 x <3 –9/2 < x <3/2 Решение исходного неравенства по модулю, | 2 x + 3 | <6, это интервал: Другой случай неравенства абсолютных значений — это случай «больше чем». Сначала я начну с числовой строки. Решением данного неравенства будет набор всех точек, отстоящих от нуля более чем на две единицы. Например, –3 будет работать, как и +3; –4 будет работать, как и +4. Но –1 не сработает, равно как и +1, потому что они слишком близки к нулю.Даже –2 не будет работать, как и +2 (хотя они на грани), потому что это неравенство «больше» (но не равно). Однако +2.01 будет работать, как и –2.01. Другими словами, решением будет , две отдельные секции : одна секция будет содержать все точки больше двух единиц от нуля слева , а другая секция будет содержать все точки больше двух единиц от нуля до правый . Графически решение выглядит так: Переводя это графическое решение в символы, я получаю: Обратите внимание! Решением этого неравенства «больше чем» по модулю являются ДВА регулярных неравенства, а не одно.НЕ пытайтесь записать это как одно неравенство. Если вы попытаетесь записать это решение как «–2> x > 2», ваш ответ будет засчитан неверно. Почему? Потому что, если вы вытащите x посередине, вы увидите, что скажете «–2> 2», что определенно будет , а не правдой. Потратьте лишние полсекунды и напишите решение правильно. Этот шаблон для неравенства «больше чем» по абсолютной величине всегда верен: Учитывая неравенство | x | > a , решение всегда начинается с разделения неравенства на две части: x <- a или x > a . И, кстати, правильное союз — «или», а не «и». Почему? Потому что переменная не может находиться в обоих интервалах решения и в одно и то же время. В приведенном выше примере x не может одновременно быть «меньше –2» и «больше +2» . Поэтому мы используем «или» для таких решений. Филиал Даже когда неравенства усложняются, вышеупомянутая картина все еще сохраняется. Первое, что мне нужно сделать, это очистить полосы абсолютного значения, разделив неравенство на две части. Затем я решу два регулярных неравенства. | 2 x — 3 | > 5 2 x — 3 <–5 или 2 x — 3> 5 Это модель неравенства «больше чем» по абсолютной величине. 2 x <–2 или 2 x > 8 x <–1 или x > 4 Эта ПАРА неравенств является решением исходного неравенства по абсолютной величине. Есть еще одна ситуация, с которой вы можете столкнуться: вам будет дана пара неравенств, и вам будет предложено найти соответствующее неравенство по абсолютным значениям.Этот процесс может показаться немного странным, поэтому я приведу пару примеров того, как он работает. Чтобы понять это, я сначала смотрю на конечные точки. Минус два и плюс четыре — это шесть единиц. Половина шести — это три. Это говорит мне, что я хочу скорректировать это неравенство так, чтобы оно относилось к –3 и +3, а не к –2 и +4.Для этого я вижу, что могу отрегулировать значения на левом и правом концах, вычитая 1 из всех трех «сторон» неравенства: –2 < x <4 –2 — 1 < x — 1 <4 - 1 –3 < x — 1 <3 Поскольку последняя строка выше находится в формате «меньше чем» для неравенств абсолютных значений, мое неравенство решения будет иметь форму «абсолютное значение (чего-то) меньше 3».(Что-то) — это кусок посередине, где находится переменная. Итак, я могу преобразовать мою последнюю строку выше в следующее: То, что они дали мне, состоит из двух частей, соединенных знаком «или», поэтому я знаю, что это будет неравенство «больше, чем» по абсолютной величине. Для начала смотрю на конечные точки. Девятнадцать и 24 — это пять единиц. Половина из пяти — 2,5. Поэтому я хочу скорректировать неравенство, чтобы оно относилось к –2,5 и +2,5, а не к +19 и +24. Поскольку 19 — (–2,5) = 21,5 и 24 — 2,5 = 21,5, я вижу, что мне нужно вычесть всего 21,5: x ≤ 19 или x ≥ 24 x — 21,5 ≤ 19 — 21,5 или x — 21.5 ≥ 24 — 21,5 x — 21,5 ≤ –2,5 или x — 21,5 ≥ 2,5 Поскольку последняя строка выше — это формат «больше чем», неравенство абсолютных значений будет иметь форму «абсолютное значение (чего-то) больше или равно 2,5». (Что-то) будет частью с переменной в нем. Итак, я могу преобразовать мою последнюю строку выше в: Предупреждение: есть один вопрос типа «уловка» для такого рода задач, когда они попытаются сбить вас с толку при выполнении домашнего задания или тестов.Они попросят вас решить что-то вроде «| x + 2 | <–1». Но может ли абсолютное значение когда-либо быть отрицательным, не говоря уже о том, чтобы было меньше, чем отрицательным? Нет! Таким образом, это неравенство не имеет решения; это даже не имеет смысла. Не тратьте много времени на то, чтобы «решить» эту проблему; просто напишите «нет решения». Точно так же, если вам дано что-то вроде «| x — 2 |> –3», первое, что следует отметить, это то, что все абсолютные значения равны нулю или положительны.В частности, они никогда не отрицательные. Они просят вас ввести значения x , которые сделают выражение абсолютного значения больше отрицательного числа. Поскольку абсолютное значение всегда больше, чем любого отрицательного числа , решением должно быть «все x » или «все действительные числа». Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении абсолютных неравенств. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку и выберите «Решить для x», чтобы сравнить свой ответ с ответом Матвея. (Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.) URL: https://www.purplemath.com/modules/absineq.htm 1 2
Линейные неравенства по одной переменной 3
Неравенство с одной переменной в первой степени.например: 2x-3 <8 Решение - это значение переменной, которое делает неравенство истинным. x может равняться -3, 0, 1 и т. д. Линейные неравенства в одной переменной 4
Преобразования для неравенств Сложить / вычесть одно и то же число с каждой стороны неравенства (как с линейным уравнением) Умножить / разделить на одно и то же положительное число с каждой стороны неравенства Если вы умножаете или делите на отрицательное число, вы ДОЛЖНЫ перевернуть знак неравенства! 5
Пример: Решите неравенство 2x-3 <8 +3 +3 2x <11 2 2 x <5.5 Переверните знак при делении на -3! 6
Вспомните построение графика линейного равенства с одной переменной… .. x = 4 Обратите внимание, что круг замкнут 7
Построение графика линейного неравенства с одной переменной… .. x <4 Обратите внимание, что кружок открыт 8
Построение графика линейного неравенства с одной переменной….. x> -2 Обратите внимание, что круг открыт 9
Построение графика линейного неравенства с одной переменной… .. x <4 Обратите внимание, что круг замкнут 10
Построение графика линейного неравенства с одной переменной… .. x ≥ -2 Обратите внимание, что круг замкнут 11
Круг будет замкнутым или открытым? 1.) x = 6 2.) x> 0 3.) x <-3 4.) x> -1 5.) x <7 1.) закрыто 2.) открыто 3.) открыто 4.) закрыто 5.) закрыто 12
Решение линейного неравенства p + 5> 3 p + 5-5> 3-5 p> -2 Решите следующее линейное уравнение и проиллюстрируйте свой ответ графически. 13
Решение линейного неравенства 3x <9 3x / 3 <9/3 x <3 14
Решение линейного неравенства -x <4 -x / -1 <4 / -1 x> -4 Знак меняется при умножении или делении на отрицательное 15
Решение трехэтапного неравенства 2x — 4 <4x - 1 2x -4x - 4 <4x -4x - 1 -2x - 4 <- 1 -2x -4 + 4 <- 1 + 4 -2x <3 -2x / - 2 <3 / -2 16
2x — 4 <4x - 1 x> -3/2 17
Решение составного неравенства Чтобы решить составное неравенство, примените те же правила, что и раньше, но примените их к обеим сторонам неравенства: -3 <2x-1 ≤ 5 (добавьте 1 к обеим сторонам неравенства) -2 <2x ≤ 6-1 Содержание : Эта страница соответствует § 2.5 (стр. 216) текст. Предлагаемые задачи из текста: с. 225 # 11, 12, 13, 14, 16, 28, 33, 35, 38, 41, 53, 56, 62, 63, 68, 69 Неравенство — это сравнение выражений на «меньше чем» (<), «меньше или равно»
на "(<=)," больше "(>) или» больше или равно «(> =).Обратите внимание, что Html
не поддерживает стандартные символы «меньше или равно» и «больше или равно»,
поэтому мы используем <= и> = для этих отношений. Пример 1 . х + 3 <= 10 Решение для неравенства в x — это число, такое, что когда мы подставляем это число вместо x, мы имеем
верное заявление. Итак, 4 — это решение, например 1, а 8 — нет. набор решений неравенства:
набор всех решений.Обычно неравенство имеет бесконечно много решений, и множество решений легко
описывается с использованием обозначения интервалов. Набор решений в примере 1 — это набор всех x <= 7. В интервальной записи это набор (-inf, 7], где
мы используем inf для обозначения бесконечности. Линейное неравенство — это такое неравенство, что если бы мы заменили неравенство соотношением равенства, то мы имели бы
линейное уравнение.
Решение линейных неравенств очень похоже на решение линейных уравнений с одним важным отличием. Когда вы умножаете или делите обе стороны неравенства на отрицательное число, направление
неравенство обращено вспять. Вы можете увидеть это, используя неравенство без переменных. Пример 2 . 3 <7. Это ИСТИНА. (3) (- 2) <(7) (- 2). Это ЛОЖЬ, потому что -6 находится справа от -14 в числовой строке.Следовательно, -6> -14. (3) (- 2)> (7) (- 2). Это верно. Итак, когда мы умножаем исходное неравенство на -2, мы должны перевернуть
направление, чтобы получить еще одно верное утверждение. Примечание : Как правило, мы не можем умножать или делить обе стороны неравенства на выражение с переменной,
потому что некоторые значения переменной могут сделать выражение положительным, а некоторые — отрицательным. Пример 3 . 7 — 2x <3. -2x <-4. х> 2. Примечание : Когда мы разделили обе стороны неравенства на -2, мы изменили направление неравенства. Посмотрите на графики функций по обе стороны от неравенства. Для выполнения неравенства 7 — 2x должно быть меньше 3. Итак, мы ищем такие числа x, что точка
на графике y = 7 — 2x находится ниже точки на графике y = 3.Это верно для x> 2. В интервале
обозначение множество решений — (2, inf). Есть еще один способ использовать графическую утилиту для решения этого неравенства. В Java Grapher выражение
(7-2 * x) L3 имеет значение 1 для чисел x, удовлетворяющих неравенству, и значение 0 для других чисел
Икс. На рисунке ниже показан график (7-2 * x) L3, нарисованный Grapher. Упражнение 1: Решите неравенство 4 — x> 1 + 3x.Ответ Вернуться к содержанию Пример 4 . Найдите все числа x такие, что -3 <5 - 2x и 5 — 2x <9. -3 <5 - 2x -8 <-2x 4> x (-inf, 4) И 5 — 2x <9 -2x <4 x> -2 (-2, инф) Чтобы удовлетворить обоим неравенствам, число должно быть в обоих наборах решений.Итак, числа, удовлетворяющие обоим
неравенства — это значения на пересечении двух наборов решений, которые представляют собой набор (-2, 4) в интервале
обозначение. Приведенная выше задача обычно записывается как двойное неравенство . -3 <5 - 2x <9 означает -3 <5 - 2x и 5 — 2x <9. Примечание: Когда мы решили два неравенства по отдельности, шаги в двух задачах были
одно и тоже.Следовательно, для одновременного решения неравенств можно использовать обозначение двойного неравенства. -3 <5 - 2x <9. -8 <-2x <4. 4> х> -2. В терминах графиков эта задача соответствует нахождению таких значений x, что соответствующая точка на
график y = 5 — 2x находится между графиками y = -3 и y = 9. Пример 5 . Найдите все числа x такие, что x + 1 <0 или x + 1> 3. В примере 4 выше мы искали числа, удовлетворяющие обоим неравенствам. Здесь мы хотим найти числа
удовлетворяющие любому из неравенств. Это соответствует объединению наборов решений вместо пересечения. Не используйте в этой ситуации обозначение двойного неравенства. x <-1 (-inf, -1) x> 2 (2, инф) Набор решений — это объединение двух интервалов (-inf, -1) и (2, inf). Упражнение 2: (а) 1 <3 + 5x <7 Ответ (b) 2 — x <1 или 2 - x> 5 Ответ Вернуться к содержанию Неравенства, включающие абсолютные значения, можно переписать как комбинации неравенств. Пусть a будет положительным числом. Что такое сложное неравенство?
Как решить сложные неравенства?
Решение сложных неравенств зависит от того, используются ли слова «и» или «или» для связи отдельных утверждений.
Предыдущий урок | Главная страница | Следующий урок Неравенства в графике на числовой прямой
12.Каково значение x в неравенстве 2x — 4> 4? А.x
< 1B.x > 4C. х < 4 D. x > 8 Решите составное неравенство 2x -4 5
Абсолютные неравенства | Purplemath
Purplemath
MathHelp.com
Решить |
x | <3 и изобразите его решение. Решить | 2
x + 3 | <6. Решить |
x | > 2 и график. Решить | 2
x — 3 | > 5. Найдите утверждение о неравенстве абсолютного значения, которое соответствует –2
< x <4. Найдите утверждение о неравенстве абсолютного значения, которое соответствует неравенствам
x ≤ 19 или x ≥ 24 Линейные неравенства с одной переменной Неравенство с одной переменной в первой степени.например: 2x-3
Презентация на тему: «Линейные неравенства по одной переменной Неравенство с одной переменной в первой степени. Например: 2x-3
<8 Решение - это значение переменной, которая производит» - стенограмма презентации: ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]> Неравенство
Неравенство Линейные неравенства
Сочетания неравенств
Неравенства, связанные с абсолютными значениями
Полиномиальные неравенства
Рациональное неравенство
Линейные неравенства
Сочетания неравенств
x + 1 <0 ИЛИ x + 1> 3 Неравенства, связанные с абсолютными значениями
