|
№ п/п |
Задание |
Варианты ответов |
Правильный ответ |
|
1 |
В продукции фабрики изделия второго составляют 15%. Магазин получил 1000 изделий этой фабрики. Какова вероятность того, что в полученной партии изделия второго сорта будут находиться в границах 15% ± 2%. |
|
0,9235 |
|
2. |
Математическое ожидание нормально распределённой случайной величины равно 10, а дисперсия 4. Найти вероятность того, что в результате испытания случайная величина примет значение из интервала [12;14]. |
|
0.6827 |
|
3. |
Установлено, что 20% студентов учатся на «хорошо» и «отлично». Случайно отобрали 1600 студентов. Найти границы, в которых находится число студентов, обучающихся на «хорошо» и «отлично», с гарантией в 95%. |
1) (200;300) 2) (320;900) 3) (288;352) 4) (600;800) 5) (254;418) |
(288;352) |
|
4. |
При массовом производстве 5% продукции составляет брак. Сколько изделий должно быть в упаковке, чтобы с вероятностью 0,95 можно было гарантировать, что доля бракованных изделий в ней будет находиться в пределах 5%2%? |
|
457 |
|
5. |
Случайная величина Х распределена по нормальному закону с математическим ожиданием, а=40 и дисперсией = 100. Найти вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (20;60) |
|
0,9545 |
|
6. |
90% населения пользуются общественным транспортом. Найти вероятность того, что из 5 наудачу отобранных жителей не менее четырёх из них пользуются общественным транспортом. |
|
0,919 |
|
7. |
Установлено, что 64% водителей страхуют свой транспорт. Найти вероятность того, что среди 625 случайно отобранных водителей, транспорт застрахован у 415. |
|
0,0152 |
|
8. |
При транспортировке 0,04 % всех изделий получают повреждения. Какова вероятность того, что при транспортировке 5000 изделий повреждения получат не более пяти. |
|
0,9835 |
|
9. |
Вероятность поражения цели при каждом выстреле равна 0,6. Найти вероятность того, что при 600 выстрелах число попаданий будет находиться в границах от 330 до 375. |
|
0,8882 |
|
10. |
Можно считать, что длина детали является случайной величиной, распределённой по нормальному закону. Стандартная длина (математическое ожидание) детали, а= 40 см, среднее квадратическое отклонение = 0,4 см. Найти вероятность того, что отклонение длины наудачу взятой детали от её стандартной длины по модулю не превзойдёт 0,6 см. |
|
0,8664 |
|
11. |
Прибор состоит из 4 узлов. Вероятность безотказной работы каждого узла равна 0,8. Узлы выходят из строя независимо один от другого. Найти вероятность того, что из строя выйдут не менее двух узлов. |
|
0,1808 |
|
12. |
Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что событие наступит 1950 раз в 2500 испытаниях. |
|
0,0009 |
studrb.ru
Теория вероятностей и математическая статистика Тема 1-2
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Чем отличаются друг от друга различные перестановки из “n” элементов?
Количеством элементов
Нет ни одного верного варианта ответа
Количеством и составом элементов
Ничем не отличаются
Составом элементов
+Только порядком расположения элементов
Какое событие называется противоположным событию А?
Событие, всегда наступающее в результате опыта
Событие, никогда не наступающее в результате опыта
Нет ни одного верного варианта ответа
+Событие, состоящее в ненаступлении события А
Какое событие называется произведением AB событий А и В?
Событие, состоящее в наступлении хотя бы одного из событий А или В
+Событие, состоящее в их совместном наступлении
Нет ни одного верного варианта ответа
Событие А происходит, а В − не происходит
Событие, состоящее в наступлении только одного из событий A или В
Чем отличаются друг от друга различные размещения из “n” элементов по “m” ?
Количеством элементов
Ничем не отличаются
Нет ни одного верного варианта ответа
+Порядком расположения элементов либо их составом
Только составом элементов
Друзья, более 600 собак Воронежского приюта Дора https://vk.com/priyt_dora очень нуждаются в поддержке! Приют бедствует, не хватает средств на корм и лечение. Не откладывайте добрые дела, перечислите прямо сейчас любую сумму на «Голодный телефон» +7 960 111 77 23 или карту сбербанка 4276 8130 1703 0573. По всем вопросам обращаться +7 903 857 05 77 (Шамарин Юрий Иванович)
Чем отличаются друг от друга различные сочетания из “n” элементов по “m” ?
Порядком расположения элементов либо их составом
Количеством и составом элементов
Ничем не отличаются
Только порядком расположения элементов
Нет ни одного верного варианта ответа
+Только составом элементов
Чему равна вероятность суммы двух произвольных событий?
Произведению вероятностей этих событий
+Сумме вероятностей этих событий минус вероятность их произведения
Сумме вероятности одного из событий и условной вероятности другого, вычисленной при условии, что первое событие наступило
Сумме вероятностей этих событий
Нет ни одного верного варианта ответа
Чему равна вероятность произведения двух произвольных событий?
Нет ни одного верного варианта ответа
Сумме вероятностей этих событий минус вероятность их произведения
Произведению вероятностей этих событий
Сумме вероятностей этих событий
+Произведению вероятности одного из событий на условную вероятность второго, вычисленную при условии, что первое событие наступило
Когда несколько событий образуют полную группу?
Если все вместе происходят в одном опыте
+Если они попарно несовместны и в сумме равны достоверному событию
Нет ни одного верного варианта ответа
+Если в результате опыта обязательно происходит одно и только одно из них
Какие события называются несовместными?
+Не могут произойти вместе в одном опыте
Нет ни одного верного варианта ответа
+Наступление одного исключает наступление другого
Никогда не наступают в результате опыта
Хотя бы одно наступит в результате опыта
Какое событие называется суммой A+B событий А и В?
Событие, состоящее в их совместном наступлении
Событие, состоящее в наступлении только одного из событий А или В
Нет ни одного верного варианта ответа
+Событие, состоящее в наступлении хотя бы одного из событий А или В
Какие из следующих утверждений относительно дискретной случайной величины верны?
Её значения непрерывно меняются на некотором промежутке
Нет ни одного верного варианта ответа
Её значения обязательно целые
+Множество её значений дискретное или счётное
Для дискретных случайных величин существует плотность вероятности
Она не может принимать отрицательные значения
+Её значения изолированы друг от друга
Какие из следующих утверждений относительно непрерывной случайной величины верны?
Её значения изолированы друг от друга
Множество её значений дискретное или счётное
Её значения всегда положительны
+Её значения непрерывно меняются на некотором промежутке
Для неё существует ряд распределения
+Множество её значений несчётное
Нет ни одного верного варианта ответа
Это неотрицательная функция
Это неубывающая функция
Может принимать значения любого знака
Нет ни одного верного варианта ответа
+Плотность вероятности нормирована на единицу
В каких случаях применима формула Пуассона? :
а) Всегда применима
б) При большом числе опытов применима всегда
в) Нет ни одного верного варианта ответа
+г) Применима только в том случае, если число опытов n велико () вероятность p события А мала и произведение
Может ли в схеме испытаний Бернулли меняться от опыта к опыту вероятность наступления события А?
Может
+Должна оставаться постоянной
Всегда меняется
Нет ни одного верного варианта ответа
Для каких случайных величин существует функция распределения?
Только для величин, принимающих целые значения
Только для непрерывных
Только для величин, принимающих положительные значения
+Для любых
Только для дискретных
Может ли в схеме испытаний Бернулли факт наступления события А в одном из опытов влиять на возможность его появления в остальных опытах?
+Не может влиять
Всегда влияет
Влияет только при большом числе опытов
Нет ни одного верного варианта ответа
Не влияет только при малой вероятности события А
Возможно ли совместное наступление двух или более из гипотез при использовании формулы полной вероятности или формулы Байеса?
+Нет, гипотезы должны взаимно исключать друг друга
Конечно возможно, только так и бывает
Возможно, если событие А не зависит от гипотез
Нет ни одного верного варианта ответа
Возможно, если событие А зависит от гипотез
Какие утверждения относительно гипотез в формуле полной вероятности и в формуле Байеса верны?
Событие А не зависит от гипотез
Нет ни одного верного варианта ответа
+Событие А обязательно наступает в совокупности с одной из гипотез, т.е зависит от них
+Сумма вероятностей гипотез всегда равна единице
Гипотезами могут быть произвольные события
+Гипотезы обязательно образуют полную группу попарно несовместных событий
Какие из следующих утверждений относительно функции распределения случайной величины верны?
Функция может принимать любые значения
Имеются участки возрастания и убывания функции
+При бесконечном увеличении аргумента функция стремится к единице
Она может быть и положительна и отрицательна
+Это неубывающая функция
При бесконечном уменьшении аргумента функция стремится к единице
+Она всегда заключена между нулём и единицей
test-for-you.ru
Тесты по курсу: «теория вероятностей и математическая статистика»
ТЕСТЫ ПО КУРСУ:
«ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
(дополнение)
РАЗДЕЛ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Тема 1. Случайные события
Вопрос 1. Из букв слова ТЕОРЕМА наугад выбирают 5 букв. Тогда вероятность того, что из выбранных букв можно составить слово МОРЕ, равна:
Вопрос 2. Из букв слова КОРОБКА наугад выбирают 5 букв. Тогда вероятность того, что из выбранных букв можно составить слово КРАБ, равна:
Вопрос 3. Из букв слова КОРОБКА наугад выбирают 5 букв. Тогда вероятность того, что из выбранных букв можно составить слово БОР, равна:
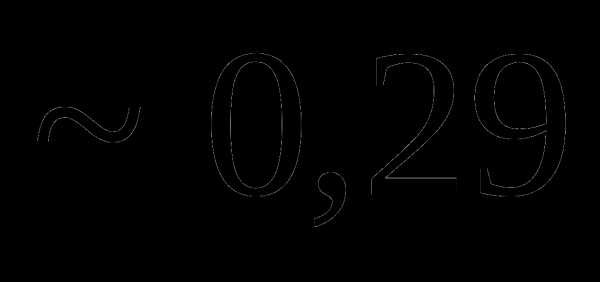
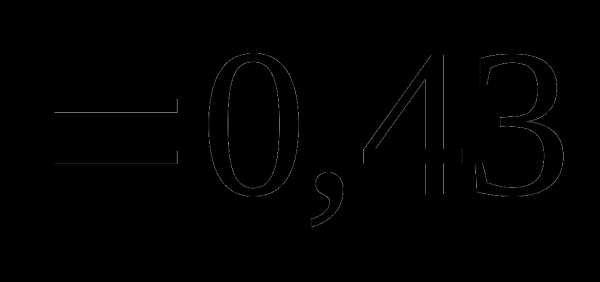
Вопрос 4. Двое по очереди по одному разу подбрасывают игральную кость. Выигрывает тот, у которого выпадает больше очков. Тогда вероятность того, что начинающий игру победит, равна:
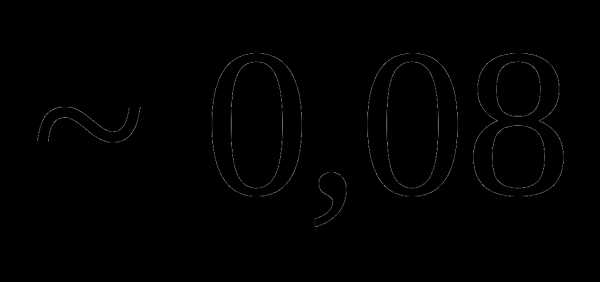
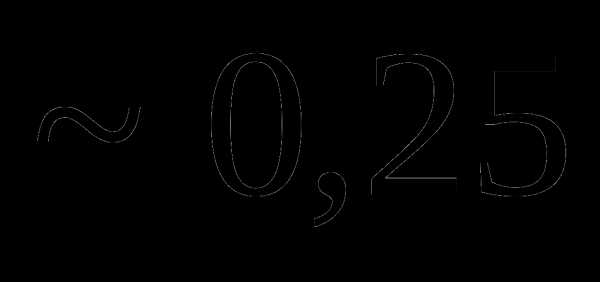
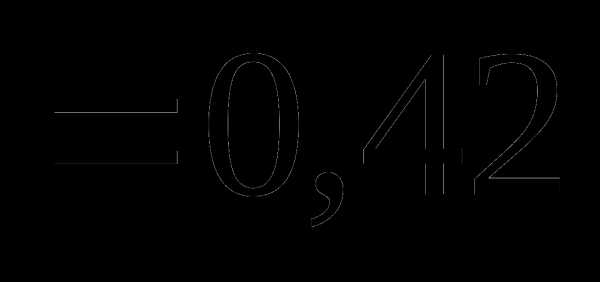
Вопрос 5. Двое поочередно подбрасывают монету. Выигрывает тот, у которого раньше выпадает герб. Тогда вероятность выигрыша игрока, начавшим подбрасывание монеты первым, равна:
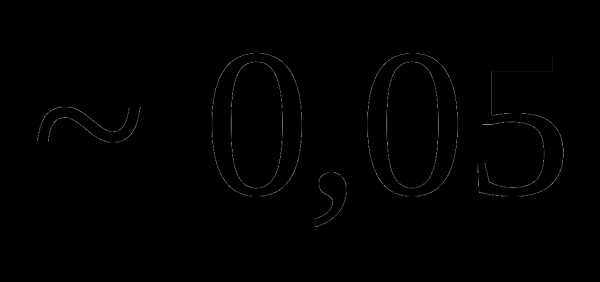
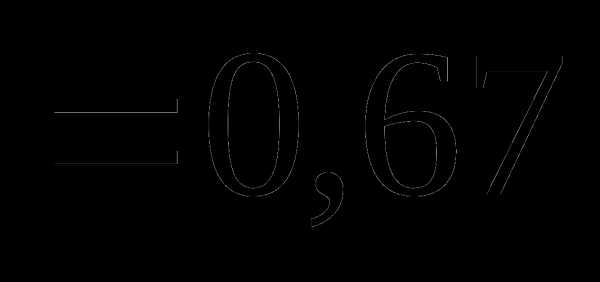
Вопрос 6. Двое поочередно подбрасывают монету. Выигрывает тот, у которого раньше выпадает герб. Тогда вероятность выигрыша игрока, начавшим подбрасывание монеты вторым, равна:
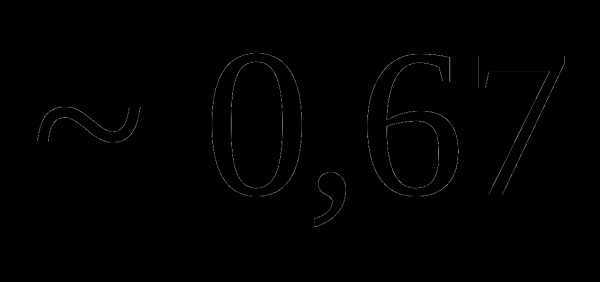
Вопрос 7. Монета подбрасывается 5 раз. Тогда вероятность того, что герб выпадает по меньшей мере три раза подряд равна:
Вопрос 8. Случайные события A, B и C независимы в совокупности и вероятности их появления, соответственно, равны 0,2, 0,3 и 0,5. Тогда вероятность события D = A + B + C равна:
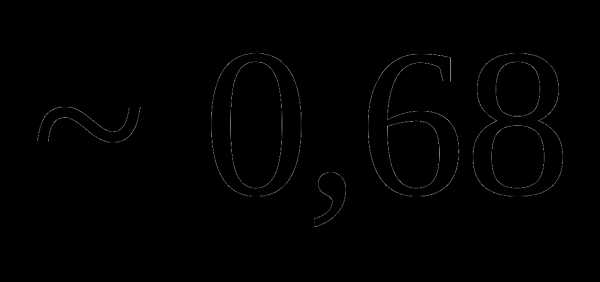
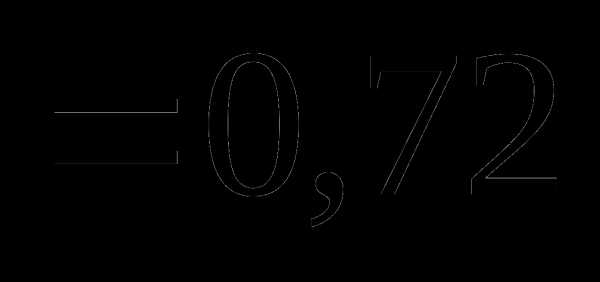
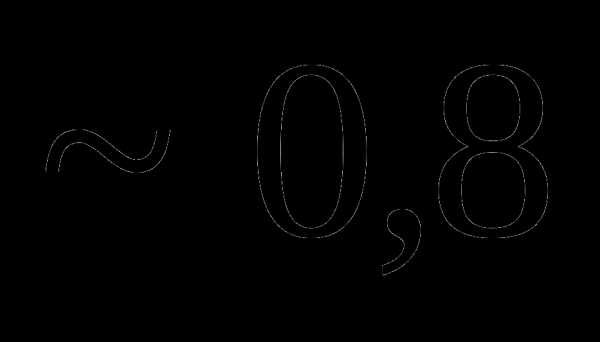
Вопрос 9. Игральная кость бросается 5 раз. Тогда вероятность того, что шестерка выпадает не менее трех раз подряд, равна:
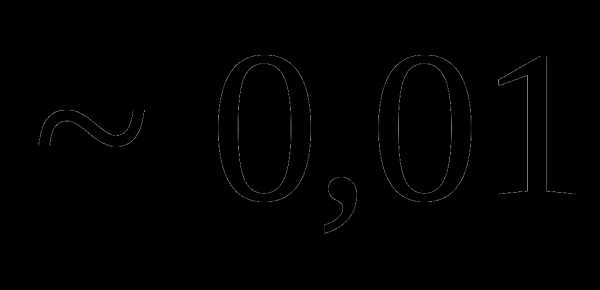
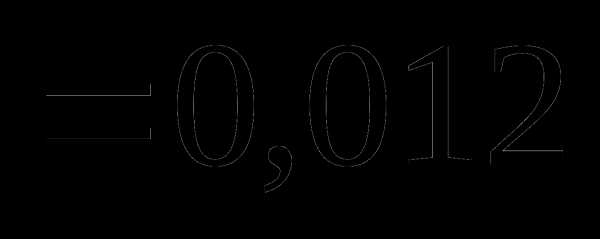
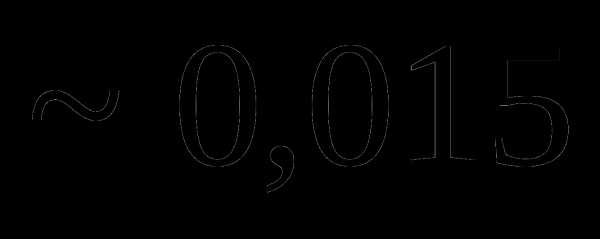
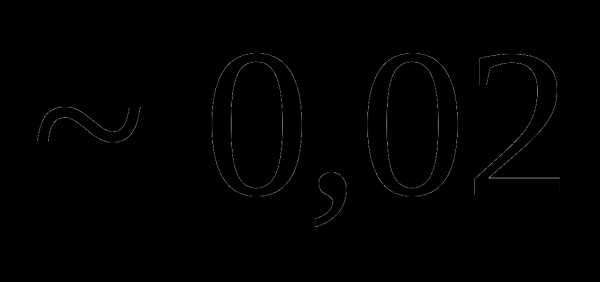
Вопрос 10. Двое поочередно извлекает шары (без возвращения) из урны, содержащей 3 белых и 4 черных шара. Выигрывает тот, кто первым вынет белый шар. Тогда вероятность выигрыша участника, начинающего игру, равна:
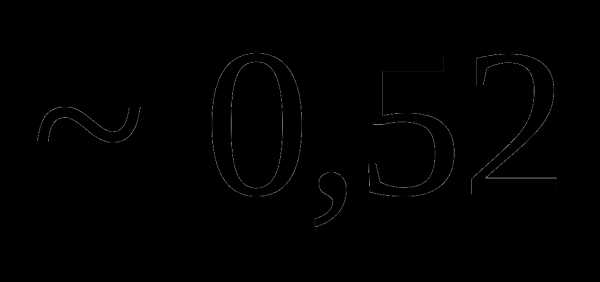
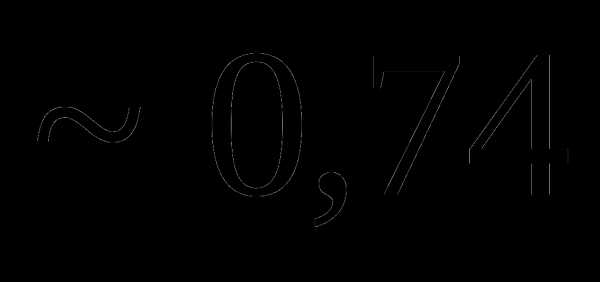
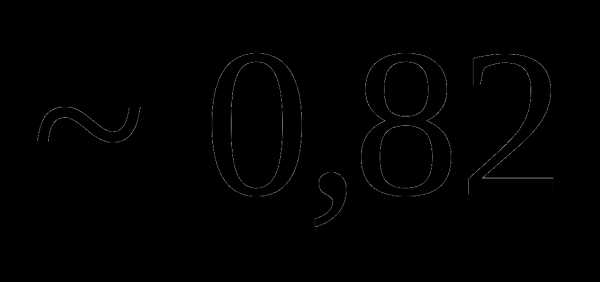
Вопрос 11. Монета подбрасывается до тех пор, пока не выпадает герб. Тогда вероятность того, что монету придется подбрасывать не более 5 раз, равна:
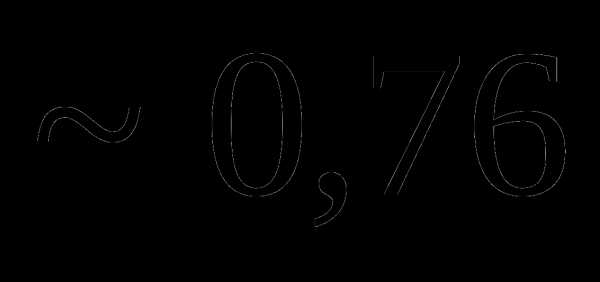
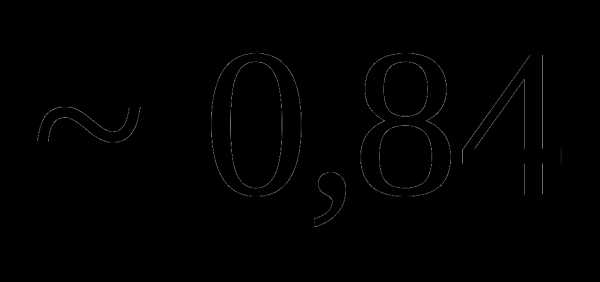
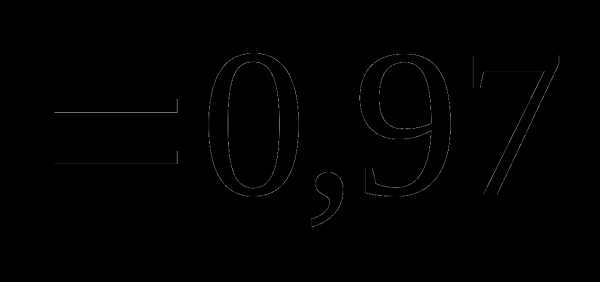
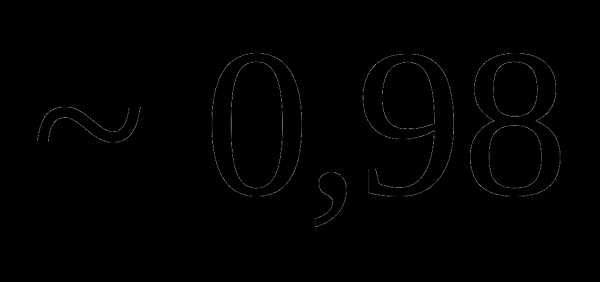
Вопрос 12. Из букв слова ЛАМБАДА наугад выбирают 5 букв. Тогда вероятность того, что из выбранных букв можно составить слово ЛАДА, равна:
Вопрос 13. Из букв слова ЛАМБАДА наугад выбирают 5 букв. Тогда вероятность того, что из выбранных букв можно составить слово БАЛ, равна:
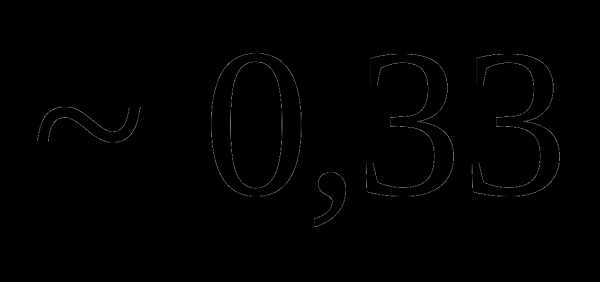
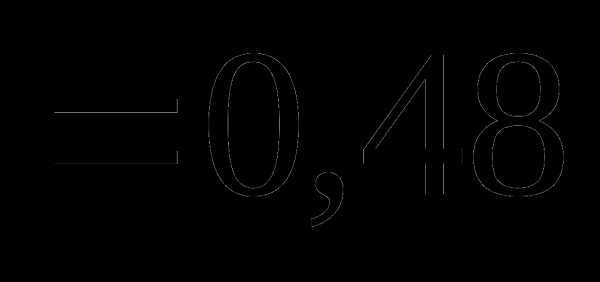
Вопрос 14. Из урны, в которой имелось 4 черных и 6 белых шаров, потерян шар неизвестного цвета. Для того, чтобы определить состав шаров в урне, из нее наугад извлекают 2 шара. Один из них оказался белым, другой – черным. Тогда вероятность того, что был утерян белый шар, равна:
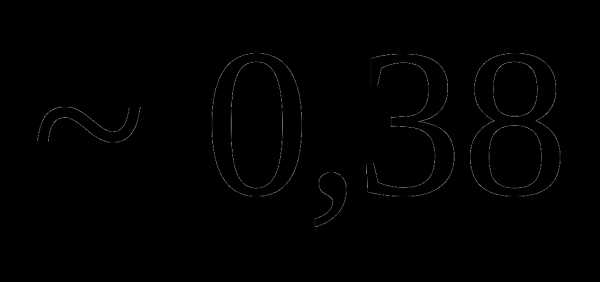
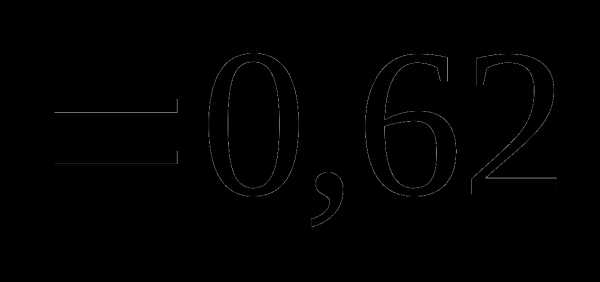
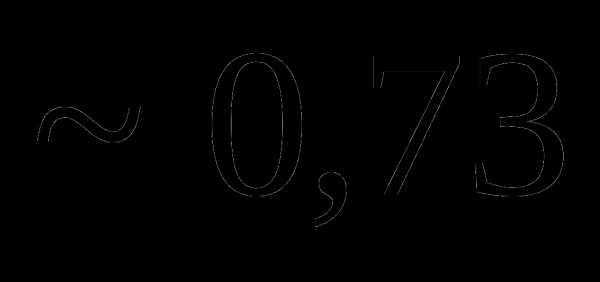
Вопрос 15. Из урны, в которой имелось 4 черных и 6 белых шаров, потерян шар неизвестного цвета. Для того, чтобы определить состав шаров в урне, из нее наугад извлекают 2 шара. Один из них оказался белым, другой – черным. Тогда вероятность того, что был утерян черный шар, равна:
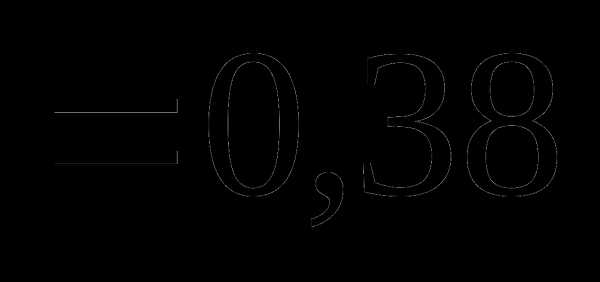
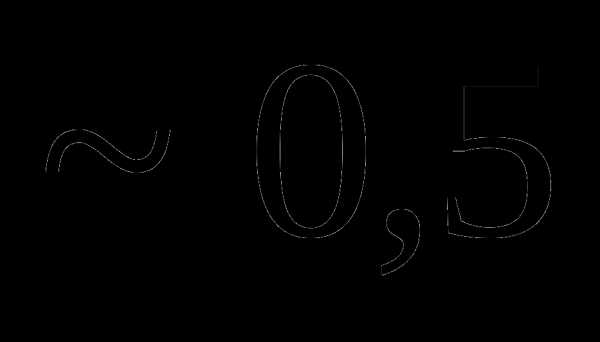
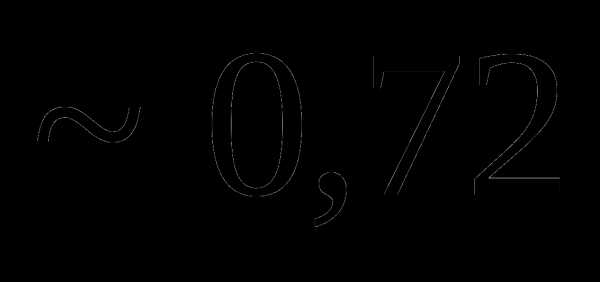
Вопрос 16. Из урны, в которой имелось 4 белых и 6 черных шаров, потеряны 2 шара неизвестного цвета. Для того, чтобы определить состав шаров в урне, из нее наудачу извлекли 2 шара. Они оказались черными. Тогда вероятность того, что были утеряны 1 белый и 1 черный шары, равна:
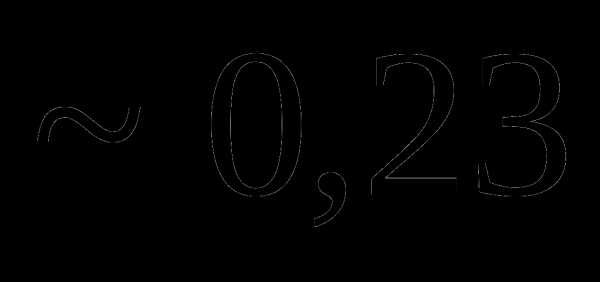
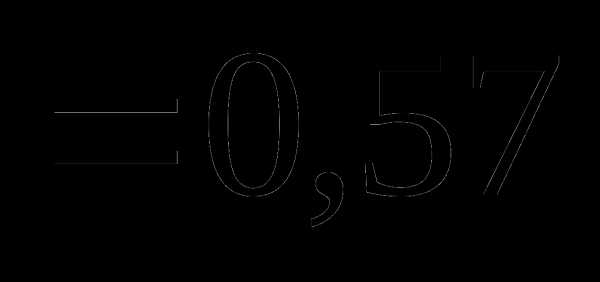
Вопрос 17. Из урны, в которой имелось 4 белых и 6 черных шаров, потеряны 2 шара неизвестного цвета. Для того, чтобы определить состав шаров в урне, из нее наудачу извлекли 2 шара. Они оказались черными. Тогда вероятность того, что были утеряны 2 белых шара, равна:
Вопрос 18. Из урны, в которой имелось 4 белых и 6 черных шаров, потеряны 2 шара неизвестного цвета. Для того, чтобы определить состав шаров в урне, из нее наудачу извлекли 2 шара. Они оказались черными. Тогда вероятность того, что были утеряны 2 черных шара, равна:
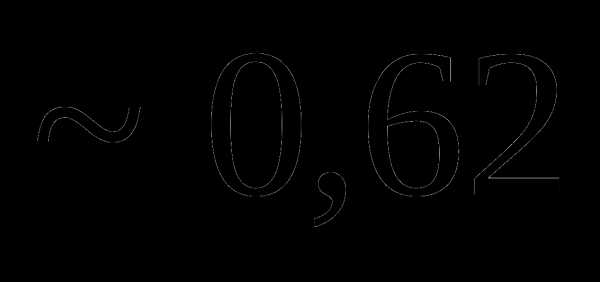
Вопрос 19. На молодежную газету в среднем подписывается 25% студентов. Тогда наиболее вероятное число подписчиков на эту газету на потоке, насчитывающем 100 студентов, равно:
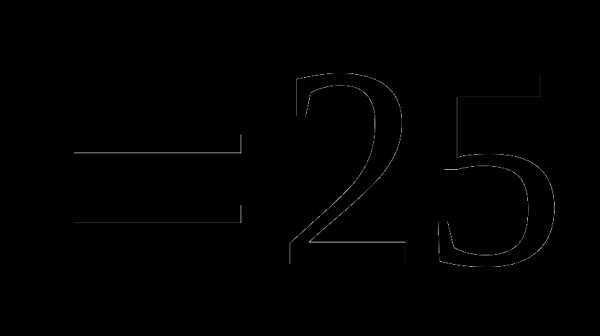
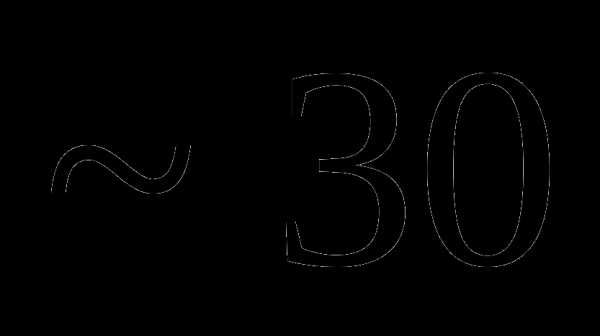
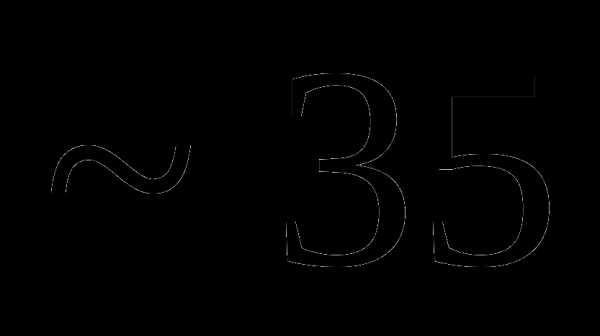
Вопрос 20. В круг вписан квадрат. В круг наугад бросается 4 точки. Тогда наиболее вероятное число точек, попавших в квадрат, равно:
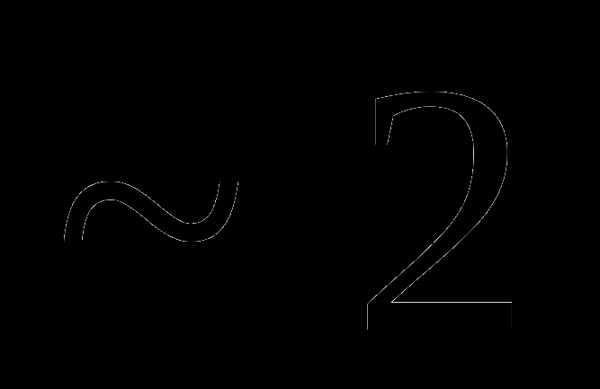
Вопрос 21. В круг вписан квадрат. В круг наугад бросается 4 точки. Тогда вероятность того, что из четырех точек только одна попадет внутрь квадрата, равна:
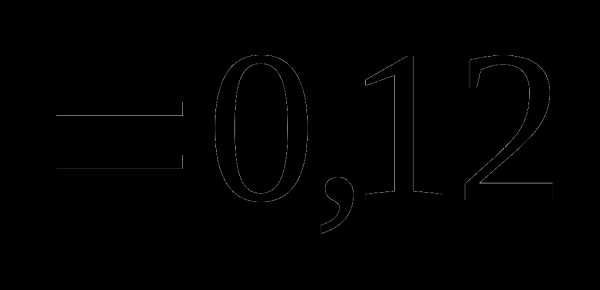
Вопрос 22. В круг вписан квадрат. В круг наугад бросается 4 точки. Тогда вероятность того, что из четырех точек хотя бы одна попадет внутрь квадрата, равна:
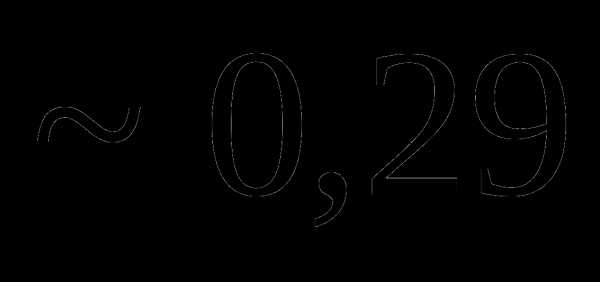
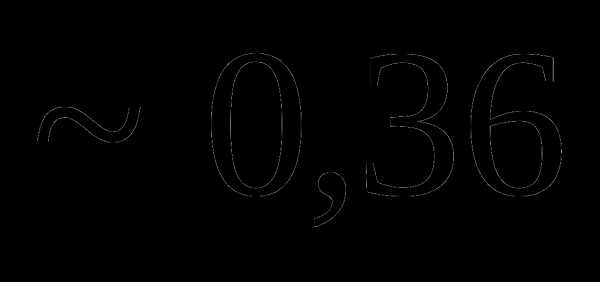
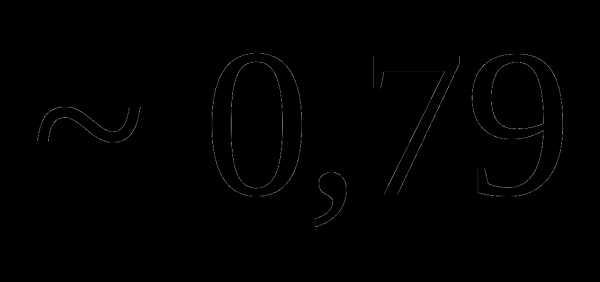
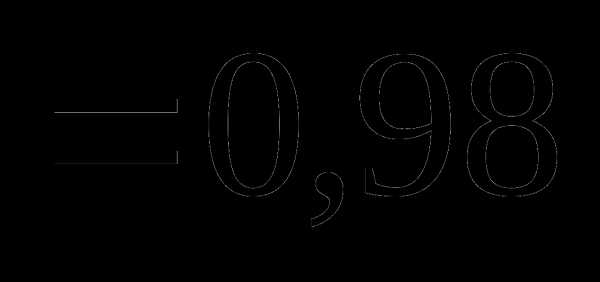
Тема 2. Случайные величины
Вопрос 23. Дан закон распределения дискретной случайной величины X:
X | 0 | 1 | 2 | 3 |
P | P1 | 1/3 | P3 | 1/6 |
Известно, что mx = 1. Тогда Dx равна:
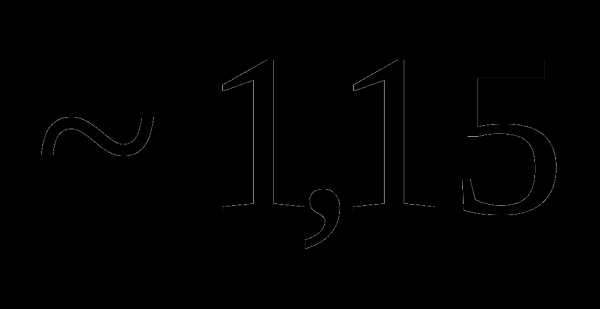

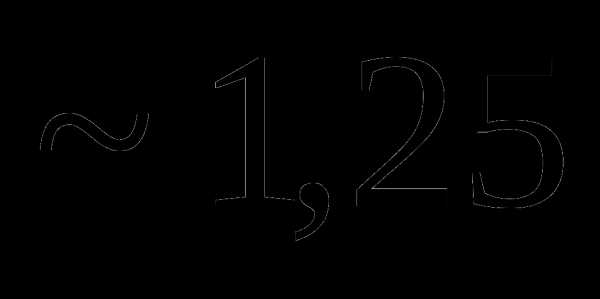
Вопрос 24. Случайная величина X принимает 3 значения: –1, 0, 1. Известно, что mx = 0, Dx = 0,5. Тогда P (X = -1) равна:
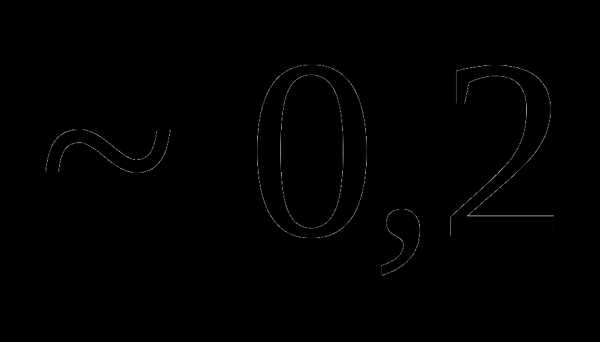
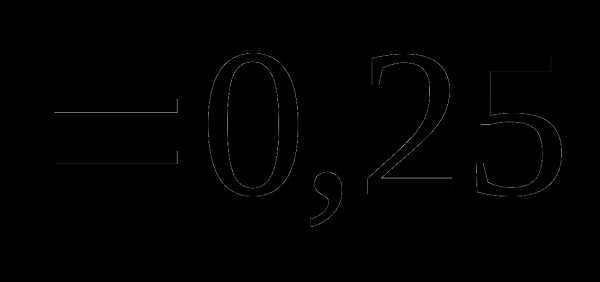
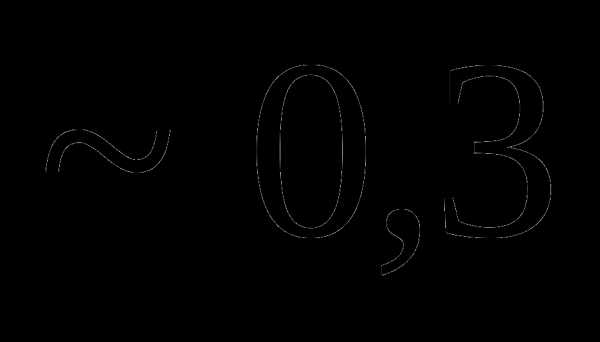
Вопрос 25. Случайная величина X принимает 3 значения: –1, 0, 1. Известно, что mx = 0, Dx = 0,5. Тогда P (X = 0) равна:
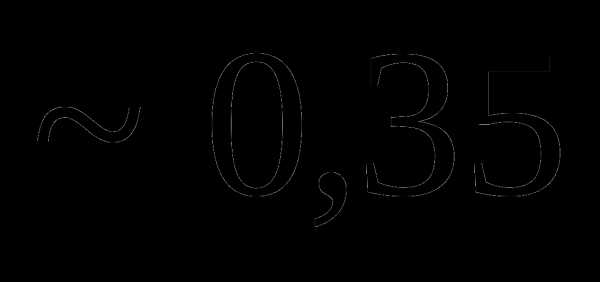
Вопрос 26. Случайная величина X принимает 3 значения: –1, 0, 1. Известно, что mx = 0, Dx = 0,5. Тогда P (X = 1) равна:
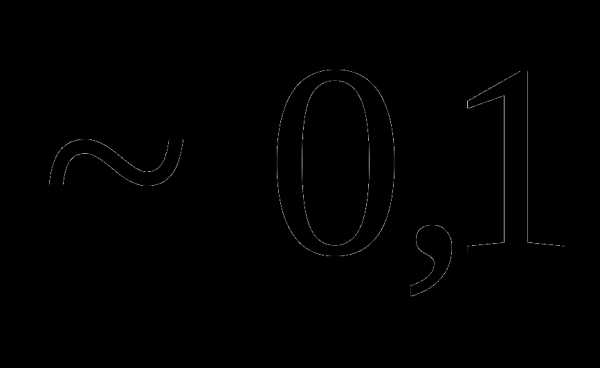
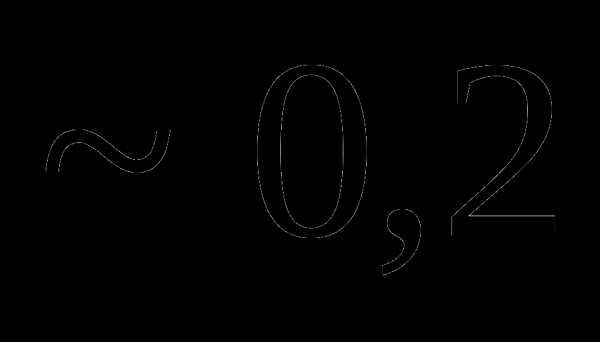
Вопрос 27. Случайная величина X распределена равномерно в некотором интервале [a;b], причем P (X P (X mx равно:
Вопрос 28. Случайная величина X распределена равномерно в некотором интервале [a;b], причем P (X P (X Dx равно:
Вопрос 29. Случайная величина X распределена равномерно в некотором интервале [a;b], причем P (X P (X a равно:
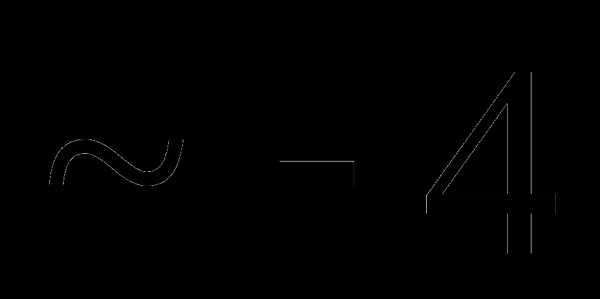
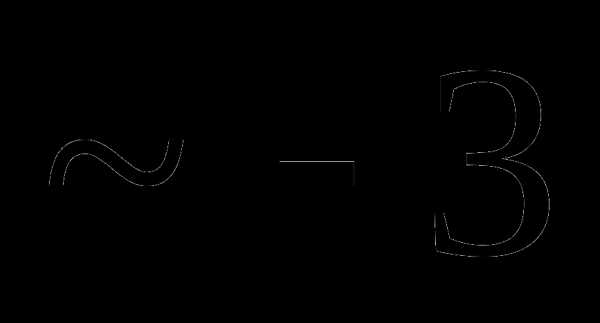
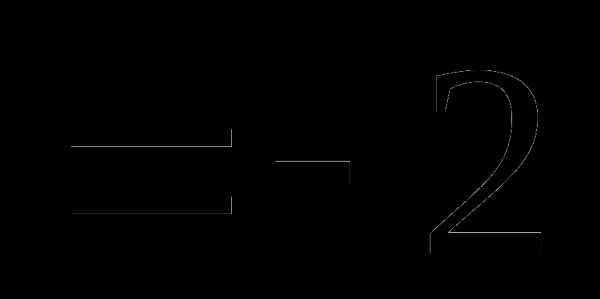
Вопрос 30. Случайная величина X распределена равномерно в некотором интервале [a;b], причем P (X P (X b равно:
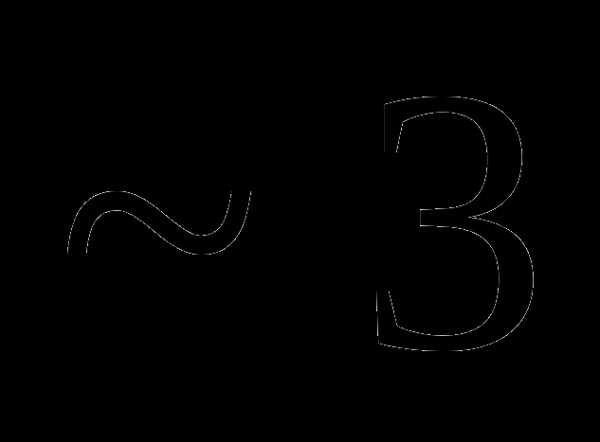

Вопрос 31. Случайная величина X распределена равномерно в интервале [a;b]. Известно, что mx = 2, Dx = 0,75. Тогда a равно:
Вопрос 32. Случайная величина X распределена равномерно в интервале [a;b]. Известно, что mx = 2, Dx = 0,75. Тогда b равно:
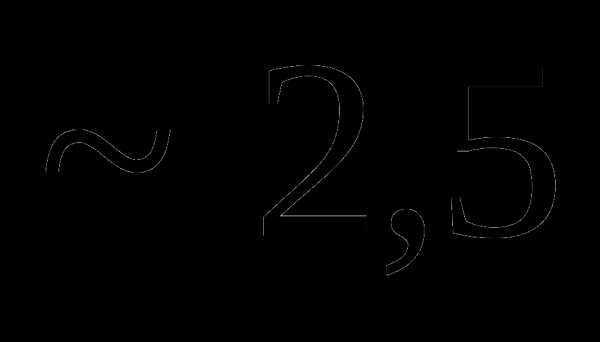
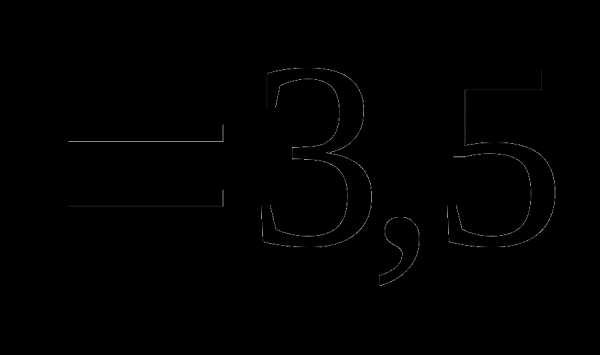
Вопрос 33. Случайная величина X распределена по нормальному закону с mx = –2 и Dx = 9. Тогда M((3 – X)(X + 5)) равно:
Тема 3. Системы двух случайных величин
Вопрос 34. Распределение двух дискретных случайных величин X и Y задано таблицей:
yj
xi
–1
0
1
–1
1/6
1/12
7/24
1
1/8
1/3
0
Тогда mx равно:
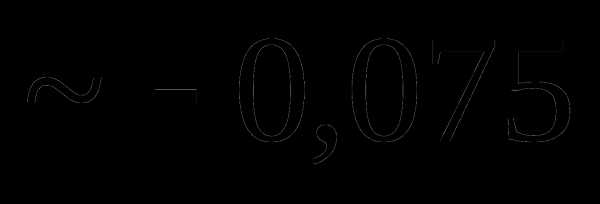
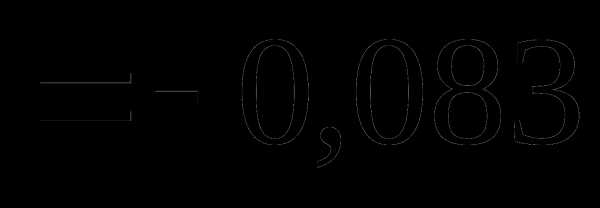
Вопрос 35. Распределение двух дискретных случайных величин X и Y задано таблицей:
yj
xi
–1
0
1
–1
1/6
1/12
7/24
1
1/8
1/3
0
Тогда my равно:
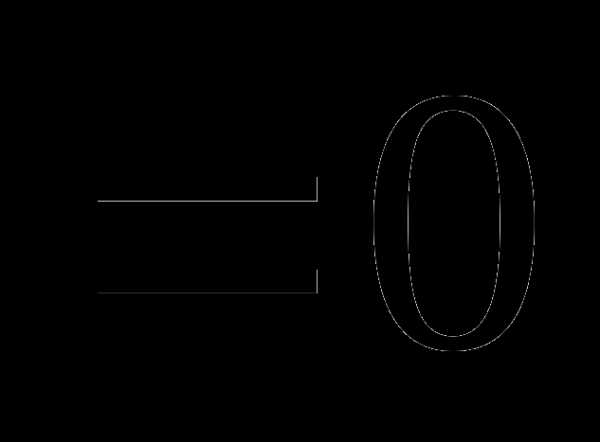
Вопрос 36. Распределение двух дискретных случайных величин X и Y задано таблицей:
yj xi | –1 | 0 | 1 |
–1 | 1/6 | 1/12 | 7/24 |
1 | 1/8 | 1/3 | 0 |
Тогда Dx равно:
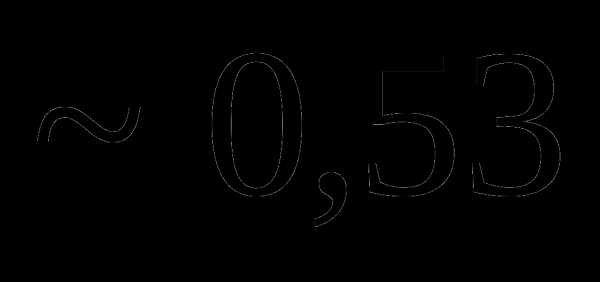
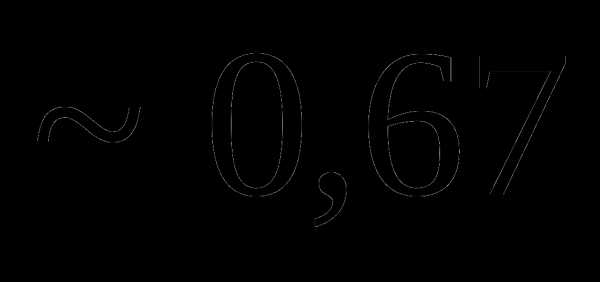
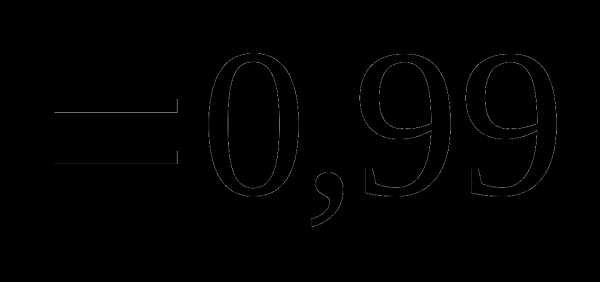
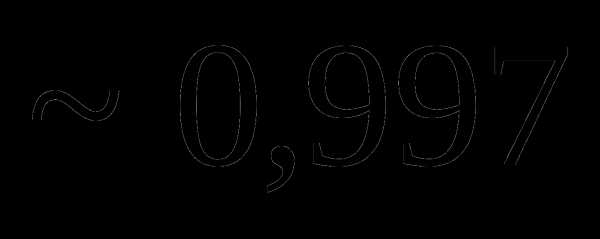
Вопрос 37. Распределение двух дискретных случайных величин X и Y задано таблицей:
yj xi | –1 | 0 | 1 |
–1 | 1/6 | 1/12 | 7/24 |
1 | 1/8 | 1/3 | 0 |
Тогда Dy равно:
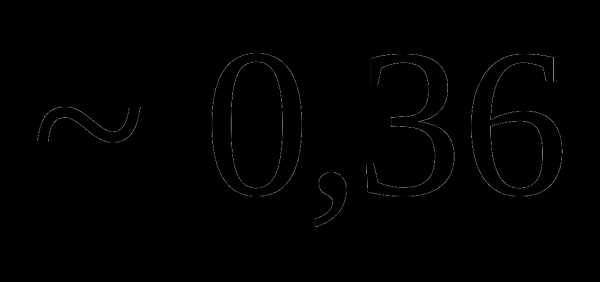
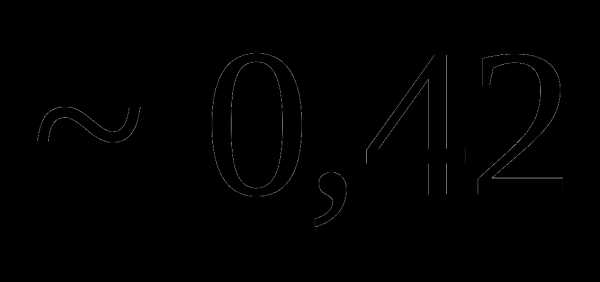
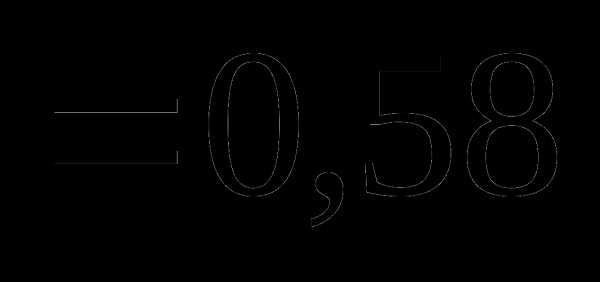
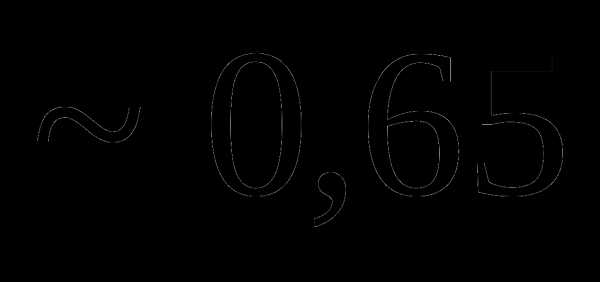
Вопрос 38. Распределение двух дискретных случайных величин X и Y задано таблицей:
yj xi | –1 | 0 | 1 |
–1 | 1/6 | 1/12 | 7/24 |
1 | 1/8 | 1/3 | 0 |
Тогда Kxy равно:
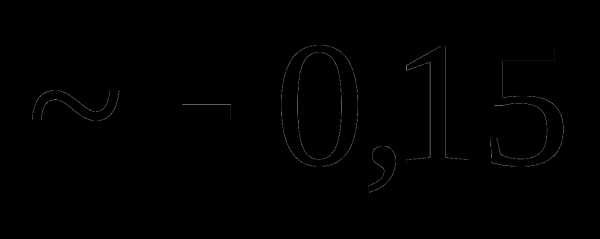
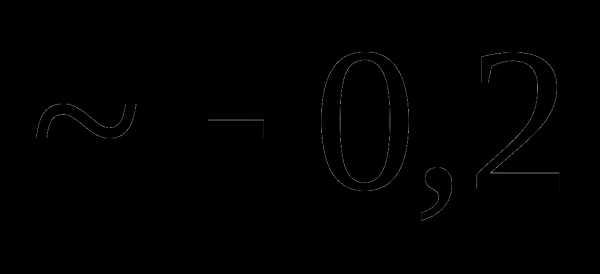
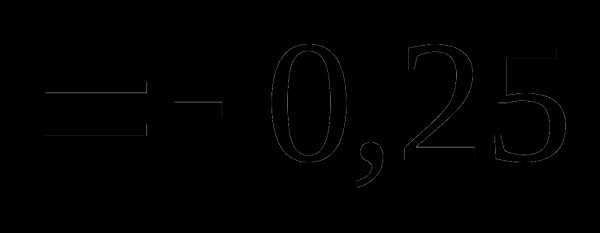
Вопрос 39. Распределение двух дискретных случайных величин X и Y задано таблицей:
yj xi | –1 | 0 | 1 |
–1 | 1/6 | 1/12 | 7/24 |
1 | 1/8 | 1/3 | 0 |
Тогда rxy равно:
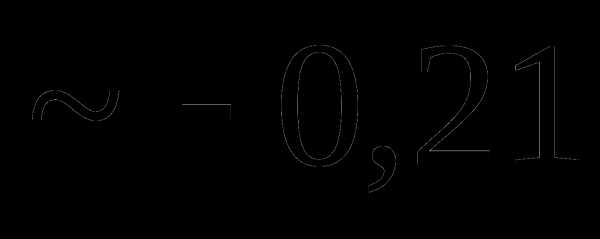
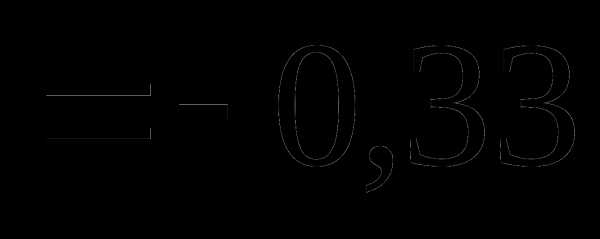
Тема 4. Функции случайных величин
Вопрос 40. Плотность распределения случайной величины X задана выражением (закон Релея):
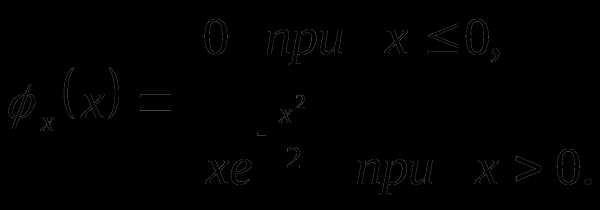
Тогда вероятность попадания случайной величины Y = X2 в интервал (0;2) равна:
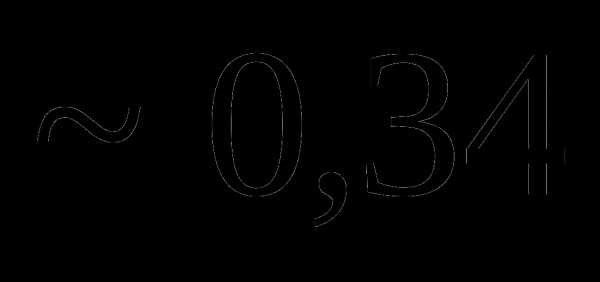
Вопрос 41. Плотность распределения случайной величины X задана выражением:
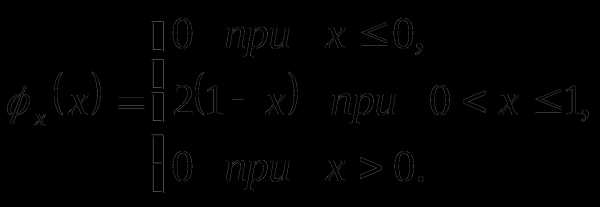
Тогда вероятность попадания случайной величины Y = X2 в интервал (0;0,25) равна:
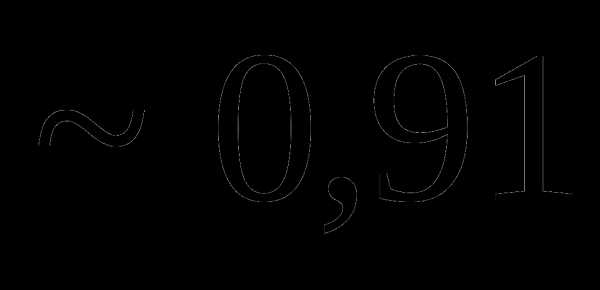
Вопрос 42. Плотность распределения случайной величины X задана выражением:
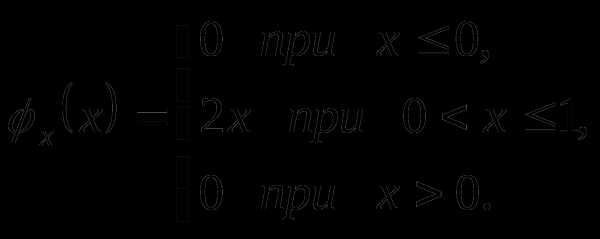
Тогда P(Y > 0,25), где Y = X2, равна:

Вопрос 43. Известна плотность случайной величины X в виде:
Тогда математическое ожидание случайной величины Y = 5 + 3X равно:

Вопрос 44. Известна плотность случайной величины X в виде:
Тогда дисперсия случайной величины Y = 5 + 3X равно:
Вопрос 45. Числовые характеристики случайных величин X, Y и Z, входящих в случайную величину U = X – 2Y + Z – 4, заданы в виде: mx = my = mz = 1 и
Тогда mu равно:
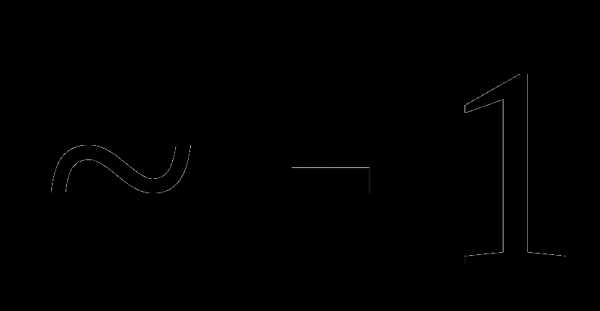
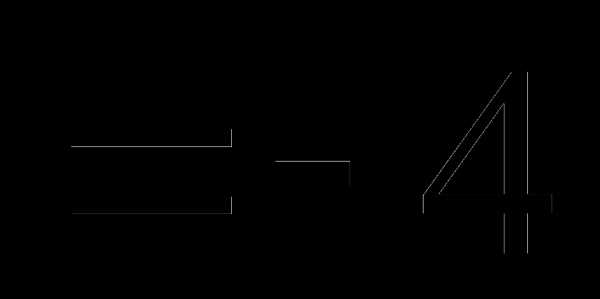
Вопрос 46. Числовые характеристики случайных величин X, Y и Z, входящих в случайную величину U = X – 2Y + Z – 4, заданы в виде: mx = my = mz = 1 и
Тогда Du равна:
Вопрос 47. Известны числовые характеристики системы двух случайных величин {X,Y}: mx = 2, my = 3, Тогда для случайной величины Z = = 3X – 5Y + 3 mz равно:
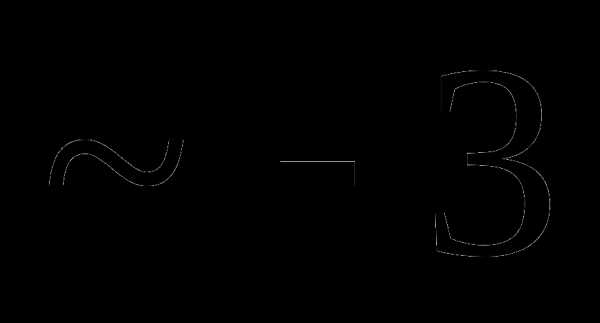
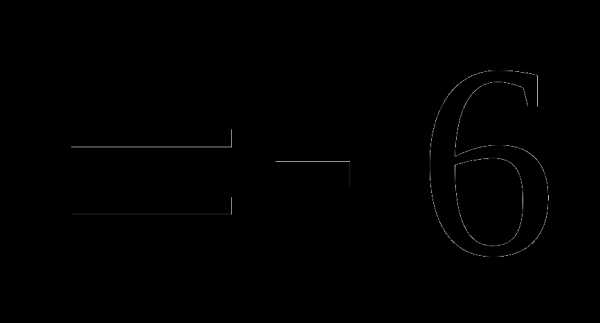
Вопрос 48. Известны числовые характеристики системы двух случайных величин {X,Y}: mx = 2, my = 3, Тогда для случайной величины Z = = 3X – 5Y + 3 Dz равна:

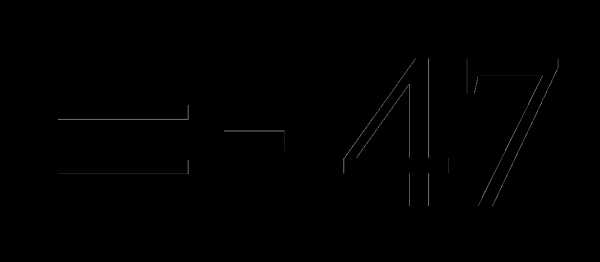
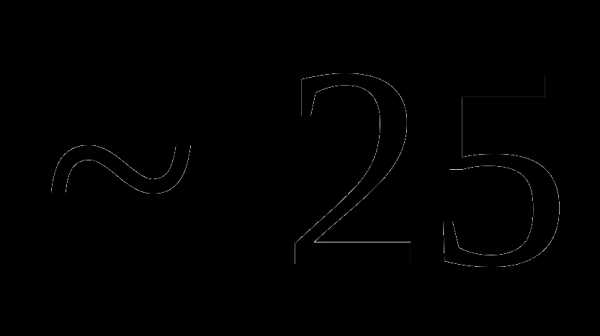
Вопрос 49. Известны числовые характеристики системы трех случайных величин Тогда для случайной величины Y = 2X1 – 3X2 + 4X3 + 1 my равно:
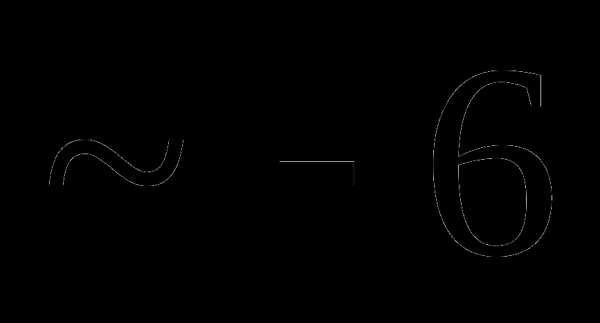
Вопрос 50. Известны числовые характеристики системы трех случайных величин Тогда для случайной величины Y = 2X1 – 3X2 + 4X3 + 1 Dy равна:
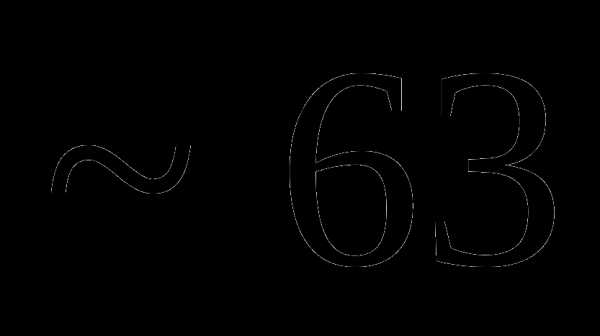
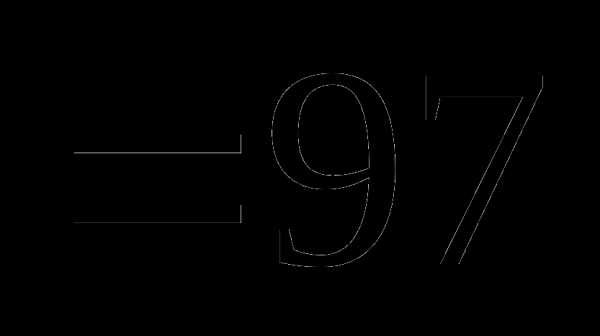

gigabaza.ru
ТЕСТЫ ТВиМС с ответами
ТЕСТЫ
по курсу «Теория вероятностей и математическая статистика»
Вероятность события
 это:
это:
; 2.; 3.
2. Какие способы задания вероятностей вы знаете:
классический, динамический, точечный, геометрический;
статистический, геометрический, биноминальный, классический;
геометрический, классический, дискретный, статистический;
классический, геометрический, точечный, статистический;
классический, геометрический, статистический, комбинаторный.
3. Когда применяется классический способ задания вероятности:
пространство элементарных событий бесконечно, все события равновозможные и независимые;
пространство элементарных событий замкнуто, все события независимы;
пространство элементарных событий конечно, все события равновозможные;
пространство элементарных событий конечно, все элементарные события независимы.
4. Когда применяется геометрический способ задания вероятности:
пространство элементарных событий бесконечно, все события равновозможные и независимые;
пространство элементарных событий замкнуто, все события независимы;
пространство элементарных событий конечно, все события равновозможные;
пространство элементарных событий конечно, все элементарные события независимы.
5. Назовите основные аксиомы вероятностей:
6. Суммой двух событий  и
и называют:
называют:
событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;
7.
Произведением двух событий  и
и называют:
называют:
событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;
Вероятность суммы двух совместных событий
 равна:
равна:
Вероятность произведения двух совместных событий рана:
Формула полной вероятности:
Законы распределения случайной дискретной величины представляются в виде:
Законы распределения непрерывной случайной величины представляются в виде:
Функция распределения случайной величины это:
Вероятность того, что
Вероятность того, что
Вероятность того, что
Вероятность того, что
Вероятность того, что.
Функция плотности распределения случайной величины
 это:
это:
Основные числовые характеристики дискретных случайных величин это:
Среднее арифметическое, дисперсия, квантиль, моменты
 -того
порядка, мода и медиана;
-того
порядка, мода и медиана;Дисперсия, центральные и начальные моменты
 -того
порядка, среднее геометрическое, мода
и медиана;
-того
порядка, среднее геометрическое, мода
и медиана;Математическое ожидание, мода, медиана, дисперсия, среднее квадратичное отклонение, центральные и начальные моменты
 -того
порядка.
-того
порядка.Математическое ожидание, среднее арифметическое, дисперсия, среднее квадратичное отклонение, мода, медиана, центральные и начальные моменты
 -того
порядка.
-того
порядка.Математическое ожидание, мода, медиана, дисперсия, среднее квадратичное отклонение, центральные и начальные моменты
 -того
порядка, эксцесс, асимметрия.
-того
порядка, эксцесс, асимметрия.
Функция распределения
 и
функция плотности распределения имеют
и
функция плотности распределения имеют следующие
свойства:
следующие
свойства:
Дисперсия случайно величины равна:
Математическое ожидание непрерывной случайной величины равно:
Нормальный закон распределения имеет следующую функцию плотности распределения
 :
:
Для нормального закона распределения вероятность попадания случайной величины в интервал
 равен:
равен:
Сущность предельных теорем и закона больших чисел заключается:
В определении числовых характеристик случайных величин при большом числе наблюдаемых данных;
В поведении числовых характеристик и законов распределения наблюдаемых значений случайных величин;
В определении области применения нормального закона распределения случайных величин при сложении большого количества случайных величин;
В поведении числовых характеристик и законов распределения случайных величин при увеличении числа наблюдений и опытов.
В определении суммарных значений основных характеристик законов распределения.
Коэффициент корреляции случайных величин характеризует:
Степень независимости между случайными величинами;
Степень нелинейной зависимости между случайными величинами;
Степень линейной зависимости между случайными величинами;
Степень регрессии между случайными величинами;
Степень разброса двух величин относительно математического ожидания.
Степень отклонения двух величин от их математических ожиданий.
Марковским случайным процессом называют такие процессы, у которых:
Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;
Марковскими цепями называю случайных процесс, у которого:
Сама функция подчиняется нормальному закону распределения;
Сама функция подчиняется показательному закону распределения;
Сама функция имеет дискретный характер;
Сама функция имеет непрерывный характер;
Сама функция подчиняется биноминальному закону распределения;
К оценкам генеральной совокупности предъявляются следующие требования:
Оценка должна быть стационарной, эргодичной и эффективной;
Оценка должна быть состоятельной, эргодичной и эффективной;
Оценка должна быть состоятельной, стационарной и эргодичной ;
Оценка должна быть состоятельной, эффективной и несмещенной;
Оценка должна быть несмещенной, стационарной и эффективной;
Статистической гипотезой называют:
Предположение относительно параметров и вида закона распределения генеральной совокупности;
Предположение относительно объема генеральной совокупности;
Предположение относительно параметров и вида закона распределения выборки;
Предположение относительно объема выборочной совокупности;
Предположение относительно статистического критерия ;
При проверки статистической гипотезы ошибка первого рода это:
Принятие в действительности неверной гипотезы;
Отвержение в действительности правильной гипотезы;
Принятие в действительности правильной гипотезы;
Отвержение в действительности неправильной гипотезы;
В критерии Колмогорова за меру качества согласия эмпирического и теоретического распределения принимается:
Относительное расхождение между теоретической и эмпирической частотами попадания случайной величины в интервал;
Максимальное расхождение по модулю между теоретической и эмпирической частотами попадания случайной величины в интервал;
Среднее квадратичное отклонение между теоретической и эмпирической частотами попадания случайной величины в интервал;
Максимальное расхождение модуля разности между эмпирической и теоретической функциями распределения;
Максимальное расхождение модуля разности между эмпирической и теоретической функциями плотности распределения;
Дисперсионный анализ позволяет:
Установить степень влияния фактора на изменчивость признака;
Установить количество факторов влияния на изменчивость признака;
Установить степень влияния факторов на дисперсию;
Установить степень влияния фактора на среднее значение;
Установить степень влияния фактора на числовые характеристики случайной величины;
Задачами регрессионного анализа являются:
Выявление связи между случайными величинами и оценка их тесноты;
Выявление связи между случайными величинами и их числовыми характеристиками;
Выявление уравнения связи между случайными величинами;
Выявление уравнения связи между случайной зависимой переменной и неслучайными независимыми переменными и оценка неизвестных значений зависимой переменной;
Выявление уравнения связи между неслучайной зависимой переменной и случайными независимыми переменными и оценка неизвестных значений независимой переменной;
Выявление уравнения связи между неслучайной независимой переменной и случайными независимыми переменными и оценка неизвестных значений зависимой переменной;
Задачи
В урне 6 белых и 4 черных шара. Из нее вынимают подряд 3 шара. Найти вероятность того, что оба шара черные?
Продавец мороженного в солнечный день может заработать 10 $., а в дождливый – 3. Чему равна ожидаемая выручка, если вероятность того, что день окажется дождливым, равна 0,4?
В банк подано 5 заявок фирм на получение кредита. Вероятность получить кредит для каждой фирмы равна 0,5. Найти вероятность того, что из пяти фирм кредит получит ровно 3 фирмы?
Случайная величина задана функцией распределения:
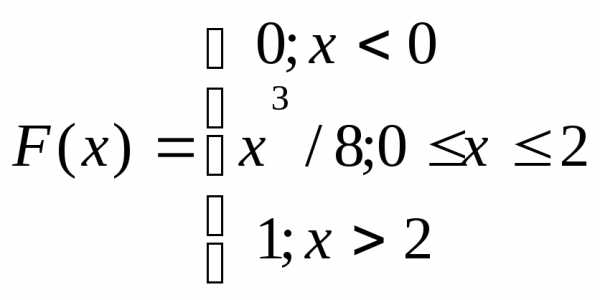
Найти плотность распределения случайной величины и вычислить
вероятность того, что  .
.
Коробки с шоколадом упаковываются автоматики чески: средний вес коробки равен 1,06 кГ, а его среднее квадратичное отклонение равно 0,25 кГ. Найти практически возможный максимальный вес одной коробки, если масса коробок поднимается нормальному закону распределения.
В урне 2 белых и 7 черных шара. Из нее вынимают подряд 2 шара. Найти вероятность того, что оба шара черные?
Продавец мороженного в солнечный день может заработать 5 $., а в дождливый – 2. Чему равна ожидаемая выручка, если вероятность того, что день окажется дождливым, равна 0,5?
В банк подано 3 заявок фирм на получение кредита. Вероятность получить кредит для каждой фирмы равна 0,6. Найти вероятность того, что из пяти фирм кредит получит ровно 2 фирмы?
Случайная величина задана функцией распределения:
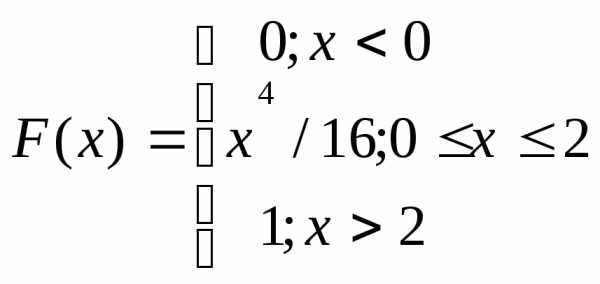
Найти плотность распределения случайной величины и вычислить
вероятность того, что  .
.
Коробки с шоколадом упаковываются автоматики чески: средний вес коробки равен 1,0 кГ, а его среднее квадратичное отклонение равно 0,2 кГ. Найти практически возможный максимальный вес одной коробки, если масса коробок поднимается нормальному закону распределения.
В урне 4 белых и 4 черных шара. Из нее вынимают подряд 2 шара. Найти вероятность того, что оба шара черные?
Продавец мороженного в солнечный день может заработать 12 $., а в дождливый – 6. Чему равна ожидаемая выручка, если вероятность того, что день окажется дождливым, равна 0,8?
В банк подано 7 заявок фирм на получение кредита. Вероятность получить кредит для каждой фирмы равна 0,8. Найти вероятность того, что из пяти фирм кредит получит ровно 4 фирмы?
Случайная величина задана функцией распределения:
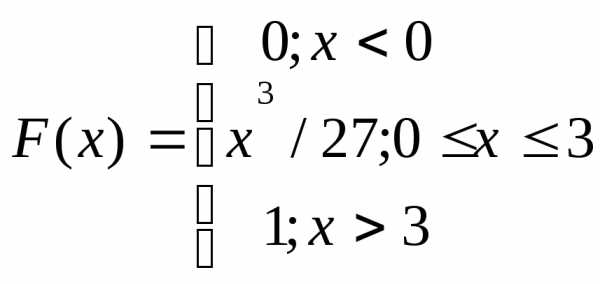
Найти плотность распределения случайной величины и вычислить
вероятность того, что  .
.
Коробки с шоколадом упаковываются автоматики чески: средний вес коробки равен 0,5 кГ, а его среднее квадратичное отклонение равно 0,1 кГ. Найти практически возможный максимальный вес одной коробки, если масса коробок поднимается нормальному закону распределения.
Из группы деталей делается случайная выборка ( с возвратом) 20 штук. Найти доверительный интервал для генерального среднего с вероятностью 0,95, если результаты выборки представлены в таблице:
Вес деталей, кГ
500
510
520
530
Количество (частота)
3
6
10
1
Предполагается произвести выборочное обследование 2000 ламп с целью установления продолжительности их горения. Каким должен быть объем повторной выборки, чтобы можно было гарантировать с вероятностью 0,9, что генеральное среднее отличается от выборочного по абсолютной величине меньше, чем на 20 часов, если генеральная дисперсия меньше 10000 часов.
Распределение признака Х в выборке дается следующим вариационным рядом:
3,0-3,6 | 3,6-4,2 | 4,2-4,8 | 4,8-5,4 | 5,4-6,0 | 6,0-6,6 | 6,6-7,2 |
2 | 8 | 35 | 43 | 22 | 15 | 5 |
При уровне значимости 0,01 проверить гипотезу о нормальном законе распределения по критерию Пирсона.
Из партии деталей делается случайная выборка 10 штук. Найти доверительный интервал для генерального среднего с вероятностью 0,95, если результаты выборки представлены в таблице
Вес деталей, кг | 400 | 410 | 420 | 430 |
Количество (частота) | 2 | 2 | 5 | 1 |
studfiles.net
Тест по «Теории вероятности и математической статистике» — тест
Ответ: распределение Стьюдента
Вопрос: 172 — й
При проверке гипотезы об однородности ряда вероятностей в случае полиномиального распределения используется:
Ответ: распределение Пирсона
Вопрос: 173 — й
При проверке значимости коэффициента корреляции с помощью таблицы Фишера-Иейтса коэффициент корреляции считается значимым, если:
Ответ: рассчитанное по выборке значение коэффициента корреляции превышает по модулю найденное по таблице критическое значение
Вопрос: 174 — й
Произведение каких событий есть событие невозможное?
Ответ: несовместных
Вопрос: 175 — й
Простой называют статистическую гипотезу:
Ответ: однозначно определяющую закон распределения
Вопрос: 176 — й
Симметричный ли интервал строится при оценивании генеральной дисперсии для заданной надѐжности γ?
Ответ: нет
Вопрос: 177 — й
Симметричный ли интервал строится при оценивании генеральной доли (вероятности) в случае большого объѐма наблюдений для заданной надѐжности γ?
Ответ: да
Вопрос: 178 — й
Симметричный ли интервал строится при оценивании генеральной средней для заданной надѐжности γ?
Ответ: да
Вопрос: 179 — й
Сколькими способами можно поставить 5 человек в очередь?
Ответ: 120
Вопрос: 180 — й
Сколькими способов жеребьѐвки существует для 5 участников конкурса?
Ответ: 120
Вопрос: 181 — й
Сколько различных двухбуквенных бессмысленных слов можно составить из букв К, Н, И, Г, А?
Ответ: 20
Вопрос: 182 — й
Сколько различных трѐхбуквенных бессмысленных слов можно составить из букв К, Н, И, Г, А?
Ответ: 60
Вопрос: 183 — й
Сложной называют статистическую гипотезу:
Ответ: не определяющую однозначно закон распределения
Вопрос: 184 — й
Согласно методу наименьших квадратов, в качестве оценок параметров двумерной линейной регрессионной модели следует использовать такие значения b0, b1, которые минимизируют сумму квадратов отклонений:
Ответ: фактических значений зависимой переменной от ее расчетных значений
Вопрос: 185 — й
Статистическим критерием
Ответ: правило, устанавливающее условия, при которых проверяемую гипотезу следует либо отвергнуть, либо не отвергнуть
Вопрос: 186 — й
Статистической гипотезой
Ответ: о виде или параметрах неизвестного закона распределения случайной величины
Вопрос: 187 — й
Сумма каких событий есть событие достоверное?
Ответ: противоположных
Вопрос: 188 — й
Точечную оценку называют эффективной, если она:
Ответ: обладает минимальной дисперсией среди всех несмещенных оценок
Вопрос: 189 — й
У какого распределения случайной величины вероятности рассчитываются по формуле Бернулли?
Ответ: биномиального
Вопрос: 190 — й
У какого распределения случайной величины вероятности рассчитываются по формуле Пуассона?
Ответ: Пуассоновского
Вопрос: 191 — й
Уравнение регрессии имеет вид ŷ=1,7+5,1x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:
Ответ: увеличится на 5,1
Вопрос: 192 — й
Уравнение регрессии имеет вид ŷ=1,7-5,1x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:
Ответ: уменьшится на 5,1
Вопрос: 193 — й
Уравнение регрессии имеет вид ŷ=5,1+1,7x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:
Ответ: увеличится на 1,7
Вопрос: 194 — й
Уравнение регрессии имеет вид ŷ=5,1-1,7x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:
Ответ: уменьшится на 1,7
Вопрос: 195 — й
Функция плотности вероятности непрерывной случайной величины есть … еѐ функции распределения
Ответ: производная
Вопрос: 196 — й
Функция распределения дискретной случайной величины есть функция:
Ответ: разрывная
Вопрос: 197 — й
Функция распределения любой случайной величины есть функция:
Ответ: неубывающая
Вопрос: 198 — й
Функция распределения непрерывной случайной величины есть функция:
Ответ: непрерывная
Вопрос: 199 — й
Функция распределения непрерывной случайной величины есть … еѐ функции плотности вероятности
Ответ: первообразная
Вопрос: 200 — й
Человек забыл последние две цифры номера телефона своего знакомого и, помня лишь, что они различны, пытается набрать номер наугад. Какова вероятность, что он дозвонится с первого раза?
Ответ: 1/90
Вопрос: 201 — й
Чем достигается репрезентативность выборки?
Ответ: случайностью отбора
Вопрос: 202 — й
Чему равна вероятность
Ответ: 1
Вопрос: 203 — й
Чему равна вероятность любого отдельно взятого значения непрерывной случайной величины?
Ответ: 0
Вопрос: 204 — й
Чему равна вероятность
Ответ: 0
Вопрос: 205 — й
Чему равна дисперсия
Ответ: 0
Вопрос: 206 — й
Чему равна дисперсия
Ответ: 8
Вопрос: 207 — й
Чему равна дисперсия
Ответ: 12
Вопрос: 208 — й
Чему равна дисперсия
Ответ: 12
Вопрос: 209 — й
Чему равна дисперсия
Ответ: 8
Вопрос: 210 — й
Чему равна дисперсия
Ответ: 8
Вопрос: 211 — й
Чему равна дисперсия
Ответ: 18
Вопрос: 212 — й
Чему равна сумма вероятностей всех значений дискретной случайной величины?
Ответ: 1
Вопрос: 213 — й
Чему равна сумма
Ответ: 1
Вопрос: 214 — й
Чему равно математическое ожидание случайной величины Y=2X+2, если математическое ожидание X равно 3?
Ответ: 8
Вопрос: 215 — й
Чему равно математическое ожидание случайной величины Y=2X-2, если математическое ожидание X равно 4?
Ответ: 6
Вопрос: 216 — й
Чему равно математическое ожидание случайной величины Y=2X-2, если математическое ожидание X равно 5?
Ответ: 8
Вопрос: 217 — й
Чему равно математическое ожидание случайной величины Y=4X+2, если математическое ожидание X равно 3?
Ответ: 14
Вопрос: 218 — й
Чему равно математическое ожидание постоянной величины?
Ответ: этой величине
Вопрос: 219 — й
Чему равно математическое ожидание произведения независимых случайных величин?
Ответ: произведению их математических ожиданий
Вопрос: 220 — й
Чему равно математическое ожидание суммы случайных величин?
Ответ: сумме их математических ожиданий
Вопрос: 221 — й
Что называют мощностью критерия 1-β?
Ответ: Нулевая гипотеза не верна и ее отвергают согласно критерию
Вопрос: 222 — й
Что называют мощностью критерия1-β?
Ответ: вероятность не допустить ошибку второго рода
Вопрос: 223 — й
Что называют ошибкой второго рода β ?
Ответ: Нулевая гипотеза не верна, но ее принимают согласно критерию
Вопрос: 224 — й
Что называют ошибкой первого рода α?
Ответ: Нулевая гипотеза верна, но ее отвергают согласно критерию
Вопрос: 225 — й
Что показывает множественный коэффициент корреляции?
Ответ: тесноту связи между одной величиной и совместным действием остальных величин
Вопрос: 226 — й
Что показывает парный коэффициент корреляции?
Ответ: тесноту связи между величинами X и Y на фоне действия остальных переменных
Вопрос: 227 — й
Что показывает частный коэффициент корреляции?
Ответ: тесноту связи между двумя переменными при фиксированном значении остальных
Вопрос: 228 — й
Что является несмещѐнной точечной оценкой генеральной дисперсии?
Ответ: исправленная выборочная дисперсия
Вопрос: 229 — й
Что является точечной оценкой генеральной дисперсии?
Ответ: выборочная дисперсия
Вопрос: 230 — й
Что является точечной оценкой генеральной доли или вероятности p?
Ответ: частость (относительная частота) события
Вопрос: 231 — й
Что является точечной оценкой математического ожидания?
Ответ: средняя арифметическая
Вопрос: 232 — й
Что является центром при построении доверительного интервала для генеральной доли или вероятности?
Ответ: частость (относительная частота) события
Вопрос: 233 — й
Что является центром при построении доверительного интервала для генеральной средней?
Ответ: средняя арифметическая
Вопрос: 234 — й
Ширина доверительного интервала при построении интервальных оценок зависит от:
Ответ: доверительной вероятности (надѐжности) и числа наблюдений
yaneuch.ru
Тест « Элементы теории вероятностей и математической статистики». II-ОЙ КУРС НПО.
ГПОБУ СПО СТ №30 г. МОСКВА
Учитель математики Хасянова Т.Г.
Тест « Элементы теории вероятностей и математической статистики»
II-ОЙ КУРС НПО
№1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
1) 30 2) 100 3) 120 4) 5
№2. В 9«Б» классе 32 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
1) 128 2) 35960 3) 36 4)46788
№3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
1) 10 2) 60 3) 20 4) 30
№4. Вычислить: 6! -5!
1) 600 2) 300 3) 1 4) 1000
№5. В ящике находится 45 шариков, из которых 17 белых. Потеряли 2 не белых шарика. Какова вероятность того, что выбранный наугад шарик будет белым?
1) 2) 3) 4)
№6. Бросают три монеты. Какова вероятность того, что выпадут два орла и одна решка?
1) 2) 0,5 3) 0,125 4)
№7. В денежно-вещевой лотерее на 1000000 билетов разыгрывается 1200 вещевых и 800 денежных выигрышей. Какова вероятность выигрыша?
1) 0,02 2) 0,00012 3) 0,0008 4) 0,002
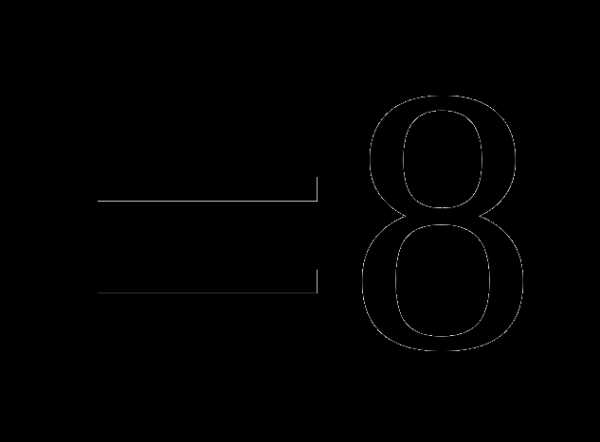
№8. ξ- непрерывная случайная величина с плотностью распределения φ(Х), заданной следующим образом:
φ(Х)=
Найти М(ξ), D(ξ).
3 и 0,078 2) 0,9 и 9/97 3) 9/12 и 0,076 4) 7,8 и 8,7
Ключи ответов.
№ задания
1
2
3
4
5
6
7 8
№ ответа
3
2
4
1
2
3
4 4
infourok.ru
Тесты по дисциплине «Теория вероятностей и математическая статистика»
Тесты по дисциплине «Теория вероятностей и математическая статистика»
Вариант 1
Случайным событием называется всякий факт, который обязательно происходит в результате опыта.
а) верно; б) неверно.Противоположные события представляют собой простейший случай полной группы событий.
а) да; б) нет.Из 4 букв разрезной азбуки составлено слово (стол). Найти вероятность того, что эти буквы, собранные в произвольном случайном порядке образуют (стол).
а) 1/24; б) 1/4; в) 0,5; г) 1/16; д) 4/9.Три орудия ведут огонь по цели, вероятность попадания в которую при одном выстреле из первого орудия 0,5, из второго – 0,6, из третьего – 0,7. Каждое орудие стреляет один раз. Чему равна вероятность поражения цели, если для этого достаточно двух попаданий?
а) 0,21; б) 0,35; в) 0,30; г) 0,5; д) 0,65.Игральная кость бросается четыре раза. Определить, чему равна вероятность того, что местерка появится хотя бы один раз?
а) 0,2; б) 0,4; в) 0,52; г) 1/6; д) 0,84.Используя общую теорему повторения опытов, можно найти вероятность того, что событие А появится в n опытах ровно m раз для случаев, когда в каждом опыте вероятность события А различна.
а) верно; б) неверно.Дисперсия постоянной величины равна:
а) единице; б) нулю; в) самой постоянной; г) квадрату самой постоянной.Имеется шесть ключей, из которых только один подходит к замку. Пусть Х = число попыток открыть замок, если ключ, не подошедший к замку, отбрасывается. Чему равно математическое ожидание случайной величины Х?
а) 3,5; б) 0,6; в) 1,5; г) 1/6; д) 0,5.Математическое ожидание случайной величины Х, распределенной по биномиальному закону равна:
а) npq; б) np; в) nq; г) pq.Случайная величина Х распределена по гауссовому закону. Найти вероятность того, что она отклонится от своего математического ожидания на величину большую, чем
 .
.
а) 0,5; б) 0,9; в) 0,3; г) 0,0027; д) 0.Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы двух случайных величин равен:
а) 0; б) +; в) -; г) 0,5; д) 1.
Матрица распределения системы двух дискретных случайных величин (Х,Y) задано таблицейyi xi
0
2
5
1
0,1
0
0,2
2
0
0,3
0
4
0,1
0,3
0
Чему равно математическое ожидание случайной величины Х?
а) 1; б) 2; в) 4; г) 2,5; д) 3,5.
Математическое ожидание произведения двух случайных величин X и Y выражается формулой
а) верно; б) неверно.Заданы ряды распределения двух независимых случайных величин X и Y:
| 0 | 1 | ||||||||||
qJ | 0,4 | 0,6 | ||||||||||
Чему равно математическое ожидание случайной величины ?
а) 0,5; б) 0; в) 0,3; г) 2,2; д) 3.
Теорема Чебышева устанавливает связь между частотой события и его вероятностью.
а) верно; б) неверно.Чему равно необходимое число опытов, которое нужно провести, чтобы отклонение частоты появления события А от вероятности его появления в отдельном опыте, равной 0,75, не превзошло по абсолютной величине 0,05 с вероятностью 0,96?
а) ≥1000; б) ≥500; в) ≥1875; г) ≤0,6; д) ≥2125.Математическая статистика – это наука, занимающаяся методами обработки результатов опытов или наблюдений над случайными явлениями.
а) верно; б) неверно.Оценка, для которой , называется:
а) состоятельной; б) эффективной;
в) несмещенной.Произведено п=400 опытов с целью определения вероятности р события А. Из этих 400 опытов в 101 появилось событие А. Найти вероятность того, что приняв
 , мы не сделаем ошибки больше, чем
, мы не сделаем ошибки больше, чем  =0,02.
=0,02.
а) 0,54; б) 0,642; в) 0,287; г) 0,43; д) 0,91.С помощью измерительного прибора, практически не имеющего систематической ошибки, было сделано восемь измерений некоторой величины. Результаты измерений следующие:
Номер измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
xi | 2504 | 2486 | 2525 | 2495 | 2515 | 2528 | 2492 | 2494 |
Определить несмещенную оценку дисперсии.
а) 48,5; б) 341,7; в) 12,9; г) 63,42; д) 221,1.
Вариант 2
Является ли событие «хотя бы раз при трехкратном бросании игрального кубика появится двойка» составным?
а) да; б) нет.Вероятностью случайного события А называется число, около которого группируются частоты этого события по мере увеличения количества опытов.
а) да; б) нет.В урне 3 белых и 5 черных шаров. Их урны вынимается один шар, отмечается его цвет и шар возвращается в урну. После чего из урны берется еще один шар. Чему равна вероятность того, что оба шара будут белыми?
а) 3/5; б) 3/8; в) 9/64; г) 9/25; д) 3/25.Абонент забыл последнюю цифру номера телефона и набирает ее наугад. Чему равна вероятность того, что ему придется звонить не более, чем четыре раза?
а) 0,4; б) 0,5; в) 0,6; г) 0,7; д) 0,8.Вероятности отказа одного из четырех приборов при независимых испытаниях различны и равны: 0,1; 0,2; 0,3; 0,4. Чему равна вероятность того, что откажут ровно два прибора?
а) 0,21; б) 0,42; в) 0,86; г) 0,6; д) 0,34.Случайной величиной называется величина Х, которая в результате опыта может принимать то или иной (но только одно) значение, причем, до опыта не известно, какое именно.
а) верно; б) неверно.Математическое ожидание имеет размерность квадрата размерности случайной величины.
а) верно; б) неверно.Имеется группа, состоящая из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна . Для решения этой задачи используют:
а) Формулу Бернулли ; б) Локальную теорему Лапласа ; в) Интегральную теорему Лапласа; г) Формулу Пуассона.
Математическое ожидание случайной величины Х, распределенной по биномиальному закону равна:
а) npq; б) np; в) nq; г) pq.Функция Лапласа обладает следующим свойством: Ф(0)=0.
а) верно; б) неверно.Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами
а) верно; б) неверно.Матрица распределения системы двух дискретных случайных величин (Х,Y) задано таблицей
yi xi | 0 | 2 | 5 |
1 | 0,1 | 0 | 0,2 |
2 | 0 | 0,3 | 0 |
4 | 0,1 | 0,3 | 0 |
Чему равна дисперсия случайной величины Y.
а) 2; б) 5; в) 3,5; г) 2,56; д) 2,2.
Формула верна, если X и Y
а) независимы; б) некоррелированы.Заданы ряды распределения двух независимых случайных величин X и Y:
| 0 | 1 | ||||||||||
qJ | 0,4 | 0,6 | ||||||||||
Чему равна дисперсия случайной величины ?
а) 0,9; б) 0,3; в) 1,15; г) 5,6; д) 0,21.
Теорема Бернулли устанавливает свойство устойчивости среднеарифметического.
а) верно; б) неверно.Вероятность наступления события А в каждом независимом опыте равна 0,4. Чему равна вероятность того, что в 20 000 испытаний отклонение частоты события А от его вероятности не превзойдет по абсолютной величине 0,01?
а) ≥0,58; б) ≤0,2; в) ≥0,42; г) ≥0,88; д) ≥0,24.Математическая статистика – это наука, занимающаяся методами обработки результатов опытов или наблюдений над случайными явлениями.
а) верно; б) неверно.Эффективной называется такая оценка
 , которая при увеличении числа опытов сходилась бы по вероятности к исходному значению
, которая при увеличении числа опытов сходилась бы по вероятности к исходному значению  .
.
а) верно; б) неверно.Произведено 400 опытов с целью определения вероятности р события А. Из этих 400 опытов в 101 появилось событие А. Сколько опытов надо произвести, чтобы ошибка приближенного равенства
 не превысила 0,02 с вероятностью не меньше, чем 0,9?
не превысила 0,02 с вероятностью не меньше, чем 0,9?
а) ≥500; б) ≥1000; в) ≤180; г) ≥1271; д) ≥1645.Какой из критерий согласия используется для проверки гипотезы о виде закона распределения, когда параметры предлагаемого закона определяются на основании опытных данных?
а) критерий согласия х2; б) критерий Колмогорова.
multiurok.ru

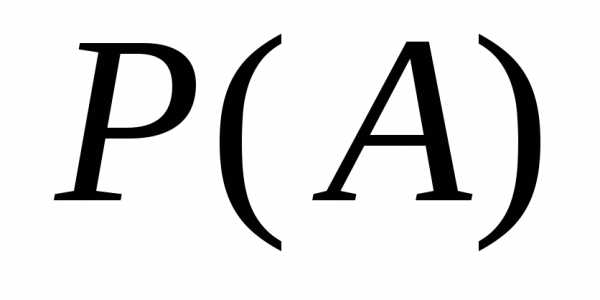 это:
это: ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;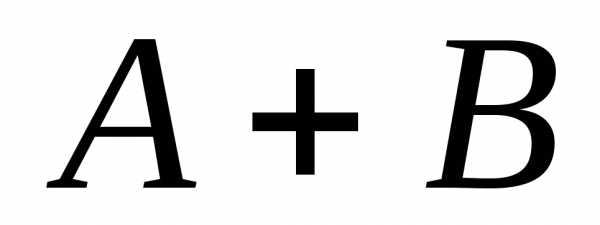 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;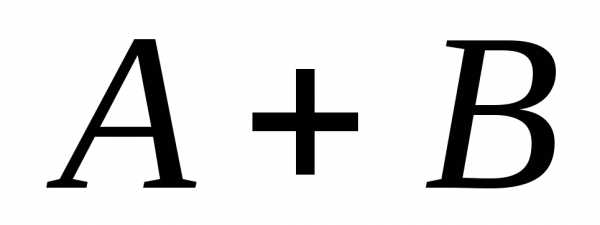 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
; ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;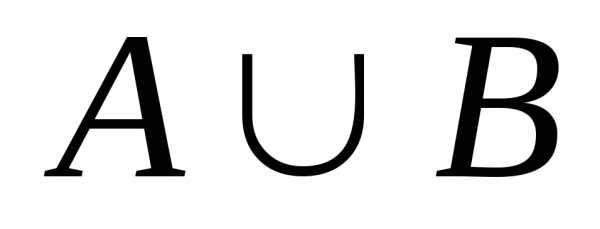 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
; ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;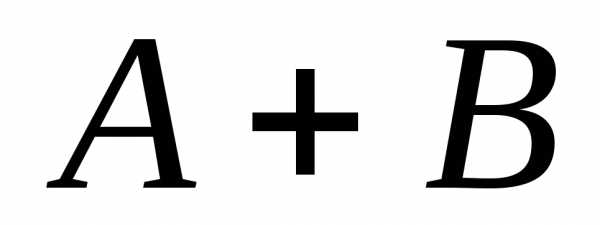 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию или
или ;
;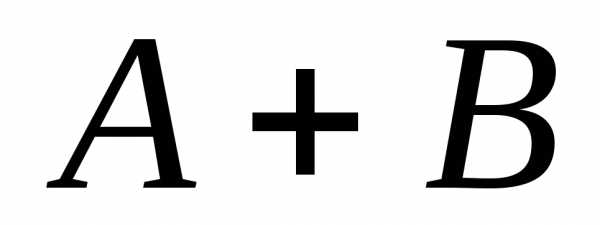 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
; ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;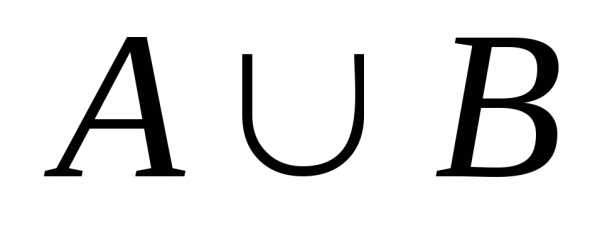 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию и
и ;
;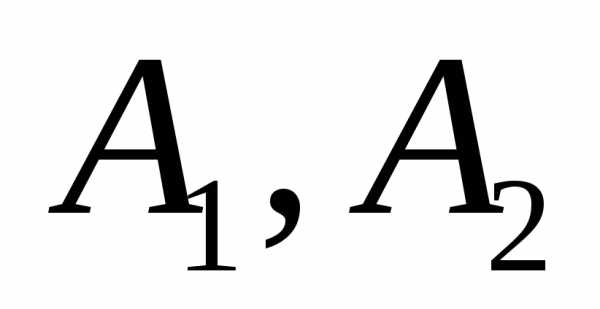 равна:
равна: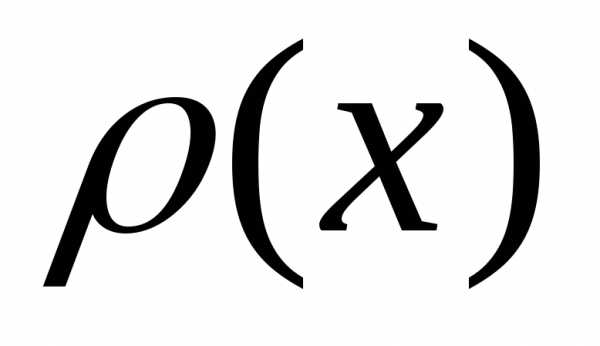 это:
это: -того
порядка, мода и медиана;
-того
порядка, мода и медиана; -того
порядка, среднее геометрическое, мода
и медиана;
-того
порядка, среднее геометрическое, мода
и медиана; -того
порядка.
-того
порядка. -того
порядка.
-того
порядка. -того
порядка, эксцесс, асимметрия.
-того
порядка, эксцесс, асимметрия.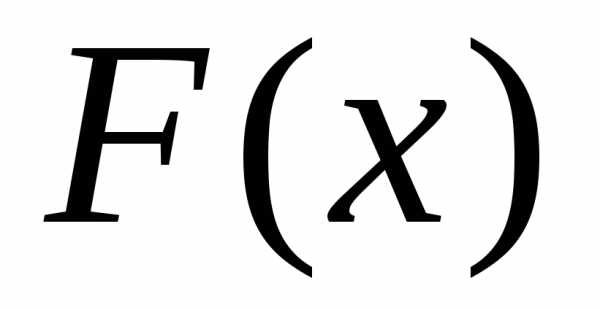 и
функция плотности распределения имеют
и
функция плотности распределения имеют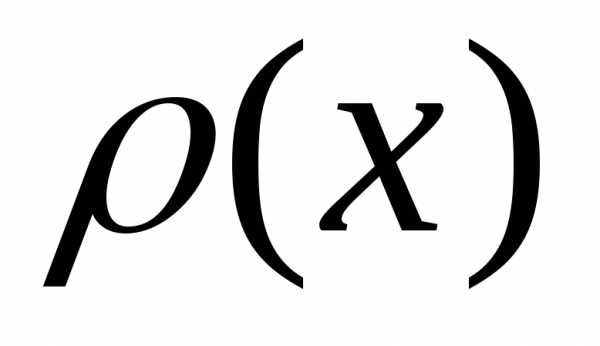 следующие
свойства:
следующие
свойства: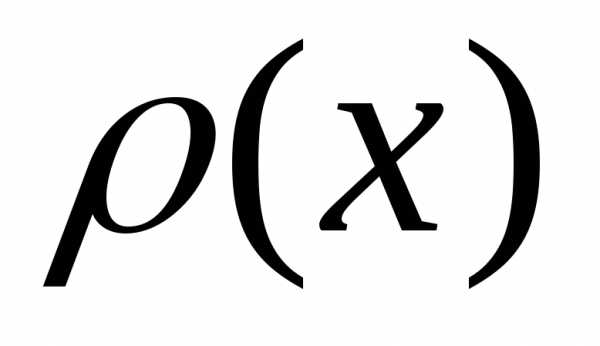 :
: равен:
равен: сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;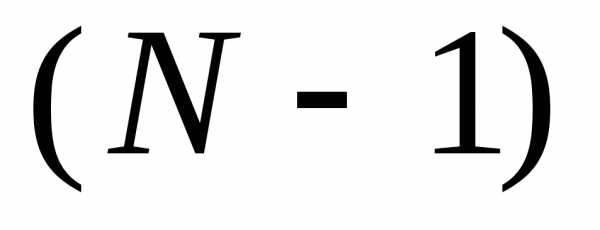 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;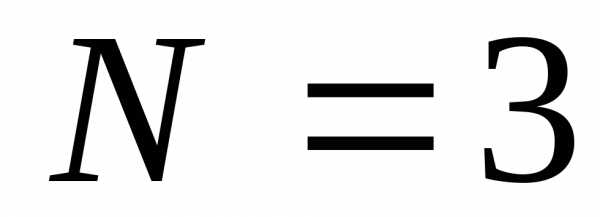 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;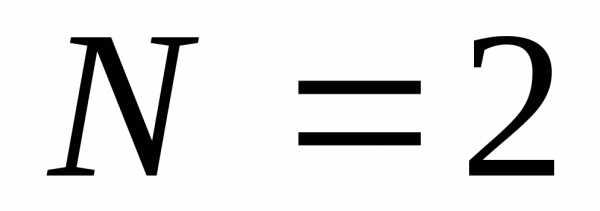 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;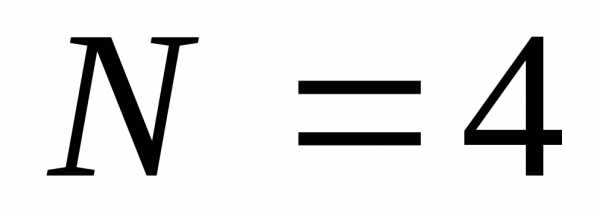 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса; .
.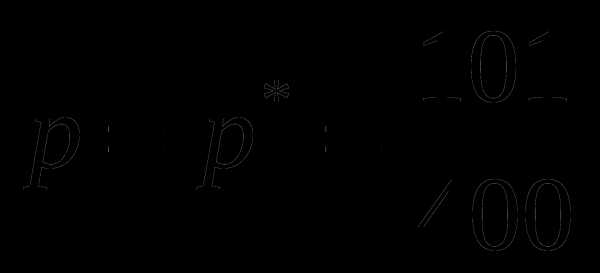 , мы не сделаем ошибки больше, чем
, мы не сделаем ошибки больше, чем  =0,02.
=0,02. , которая при увеличении числа опытов сходилась бы по вероятности к исходному значению
, которая при увеличении числа опытов сходилась бы по вероятности к исходному значению  .
. не превысила 0,02 с вероятностью не меньше, чем 0,9?
не превысила 0,02 с вероятностью не меньше, чем 0,9?