Решите неравенство х 2 х 3 больше 0: Решите неравенство х-2 / 3-х больше или равно 0

Содержание

Решение Неравенств через Метод Интервалов

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

a, b, c — числа,

при этом а ≠ 0.

Квадратное неравенство можно решить двумя способами:

графический метод;
метод интервалов.

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную онлайн-школу Skysmart.

Наши преподаватели понятно объяснят что угодно — от дробей до неравенств — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, <, ≤, ≥.

Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.

Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. 2 + bx + c из левой части квадратного неравенства.

Изобразить координатную прямую и при наличии корней отметить их на ней.

Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.

Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками.

Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.

В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.

Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −. 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.

Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.

Когда квадратный трехчлен корней не имеет (D < 0), то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.

Теперь мы знаем пошаговый алгоритм. 2 — 5x + 6 ≥ 0.

Как решаем:

Разложим квадратный трехчлен на множители.
Неравенство примет вид:
(х — 3) * (х — 2) ≥ 0

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х < 0 это выражение отрицательно: х — 3 < 0, а при х > 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.
х < 0 — на этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию, можно взять любое значение из этого интервала и подставить его в произведение. Например: х = -1. Подставляем:
(-1 — 3) * (-1 — 2) = -4 * (-3) = 12
12 > 0
Вывод: при х < 0 верно неравенство (х — 3) * (х — 2) > 0.
Отобразим эти данные на чертеже:

2 < x < 3 — на этом интервале ситуация не меняется, значит, для того, чтобы определить ситуацию нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 2,5.

Подставляем:
- (2,5 — 3) (2,5 — 2) = -0,5 * 0,5 = — 0,25 < 0
Вывод: при 2 < x < 3 верно неравенство (х — 3) * (х — 2) < 0. Отметим на чертеже:

х > 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
Подставляем:
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
(x — 3) * (x + 3/2) > 0.
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3 < 0.

Как решить неравенство методом интервалов нам уже известно. Поэтому можем оформить решение кратко:

Ответ: -3 < x < -2.

Пример 3. Выполнить решение квадратного неравенства методом интервалов:

Как решаем:

Находим корни квадратного трехчлена, который находится в левой части:

Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:

Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞).
Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус.

Фиксируем знаки: −, −:
Так как мы решаем неравенство со знаком <, то изобразим штриховку над интервалами со знаками минус:
Очевидно, решениями являются оба промежутка (−∞, 7), (7, +∞).

Ответ: (−∞, 7), (7, +∞).

В онлайн-школе Skysmart ученики решают такие задачки на специальной онлайн-доске. А еще отслеживают личный прогресс и получают поддержку учителя по самым коварным вопросам.

Запишите ребенка на бесплатный вводный урок математики: покажем, как у нас все устроено и вдохновим на учебу!

Внеклассный урок — Уравнения и неравенства с модулем

Уравнения и неравенства с модулем

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.

Например, модулем числа 6 является 6, модулем числа –6 тоже является 6.

То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.

Обозначается так: |6|, |х|, |а| и т.д.

(Подробнее – в разделе «Модуль числа»).

Уравнения с модулем.

Пример 1. Решить уравнение

|10х – 5| = 15.

Решение.

В соответствии с правилом, уравнение равносильно совокупности двух уравнений:

│10х – 5 = 15
│10х – 5 = –15

Решаем:

│10х = 15 + 5 = 20
│10х = –15 + 5 = –10

↕

│х = 20 : 10
│х = –10 : 10

↕

│х = 2
│х = –1

Ответ: х₁ = 2, х₂ = –1.

Пример 2. Решить уравнение

|2х + 1| = х + 2.

Решение.

Поскольку модуль – число неотрицательное, то х + 2 ≥ 0. Соответственно:

х ≥ –2.

Составляем два уравнения:

│2х + 1 = х + 2
│2х + 1 = –(х + 2)

Решаем:

│2х + 1 = х + 2
│2х + 1 = –х – 2

↕

│2х – х = 2 – 1
│2х + х = –2 – 1

↕

│х = 1
│х = –1

Оба числа больше –2. Значит, оба являются корнями уравнения.

Ответ: х₁ = –1, х₂ = 1.

Пример 3. Решить уравнение

|х + 3| – 1
————— = 4
х – 1

Решение.

Уравнение имеет смысл, если знаменатель не равен нулю – значит, если х ≠ 1. Учтем это условие. Наше первое действие простое – не просто освобождаемся от дроби, а преобразуем ее так, чтобы получить подмодульное выражение в чистом виде:

|х + 3| – 1 = 4 · (х – 1),

|х + 3| – 1 = 4х – 4,

|х + 3| = 4х – 4 + 1,

|х + 3| = 4х – 3.

Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.

Модуль числа есть неотрицательное число – то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:

4х – 3 ≥ 0

4х ≥ 3

х ≥ 3/4

Таким образом, у нас появилось второе условие: корень или корни уравнения должны быть не меньше 3/4.

В соответствии с правилом модуля составляем совокупность двух уравнений и решаем их:

│х + 3 = 4х – 3
│х + 3 = –(4х – 3)

↕

│ х + 3 = 4х – 3
│ х + 3 = –4х + 3

↕

│х – 4х = –3 – 3
│х + 4х = 3 – 3

↕

│х = 2
│х = 0

Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.

У нас было два условия: корень уравнения должен быть не меньше 3/4, но не может быть равен 1. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.

Ответ: х = 2.

Неравенства с модулем.

Пример 1. Решить неравенство:

|х — 3| < 4

Решение.

Правило модуля гласит:

|а| = а, если а ≥ 0.
|а| = –а, если а < 0.

Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая:
х – 3 ≥ 0 и х – 3 < 0.

1) При х – 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:

х – 3 < 4.

2) При х – 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

–(х – 3) < 4. Раскрыв скобки, получаем:

–х + 3 < 4.

Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:

│ х – 3 ≥ 0
│ х – 3 < 4

│ х – 3 < 0
│–х + 3 < 4

Решим их:

│х ≥ 3
│ х < 7

│х < 3
│х > –1

Итак, у нас в ответе объединение двух множеств:

3 ≤ х < 7 U –1 < х < 3.

Определяем наименьшее и наибольшее значения. Это –1 и 7. При этом х больше –1, но меньше 7. Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от –1 до 7, исключая эти крайние числа.

Ответ: –1 < х < 7.

Или: х ∈ (–1; 7).

Дополнения.

1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).

Выражение |х — 3| < 4 означает, что расстояние от точки х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа – к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.

При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:

–1 < х < 7.

2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:

–4 < х – 3 < 4.

Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число –4 являются границами решения неравенства.

Далее мы просто переносим влево и вправо число –3 с обратным знаком, оставляя х в одиночестве:

–4 + 3 < х < 4 + 3

–1 < х < 7.

Пример 2. Решить неравенство

|х – 2| ≥ 5

Решение.

Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны –3 и больше или равны 7. А значит, мы уже получили ответ.

Ответ: –3 ≥ х ≥ 7.

Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:

–5 ≥ х – 2 ≥ 5

–5 + 2 ≥ х ≥ 5 + 2

Ответ тот же: –3 ≥ х ≥ 7.

Или: х ∈ [–3; 7]

Пример решен.

Пример 3. Решить неравенство:

6х² – |х| – 2 ≤ 0

Решение.

Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х < 0. При х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:

6х² – х – 2 ≤ 0.

Теперь о втором случае: если х < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6х² – (–х) – 2 ≤ 0.

Раскрываем скобки:

6х² + х – 2 ≤ 0.

Таким образом, мы получили две системы уравнений:

│6х² – х – 2 ≤ 0
│ х ≥ 0

│6х² + х – 2 ≤ 0
│ х < 0

Надо решить неравенства в системах – а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.

Начнем с первого:

6х² – х – 2 = 0.

Как решается квадратное уравнение – см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:

х₁ = –1/2, х₂ = 2/3.

Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от –1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[–1/2; 2/3].

Теперь решим второе квадратное уравнение:

6х² + х – 2 = 0.

Его корни:

х₁ = –2/3, х₂ = 1/2.

Вывод: при х < 0 корнями исходного неравенства являются также все числа от –2/3 до 1/2.

Объединим два ответа и получим итоговый ответ: решением является все множество чисел от –2/3 до 2/3, включая и эти крайние числа.

Ответ: –2/3 ≤ х ≤ 2/3.

Или: х ∈ [–2/3; 2/3].

x 2 x больше или равно 0

Вы искали x 2 x больше или равно 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x 2 больше или равно 0, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x 2 x больше или равно 0».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как x 2 x больше или равно 0,x 2 больше или равно 0,решите неравенство x2 x больше или равно 0,х 2 х больше или равно 0.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и x 2 x больше или равно 0. Просто введите задачу в окошко и нажмите «решить» здесь (например, решите неравенство x2 x больше или равно 0).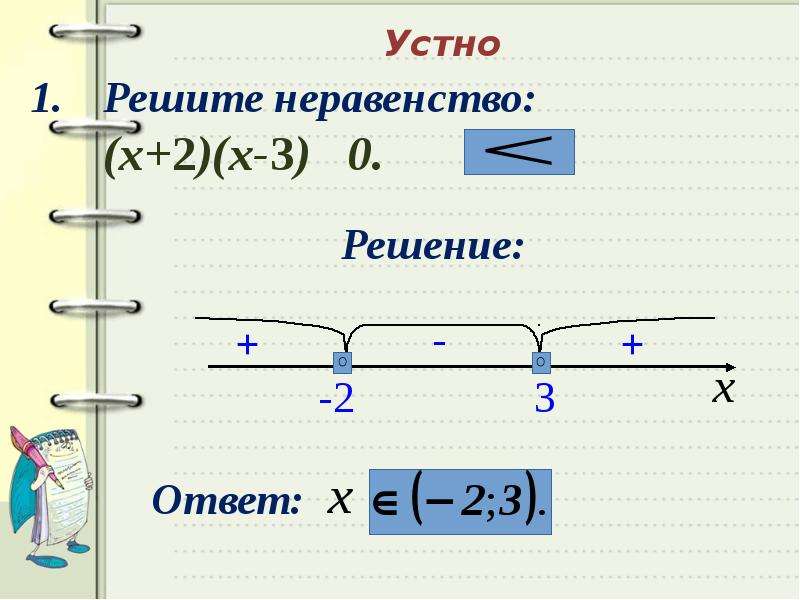

Где можно решить любую задачу по математике, а так же x 2 x больше или равно 0 Онлайн?

Решить задачу x 2 x больше или равно 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Квадратное неравенство

Квадратное неравенство – «ОТ и ДО». В этой статье мы с вами рассмотрим решение квадратных неравенств что называется до тонкостей. Изучать материал статьи рекомендую внимательно ничего не пропуская. Осилить статью сразу не получится, рекомендую сделать это за несколько подходов, информации много.

Содержание:

Вступление. Важно!
Алгоритм решения квадратного неравенства. Метод интервалов. Примеры.
Использование графика квадратичной функции. Рекомендую!
Решение квадратного неравенства. Все случаи…

Вступление. Важно!

Рекомендую повторить формулы для решения квадратного уравнения и научиться быстро его решать. Без этого о решении квадратных неравенств речи быть не может.

Квадратное неравенство – это неравенство вида:

Если взять квадратное уравнение и заменить знак равенства на любой из указанных выше, то получится квадратное неравенство. Решить неравенство — это значит ответить на вопрос, при каких значениях х данное неравенство будет верно. Примеры:

10x²– 6x+12 ≤ 0

2x²+ 5x –500 > 0

– 15x²– 2x+13 > 0

8x²– 15x+45≠ 0

Квадратное неравенство может быть задано в неявном виде, например:

10x²– 6x+14x² –5x +2≤ 56

2x² > 36

8x²<–15x²– 2x+13

0> – 15x²– 2x+13

В этом случае необходимо выполнить алгебраические преобразования и привести его к стандартному виду (1).

*Коэффициенты могут быть и дробными и иррациональными, но в школьной программе такие примеры редкость, а в заданиях ЕГЭ не встречаются вообще. Но вы не пугайтесь, если, например, встретите:

Это тоже квадратное неравенство.

Сначала рассмотрим простой алгоритм решения, не требующий понимания того, что такое квадратичная функция и как её график выглядит на координатной плоскости относительно осей координат. Если вы способны запоминать информацию крепко и надолго, при этом регулярно подкрепляете её практикой, то алгоритм вам поможет. Так же если вам, как говорится, нужно решить такое неравенство «наразок», то алгоритм вам в помощь. Следуя ему вы без труда осуществите решение.

Если же вы учитесь в школе, то настоятельно рекомендую вам начать изучение статьи со второй части, где рассказывается весь смысл решения (смотрите ниже с пункта – использование графика квадратичной функции). Если будет понимание сути, то не учить, не запоминать указанный алгоритм будет не нужно, вы без труда быстро решите любое квадратное неравенство.

Конечно, следовало бы сразу начать разъяснение именно с графика квадратичной функции и oбъяснения самого смысла, но решил «построить» статью именно так.

Ещё один теоретический момент! Посмотрите формулу разложения квадратного трёхчлена на множители:

где х₁ и х₂ — корни квадратного уравнения ax²+bx+c=0

*Для того, чтобы решить квадратное неравенство, необходимо будет квадратный трёхчлен разложить на множители.

Представленный ниже алгоритм называют ещё методом интервалов. Он подходит для решения неравенств вида f(x)>0, f(x)<0, f(x)≥0 и f(x)≤0. Обратите внимание, что множителей может более двух, например:

(х–10)(х+5)(х–1)(х+104)(х+6)(х–1)<0

Алгоритм решения. Метод интервалов. Примеры.

Дано неравенство ax²+ bx + с > 0 (знак любой).

1. Записываем квадратное уравнение ax²+ bx + с = 0 и решаем его. Получаем х₁ и х₂ – корни квадратного уравнения.

2. Подставляем в формулу (2) коэффициент a и корни. Записываем неравенство в виде:

a (x – x₁)(x – x₂)>0

3. Определяем интервалы на числовой прямой (корни уравнения делят числовую ось на интервалы):

4. Определяем «знаки» на интервалах (+ или –) путём подстановки произвольного значения «х» из каждого полученного интервала в выражение:

a (x – x₁)(x – x₂)

и отмечаем их.

5. Остаётся лишь выписать интересующие нас интервалы, они отмечены:

— знаком «+», если в неравенстве стояло «>0» или «≥0».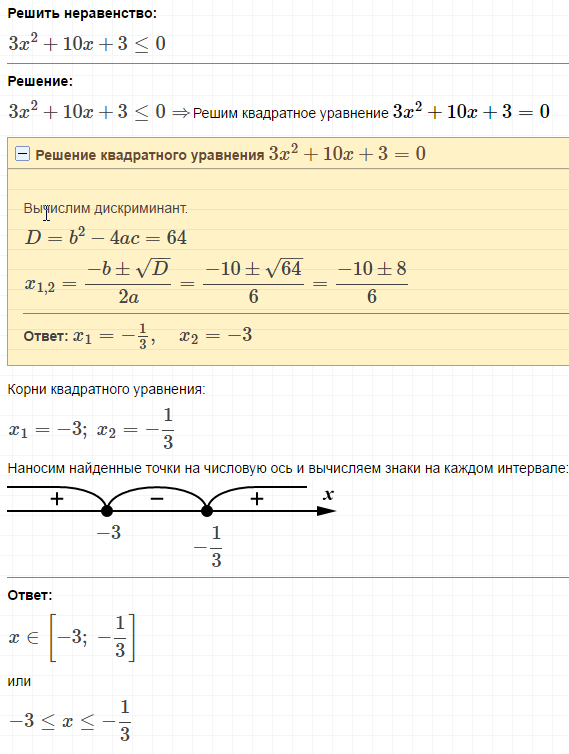

— знаком «–», если в неравенстве было «<0» или «≤0».

Далее записываем ответ.

ОБРАТИТЕ ВНИМАНИЕ!!! Сами знаки в неравенстве могут быть:

строгими – это «>», «<» и нестрогими – это «≥», «≤».

Как это влияет на результат решения?

При строгих знаках неравенства границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде (x₁;x₂) – скобки круглые.

При нестрогих знаках неравенства границы интервала ВХОДЯТ в решение, и ответ записывается в виде [x₁;x₂] – скобки квадратные.

*Это касается не только квадратных неравенств. Квадратная скобка означает, что сама граница интервала включена в решение.

На примерах вы это увидите. Давайте разберём несколько, чтобы снять все вопросы по этому поводу. В теории алгоритм может показаться несколько сложным, на самом деле всё просто.

ПРИМЕР 1: Решить x²– 60x+500 ≤ 0

Решаем квадратное уравнение x²–60x+500=0

D = b²–4ac = (–60)²–4∙1∙500 = 3600–2000 = 1600

Находим корни:

Подставляем коэффициент a и корни в формулу (2), получаем:

x²–60x+500 = (х–50)(х–10)

Записываем неравенство в виде (х–50)(х–10) ≤ 0

Корни уравнения делят числовую ось на интервалы. Покажем их на числовой прямой:

Мы получили три интервала (–∞;10), (10;50) и (50;+∞).

Определяем «знаки» на интервалах, делаем это путём подстановки в выражение (х–50)(х–10) произвольных значений их каждого полученного интервала и смотрим соответствие полученного «знака» знаку в неравенстве (х–50)(х–10) ≤ 0:

при х=2 (х–50)(х–10) = 384 > 0 неверно

при х=20 (х–50)(х–10) = –300 < 0 верно

при х=60 (х–50)(х–10) = 500 > 0 неверно

Решением будет являться интервал [10;50].

При всех значениях х из этого интервала неравенство будет верным.

*Обратите внимание, что мы поставили квадратные скобки.

При х = 10 и х = 50 неравенство также будет верно, то есть границы входят в решение.

Ответ: x∊[10;50]

Ещё раз:

— Границы интервала ВХОДЯТ в решение неравенства тогда, когда в условии стоит знак ≤ или ≥ (нестрогое неравенство). При этом на эскизе принято полученные корни отображать ЗАШТРИШОВАННЫМ кружком.

— Границы интервала НЕ ВХОДЯТ в решение неравенства тогда, когда в условии стоит знак < или > (строгое неравенство). При этом на эскизе принято корень отображать НЕЗАШТРИХОВАННЫМ кружком.

ПРИМЕР 2: Решить x²+ 4x–21 > 0

Решаем квадратное уравнение x²+ 4x–21 = 0

D = b²–4ac = 4²–4∙1∙(–21) =16+84 = 100

Находим корни:

Подставляем коэффициент a и корни в формулу (2), получаем:

x²+ 4x–21 = (х–3)(х+7)

Записываем неравенство в виде (х–3)(х+7) > 0.

Корни уравнения делят числовую ось на интервалы. Отметим их на числовой прямой:

*Неравенство нестрогое, поэтому обозначения корней НЕзаштрихованы. Получили три интервала (–∞;–7), (–7;3) и (3;+∞).

Определяем «знаки» на интервалах, делаем это путём подстановки в выражение (х–3)(х+7) произвольных значений их этих интервалов и смотрим соответствие неравенству (х–3)(х+7)> 0:

при х= –10 (–10–3)( –10 +7) = 39 > 0 верно

при х= 0 (0–3)(0 +7) = –21 < 0 неверно

при х=10 (10–3)(10 +7) = 119 > 0 верно

Решением будут являться два интервала (–∞;–7) и (3;+∞). При всех значениях х из этих интервалов неравенство будет верным.

*Обратите внимание, что мы поставили круглые скобки. При х = 3 и х = –7 неравенство будет неверным – границы не входят в решение.

Ответ: x∊(–∞;–7) U (3;+∞)

ПРИМЕР 3: Решить –x²–9x–20 > 0

Решаем квадратное уравнение –x²–9x–20 = 0.

a = –1 b = –9 c = –20

D = b²–4ac = (–9)²–4∙(–1)∙ (–20) =81–80 = 1.

Находим корни:

Подставляем коэффициент a и корни в формулу (2), получаем:

–x²–9x–20 =–(х–(–5))(х–(–4))= –(х+5)(х+4)

Записываем неравенство в виде –(х+5)(х+4) > 0.

Корни уравнения делят числовую ось на интервалы. Отметим на числовой прямой:

*Неравенство строгое, поэтому обозначения корней незаштрихованы. Получили три интервала (–∞;–5), (–5; –4) и (–4;+∞).

Определяем «знаки» на интервалах, делаем это путём подстановки в выражение –(х+5)(х+4) произвольных значений их этих интервалов и смотрим соответствие неравенству –(х+5)(х+4)>0:

при х= –10 – (–10+5)( –10 +4) = –30 < 0 неверно

при х= –4,5 – (–4,5+5)(–4,5+4) = 0,25 > 0 верно

при х= 0 – (0+5)(0 +4) = –20 < 0 неверно

Решением будут являться интервал (–5;–4). При всех значениях «х» принадлежащих ему неравенство будет верным.

*Обратите внимание, что границы не входят в решение. При х = –5 и х = –4 неравенство будет неверным.

ЗАМЕЧАНИЕ!

При решении квадратного уравнения у нас может получится один корень или корней не будет вовсе, тогда при использовании данного метода вслепую могут возникнуть затруднения в определении решения.

Небольшой итог! Метод хорош и использовать его удобно, особенно если вы знакомы с квадратичной функцией и знаете свойства её графика. Если нет, то прошу ознакомиться, приступим к следующему разделу.

Использование графика квадратичной функции. Рекомендую!

Квадратичная это функция вида:

Её графиком является парабола, ветви параболы направлены вверх, либо вниз:

График может быть расположен следующим образом: может пересекать ось х в двух точках, может касаться её в одной точке (вершиной), может не пересекать. Об этом подробнее в дальнейшем.

Теперь рассмотрим этот подход на примере.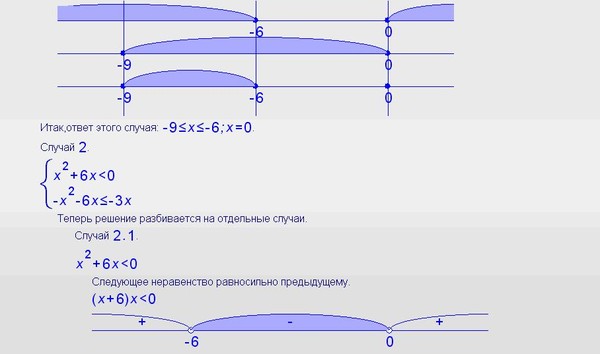 Весь процесс решения состоит из трёх этапов. Решим неравенство x²+2x –8 >0.

Первый этап

Решаем уравнение x²+2x–8=0.

D = b²–4ac = 2²–4∙1∙(–8) = 4+32 = 36

Находим корни:

Получили х₁=2 и х₂ = – 4.

Второй этап

Строим параболу у= x²+2x–8 по точкам:

Точки – 4 и 2 это точки пересечения параболы и оси ох. Всё просто! Что сделали? Мы решили квадратное уравнение x²+2x–8=0. Посмотрите его запись в таком виде:

0 = x²+2x – 8

Ноль у нас это значение «у». При у = 0, мы получаем абсциссы точек пересечения параболы с осью ох. Можно сказать, что нулевое значение «у» это есть ось ох.

Теперь посмотрите при каких значениях х выражение x²+2x – 8 больше (или меньше) нуля? По графику параболы это определить несложно, как говорится, всё на виду:

1. При х < – 4 ветвь параболы лежит выше оси ох. То есть при указанных х трёхчлен x²+2x –8 будет положительным.

2. При –4 < х < 2 график ниже оси ох. При этих х трёхчлен x²+2x –8 будет отрицательным.

3. При х > 2 ветвь параболы лежит выше оси ох. При указанных х трёхчлен x²+2x –8 будет положительным.

Третий этап

По параболе нам сразу видно, при каких х выражение x²+2x–8 больше нуля, равно нулю, меньше нуля. В этом заключается суть третьего этапа решения, а именно увидеть и определить положительные и отрицательные области на рисунке. Сопоставляем полученный результат с исходным неравенством и записываем ответ. В нашем примере необходимо определить все значения х при которых выражение x²+2x–8 больше нуля. Мы это сделали во втором этапе.

Остаётся записать ответ.

Ответ: x∊(–∞;–4) U (2;∞).

Подведём итог: вычислив в первом шаге корни уравнения, мы можем отметить полученные точки на оси ох (это точки пересечения параболы с осью ох). Далее схематично строим параболу и уже можем увидеть решение. Почему схематично? Математически точный график нам не нужен. Да и представьте, например, если корни получатся 10 и 1500, попробуй-ка построй точный график на листе в клетку с таким разбегом значений. Возникает вопрос! Ну получили мы корни, ну отметили их на оси ох, а зарисовать расположение самой парабола – ветвями вверх или вниз? Тут всё просто! Коэффициент при х² вам подскажет:

— если он больше нуля, то ветви параболы направлены вверх.

— если меньше нуля, то ветви параболы направлены вниз.

В нашем примере он равен единице, то есть положителен.

*Примечание! Если в неравенстве будет стоять знак нестрогий, то есть ≤ или ≥, то корни на числовой прямой следует заштриховать, этим условно обозначается, что сама граница интервала входит в решение неравенства. В данном случае корни не заштрихованы (выколоты), так как неравенство у нас строгое (стоит знак «>»). При чем в ответе, в данном случае, ставятся круглые скобки, а не квадратные (границы не входят в решение).

Написано много, кого-то запутал, наверное. Но если вы решите минимум 5 неравенств с использованием парабол, то восхищению вашему предела не будет. Всё просто!

Итак, кратко:

1. Записываем неравенство, приводим к стандартному.

2. Записываем квадратное уравнение и решаем его.

3. Рисуем ось ох, отмечаем полученные корни, схематично рисуем параболу, ветвями вверх, если коэффициент при х² положителен, или ветвями вниз, если он отрицателен.

4. Определяем визуально положительные или отрицательные области и записываем ответ по исходному неравенству.

Рассмотрим примеры.

ПРИМЕР 1: Решить x²–15x+50 > 0

Первый этап.

Решаем квадратное уравнение x²–15x+50=0

D = b²–4ac = (–15)²–4∙1∙50 = 225–200 = 25

Находим корни:

Второй этап.

Строим ось ох. Отмечем полученные корни. Так как неравенство у нас строгое, то заштриховывать их не будем. Схематично строим параболу, расположена она ветвями вверх, так как коэффициент при х² положительный:

Третий этап.

Определяем визуально положительные и отрицательные области, здесь мы их отметили разными цветами для наглядности, можно этого и не делать.

Записываем ответ.

Ответ: x∊(–∞;5) U (10;∞).

*Знак U обозначает объёдинение решение. Образно можно выразиться так, решением является «этот» И « ещё этот» интервал.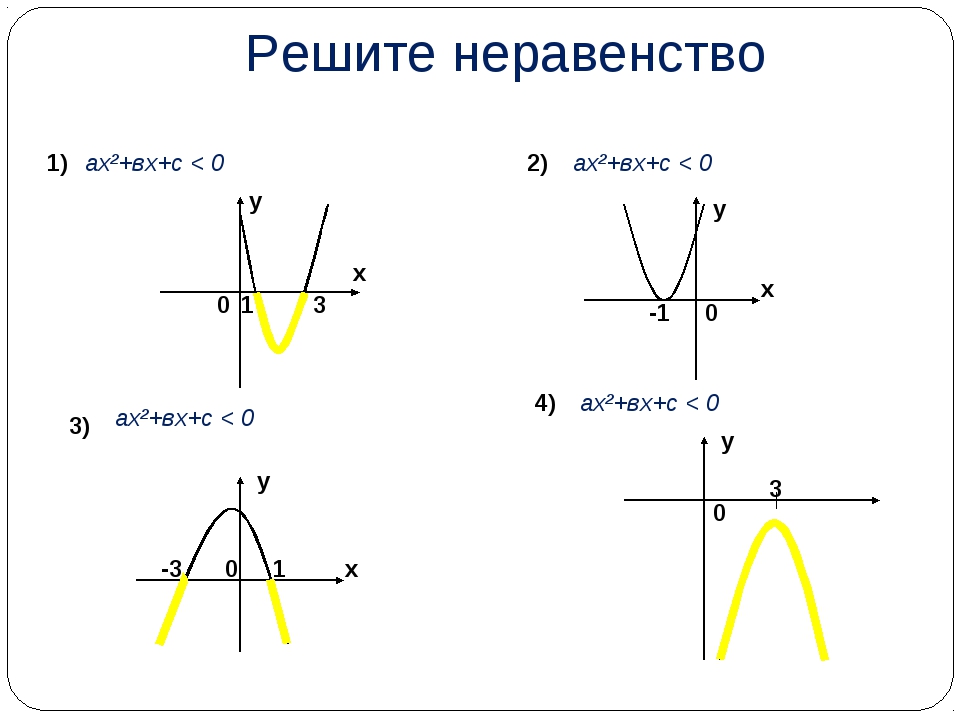

ПРИМЕР 2: Решить –x²+x+20 ≤ 0

Первый этап.

Решаем квадратное уравнение –x²+x+20=0

D = b²–4ac = 1²–4∙(–1)∙20 = 1+80 = 81

Находим корни:

Второй этап.

Строим ось ох. Отмечем полученные корни. Так как неравенство у нас нестрогое, то заштрихуем обозначения корней. Схематично строим параболу, расположена она ветвями вниз, так как коэффициент при х² отрицательный (он равен –1):

Третий этап.

Определяем визуально положительные и отрицательные области. Сопоставляем с исходным неравенством (знак у нас ≤ 0). Неравенство будет верно при х ≤ – 4 и х ≥ 5.

Записываем ответ.

Ответ: x∊(–∞;–4] U [5;∞).

*Указаны квадратные скобки – это обозначает, что границы интервала входят в решение. Ось оу мы на эскизах не указали, так как она в данной ситуации не играет никакой роли, то есть при построении эскиза ось оу строить необязательно.

Теперь ещё один важный момент! Мы рассмотрели примеры, в которых при решении квадратного уравнения получается два корня, то есть парабола пересекает ось ох в двух точках. Процесс решения понятен. Но возникают вопросы: а если при решении квадратного уравнения получится один корень или вообще не будет корней (дискриминант отрицательный), то как это осмыслить и как определить есть ли решение?

Некоторые ответы очевидны:

— Если получится один корень (дискриминант равен нулю), то парабола будет касаться оси ох в одной точке, а именно своей вершиной.

— Если решения квадратного уравнения нет (дискриминант отрицательный), то парабола вообще не будет касаться оси ох.

Тогда возникает вопрос, что делать в этих ситуациях и как определять ответ?

И вот тут прошу вас обратить внимание на один ключевой момент, который уже оговаривался в этой статье! В неравенстве при х² у нас может стоять положительный или отрицательный коэффициент. При положительном коэффициенте ветви параболы направлены вверх, при отрицательном вниз. А теперь переходим к следующему разделу статьи.

Решение квадратного неравенства. Все случаи!

Ниже для вас представлены все варианты расположения парабол, которые могут иметь место при решении квадратных неравенств:

Первая группа графиков

(коэффициент а > 0, то есть ветви параболы направлены вверх)

Вторая группа графиков

(коэффициент а < 0, то есть ветви параболы направлены вниз)

Что касается оговоренных выше вопросов по поводу случая, когда квадратное уравнение не имеет решения, обратите внимание на рисунки 9,10,11,12, 21,22,23,24 и всё поймёте. Подробнее:

Например, при решении квадратного уравнения вы обнаружили, что дискриминант отрицательный, то есть коней нет. Что это означает? А то, что ветви параболы не пересекают ось ох, то есть она расположена либо выше оси ох и её ветви направлены вверх, либо ниже оси и её ветви направлены вниз. И тут нам необходимо разобраться куда в вашем случае направлены ветви. Смотрим на коэффициент при х²:

— если он положительный, то схематично рисуем параболу выше оси ох с ветвями направленными вверх.

— если он отрицательный, то схематично рисуем параболу ниже оси ох с ветвями направленными вниз.

Далее только остаётся сопоставить наш рисунок с данным неравенством и учитывая знак в нём просто записать ответ. Всё!!!

Пример: х² +2х+16 < 0

Решаем квадратное уравнение x²+2x+16=0

D = b²–4ac = 2²–4∙2∙16 = 4–128 = –124

Дискриминант отрицательный, коней нет. Значит парабола не пересекает ось ох.

Коэффициент при х² положительный (равен 1), значит парабола расположена следующим образом – её ветви направлены вверх и расположена она выше оси ох (как на рис. 12).

Нам необходимо записать значения х, при которых х² +2х+16 отрицательно. Таких «х» нет, это видно по графику (рис 12).

Ответ: x∊∅ (решения нет).

*Если бы знак в этом неравенстве был «>», то решением были бы все действительные числа (рис. 10).

Теперь завершающий момент который стороной никак обойти нельзя, мы ещё не рассматривали решение неравенства вида:

Тут всё просто. Если вы детально изучили материал изложенный выше в статье и пропустили информацию, что называется, через себя, то здесь на эти вопросы вы ответите без труда.

Возможны три случая, если при решении aх²+bх+c = 0 получаем:

1. Два корня, то решением неравенства будет x∊(–∞;х₁) U (х₁;х₂) U (х₂;+∞).

2. Один корень, то решением будет x∊(–∞;х) U (х;+∞).

3. Нет корней, то решением будет вся числовая ось x∊(–∞;+∞).

Получить материал статьи в PDF

Понравилась статья — делитесь с коллегами и друзьями, социальные кнопки к вашим услугам. Также можете скачанный файл свободно распространять в сети.

На этом всё, благодарю за внимание. Ёмкая получилась статейка.

С уважением, Александр крутицких

P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.

Иррациональные неравенства. Исчерпывающий гид (ЕГЭ — 2021)

Определение

Иррациональное неравенство – это неравенство, содержащее переменную под корнем

Неравенства вида \( \sqrt{A}\ge \sqrt{B}\)

\( \sqrt{A}\ge \sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A\ge B\\B\ge 0\end{array} \right.\)

или

\( \sqrt{A}>\sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A>B\\B\ge 0\end{array} \right.\)

Неравенства вида \( A\sqrt{B}>0\) или \( A\sqrt{B}<0\)

\( A\sqrt{B}>0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A>0\end{array} \right. 2\) \(D=1-4 \cdot (-9) \cdot 8=289\)
\(x_1=\frac{6-10}{2}=-2\) \(x_1=\frac{-1+17}{-18}=\frac{16}{-18}=-\frac{8}{9}\) \(x_2=\frac{6+10}{2}=8\) \(x_2=\frac{-1-17}{-18}=\frac{-18}{-18}=1\)

\((x-8)(x+2)<0\) \(-9(x+\frac{8}{9})(x-1)≤0\)

Начертите числовую ось и отметьте на ней найденные корни. Если неравенство строгое (со знаком \(<\) или \(>\)) то точки должны быть выколоты, если неравенство нестрогое (со знаком \(≤\) или \(≥\)), то точки должны быть закрашены.

Нанесенные корни разбивают числовую ось на несколько интервалов.
В первом справа интервале поставьте:
\(-\) знак плюс если перед скобками ничего не стоит или стоит положительное число
\(-\) знак минус если перед скобками стоит знак минус.
В следующих за ним интервалах поставьте чередующиеся знаки.

Заштрихуйте подходящие интервалы, то есть числовые промежутки:
\(-\) со знаком «\(+\)», если в неравенстве стояло «\(>0\)» или «\(≥0\)»
\(-\) со знаком «\(-\)», если в неравенстве стояло «\(<0\)» или «\(≤0\)»

Выпишите в ответ те интервалы, которые вы заштриховали.
Внимание! При строгих знаках неравенства (\(<\) или \(>\)) границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде \((x_1;x_2)\) – скобки круглые. При нестрогих знаках неравенства (\(≤\) или \(≥\)) — границы интервала ВХОДЯТ в решение, и ответ записывается в виде \([x_1;x_2]\), с квадратными скобками на точках.

Ответ: \((-2;8)\) Ответ: \((-∞;\frac{8}{9}]∪[1;∞)\)

Пример. 2\)
\(x_1=\frac{-10-14}{6}=-4\) \(x_2=\frac{-10+14}{6}=\frac{2}{3}\)

Когда корни найдены, запишем неравенство в разложенном на множители виде.

\(3(x+4)(x-\frac{2}{3})≥0\)

Теперь начертим числовую ось, отметим на ней корни и расставим знаки на интервалах.

Выпишем в ответ интересующие нас интервалы . Так как знак неравенства \(≥\), то нам нужны интервалы со знаком \(+\), при этом сами корни мы включаем в ответ (скобки на этих точках – квадратные).

Ответ: \(x∈(-∞;-4]∪[ \frac{2}{3};∞)\)
Квадратные неравенства с отрицательным и равным нулю дискриминантом
Алгоритм выше работает, когда дискриминант больше нуля, то есть квадратный трехчлен имеет \(2\) корня. 2-64<0\)
\(D=-4 \cdot 64<0\)

Когда выражение слева меньше нуля?

Всегда. Значит неравенство выполняется при любых \(x\).

Ответ: \(x∈(-∞;∞)\)

Смотрите также:
Дробно-рациональные неравенства

Скачать статью
Алгебра для 8 класса
Необходимо решить уравнение: х*(143)=2х-30:
1
-2
2
Необходимо решить уравнение: 2*(х2х3х4х)=600:
30
20
4
Необходимо решить уравнение: 3*(5х7х)2=576:
7
9
8
Какие из представленных значений С и М соответствует уравнению С(ХМ)=0, если Х=-7. С и М – больше нуля:
М=3
С=0
М=0
С=0
М=7
С=2
Укажите квадратный корень из 16:
-4
8
4
Укажите квадратный корень из 25:
10
5
2,5
Укажите квадратный корень из 64:
16
18
8
При каких значениях x график функции y=2x-7 расположен выше оси x:
при x>3,5
при x< -3,5
при x< 3,5
Необходимо найти наименьшее целочисленное решение неравенства 2x-5< 4×7:
6
1
-5
Необходимо решить уравнение х2 – 2х = 0. В ответе укажите сумму корней:
1
2
4
Если дискриминант квадратного уравнения отрицательный, то уравнение:
не имеет корней
имеет 1 корень
имеет 2 корня
Книга стоила 320 р. , цена была увеличена на 20%. Сколько стоит эта книга теперь:
364
384
380
Понятие этих чисел вызвано потребностью счёта предметов. Какое они название носят:
Натуральные
простые
целые
Какие цифры мы используем в школе:
Римские
Индийские
Арабские и Римские
Какое из чисел является решением неравенства 3х > х 3:
0
-2
3
Неравенству х < 5 соответствует промежуток:
[5; ∞)
( – ∞; 5)
(5; ∞)
Необходимо решить неравенство: 3х < 18:
[6; ∞)
(6; ∞)
( – ∞; 6)
Какое из чисел является решением неравенства 4х – 3 > х:
0
2
1
Неравенству х > 4 соответствует промежуток:
(-∞; 4]
(-∞; 4)
(4; ∞)
Необходимо решить неравенство: 6х ≤ 30:
(5; ∞)
( – ∞; 5]
[5; ∞)
Какое из чисел не является решением неравенства 4,5 3у >0:
-1,5
3
4,5
Необходимо решить неравенство: 6 -7х > 3х – 7:
(0,1; ∞)
(-∞; 1,3)
(-∞; 0,1)
Сколько целых решений неравенства 2с < -1,3 принадлежит промежутку (-6; 3]:
4
3
5
Какое из предложенных неравенств является верным при любых значениях х и у, удовлетворяющих условию х > у:
у – х < -1
х – у > -2
х – у > 3
Какое из чисел не является решением неравенства 2,6 2у < 0
4,5
-3
-1,3
Необходимо решить уравнение: 3х-4*(82х)-710х=2х3*(6х7):
-2
-4
2
Выберите число, заключенное между числами 3,128 и 3,131:
3,12(8)
3,127
3,1(3)
Необходимо сравнить числа 0,791(6) и 37/48:
0,791(6) < 37/48
0,791(6) = 37/48
0,791(6) > 37/48
Порядок числа 20331,22 равен:
6
4
2
Наибольшее из предложенных цифр:
2,5
√7
√5
Решение квадратичных неравенств
. .. и более …
Квадратичный
Квадратное уравнение (в стандартной форме) выглядит так:

Квадратичное уравнение в стандартной форме
( a , b и c могут иметь любое значение, за исключением того, что a не может быть 0.)
Выше приведено уравнение (=), но иногда нам нужно решить такие неравенства:
Символ
слов
Пример
>
больше
x ² + 3x> 2
<
менее
7x ² <28
≥
больше или равно
5 ≥ х ² — х
≤
меньше или равно
2 года ² + 1 ≤ 7 лет
Решение
Решение неравенств очень похоже на решение уравнений. .. мы делаем почти то же самое.
При решении уравнений мы пытаемся найти точек ,
, например, помеченные «= 0»
Но когда мы решаем неравенства мы пытаемся найти интервал (с) ,
, например, помеченные «> 0» или «<0"
Итак, что мы делаем:
найти «= 0» точек
между точками «= 0», это интервалов , которые либо
больше нуля (> 0) или
меньше нуля (<0)
, затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)
Вот пример:
Пример: x
² — x — 6 <0
x ² — x — 6 имеет эти простые коэффициенты (потому что я хотел упростить!):
(х + 2) (х − 3) <0
Сначала , найдем где равно ноль:
(х + 2) (х − 3) = 0
Равно нулю, когда x = −2 или x = +3.
, потому что, когда x = −2, тогда (x + 2) равно нулю
или когда x = +3, то (x − 3) равно нулю
Итак, между −2 и +3, функция будет либо
всегда больше нуля или
всегда меньше чем ноль
Мы не знаем какой… еще!
Давайте выберем промежуточное значение и проверим его:
При x = 0: x ² — x — 6
= 0–0–6
= −6
Таким образом, между -2 и +3 функция будет на меньше, чем на , чем ноль.
И это тот регион, который нам нужен, так что …
x ² — x — 6 <0 в интервале (−2, 3)
Примечание: x ² — x — 6> 0 на интервале (−∞, −2) и (3, + ∞)
А вот график x ² — x — 6:
Уравнение равно нулю при −2 и 3
Неравенство «<0» истинно между −2 и 3.
Также попробуйте Grapher неравенства.
Что делать, если он не проходит через ноль?
Вот график x ² — x + 1
Нет баллов «= 0»!
Но от этого все становится проще!
Поскольку линия не пересекает y = 0, это должно быть либо:
всегда> 0 или
всегда <0
Итак, все, что нам нужно сделать, это проверить одно значение (скажем, x = 0), чтобы увидеть, выше или ниже оно.
A «Реальный мир» Пример
Каскадер прыгнет с 20-метрового здания.
Высокоскоростная камера готова снимать его на высоте от 15 до 10 метров над землей.
Когда его снимать на камеру?
Мы можем использовать эту формулу для расстояния и времени:
d = 20 — 5т ²
d = расстояние от земли (м) и
t = время от прыжка (секунды)
(Примечание: если вам интересна формула, она упрощена: d = d ₀ + v ₀ t + ½a ₀ t ² , где d ₀ = 20 , v ₀ = 0 и a ₀ = −9. 81 , г. то ускорение свободного падения.)
Ладно, поехали.
Сначала , давайте набросаем вопрос:
Требуемое расстояние от 10 м до 15 м :
10
И мы знаем формулу для d:
10 <20 - 5 т ² <15
Теперь решим!
Сначала вычтем 20 с обеих сторон:
−10 <−5 т ² <−5
Теперь умножьте обе стороны на — (1/5). Но поскольку мы умножаем на отрицательное число, неравенства изменят направление… прочтите «Решение неравенств», чтобы понять, почему.
2> т ²> 1
Для аккуратности, меньшее число должно быть слева, а большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства по-прежнему указывают правильно):
1 2 <2
Наконец, мы можем безопасно извлекать квадратные корни, поскольку все значения больше нуля:
√1
Съемочную группу можем сказать:
«Фильм из 1. От 0 до 1,4 секунды после прыжка »
Выше квадратичного
Те же идеи могут помочь нам решить более сложные неравенства:
Пример: x
³ + 4 ≥ 3x ² + x
Во-первых, приведем его в стандартном виде:
x ³ — 3x ² — x + 4 ≥ 0
Это кубическое уравнение (наивысший показатель — куб, т. Е. X ³), и его сложно решить, поэтому давайте изобразим его вместо этого:
Нулевые точки: приблизительно :
А на графике мы видим интервалы, где он больше (или равен) нулю:
Из −1.1 до 1,3 и
с 2,9 по
В интервальной записи можно записать:
Примерно: [-1,1, 1,3] U [2,9, + ∞)
Решение рациональных неравенств
Рациональный
Рациональное выражение выглядит так:
Неравенства
Иногда нам нужно решить такие рациональные неравенства:
Символ
слов
Пример

>
больше
(х + 1) / (3-х)> 2
<
менее
х / (х + 7) <−3
≥
больше или равно
(x − 1) / (5 − x) ≥ 0
≤
меньше или равно
(3−2x) / (x − 1) ≤ 2

Решение
Решение неравенств очень похоже на решение уравнений. .. вы делаете почти то же самое.
Когда мы решаем неравенства
, мы пытаемся найти интервалов ,
, например, отмеченные «<0» или «> 0»
Это шаги:
найти «достопримечательности»:
точек «= 0» (корни) и
«вертикальные асимптоты» (где функция не определена)
между «точками интереса», функция либо больше нуля (> 0), либо меньше нуля (<0)
, затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)
Вот пример:
Пример:
3x − 10 x − 4 > 2
Первый , давайте упростим!
Но вы не можете умножить на (x − 4)
Потому что «x − 4» может быть положительным или отрицательным. … мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».
Вместо этого переместите «2» влево:
3x − 10 x − 4 -2> 0
Затем умножьте 2 на (x − 4) / (x − 4):
3x − 10 x − 4 -2 x − 4 x − 4 > 0
Теперь у нас есть общий знаменатель, давайте все вместе:
3x − 10-2 (x − 4) x − 4 > 0
Упростить:
x − 2 x − 4 > 0
Второй , поищем «достопримечательности».
При x = 2 имеем: (0) / (x − 4)> 0, что является точкой «= 0», или корень
При x = 4 имеем: (x − 2) / (0)> 0, что равно undefined
Третий , сделайте контрольные точки, чтобы увидеть, что он делает между:
При x = 0:
x − 2 = −2, что равно отрицательным
x − 4 = −4, что также является отрицательным
Итак, (x − 2) / (x − 4) должно быть положительным
Мы можем сделать то же самое для x = 3 и x = 5 и получить следующие результаты:
х = 0 х = 2 х = 3 х = 4 х = 5
х − 2 <0 х − 2> 0 х − 2> 0
х − 4 <0 х − 4 <0 х − 4> 0
(x − 2) / (x − 4) равно > 0 0 <0 undefined > 0
Это дает нам полную картину!
А где это> 0?
Итак, наш результат:
(−∞, 2) U (4, + ∞)
Все это мы сделали без рисования сюжета!
Но вот график (x − 2) / (x − 4), поэтому вы можете видеть:
Решите неравенство и обозначьте интервалы: 2x ^ 3-2x≥0
Чтобы решить полиномиальные неравенства, вы хотите начать с рассмотрения их как уравнений. 2 -1) = 0. Что касается неравенств, представьте себе числовую прямую. Любая точка в числе, левая часть вашего неравенства либо положительная, либо отрицательная, либо 0. Мы ищем> = 0, поэтому нам нужны значения, где оно положительно или 0. Мы уже знаем, где оно равно 0, а те также являются единственными точками, где он изменится с положительного на отрицательный. По сути, мы только что разорвали числовую линию на три точки:
___________________________ | ______________ | ________________ | ___________________________
-1 0 1
Выберите контрольную точку в каждом из этих интервалов, число меньше -1, число от -1 до 0, число от 0 до 1 и число больше 1.2 — 1) = 4 (3) = 12 … мы положительны справа от 1
Итак, опять же, наши решения — любые значения, у которых левая сторона была равна нулю или положительна. Для обозначения интервалов ваши интервалы дают начальные и конечные значения, где у вас есть решения. Вы используете скобки, если начальное или конечное значение является решением (если оно включено).
У нас есть решения от -1 до 0 (включая AT -1 и 0) и все, что больше 1 (включая AT one). Это означает, что нам нужны два разных интервала, и они соединены символом объединения:
[-1, 0] U [1, inf)
Решение линейных неравенств — ChiliMath
Большинство правил или методов, используемых при решении многоэтапных уравнений, должно быть легко преобразовано в решение неравенств.
Единственная большая разница заключается в том, как символ неравенства переключает направление , когда отрицательное число умножается или делится на обе стороны уравнения.
В этом уроке я рассмотрю семь (7) рабочих примеров с разным уровнем сложности, чтобы обеспечить достаточную практику.
Символы неравенства с примерами и иллюстрациями на числовых строках
БОЛЬШЕ, ЧЕМ
БОЛЬШЕ ИЛИ РАВНО
МЕНЬШЕ
МЕНЬШЕ ИЛИ РАВНО
Примеры решения и построения графика линейных неравенств
Пример 1: Решите и изобразите решение неравенства
.
Чтобы решить это неравенство, мы хотим найти всех значений x, которые могут ему удовлетворить.Это означает, что существует почти бесконечное количество значений x, которые при замене дадут истинные утверждения.
Проверьте значения x = 0, x = 1, x = 2, x = 3, x = 5, x = 6 и x = 7.
Какое из этих значений x является верным?
После выполнения некоторых обратных замен вы должны согласиться, что работают только 5, 6 и 7; а остальные терпят неудачу. Но вопрос в том, есть ли больше значений x, кроме упомянутых? Ответ положительный! Теперь давайте решим неравенство, чтобы выяснить весь набор значений, которые могут сделать его истинным.
Напишите исходную задачу.
Добавьте 17 с обеих сторон, чтобы переменные оставались слева, а константа — справа.
Неравенство сводится к этому после упрощения.
Разделим обе части неравенства на коэффициент при x.
Используйте открытое отверстие, чтобы указать, что 3 не является частью решения. Решение неравенства x> 3 включает все значения справа от 3, но исключая само 3.Теперь вы понимаете, почему все числа больше 3 являются решениями?
Пример 2: Решите и изобразите решение неравенства
.
Этот пример показывает, что происходит с символом неравенства при делении на отрицательное число.
Напишите исходную задачу.
Чтобы изолировать переменную x слева от неравенства, я добавлю обе части на 2.
Вот как это выглядит после того, как я упростил, используя вышеуказанный шаг.
Теперь, чтобы найти x, я разделю обе части на — \, 3.
ВСЕГДА меняет направление неравенства всякий раз, когда вы делите или умножаете отрицательное число на обе стороны неравенства.
Используйте закрытое или закрашенное отверстие , чтобы указать, что 7 является частью решения. Решение неравенства x \ le 7 включает 7 и все, что находится слева от него.
Пример 3: Решите и изобразите решение неравенства
.
В этой задаче у меня есть переменные по обе стороны неравенства.Хотя не имеет значения, где мы храним переменную, слева или справа, имеет смысл всегда быть последовательным, изолировав ее слева. Думаю, это просто «стандартный» способ.
Однако, если вы попытаетесь сохранить переменную справа, убедитесь, что вы знаете об их тонкостях. Например, ответ на эту проблему: x <- \, 6, что совпадает с - \, 6> x. Они эквивалентны, потому что начало неравенства также указывает на — \, 6. Следовательно, это означает, что если я переключаю переменную и константу в своем окончательном ответе, я также должен изменить направление символа, чтобы значение оставалось неизменным.
Напишите исходную задачу.
Я хочу оставить x слева. Я сделаю это, добавив 6x к обеим сторонам на
После шага выше мне нужно переместить константу вправо.
Вычтем обе стороны на 7.
Чтобы окончательно выделить x слева, разделите обе стороны на коэффициент при x, равный 2.
Обратите внимание, что I не изменил направление неравенства, потому что I разделил обе стороны на положительное число.
Используйте открытое отверстие , чтобы указать, что — \, 6 — это , а не часть решения. Решение неравенства x <- \, 6 включает все значения слева от - \, 6, кроме самого - \, 6.
Пример 4: Решите и изобразите решение неравенства
.
Я построил эту задачу, чтобы подчеркнуть шаг, необходимый для работы с символом круглой скобки . Я знаю, что это вас не смутит, потому что вы уже видели это раньше, когда решали линейные уравнения, верно? Шаг, необходимый для того, чтобы избавиться от скобок, — применить распределительное свойство умножения над сложением.Однако я должен предостеречь вас, чтобы вы были осторожны со знаками в процессе умножения. Помните, что произведение двух членов с одинаковыми знаками является положительным, а если знаки не совпадают, произведение отрицательное.
Напишите исходную задачу. Сначала я удалю круглые скобки, распределив это — \, 4 в бином \ left ({x — 5} \ right).
Упростите и будьте осторожны при распространении. Помните, вы получите положительный продукт, если знаки одинаковые, и отрицательный, если знаки разные.
При решении неравенств я делаю привычкой «всегда» оставлять переменную слева. Хотя держать его справа тоже правильно. Это всего лишь вопрос предпочтения. Чтобы оставить x слева, вычтите обе стороны на 3x.
Поскольку я хочу, чтобы константа оставалась справа, становится ясно, что моим следующим шагом будет удаление 20 слева.
Вычтем обе стороны на 20.
Очевидно, я разделю обе части на отрицательный коэффициент и заменю неравенство.
Чтобы найти x, разделите обе части на — \, 7, что оставит нам окончательный ответ.
Используйте закрытое или закрашенное отверстие , чтобы указать, что 5 является частью решения. Решение неравенства x \ ge 5 включает 5 и все справа от него.
Пример 5: Решите и изобразите решение неравенства
.
Мой общий подход здесь состоит в том, чтобы немедленно исключить круглые скобки, используя свойство распределения, объединить одинаковые термины с обеих сторон и, наконец, оставить x слева, а константу — с противоположной стороны.
Напишите исходную задачу. Я дважды применю свойство распределения к левой части двух круглых скобок.
Что касается правой стороны, это похожие термины, поэтому я просто объединю их.
Упростить. На этом этапе я объединю похожие термины слева. Объедините вместе x и константы.
Это то, что я получил после выполнения вышеуказанного шага.
Переместите константы вправо, добавив обе стороны на 6.
Теперь переместите все переменные влево, добавив обе стороны в 4 раза.
Разделите обе стороны на — \, 3, чтобы выделить x. Однако я должен изменить ориентацию символа неравенства, поскольку я разделил обе стороны отрицательным числом.
Используйте открытое отверстие , чтобы указать, что — \, 2 — это , а не часть решения. Решение неравенства x> — 2 подразумевает все значения справа от — \, 2, кроме — \, 2.
Пример 6: Решите и изобразите решение неравенства
.
«Сложность» этой проблемы не должна вас беспокоить. Ключом к успешному решению этой проблемы является применение всех техник, которые вы уже усвоили из наших предыдущих примеров. Если вам нужен обзор, пожалуйста, оглядывайтесь назад.
Попробуйте решить эту проблему, не просматривая подробное решение. Каждый раз, когда вы думаете, что закончили, сравните то, что у вас есть на бумаге, с ответом ниже.
Напишите исходную задачу. Избавьтесь от скобок с обеих сторон неравенства, применив свойство распределенности.
Упростить. Совместите одинаковые термины с обеих сторон.
Вот как это выглядит после объединения одинаковых терминов.
Вычтите обе части на 12, чтобы оставить x слева.
Вычтите обе стороны в 5 раз, чтобы постоянная оставалась справа.
Решите x, разделив обе части на — 10, однако не забудьте также изменить направление неравенства.
Используйте открытое отверстие, чтобы указать, что 2 не является частью решения. Решение неравенства включает все значения выше 2, но исключая 2.
Пример 7: Решите и изобразите решение неравенства
.
Давайте закончим, сделав последний пример мастерства! Опять же, сначала сделайте это самостоятельно на бумаге, а затем сравните свое решение с ответом ниже.
Напишите исходную задачу. Объедините члены x в левой части, а затем дважды примените свойство дистрибуции к правой части неравенства.
Это то, что мы получили после выполнения описанного выше шага.
Затем упростите правую часть, объединив похожие термины, появившиеся после распространения.
Чтобы выделить x слева, вычтите обе части на 5.
Избавьтесь от переменных справа, вычтя 7x.
Наконец, разделите обе стороны на — \, 3, чтобы изолировать x. Убедитесь, что мы изменили направление символа неравенства, чтобы компенсировать деление отрицательного числа.
Используйте закрытое или закрашенное отверстие , чтобы указать, что — \, 1 является частью решения. Решение неравенства x \ ge — 1 включает — \, 1 и все значения справа от него, как показано направлением стрелки.
Практика с рабочими листами
Возможно, вас заинтересует:
Шаги по построению графика линейных неравенств
Графические примеры линейных неравенств
Графические системы линейных неравенств
Решение сложных неравенств
Решение полиномиальных неравенств
Решение полиномиальных неравенств Вот шаги, необходимые для решения полиномиальных неравенств:
Шаг 1 : Запишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите.
Шаг 3 : Сделайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. Знак этого ответа (положительный или отрицательный) будет знаком всего раздела. Вы можете проверить другой номер из того же раздела, если хотите проверить свой ответ.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству.Если неравенство меньше нуля или меньше или равно нулю, тогда вы хотите, чтобы все отрицательные участки были найдены в диаграмме анализа знаков. Если неравенство больше нуля или больше или равно нулю, тогда вы хотите, чтобы все положительные участки были найдены в диаграмме анализа знаков.
Шаг 6 : Используйте обозначение интервалов, чтобы написать окончательный ответ.
Пример 1 — График:
Шаг 1 : Напишите многочлен в правильной форме.Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –3, что дает +7, x = 0, что дает –8, и x = 5, что дает +7.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас больше или равно нулю, поэтому нам нужны все положительные секции.
Шаг 6 : Используйте интервальную нотацию для записи окончательного ответа.
Пример 2 — График:
Шаг 1 : Напишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –4, что дает +3, x = –2, что дает –1, и x = 0, что дает +3.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас меньше или равно нулю, поэтому нам нужна отрицательная секция.
Шаг 6 : Используйте интервальную нотацию для записи окончательного ответа.
Щелкните здесь для практических задач
Пример 3 — График:
Шаг 1 : Напишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –4, что дает –35, x = 0, что дает +9, x = 2, что дает –5, и x = 4, что дает +21.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас меньше нуля, поэтому нам нужны все отрицательные секции.
Шаг 6 : Используйте интервальную нотацию для записи окончательного ответа.
Щелкните здесь для практических задач
Пример 4 — График:
Шаг 1 : Напишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –5, что дает +56, x = –2, что дает –16, x = 0, что дает +16, и x = 3, что дает –56.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас больше нуля, поэтому нам нужны все положительные секции.
Шаг 6 : Используйте интервальную нотацию для записи окончательного ответа.
Щелкните здесь для практических задач
Квадратичные неравенства — объяснение и примеры
Подобно тому, как уравнения имеют разные формы, неравенства также существуют в разных формах, и квадратное неравенство является одним из них.
Квадратичное неравенство — это уравнение второй степени, в котором вместо знака равенства используется знак неравенства.
Решения квадратного неравенства всегда дают два корня. Природа корней может быть разной и определяется дискриминантом (b ² — 4ac).
Общие формы квадратичных неравенств:
топор ² + bx + c <0
ах ² + bx + c ≤ 0
топор ² + bx + c> 0
топор ² + bx + c ≥ 0
Примеры квадратичных неравенств:
x ² — 6x — 16 ≤ 0, 2x ² — 11x + 12> 0, x ² + 4> 0, x ² — 3x + 2 ≤ 0 и т. Д.
Как решить квадратичные неравенства?
Квадратичное неравенство — это уравнение второй степени, в котором вместо знака равенства используется знак неравенства.
Примеры квадратичных неравенств: x ² — 6x — 16 ≤ 0, 2x ² — 11x + 12> 0, x ² + 4> 0, x ² — 3x + 2 ≤ 0 пр.
Решение квадратного неравенства в алгебре аналогично решению квадратного уравнения. Единственное исключение состоит в том, что в квадратных уравнениях вы приравниваете выражения к нулю, а в случае неравенств вам интересно знать, что находится по обе стороны от нуля i.е. отрицательные и положительные стороны.
Квадратные уравнения могут быть решены либо методом факторизации , либо с помощью квадратной формулы . Прежде чем мы научимся решать квадратные неравенства, давайте вспомним, как решаются квадратные уравнения, на нескольких примерах.
Как квадратные уравнения решаются методом факторизации?
Поскольку мы знаем, что можем решать квадратные неравенства аналогично квадратным уравнениям, полезно понять, как факторизовать данное уравнение или неравенство.
Давайте посмотрим здесь несколько примеров.
6x ² — 7x + 2 = 0
Решение
⟹ 6x ² — 4x — 3x + 2 = 0
Разложите выражение на множители;
⟹ 2x (3x — 2) — 1 (3x — 2) = 0
⟹ (3x — 2) (2x — 1) = 0
⟹ 3x — 2 = 0 или 2x — 1 = 0
⟹ 3x = 2 или 2x = 1
⟹ x = 2/3 или x = 1/2
Следовательно, x = 2/3, ½
Решить 3x ² — 6x + 4x — 8 = 0
Решение
Разложите выражение в левой части на множители.
⟹ 3x ² — 6x + 4x — 8 = 0
⟹ 3x (x — 2) + 4 (x — 2) = 0
⟹ (x — 2) (3x + 4) = 0
⟹ x — 2 = 0 или 3x + 4 = 0
⟹ x = 2 или x = -4/3
Следовательно, корни квадратного уравнения равны, x = 2, -4/3.
Решите 2 (x ² + 1) = 5x
Решение
2x ² + 2 = 5x
⟹ 2x ² — 5x + 2 = 0
⟹ 2x ² — 4x — x + 2 = 0
⟹ 2x (x — 2) — 1 (x — 2) = 0
⟹ (х — 2) (2x — 1) = 0
⟹ x — 2 = 0 или 2x — 1 = 0
⟹ x = 2 или x = 1/2
Следовательно, решения x = 2, 1/2.
(2x — 3) ² = 25
Решение
Разверните и разложите выражение на множители.
(2x — 3) ² = 25
⟹ 4x ² — 12x + 9-25 = 0
⟹ 4x ² — 12x — 16 = 0
⟹ x ² — 3x — 4 = 0
⟹ (х — 4) (х + 1) = 0
⟹ x = 4 или x = -1
Решить x ² + (4 — 3y) x — 12y = 0
Решение
Разверните уравнение;
x ² + 4x — 3xy — 12y = 0
Факторизация;
⟹ х (х + 4) — 3у (х + 4) = 0
х + 4) (х — 3у) = 0
⟹ x + 4 = 0 или x — 3y = 0
⟹ x = -4 или x = 3y
Таким образом, x = -4 или x = 3y
Чтобы решить квадратное неравенство, мы также применяем тот же метод, который проиллюстрирован в процедуре ниже:
Запишите квадратное неравенство в стандартной форме: ax ² + bx + c, где a, b и — коэффициенты, а a ≠ 0
Определите корни неравенства.
Запишите решение в виде неравенств или интервалов.
Если квадратное неравенство имеет вид: (x — a) (x — b) ≥ 0, то a ≤ x ≤ b, а если оно имеет вид: (x — a) (x — b) ≤ 0 , когда a
Пример 1
Решите неравенство x ² — 4x> –3
Решение
Сначала сделайте одну сторону неравенства равной нулю, прибавив обе стороны по 3.
x ² — 4x> –3 ⟹ x ² — 4x + 3> 0
Учтите левую часть неравенства.
x ² — 4x + 3> 0 ⟹ (x — 3) (x — 1)> 0
Найти все нули неравенства;
Для, (x — 1)> 0 ⟹ x> 1 и для, (x — 3)> 0 ⟹ x> 3
Поскольку y положительно, мы выбираем значения x, при которых кривая будет выше оси x.
x <1 или x> 3
Пример 2
Решите неравенство x ² — x> 12.
Решение
Чтобы записать неравенство в стандартной форме, вычтите обе части неравенства на 12.
x ² — x> 12 ⟹ x ² — x — 12> 0.
Факторизуйте квадратное неравенство, чтобы добраться до;
( x -4) ( x + 3)> 0
Найти все нули неравенства;
Для, (x + 3)> 0 ⟹ x> -3
Для x — 4> 0 ⟹ x> 4
Значения x <–3 или x> 4, следовательно, являются решением этого квадратичного неравенства.
Пример 3
Решить 2x ² <9x + 5
Решение
Запишите неравенство в стандартной форме, приравняв одну сторону неравенства к нулю.
2x ² <9x + 5 ⟹ 2x ² — 9x — 5 <0
Разложите на множители левую часть квадратного неравенства.
2x ² — 9x — 5 <0 ⟹ (2x + 1) (x - 5) <0
Решить относительно всех нулей неравенства
Для, (x — 5) <0 ⟹ x <5 и для (2x + 1) <0 ⟹ x <-1/2
Поскольку y отрицателен для уравнения 2x ² — 9x — 5 <0, мы выбираем значения x, при которых кривая будет ниже оси x.
Следовательно, решение -1/2
Пример 4
Решить — x ² + 4 <0.
Решение
Поскольку неравенство уже имеет стандартную форму, мы факторизуем выражение.
-x ² + 4 <0 ⟹ (x + 2) (x - 2) <0
Решить относительно всех нулей неравенства
Для, (x + 2) <0 ⟹ x <-2 и для, (x - 2) <0 ⟹ x <2
Значение y для –x ² + 4 <0 отрицательно; поэтому мы выбираем значения x, при которых кривая будет ниже оси x: –2 2
Пример 5
Решить 2x ² + x — 15 ≤ 0.
Решение
Разложите квадратное уравнение на множители.
2x ² + x — 15 = 0
2x ² + 6x — 5x− 15 = 0
2x (x + 3) — 5 (x + 3) = 0
(2x — 5) (x + 3) = 0
Для, 2x — 5 = 0 ⟹ x = 5/2 и для, x + 3 = 0 ⟹ x = -3
Поскольку y для 2x ² + x — 15 ≤ 0 отрицательно, мы выбираем значения x, при которых кривая будет ниже оси x. Следовательно, x ≤ -3 или x ≥5 / 2 — решение.
Пример 6
Решить — x ² + 3x — 2 ≥ 0
Решение
Умножьте квадратное уравнение на -1 и не забудьте изменить знак.
x ² — 3x + 2 = 0
x ² — 1x — 2x + 2 = 0
х (х — 1) — 2 (х — 1) = 0
(х — 2) (х — 1) = 0
Для, x — 2 = 0 ⟹ x = 2 и для, x — 1 = 0 ⟹x = 1
Следовательно, решение квадратного неравенства 1 ≤ x ≤ 2
Пример 7
Решить x ² — 3x + 2> 0
Решение
Разложите выражение на множители, чтобы получить;
x ² — 3x + 2> 0 ⟹ (x — 2) (x — 1)> 0
Теперь найдите корни неравенства как;
(х — 2)> 0 ⟹ х> 2
(х — 1)> 0 ⟹x> 1
Кривая для x ² — 3x + 2> 0 имеет положительное значение y, поэтому выбираются значения x, при которых кривая будет выше оси x.Следовательно, решение x <1 или x> 2.
Пример 8
Решить −2x ² + 5x + 12 ≥ 0
Решение
Умножить все выражение на -1 и изменить знак неравенства
−2x ² + 5x + 12 ≥ 0 ⟹2x ² — 5x — 12 ≤ 0
Разложите выражение на множители, чтобы получить;
(2x + 3) (x — 4) ≤ 0.
Решите корни;
(2x + 3) ≤ 0 ⟹ x ≤ -3/2.
(x — 4) ≤ 0 ⟹ x ≤ 4.
Применяя правило; (x — a) (x — b) ≥ 0, тогда a ≤ x ≤ b, мы можем удобно записать решения этого квадратичного неравенства в виде:
-3/2 ≤ х ≤ 4.
Пример 9
x ² — x — 6 <0
Решение
Разложите на множители x ² — x — 6, чтобы получить;
(х + 2) (х — 3) <0
Найдите корни уравнения как;
(х + 2) (х — 3) = 0
x = −2 или x = +3
Поскольку y отрицателен для x ² — x — 6 <0, то мы выбираем интервал, в котором кривая будет ниже оси x.Следовательно, -2
Практические вопросы
(x — 3) (x + 1) <0
x ² + 5x + 6 ≥ 0
(2x — 1) (3x + 4)> 0
10x ² — 19x + 6 ≤ 0
5 — 4x — x ²> 0
1 — x — 2x ² <0
(x — 3) (x + 2)> 0.
x ² −2x − 3 <0.
Ответы
-1 <х <3
x <−3 или x> −2
x <−4/3 или x> ½
2/5 ≤ х ≤ 3/2
−5 <х <1
x <−1 или x> ½
x <–2 или x> 3
−1≤ х ≤ 3
Предыдущий урок | Главная страница | Следующий урок
Литература: Устранение неравенств за один шаг | Конечная математика
Неравенства похожи на уравнения в том, что они показывают взаимосвязь между двумя выражениями.Мы решаем и графически изображаем неравенства аналогично уравнениям. Однако есть некоторые отличия, о которых мы поговорим в этой главе. Основное отличие состоит в том, что для линейных неравенств ответом является интервал значений, тогда как для линейного уравнения ответом чаще всего является одно значение.
При написании неравенств мы используем следующие символы
> больше
[латекс] \ ge [/ latex] больше или равно
<меньше
[латекс] \ le [/ latex] меньше или равно
Запишите и изобразите неравенства в одной переменной в числовой строке
Начнем с простого неравенства x> 3
Мы читаем это неравенство как «x больше 3.«Решение — это набор всех действительных чисел, которые больше трех. Мы часто представляем множество решений неравенства числовой линией.
Рассмотрим еще одно простое неравенство [латекс] x \ le4 [/ latex]
Мы читаем это неравенство как «x меньше или равно 4». Решение — это набор всех действительных чисел, которые равны четырем или меньше четырех. Построим это множество решений на числовой прямой.
В графе мы используем пустой кружок для конечной точки строгого неравенства (x> 3) и закрашенный кружок, если включен знак равенства (x [latex] \ le [/ latex] 4).
Пример 1
На числовой прямой нанесите следующие неравенства.
х <−3
[латекс] x \ ge6 [/ латекс]
х> 0
[латекс] x \ le8 [/ латекс]
Решения
Неравенство x <−3 представляет все действительные числа, которые меньше −3. Число −3 не входит в решение и обозначено белым кружком на графике.
Неравенство [латекс] x \ ge6 [/ latex] представляет все действительные числа, которые больше или равны шести.Число шесть включено в решение и обозначено на графике замкнутым кружком.
Неравенство x > 0 представляет все действительные числа, которые больше нуля. Число ноль не входит в решение и обозначено белым кружком на графике.
Неравенство [латекс] x \ le8 [/ latex] представляет все действительные числа, которые меньше или равны восьми. Число восемь включено в решение и обозначено на графике замкнутым кружком.
Пример 2
Напишите неравенство, которое представлено на каждом графике.
Решения
x <−12
x > 540
x <65
[латекс] x \ ge83 [/ латекс]
В реальной жизни неравенство проявляется повсюду. Вот несколько простых примеров реальных приложений.
Пример 3
Запишите каждое утверждение в виде неравенства и обозначьте его числовой прямой.
Чтобы получить бесплатную проверку, вы должны поддерживать баланс не менее 2500 долларов на текущем счете.
Чтобы кататься на американских горках «Тандерболт», вы должны быть ростом не менее 48 дюймов.
Для бесплатного посещения зоопарка Сан-Диего вам должно быть меньше 3 лет.
Ограничение скорости на межштатной автомагистрали составляет 65 миль в час.
Решения
Неравенство записывается как [латекс] х \ ge2500 [/ латекс]. Слова «как минимум» означают, что в набор решений включена стоимость 2500 долларов.
Неравенство записывается как [латекс] x \ ge48 [/ latex]. Слова «по крайней мере» означают, что значение 48 дюймов включено в набор решений.
Неравенство записывается как x <3.
Ограничение скорости означает наивысшую допустимую скорость, поэтому неравенство записывается как [latex] x \ le65 [/ latex].
Чтобы решить неравенство, мы должны изолировать переменную с одной стороны от знака неравенства. Чтобы изолировать переменную, мы используем те же базовые методы, которые используются при решении уравнений.Для неравенств этого типа:
x — a < b или x — a > b
Мы изолируем x, добавив константу a к обеим сторонам неравенства.
Пример 4
Решите каждое неравенство и изобразите набор решений.
х − 3 <10
х − 1> −10
[латекс] x − 1 \ le − 5 [/ латекс]
[латекс] x − 20 \ ge14 [/ латекс]
Решения
Для решения неравенства x- 3 <10 Упростите:
x <13

Решить неравенство x — 1> -10
Решить неравенство [латекс] x-1 \ le-5 [/ latex].Упростить:
[латекс] x \ le-4 [/ латекс]

Решить неравенство [латекс] x-20 \ le14 [/ latex]
Для неравенств этого типа:
x + 1 b
Мы выделяем x, вычитая константу a с обеих сторон неравенства.
Пример 5
Решите каждое неравенство и изобразите набор решений.
[латекс] x + 2 <7 [/ латекс]
[латекс] x + 8 \ le-7 [/ латекс]
[латекс] x + 4> 13 [/ латекс]
Решения
Чтобы решить неравенство x + 2 <7, вычтите 2 с обеих сторон неравенства. x + 2-2 <7-2
Упростить: x <5
Чтобы решить неравенство [латекс] x + 8 \ le – 7 [/ latex], вычтите 8 с обеих сторон неравенства. [латекс] x + 8 — 8 \ le-7 — 8 [/ latex] Упростить:
[латекс] x \ ge – 15 [/ латекс]
Чтобы решить неравенство x + 4> 13, вычтите 4 с обеих сторон неравенства. x + 4-4> 13-4 Упростить:
x > 9
Рассмотрим проблему:
[латекс] \ frac {x} {5} \ le 3 [/ latex]
Чтобы найти решение, умножаем обе части на 5:
[latex] (5) \ frac {x} {5} \ le 3 (5) [/ latex]
Получаем
[латекс] х \ le 15 [/ латекс].
Ответ неравенства может быть выражен четырьмя различными способами:
Обозначение неравенства Ответ выражается просто как x <15.
Обозначение набора Ответ: x | x <15. Вы читаете это как «набор всех значений x, таких, что x является действительным числом меньше 15».
Интервальное обозначение использует скобки для обозначения диапазона значений в решении. Интервальное обозначение решения для нашей задачи — (-∞, 15). В обозначении интервалов также используется понятие бесконечности ∞ и отрицательной бесконечности −∞.Круглые или открытые скобки «(» и «)» означают, что число рядом со скобкой не входит в набор решений. Квадратные или закрытые скобки «[» и «]» означают, что число рядом со скобкой включено в набор решений.
График решения показывает решение в виде вещественной числовой прямой. Закрашенный кружок на цифре означает, что номер включен в набор решений. Белый кружок указывает на то, что номер не входит в набор. Для нашего примера здесь нарисован график решения.
Пример 6
[−4,6] говорит, что решения — это все числа от −4 до 6 , включая −4 и 6.
(8,24) говорит, что решением являются все числа от 8 до 24, но не включает числа 8 и 24.
[3,12) говорит, что решением являются все числа от 3 до 12, включая 3, но не включая 12.
(−5, ∞) говорит, что решением являются все числа больше −5, , исключая −5.
(−∞, ∞) говорит, что решение — все действительные числа.
Решаем неравенство
[латекс] 2x \ ge 12 [/ latex] делением обеих сторон на 2:
[латекс] \ frac {2x} {2} \ ge \ frac {12} {2} [/ латекс]
Упростить:
[латекс] x \ ge 6 [/ латекс]
Давайте запишем решение в четырех различных обозначениях, которые вы только что выучили:
Обозначение неравенства [латекс] x \ ge 6 [/ латекс]
Обозначение набора [латекс] {x | x \ ge 6} [/ латекс]
Обозначение интервалов [латекс] [6, [/ латекс] ∞]
График решения
Мы решаем неравенство аналогично решению обычного уравнения.Мы можем складывать или вычитать числа по обе стороны неравенства. Мы также можем умножать или делить положительные числа по обе стороны неравенства, не меняя решения.
Что-то другое происходит, если мы умножаем или делим на отрицательные числа. В этом случае знак неравенства меняет направление.
Например, чтобы решить −3x <9
Делим обе части на –3. Знак неравенства меняется с <на>, потому что мы делим на отрицательное число.
[латекс] \ frac {-3x} {- 3} \ gt \ 6 \ frac {9} {- 3} [/ латекс]
[латекс] x \ gt \ -3 [/ латекс]
Мы можем объяснить, почему это происходит, на простом примере.Мы знаем, что два меньше трех, поэтому можем записать неравенство.
2 <3
Если мы умножим оба числа на −1, мы получим −2 и −3, но мы знаем, что −2 больше −3.
−2> −3
Вы видите, что умножение обеих сторон неравенства на отрицательное число привело к изменению направления знака неравенства. Это также происходит, если мы делим на отрицательное число.
Пример 7
Решите каждое неравенство. Приведите решение в обозначениях неравенств и интервалов.
[латекс] 4x \ lt 24 [/ latex] [латекс] \ displaystyle {4} {x} lt {24} [/ latex]
[латекс] -9x \ le \ frac {3} {5} [/ латекс]
[латекс] \ displaystyle- {5} {x} \ le {21} [/ latex]
[латекс] \ displaystyle {12} {x} \ gt- {30} [/ latex]
Решения
[latex] \ displaystyle {4} {x} \ lt {24} [/ latex] Разделите обе стороны на 4: [latex] \ displaystyle \ frac {{{4} {x}}} {{4}} \ lt \ frac {{24}} {{4}} [/ latex] Упростите, чтобы получить ответ:
[latex] \ displaystyle {x} \ lt {6} [/ latex]
[latex] \ displaystyle- {9} {x} \ le- \ frac {{3}} {{5}} [/ latex] Разделите обе стороны на –9:
[latex] \ displaystyle \ frac {{- {9} {x}}} {{- {9}}} \ ge- \ frac {{3}} {{5}} (- \ frac {{1}} {{9}}) [/ latex] .Направление неравенства изменилось. Чтобы получить ответ, упростите:
[latex] \ displaystyle {x} \ ge \ frac {{1}} {{15}} [/ latex]
[латекс] \ displaystyle- {5} {x} \ le {21} [/ latex] Разделите обе стороны на –5:
[латекс] \ displaystyle \ frac {{- {5} {x}}} {{ — {{5}}}} \ ge \ frac {{21}} {{- {{5}}}} [/ latex] Направление неравенства изменено. Упростите, чтобы получить ответ
[latex] \ displaystyle {x} \ ge- \ frac {{21}} {{5}} [/ latex]
[latex] \ displaystyle {12} {x} \ gt- {30} [/ latex] Разделите обе стороны на 12: [latex] \ displaystyle \ frac {{{12} {x}}} {{12}} \ gt- \ frac {{30}} {{12}} [/ latex] Упростите, чтобы получить ответ
[latex] \ displaystyle {x} \ gt- \ frac {{5}} {{2}} [/ латекс]
Пример 8
Решите каждое неравенство.Приведите решение в обозначениях неравенств.
[латекс] \ displaystyle \ frac {{x}} {{2}} \ gt {40} [/ latex]
[латекс] \ displaystyle \ frac {{x}} {{- {3}}} \ le- {12} [/ latex]
[латекс] \ displaystyle \ frac {{x}} {{25}} \ lt \ frac {{3}} {{2}} [/ latex]
[латекс] \ displaystyle \ frac {{x}} {{- {7}}} \ ge {9} [/ latex]
Решения
[латекс] \ displaystyle \ frac {{x}} {{2}} \ gt {40} [/ latex] Умножьте обе стороны на 2: [латекс] \ displaystyle {2} (\ frac {{x}} {{2}}) \ gt {40} ({2}) [/ latex] Упростить: [latex] \ displaystyle {x} \ gt {80} [/ latex]
[латекс] \ displaystyle \ frac {{x}} {{- {3}}} \ le {12} [/ latex] Умножьте обе стороны на –3:
[латекс] \ displaystyle- {3} (\ frac {{x}} {{- {3}}}) \ ge- {12} (- {3}) [/ latex] Направление неравенства изменено.Упростить: [latex] \ displaystyle {x} \ ge {36} [/ latex]
.
[латекс] \ displaystyle \ frac {{x}} {{25}} \ lt \ frac {{3}} {{2}} [/ latex] Умножьте обе стороны на 25 [латекс] \ displaystyle {25} ( \ frac {{x}} {{25}}) \ lt \ frac {{3}} {{2}} ({25}) [/ latex] Упростить:
[латекс] \ displaystyle {x} \ lt \ гидроразрыв {{75}} {{2}} [/ latex] или 37,5
[латекс] \ displaystyle \ frac {{x}} {{- {7}}} \ ge {9} [/ latex] Умножьте обе стороны на –7: [латекс] \ displaystyle (- {7}) \ frac {{x}} {{- {7}}} \ le {9} (- {7}) [/ latex] Направление неравенства изменено. Упростите: [latex] \ displaystyle {x} \ le- {63} [/ латекс]
Ответом на неравенство часто бывает интервал значений.Распространенные неравенства:
ge больше или равно
le меньше или равно
Решение неравенств с помощью сложения и вычитания работает так же, как решение уравнения. Чтобы решить, мы изолируем переменную на одной стороне уравнения.
No related posts.