Решение неравенств методом интервалов
Разделы: Математика, Внеклассная работа
Цели:
- Обобщить использование метода интервалов для решения неравенств,
- Показать широкие возможности этого метода для решения неравенств, содержащих переменные под знаком log, , и тригонометрические функции.
Мы будем рассматривать неравенства, правая часть которых равна нулю, а левая часть представлена в виде произведения или частного функций.
Идея метода: Знак произведения или частного определяется знаком сомножителей.
Рис.1
Линейная функция с ненулевым угловым коэффициентом меняет знак при переходе через нуль функции, причём справа от нуля знак функции совпадает со знаком углового коэффициента.
Рис.2
Эти соображения приводят к следующей схеме решения неравенства:
Пример 1:[1]
- Найдём нули числителя: , , .
- Найдём нули знаменателя: .
- Наносим найденные нули на числовую ось. Т.к. неравенство строгое, то все нули изображаем выколотыми точками, которые разбивают числовую ось на интервалы:
Рис. 3
На самом правом из них знак каждого сомножителя совпадает со знаком его старшего коэффициента:
Следовательно, дробь на этом промежутке тоже отрицательна.
- При переходе через каждый из отмеченных нулей, один и только один из сомножителей меняет знак, и поэтому каждый раз меняется знак дроби. Учитывая это, расставляем в интервалах знаки (как показано на Рис.3).
- Выбираем интервалы, на которых дробь отрицательна.
- Записываем ответ: .
В рассмотренном примере 1, знаки в промежутках знакопостоянства функции чередуются. Однако делать обобщение, что так будет происходить всегда, разумеется, не следует.
Пример 2:
- нули числителя:
-2 – нуль второй кратности
- нули знаменателя:
- наносим найденные нули на числовую ось, т.к. неравенство не строгое, то нули числителя изображаем заштрихованными точками, а нуль знаменателя мы выкалываем, т.к. это число не входит в область определения неравенства:
Рис.4
Обозначим нуль второй кратности галочкой, чтобы не забыть. Т.к. числитель всегда принимает положительные значения, то на правом крайнем промежутке знак будет зависеть от знака старшего коэффициента знаменателя, т.е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется:
Рис.5
Это поможет понять следующая геометрическая картинка (Рис.6):
Рис.6
- Для записи ответа выбираем промежуток, где стоит знак «+» и заштрихованную точку , при которой дробь обращается в нуль.
Ответ:
Вывод: при переходе через нуль чётной кратности, знак не меняется.
Решить по вариантам, с последующим обсуждением у доски.
I вариант
Пример 3:
- нули числителя:
;
- нули знаменателя:
;
— нуль второй кратности
Рис.7
Ответ:
II вариант
Пример 4:
- нули числителя:
— нуль второй кратности - нули знаменателя:
;
— нуль третьей кратности
Рис.8
Ответ:
Применение метода интервалов не ограничивается решением рациональных неравенств.
Универсальность метода основана на достаточно наглядном свойстве непрерывных функций: «Если на интервале (a;b) функция f(x) непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак».
Пример 5: [1] ,
Будем решать это неравенство по той же схеме, но не на всей оси, а на области определения логарифмической функции, т.е. на промежутке (*):
- нули числителя:
; — не входит в (*) - нули знаменателя:
;
Рис. 9
- на самом правом промежутке
, ,
Следовательно на этом промежутке левая часть неравенства отрицательна
- при переходе через каждый корень меняет знак один и только один из сомножителей. Учитывая это, расставляем знаки на остальных промежутках.
Ответ: .
Пример 6:
- нули числителя:
корней нет - нули знаменателя:
- решение изображаем на рис. 10:
Рис.10
Квадратный трёхчлен в числителе не имеет корней и не меняет свой знак. Его знак совпадает со знаком старшего коэффициента, т.е. «+».
Ответ:.
Пример 7: ОДЗ:
Приведём неравенство к такому виду, чтобы в правой части был «0»:
- нули числителя:
;;;
- нули знаменателя:
- решение изображаем на рис. 11:
Рис.11
Ответ:.
Пример 8:
ОДЗ:
Рис.12
- нули числителя:
- нули знаменателя:
, но ОДЗ удовлетворяет только
- решение изображаем на рис. 13:
Рис.13
Ответ:.
- Ответ:.
- Ответ:.
- Ответ:.
- Ответ: .
- Ответ:.
Задания для факультативный занятий предоставлены в Приложении2.
Вывод: Как известно, линейная, квадратичная, степенная, показательная, логарифмическая и тригонометрические функции, а так же их композиции и функции, получаемые из них с помощью арифметических действий, непрерывны в своей области определения. Поэтому метод интервалов можно применять при решении практически всех неравенств школьного курса. Метод интервалов позволяет представить множество решений неравенства в виде объединения промежутков, границы которых либо корни соответствующего уравнения, либо граничные точки области определения.
Список литературы:
[1] «Метод интервалов» //Журнал «Квант» No12, 1985 г.
11.08.2009
Поделиться страницей:urok.1sept.ru
Решение рациональных неравенств методом интервалов
Метод интервалов — это универсальный способ решения практически любых неравенств, которые встречаются в школьном курсе алгебры. Он основан на следующих свойствах функций:
1. Непрерывная функция g(x) может изменить знак только в той точке, в которой она равна 0. Графически это означает, что график непрерывной функции может перейти из одной полуплоскости в другую, только если пересечет ось абсцисс (мы помним, что ордината любой точки, лежащей на оси ОХ (оси абсцисс) равна нулю, то есть значение функции в этой точке равно 0):
Мы видим, что функция y=g(x), изображенная на графике пересекает ось ОХ в точках х= -8, х=-2, х=4, х=8. Эти точки называются нулями функции. И в этих же точках функция g(x) меняет знак.
2. Функция также может менять знак в нулях знаменателя — простейший пример хорошо известная функция :
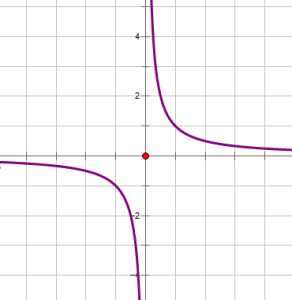
Мы видим, что функция меняет знак в корне знаменателя, в точке , но при этом не обращается в ноль ни в одной точке. Таким образом, если функция содержит дробь, она может менять знак в корнях знаменателя.
2. Однако, функция не всегда меняет знак в корне числителя или в корне знаменателя. Например, функция y=x2 не меняет знак в точке х=0:
Т.к. уравнение x2 =0 имеет два равных корня х=0, в точке х=0 функция как бы дважды обращается в 0. Такой корень называется корнем второй кратности.
Функция меняет знак в нуле числителя, , но не меняет знак в нуле знаменателя: , так как корень — корень второй кратности, то есть четной кратности:
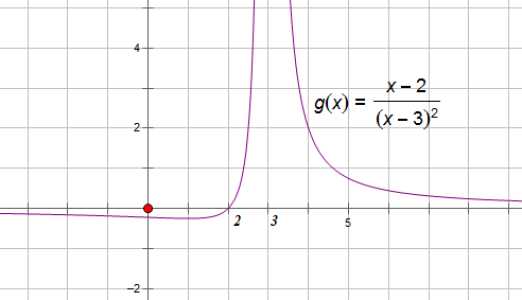
Важно! В корнях четной кратности функция знак не меняет.
Обратите внимание! Любое нелинейное неравенство школьного курса алгебры, как правило, решается с помощью метода интервалов.
Предлагаю вам подробный алгоритм решения неравенств методом интервалов, следуя которому вы сможете избежать ошибок при решении нелинейных неравенств.
1. Для начала необходимо привести неравенство к виду
Р(х)V0,
где V- знак неравенства: <,>,≤ или ≥. Для этого необходимо:
а) перенести все слагаемые в левую часть неравенства,
б) найти корни получившегося выражения,
в) разложить левую часть неравенства на множители
г) одинаковые множители записать в виде степени.
Внимание! Последнее действие необходимо сделать, чтобы не ошибиться с кратностью корней — если в результате получится множитель в четной степени, значит, соответствующий корень имеет четную кратность.
2. Нанести найденные корни на числовую ось.
3. Если неравенство строгое, то кружки, обозначающие корни на числовой оси оставляем «пустыми», если неравенство нестрогое, то кружки закрашиваем.
4. Выделяем корни четной кратности — в них Р(х) знак не меняет.
5. Определяем знак Р(х) на самом правом промежутке. Для этого берем произвольное значение х0, которое больше большего корня и подставляем в Р(х).
Если P(x0)>0 (или ≥0), то в самом правом промежутке ставим знак «+».
Если P(x0)<0 (или ≤0), то в самом правом промежутке ставим знак «-«.
6. Далее двигаемся влево по числовой прямой и расставляем знаки: при переходе через точку, обозначающую корень нечетной кратности происходит смена знака.
При переходе через точку, обозначающую корень четной кратности знак НЕ МЕНЯЕТСЯ.
7. Еще раз смотрим на знак исходного неравенства, и выделяем промежутки нужного нам знака.
8. Внимание! Если наше неравенство НЕСТРОГОЕ, то условие равенства нулю проверяем отдельно.
9. Записываем ответ.
Если исходное неравенство содержит неизвестное в знаменателе, то также переносим все слагаемых влево, и приводим левую часть неравенства к виду
(где V- знак неравенства: < или >)
Строгое неравенство такого вида равносильно неравенству
НЕстрогое неравенство вида
равносильно системе:
На практике, если функция имеет вид , то поступаем следующим образом:
- Находим корни числителя и знаменателя.
- Наносим их на ось. Все кружки оставляем пустыми. Затем, если неравенство не строгое, то корни числителя закрашиваем, а корни знаменателя всегда оставляем пустыми.
- Далее следуем общему алгоритму:
- Выделяем корни четной кратности (если числитель и знаменатель содержат одинаковые корни, то считаем, сколько раз встречаются одинаковые корни). В корнях четной кратности смены знака не происходит.
- Выясняем знак на самом правом промежутке.
- Расставляем знаки.
- В случае нестрого неравенства условие равенства условие равенства нулю проверяем отдельно.
- Выделяем нужные промежутки и отдельно стоящие корни.
- Записываем ответ.
Чтобы лучше понять алгоритм решения неравенств методом интервалов, посмотрите ВИДЕОУРОК, в котором подробно разбирается пример решения неравенства методом интервалов.
ege-ok.ru
Решение неравенств методом интервалов
Решим неравенство:
Чтобы решить такое неравенство, нужно рассмотреть функцию, решив ее, получим:
Задача сводится к нахождению промежутков знакопостоянства. Для этого необходимо найти нули функции:
Решением системы будет:
Можно ли использовать такой приём при наличии большего количества множителей? Хоть внешний вид графика нам будет неизвестен, но нули такой функции найти не трудно.
Найдём нули функции. Отметим их на оси икс:
Они разбили числовую прямую на части. Как же разобраться со знаком функции на каждом промежутке. В правой части формулы, задающей функцию, записано произведение линейных множителей:
Если вспомним график линейной функции, то станет понятно, что каждый линейный множитель меняет знак в своём нуле с + на — или наоборот, с минуса на плюс. Причём остальные множители свой знак менять не будут. Если изменится знак одного множителя в произведении, то и знак всего произведения тоже изменится.
Свойство:
В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
Этим свойством и пользуются при решении неравенств, такой приём называют методом интервалов.
Пример.
Решить неравенство:
Преобразуем:
Знак неравенства поменялся, так как неравенство умножили на отрицательное число.
Рассмотрим соответствующую функцию и найдём её нули:
Вернёмся к неравенству. Его знак: строго меньше нуля. Значит, все точки изображённые на числовой прямой, являются выколотыми, ведь не допускается равенство нулю.
Эти значения разбили область определения на промежутки:
Для того чтобы определим знак этой функции нужно в функцию подставить значение из этого промежутка.
Решением неравенства будет:
Пример.
Решить неравенство:
Приведём левую часть неравенства к виду:
Рассмотрим соответствующую функцию и найдём её нули:
Отметим их на числовой прямой:
Область определения разбили на промежутки. Определили знаки функции. Вернёмся к неравенству, так как его знак ≥0. Допускается равенство нулю, поэтому точки будут закрашенными.
Решением данного неравенства будет:
Пример.
Решить неравенство:
Так как знак этой дроби совпадает со знаком ее произведения, перейдем к решению неравенства:
Найдем нули функции:
Отметим их на числовой прямой:
Решение данного неравенства:
Пример.
Решить неравенство:
Перейдём к произведению:
Найдём нули функции:
Определим их:
Решением данного неравенства будет:
Пример.
Решить неравенство:
Преобразуем неравенство:
Найдем нули функции и отметим их на числовой прямой:
Если нуль функции имеет чётную кратность, то при переходе через этот нуль функция сохраняет знак. Если же нуль функции имеет нечётную кратность, то при переходе через этот нуль функция меняет знак.
Решением данного неравенства будет:
videouroki.net
Решение неравенств методом интервалов: разбираем на конкретном примере
Одним из методов решения различных неравенств является метод интервалов. Он применяется для неравенств вида:
- f(x)>0,
- f(x)>=0,
- f(x)
- f(x)
- f(x)/g(x) >0,
- f(x)/g(x)>=0,
- f(x)/g(x)<0,
- f(x)/g(x)<=0.
Где f(x) и g(x) это некоторые многочлены, которые разложены на простейшие множители.
Простейшие множители, это множители вида (х-а).
Разберем метод интервалов на достаточно общем конкретном примере.
Метод интервалов на конкретном примере
Пусть в результате преобразований исходного неравенства мы пришли к следующему неравенству:
(x-3)2*(x-7)3*(x+1) / (x-2)*(x+4)2 >= 0.
Обратите внимание, что в каждом из сомножителей переменная стоит на первом месте, то есть (х-2) а не (2-х).К такому виду всегда можно привести данные скобки умножая их на -1, и при этом не забывая менять знак.
Теперь нам необходимо на числовой прямой отметить все точки в которых в числителе или знаменателе получается нуль. Так как неравенство не строгое (>=), то нули числителя отмечаем обычными точками, а нули знаменателя выколотыми точками. Если бы неравенство было строгим, то все точки надо было бы рисовать выколотыми. Эти точки разбили нашу прямую на несколько интервалов.
Теперь надо расставить знаки. В самый правый интервал ставим знак «плюс». Далее знаки в каждом промежутке расставляются в соответствии со следующим правилом.
- Знак меняется, если у скобки была нечетная степень.
- Знак не меняется, если у скобки была четная степень.
Например, у нас. Сначала был знак «плюс». Далее точка 7. Смотрим неравенство, у нас там множитель с семеркой (х-7)^3 имеет третью степень. Тройка нечетное число, значит знак меняем и записываем его над промежутком. Следующая точка 3. Смотрим неравенство. Тройка имеется в множителе (x-3)^2. Степень четная значит знак остается таким же «минус». И так продолжаем до конца, пока у каждого промежутка не будет свой знак.
Получится следующая картинка.
Теперь остаётся только записать ответ. По условию нам нужно выписать все значения, при которых неравенство больше либо равно нулю. Значит в ответ включаем все интервалы где у нас стоит знак «плюс».
- Х принадлежит [-1,2)U{3}U[7,+∞).
Если точка выколотая, значит она не включается в ответ, и у неё рисуется круглая скобка, если точка обычная, то она включается в ответ и у неё пишется квадратная скобка.
Важно не забыть отдельные точки, как например точку 3 в нашем примере. Она обычная, и в ней указанная дробь будет равняться нулю, значит её тоже надо записать в ответ.
Нужна помощь в учебе?
Предыдущая тема: Решение неравенств второй степени с одной переменной: приводим примеры
Следующая тема:   Целое уравнение и его корни: четыре степени уравнений
Все неприличные комментарии будут удаляться.
www.nado5.ru
