ВЕКТОРНАЯ АЛГЕБРА — это… Что такое ВЕКТОРНАЯ АЛГЕБРА?
— раздел векторного исчисления, в к-ром изучаются простейшие операции над (свободными) векторами. К числу этих операций относятся линейные операции над векторами: операция сложения векторов и умножения вектора на число.
Суммой векторов наз. вектор, проведенный из начала к концу , если конец и начало
совмещены. Операция сложения векторов обладает свойствами:
где — нулевой вектор,- есть вектор, противоположный вектору . Разностью векторов наз.
вектор такой, что
Произведением вектора на число в случае пал. вектор, модуль к-рого равен и к-рый направлен в ту же сторону, что и вектор , если , и в противоположную, если . Если или (и) , то . Операция умножения вектора на число обладает свойствами:
(дистрибутивность относительно сложения векторов),
(дистрибутивность относительно сложения чисел),
(ассоциативность), (умножение на единицу). Множество всех векторов пространства с введенными в нем операциями сложения и умножения на число образует векторное пространство (линейное пространство). В В. а. важное значение имеет понятие линейной зависимости векторов. Векторы наз. линейно зависимыми векторами, если существуют числа из к-рых хотя бы одно отлично от нуля, такие, что справедливо равенство
Для линейной зависимости двух векторов необходима и достаточна их коллинеарность, для линейной зависимости трех векторов необходима и достаточна их компланарность. Если один из векторов нулевой, то они линейно зависимы. Векторы наз. линейно независимым и, если из равенства (1) следует, что числа равны нулю. На плоскости существует не более двух, а в трехмерном пространстве не более трех линейно независимых векторов.
Совокупность трех (двух) линейно независимых векторов трехмерного пространства (плоскости), взятых в определенном порядке, образует б а-з и с. Любой вектор единственным образом представляется в виде суммы:
Числа наз. координатами (компонентами) вектора в данном базисе и пишут .
Два вектора н равны тогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе. Необходимым в достаточным условием коллинеарности векторов является пропорциональность их соответствующих координат: Необходимым и достаточным условием компланарности трех векторов является равенство
Линейные операции над векторами сводятся клинейным операциям над координатами. Координаты суммы векторов и равны суммам соответствующих координат: Координаты произведения вектора ана число равны произведениям координат на :
Скалярным произведением ненулевых векторов наз. произведение их модулей на косинус угла между ними:
За j принимается угол между векторами, не превосходящий . Если или , то скалярное произведение полагают равным нулю. Скалярное произведение обладает свойствами:
(коммутативность),
(дистрибутивность относительно сложения векторов),
(сочетательность относительно умножения на число),
лишь если
Для вычисления скалярных произведений векторов часто пользуются декартовыми прямоугольными координатами, т. е. координатами векторов в базисе, состоящем из единичных взаимно перпендикулярных векторов (ортов) (ортонормированный базис). Скалярное произведение векторов
заданных в ортонормированием базисе, вычисляется по формуле:
Косинус угла между ненулевыми векторами и может быть вычислен по формуле
Косинусы углов вектора с векторами базиса наз. направляющими косинусами вектора
Направляющие косинусы обладают следующим свойством:
Осью наз. прямая с лежащим на ней единичным вектором — ортом, задающим положительное направление на прямой. Проекцией вектора на ось наз. направленный отрезок на оси, алгебраич. значение к-рого равно скалярному произведению вектора на вектор . Проекции обладают свойствами:
Каждая координата вектора в ортонормированием базисе равна проекции этого вектора на ось, определяемую соответствующим вектором базиса.
В пространстве различают правые н левые тройки векторов. Тройка некомпланарных векторов наз. правой, если наблюдателю из их общего начала обход концов векторов в указанном порядке кажется совершающимся по часовой стрелке. В противном случае — левая тройка. Правая (левая) тройка векторов располагается так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки (см. рис.).
Все правые (или левые) тройки векторов наз. одинаково ориентированными. Ниже тройка векторов базиса считается правой.
Пусть на плоскости задано направление положительного вращения (от к |. Псевдоскалярным произведением ненулевых векторов и наз. произведение их модулей на синус угла положительного вращения от к :
Псевдоскалярное произведение нулевых векторов полагают равным нулю. Псевдоскалярное произведение обладает свойствами:
(антикоммутативность),
(дистрибутивность относительно сложения векторов),
(сочетательность относительно умножения на число),
лишь если или (и) или кол-ливеарны.
Если в ортонормированием базисе векторы имеют координаты и то
Векторным произведением ненулевых и неколлинеарных векторов наз. вектор, модуль к-рого равен произведению их модулей на синус угла между ними, перпендикулярный и направленный так, что тройка векторов — правая:
Векторное произведение полагают равным нулю, если или (и) или они коллинеарны. Векторное произведение обладает свойствами:
(антикоммутативность),
(дистрибутивность относительно сложения векторов),
(сочетательность относительно умножения на число),
лишь если или(и) или коллинеарны.
Если в ортонормпрованном базисе векторы имеют координаты и , то
Смешанным произведением векторов наз. скалярное произведение вектора на векторное произведение векторов :
Смешанное произведение обладает свойствами:
лишь если или (и) или (и) или векторы компланарны.
если тройка векторов — правая, если — тройка левая.
Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах Если в ортонормированном базисе векторы имеют координаты то
Двойным векторным произведением векторов наз. векторное произведение .
При вычислении двойного векторного произведения имеют место формулы:
Лит.:[1] Александров П. С., Лекции по аналитической геометрии…, М., 1968; [2] Ефимов Н. В., Краткий курс аналитической геометрии, 9 изд., М., 1967; [3] Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1968; [4] Погорелов А. В., Аналитическая геометрия, 3 изд., М., 1968. Ю. П. Пытьев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Векторная алгебра | Решение задач по математике и другим предметам!!! |
Решение типового варианта контрольной работы. Векторная алгебра.
Задание 1: Коллинеарны ли векторы и , разложенные по векторам и , где
Решение:
1. Вычислим проекции векторов на оси координат:
2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:
не коллинеарны.
Задание 2: Перпендикулярны ли векторы ?
Решение: Два вектора перпендикулярны, если их скалярное произведение равно 0,скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле:, где вычислим скалярное произведение:
Векторы не перпендикулярны.
Задание 3: Компланарны ли векторы ?
Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле: , гдеВычислим смешанное произведение векторов:
Векторы не компланарны.
Задание 4: При каком значении векторы где , перпендикулярны?
Решение:
1) Для определения , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) мы сможем найти из условия: , для этого найдем проекции векторов и на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора
Итак: векторы и перпендикулярны при и при
Задание 5: Даны точки:
Найти:
1. пр;
2. ;
3. ;
4. орт вектора ;
5. ;
6. ;
7.
Решение:
1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: пр где скалярное произведение векторов вычисляется по формуле: Где и длина вектора: итак ,в нашем случае, формула принимает вид: для нахождения необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:

на основании формулы, выше написанной, получим :
Пр;
2. Для нахождения длины вектора воспользуемся формулой:, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:
;
Итак:
3. Угол между векторами можно найти из определения скалярного произведения: в нашем случае формула принимает вид: находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:
Итак
4. Направление вектора Определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам: Направляющие косинусы вектора связаны соотношением Мы имеем вектор единичной длины, такой вектор называется ортом для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину Орт вектора .
Итак: орт вектора
5. Скалярное произведение векторов вычисляем по формуле:
(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :
Итак:
6. Векторное произведение векторов вычисляется по формуле:
, где
Находим проекции векторов на оси координат:

Итак:
7. Смешанное произведение векторов вычисляется по формуле:
, где Итак:
Задание 6: Даны координаты вершин пирамиды:
Вычислить:
1. объем пирамиды;
2. длину ребра ;
3. площадь грани ;
Решение:
1. Объем пирамиды равен объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения объем
Параллелипипеда, построенного на векторах как на ребрах равен:
Найдем проекции соответствующих векторов на оси координат:
Тогда объем пирамиды равен:
Вычислим объем по указанной формуле:
;
2. Длина ребра
; (смотри пункт 5,3)
3. Площадь грани вычисляется по формуле:
так как грань треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения найдем проекции векторов на оси координат:
;
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Векторная алгебра
6. Векторная алгебра
В математике исследуются различные объекты. К числу основных относятся скалярные и векторные величины. Знакомство с ними состоялось еще в средней школе.
Известно, что скалярная величина (скаляр) определяется одним параметром – величиной, например, 3, -5, 3.14 и так далее. В дальнейшем скаляры будем обозначать буквами и так далее.
Вектор – это
направленный отрезок, характеризуемый
двумя параметрами – длиной и направлением.
Чтобы отличать векторы от скаляров, их
будем задавать следующим образом 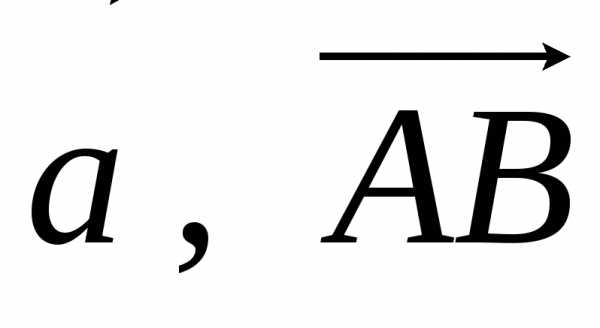 ,
в последнем случае
,
в последнем случае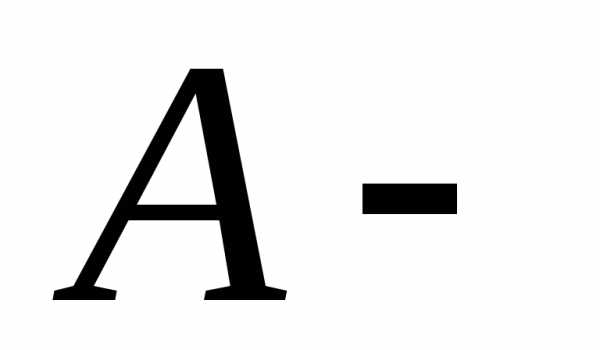 начальная,
начальная,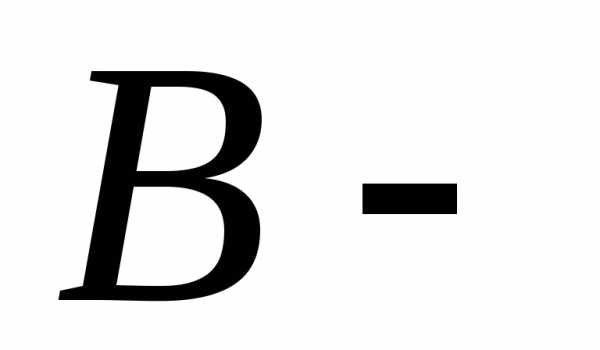 конечная
точки вектора. Иногда их обозначают
жирным шрифтомa .
конечная
точки вектора. Иногда их обозначают
жирным шрифтомa .
Исторически сложилось, что геометрия оперирует со свободными векторами. Два вектора считаются равными, если одинаковы их длины и они сонаправлены (параллельны и направлены в одну сторону). Другими словами, действие вектора на объект не зависит от точки его приложения.
Э

Итак, векторная алгебра строится для свободных векторов, что значительно упрощает теорию. При переходе к силам, действующим на тело, делаются определенные поправки (вводятся моменты сил), чем устраняется указанное противоречие.
Введем понятие
орта — единичного вектора, то есть
вектора, длина которого равна единице.
Обозначим длину, или модуль вектора  ,
тогда единичный вектор
,
тогда единичный вектор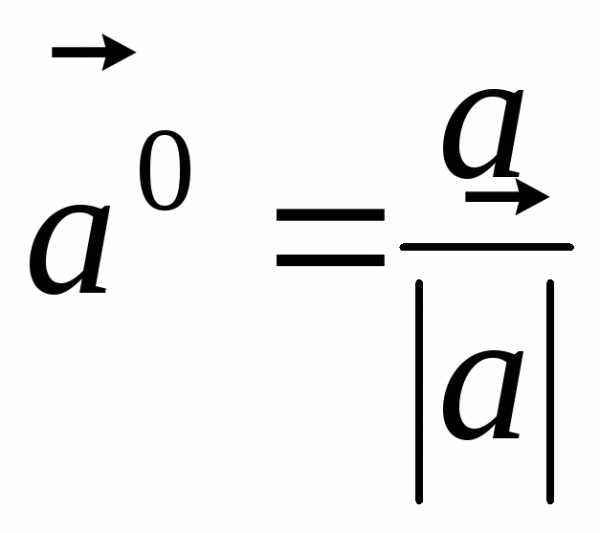 .
.
Проекцией вектора  на направление
на направление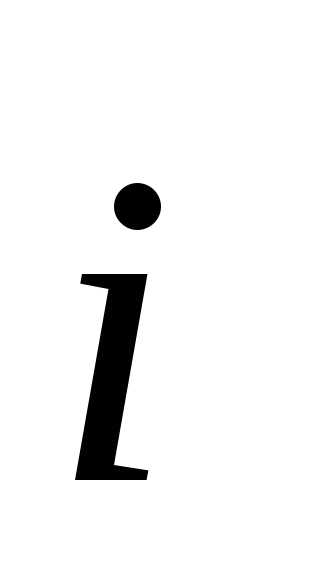 ,
где
,
где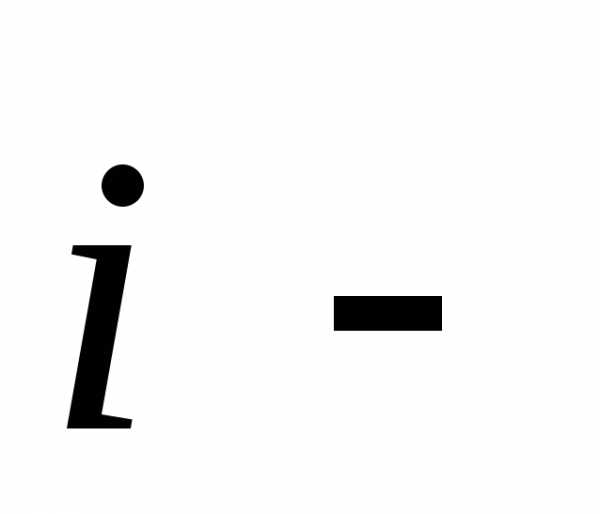 единичный
вектор, показывающий направление от
единичный
вектор, показывающий направление от к
к ,
является скалярная величина
,
является скалярная величина .
В соответствии с рисунком,
следовательно, если угол между векторами
.
В соответствии с рисунком,
следовательно, если угол между векторами и
и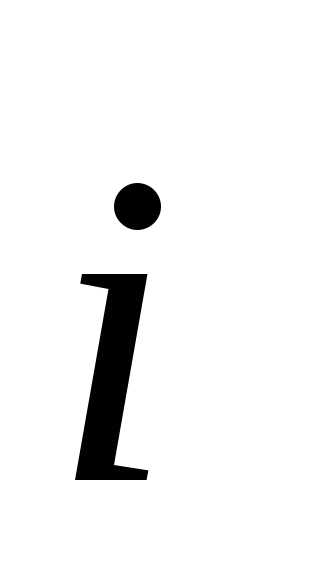 острый,
острый, ,
в противном случае проекция отрицательна.
,
в противном случае проекция отрицательна.
Рисунок 1.
Векторы называются коллинеарными, если лежат на параллельных прямых.
Векторы называются ортогональными, если угол между ними прямой.
Векторы, лежащие в некоторой плоскости или параллельные плоскости, называются компланарными. Компланарные векторы могут быть перемещены в одну плоскость, сто следует из определения свободных векторов.
Линейными операциями над векторами называются сложение векторов, их вычитание, умножение на число (скаляр).
Правило параллелограмма.
Сложение двух векторов осуществляется следующим образом. В силу того, что векторы свободны, с помощью параллельного переноса совмещаются их начальные точки, затем на этих векторах, как на сторонах, строится параллелограмм. Диагональ параллелограмма, идущая из общей начальной точки является суммарным вектором этих дух векторов.
Рисунок 2.
Это правило установлено еще в древности путем наблюдений за передвижением предметов под действием двух сил.
Из правила
параллелограмма можно получить правило
треугольника суммирования двух векторов. Сумму
векторов можно получить, построив
вначале вектор  ,
затем из его конца провести вектор
,
затем из его конца провести вектор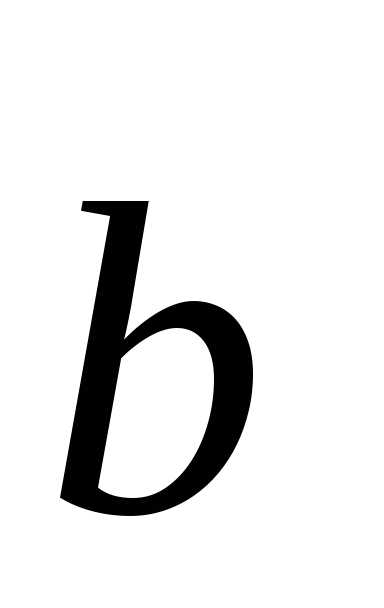 .
Вектор, идущий из начала первого вектора
в конец второго является суммой этих
двух векторов, что непосредственно
следует из рисунка 2.
.
Вектор, идущий из начала первого вектора
в конец второго является суммой этих
двух векторов, что непосредственно
следует из рисунка 2.
Сложение большего количества векторов осуществляется по правилу многоугольника. Заключается оно в следующем. Строится первый вектор, из его конца проводится второй вектор, из конца второго третий и так далее, затем соединяется начальная точка первого вектора с концом второго это и будет суммарным вектором.
Правило доказывается с помощью несколько раз примененного правила треугольника.
Рисунок 3.
Правило вычитания векторов
Разностью векторов 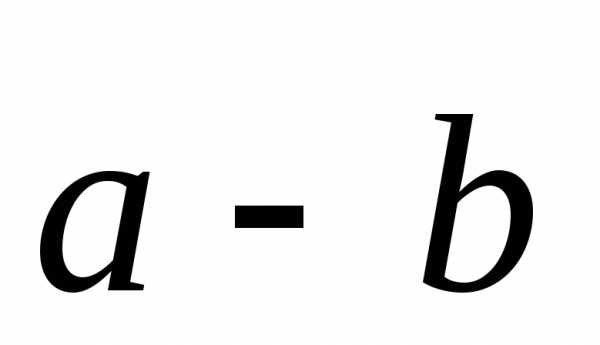 является вторая диагональ параллелограмма,
проведенная из конца вычитаемого вектора
в конец уменьшаемого. Это правило
доказывается с помощью рисунка 4.
является вторая диагональ параллелограмма,
проведенная из конца вычитаемого вектора
в конец уменьшаемого. Это правило
доказывается с помощью рисунка 4.
Рисунок 4.
Представим вектор 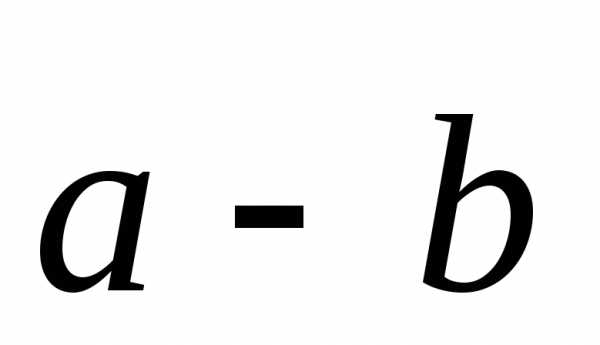 как сумму вектора
как сумму вектора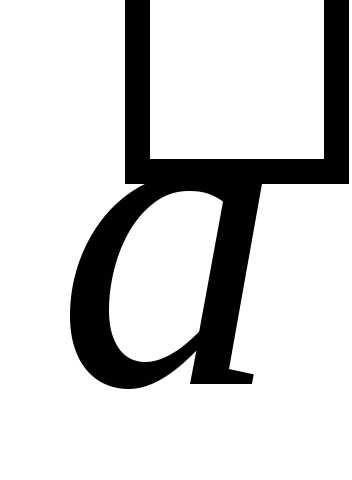 с вектором, обратным вектору
с вектором, обратным вектору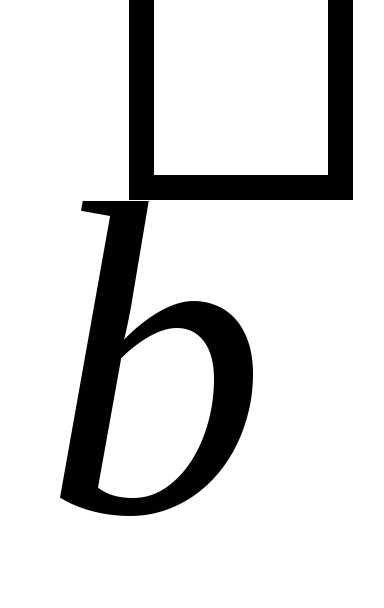 ,
то есть с
,
то есть с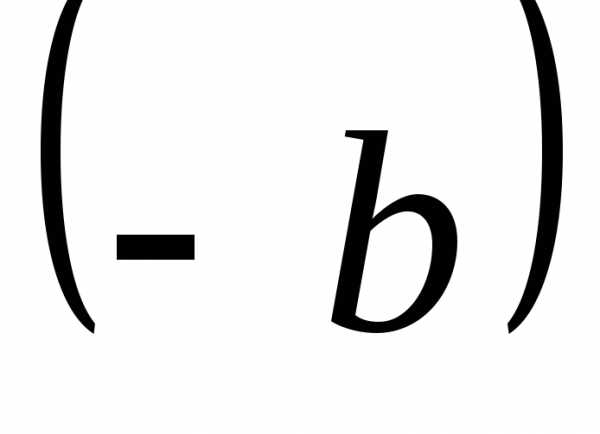 .
Очевидно,,
но эта сумма 0 — есть диагональ нижнего
параллелограмма. Из среднего параллелограмма
видно, полученный вектор совпадает с
вектором, являющимся второй диагональю
исходного (верхнего) параллелограмма,
что требовалось доказать.
.
Очевидно,,
но эта сумма 0 — есть диагональ нижнего
параллелограмма. Из среднего параллелограмма
видно, полученный вектор совпадает с
вектором, являющимся второй диагональю
исходного (верхнего) параллелограмма,
что требовалось доказать.
Правило умножения вектора на число
Вектор 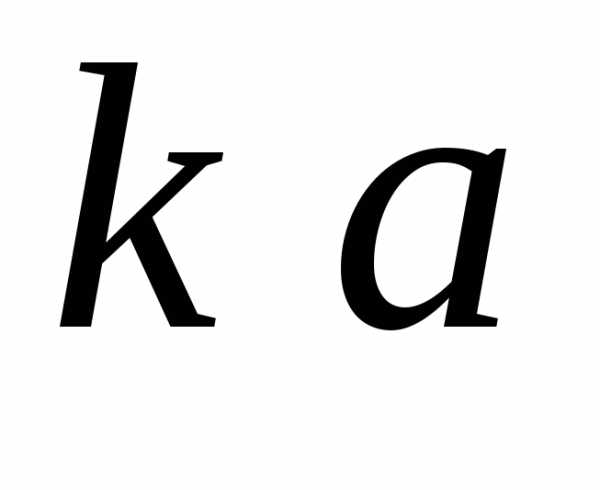 ,
где
,
где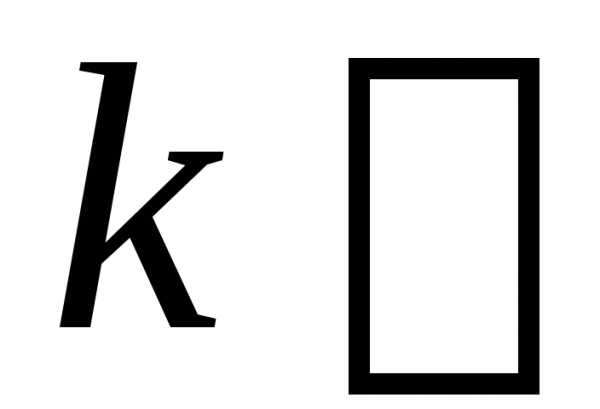 скаляр,
представляет собой вектор, длина которого
в
скаляр,
представляет собой вектор, длина которого
в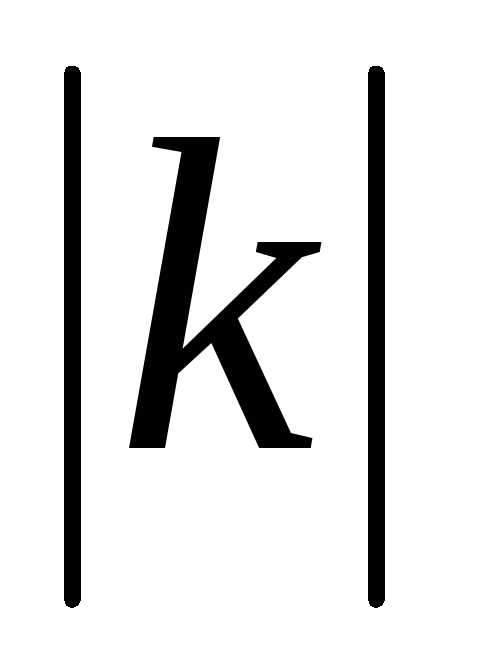 раз больше длины вектора
раз больше длины вектора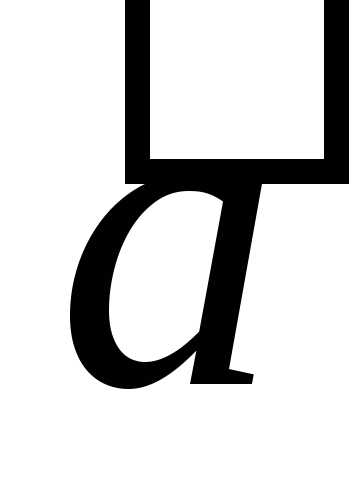 ,
и направлен он вдоль вектора
,
и направлен он вдоль вектора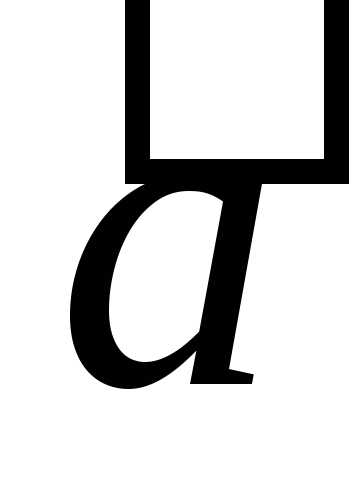 при
при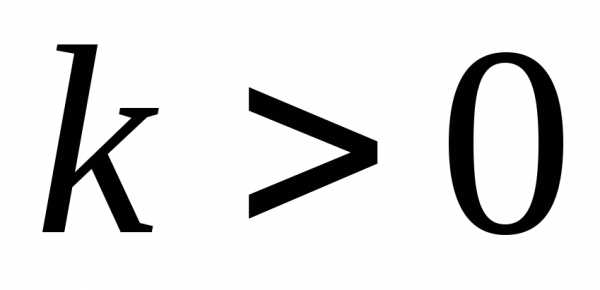 и в противоположном направлении при
и в противоположном направлении при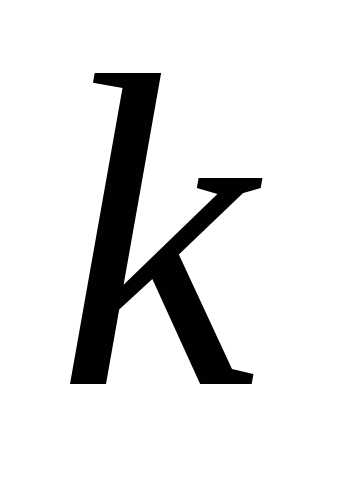 отрицательном.
отрицательном.
Примечание. Приведенные выше правила требуют решения соответствующих задач построением, то есть с помощью чертежей, что не всегда удобно ввиду неизбежных погрешностей построения.
Встает вопрос, как свести эти ошибки к минимуму. Одним из решений этого вопроса явилось введение базисов, о чем пойдет речь ниже.
Базисы на плоскости и в трехмерном пространстве
Определение 1. Любые два неколлинеарных вектора могут быть выбраны в качестве базиса на плоскости.
Определение 2. Любые три некомпланарных вектора могут быть выбраны в качестве базиса в трехмерном пространстве.
Определение 3. Базис называется ортогональным, если углы между базисными векторами прямые.
Определение 4. Базис называется нормированным, если базисные векторы единичные.
Определение 5.
Базис называется ортонормированным,
если он ортогональный и нормированный.
Векторы ортонормированного базиса в
соответствии с существующими традициями
обозначаются  .
.
Определение 6. Линейной комбинацией векторов называется выражение, гденекоторые числа (скаляры).
Теорема 1. Любой
вектор  плоскости может быть представлен в виде
линейной комбинации базисных векторов
плоскости может быть представлен в виде
линейной комбинации базисных векторов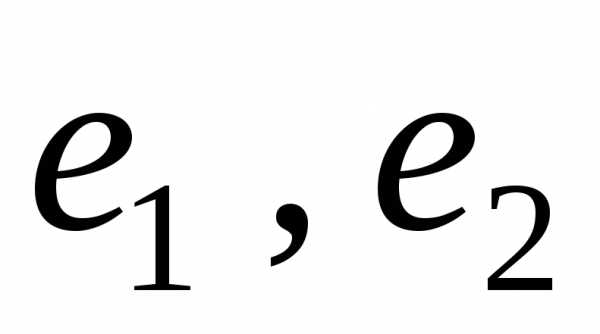 :.
:.
Доказательство.
Совместим начальные точки базисных
векторов и вектора  ,
назовем эту точку
,
назовем эту точку ,
из конца вектора
,
из конца вектора (точка
(точка )
проведем прямые, параллельные векторам
)
проведем прямые, параллельные векторам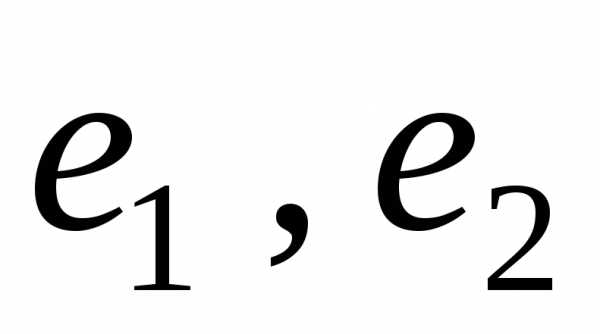 до пересечения их с продолжениями
векторов
до пересечения их с продолжениями
векторов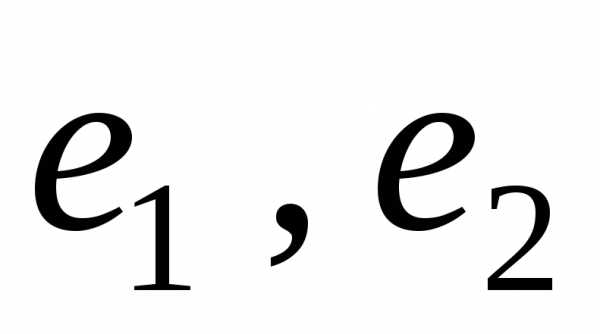 ,
точки пересечения прямых обозначим
,
точки пересечения прямых обозначим и.
В результате получен параллелограмм
и.
В результате получен параллелограмм (рисунок 5). Из правила сложения векторов
следует
(рисунок 5). Из правила сложения векторов
следует
.
Поскольку векторы
и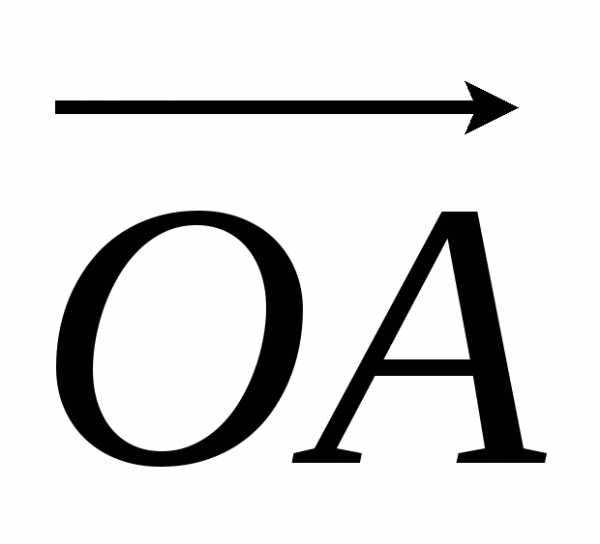 коллинеарны, можно
записать
коллинеарны, можно
записать 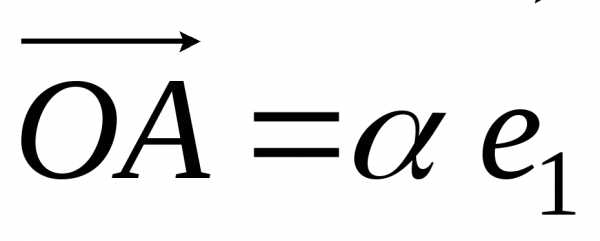 ,
где
,
где 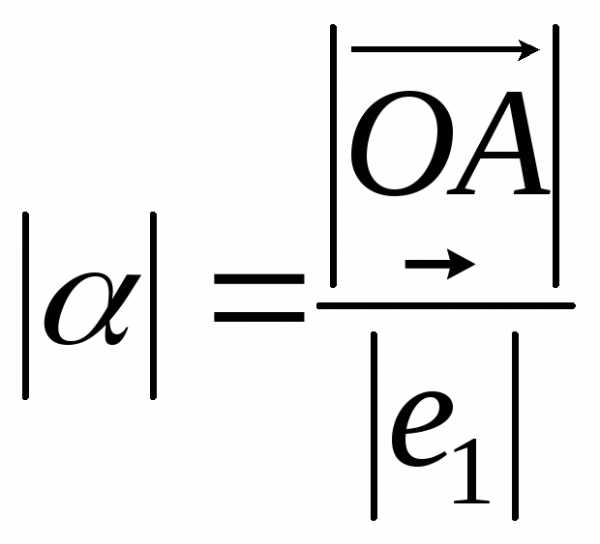 .
Аналогично
.
Аналогично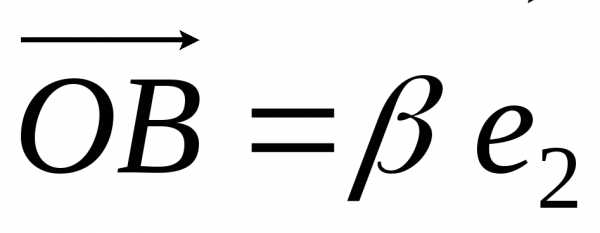 ,
где,
причем
,
где,
причем и
и могут быть как положительными, так и
отрицательными числами в зависимости
от направлений базисных векторов и
вектора
могут быть как положительными, так и
отрицательными числами в зависимости
от направлений базисных векторов и
вектора .
Теорема доказана.
.
Теорема доказана.
Рисунок 5.
Очевидно, векторы 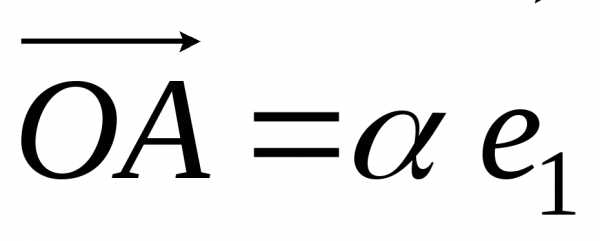 и
и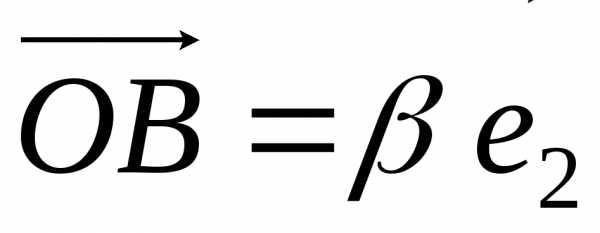 являются проекциями вектора
являются проекциями вектора на направления
на направления соответственно. Если базис нормированный,
то числа
соответственно. Если базис нормированный,
то числа и
и называют координатами (компонентами)
вектора в данном базисе.
называют координатами (компонентами)
вектора в данном базисе.
Теорема 2. Любой вектор трехмерного пространства может быть представлен в виде линейной комбинации базисных векторов.
Докажем теорему для ортонормированного базиса, то есть, что
.
Пусть точка  начальная точка векторов
начальная точка векторов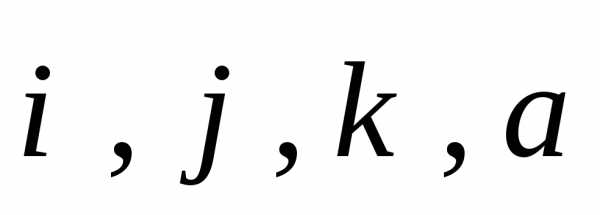 ,
, конечная
точка вектора
конечная
точка вектора ,
, основание
перпендикуляра, опущенного из точки
основание
перпендикуляра, опущенного из точки на плоскость
на плоскость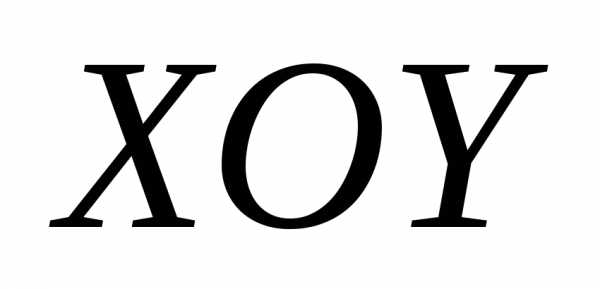 .
Из треугольника
.
Из треугольника ,
изображенного на рисунке 6, следует.
Из первой теоремы следует,
из коллинеарности векторов
,
изображенного на рисунке 6, следует.
Из первой теоремы следует,
из коллинеарности векторов и
и следует
следует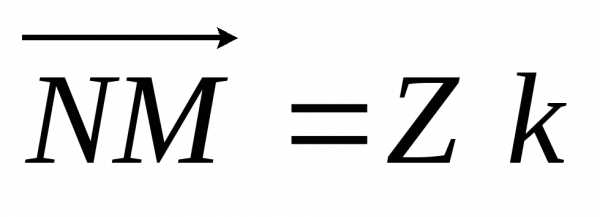 ,
очевидно,.
,
очевидно,.
Рисунок 6.
Следствие. Векторы считаются равными, если равны их соответствующие координаты в одном и том же базисе. То есть
, если .
Вместо обозначения можно использовать сокращенную запись, если базисные векторы заданы ранее.
Имеют место две теоремы о проекциях векторов:
1. ,
2.
где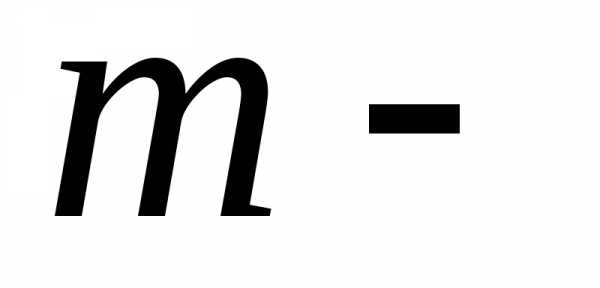 число
(скаляр).
число
(скаляр).
Из этих теорем следуют правила сложения, вычитания векторов, заданных в базисе, умножения вектора на скаляр. Итак,
Пусть ,, тогда
, или
Таким образом, чтобы просуммировать два, или большее количество векторов, заданных в едином базисе, необходимо просуммировать их одноименные проекции.
Аналогично
,
(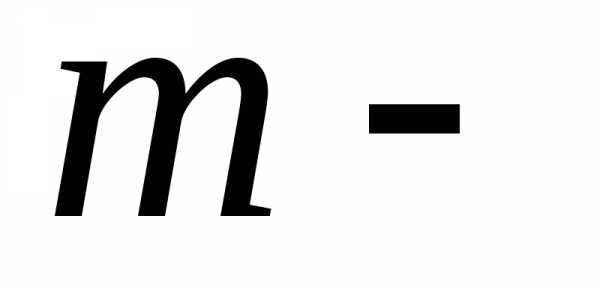 скаляр),
скаляр),
или .
Скалярное произведение векторов
Определение.
Скалярным произведением двух векторов 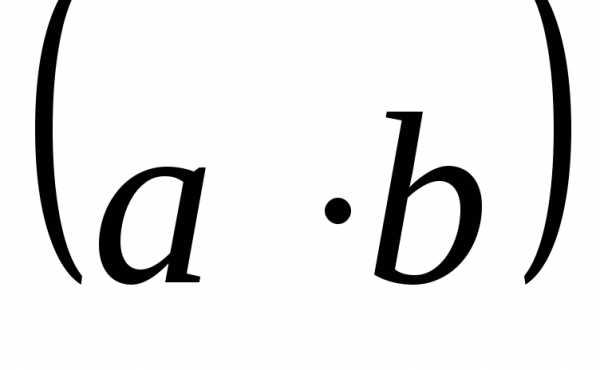 называется число, равное произведению
модулей этих векторов на косинус угла
между ними.
называется число, равное произведению
модулей этих векторов на косинус угла
между ними.
.
Знак скалярного произведения определяется знаком косинуса.
Очевидно, скалярное произведение можно представить в виде
.
Как уже говорилось ранее, правило суммирования векторов было получено еще в древности из наблюдений за движением тел под действием нескольких сил. Правило вычитания векторов следовало из правила их суммирования. Правило умножения вектора на число также следовало из наблюдений за действием на тело сил.
Скалярное
произведение также следует из практических
потребностей. В самом деле, если тело
под действием силы  движется в
направлении
движется в
направлении  ,
то работу совершает только проекция
этой силы на направление
,
то работу совершает только проекция
этой силы на направление ,
перпендикулярная ей проекция работы
не совершает. Тогда работа, совершаемая
силой
,
перпендикулярная ей проекция работы
не совершает. Тогда работа, совершаемая
силой на пути
на пути ,
вычисляется по формуле
,
вычисляется по формуле
,
то есть совершаемая
работа вычисляется посредством скалярного
произведения. Если угол  острый, работа положительная (активная).
При тупом угле между векторами, работа
отрицательная, то есть совершается
силами, противодействующими движению
(например, силой трения).
острый, работа положительная (активная).
При тупом угле между векторами, работа
отрицательная, то есть совершается
силами, противодействующими движению
(например, силой трения).
Свойства скалярного произведения
1.
.
Поскольку угол
между первым и вторым векторами
произведения, в левом и правом произведениях
эти углы отличаются знаком, и в силу
четности косинуса не влияют на величину
произведения.
угол
между первым и вторым векторами
произведения, в левом и правом произведениях
эти углы отличаются знаком, и в силу
четности косинуса не влияют на величину
произведения.
2.
,
если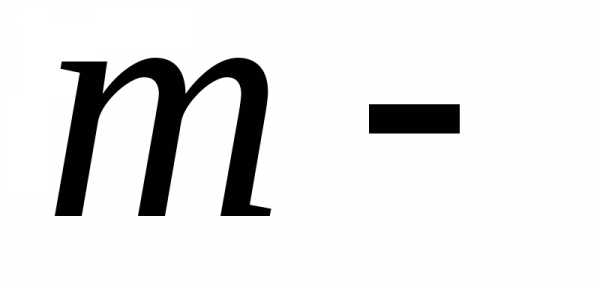 скаляр.
Для
скаляр.
Для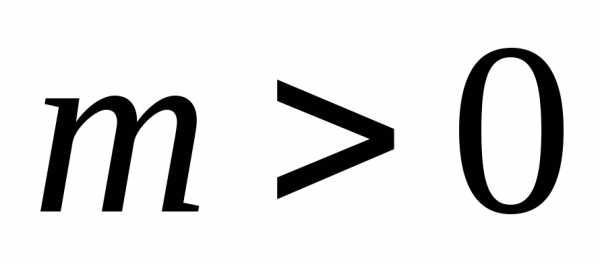 это свойство очевидно: поскольку
это свойство очевидно: поскольку  и
и в этом случае сонаправлены,
в этом случае сонаправлены,
.
Доказательство
для случая 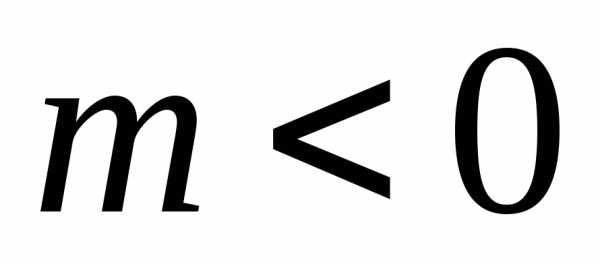 не приводится.
не приводится.
3. .
Доказательство. .
4. 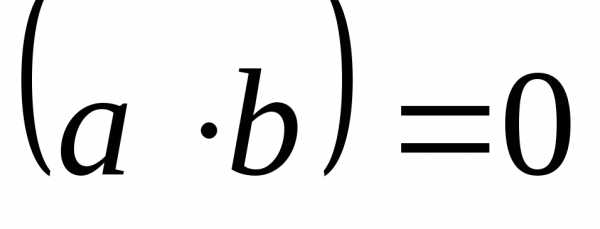 ,
когда
,
когда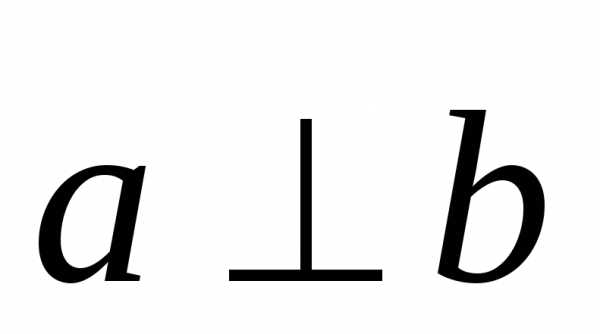 .
Если исключить из рассмотрения
нуль-векторы, то скалярное произведение
равно нулю при,
то есть при
.
Если исключить из рассмотрения
нуль-векторы, то скалярное произведение
равно нулю при,
то есть при .
.
5. 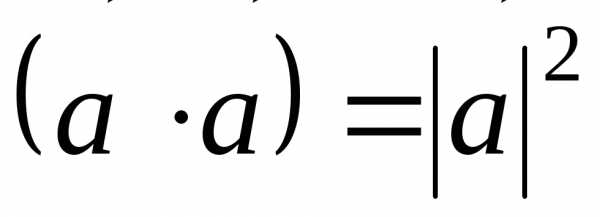 ,
то есть квадрат длины вектора равен
скалярному произведению вектора на
себя.
,
то есть квадрат длины вектора равен
скалярному произведению вектора на
себя.
Скалярное произведение векторов в ортонормированном базисе
Пусть ,, тогда , то есть скалярное произведение векторов в этом случае – есть сумма произведений одноименных проекций перемножаемых векторов.
Доказательство.
Данный результат следует из 3 – го свойства скалярного произведения.
Поскольку базис  — ортонормированный, векторы, входящие
во второе, третье, четвертое, шестое,
седьмое и восьмое скалярные произведения,
ортогональны, следовательно, эти
произведения равны нулю (четвертое
свойство). Кроме того, из второго и
пятого свойств имеем,,.
Теорема доказана.
— ортонормированный, векторы, входящие
во второе, третье, четвертое, шестое,
седьмое и восьмое скалярные произведения,
ортогональны, следовательно, эти
произведения равны нулю (четвертое
свойство). Кроме того, из второго и
пятого свойств имеем,,.
Теорема доказана.
Приложения скалярного произведения
1. Условие
ортогональности векторов: из 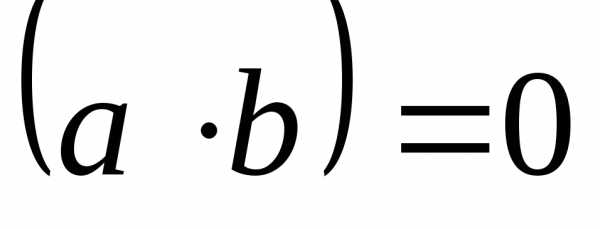 следует
.
следует
.
2. Длина вектора .
3. Угол между
векторами. Из определения скалярного
произведения 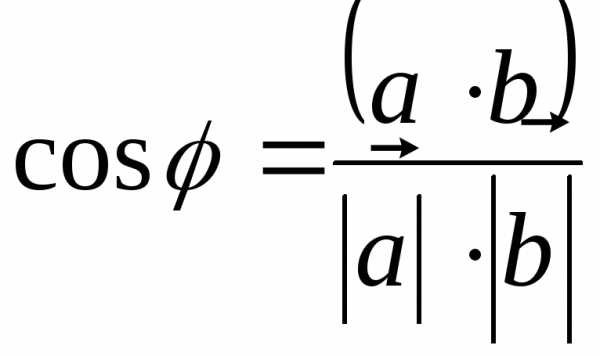 следует
следует
.
4. Расстояние между точками. Для получения этого результата введем декартову систему координат, которая известна еще со школы.
Осью координат
(координатной осью) называют прямую, на
которой выбрана начальная точка (начало
отсчета), положительное направление и
единица масштаба. Совместим начальные
точки векторов ортонормированного
базиса  ,
назовем эту точку началом координат,
проведем три прямые в направлении
базисных векторов. Поскольку положительное
направление каждой прямой и масштаб
определены направлением базисного
вектора и его длиной, точка отсчета
совпадает с началом координат, имеем
систему трех взаимно перпендикулярных
осей. Ее называют прямоугольной декартовой
системой координат
,
назовем эту точку началом координат,
проведем три прямые в направлении
базисных векторов. Поскольку положительное
направление каждой прямой и масштаб
определены направлением базисного
вектора и его длиной, точка отсчета
совпадает с началом координат, имеем
систему трех взаимно перпендикулярных
осей. Ее называют прямоугольной декартовой
системой координат .
Базисный вектор
.
Базисный вектор направлен вдоль
оси абсцисс
направлен вдоль
оси абсцисс 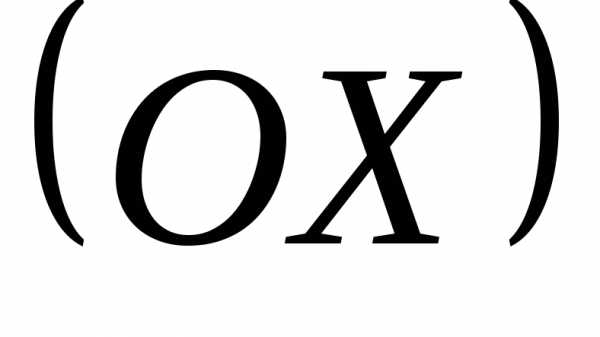 ,
вектор
,
вектор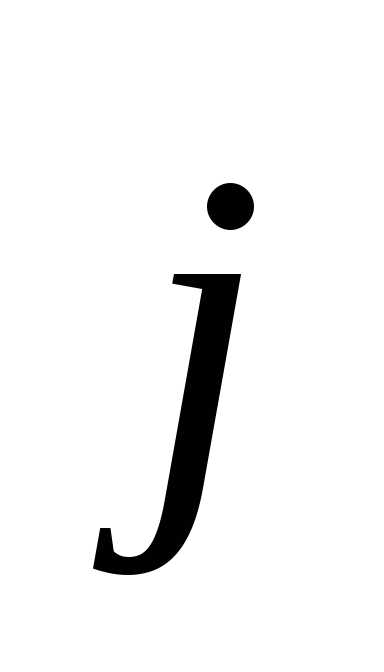 — по оси ординат
— по оси ординат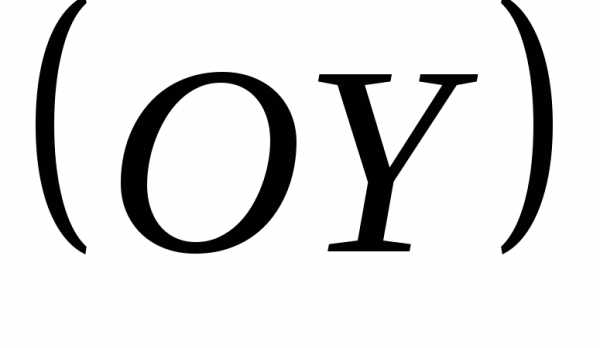 ,
вектор
,
вектор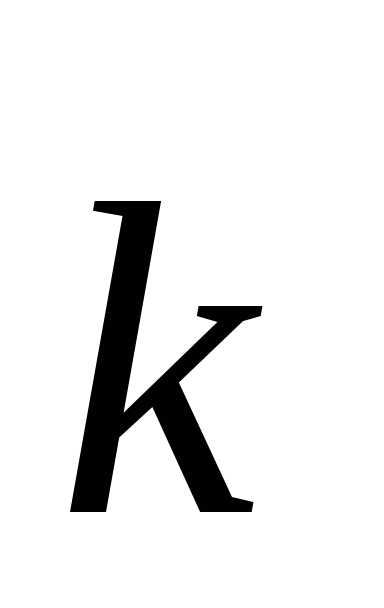 по оси аппликат
по оси аппликат .
.
Введение системы
координат дает возможность применить,
так называемый, координатный метод,
увязывающий точку, как геометрический
объект, с тройкой чисел, называемых
координатами точки. Тройка называется
упорядоченной, поскольку взаиморасположение
чисел зафиксировано. Первое число — есть
координата вдоль оси 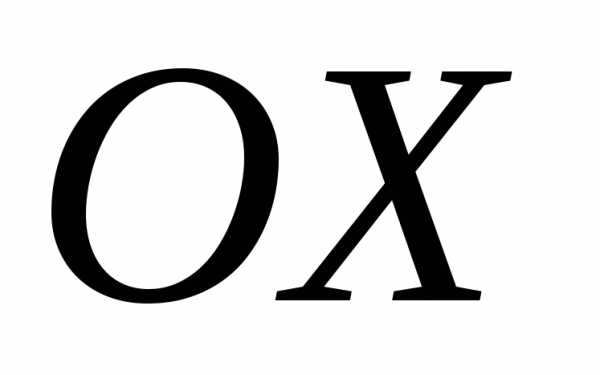 ,
второе – вдоль
,
второе – вдоль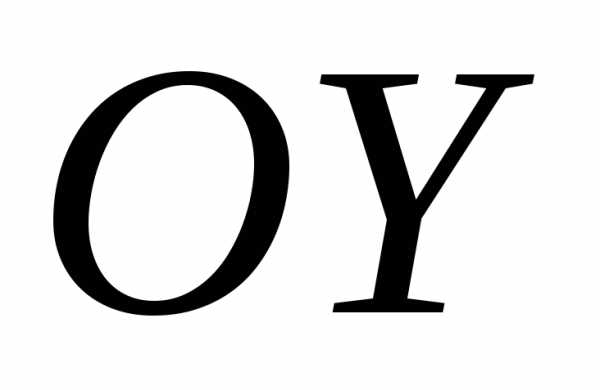 ,
третье – расстоянии вдоль оси
,
третье – расстоянии вдоль оси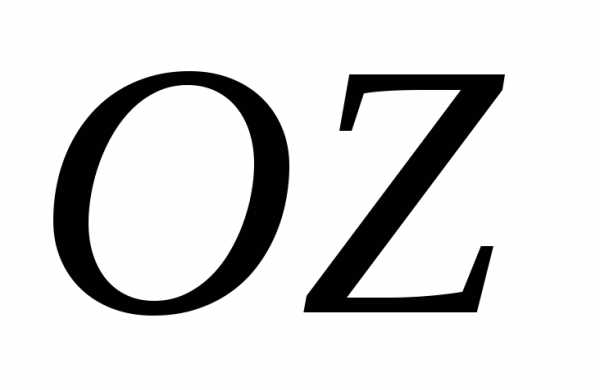 .
Меняя местами любые из этих чисел,
получаем другую точку пространства.
Например,и-
разные точки пространства. Начало
координат соответствует тройке
.
Меняя местами любые из этих чисел,
получаем другую точку пространства.
Например,и-
разные точки пространства. Начало
координат соответствует тройке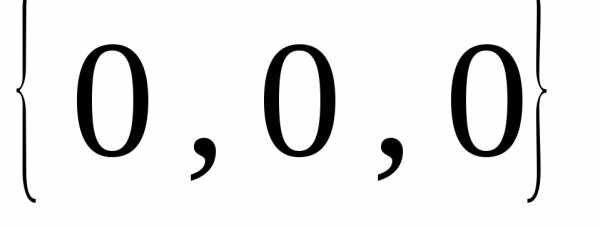 .
.
Любой объект теперь можно считать множеством точек.
Введем понятие радиуса-вектора
точки  – это вектор, начальной точкой которого
является начало координат, конечной –
точка
– это вектор, начальной точкой которого
является начало координат, конечной –
точка  .
Если точке
.
Если точке соответствуют координаты
соответствуют координаты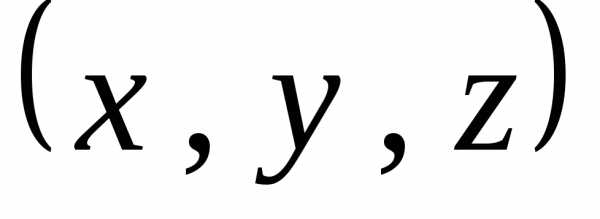 ,
нетрудно заметить, что радиус-вектор
точки может быть представлен в виде.
,
нетрудно заметить, что радиус-вектор
точки может быть представлен в виде.
Пусть даны две
точки
и.
Вместе с вектором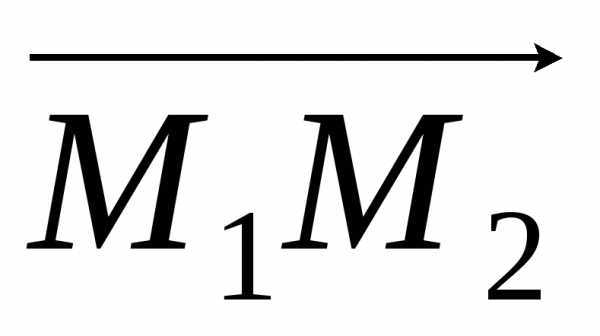 радиусы-векторы точек
радиусы-векторы точек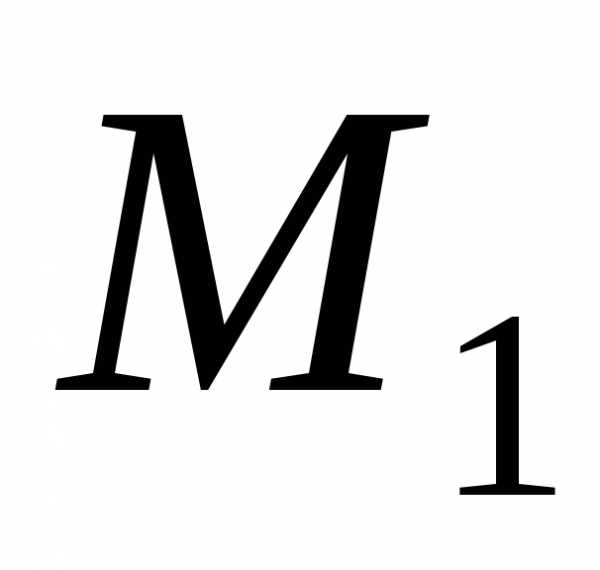 и
и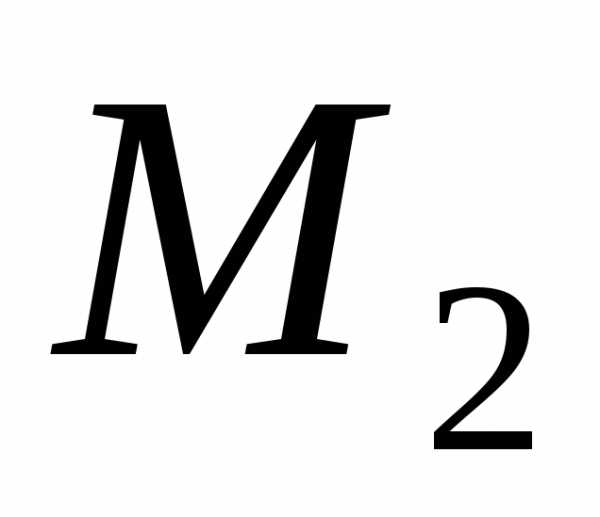 представляют треугольник
представляют треугольник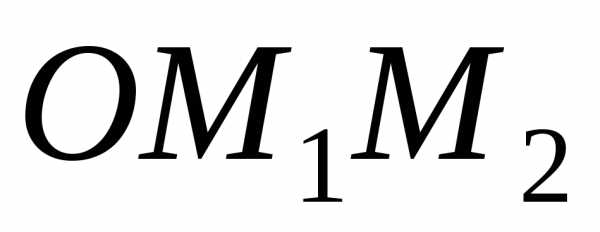 ,
причем
,
причем
.
Таким образом,
длина вектора 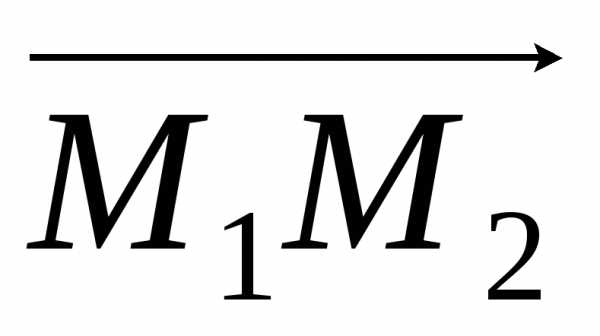 ,
совпадающая с расстоянием между точками
,
совпадающая с расстоянием между точками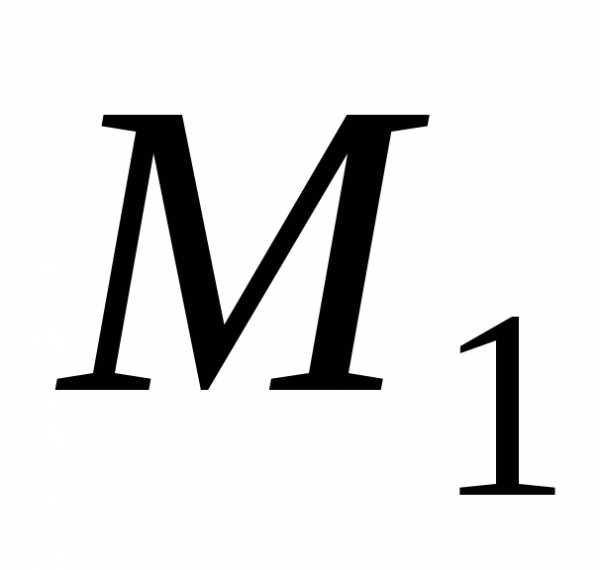 и
и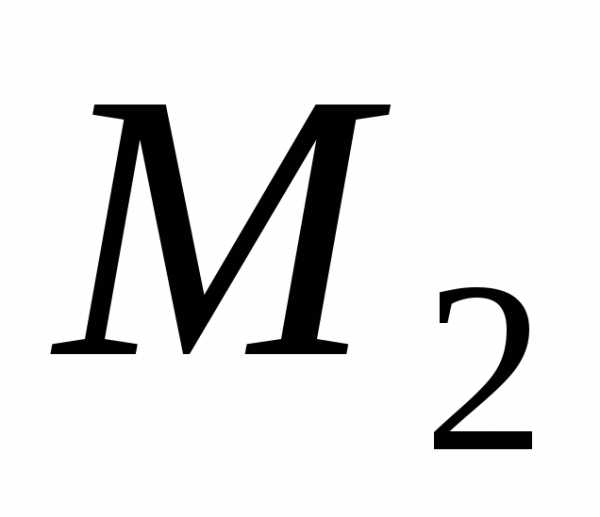 ,
вычисляется по формуле
,
вычисляется по формуле
.
Пример.
1. Задан треугольник
с вершинами
.
Определить длину стороны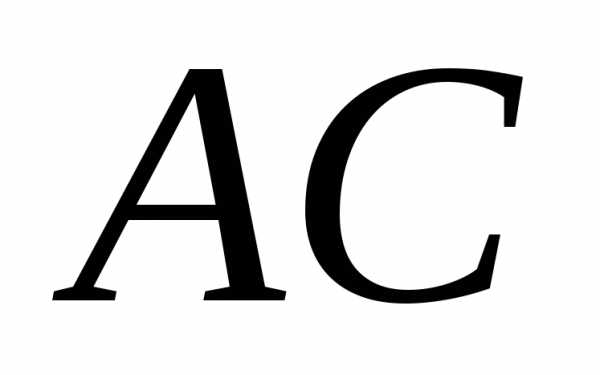 и угол при вершине
и угол при вершине .
.
Длину стороны определяем как расстояние между вершинами, тогда
.
Определим векторы ,
.
Угол между этими
векторами есть угол при вершине  .
Очевидно,
.
Очевидно,
.
Угол теперь определяется с помощью таблиц или калькулятора рад.
Векторное произведение
Как уже говорилось выше, скалярное произведение векторов имеет практическое значение. В частности, с его помощью определяется работа силы на участке пути.
Векторное произведение также имеет практический смысл. С его помощью определяют моменты сил, придающие телам вращение.
Правая и левая тройки векторов
Определение 1. Тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки.
Определение 2. Тройка некомпланарных векторов называется левой, если с конца третьего вектора кратчайший поворот от первого вектора ко второму видится по часовой стрелке.
Можно проверить, что правая тройка векторов связана на практике с правой резьбой, левая тройка – с левой резьбой.
Это обстоятельство
привело к тому, что до середины XX
века наука о движении (механика) излагалась
как в правой, так и в левой декартовых
системах координат, что затрудняло
изучение литературы по предмету. В
середине XX
века договорились использовать только
правую тройку векторов, а, следовательно,
правую декартову систему координат. На
рисунке 7 тройка базисных векторов  — правая,левая.
— правая,левая.
Рисунок 7.
Определение векторного произведения, его свойства.
Векторным произведением двух векторов называется третий вектор, длина которого равна произведению модулей перемножаемых векторов на синус угла между ними, направлен этот вектор перпендикулярно плоскости, в которой расположены перемножаемые векторы, образуя с ними правую тройку.
studfiles.net
Вектор (математика) Википедия
| Классическая механика |
| d(mv→)dt=F→{\displaystyle {\frac {\mathrm {d} (m{\vec {v}})}{\mathrm {d} t}}={\vec {F}}}Второй закон Ньютона |
| История… |
Фундаментальные понятия Пространство · Время · Масса· Скорость · Сила · Механическая работа · Энергия · Импульс |
Формулировки Ньютоновская механика · Лагранжева механика · Гамильтонова механика · Формализм Гамильтона — Якоби · Уравнения Рауса · Уравнения Аппеля · Теория Купмана — фон Неймана |
Разделы Прикладная механика · Небесная механика · Механика сплошных сред · Геометрическая оптика · Статистическая механика |
Учёные Галилей · Кеплер · Ньютон · Эйлер · Лаплас · Д’Аламбер · Лагранж · Гамильтон · Коши |
| См. также: Портал:Физика |
Ве́ктор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости)[1].
Примеры: радиус-вектор, скорость, момент силы. Если в пространстве задана система координат, то вектор однозначно задаётся набором своих координат. Поэтому в матема
ru-wiki.ru
Векторная алгебра. Справочная информация | Perpetuum mobile: «свободная энергия» и вечные двигатели.
Векторная алгебра
Векторная алгебра описывает способы выполнения различных операций над векторами, в том числе сложение, вычитание, разные типы перемножения. Здесь приводится лишь часть этого раздела математики, непосредственно относящаяся к задачам, наиболее часто возникающим в физической и инженерной практике.
Понятие вектора
Ограничения
Основные понятия
Проекции и координаты вектора
Некоторые определения
Операции над векторами
Сложение векторов
Вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Вычисление скалярного произведения
Свойства скалярного произведения
Векторное произведение векторов
Вычисление векторного произведения
Свойства векторного произведения
Понятие вектора
В геометрическом смысле вектор — это направленный отрезок, определяемый точками своего начала и конца. В физическом смысле под векторами обычно понимаются величины, имеющие направление в трёхмерном пространстве. Как правило, они характеризуются абсолютной величиной, направлением и точкой приложения (точкой привязки). Во времена Ньютона эти три категории были достаточно автономны и их увязка была своего рода искусством. Применение концепции векторов позволило формализовать естественную взаимосвязь этих категорий и сделать операции над ними более наглядными и удобными.
Ограничения
В силу специфики сайта векторные операции рассматриваются для наиболее частого случая — трёхмерного пространства, описываемого в декартовой системе координат (три взаимно ортогональные оси отсчёта). Для пространств меньшей мерности (двухмерной плоскости и одномерной прямой) обычно достаточно обнулить «неиспользуемые» координаты. Пространства большей мерности не рассматриваются, поскольку до сих пор являются физической экзотикой. Для работы с ними следует изучить курс векторной алгебры более серьёзно.
В связи с малой практической востребованностью не рассматривается выполнение операций над векторами в полярных и других недекартовых системах координат. Не рассматривается и матричное исчисление, поскольку для трёхмерного пространства алгебраическая форма векторных операций является достаточно простой и удобной, хотя и не столь универсальной. Кроме того, матричное исчисление требует довольно специфического подхода, что затрудняет его применение теми, кто с прежде с матрицами не сталкивался.
Основные понятия
Рассмотрим основные понятия, используемые на этой странице.
Проекции и координаты вектора
Любой трёхмерный вектор можно спроецировать на три взаимно перпендикулярные оси отсчёта, пересекающиеся в одной точке (декартовы оси координат). Выбор точки отсчёта и положение осей (базис системы координат) теоретически непринципиален, но на практике обычно выбирается так, чтобы как можно большее число участвующих в расчёте векторов было направлено вдоль какой-либо из осей координат — это упрощает вычисления.
Каждый вектор можно охарактеризовать координатами двух точек — его начала и конца, — либо проекциями на оси координат и координатами точки привязки (обычно точкой привязки является начало вектора, но иногда бывает удобнее использовать в этом качестве его конец). В физике чаще применяется второй подход. В этом случае в трёхмерном пространстве вектор a описывается шестью величинами — координатами его точки привязки xa, ya, za и проекциями на оси ax, ay и az. Иногда точка привязки не имеет принципиального значения либо подразумевается неявно, и тогда обходятся тремя значениями — проекциями векторной величины на оси координат (ax, ay, az).
Некоторые определения
Модулем вектора |a| в геометрии называется его длина, а в физике — абсолютное значение направленной величины (т.е. значение, измеренное вдоль направления её действия). В ортогональной системе координат модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Среди всевозможных взаимных ориентаций векторов выделяют коллинеарные и ортогональные вектора.
Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направлеными строго в противоположные стороны.
Ортогональными называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны.
Понятие равных векторов менее однозначно. Иногда под этим понимают любые сонаправленные вектора одного размера, расположение точки привязки которых безразлично и может быть в любом месте пространства. Более строгое определение подразумевает и совпадение точек привязки. В физике под «равенством векторов» обычно имеют в виду первый случай (величины и направления одинаковы, положение точки привязки произвольно). Если же одинаковы и точки привязки, то речь идёт о совпадающих (эквивалентных) векторах.
Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления. Иногда нулевой вектор трактуют как всенаправленный, хотя в строгом смысле это не так.
Операции над векторами
Сложение векторов
В алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака:
сx = ax + bx ;сy = ay + by ;
сz = az + bz .
Если точка привязки не важна, а важна лишь величина (длина и направление) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). В противном случае точка привязки результирующего вектора определяется исходя из физического смысла производимой операции (как правило, в физике точки привязки всех складываемых векторов и суммарного вектора совпадают, — то есть и все слагаемые, и их сумма применимы к одной и той же точке пространства или к одной и той же материальной точке).
Вычитание векторов
Вычитание векторов с = a – b можно представить как сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак:
сx = ax – bx ;сy = ay – by ;
сz = az – bz .
Умножение вектора на число
При умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число:
bx = k · ax ;by = k · ay ;
bz = k · az .
В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи.
Операция умножения на число является коммутативной a · k = k · a (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет нулевой вектор, говорить о направлении которого некорректно.
Операция умножения на число является дистрибутивной k · (a + b) = k · a + k · b (произведение суммы векторов на число равно сумме произведений слагаемых на это же число).
Скалярное произведение векторов
Результатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними.
Вычисление скалярного произведения
В алгебраической форме скалярное произведение d = a · b вычисляется как
d = ax · bx + ay · by + az · bz .Свойства скалярного произведения
Коммутативность: a · b = b · a .
Дистрибутивность: a · (b + c) = a · b + a · c .
Сочетательность (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b) .
Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|2 (норма вектора).
Векторное произведение векторов
Правая тройка векторов и правая система координат. |
Результатом векторного перемножения двух векторов a и b является вектор c, длина которого равна произведению их модулей, умноженному на синус угла между ними, а сам вектор ориентирован таким образом, что перпендикулярен обоим исходным векторам, и тройка a b c является правой.
Вычисление векторного произведения
В алгебраической форме векторное произведение c = [a × b] в правой системе координат вычисляется как
сx = ay · bz – az · by ;сy = az · bx – ax · bz ;
сz = ax · by – ay · bx .
В левой системе координат знаки слагаемых меняются на противоположные.
В физике обычно подразумевается, что точки привязки всех перемножаемых векторов и результирующего вектора совпадают (и вектора-сомножители, и результат их векторного произведения действуют в одной и той же точке пространства).
Свойства векторного произведения
Антикоммутативность: [a × b] = –[b × a] .
Дистрибутивность: [a × (b + c)] = [a × b] + [a × c] .
Сочетательность относительно скалярного множителя: k · [a × b] = [(k · a) × b] = [a × (k · b)] .
Смешанное произведение: a · [b × c] = [a × b] · c .
Векторный квадрат вектора всегда является нулевым вектором: [a × a] = 0 . Поэтому, когда говорят о «квадрате вектора» без уточнения типа перемножения, имеют в виду скалярный квадрат (квадрат модуля вектора).
♦
khd2.narod.ru
Вектор (математика) — Википедия
Вектор У этого термина существуют и другие значения, см. Вектор.Ве́ктор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости)[1].
Примеры: радиус-вектор, скорость, момент силы. Если в пространстве задана система координат, то вектор однозначно задаётся набором своих координат. Поэтому в математике, информатике и других науках упорядоченный набор чисел часто тоже называют вектором. В более общем смысле вектор в математике рассматривается как элемент некоторого векторного (линейного) пространства.
Является одним из основополагающих понятий линейной алгебры. При использовании наиболее общего определения векторами оказываются практически все изучаемые в линейной алгебре объекты, в том числе матрицы, тензоры, однако, при наличии в окружающем контексте этих объектов, под вектором понимаются соответственно вектор-строка или вектор-столбец, тензор первого ранга. Свойства операций над векторами изучаются в векторном исчислении.
Вектор, представленный набором элементов (компонент) обозначают следующими способами:
- .
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
Сложение векторов почти всегда обозначается знаком плюс:
- .
Умножение на число — просто написанием рядом, без специального знака, например:
- ,
причём число при этом обычно пишут слева.
Умножение на матрицу также обозначают написанием рядом, без специального знака, но здесь перестановка сомножителей в общем случае влияет на результат. Действие линейного оператора на вектор также обозначается написанием оператора слева, без специального знака.
Интуитивно вектор понимается как объект, имеющий величину, направление и (необязательно) точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831). Развитые операции с векторами опубликовал Гамильтон как часть своего кватернионного исчисления (вектор образовывали мнимые компоненты кватерниона). Гамильтон предложил сам термин вектор (лат. vector, несущий) и описал некоторые операции векторного анализа. Этот формализм использовал Максвелл в своих трудах по электромагнетизму, тем самым обратив внимание учёных на новое исчисление. Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.
В геометрии под векторами понимают направленные отрезки. Эту интерпретацию часто используют в компьютерной графике, строя карты освещения, с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов, а также объёмы тел: тетраэдра и параллелепипеда.
Иногда с вектором отождествляют направление.
Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Действительно, любой направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства, и обратно, параллельный перенос однозначно определяет собой единственный направленный отрезок (однозначно — если считать равными все направленные отрезка одинакового направления и длины — то есть рассматривать их как свободные векторы.
Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.
В линейной алгебре[править]
В линейной алгебре вектором называется элемент линейного пространства, что соответствует общему определению, приведённому ниже. Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
Данным понятием вектора чаще всего пользуются при решении систем линейных алгебраических уравнений, а также при работе с линейными операторами (пример линейного оператора — оператор поворота).
Часто это определение расширяют, определяя норму или скалярное произведение (возможно, и то и другое вместе), после чего оперируют уже с нормированными и евклидовыми пространствами, со скалярным произведением связывают понятие угла между векторами, а с нормой — понятие длины вектора.
Многие математические объекты (например, матрицы, тензоры и т. д.), в том числе обладающие структурой более общей, чем конечный (а иногда даже и чем счётный) упорядоченный список, удовлетворяют аксиомам векторного пространства, то есть являются с точки зрения алгебры векторами.
В функциональном анализе[править]
В функциональном анализе рассматриваются функциональные пространства — бесконечномерные линейные пространства. Их элементами могут являться функции. На основании такого представления функции выстроена теория рядов Фурье. Аналогично с линейной алгеброй часто вводят норму, скалярное произведение или метрику на пространстве функций. На понятии функции как элемента гильбертова пространства основываются некоторые методы решения дифференциальных уравнений, например метод конечных элементов.
Общее определение[править]
Наиболее общее определение вектора даётся средствами общей алгебры. Пусть — некоторое поле с аддитивной операцией , мультипликативной операцией , аддитивной единицей и мультипликативной единицей . Пусть — некоторая абелева группа с единицей . Если существует операция , такая что для любых и для любых выполняются соотношения:
- ,
- ,
- ,
- ,
тогда называется векторным пространством над полем (или линейным пространством), элементы называются векторами, элементы — скалярами, а указанная операция — умножением вектора на скаляр.
Многие результаты линейной алгебры обобщены до унитарных модулей над некоммутативными телами и даже произвольных модулей над кольцами, таким образом, в наиболее общем случае, в некоторых контекстах, вектором может быть назван как любой элемент модуля над кольцом.
Физическая интерпретация[править]
Вектор, как структура, имеющая одновременно величину (модуль) и направление, рассматривается в физике как математическая модель скорости, силы, и связанных с ними величин, кинематических или динамических. Математической моделью многих физических полей (например, электромагнитного поля или поля скорости жидкости) являются векторные поля.
Абстрактные многомерные и бесконечномерные (в духе функционального анализа) векторные пространства используются в лагранжевом и гамильтоновом формализме применительно к механическим и другим динамическим системам, а также в квантовой механике (см. Вектор состояния).
Вектор как последовательность[править]
Вектор — (последовательность, кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычным аксиомам линейного пространства. Именно в таком виде вектор понимается в программировании, где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object[]). Перечень свойств моделирует принятое в теории систем определение класса и состояния объекта. Так типы элементов вектора определяют класс объекта, а значения элементов — его состояние. Впрочем, вероятно, это употребление термина уже выходит за рамки обычно принятого в алгебре, да и в математике вообще.
www.wikiznanie.ru
Вектор (математика) — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Вектор.Ве́ктор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости)[1].
Примеры: радиус-вектор, скорость, момент силы. Если в пространстве задана система координат, то вектор однозначно задаётся набором своих координат. Поэтому в математике, информатике и других науках упорядоченный набор чисел часто тоже называют вектором. В более общем смысле вектор в математике рассматривается как элемент некоторого векторного (линейного) пространства.
Является одним из основополагающих понятий линейной алгебры. При использовании наиболее общего определения векторами оказываются практически все изучаемые в линейной алгебре объекты, в том числе матрицы, тензоры, однако, при наличии в окружающем контексте этих объектов, под вектором понимаются соответственно вектор-строка или вектор-столбец, тензор первого ранга. Свойства операций над векторами изучаются в векторном исчислении.
Обозначения
Вектор, представленный набором <math>n</math> элементов (компонент) <math>a_1, a_2, \ldots, a_n</math> обозначают следующими способами:
- <math>\langle a_1, a_2, \ldots, a_n\, \rangle,\ \left ( a_1, a_2, \ldots, a_n\, \right ), \{ a_1, a_2, \ldots, a_n\, \} </math>.
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
- <math>\bar a,\ \vec a, \mathbf a, \mathfrak A,\ \mathfrak a.</math>
Сложение векторов почти всегда обозначается знаком плюс:
- <math>\vec{a} + \vec{b}</math>.
Умножение на число — просто написанием рядом, без специального знака, например:
- <math>k \vec{b}</math>,
причём число при этом обычно пишут слева.
Умножение на матрицу также обозначают написанием рядом, без специального знака, но здесь перестановка сомножителей в общем случае влияет на результат. Действие линейного оператора на вектор также обозначается написанием оператора слева, без специального знака.
История
Интуитивно вектор понимается как объект, имеющий величину, направление и (необязательно) точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831). Развитые операции с векторами опубликовал Гамильтон как часть своего кватернионного исчисления (вектор образовывали мнимые компоненты кватерниона). Гамильтон предложил сам термин вектор (лат. vector, несущий) и описал некоторые операции векторного анализа. Этот формализм использовал Максвелл в своих трудах по электромагнетизму, тем самым обратив внимание учёных на новое исчисление. Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.
В геометрии
В геометрии под векторами понимают направленные отрезки. Эту интерпретацию часто используют в компьютерной графике, строя карты освещения, с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов, а также объёмы тел: тетраэдра и параллелепипеда.
Иногда с вектором отождествляют направление.
Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Действительно, любой направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства, и обратно, параллельный перенос однозначно определяет собой единственный направленный отрезок (однозначно — если считать равными все направленные отрезка одинакового направления и длины — то есть рассматривать их как свободные векторы.
Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.
В линейной алгебре
В линейной алгебре вектором называется элемент линейного пространства, что соответствует общему определению, приведённому ниже. Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
Данным понятием вектора чаще всего пользуются при решении систем линейных алгебраических уравнений, а также при работе с линейными операторами (пример линейного оператора — оператор поворота).
Часто это определение расширяют, определяя норму или скалярное произведение (возможно, и то и другое вместе), после чего оперируют уже с нормированными и евклидовыми пространствами, со скалярным произведением связывают понятие угла между векторами, а с нормой — понятие длины вектора.
Многие математические объекты (например, матрицы, тензоры и т. д.), в том числе обладающие структурой более общей, чем конечный (а иногда даже и чем счётный) упорядоченный список, удовлетворяют аксиомам векторного пространства, то есть являются с точки зрения алгебры векторами.
В функциональном анализе
В функциональном анализе рассматриваются функциональные пространства — бесконечномерные линейные пространства. Их элементами могут являться функции. На основании такого представления функции выстроена теория рядов Фурье. Аналогично с линейной алгеброй часто вводят норму, скалярное произведение или метрику на пространстве функций. На понятии функции как элемента гильбертова пространства основываются некоторые методы решения дифференциальных уравнений, например метод конечных элементов.
Общее определение
Наиболее общее определение вектора даётся средствами общей алгебры. Пусть <math>\mathfrak F= \langle F;+,* \rangle </math> — некоторое поле с аддитивной операцией <math>+</math>, мультипликативной операцией <math>*</math>, аддитивной единицей <math>0</math> и мультипликативной единицей <math>1</math>. Пусть <math>\mathfrak V= \langle V;+ \rangle </math> — некоторая абелева группа с единицей <math>\mathbf 0</math>. Если существует операция <math>F \times V \to V</math>, такая что для любых <math>a,b \in F</math> и для любых <math>\mathbf x ,\mathbf y \in V </math> выполняются соотношения:
- <math>(a+b)\mathbf x=a\mathbf x + b\mathbf x</math>,
- <math>a(\mathbf x + \mathbf y )=a\mathbf x + a\mathbf y</math>,
- <math>(a*b)\mathbf x = a(b\mathbf x )</math>,
- <math>1\mathbf x =\mathbf x</math>,
тогда <math>\mathfrak V</math> называется векторным пространством над полем <math>\mathfrak F</math> (или линейным пространством), элементы <math>V</math> называются векторами, элементы <math>F</math> — скалярами, а указанная операция <math>F \times V \to V</math> — умножением вектора на скаляр.
Многие результаты линейной алгебры обобщены до унитарных модулей над некоммутативными телами и даже произвольных модулей над кольцами, таким образом, в наиболее общем случае, в некоторых контекстах, вектором может быть назван как любой элемент модуля над кольцом.
Физическая интерпретация
Вектор, как структура, имеющая одновременно величину (модуль) и направление, рассматривается в физике как математическая модель скорости, силы, и связанных с ними величин, кинематических или динамических. Математической моделью многих физических полей (например, электромагнитного поля или поля скорости жидкости) являются векторные поля.
Абстрактные многомерные и бесконечномерные (в духе функционального анализа) векторные пространства используются в лагранжевом и гамильтоновом формализме применительно к механическим и другим динамическим системам, а также в квантовой механике (см. Вектор состояния).
Вектор как последовательность
Вектор — (последовательность, кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычным аксиомам линейного пространства. Именно в таком виде вектор понимается в программировании, где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object[]). Перечень свойств моделирует принятое в теории систем определение класса и состояния объекта. Так типы элементов вектора определяют класс объекта, а значения элементов — его состояние. Впрочем, вероятно, это употребление термина уже выходит за рамки обычно принятого в алгебре, да и в математике вообще.
См. также
Напишите отзыв о статье «Вектор (математика)»
Литература
Ссылки
Примечания
Отрывок, характеризующий Вектор (математика)
После князя Андрея к Наташе подошел Борис, приглашая ее на танцы, подошел и тот танцор адъютант, начавший бал, и еще молодые люди, и Наташа, передавая своих излишних кавалеров Соне, счастливая и раскрасневшаяся, не переставала танцовать целый вечер. Она ничего не заметила и не видала из того, что занимало всех на этом бале. Она не только не заметила, как государь долго говорил с французским посланником, как он особенно милостиво говорил с такой то дамой, как принц такой то и такой то сделали и сказали то то, как Элен имела большой успех и удостоилась особенного внимания такого то; она не видала даже государя и заметила, что он уехал только потому, что после его отъезда бал более оживился. Один из веселых котильонов, перед ужином, князь Андрей опять танцовал с Наташей. Он напомнил ей о их первом свиданьи в отрадненской аллее и о том, как она не могла заснуть в лунную ночь, и как он невольно слышал ее. Наташа покраснела при этом напоминании и старалась оправдаться, как будто было что то стыдное в том чувстве, в котором невольно подслушал ее князь Андрей.
Князь Андрей, как все люди, выросшие в свете, любил встречать в свете то, что не имело на себе общего светского отпечатка. И такова была Наташа, с ее удивлением, радостью и робостью и даже ошибками во французском языке. Он особенно нежно и бережно обращался и говорил с нею. Сидя подле нее, разговаривая с ней о самых простых и ничтожных предметах, князь Андрей любовался на радостный блеск ее глаз и улыбки, относившейся не к говоренным речам, а к ее внутреннему счастию. В то время, как Наташу выбирали и она с улыбкой вставала и танцовала по зале, князь Андрей любовался в особенности на ее робкую грацию. В середине котильона Наташа, окончив фигуру, еще тяжело дыша, подходила к своему месту. Новый кавалер опять пригласил ее. Она устала и запыхалась, и видимо подумала отказаться, но тотчас опять весело подняла руку на плечо кавалера и улыбнулась князю Андрею.
«Я бы рада была отдохнуть и посидеть с вами, я устала; но вы видите, как меня выбирают, и я этому рада, и я счастлива, и я всех люблю, и мы с вами всё это понимаем», и еще многое и многое сказала эта улыбка. Когда кавалер оставил ее, Наташа побежала через залу, чтобы взять двух дам для фигур.
«Ежели она подойдет прежде к своей кузине, а потом к другой даме, то она будет моей женой», сказал совершенно неожиданно сам себе князь Андрей, глядя на нее. Она подошла прежде к кузине.
«Какой вздор иногда приходит в голову! подумал князь Андрей; но верно только то, что эта девушка так мила, так особенна, что она не протанцует здесь месяца и выйдет замуж… Это здесь редкость», думал он, когда Наташа, поправляя откинувшуюся у корсажа розу, усаживалась подле него.
В конце котильона старый граф подошел в своем синем фраке к танцующим. Он пригласил к себе князя Андрея и спросил у дочери, весело ли ей? Наташа не ответила и только улыбнулась такой улыбкой, которая с упреком говорила: «как можно было спрашивать об этом?»
– Так весело, как никогда в жизни! – сказала она, и князь Андрей заметил, как быстро поднялись было ее худые руки, чтобы обнять отца и тотчас же опустились. Наташа была так счастлива, как никогда еще в жизни. Она была на той высшей ступени счастия, когда человек делается вполне доверчив и не верит в возможность зла, несчастия и горя.
Пьер на этом бале в первый раз почувствовал себя оскорбленным тем положением, которое занимала его жена в высших сферах. Он был угрюм и рассеян. Поперек лба его была широкая складка, и он, стоя у окна, смотрел через очки, никого не видя.
Наташа, направляясь к ужину, прошла мимо его.
Мрачное, несчастное лицо Пьера поразило ее. Она остановилась против него. Ей хотелось помочь ему, передать ему излишек своего счастия.
– Как весело, граф, – сказала она, – не правда ли?
Пьер рассеянно улыбнулся, очевидно не понимая того, что ему говорили.
– Да, я очень рад, – сказал он.
«Как могут они быть недовольны чем то, думала Наташа. Особенно такой хороший, как этот Безухов?» На глаза Наташи все бывшие на бале были одинаково добрые, милые, прекрасные люди, любящие друг друга: никто не мог обидеть друг друга, и потому все должны были быть счастливы.
На другой день князь Андрей вспомнил вчерашний бал, но не на долго остановился на нем мыслями. «Да, очень блестящий был бал. И еще… да, Ростова очень мила. Что то в ней есть свежее, особенное, не петербургское, отличающее ее». Вот всё, что он думал о вчерашнем бале, и напившись чаю, сел за работу.
Но от усталости или бессонницы (день был нехороший для занятий, и князь Андрей ничего не мог делать) он всё критиковал сам свою работу, как это часто с ним бывало, и рад был, когда услыхал, что кто то приехал.
Приехавший был Бицкий, служивший в различных комиссиях, бывавший во всех обществах Петербурга, страстный поклонник новых идей и Сперанского и озабоченный вестовщик Петербурга, один из тех людей, которые выбирают направление как платье – по моде, но которые по этому то кажутся самыми горячими партизанами направлений. Он озабоченно, едва успев снять шляпу, вбежал к князю Андрею и тотчас же начал говорить. Он только что узнал подробности заседания государственного совета нынешнего утра, открытого государем, и с восторгом рассказывал о том. Речь государя была необычайна. Это была одна из тех речей, которые произносятся только конституционными монархами. «Государь прямо сказал, что совет и сенат суть государственные сословия ; он сказал, что правление должно иметь основанием не произвол, а твердые начала . Государь сказал, что финансы должны быть преобразованы и отчеты быть публичны», рассказывал Бицкий, ударяя на известные слова и значительно раскрывая глаза.
– Да, нынешнее событие есть эра, величайшая эра в нашей истории, – заключил он.
Князь Андрей слушал рассказ об открытии государственного совета, которого он ожидал с таким нетерпением и которому приписывал такую важность, и удивлялся, что событие это теперь, когда оно совершилось, не только не трогало его, но представлялось ему более чем ничтожным. Он с тихой насмешкой слушал восторженный рассказ Бицкого. Самая простая мысль приходила ему в голову: «Какое дело мне и Бицкому, какое дело нам до того, что государю угодно было сказать в совете! Разве всё это может сделать меня счастливее и лучше?»
И это простое рассуждение вдруг уничтожило для князя Андрея весь прежний интерес совершаемых преобразований. В этот же день князь Андрей должен был обедать у Сперанского «en petit comite«, [в маленьком собрании,] как ему сказал хозяин, приглашая его. Обед этот в семейном и дружеском кругу человека, которым он так восхищался, прежде очень интересовал князя Андрея, тем более что до сих пор он не видал Сперанского в его домашнем быту; но теперь ему не хотелось ехать.
В назначенный час обеда, однако, князь Андрей уже входил в собственный, небольшой дом Сперанского у Таврического сада. В паркетной столовой небольшого домика, отличавшегося необыкновенной чистотой (напоминающей монашескую чистоту) князь Андрей, несколько опоздавший, уже нашел в пять часов собравшееся всё общество этого petit comite, интимных знакомых Сперанского. Дам не было никого кроме маленькой дочери Сперанского (с длинным лицом, похожим на отца) и ее гувернантки. Гости были Жерве, Магницкий и Столыпин. Еще из передней князь Андрей услыхал громкие голоса и звонкий, отчетливый хохот – хохот, похожий на тот, каким смеются на сцене. Кто то голосом, похожим на голос Сперанского, отчетливо отбивал: ха… ха… ха… Князь Андрей никогда не слыхал смеха Сперанского, и этот звонкий, тонкий смех государственного человека странно поразил его.
Князь Андрей вошел в столовую. Всё общество стояло между двух окон у небольшого стола с закуской. Сперанский в сером фраке с звездой, очевидно в том еще белом жилете и высоком белом галстухе, в которых он был в знаменитом заседании государственного совета, с веселым лицом стоял у стола. Гости окружали его. Магницкий, обращаясь к Михайлу Михайловичу, рассказывал анекдот. Сперанский слушал, вперед смеясь тому, что скажет Магницкий. В то время как князь Андрей вошел в комнату, слова Магницкого опять заглушились смехом. Громко басил Столыпин, пережевывая кусок хлеба с сыром; тихим смехом шипел Жерве, и тонко, отчетливо смеялся Сперанский.
Сперанский, всё еще смеясь, подал князю Андрею свою белую, нежную руку.
– Очень рад вас видеть, князь, – сказал он. – Минутку… обратился он к Магницкому, прерывая его рассказ. – У нас нынче уговор: обед удовольствия, и ни слова про дела. – И он опять обратился к рассказчику, и опять засмеялся.
Князь Андрей с удивлением и грустью разочарования слушал его смех и смотрел на смеющегося Сперанского. Это был не Сперанский, а другой человек, казалось князю Андрею. Всё, что прежде таинственно и привлекательно представлялось князю Андрею в Сперанском, вдруг стало ему ясно и непривлекательно.
За столом разговор ни на мгновение не умолкал и состоял как будто бы из собрания смешных анекдотов. Еще Магницкий не успел докончить своего рассказа, как уж кто то другой заявил свою готовность рассказать что то, что было еще смешнее. Анекдоты большею частью касались ежели не самого служебного мира, то лиц служебных. Казалось, что в этом обществе так окончательно было решено ничтожество этих лиц, что единственное отношение к ним могло быть только добродушно комическое. Сперанский рассказал, как на совете сегодняшнего утра на вопрос у глухого сановника о его мнении, сановник этот отвечал, что он того же мнения. Жерве рассказал целое дело о ревизии, замечательное по бессмыслице всех действующих лиц. Столыпин заикаясь вмешался в разговор и с горячностью начал говорить о злоупотреблениях прежнего порядка вещей, угрожая придать разговору серьезный характер. Магницкий стал трунить над горячностью Столыпина, Жерве вставил шутку и разговор принял опять прежнее, веселое направление.
wiki-org.ru
