Решите неравенство x 2 2x 3 0: Решить неравенство: x² -2x -3 ≥0;

Содержание

СУНЦ УрФУ

Расписание

Электронный журнал

Поступающим

Олимпиады, турниры, конкурсы

Планы работы

Подготовительные курсы

Новости:

14.02.2023

«Науки юношей питают…» (М. Ломоносов)

В СУНЦ УрФУ в День российской науки состоялись тематические мероприятия.

12.02.2023

Lecture on the world economy Pupils 10Z and 11Z, или Приглашение на кейс-чемпионат

Математико-экономические классы СУНЦ встретились с представителями УрФУ.

10.02.2023

Урал… Уралу… Об Урале!

В общежитии состоялся поэтический вечер, посвященный Уралу.

09.02.2023

День Российской науки: астрономия с автором учебника

Лицеисты встретились с Владимиром Георгиевичем Сурдиным, автором учебника астрономии.

09.02.2023

Юрий Казарин о Тютчеве, интерфизике и «чуваках»

В СУНЦ прошла встреча с уральским поэтом, организованная кафедрой филологии.

06.02.2023

В СУНЦ УрФУ состоялся форум выпускников

Выпускники СУНЦ разных лет встретились с нынешними лицеистами.

Больше новостей

Видеогалерея:

Новогодние поздравления (декабрь 2022)

СУНЦ.АРТ (ноябрь 2022)

«Горнозаводской Урал» (октябрь 2022)

Больше видео

О нас:

Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).

В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.

Иногородние обучающиеся проживают в уютном общежитии.

Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.

Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».

Как нас найти:

Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝

Проезд:

автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;

троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.

Алгебра 8 Мордкович (упр. 37.1

Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). § 37. Решение квадратных неравенств. ОТВЕТЫ на упражнения 37.1 — 37.46. ГЛАВА 5. НЕРАВЕНСТВА. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.

§ 37. Решение квадратных неравенств.

Задание № 37.1. Постройте график функции у = x² – 4х + 3. С помощью графика решите неравенство:
а) x² – 4х + 3 > 0; б) x² – 4х + 3 ≤ 0; в) x² – 4х + 3 < 0; г) х² – 4х + 3 ≥ 0.

Смотреть ответы на № 37.1

Задание № 37.2. Решите неравенство:
а) x² – 6х – 7 > 0; б) x² + 2х – 48 ≤ 0; в) x² + 4х + 3 ≥ 0; г) x² – 12x – 45 < 0.

Смотреть ответы на № 37.2

Решите неравенство:
Задание № 37.3. а) –x² + 6x – 5 < 0; б) –x²– 2х + 8 ≥ 0; в) –x²

+ 16x – 28 > 0; г) –x² + 4x – 3 < 0.

Смотреть ответы на № 37. 3

Задание № 37.4. а) 2x² – х – 6 > 0; б) 3x² – 7x + 4 ≤ 0; в) 2x² + 3x + 1 < 0; г) 5x² – 11x + 2 ≥ 0.

Смотреть ответы на № 37.4

Задание № 37.5. а) –5x² + 4x + 1 > 0; б) –2x² – 5x + 18 ≤ 0; в) –6x² + 13x + 5 < 0; г) –3x² + 5x – 2 ≥ 0.

Смотреть ответы на № 37.5

Задание № 37.6. а) (x – 2)(x + 3) > 0; б) (x + 5)(x + 1) ≤ 0; в) (x + 7)(x – 5) < 0; г) (x – 4)(x – 6) > 0.

Смотреть ответы на № 37.6

Задание № 37.7.

Смотреть ответы на № 37.7

Задание № 37.8.

Смотреть ответы на № 37.8

Задание № 37.9.

Смотреть ответы на № 37.9

Задание № 37.10.

Смотреть ответы на № 37.10

Задание № 37.11.

Смотреть ответы на № 37.11

Задание № 37.12.

Смотреть ответы на № 37.12

Задание № 37.13.

Смотреть ответы на № 37.13

Задание № 37. 14.

Смотреть ответы на № 37.14

Задание № 37.15.

Смотреть ответы на № 37.15

Задание № 37.16.

Смотреть ответы на № 37.16

Задание № 37.17.

Смотреть ответы на № 37.17

Задание № 37.18.

Смотреть ответы на № 37.18

Задание № 37.19. Решите неравенство: а) x² ≥ 25x; б) 0,3x² < 0,6x; в) x² ≤ 36x; г) 0,2x² > 1,8x.

Смотреть ответы на № 37.19

Задание № 37.20. При каких значениях x:
а) трехчлен 2x² + 5x + 3 принимает положительные значения;
б) трехчлен –x² – x/3 – 1/36 принимает неотрицательные значения?

Смотреть ответы на № 37.20

Задание № 37.21. а) Сколько целочисленных решений имеет неравенство x² – 5x – 6 < 0?
б) Сколько целочисленных решений имеет неравенство x² – 6x ≤ 7?

Смотреть ответы на № 37.21

Задание № 37.22. а) Найдите наименьшее целочисленное решение неравенства x² + 7x ≤ 30.
б) Найдите наибольшее целочисленное решение неравенства 3x – x² > –40.

Смотреть ответы на № 37.22

Задание № 37.23.

Смотреть ответы на № 37.23

Задание № 37.24.

Смотреть ответы на № 37.24

Задание № 37.25.

Смотреть ответы на № 37.25

Задание № 37.26.

Смотреть ответы на № 37.26

Задание № 37.27.

Смотреть ответы на № 37.27

Задание № 37.28.

Смотреть ответы на № 37.28

Задание № 37.29.

Смотреть ответы на № 37.29

Задание № 37.30.

Смотреть ответы на № 37.30

Задание № 37.31.

Смотреть ответы на № 37.31

Задание № 37.32.

Смотреть ответы на № 37.32

Задание № 37.33.

Смотреть ответы на № 37.33

Задание № 37.34. а) Сколько целочисленных решений имеет неравенство x² + 5х – 8 < 0?
б) Сколько целочисленных решений имеет неравенство 15 – x² + 10х > 0?

Смотреть ответы на № 37.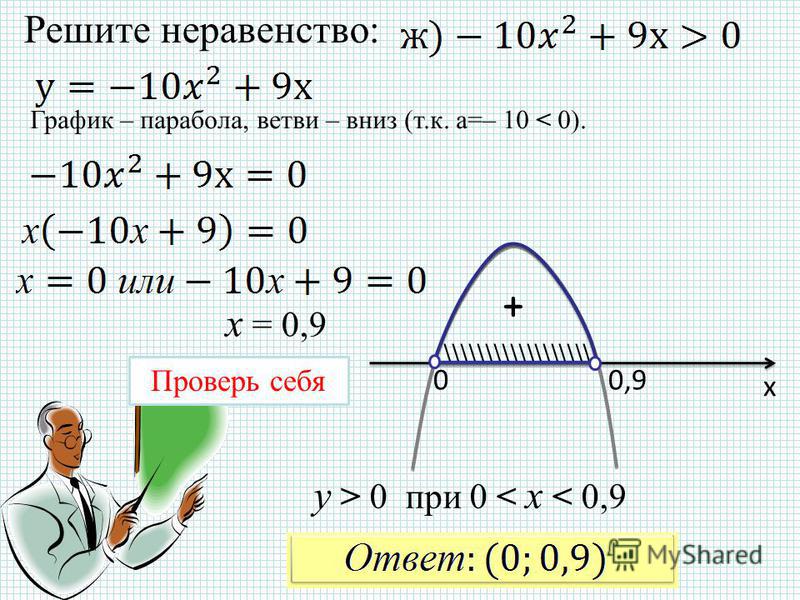 34

Задание № 37.35. а) Найдите наименьшее целочисленное решение неравенства x² + 10х < –12.
б) Найдите наибольшее целочисленное решение неравенства 3x² + 5х ≤ 4.

Смотреть ответы на № 37.35

Задание № 37.36. При каких значениях параметра р квадратное уравнение 3x² – 2рх – р + 6 = 0:
а) имеет два различных корня; б) имеет один корень; в) не имеет корней?

Смотреть ответы на № 37.36

Задание № 37.37. При каких значениях параметра р квадратное уравнение 2x² – 2рх + р + 12 = 0:
а) имеет два различных корня; б) имеет один корень; в) не имеет корней?

Смотреть ответы на № 37.37

Задание № 37.38. При каких значениях параметра р квадратное уравнение x² + 6рх + 9 = 0:
а) имеет два различных корня; б) имеет один корень; в) не имеет корней?

Смотреть ответы на № 37.38

Задание № 37.39. Найдите все значения параметра р, при которых не имеет действительных корней уравнение:
а) (р – 1)x² – 4х + 5 = 0;
б) (р – 15)x² + 4px – 3 = 0;
в) (2p + 3)x² – 6х + 8 = 0;
г) (3p – 5)x² – (6p – 2)х + 3p – 2 = 0.

Смотреть ответы на № 37.39

Задание № 37.40. Найдите все значения параметра р, при которых имеет действительные корни уравнение:
а) x² – 6х + p² = 0; б) x² – 12px – 3p = 0; в) x² – 4х – 2p = 0; г) x² + 2px + р + 2 = 0.

Смотреть ответы на № 37.40

Задание № 37.41. Найдите все значения параметра р, при которых имеет действительные корни уравнение:
а) 3px² – 6px + 13 = 0;
б) (1 – 3p)x² – 4х – 3 = 0;
в) px² – 3рх – 2 = 0;
г) (р – 1)x² – (2p – 3)х + р + 5 = 0.

Смотреть ответы на № 37.41

Задание № 37.42. При каких целочисленных значениях параметра р неравенство (х – 2)(х – р) < 0 имеет три целочисленных решения?

Смотреть ответы на № 37.42

Задание № 37.43. При каких значениях параметра р неравенство x² ≤ 9р² имеет одно целочисленное решение?

Смотреть ответы на № 37.43

Задание № 37.

44. Длина прямоугольника на 2 см больше его ширины. Чему равна длина прямоугольника, если известно, что его площадь не превосходит 224 см²?

Смотреть ответы на № 37.44

Задание № 37.45. Непараллельные стороны квадрата увеличили на 6 см и 4 см. Чему равна сторона квадрата, если известно, что площадь полученного прямоугольника меньше удвоенной площади квадрата?

Смотреть ответы на № 37.45

Задание № 37.46. Две группы туристов вышли с турбазы по направлениям, которые образуют прямой угол. Первая группа шла со скоростью 4 км/ч, а вторая со скоростью 5 км/ч. Группы поддерживали связь по радио, причем переговариваться можно было на расстоянии не более чем 13 км. Какое время после выхода второй группы могли поддерживать между собой связь туристы, если известно, что вторая группа вышла на маршрут через 2 ч после первой?

Смотреть ответы на № 37.46

Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). ГЛАВА 5. НЕРАВЕНСТВА. § 37. Решение квадратных неравенств. ОТВЕТЫ на задачи 37.1 — 37.46. Вернуться в ОГЛАВЛЕНИЕ.

2 — 6x + 10 = 0.
Dauer: 1:02
Прислан: 13.06.2017

Решаем квадратные уравнения x2-6x+10=0 -6x_10=0

Tiger шаг за шагом покажет вам, как решать ВАШИ квадратные уравнения x2-6x+10=0, заполнив формулу квадрата, квадрата или, если возможно, …

Решить квадратное уравнение x2- 6x=10 Tiger Algebra Solver

www.tiger-алгебра.com › тренировка › x2-6x=10 92-6x+10=0 формула квадратов

X2 6x 10=0 мозгов

Y = x 2 6x+10

2x 2 6x + 10 = 0

X2 6x 10=0 дискриминант -2

решить 4 x 3 2 x 1 0

AlleBilderVideosShoppingMapsNewsBücher

suchoptionen

Tipp: Begrenze diesuche auf deutschsprachige Ergebnisse. Du kannst deinesuchsprache in den Einstellungen ändern.

Решить 4(x — 3) — 2(x — 1) > 0. — Brainly.com

brainly.com › Математика › Высшая школа

Решить 4(x — 3) — 2(x — 1) > 0. · Ответ · Ответ · Возможно, вас заинтересуют · Новые вопросы по математике.

Решить x 4(x-3)-2(x-1)>0 — Mathway

www.mathway.com › Popular-Problems › Algebra

Бесплатный решатель математических задач отвечает на ваши вопросы по алгебре, геометрии, тригонометрии домашние задания по математике и статистике с пошаговыми объяснениями, …

Решение линейных неравенств 4(x-3)-2(x-1)>0 Tiger Algebra Solver 92-x+1=0 …
Добавлено: 8:33
Прислано: 07.03.2021

Решайте неравенства с помощью Пошагового решения математических задач — QuickMath

quickmath.com › уравнения › решать › основные

4x — 2 = 3x + 1. Решение Подставим значение 3 вместо x в уравнение и посмотрим, равен ли левый член правому. 4(3) — 2 = 3(3) + 1.

Как решить (4x – 3) ² – (2x – 1) ² = 0? | Socratic

socratic.