Новые вопросы
Ответы
Решение смотри на фото)
Похожие вопросы
Сумма боковых сторон равнобедренного треугольника равна 12см.Каким может быть основание если периметр больше 17?
а)x больше 5
б)5 меньше x меньше 12
в)x меньше 6
г)5 меньше x меньше 11…
Найти первые шесть членов последовательности аn=1/n+2…
2x»3+7x*2-10x-63помогите решить…
Срочно нужно решение. Решите неравенство: -8x + 9 < 12x + 209. В ответе укажите его наименьшее целое решение….
A) 4a^3 b * (-2. 2…
2…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська моваУкраїнська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Решите неравенство: x^2-3x+2
Алгебра, 17. 06.2019 11:30, VoDarks
06.2019 11:30, VoDarks
Показать ответы
Другие вопросы по: Алгебра
Синус пи делённый на 7 как вычислить?…
Опубликовано: 27.02.2019 06:40
Ответов: 3
Частота вращения воздушного винта самолёта 1500 об/мин. сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч?…
Опубликовано: 28.02.2019 17:50
Ответов: 2
Найти сумму семи первых членов арифметической прогрессии. если ее второй член в два раза больше первого. а четвертый член равен 12…
Опубликовано: 01.03.2019 04:30
Ответов: 3
Показать решение ! мотоциклист проехал 4 ч по грунтовой дороге и 3 ч по шоссе. весь путь составил 195 км. скорость мотоциклиста по шоссе была на 30 км/ч больше скорости по грунтово. 2-3x+2< 0…
2-3x+2< 0…
Популярные вопросы
Пригадай, який вигляд має калиновий кущ навесні й восени. напиши про це текст-опис (5-7 речень)….
Опубликовано: 28.02.2019 03:30
Ответов: 1
Искуство это нектар души собранный в трудах и муках раскройте смысл этой фразы…Опубликовано: 01.03.2019 03:20
Ответов: 3
Почему швабрин вызывает презрение читателя? а есть ли в его характере хотя бы одно светлое пятнышко? какое? чем можно объяснить, что пушкин не рисовал швабрина сплошь чёрной кра…
Опубликовано: 01.03.2019 04:30
Ответов: 2
Какова разность потенциалов двух точек электростатического поля , если для перемещения заряда 2мккл между этими точками совершена работа 8*(10*-4)?…
Опубликовано: 02. 03.2019 16:20
03.2019 16:20
Ответов: 3
Сколько всего книг о животных и книг с рассказами в библиотеке, если книг с рассказами 45,книг о животных 38, а книг с рассказами о животных 17?…
Опубликовано: 03.03.2019 02:30
Ответов: 3
Представьте число 8000 в виде произведения степеней простых чисел…
Опубликовано: 03.03.2019 12:50
Ответов: 3
Сочинение на тему любимый праздник на решите…
Опубликовано: 03.03.2019 17:30
Ответов: 2
h4po4+nacl h4po4+mg написать ионное уравнение реакций…
Опубликовано: 03.03.2019 23:50
Ответов: 2
:перед ремонтом зоопарка животных вывезли в специальных автофургонах. было сделано 150 рейсов. каждым рейсом отправлялось одно и то же количество животных. после ремонта зоопарка с…
каждым рейсом отправлялось одно и то же количество животных. после ремонта зоопарка с…
Ответов: 2
Написать сложноподчиненные предложения с несколькими придаточными из худ, по 2 примера…
Опубликовано: 04.03.2019 21:20
Ответов: 3
Больше вопросов по предмету: Алгебра Случайные вопросы
Популярные вопросы
Квадратные неравенства с первого взгляда
Помните, когда мы рассматривали линейные неравенства? В какой-то момент мы сказали: «Мы обещаем, что позже постараемся заставить ваш мозг болеть сильнее». Мы всегда выполняем свои обещания, так что берите пакет со льдом и пристегивайтесь, потому что сейчас мы рассмотрим квадратные неравенства.
Пример задачи
Решить x 2 – 5 x < -4.
Когда мы решаем неравенство, нам нужны все значения x , что делает утверждение верным. Таким образом, наши ответы будут не одиночными значениями, а большими обширными областями числового пространства. Затем вы можете отгородить эти регионы и разводить на них коров.
Таким образом, наши ответы будут не одиночными значениями, а большими обширными областями числового пространства. Затем вы можете отгородить эти регионы и разводить на них коров.
Мы в Shmoop любим знак равенства. Хорошо, что первым шагом решения неравенства является представление о том, что неравенство представляет собой знак равенства. Установите уравнение «равно» нулю, а затем решите, чтобы найти корни уравнения. Они пригодятся через мгновение.
х 2 -5 x <-4
x 2 -5 x + 4 <0
( x -1) ( x -4) <0
Хорошо,. наши корни х = 1 и х = 4. И что? Посмотрите на график этого уравнения.
Парабола — это гладкая непрерывная кривая. Единственные места, где он может изменить знак (с нуля на меньшую или наоборот), находятся в корнях. Мы будем использовать это, чтобы помочь нам найти наши решения.
Эй, подождите минутку сюда! Не могли бы мы просто нарисовать уравнение и решить его визуально? Мы могли бы, но есть две веские причины не делать этого. Во-первых, часто бывает так же или даже сложнее изобразить уравнение в виде графика, чем решить его другим способом (см. следующий пример задачи). Во-вторых, мы также можем использовать эту технику для решения всех видов полиномиальных неравенств, а не только квадратичных (см. пример задачи после этого).
Во-первых, часто бывает так же или даже сложнее изобразить уравнение в виде графика, чем решить его другим способом (см. следующий пример задачи). Во-вторых, мы также можем использовать эту технику для решения всех видов полиномиальных неравенств, а не только квадратичных (см. пример задачи после этого).
Итак, вернемся к разгадке. Теперь мы установим наши корни на числовой прямой, вот так.
Теперь у нас отгорожены три области. Нам нужно выбрать точку из каждой области, чтобы проверить, является ли она положительной или отрицательной в пределах этой области. Те области, которые отрицательны, будут нашими решениями (поскольку наше неравенство заканчивается на «< 0»). После этого мы поместим наших коров в положительные регионы, чтобы поднять боевой дух коров.
Все значения x от 1 до 4 приведут к истинности неравенства. Таким образом, наши решения 1 < x < 4. Если вы посмотрите на график уравнения, вы увидите, что это область, где оно опускается ниже нуля.
Пример задачи
Решить -2 x 2 ≤ 6 x + 1.
Мы снова начинаем с того, что получаем все наши данные с одной стороны неравенства, оставляя большой жирный нуль с другой стороны .
0 ≤ 2 x 2 + 6 x + 1
2 x 2 + 6 x + 1 ≥ 0
. Не в этот раз, бако. Теперь нам нужно использовать квадратную формулу, чтобы найти наши корни.
Наш калькулятор говорит нам, что это х = -0,177 и х = -2,823. Теперь настроим числовую прямую и проверим знаки каждого региона.
На этот раз нам нужны области больше нуля, поэтому решения следующие: повредить? Эта следующая проблема — последняя, так что держитесь с ней немного дольше.
Пример задачи
Решить ( x + 3) 2 (3 x 2 – 6) < 0.
Это неравенство определенно не является квадратичным, но методом нахождения решения является такой же.
Выражение меньше нуля, когда -√2 < x < √2.
При работе с полиномами большими, чем квадратичные, может быть более двух корней, и нам нужно проверять знак каждой области. Для каждого неравенства знак не обязательно будет следовать предсказуемой схеме от одного корня к другому.
Ваш мозг пульсирует от знаний? Звучит не очень приятно, но, по крайней мере, благодаря этому опыту вы стали немного умнее.
Решите квадратичное неравенство-DUMMIES
BY: Мэри Джейн Стерлинг и
Обновлено: 03-26-2016
Из книги: Algebra II для Dummies
00160016016001600101600101600160016002. Купить книгу на Amazon
В алгебре решение квадратного неравенства очень похоже на решение квадратного уравнения. Разница в том, что с квадратными уравнениями вы устанавливаете выражения равными нулю, а с неравенствами вас интересует, что находится по обе стороны от нуля (положительные и отрицательные).
Разница в том, что с квадратными уравнениями вы устанавливаете выражения равными нулю, а с неравенствами вас интересует, что находится по обе стороны от нуля (положительные и отрицательные).
Чтобы решить квадратное неравенство, выполните следующие действия:
Переместите все члены в одну сторону от знака неравенства.
Фактор, если возможно.
Определить все нули (корни или решения).
Нули — это значения переменной, которые делают каждое факторизованное выражение равным нулю.
Расставьте нули по порядку в числовой строке.
Создайте линию знака, чтобы показать, где выражение в неравенстве положительное или отрицательное.
Линия знаков показывает знаки различных факторов в каждом интервале. Если выражение факторизовано, укажите знаки отдельных факторов.
Найдите решение, записав его в виде неравенства или в виде интервала.
Вот пример: Решите неравенство x 2 – x > 12.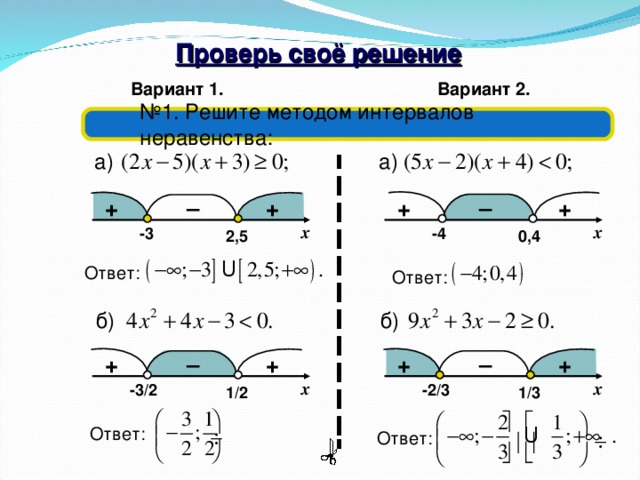
Здесь вам нужно определить, какие значения x вы можете возвести в квадрат, чтобы при вычитании исходного числа ваш ответ был больше 12.
Следуйте инструкциям:
Вычтите 12 из каждой стороны неравенства x 2 – x > 12, чтобы переместить все члены в одну сторону.
Вы получите x 2 – x – 12 > 0.
Разлагая на множители левую часть неравенства, получаем ( x – 4)( x + 3) > 0,
Определите, что все нули неравенства равны х = 4 и х = –3.
Расположите нули по порядку в числовой строке, как показано на следующем рисунке.
Создайте линию знаков, чтобы показать знаки различных факторов в каждом интервале.
Между –3 и 4 попробуйте установить x = 0 (вы можете использовать любое число от –3 до 4). Когда x = 0, коэффициент ( x – 4) отрицательный, а коэффициент ( x + 3) положительный.
 Поместите эти знаки на линии знаков, чтобы они соответствовали факторам. Сделайте то же самое для интервала чисел слева от –3 и справа от 4 (см. следующую иллюстрацию).
Поместите эти знаки на линии знаков, чтобы они соответствовали факторам. Сделайте то же самое для интервала чисел слева от –3 и справа от 4 (см. следующую иллюстрацию).Имейте в виду, что значения x в каждом интервале на самом деле выбираются случайным образом (как видно из вариантов выбора в этом примере x = –5 и x = 10). Любое число в каждом из интервалов дает вам одно и то же положительное или отрицательное значение фактора.
Чтобы определить решение, посмотрите на знаки факторов; вы хотите, чтобы выражение было положительным, соответствующим неравенству больше нуля.
Интервал слева от –3 имеет отрицательное значение, умноженное на отрицательное, что является положительным. Итак, любое число слева от -3 работает. Вы можете записать эту часть решения как x < –3 или, в интервальных обозначениях,
Интервал справа от 4 имеет положительное значение, умноженное на положительное, что является положительным.
 Итак, x > 4 — это решение; вы можете написать это как
Итак, x > 4 — это решение; вы можете написать это какИнтервал между –3 и 4 всегда отрицательный; у вас есть отрицательный раз положительный. В полном решении перечислены оба интервала, которые имеют рабочие значения в неравенстве.
Решение неравенства х 2 – х > 12, следовательно, равно x < –3 или x > 4. Записывая этот результат в интервальной записи, вы заменяете слово «или» символом
и запишите как
Эта статья из книги:
- Алгебра II для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором Алгебра I для чайников, Algebra Workbook9 For2000, and many0 Dummies прочее Для чайников книг. Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.

 Поместите эти знаки на линии знаков, чтобы они соответствовали факторам. Сделайте то же самое для интервала чисел слева от –3 и справа от 4 (см. следующую иллюстрацию).
Поместите эти знаки на линии знаков, чтобы они соответствовали факторам. Сделайте то же самое для интервала чисел слева от –3 и справа от 4 (см. следующую иллюстрацию).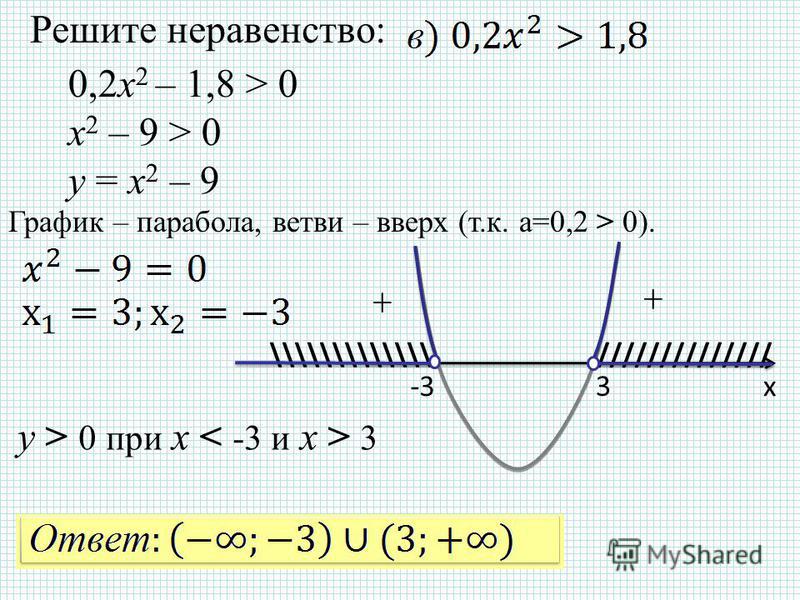 Итак, x > 4 — это решение; вы можете написать это как
Итак, x > 4 — это решение; вы можете написать это как