3.
 Решение нелинейных неравенств
Решение нелинейных неравенствДругой способ решения неравенств состоит в том, чтобы выразить данное неравенство с нулем в правой части, а затем определить знак результирующая функция по обе стороны от корня функция.
Шаги следующие:
- Перепишите неравенство так, чтобы на правая сторона.
- Найти все линейные множители функции.
- Чтобы найти критические значения, установите для каждой линейной функции значение ноль и решить для х .
- Определить знак функции на интервалах формируется критическими значениями.
- Решением будут те интервалы, в которых функция имеет правильные знаки, удовлетворяющие неравенству.
Пример 1
Решите неравенство х 2 − 3 > 2 х
Ответ
Сначала переставим неравенство с нулем на справа:
х 2 − 2 х − 3 > 0
, что можно разложить на множители, чтобы получить:
`(х + 1)(х — 3) > 0`
Приравняв оба множителя к нулю, получим:
`(х + 1) = 0 и (х — 3) = 0`
`х = -1 и х = 3`
Следовательно, критические значения равны
`х = -1 и х = 3`.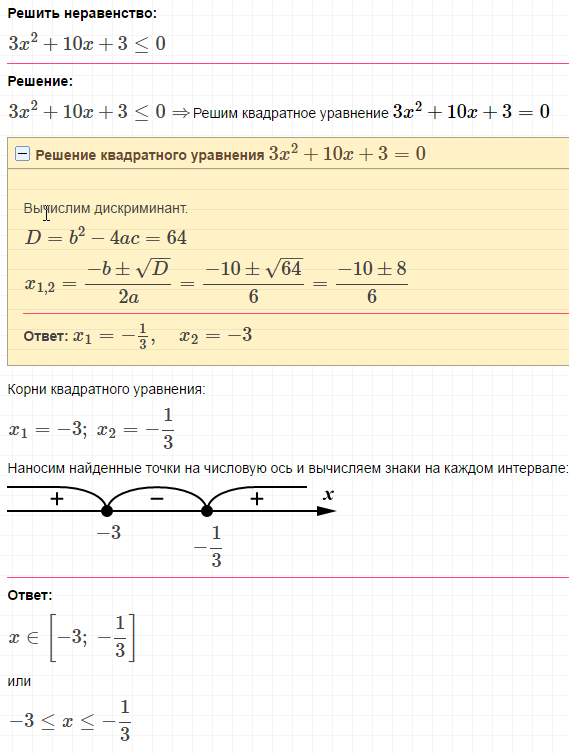
Эти критические значения делят числовую прямую на 3 интервалы:
`х < -1`,
`-1 < x < 3` и
`х > 3`.
Далее нам нужно определить знак (плюс или минус) функции в каждом из 3-х интервалов.
Для первого интервала `x < -1`,
Значение `(x + 1)` будет отрицательным (для проверки подставьте несколько значений `x` меньше, чем `-1`),
Значение `(x − 3)` также будет отрицательным
Таким образом, в интервале `x < -1` значение функции x 2 − 2 x − 3 будет равно
.отрицательное × отрицательное = положительное
Продолжаем делать это для двух других интервалов и суммируем результаты в этой таблице:
| Интервал | `(х + 1)` | `(х — 3)` | знак из f ( x ) |
| `x < -1` | − | − | + |
| `-1 < x < 3` | + | − | − |
| `х > 3` | + | + | + |
Решаем на
`(х + 1)(х — 3) > 0`
Интервалы, удовлетворяющие этому неравенству, будут такими, где f ( x ) имеет положительный знак.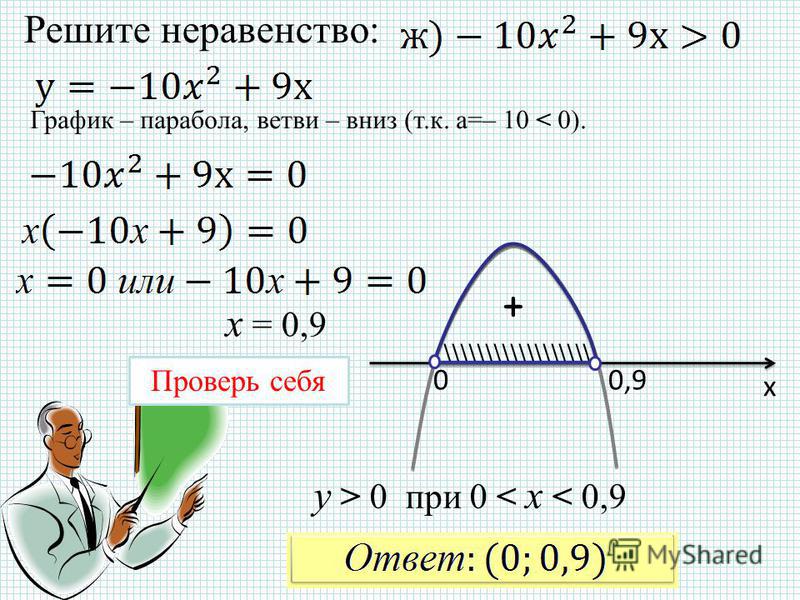
Следовательно, решение: `x < -1` или `x > 3`.
Вот график нашего решения:
123450-1-2-3-4xОткрыть изображение на новой страницеПример 2
Решите неравенство х 3 – 4 х 2 + х + 6 < 0
Ответить
Используя методы, изученные в предыдущих главах (см. теоремы об остатках и факторах), выражение можно быть учтено, чтобы дать:
( х + 1)(
х — 2)( х — 3) < 0
Приравняв множители к нулю, получим:
( х + 1) = 0
( х — 2) = 0
( х — 3) = 0
Итак, `x = −1`, `x = 2` или `x = 3`.
Следовательно, критическими значениями являются
`x = −1`, `x = 2` и `x = 3`.
Эти критические значения делят числовую прямую на 4 интервалы:
x < −1,
−1 < x < 2,
2 < x < 3 и
x > 3.
Далее определим знак функции следующим образом метод:
| Интервал | `(х + 1)` | `(х — 2)` | `(х — 3)` | знак ф ( х ) |
| `x < −1` | − | − | − | − |
| `−1 < x < 2` | + | − | − | + |
| `2 < x < 3` | + | + | − | − |
| `х > 3` | + | + | + | + |
Поскольку мы хотим, чтобы `f(x) < 0`, интервалы, которые
удовлетворять этому неравенству будут те, которые имеют отрицательный знак.
Следовательно, решение: `x < −1` или `2 < х < 3`.
Вот график нашего решения:
123450-1-2-3-4xОткрыть изображение на новой странице 92(х+3))/(4−х)`Поскольку мы хотим, чтобы `f(x) < 0`, интервалы, которые удовлетворять этому неравенству будут те, которые имеют отрицательный знак. 92 >= 0`
Наши критические значения: `x=0 или 1`.
Выполнив описанное выше тестирование, мы обнаружили, что наш набор решений: `x>
=0`.
Вот график решения:
123450-1-2-3-4xОткрыть изображение на новой странице2. Масса м , в Мг, топлива в ракета после запуска
м = 2000 − т 2 − 140 т
, где t измеряется в минутах. В течение в какое время масса топлива больше `500\ «Мг»`? 92+ 140т − 1500 < 0`
`(t + 150)(t − 10) < 0`
Итак, `−150 < t < 10`.
Но t не может быть отрицательным, поэтому `0 ≤ t < 10`.
График решения:
246810120-2tОткрыть изображение на новой странице3. Расстояние до объекта p , и расстояние изображения q , для камеры фокусного длина 3 см дается по:
`р=(3q)/(q-3)`
Для каких значений q р > 12 см?
Ответить
Запишем неравенство следующим образом:
`(3q)/(q−3)>12`
Первым логическим шагом было бы умножить обе части на ( q − 3).
