Решите неравенство с дробями » задачи
неравенства »
решите неравенство x-(5x/2+x дробью)≥0
Решение: x-(5x/2+x дробью)≥0зводим до спільного знаменника
x множим на (х + 2 )
2х + х квадрат — 5х ≥ 0
х квадрат — зх ≥ 0
Д= 9 — 4 помножити на 1 і 0 = 9 = 3 в квадраті
хперше 3+3/ 1 = 6 не задовольняє нерівність
х друге 3-3 /1 = 0
отже, 0 ≥ 0
відповідь: квадратна дужка 0 до + нескінченності — кругла дужка
1)11/x+5=11/5(дробью) 2)найти значение выражения 1/7x-7x+2y/14xy(дробью) при x = корень из 10, y=1/2
3)решить неравенство x в квадрате-4x-12 меньше 0
Решение: 1.накрест перемножаем числа и получается:
11*5=11(х+5)
55=11х+55
11х=0
х=0
ответ:0
3. 1)задаем функцию.
у=х²-4х-12
2)Область определения функции R,т.е. все действительные числа
3)находим нули функции: у=0; х²-4х-12=0
D=4+12=16
х1=2+4=6
х2=2-4=-6
4) наносим полученные числа на прямую.
ответ получается промежуток (-2;6)Решите неравенство дробь: 3x-1/3x+1
Решение: 3х-1=3x=x,=
Не верно предыдущее решение.
нужно писать 2 системы
3х-1>=0. 3х-13х+103х>=1. 3х3х-1
х>=1/3. хх-1/3
ответ (-1/3;1/3]
скобки и знаки должны быть как написаноРешите неравенство /-дробьx+3/x-5 < 0
Решение: Решаем неравенство методом интервалов.
Находим нули функции у=(x+3)/(х-5)
x+3=0
х=-3
Находим нуль знаменателя
х-5=0
х=5
Отмечаем точки на числовой прямой пустым кружком (здесь это круглые скобки) и расставляем знаки : + — +
при х =10 получаем (10+3)(10-5)>0
поэтому на интервале, содержащем точку (10), ставим знак «плюс», далее знаки чередуем.
+ _ +
————-(-3)————(5)————————Ответ: (−3;5)
Решите неравенство дробь в числителе 4x в знаменателе x+1 потом + дробь в числителе 6 в знаменателе x²-x-2 потом +1 ≤ 0
Решение: $$ \frac{4x}{x+1} + \frac{6}{x^2-x-2} +1 \leq 0 $$
ОДЗ:$$ \left \{ {{x+1 eq 0} \atop {x^2-x-2 eq 0}} \right. 2-x-12) < дробь (25x-47)/(10x-15) минус дробь 3/(3x+4)
Решение: 6x²-x-12=6(x+4/3)(x-3/2)=(3x+4)(2x-3)
D=1+288=289
x1=(1-17)/12=-4/3 U x2=(1+17)/12=3/2
————————
3/[(3x+4)(2x-3)]-(25x-47)/[5(2x-3)+3/(3x+4)<0
(15-75x²+141x-100x+188+30x-45)/[5(3x+4)(2x-3)<0
(-75x²+71x+158)/[5(3x+4)(2x-3)<0
(75x²-71x-158)/[5(3x+4)(2x-3)>0
75x²-71x-158=0
D=5041+47400=52441
√D=229
x1=(71-229)/100=-1,58
x2=(71+229)/100=3
3x+4=0⇒x=-4/3
2x-3=0⇒x=1,5
+ _ + _ +
————(-1,58)———(-1 1/3)———(1,5)———-(3)—————-
x∈(-∞;-1,58) U (-1 1/3;1,5) U (3;∞)объясните как решить неравенство: дробь 3х-1/х+9>0
Решение: Дробь решается методом интервалов:1)3x-1=0
x=1/3
2)x+9 не =0
x не = -9
+ — +
—- -9 —- 1/3 ——>x
x=(-;-9)U(1/3;+)
Решить неравенства с дробями:
1. {2}(+-)bx(+-)c=0 $$, а здесь просто х выносите за скобки…
х2-3х≥0
х(х-3)≥0, х1≥х2≥3
На координатной прямой строим,
___________0 //////// 3////////////////////////////>
ответ получается промежуток (-2;6)
2-x-12) < дробь (25x-47)/(10x-15) минус дробь 3/(3x+4)
{2}(+-)bx(+-)c=0 $$, а здесь просто х выносите за скобки…1 2 > >>
Предварительное вычисление по алгебре — Решить неравенство: $-5
спросил
Изменено 8 лет, 3 месяца назад
Просмотрено 234 раза
$\begingroup$
Решить неравенство: $-5 < \frac{1}{x} < 0$
Я думал о том, как я могу решить эту проблему.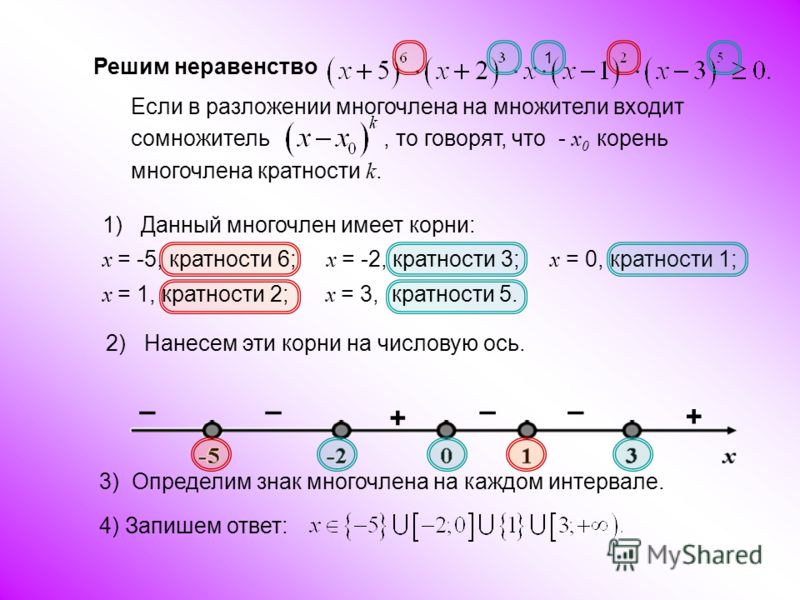
Если я умножу все стороны на $x$, боюсь, я удалю ответ, потому что $\frac{x}{x}=1$. И когда $x$ «уходит» из неравенства, я остаюсь без буквы.
Как получить только $x$ посередине, не добавляя $x$ к другим сторонам и не удаляя $x$?
Верно ли это? Если нет, то что я сделал не так?
- алгебра-предварительное исчисление
- неравенство
$\endgroup$
$\begingroup$
Поскольку вы знаете, что $x\neq 0$, вы можете умножить на $x$. Просто помните, что $x<0$. Таким образом, умножение на $x$ меняет неравенства на противоположные.
Тогда вы получите $-5x>1>0$. Это дает $-5x>1$. Теперь разделите на $-5$.
$\endgroup$
4
$\begingroup$
Вам не обязательно ставить $x$ прямо в центр.
Один из способов решения такого двойного неравенства — разбить его на систему из двух неравенств:
$$\begin{cases}-5<\frac1x\\ \frac1x<0\end{cases}$$
Из второго получается $x<0$, а из первого можно получить $x<-\frac15$ (не забывая, что $x<0$) .
Теперь ответом является пересечение двух интервалов: $x\in(-\infty,0)\cap(-\infty,-\frac15)=(-\infty,-\frac15)$.
$\endgroup$
7
$\begingroup$
Обратите внимание, что при $-5\lt \frac 1x \lt 0$ мы знаем, что $$\frac 1x < 0 \имеет x< 0$$. Поэтому, когда вы умножаете на $x$, чтобы удалить его из знаменателя, вам нужно поменять направления неравенств на противоположные.
$$-5 \lt \frac 1x \iff -5x \gt 1\iff x \lt -\frac 15 $$ и $$\frac 1x <0 \iff x\lt 0$$ Второе неравенство мы уже известно, и поэтому первое неравенство является более строгим из двух, которые должны быть соблюдены, чтобы оба неравенства выполнялись.