влияние прививки на холерную инфекцию
В таблице ниже приведены сведения о числе людей, заболевших или не заболевших холерой, с указанием, была ли им сделана противохолерная прививка.
Фрагмент таблицы с исходными данными
Файл содержит данные по 2663 пациентам.
В первой переменной указано была ли сделана пациенту прививка, а во второй – был ли зафиксирован факт заболевания холерой после прививки.
Задача: Требуется выяснить, эффективна прививка или нет.
Мы критикуем прививку и выдвигаем гипотезу: связи между заболеваемостью и прививкой нет.
Наблюдаемые частоты: Для решения задачи построим таблицу сопряженности, т.е. сопряжем признаки:
Таблица с наблюдаемыми частотами
Четыре элемента таблицы, а именно 1022, 11, 1625, 5 — это частоты; мы имеем, таким образом, таблицу в виде квадрата вместо привычного ряда столбцов.
По ней строится критерий согласия хи-квадрат с некоторой выдвинутой гипотезой:
Нулевая гипотеза:
Переформулируем нашу задачу.
Значимо ли воздействие прививки на вероятность заболевания?
Попробуем принять в качестве нулевой гипотезы, что прививка не оказывает воздействия на заболевание и что видимый эффект от прививки есть результат случайных флуктуаций.
Мы должны, следовательно, сравнить элементы в таблице с соответствующими ожидаемыми элементами в предположении справедливости гипотезы.
Ожидаемые частоты. Из гипотезы следует, что для 2663 человек, находящихся в группе риска, ожидаемая доля заболевших после прививки будет той же, что и ожидаемая доля заболевших среди тех, кому прививку не делали; общее значение этих долей совпадает с долей заболевших во всей выборке, а именно p = 16/2663 (~0,006). Эти ожидаемые доли представлены в таблице ниже:
Подставляя, полученное значение p:
Таблица с ожидаемыми частотами
При нулевой гипотезе ожидаемая частота в любой ячейке может быть найдена умножением доли (p или 1-p) на маргинальное общее число соответствующей строки (1630 — для категории привитых, 1033 — для остальных).
В принципе, только один элемент следует вычислять умножением маргинально частоты на ожидаемую долю; остальные элементы находятся вычитанием.
Значение Xи-квадрат используется для оценки меры рассогласованности наблюдаемого и ожидаемого результата. Если, согласно нулевой гипотезе, ожидаемый результат будет сильно отличаться от наблюдаемых значений, значит стоит поставить под сомнение справедливость гипотезы.
Перед тем, рассчитывать значение хи-квадрат, рассмотрим некоторые особенности таблиц 2х2, которые заслуживают специального упоминания.
В некоторых случаях необходимо делать «поправку на непрерывность» (так называемая «поправка Йетса»). Такие расхождения могут возникать, когда в таблице встречаются малые частоты (меньше 10).
Математически, «поправка на непрерывность» уменьшает погрешность, возникающую при аппроксимации непрерывным распределением хи-квадрат точного выборочного распределения, которое является дискретным.
Вычислим значение хи-квадрат без поправки Йетса. Значение представляет собой сумму квадратов разностей наблюдаемой и ожидаемой частоты, деленную на соответствующую ожидаемую частоту:
(Смотрите значения в таблицах с наблюдаемыми и ожидаемыми частотами выше.)
Отметим, что в нашем случае, для более точного вычисления статистики хи-квадрат необходимо использовать поправку Йетса (пять пациентов заболели, несмотря на сделанную противохолерную прививку).
Поправка Йетса немного изменит таблицу наблюдаемых частот:
Модифицированная таблица с наблюдаемыми частотами
В модифицированной таблице частота «5» заменена на «5,5», а все остальные элементы изменены так, чтобы общие суммарные (маргинальные) частоты сохранились.
Отметим, что при такой модификации ожидаемые частоты остаются без изменения.
Теперь вычислим значение хи-квадрат с поправкой Йетса, пользуясь той же формулой, но в качестве наблюдаемых частот берем значения из модифицированной таблицы:
Чтобы оценить какова вероятность получить такое или большее значение хи-квадрат, при условии истинности нулевой гипотезы, необходимо вычислить уровень значимости (p-уровень).
Если он окажется маленьким (обычно берется меньше 0,05), то нулевую гипотезу следует отклонить.
Использование калькулятора таблиц сопряженности 2 на 2.Заполняем таблицу в интерактивном калькуляторе таблиц сопряженности 2х2
Согласно таблице наблюдаемых частот (номера групп и вариантов заменяем на удобные для нас обозначения).
- Устанавливаем галочку напротив поправки Йетса (поправка для случая малых частот).
- Нажимаем кнопку «Вычислить».
Полученные результаты (p-уровень значимости ~ 0.014 < 0.05) говорят о том, что нулевую гипотезу о независимости следует отвергнуть: прививка в действительности имеет некоторый предупредительный эффект.
В нашем случае, значение величины «Отношение шансов» говорит о том, что шанс заболеть у группы непривитых больше, чем у группы привитых. Этот факт подтверждается проведенным выше анализом.
Таким же образом могут быть проверены гипотезы о прививках против гриппа, эффективности диспансеризации и т.д.
В начало
Содержание портала
HTML таблицы основы — Изучение веб-разработки
- Обзор: Tables
- Далее
Этот раздел познакомит вас с таблицами HTML, представив самые базовые понятия — строки и ячейки, заголовки, слияние строк и столбцов, а также объединение всех ячеек в столбце в целях стилизации.
| Начальные условия: | Знание основ HTML (читайте Введение в HTML — Introduction to HTML). |
|---|---|
| Цель: | Общее знакомство с таблицами HTML. |
Таблица — это структурированный набор данных, состоящий из строк и столбцов (табличных данных). Таблицы позволяют быстро и легко посмотреть значения, показывающие некоторую взаимосвязь между различными типами данных, например — человек и его возраст, или расписание в плавательном бассейне.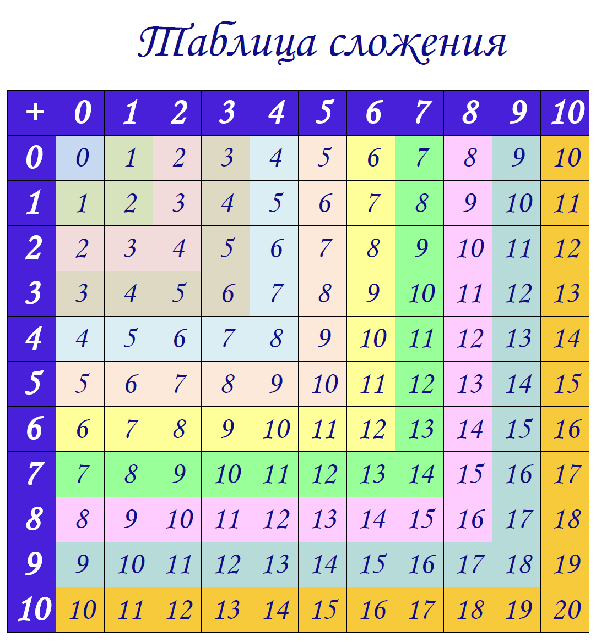
Люди постоянно используют таблицы, причём уже давно, как показывает документ по переписи в США, относящийся к 1800 году:
Так что не удивительно, что создатели HTML включили в него средства для структурирования и представления табличных данных в сети.
Как работает таблица?
Смысл таблицы в том, что она жёсткая. Информацию легко интерпретировать, визуально сопоставляя заголовки строк и столбцов. Например, посмотрите на приведённую ниже таблицу и найдите единственное личное местоимение, используемое в третьем лице , с полом ♀, выступающее в качестве объекта в предложении. Ответ можно найти, сопоставив соответствующие заголовки столбцов и строк.
| Субъект | Объект | |||
|---|---|---|---|---|
| 1 Лицо | Я | меня | ||
| 2 Лицо | ты | тебя | ||
| 3 Лицо | ♂ | он | его | |
| ♀ | она | её | ||
| o | оно | его | ||
Множ. числ. числ. | 1 Лицо | мы | нас | |
| 2 Лицо | вы | вас | ||
| 2 Лицо | они | их | ||
Если правильно представить таблицу HTML, интерпретировать её данные смогут даже люди, имеющие проблемы со зрением.
Оформление таблиц
Исходный код HTML (HTML source code) вышеприведённой таблице есть в GitHub; посмотрите его и живой пример (look at the live example)! Вы заметите, что таблица там выглядит иначе — это потому, что на сайте MDN к этим данным была применена таблица стилей, а приведённый в GitHub пример информации о стиле не имеет.
Не питайте ложных иллюзий — чтобы эффективно представлять таблицы в веб, необходимо придать им хорошую структуру в HTML и применить к ним таблицы стилей (CSS). В данном разделе мы сфокусируемся на HTML, чтобы узнать о том, что касается CSS, вам надо обратиться к статье Стилизация таблиц.
В этом разделе мы не фокусируемся на CSS, но всё же дали простейшую таблицу стилей CSS, чтобы сделать таблицы более читабельными. Эту таблицу стилей можно найти здесь, можно также использовать шаблон HTML, применяющий эту стаблицу стилей — вместе они дадут вам хорошую основу для экспериментов с таблицами HTML.
Примечание: Посмотрите также таблицу personal_pronouns с применённым к ней стилем, чтобы получить представление о том, как она выглядит.
Когда не надо использовать таблицы HTML?
HTML-таблицы следует использовать для табличных данных — это то, для чего они предназначены. К сожалению, многие используют таблицы HTML для оформления веб-страниц, например, одна строка для заголовка, одна для содержимого, одна для сносок, и тому подобное. Подробнее об этом можно узнать в разделе Вёрстка на Начальном обучающем модуле доступности. Это происходило из-за плохой поддержки CSS в разных браузерах; в наше время такое встречается гораздо реже, но иногда всё же попадается.
Короче говоря, использование таблиц в целях оформления вместо методов CSS является плохой идеей по следующим причинам :
- Таблицы, используемые для оформления, уменьшают доступность страниц для людей, имеющих проблемы со зрением: Скринридеры (Screenreaders (en-US)), используемые ими, интерпретируют HTML-теги и читают содержимое пользователю. Поскольку таблицы не являются средством для представления структуры таблицы, и разметка получается сложнее, чем при использовании методов CSS, скринридеры вводят пользователей в заблуждение.
- Таблицы создают путаницу тегов: Как уже упоминалось, оформление страниц с помощью таблиц даёт более сложную структуру разметки, чем специально предназначенные для этого методы. Соответственно, такой код труднее писать, поддерживать и отлаживать.
- Таблицы не реагируют автоматически на тип устройства: У надлежащих контейнеров (например,
<header>,<section>,<article>, или<div>) ширина по умолчанию равна 100% от их родительского элемента. У таблиц же размер по умолчанию подстраивается под их содержимое, так что чтобы они одинаково хорошо работали на разных типах устройств необходимо принимать дополнительные меры.
У таблиц же размер по умолчанию подстраивается под их содержимое, так что чтобы они одинаково хорошо работали на разных типах устройств необходимо принимать дополнительные меры.
Итак, мы уже достаточно говорили о теории, теперь возьмём конкретный пример и построим таблицу.
- Прежде всего, создайте локальную копию blank-template.html и minimal-table.css в новой папке на вашем компьютере.
- Содержимое любой таблицы заключается между двумя тегами :
<table></table>. Добавьте их в тело HTML. - Самым маленьким контейнером в таблице является ячейка, она создаётся элементом
<td>(‘td’ — сокращение от ‘table data’). Введите внутри тегов table следующее:<td>Hi, I'm your first cell.</td>
- Чтобы получить строку из четырёх ячеек, необходимо скопировать эти теги три раза. Обновите содержимое таблицы так, чтобы она выглядела следующим образом:
<td>Hi, I'm your first cell.
 </td> <td>I'm your second cell.</td> <td>I'm your third cell.</td> <td>I'm your fourth cell.</td>
</td> <td>I'm your second cell.</td> <td>I'm your third cell.</td> <td>I'm your fourth cell.</td>
Как видите, ячейки не располагаются одна под другой, на самом деле они автоматически выравниваются по отношению к другим ячейкам той же строки. Каждый элемент <td> создаёт отдельную ячейку, а все вместе они создают первую строку. Каждая добавленная ячейка удлиняет эту строку.
Чтобы эта строка перестала расти, а новые ячейки перешли на вторую строку, необходимо использовать элемент <tr> (‘tr’ — сокращение от ‘table row’). Попробуем, как это получится.
- Поместите четыре уже созданных ячейки между тегами
<tr>как здесь показано:<tr> <td>Hi, I'm your first cell.</td> <td>I'm your second cell.</td> <td>I'm your third cell.</td> <td>I'm your fourth cell.</td> </tr>
- Теперь, когда одна строка уже есть, добавим ещё — каждую строку надо вложить в дополнительный элемент
<tr>, а каждая ячейка должна быть внутриэлемента <td>.
В результате получится таблица, которая будет выглядеть примерно так:
| Hi, I’m your first cell. | I’m your second cell. | I’m your third cell. | I’m your fourth cell. |
|---|---|---|---|
| Second row, first cell. | Cell 2. | Cell 3. | Cell 4. |
Примечание: Этот пример можно также найти на GitHub под названием simple-table.html (see it live also).
Теперь обратимся к табличным заголовкам — особым ячейкам, которые идут вначале строки или столбца и определяют тип данных, которые содержит данная строка или столбец (как «Person» и «Age» в первом примере данной статьи). Чтобы показать, для чего они нужны, возьмём следующий пример. Сначала исходный код:
<table>
<tr>
<td> </td>
<td>Knocky</td>
<td>Flor</td>
<td>Ella</td>
<td>Juan</td>
</tr>
<tr>
<td>Breed</td>
<td>Jack Russell</td>
<td>Poodle</td>
<td>Streetdog</td>
<td>Cocker Spaniel</td>
</tr>
<tr>
<td>Age</td>
<td>16</td>
<td>9</td>
<td>10</td>
<td>5</td>
</tr>
<tr>
<td>Owner</td>
<td>Mother-in-law</td>
<td>Me</td>
<td>Me</td>
<td>Sister-in-law</td>
</tr>
<tr>
<td>Eating Habits</td>
<td>Eats everyone's leftovers</td>
<td>Nibbles at food</td>
<td>Hearty eater</td>
<td>Will eat till he explodes</td>
</tr>
</table>
Теперь как выглядит таблица:
| Knocky | Flor | Ella | Juan | |
|---|---|---|---|---|
| Breed | Jack Russell | Poodle | Streetdog | Cocker Spaniel |
| Age | 16 | 9 | 10 | 5 |
| Owner | Mother-in-law | Me | Me | Sister-in-law |
| Eating Habits | Eats everyone’s leftovers | Nibbles at food | Hearty eater | Will eat till he explodes |
Проблема в том, что, хотя вы и можете представить, о чем идёт речь, ссылаться на эти данные не так легко, как хотелось бы.
Упражнение: заголовки
Попробуем улучшить эту таблицу.
- Сначала создайте локальную копию dogs-table.html и minimal-table.css в новой папке на вашем компьютере. HTML содержит пример Dogs, который вы уже видели выше.
- Чтобы опознавать заголовки таблицы в качестве заголовков, визуально и семантически, можно использовать элемент
<th>(‘th’ сокращение от ‘table header’). Он работает в точности как<td>, за исключением того, что обозначает заголовок, а не обычную ячейку. Замените в своём HTML все элементы<td>, содержащие заголовки, на элементы<th>. - Сохраните HTML и загрузите его в браузер, и вы увидите, что заголовки теперь выглядят как заголовки.
Примечание: Законченный пример можно найти на dogs-table-fixed.html в GitHub (посмотрите живой пример).
Для чего нужны заголовки?
Мы уже частично ответили на этот вопрос — когда заголовки выделяются, легче искать данные и таблица выглядит лучше.
Примечание: По умолчанию к заголовкам таблицы применяется определённый стиль — они выделены жирным шрифтом и выровнены по центру, даже если вы не задавали для них стиль специально.
Заголовки дают дополнительное преимущество — вместе с атрибутом scope (который мы будем изучать в следующей статье) они помогают улучшить связь каждого заголовка со всеми данными строки или столбца одновременно, что довольно полезно
Иногда нам нужно, чтобы ячейки распространялись на несколько строк или столбцов. Возьмём простой пример, в котором приведены имена животных. Иногда бывает нужно вывести имена людей рядом с именами животных. А иногда это не требуется, и тогда мы хотим, чтобы имя животного занимало всю ширину.
Исходная разметка выглядит так:
<table>
<tr>
<th>Animals</th>
</tr>
<tr>
<th>Hippopotamus</th>
</tr>
<tr>
<th>Horse</th>
<td>Mare</td>
</tr>
<tr>
<td>Stallion</td>
</tr>
<tr>
<th>Crocodile</th>
</tr>
<tr>
<th>Chicken</th>
<td>Cock</td>
</tr>
<tr>
<td>Rooster</td>
</tr>
</table>
Но результат не такой, как хотелось бы:
| Animals | |
|---|---|
| Hippopotamus | |
| Horse | Mare |
| Stallion | |
| Crocodile | |
| Chicken | Cock |
| Rooster |
Нужно, чтобы «Animals», «Hippopotamus» и «Crocodile» распространялись на два столбца, а «Horse» и «Chicken» — на две строки. К счастью, табличные заголовки и ячейки имеют атрибуты
К счастью, табличные заголовки и ячейки имеют атрибуты colspan и rowspan, которые позволяют это сделать. Оба принимают безразмерное числовое значение, которое равно количеству строк или столбцов, на которые должны распространяться ячейки. Например, colspan="2" распространяет ячейку на два столбца.
Воспользуемся colspan и rowspan чтобы улучшить таблицу.
- Сначала создайте локальную копию animals-table.html и minimal-table.css в новой папке на вашем компьютере. Код HTML содержит пример с животными, который вы уже видели выше.
- Затем используйте атрибут
colspanчтобы распространить «Animals», «Hippopotamus» и «Crocodile» на два столбца. - Наконец, используйте атрибут
rowspanчтобы распространить «Horse» и «Chicken» на две строки. - Сохраните код и откройте его в браузере, чтобы увидеть улучшения.
Примечание: Законченный пример можно посмотреть в animals-table-fixed. html на GitHub (живой пример).
html на GitHub (живой пример).
И последняя возможность, о которой рассказывается в данной статье. HTML позволяет указать, какой стиль нужно применять к целому столбцу данных сразу — для этого применяют элементы <col> и <colgroup>. Их ввели, поскольку задавать стиль для каждой ячейки в отдельности или использовать сложный селектор вроде :nth-child() (en-US) было бы слишком утомительно.
Возьмём простой пример:
<table>
<tr>
<th>Data 1</th>
<th>Data 2</th>
</tr>
<tr>
<td>Calcutta</td>
<td>Orange</td>
</tr>
<tr>
<td>Robots</td>
<td>Jazz</td>
</tr>
</table>
Что даёт нам:
| Data 1 | Data 2 |
|---|---|
| Calcutta | Orange |
| Robots | Jazz |
Он не идеален, поскольку нам пришлось повторить информацию о стиле для всех трёх ячеек в столбце (в реальном проекте, возможно, придётся вводить class на всех трёх и вводит правило в таблице стилей). Вместо этого, мы можем задать информацию один раз, в элементе
Вместо этого, мы можем задать информацию один раз, в элементе <col>. Элемент <col> задаётся в контейнере <colgroup> сразу же за открывающим тегом <table>. Эффект, который мы видели выше, можно задать так:
<table>
<colgroup>
<col>
<col>
</colgroup>
<tr>
<th>Data 1</th>
<th>Data 2</th>
</tr>
<tr>
<td>Calcutta</td>
<td>Orange</td>
</tr>
<tr>
<td>Robots</td>
<td>Jazz</td>
</tr>
</table>
Мы определяем два «стилизующих столбца». Мы не применяем стиль к первому столбцу, но пустой элемент <col> ввести необходимо — иначе к первому столбцу не будет применён стиль.
Если бы мы хотели применить информацию о стиле к обоим столбцам, мы могли бы просто ввести один элемент <col> с атрибутом span, таким образом:
<colgroup> <col span="2"> </colgroup>
Подобно colspan и rowspan, span принимает безразмерное числовое значение, указывающее, к какому количеству столбцов нужно применить данный стиль.
Упражнение: colgroup и col
Теперь попробуйте сами.
Ниже приведена таблица уроков по языкам. В пятницу (Friday) новый класс целый день изучает голландский (Dutch), кроме того, во вторник (Tuesday) и четверг (Thursdays) есть занятия по немецкому (German). Учительница хочет выделить столбцы, соответствующие дням, когда она преподаёт.
| Mon | Tues | Wed | Thurs | Fri | Sat | Sun | |
|---|---|---|---|---|---|---|---|
| 1st period | English | German | Dutch | ||||
| 2nd period | English | English | German | Dutch | |||
| 3rd period | German | German | Dutch | ||||
| 4th period | English | English | Dutch |
Заново создайте таблицу, проделав указанные ниже действия.
- Сначала создайте локальную копию файла timetable.html в новой папке на вашем компьютере. Код HTML содержит таблицу, которую вы уже видели выше, но без информации о стиле.
- Добавьте элемент
<colgroup>вверху таблицы, сразу же под тегом<table>, куда вы сможете вставлять элементы<col>. - Первые два столбца надо оставить без стиля..
- Добавьте цвет фона для третьего столбца. Значением атрибута
styleбудетbackground-color:#97DB9A; - Задайте ширину для четвёртого столбца.
Значением атрибута styleбудетwidth: 42px; - Добавьте цвет фона для пятого столбца. Значением атрибута
styleбудетbackground-color: #97DB9A; - Добавьте другой цвет фона и границу для шестого столбца, чтобы показать, что это особый день и она ведёт новый класс. Значениями атрибута
styleбудут:background-color:#DCC48E; border:4px solid #C1437A; - Последние два дня выходные; значением атрибута style
будет width: 42px;
Посмотрите, что у вас получилось. Если застрянете, или захотите себя проверить, можете посмотреть нашу версию в timetable-fixed.html (посмотрите живой пример).
Если застрянете, или захотите себя проверить, можете посмотреть нашу версию в timetable-fixed.html (посмотрите живой пример).
Здесь приведены практически все базовые сведения о таблицах HTML. В следующей статье вы получите более продвинутые сведения на эту тему.
- Обзор: Tables
- Далее
Last modified: , by MDN contributors
Объединение таблиц 2 на 2
Критерий хи-квадрат и другие тесты для сравнения пропорций, охватываемые этим блоком, часто неправильно применяются при анализе объединенных 22 таблиц, как если бы они были получены из одного исследования. Объединение данных, в которых распространенность характеристики различается между репликами, может просто дать неправильный ответ — известный как парадокс Симпсона . Это лучше всего понять, взглянув на эти гипотетические наборы данных.
Например:
Пример 1
Обратите внимание, что скорости падения для двух процедур A и B были очень похожими в каждом центре, но различались между центрами. В первом центре падение составило 81-83%, а во втором всего 33-36%.
В первом центре падение составило 81-83%, а во втором всего 33-36%.
Итак, что произойдет, если мы просто объединим данные двух испытаний?
Теперь мы видим, что контрольная группа имеет значительно более высокую скорость падения, чем экспериментальная (69% по сравнению с 59%) с отношением риска для лечения по сравнению с контролем 0,85. Ясно, что это очень обманчивый результат. Это результат объединения данных с неравными пропорциями (общие коэффициенты падения для каждого центра составляют 0,82 против 0,34) и неравными соотношениями размеров выборки (120:210 и 105:75). Мы также потеряли ценную информацию о том, что частота падения обоих методов лечения сильно зависит от того, какой центр задействован (у нас могут быть серьезные проблемы с уходом за пациентами в центре 1!).
Чтобы правильно проанализировать данные, нам нужно вернуться к полной информации, приведенной в двух таблицах.
| ||||
Пример 2
Опять же, у нас есть бинарная переменная результата, но здесь мы полагаем, что на результат исследования повлиял такой смешанный фактор, как возраст. Поэтому мы стратифицируем результаты, чтобы исследовать этот фактор и скорректировать его влияние.
Поэтому мы стратифицируем результаты, чтобы исследовать этот фактор и скорректировать его влияние.
Наш пример здесь взят из исследования случай-контроль факторов риска заболевания крупного рогатого скота. Данные получены из 75 случаев всех возрастов по сравнению с 75 случайно выбранными контрольными группами. Мы разделяем результаты, чтобы мы могли отдельно изучить результаты для взрослых особей и телят. Мы используем отношение шансов для оценки важности фактора риска в каждой страте. Если бы мы объединили данные, то получили бы грубое отношение шансов 2,9.8 — не так явно вводит в заблуждение, как в нашем первом примере, но мы могли бы обоснованно усомниться в его релевантности, учитывая очевидную разницу между группами.
| ||||||
Лучший способ приблизиться к таким данным — сначала оценить оценку общего эффекта (либо отношение риска, либо отношение шансов) с соответствующим доверительным интервалом. Затем данные проверяются на однородность. Если данные однородны, оценку общего эффекта можно проверить на значимость. Если нет, анализ возвращается к рассмотрению каждой страты в отдельности.
Затем данные проверяются на однородность. Если данные однородны, оценку общего эффекта можно проверить на значимость. Если нет, анализ возвращается к рассмотрению каждой страты в отдельности.
Существует несколько подходов к проведению такого анализа. Наиболее популярным подходом является использование так называемых методов Mantel-Haenszel , и здесь мы сконцентрируемся на этом подходе. Альтернативный подход состоит в объединении логарифмов отношений шансов. Этот метод работает удовлетворительно, когда имеется всего несколько страт и размеры выборки в каждой из них велики. Существует также метод максимального правдоподобия, известный как метод Корнфилда-Гарта. Эти процедуры описаны Гартом (1970) и обобщены в Fleiss (2003).
Общий коэффициент риска и отношение шансов
Общий коэффициент риска Мантеля-Хензеля получают путем простого взвешивания вклада каждого отдельного коэффициента риска по мере его точности. Это делается путем взятия числителя и знаменателя отношения риска для каждого квадрата отдельно и деления каждого на количество наблюдений в этом квадрате. Затем компоненты из каждого квадрата суммируются, и числитель делится на знаменатель, чтобы получить общий коэффициент риска:
Затем компоненты из каждого квадрата суммируются, и числитель делится на знаменатель, чтобы получить общий коэффициент риска:
Алгебраически говоря —
|
Значение будет смещено в сторону отношения риска квадратов, содержащих наибольшее количество наблюдений. Следовательно, используя данные из нашего первого примера выше, мы получаем общий коэффициент риска 1,01, что больше, чем среднее арифметическое 0,9.8.
Как и прежде, асимптотический доверительный интервал (в 1,96 раза больше стандартной ошибки) вычисляется для логарифма относительного риска, а затем детрансформируется, чтобы получить интервал для самого относительного риска. Стандартная ошибка дана Greenland & Robins (1985).
Аналогичный подход используется для получения общего отношения шансов. Снова вклад каждого квадрата в общее отношение шансов взвешивается количеством наблюдений в этом квадрате:
Алгебраически говоря —
|
Используя данные из нашего второго примера выше, мы получаем общее отношение шансов 3,51. Асимптотический доверительный интервал рассчитывается для логарифма отношения шансов, а затем детрансформируется, чтобы получить интервал для самого отношения шансов. Стандартная ошибка дается Робинсом (1986). Точные доверительные интервалы предпочтительнее, когда размеры выборки малы.
Проверка на однородность/взаимодействие
В нашем первом примере мы получили центральные коэффициенты риска 1,03 и 0,93 при общем коэффициенте риска 1,01. В этой ситуации общий коэффициент риска кажется подходящей мерой суммарного эффекта для наших данных. Но во втором примере действительно ли обычное отношение шансов 3,51 подходит для описания отношения риска 2,50 для взрослых и 5,25 для телят??
Казалось бы, в этом последнем случае мы могли бы иметь взаимодействие между смешанным фактором (возрастом) и фактором риска. Другими словами, влияние фактора риска зависит от уровня искажающего фактора. Иными словами, наши разные таблицы 2 2 могут быть неоднородными. Как мы оцениваем важность этого взаимодействия или неоднородности?
Другими словами, влияние фактора риска зависит от уровня искажающего фактора. Иными словами, наши разные таблицы 2 2 могут быть неоднородными. Как мы оцениваем важность этого взаимодействия или неоднородности?
По сути, мы сравниваем наблюдаемые значения с ожидаемыми значениями, предполагая общий риск или отношение шансов. В 22-таблице, если известны итоги по строкам и столбцам, знание одной ячейки фиксирует остальные три ячейки. Следовательно, мы основываем тест на однородность, используя только одно значение в каждых 22 квадратах, обычно в верхней левой ячейке. Единственная трудность заключается в том, чтобы выяснить, какими должны быть ожидаемые значения — это просто, но довольно утомительно!
Для расчета статистики хи-квадрат взаимодействия Мантеля-Хензеля мы возвращаемся к основной форме статистики хи-квадрат Пирсона, а именно, что X 2 равно квадрату отклонений, деленному на параметрическую дисперсию при нулевой гипотезе:
Алгебраически говоря —
| |||||||||
Итак, как наши примеры работают в тесте на взаимодействие?
| ||||||
Если мы рассмотрим первый пример
, мы получим общий коэффициент риска 1,01. Наблюдаемые значения для 1 и 2 равны 100 и 35. Ожидаемые значения (выделены розовым цветом в таблице) при условии отсутствия взаимодействия составляют 98,8 для 1 и 36,3 для 2 . По этим значениям мы можем оценить другие ожидаемые значения в таблицах.
Наблюдаемые значения для 1 и 2 равны 100 и 35. Ожидаемые значения (выделены розовым цветом в таблице) при условии отсутствия взаимодействия составляют 98,8 для 1 и 36,3 для 2 . По этим значениям мы можем оценить другие ожидаемые значения в таблицах.
Близость наблюдаемых и ожидаемых значений поддерживает наше подозрение, что здесь мало свидетельств какой-либо неоднородности. Затем оцениваются отклонения для каждого квадрата и используются для получения значения X 2 . Значение P не свидетельствует о какой-либо неоднородности данных, поэтому мы принимаем коэффициент риска 1,01 в качестве разумной оценки общего коэффициента риска.
| ||||||
Для второго
например у нас есть общее отношение шансов 3,51. Наблюдаемые значения для 1 и 2 равны 25 и 30 по сравнению с ожидаемыми значениями при отсутствии взаимодействия 26,35 и 28,66.
Наблюдаемые значения для 1 и 2 равны 25 и 30 по сравнению с ожидаемыми значениями при отсутствии взаимодействия 26,35 и 28,66.
Удивительно, но наблюдаемые и ожидаемые значения кажутся довольно похожими, а тест не дает четких доказательств какой-либо неоднородности. Это не так удивительно, если принять во внимание небольшой размер выборки, а именно 70 взрослых особей и 80 телят. В этом случае мы должны признать однородность этого исследования, но очевидные различия в отношении шансов для взрослых особей и телят предполагают, что необходимо дальнейшее исследование с достаточной мощностью, чтобы выявить какие-либо различия между двумя группами.
Ассоциативный тест Мантеля-Хензеля
Остается только оценить значимость или иное значение общего риска или отношения шансов, предполагая, что выше мы продемонстрировали гомогенность. Как и прежде, мы основываем тест только на наблюдаемых и ожидаемых значениях в ячейке a каждой таблицы. Однако теперь ожидаемые значения оцениваются на основе отсутствия связи, а не на основе общего риска или отношения шансов. Если применить ее только к одному квадрату, формула алгебраически идентична хи-квадрату Пирсона, за исключением того, что она умножается на коэффициент (n и -1/n и ). Это близко к 1, за исключением небольших размеров выборки.
Однако теперь ожидаемые значения оцениваются на основе отсутствия связи, а не на основе общего риска или отношения шансов. Если применить ее только к одному квадрату, формула алгебраически идентична хи-квадрату Пирсона, за исключением того, что она умножается на коэффициент (n и -1/n и ). Это близко к 1, за исключением небольших размеров выборки.
Алгебраически говоря —
|
Важный момент-Неправильно объединенные данные из 22 таблиц могут привести к вводящим в заблуждение (= неверным) выводам из данных. Он может создавать видимые лечебные эффекты там, где их нет, и аналогичным образом скрывать важные лечебные эффекты. |
Если мы применим этот тест к первому набору данных многоцентрового исследования с общим коэффициентом риска ЗГ 1,01 (показан красным на рисунке), мы получим очень низкое значение хи-квадрат Мантеля-Хензеля всего 0,0005 ( P = 0,982).
{ Рис. 1 }
Из этого у нас явно нет доказательств связи между лечением и исходом.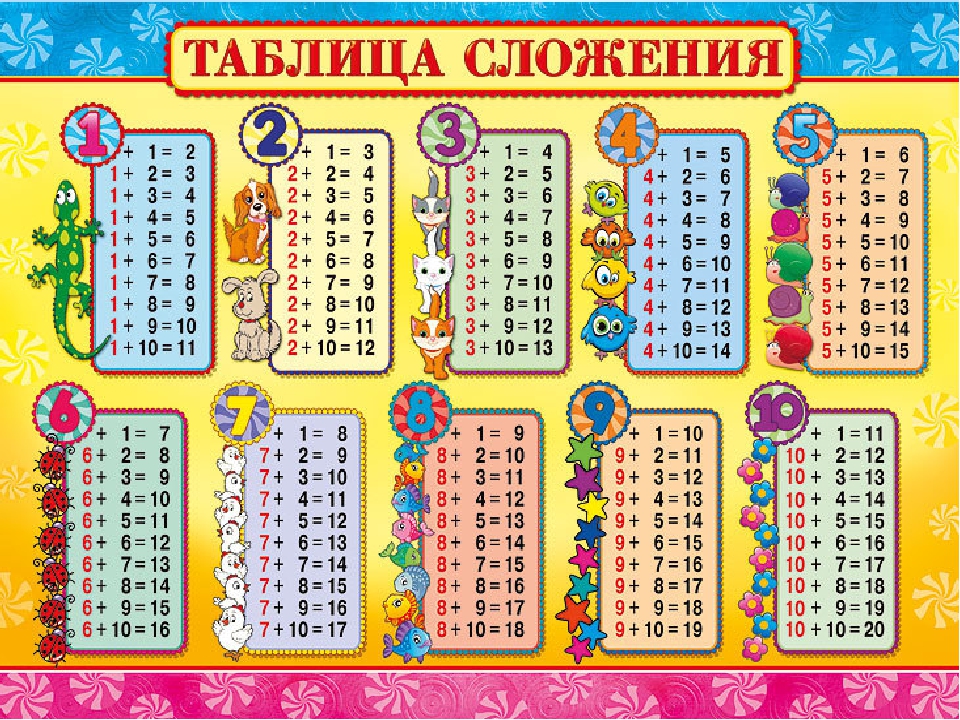
Но вспомните результат критерия хи-квадрат Пирсона для грубого коэффициента риска (показан зеленым) — он дал P значение 0,03! Использование этого подхода привело бы нас к ошибочному выводу, что лечение эффективно снижает частоту падений. Неправильное объединение данных является одной из наиболее распространенных причин неправильного статистического анализа данных в литературе.
Переходя ко второму примеру с обычным отношением шансов MH, равным 3,51 (снова показано красным на рисунке), мы получаем значение хи-квадрата Мантеля-Хензеля для ассоциации, равное 12,03 ( P = 0,0005).
{ Рис. 2 }
Таким образом, мы можем быть уверены, что фактор риска связан с возникновением заболевания.
Обратите внимание, что, поскольку это было «традиционное» исследование случай-контроль, наше отношение шансов 3,51 можно приравнять к относительному риску только в том случае, если заболевание «редкое». В этом случае поправка на смешанный фактор возраста увеличила грубое отношение шансов с 2,98 до 3,51.
В этом случае поправка на смешанный фактор возраста увеличила грубое отношение шансов с 2,98 до 3,51.
Таблицы от 2 до 20
LearnPracticeDownload
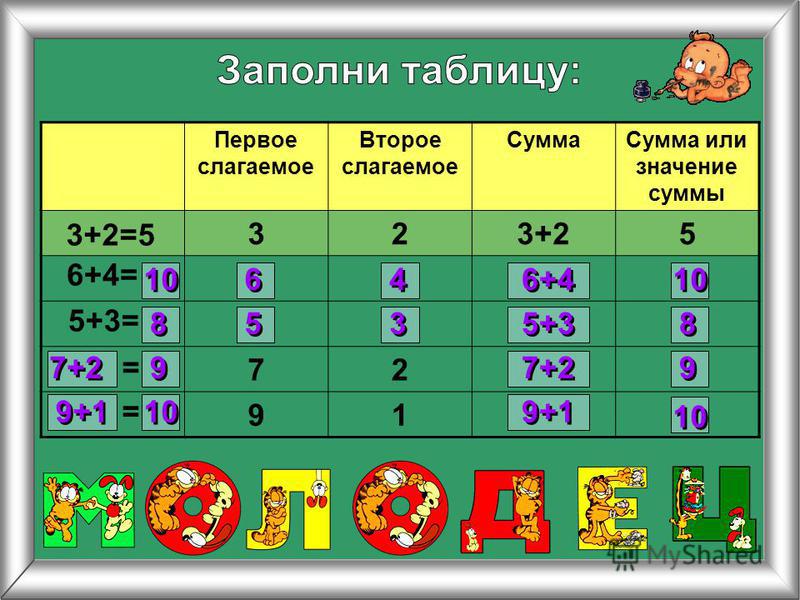
Таблицы от 2 до 20 значительно упрощают умножение и повышают ваши способности решать задачи. Даже при наличии калькуляторов запоминание таблицы умножения от 2 до 20 по-прежнему остается чрезвычайно мощным инструментом. Поэтому, если вы хотите уменьшить стресс при выполнении математических расчетов умножения, дробей, отношений и деления, вы должны распознавать числа в таблицах умножения.
Итак, вот вам решение. В этом мини-уроке вы изучите таблицу умножения от 2 до 20. Наряду с этой таблицей умножения вам будут предоставлены всевозможные советы и рекомендации для быстрых и простых вычислений. Мы также предоставили печатные таблицы умножения от 2 до 20, чтобы помочь учащимся расставить приоритеты и спланировать повторение.
1. | Таблицы со 2 по 20 |
| 2. | Математические таблицы от 2 до 20 трюков |
| 3. | Таблицы умножения от 2 до 20 PDF |
| 4. | Часто задаваемые вопросы по таблицам 2–20 |
Столы от 2 до 20
Запоминание таблицы умножения от 2 до 20 не только дает уверенность в себе, но и позволяет держать информацию под рукой. Учащиеся, лучше разбирающиеся в таблице умножения, могут решать арифметические задачи гораздо быстрее. Прочная основа на таблицах от 2 до 20 может сэкономить много вычислительного времени при решении сложных задач. Поэтому рекомендуется выучить наизусть все приведенные ниже математические таблицы от 2 до 20 для быстрых фундаментальных оценок.
☛ Таблицы с 2 по 20 Скачать PDF
Таблицы с 2 по 5
| Таблица из 2 | Таблица из 3 | Таблица из 4 | Таблица из 5 |
2 × 1 = 2 | 3 × 1 = 3 | 4 × 1 = 4 | 5 × 1 = 5 |
2 × 2 = 4 | 3 × 2 = 6 | 4 × 2 = 8 | 5 × 2 = 10 |
2 × 3 = 6 | 3 × 3 = 9 | 4 × 3 = 12 | 5 × 3 = 15 |
2 × 4 = 8 | 3 × 4 = 12 | 4 × 4 = 16 | 5 × 4 = 20 |
2 × 5= 10 | 3 × 5 = 15 | 4 × 5 = 20 | 5 × 5 = 25 |
2 × 6 = 12 | 3 × 6 = 18 | 4 × 6 = 24 | 5 × 6 = 30 |
2 × 7 = 14 | 3 × 7 = 21 | 4 × 7 = 28 | 5 × 7 = 35 |
2 × 8 = 19 | 3 × 8 = 24 | 4 × 8 = 32 | 5 × 8 = 40 |
2 × 9 = 18 | 3 × 9 = 27 | 4 × 9 = 36 | 5 × 9 = 45 |
2 × 10 = 20 | 3 × 10 = 30 | 4 × 10 = 40 | 5 × 10 = 50 |
Столы с 6 по 10
| Стол из 6 | Стол из 7 | Таблица из 8 | Таблица из 9 | Таблица из 10 |
| 6 × 1 = 6 | 7 × 1 = 7 | 8 × 1 = 8 | 9 × 1 = 9 | 10 × 1 = 10 |
6 × 2 = 12 | 7 × 2 = 14 | 8 × 2 = 16 | 9 × 2 = 18 | 10 × 2 = 20 |
6 × 3 = 18 | 7 × 3 = 21 | 8 × 3 = 24 | 9 × 3 = 27 | 10 × 3 = 30 |
6 × 4 = 24 | 7 × 4 = 28 | 8 × 4 = 32 | 9 × 4 = 36 | 10 × 4 = 40 |
6 × 5 = 30 | 7 × 5 = 35 | 8 × 5 = 40 | 9 × 5 = 45 | 10 × 5 = 50 |
6 × 6 = 36 | 7 × 6 = 42 | 8 × 6 = 48 | 9 × 6 = 54 | 10 × 6 = 60 |
6 × 7 = 42 | 7 × 7 = 49 | 8 × 7 = 56 | 9 × 7 = 63 | 10 × 7 = 70 |
6 × 8 = 48 | 7 × 8 = 56 | 8 × 8 = 64 | 9 × 8 = 72 | 10 × 8 = 80 |
6 × 9 = 54 | 7 × 9 = 63 | 8 × 9 = 72 | 9 × 9 = 81 | 10 × 9 = 90 |
6 × 10 = 60 | 7 × 10 = 70 | 8 × 10 = 80 | 9 × 10 = 90 | 10 × 10 = 100 |
Столы с 11 по 15
| Стол из 11 | Таблица из 12 | Таблица из 13 | Таблица из 14 | Таблица из 15 |
| 11 × 1 = 11 | 12 × 1 = 12 | 13 × 1 = 13 | 14 × 1 = 14 | 15 × 1 = 15 |
| 11 × 2 = 22 | 12 × 2 = 24 | 13 × 2 = 26 | 14 × 2 = 28 | 15 × 2 = 30 |
| 11 × 3 = 33 | 12 × 3 = 36 | 13 × 3 = 39 | 14 × 3 = 42 | 15 × 3 = 45 |
| 11 × 4 = 44 | 12 × 4 = 48 | 13 × 4 = 52 | 14 × 4 = 56 | 15 × 4 = 60 |
| 11 × 5 = 55 | 12 × 5 = 60 | 13 × 5 = 65 | 14 × 5 = 70 | 15 × 5 = 75 |
| 11 × 6 = 66 | 12 × 6 = 72 | 13 × 6 = 78 | 14 × 6 = 84 | 15 × 6 = 90 |
| 11 × 7 = 77 | 12 × 7 = 84 | 13 × 7 = 91 | 14 × 7 = 98 | 15 × 7 = 105 |
| 11 × 8 = 88 | 12 × 8 = 96 | 13 × 8 = 104 | 14 × 8 = 112 | 15 × 8 = 120 |
| 11 × 9 = 99 | 12 × 9 = 108 | 13 × 9 = 117 | 14 × 9 = 126 | 15 × 9 = 135 |
11 × 10 = 110 | 12 × 10 = 120 | 13 × 10 = 130 | 14 × 10 = 140 | 15 × 10 = 150 |
Столы с 16 по 20
| Стол из 16 | Стол из 17 | Таблица из 18 | Таблица из 19 | Таблица из 20 |
16 × 1 = 16 | 17 × 1 = 17 | 18 × 1 = 18 | 19 × 1 = 19 | 20 × 1 = 20 |
16 × 2 = 32 | 17 × 2 = 34 | 18 × 2 = 36 | 19 × 2 = 38 | 20 × 2 = 40 |
16 × 3 = 48 | 17 × 3 = 51 | 18 × 3 = 54 | 19 × 3 = 57 | 20 × 3 = 60 |
16 × 4 = 64 | 17 × 4 = 68 | 18 × 4 = 72 | 19 × 4 = 76 | 20 × 4 = 80 |
16 × 5 = 80 | 17 × 5 = 85 | 18 × 5 = 90 | 19 × 5 = 95 | 20 × 5 = 100 |
16 × 6 = 96 | 17 × 6 = 102 | 18 × 6 = 108 | 19 × 6 = 114 | 20 × 6 = 120 |
16 × 7 = 112 | 17 × 7 = 119 | 18 × 7 = 126 | 19 × 7 = 133 | 20 × 7 = 140 |
16 × 8 = 128 | 17 × 8 = 136 | 18 × 8 = 144 | 19 × 8 = 152 | 20 × 8 = 160 |
16 × 9 = 144 | 17 × 9 = 153 | 18 × 9 = 162 | 19 × 9 = 171 | 20 × 9 = 180 |
16 × 10 = 160 | 17 × 10 = 170 | 18 × 10 = 180 | 19 × 10 = 190 | 20 × 10 = 200 |
Математические таблицы от 2 до 20 трюков
- Каждое число в таблице умножения от 2 до 20 является целым числом.

- Таблица 2 следует образцу 2, 4, 6, 8, 0 на разряде единицы.
- В таблице 5 последняя цифра кратных либо 0, либо 5.
- Умножение четного числа на 6 дает то же четное число, что и последняя цифра произведения. Например, 6 × 4 = 24, 6 × 6 = 36, 6 × 8 = 48.
- Вы также можете обратиться к таблицам умножения на 16 и таблице умножения на 18, чтобы получить таблицу умножения на 17. В таблице умножения на 18 мы вычитаем натуральные числа (от 1 до 10) из чисел, кратных 18, а в таблице умножения на 16 мы добавляем натуральные числа (1-10) к числам, кратным 16, чтобы получить таблицу умножения на 17.
- В таблице 19 есть образец для каждых десяти кратных. Запишите первые 10 нечетных чисел в последовательности в разряде десятков. Теперь с обратной стороны начните писать цифры от 0 до 9 на месте единицы.
- Чтобы запомнить таблицу умножения на 20, вам нужно запомнить таблицу умножения на 2. Добавьте 0 к разряду единиц в числах, кратных 2, чтобы получить число, кратное 20.

Таблица умножения от 2 до 20 PDF
Здесь мы предоставили таблицы умножения от 2 до 20. Студенты могут выучить эти математические таблицы по приведенным ниже ссылкам:
Пусть ваш ребенок решит задачи из реальной жизни, используя математику
Пусть ваш ребенок применит понятия, полученные в школе, в реальном мире с помощью наших экспертов.
Запись на бесплатный пробный урок
Примеры таблиц 2–20
Пример 1: Соблюдать все таблицы от 2 до 20
а) Вычислить 2 раза 19
- б) Произведение 12 и 6
Решение:
а) Сначала рассмотрим все таблицы от 2 до 20 и запишем 2 умножить на 19 математически как, 2 умножить на 19 = 2 × 19 = 38
Следовательно, мы получим 2 умножить на 19 как 38.
б) Во-первых, мы математически запишем произведение 12 и 6. Используя таблицу умножения на 12, произведение 12 и 6 = 12 × 6 = 72
Следовательно, произведение 12 и 6 согласно таблицам 2–20 равно 72.

Пример 2: Просмотрите все таблицы нечетных чисел от 2 до 20 и оцените следующее. Проверьте, является ли результат также нечетным или четным числом.
- 3 раза 7
- 11 раз 9
- 13 раз 3
- 13 раз 3 раза 7
Решение:
а) В математике 3 умножить на 7 = 3 × 7
Согласно таблице умножения на 3, 3 × 7 = 21 (нечетное число).
б) В математике 11 умножить на 9 = 11 × 9
Согласно таблице умножения на 11, 11 × 9 = 99 (нечетное число).
c) В математике 13 умножить на 3 = 13 × 3
Согласно таблице умножения на 13, 13 × 3 = 39(нечетное число) .
d) В математике 13 умножить на 3 умножить на 7 = 13 × 3 × 7
Согласно таблице умножения на 13, таблице умножения на 3 и таблице умножения на 7, 13 × 3 × 7 = 273 (нечетное число).
Кроме того, 21 × 13 = 273. Здесь 21 тоже нечетное число.
Пример 3: Соблюдать все таблицы от 2 до 20
а) Вычислить 17 раз 9
- б) Произведение 9 и 8
Решение:
а) Сначала рассмотрим все таблицы от 2 до 20 и напишем 17 раз 9математически как 17 умножить на 9 = 17 × 9 = 153
Следовательно, мы получаем 17 умножить на 9 как 153.

б) Сначала мы математически запишем произведение 12 и 6. Используя таблицу умножения на 9, произведение 9 и 8 = 9 × 8 = 72
Следовательно, произведение 9 и 8 согласно таблицам 2–20 равно 72.
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по таблицам 2–20
Как вы читаете таблицы 2–20?
Таблицу умножения от 2 до n чисел можно читать следующим образом. Возьмем в качестве примера таблицу 2,
- два раза два (2 × 1 = 2)
- две двойки четыре (2 × 2 = 4)
- две тройки шесть (2 × 3 = 6)
- две четверки восемь (2 × 4 = 8)
- две пятерки десять (2 × 5 = 10)
- две шестерки двенадцать (2 × 6 = 12) и так далее.
Как быстрее всего выучить таблицу умножения от 2 до 5?
Следующие советы помогут вам как можно быстрее запомнить таблицу умножения от 2 до 5.
- Таблицу 2 можно запомнить, добавив каждое число дважды.


 У таблиц же размер по умолчанию подстраивается под их содержимое, так что чтобы они одинаково хорошо работали на разных типах устройств необходимо принимать дополнительные меры.
У таблиц же размер по умолчанию подстраивается под их содержимое, так что чтобы они одинаково хорошо работали на разных типах устройств необходимо принимать дополнительные меры.