Exp производная: Производная экспоненциальной функции (e^x)’

Сообщество Экспонента

• Публикация
• 30.10.2022

Системы связи

Мероприятие призвано собрать на одной площадке всех специалистов данной тематики для обмена знаний, опыта и технологий, чтобы вооруживший последними технологиями дать быстрый старт в развитии отечественного оборудования систем связи 5G. Подробная программа 09:…

Приглашаем разработчиков систем связи на семинар для всестороннего обсуждения вопросов построения отечественного оборудования систем связи 5G.

Пройдет офлайн в Москве 17 ноября в 10:00.

• MATLAB
• Simulink
• САУ
• ЦОС
• ПЛИС
• МОП
• 5G
• Модельно ориентированное проектирование

30.10.2022

• Публикация
• 26.10.2022

Встраиваемые системы

Эта статья написана совместно с нашими партнерами — компанией «РИТМ».

Компания занимается разработкой полунатурных стендов и комплексов полунатурного моделирования «РИТМ», которые используются нашими заказчиками. Клиенты в некотор…

Уже много лет мы занимаемся продвижением модельно-ориентированного проектирования в России. Поэтому наш опыт сконцентрирован вокруг инструментов модельно-ориентированного проектирования — то есть различных сред моделирования и симуляции — и применения их в инженерных разработках.

• MATLAB
• Simulink
• САУ
• ЦОС
• ПЛИС
• МОП
• fpga
• экспонента
• Модельно ориентированное проектирование

26.10.2022

• Публикация
• 26.10.2022

Электропривод и силовая электроника

Основа всех трех сценариев – цифровое моделирование в режиме жесткого реального времени. Наша команда инженеров показала, что КПМ РИТМ способен решать ряд сложных задач, которые стоят перед российской энергетикой.

Мы благодарны всем гостям и всегда рады…

13 октября в нашем офисе прошел семинар. Всего за 5 часов мы обсудили, как использовать КПМ РИТМ для:

• Тестирования микропроцессорных реле;
• Построения систем мониторинга переходных режимов;
• Исследования кибер-инцидентов в электроэнергетике.

• экспонента
• микропроцессор
• электроэнергетика
• РИТМ
• энергетика

26.10.2022

• Публикация
• 26.10.2022

Электропривод и силовая электроника

Вас ждут: Заметки по созданию цифровых двойников; Полезные статьи и видео; Анонсы вебинаров и семинаров. Подписывайтесь: https://t.me/exponenta_energy

Наша команда инженеров электроэнергетики создала канал, где вы найдёте множество материалов про то, как используют машины реального времени в энергетике.

• MATLAB
• HIL
• РИТМ
• Hardware In the Loop
• Model In the Loop

26. 10.2022

• Публикация
• 25.10.2022

Глубокое и машинное обучение(ИИ), Математика и статистика

В ходе вебинара будет рассказано о существующих подходах к организации предсказательного обслуживания. Также будет продемонстрирована экспериментальная установка, состоящая из электродвигателя, передаточного механизма, нагрузки и системы датчиков. Установка мо…

Приглашаем на вебинар «Предсказание отказов в промышленности: от теории к практике», который пройдет 8 ноября в 10:00.

Предсказание отказов промышленного оборудования достигается за счёт непрерывного мониторинга и контроля состояния оборудования.

Предсказательное обслуживание призвано существенно снизить затраты на техническое обслуживание оборудование, сократить количество поломок и время просто оборудования.

• MATLAB
• Simulink
• САУ
• ЦОС
• ПЛИС
• МОП
• ИИ
• Модельно ориентированное проектирование

25.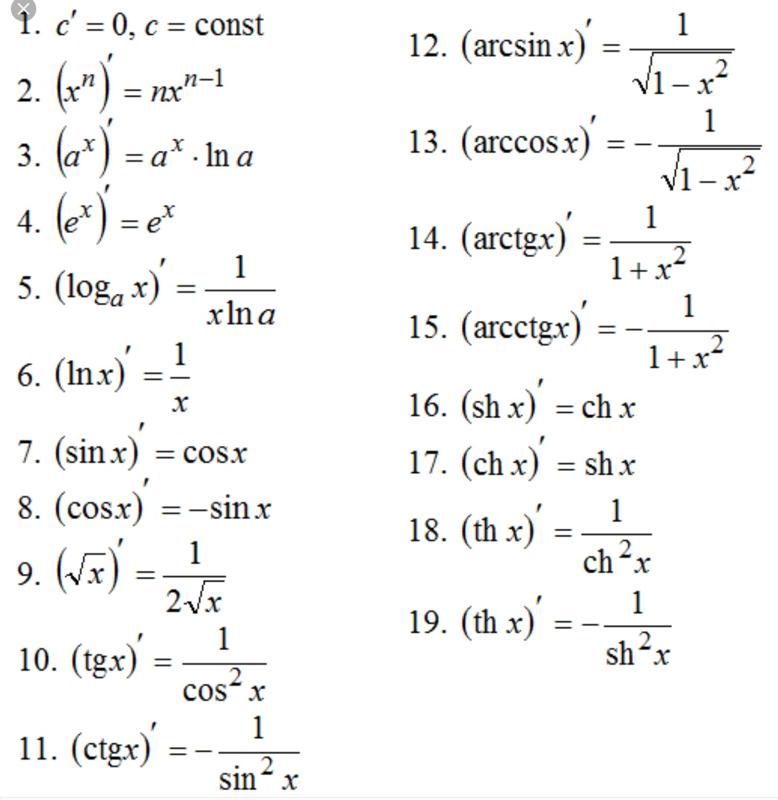 10.2022

• вопрос
• 24.10.2022

Системы связи, ПЛИС и СнК, Радиолокация, Робототехника и беспилотники, Встраиваемые системы, Цифровая обработка сигналов

Есть модуль в Симулинк детектор приамбулы. Он считает количество бит от начала на котором находится приамбула. Выдает на выходе число. Хочу это значение использовать в модуле Си но симулинк выдает оши…

Есть модуль в Симулинк детектор приамбулы. Он считает количество бит от начала на котором находится приамбула. Выдает на выходе число. Хочу это значение использовать в модуле Си но симулинк выдает оши…

• вопрос
• 19.10.2022

Математика и статистика, Цифровая обработка сигналов, Финансы

 u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка

 u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка

1 Ответ

• вопрос
• 19.10.2022

Математика и статистика, Цифровая обработка сигналов, Финансы, Другое

 u = (y³)/3 + 8xy — 9y — 4x² — 10

 u = (y³)/3 + 8xy — 9y — 4x² — 10

5 Ответов

• Публикация
• 18.
  10.2022

Другое

Введение            В настоящее время существует три основных подхода при построении криптографической системы: — алгоритмы с открытыми ключами; — симметричные алгоритмы с закрытыми ключами (блочные шифры)…

Аннотация статьи
            Разработан алгоритм генерации ключей шифрования в симметричных криптографических системах с закрытыми ключами, без использования передачи ключей по сетям связи.

            An algorithm has been developed for generating encryption keys in symmetric cryptographic systems with private keys, without using key transmission over communication networks.

           

            Ключевые слова: шифрование, симметричные криптографические системы, одноразовые блокноты, алгоритм генерации ключей, интернет вещи, (IoT), приемно-контрольные приборы.

• шифрование

18.10.2022

• Отвеченный вопрос
• 17.10.2022

Изображения и видео, Цифровая обработка сигналов, Верификация и валидация, Математика и статистика, Системы управления, Другое, Автоматизация испытаний

Здравствуйте,Необходимо смоделировать теплопередачу в емкости с водой, через которую проложена труба. Имеется разница температур жидкости в трубе и в емкости. Подскажите инструменты, статиьи, видео и…

Здравствуйте,Необходимо смоделировать теплопередачу в емкости с водой, через которую проложена труба. Имеется разница температур жидкости в трубе и в емкости. Подскажите инструменты, статиьи, видео и…

2 Ответа

• MATLAB
• теплопередача
• теплообмен

17.10.2022

U-курс

Вопрос 1: Reverse

Напиши процедуру reverse, которая принимает список lst и возвращает обращенный список.

Возможно тебе пригодится встроенная функция append.

(define (reverse lst)
    ;ТВОЙ КОД ЗДЕСЬ
    nil
)

Вопрос 2: Длиннейшая возрастающая подпоследовательность

Создай процедуру longest-increasing-subsequence, которая принимает список lst и возвращает наидлиннейшую возрастающую подпоследовательность. Элементы могут не стоять рядом в исходном списке. Например, для последовательности (1 2 3 4 9 3 4 1 10 5) наидлиннейшей возрастающей подпоследовательностью будет (1 2 3 4 9 10). Считай, что наидлиннейшая возрастающая подпоследовательность единственна для заданного списка.

Использовать встроенные процедуры length и filter — хорошая идея.

 (define (longest-increasing-subsequence lst)
    ;ТВОЙ КОД ЗДЕСЬ
    nil
)

Дифференцирование

Следующие задачи будут касаться разработки системы символьного дифференцирования алгебраических выражений. Процедура derive принимает алгебраическое выражение expr и переменную var, возвращает производную выражения expr по переменной var. Символьное дифференцирование имеет особое историческое значение для Lisp. Оно было одним из побуждающих факторов для разработки языка. Дифференцирование — рекурсивный процесс, применяющий различные правила к различным видам выражений.

; возвращает производную EXPR по VAR
(define (derive expr var)
  (cond ((number? expr) 0)
        ((variable? expr) (if (same-variable? expr var) 1 0))
        ((sum? expr) (derive-sum expr var))
        ((product? expr) (derive-product expr var))
        ((exp? expr) (derive-exp expr var))
        (else 'Error)))

Система дифференцирования использует представленные ниже абстрактные типы данных. Суммы и произведения — списки, они упрощаются в конструкторах, если это возможно.

; переменные представляются символами
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
  (and (variable? v1) (variable? v2) (eq? v1 v2)))
; числа сравниваются с помощью =
(define (=number? expr num)
  (and (number? expr) (= expr num)))
; суммы представляются списками, начинающимися с +.
(define (make-sum a1 a2)
  (cond ((=number? a1 0) a2)
        ((=number? a2 0) a1)
        ((and (number? a1) (number? a2)) (+ a1 a2))
        (else (list '+ a1 a2))))
(define (sum? x)
  (and (list? x) (eq? (car x) '+)))
(define (addend s) (cadr s))
(define (augend s) (caddr s))
; произведения представляются списками, начинающимися с *. 
(define (make-product m1 m2)
  (cond ((or (=number? m1 0) (=number? m2 0)) 0)
        ((=number? m1 1) m2)
        ((=number? m2 1) m1)
        ((and (number? m1) (number? m2)) (* m1 m2))
        (else (list '* m1 m2))))
(define (product? x)
  (and (list? x) (eq? (car x) '*)))
(define (multiplier p) (cadr p))
(define (multiplicand p) (caddr p))

Проверятель не ожидает от тебя реализации цепного правила. Хотя это было бы прикольно.

Вопрос 3: Производная суммы

Реализуй derive-sum — процедуру, которая вычисляет производную суммы, суммируя производные addend и augend. Для представления суммы используй абстрактный тип данных.

(define (derive-sum expr var)
  ;ТВОЙ КОД ЗДЕСЬ
  nil
)

Вопрос 4: Производная произведения

Реализуй процедуру derive-product, которая применяет правило произведения при вычислении производной \((f \cdot g)’ = f’ \cdot g + f \cdot g’\).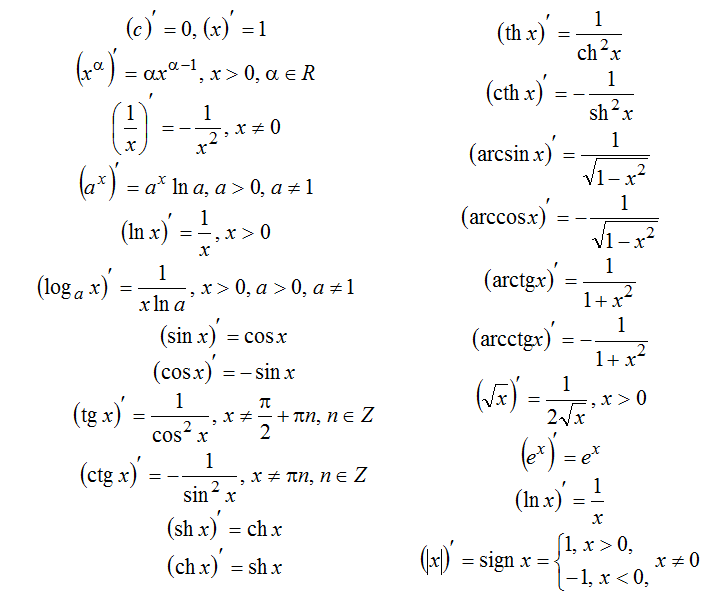 x y) 3) ‘x) обрабатывались корректно. Короче, наслаждайся!

Производная экспоненциальной функции — формула, доказательство, примеры

Прежде чем перейти к производной экспоненциальной функции , давайте вспомним концепцию экспоненциальной функции, которая определяется формулой f(x) = a ^x , a > 0. Одной из популярных форм экспоненциальной функции является f(x) = e ^x , где e — «число Эйлера», а e = 2,718…. Производная экспоненциальной функции f(x) = a ^x , a > 0 задается формулой f'(x) = a ^x ln a и производной экспоненциальной функции f(x) = e ^x определяется выражением f'(x) = e ^x .

В этой статье мы изучим понятие производной экспоненциальной функции и ее формулу, доказательство и график вместе с некоторыми решенными примерами, чтобы лучше понять.

1.	Что такое производная экспоненциальной функции?
2.	Формула производной экспоненциальной функции
3.	Производная экспоненциальной функции Доказательство
4.	График производной показательной функции
5.	Часто задаваемые вопросы о производной экспоненциальной функции

Что такое производная показательной функции?

Производная экспоненциальной функции f(x) = a ^x , a > 0 является произведением экспоненциальной функции a ^x и натурального логарифма a, то есть f'(x) = a ^х шт. Математически производная экспоненциальной функции записывается как d(a ^x )/dx = (a ^x )’ = a ^x ln a. Производная экспоненциальной функции может быть получена с использованием первого принципа дифференцирования с использованием формул пределов. График производной экспоненциальной функции меняет направление, когда a > 1 и когда a < 1.

Производная экспоненциальной функции e

^x

Теперь, когда мы знаем, что производная экспоненциальной функции определяется выражением f'(x) = ^x ln a, производная экспоненциальной функции e ^x по той же формуле будет равна e ^x ln e = e ^x (поскольку ln e = 1). Следовательно, производная показательной функции e ^x есть сама функция, то есть если f(x) = e ^x , то f'(x) = e ^x .

Формула производной экспоненциальной функции

Формула для производной экспоненциальной функции:

• f(x) = a ^x , f'(x) = a ^x ln a или d(a ^x )/dx = a ^x ln a
• f(x) = e ^x , f'(x) = e ^x или d(e ^x )/dx = e ^x

Доказательство производной экспоненциальной функции

Теперь мы докажем, что производная экспоненциальной функции a ^x равна ^x ln a, используя первый принцип дифференцирования, то есть определение пределов. Чтобы получить производную экспоненциальной функции, мы будем использовать некоторые формулы, такие как: 9x \ln a\end{align}\)

Таким образом, мы получили производную показательной функции, используя первый принцип производных.

График производной показательной функции

График показательной функции f(x) = b ^x возрастает, когда b > 1, тогда как f(x) = b ^x убывает, когда b < 1. Таким образом, график показательной функции f(x) = b ^x

• увеличивается, когда b > 1
• уменьшается, когда 0 < b < 1

Поскольку график производной показательной функции представляет собой функцию наклона касательной к графику показательной функции, поэтому график производной показательной функции f(x) = b ^x возрастает при b > 0. Даны ниже приведен график экспоненциальной функции и график производной экспоненциальной функции для b > 1 и 1 < b < 1.0176

• Экспоненциальная функция f(x) = a ^x не определена для a < 0, как и производная экспоненциальной функции.
• d(a ^x )/dx = a ^x ln a
• d(е ^х )/dx = е ^х

Связанные темы по производной экспоненциальной функции

• Экспоненциальная функция
• Производная от ln x
• Производная cos x

Часто задаваемые вопросы о производной экспоненциальной функции

Что такое производная показательной функции?

Производная экспоненциальной функции f(x) = a ^x , a > 0 является произведением экспоненциальной функции a ^x и натурального логарифма a, то есть f'(x) = a ^x Л.А.

Что такое производная экспоненциальной функции e

^x ?

Производная экспоненциальной функции e ^x есть сама функция, то есть если f(x) = e ^x , тогда f'(x) = e ^x .

Почему производная экспоненциальной функции сама по себе равна

^x ?

Производная экспоненциальной функции a ^x определяется выражением f'(x) = a ^x ln a. Мы знаем, что ln e = 1, и если a = e, то производная экспоненциальной функции e ^x определяется как e ^x ln e = e ^x

Как найти n-ю производную экспоненциальной функции e

^x ?

Поскольку первая производная показательной функции e ^x равно e ^x , поэтому, если мы продифференцируем его дальше, производная всегда будет e ^x . Следовательно, n-я производная от e ^x равна e ^x .

Является ли производная экспоненциальной функции e

^x экспоненциальной функцией?

Да, производная экспоненциальной функции e ^x является самой экспоненциальной функцией e ^x .

Что такое общая производная показательной функции?

Общая производная показательной функции a ^x задается ^x ln a.

Производные экспоненциальных функций

На этой странице мы рассмотрим, как дифференцировать экспоненциальные функции.