Решите неравенство x2 3x 0: Mathway | Популярные задачи

{2}-4*2*4=81-32=49 $$
$$ x_{1,2}= \frac{-b+- \sqrt{D} }{2a} $$
$$ x_{1,2}= \frac{9+-7}{4};\\ x_{1}= \frac{9+7}{4}= \frac{16}{4}=4;\\ x_{2}= \frac{9-7}{4}= \frac{2}{4}=0,5 $$
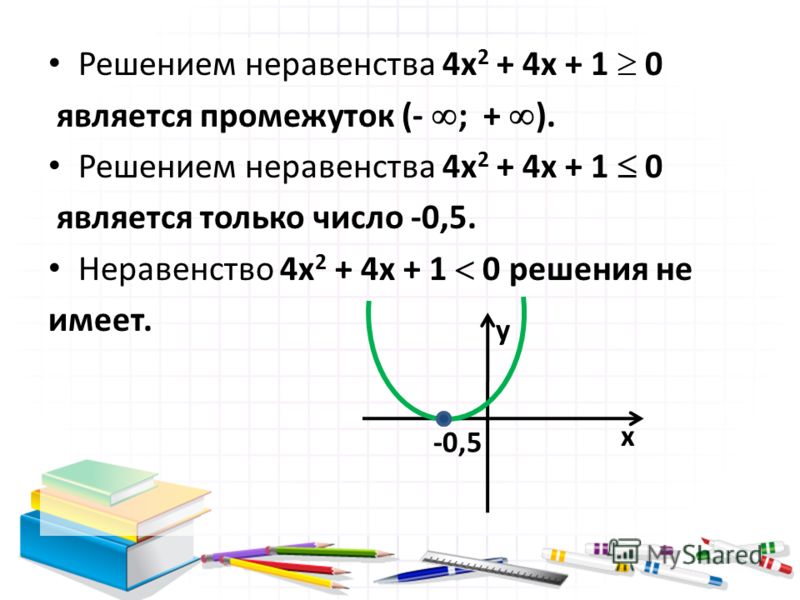
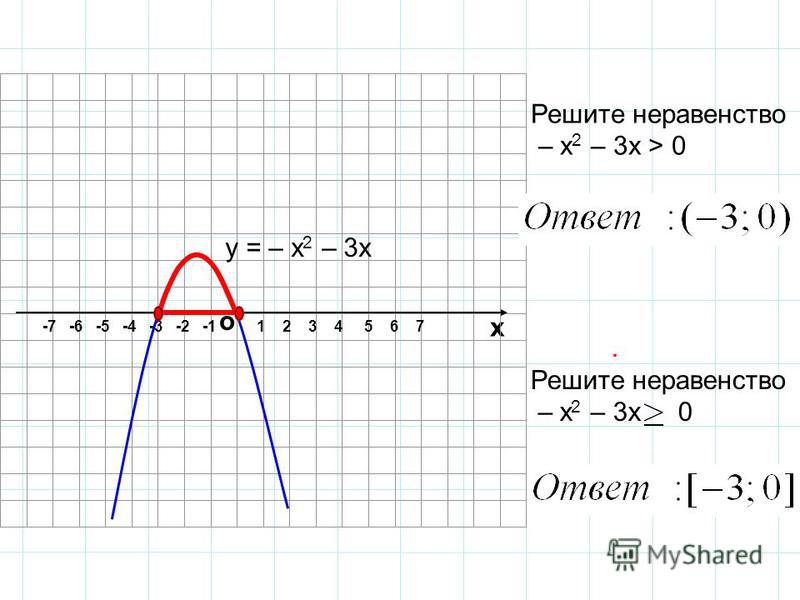
На интервале до 0,5 включительно значение функции положительно
На интервале [0,5;4] значение функции отрицательно
На интервале от 4 значение функции положительно. Т.е. ответом будут интервалы от (-бесконечности, 0,5] и от [4,+бесконечности]

1 2 > >>

Содержание

Решение неравенств второй степени с одной переменной. Подготовка к ОГЭ. 9-й класс

Ключевые слова: неравенства второй степени, ОГ, квадратные неравенства

Тип урока: урок обобщения и систематизации знаний.

Цели урока:

Обобщить и систематизировать знания учащихся по данной теме;
Закрепить навыки и умения решения неравенств с использованием графика квадратичной функции и методом интервалов;

Развить логическое мышление, навыки работы с графиками;
Сформировать умение четко и ясно излагать свои мысли.

Ход урока

I. Организационный момент

Приветствие учителя и учащихся. Ознакомление с целями и задачами урока.

II. Актуализация опорных знаний и умений учащихся

1. Фронтальная беседа с классом

— Какая функция называется квадратичной?

— Как называется график квадратичной функции?

— Как определить направление ветвей параболы?

— Как разложить квадратный трехчлен на множители?

— Как найти нули функции?

— От чего зависит количество корней квадратного уравнения?

— Приведите примеры неравенств второй степени.

— Что является решением неравенства?

— Что значит решить неравенство?

2. Устная работа

а) Решите уравнения:

x² — 64 = 0
x² + 9 = 0
3 x² = 300
(x – 7)(
x + 1,3) = 0
x² + x – 12 = 0
x² — 3x = 0

б) Найдите число корней уравнения ax² + bx + c = 0

в) Найдите промежутки, в которых функция y > 0

III. Решение неравенств

Прежде чем перейти к следующему этапу урока, давайте вспомним алгоритм решения неравенств методом интервалов и алгоритм решения неравенств второй степени через график квадратичной функции.

№1.

– x² – x + 12 0

1) Рассмотрим функцию y = – x² – x + 12

2) График функции – парабола, ветви направлены вниз (а = –1)

3) Найдем нули функции:

– x² – x + 12 = 0

x₁ = -4, x₂ = 3

4) Схематически построим график функции и выделим ту часть параболы, для которой

y 0.

5) Запишем ответ в виде промежутка

Ответ: [–4; 3]

№2.

< 0

Дробь отрицательна тогда, когда числитель и знаменатель имеют разные знаки.

-14 < 0

Следовательно, выражение x² + 2x –15 > 0

1) Рассмотрим функцию y = x² + 2x – 15

2) График функции – парабола, ветви направлены вверх (а = 1)

3) Нули функции:

x² + 2x – 15 = 0

x₁ = –5, x₂= 3

4) Схематически построим график функции и выделим ту часть параболы, для которой y > 0.

Ответ: (–; –5) U (3; +)

№3.

(x + 7)(4 – x) 0

1) Рассмотрим функцию

y = (x + 7)(4 – x)

2) Найдем нули функции:

(x + 7)(4 – x) =0

x₁ = -7; x₂ = 4

3) Отметим на оси абсцисс нули функции, определим знаки выражения на каждом промежутке, выделим промежутки, в которых функция y 0

Ответ: (–; -7] U [4; +)

№4.

x² > 121

x² – 121 > 0

(x – 11)(x +11) > 0

1) Рассмотрим функцию y = (x – 11)(x +11)

2 Нули функции: x₁ = –11, x =₂11

3) Отметим на оси абсцисс нули функции, определим знаки выражения на каждом промежутке, выделим промежутки, в которых функция y > 0

Ответ: (–; –1) U (11;+)

№5.

(x – 7)² < (x – 7)

Преобразуем данное неравенство

(x – 7)² -(x – 7) < 0

Разложим левую часть неравенства на множители
(x – 7)(x – 7 –) < 0
1) Рассмотрим функцию y = (x – 7)(x – 7 –)

2) Нули функции: x₁ = 7, x₂ = 7 +

3) Отметим на оси абсцисс нули функции, определим знаки выражения на каждом промежутке, выделим промежутки, в которых функция y < 0

Ответ: (7; 7+)

№6.

0
Разложим квадратный трехчлен x² – x – 6 на множители:

x² – x – 6 = (x – 3)(x + 2)

1) Рассмотрим функцию y =

2) Нули функции: x = 1, x = 2, x = –2, x = 3

ОДЗ: x ≠1, x≠0, x≠–1

Ответ: (-1;0) U (0;1) U (1;2] U [3;+)

IV. Самостоятельная работа с самопроверкой

Решите неравенства:

V. Итог урока

Сегодня мы вспомнили некоторые способы решения неравенств второй степени. На следующем уроке мы будем решать системы неравенств с одной переменной.

VI. Домашнее задание

Сборник ОГЭ № 8, №21 (варианты 9, 13, 17, 18, 22, 25, 28).

Логарифмические неравенства — подготовка к ЕГЭ по Математике

Решая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы.

Давайте повторим, что такое логарифмы:

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

При этом

Основное логарифмическое тождество:

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)

(Формула для логарифма степени)

Формула перехода к новому основанию:

Алгоритм решения логарифмических неравенств

Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию.

И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения .

Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение

Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов.

Перейдем к практике. Как всегда, начнем с самых простых неравенств.

1. Рассмотрим неравенство log₃x > log₃5.
Поскольку логарифмы определены только для положительных чисел, необходимо, чтобы x был положительным. Условие x > 0 называется областью допустимых значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.

Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!»

Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать?

Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно.

Так почему же мы все-таки «отбрасываем логарифмы»?

Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log

3x₁ > log₃x₂ следует, что x₁ > x₂.

Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства при этом — сохраняется.

Итак, x > 5.

Следующее логарифмическое неравенство тоже простое.

2. log₅(15 + 3x) > log₅2x

Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому

Решая эту систему, получим: x > 0.

Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется.

15 + 3x > 2x.

Получаем: x > −15.

Итак,

Ответ: x > 0.

А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться.

Приведем пример.

Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть

Решая эту систему, получим: x > 4,5.

Поскольку , логарифмическая функция с основанием монотонно убывает. А это значит, что большему значению функции отвечает меньшее значение аргумента:

И если , то
2x − 9 ≤ x.

Получим, что x ≤ 9.

Учитывая, что x > 4,5, запишем ответ:

x ∈ (4,5; 9].

В следующей задаче логарифмическое неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить.

Теперь более сложные неравенства:

4. Решите неравенство

Ответ:

5. Решите неравенство

ОДЗ:

Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ.

Сделаем замену

Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!

Ответ:

Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:

Упростим эту систему:

Это область допустимых значений неравенства.

Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что

В данном случае удобно перейти к основанию 4.

Сделаем замену

Упростим неравенство и решим его методом интервалов:

Итак,

Вернемся к переменной x:

Мы добавили условие x > 0 (из ОДЗ).

Ответ:

7. Следующая задача тоже решается с помощью метода интервалов

Как всегда, решение логарифмического неравенства начинаем с области допустимых значений. В данном случае

Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:

Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:

Видим, что условие (то есть ОДЗ) теперь выполняется автоматически. Что ж, это упрощает решение неравенства.

Решаем неравенство методом интервалов:

Ответ:

Получилось? Что же, повышаем уровень сложности:

8. Решите неравенство:

Неравенство равносильно системе:

Ответ:

9. Решите неравенство:

Выражение 5^—x²навязчиво повторяется в условии задачи. А это значит, что можно сделать замену:

Поскольку показательная функция принимает только положительные значения, t > 0. Тогда

Неравенство примет вид:

Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, (t − 3) (5⁹ · t − 1) > 0

Если это условие выполнено, то и частное будет положительным.

А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625t − 2)².

Это означает, что 625t − 2 ≠ 0, то есть

Аккуратно запишем ОДЗ

и решим получившуюся систему, применяя метод интервалов.

Итак,

Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения:

«Отбросим» логарифмы. Знак неравенства сохраняется.

Перенесем все в левую часть и разложим по известной формуле разности квадратов:

Вспомним, что (это ОДЗ неравенства) и найдем пересечение полученных промежутков.

Получим, что

Вернемся к переменной x

Поскольку

Ответ:

10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.

Запишем ОДЗ:

Воспользуемся формулой и перейдем к основанию 10:

Применим обобщенный метод интервалов. Выражение в левой части неравенства можно записать как функцию

Эта функция может менять знак в точках, где она равна нулю или не существует.

Выражение lg |x − 3| равно нулю, если |x − 3| = 1, то есть x = 4 или x = 2.

Выражение lg (|x| − 2) равно нулю, если |x| = 3, то есть в точках 3 и −3.

Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.

Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.

Ответ:

11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.

Запишем ОДЗ:

Итак, Это ОДЗ.

Обратите внимание, что .

Это пригодится вам при решении неравенства.

Упростим исходное неравенство:

Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x < 18.

Как же быть? Вспомним, что (x — 18)²=(18 — x)². Тогда:

Вторая ловушка – попроще. 2-2*x)+(7*x-19)*1/(x-3)<=(8*x+1)*1/x

Решение:

* 5 * 5 * 5 * 5 * 5 *

Удачи тебе на экзаменах! У тебя всё получится — мы в тебя верим!

Поделись этой информацией с помощью кнопок ниже (облегчи учёбу другим ученикам, и будет тебе плюс в карму!)

Задание 15 № 507658

Решите неравенство

Решение.

Сделаем замену: Тогда

Неравенство принимает вид: откуда

Это неравенство выполняется тогда и только тогда, когда Получаем:

Ответ:

Примечание.

Задача допускает решение без замены переменной: тождественными преобразованиями данное неравенство приводится к откуда также получается ответ

Задание 15 № 508212

Решите неравенство:

Решение.

Используя метод интервалов, получаем:

Ответ:

Задание 15 № 507491

Решите неравенство:

Решение.

Перепишем неравенство в виде:

Множество решений исходного неравенства:

Ответ:

Задание 15 № 508213

Решите неравенство:

Решение.

Используя метод интервалов, получаем:

Ответ:

Задание 15 № 508345

Решите неравенство:

Решение.

Приведём выражение к общему знаменателю:

Предпоследнее преобразование верно, так как модуль не может принимать отрицательных значений.

Получаем или

Ответ:

Задание 15 № 508347

Решите неравенство:

Решение.

Пусть получаем:

Возвращаясь к исходной переменной, получаем: или

Ответ:

Задание 15 № 508348

Решите неравенство:

Решение.

Сделав замену получаем:

Возвращаясь к исходной переменной, получаем:

Ответ:

Задание 15 № 508355

Решите неравенство:

Решение.

Преобразуем неравенство:

Решения неравенства: или

Ответ:

Задание 15 № 508360

Решите неравенство:

Решение.

Решим неравенство методом интервалов:

Ответ:

Задание 15 № 508364

Решите неравенство:

Решение.

Решим первое неравенство:

Ответ:

Задание 15 № 508367

Решите неравенство:

Решение.

Решим неравенство методом интервалов:

Ответ:

Задание 15 № 508371

Решите неравенство:

Решение.

Решим неравенство методом интервалов:

Ответ:

Задание 15 № 508381

Решите неравенство:

Решение.

Решим второе неравенство:

Ответ:

Задание 15 № 508429

Решите неравенство:

Решение.

Сделав замену получаем:

Значит, и

Ответ:

Задание 15 № 508432

Решите неравенство:

Решение.

Решим неравенство методом интервалов:

Ответ:

Задание 15 № 508434

Решите неравенство:

Решение.

Решим неравенство методом интервалов:

Ответ:

Задание 15 № 508442

Решите неравенство:

Решение.

По теореме Виета, сумма корней уравнения равна , а их произведение равно Поэтому корни этого уравнения — числа и Тогда неравенство можно решить так:

Ответ:

Задание 15 № 508447

Решите неравенство:

Решение.

Преобразуем неравенство:

Ответ:

Задание 15 № 508449

Решите неравенство:

Решение.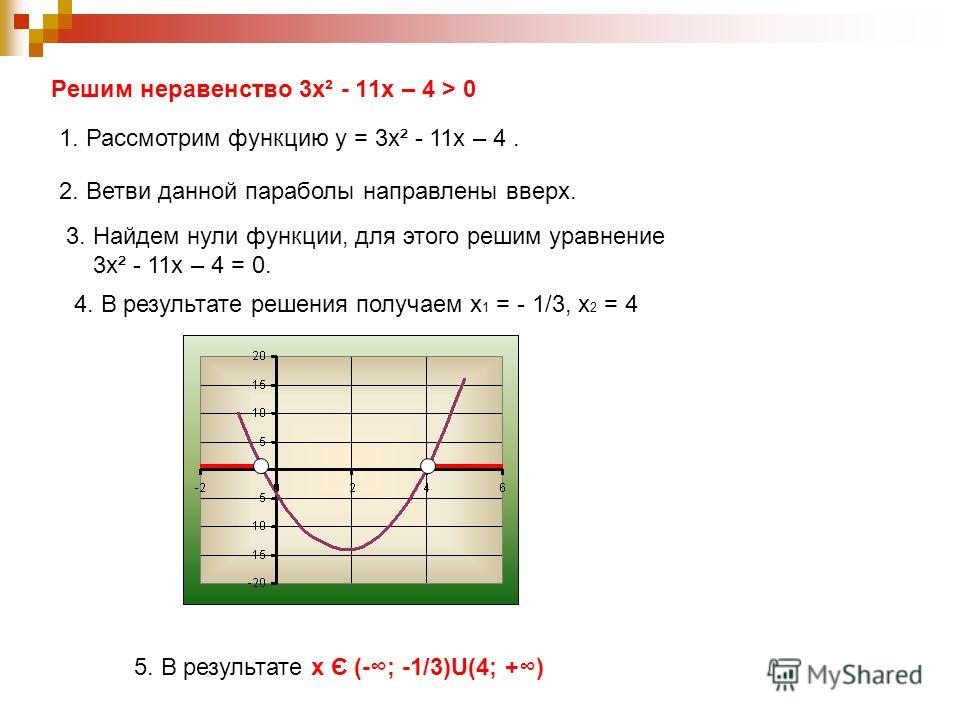

Заметим, что поэтому неравенство выполнено при всех , кроме и

Ответ:

Задание 15 № 508530

Решите неравенство:

Решение.

Последовательно получаем:

Ответ:

Задание 15 № 512484

Решите неравенство

Решение.

Преобразуем неравенство:

Учитывая, что при всех значениях x выражение x² + 3 положительно, получаем

откуда

Ответ:

Задание 15 № 507203

Решите неравенство

Решение.

Сделаем замену Получим

Следовательно,

Ответ:

Задание 15 № 515707

Решите неравенство

Решение.

Решим неравенство:

Ответ:

Задание 15 № 516402

Решите неравенство

Решение.

Преобразуем неравенство:

Ответ:

Задание 15 № 521996

Решите неравенство

Решение.

Решим неравенство методом интервалов:

откуда и

Ответ:

Задание 15 № 522124

Решите неравенство

Решение.

Решим неравенство методом интервалов:

откуда и

Ответ:

Задание 15 № 523996

Решите неравенство

Решение.

Сделаем замену Получим:

Отсюда после обратной замены получаем:

Ответ:

Задание 15 № 526726

Решите неравенство

Решение.

Преобразуем неравенство:

Решая полученное неравенство методом интервалов (см.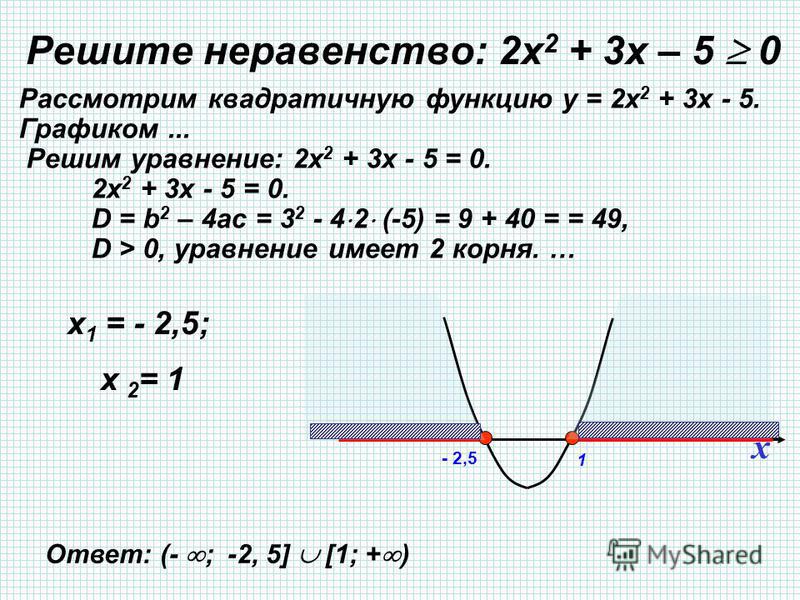 рис.), находим ответ:

Ответ:

Задание 15 № 530384

Решите неравенство:

Решение.

Заметим, что Применим эту формулу к каждому слагаемому левой части, получим:

Ответ:

Задание 15 № 530457

Решите неравенство

Решение.

Запишем исходное неравенство в виде:

Ответ:

Задание 15 № 530674

Решите неравенство

Решение.

Запишем исходное неравенство в виде:

Ответ:

Задание 15 № 530701

Решите неравенство:

Решение.

Разложим разность по формуле разности кубов, получим:

Вынесем в знаменателе общий множитель за скобки:

Ответ:

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратные неравенства – объяснение и примеры

Подобно тому, как уравнения имеют разные формы, неравенства также существуют в разных формах, и квадратное неравенство является одним из них.

Квадратное неравенство — это уравнение второй степени, в котором вместо знака равенства используется знак неравенства.

решений квадратного неравенства всегда дают два корня. Природа корней может быть разной и определяется дискриминантом (b ² – 4ac).

The general forms of the quadratic inequalities are:

ax ² + bx + c < 0

ax ² + bx + c ≤ 0

ax ² + bx + c > 0

AX ² + BX + C ≥ 0

Примеры квадратичных неравенств:

x ² — 6x — 16 ≤ 0, 2x ² — 11x + 12> 0, x ^{2 ² — 11x + 12> 0, x ^{2 ² — 11x + 12> 0, x ^{2 ² — 11x + 12> 0, x ^{2 ² — 11x + 12> 0, x ^{2 ² — 110918 0, x ² – 3x + 2 ≤ 0 и т. д.}}}}}

Как решать квадратные неравенства?

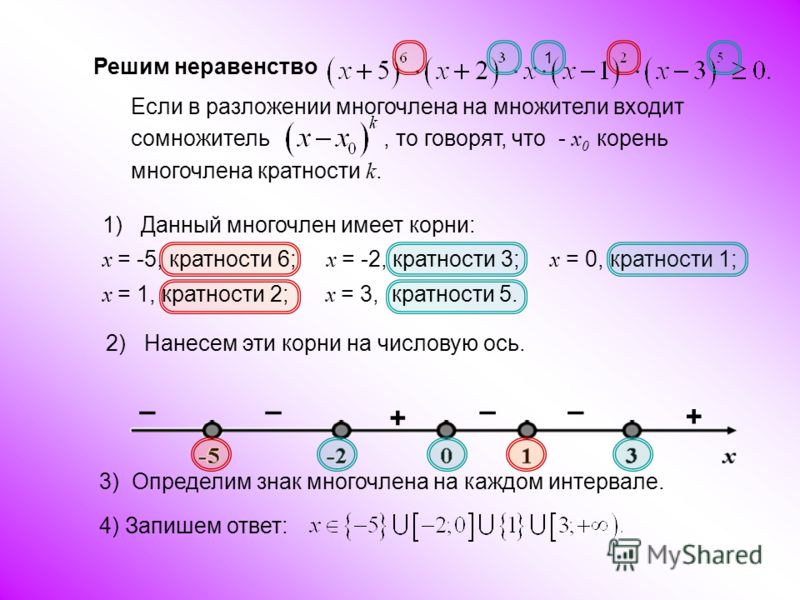
Примеры квадратных неравенств: 0 и т. д.

Решение квадратного неравенства в Алгебре аналогично решению квадратного уравнения. Единственным исключением является то, что с квадратными уравнениями вы приравниваете выражения к нулю, но с неравенствами вам интересно знать, что находится по обе стороны от нуля, то есть отрицательные и положительные.

Квадратные уравнения могут быть решены либо с помощью метода факторизации , либо с использованием квадратичной формулы . Прежде чем мы научимся решать квадратные неравенства, давайте вспомним, как решаются квадратные уравнения, на нескольких примерах.

Как решаются квадратные уравнения методом факторизации?

Поскольку мы знаем, что можем решать квадратные неравенства так же, как и квадратные уравнения, полезно понять, как разложить данное уравнение или неравенство на множители.

Давайте рассмотрим здесь несколько примеров.

6x ² — 7x + 2 = 0

Решение

⟹ 6x ² — 4x — 3x + 2 = 0

090907;

⟹ 2x (3x – 2) – 1 (3x – 2) = 0

⟹ (3x – 2) (2x – 1) = 0

⟹ 3x – 2 = 0 или 2x – 1 = 0

⟹ 3x = 2 или 2x = 1

⟹ x = 2/3 или x = 1/2

Следовательно, x = 2/3, ½

Решите 3x ² – 6x + 4x – 8 = 0

Решение

Факторизируйте выражение в левой части.

⟹ 3x ² – 6x + 4x – 8 = 0

⟹ 3x (x – 2) + 4(x – 2) = 0

⟹ (x – 2) (3x + 4) = 0

⟹ x – 2 = 0 или 3x + 4 = 0

⟹ x = 2 или x = -4/3

Следовательно, корни квадратного уравнения: x = 2, -4/3.

Решение 2(x ² + 1) = 5x

Решение

2x ² + 2 = 5x

⟹ 2x ² — 5x + 2 = 0

⟹ 2x ² — 4x — x + 2 = 0

. x – 2) = 0

⟹ (x – 2) (2x – 1) = 0

⟹ x – 2 = 0 или 2x – 1 = 0

⟹ x = 2 или x = 1/2

Следовательно , решения x = 2, 1/2.

(2x – 3) ² = 25

Решение

Разверните выражение и разложите его на множители.

(2x – 3) ² = 25

⟹ 4x ² — 12x + 9 — 25 = 0

⟹ 4x ² — 12x — 16 = 0

⟹ x ² — 3 = 4 – 4 – 4 – 4 – 40

⟹ ² — 3 – 40

⟹ ² — 3 = 0

⟹ x ² — 3 = 0

⟹ ^{— x – 4) (x + 1) = 0}

⟹ x = 4 или x = -1

Решить x ² + (4 – 3y) x – 12y = 0

Развернуть

96 уравнение;

x ² + 4x – 3xy – 12y = 0

Разложить на множители;

⟹ х (х + 4) – 3у (х + 4) = 0

х + 4) (х – 3у) = 0

⟹ x + 4 = 0 или x – 3y = 0

⟹ x = -4 или x = 3y

Таким образом, x = -4 или x = 3y

Для решения квадратного неравенства также применим тот же метод, который показан в процедуре ниже:

Запишите квадратное неравенство в стандартной форме: ax ² + bx + c, где a, b и — коэффициенты, а a ≠ 0
Определите корни неравенства.
Запишите решение в виде неравенства или в виде интервала.
Если квадратное неравенство имеет вид: (x – a) (x – b) ≥ 0, то a ≤ x ≤ b, а если оно имеет вид: (x – a) (x – b) ≤ 0, когда a < b, то a ≤ x или x ≥ b.

Пример 1

Решение неравенства x ² — 4x> –3

раствор

, первой, сделай один рад один Zeeper -neafice. x ² – 4x > –3 ⟹ x ² – 4x + 3 > 0

Фактор левой части неравенства.

x ² – 4x + 3 > 0 ⟹ (x – 3) (x – 1) > 0

Найдите все нули в неравенстве;

При (x – 1) > 0 ⟹ x > 1 и при (x – 3) > 0 ⟹ x>3

Поскольку y положителен, мы выбираем значения x, при которых кривая будет выше ось х.
x < 1 или x > 3

Пример 2

Решите неравенство x ² – x > 12,

Решение

Чтобы записать неравенство в стандартной форме, вычтите обе части неравенства на 12. квадратное неравенство, к которому нужно добраться;

( x – 4) ( x + 3) > 0

Найдите все нули неравенства;

Для (x + 3) > 0 ⟹ x > -3

Для x – 4 > 0 ⟹ x > 4

Таким образом, значения x < –3 или x > 4 являются решением этого квадратного неравенства.

Пример 3

Решите 2x ² < 9x + 5

Решение

Запишите неравенство в стандартной форме, представив одну часть неравенства.

2x ² < 9x + 5 ⟹ 2x ² – 9x – 5 < 0

Фактор левой части квадратного неравенства.

2x ² – 9x – 5 < 0 ⟹ (2x + 1) (x – 5) < 0

Найдите все нули для неравенства

Для (x – 5) < 0 ⟹ x < 5 и для (2x + 1) < 0 ⟹ x < -1/2

Поскольку y отрицательно для уравнения 2x ² – 9x – 5 < 0 , поэтому мы выбираем значения x, при которых кривая будет ниже оси x.

Следовательно, решение составляет -1/2

Пример 4

Решай-x ² + 4 <0.

Решение 9

. Уже к Actordally. форме, поэтому мы факторизуем выражение.

-x ² + 4 < 0 ⟹ (x + 2) (x – 2) < 0

Найдите все нули для неравенства

Для, (x + 2) < 0 ⟹ x < -2 и для (x – 2) < 0 ⟹ x < 2

Y для –x ² + 4 < 0 отрицательно; поэтому выбираем значения x, при которых кривая будет ниже оси x: –2 < x > 2

Решение

Фактор квадратного уравнения. (2) (x + 3) = 0

Для, 2x – 5 = 0 ⟹ x = 5/2 и для, x + 3= 0 ⟹ x = -3

Так как y для 2x ² + x − 15 ≤ 0 является отрицательным, мы выбираем значения x, при которых кривая будет ниже оси x. Следовательно, x ≤ -3 или x ≥ 5/2 является решением.

Пример 6

Решить – x ² + 3x − 2 ≥ 0

Решение

Умножьте квадратное уравнение на -1 и не забудьте изменить знак.

x ² – 3x + 2 = 0

x ² – 1x – 2x + 2 = 0

x (x – 1) – 2(x – 1) = 0

6 (x –

6) (x – 1) = 0

Для, x – 2 = 0 ⟹ x = 2 и для, x – 1= 0 ⟹x=1

Следовательно, решение квадратного неравенства 1 ≤ x ≤ 2

Пример 7

Решить x ² − 3x + 2 > 0

Решение

Разложить выражение на множители, чтобы получить;

x ² − 3x + 2 > 0 ⟹ (x − 2) (x − 1) > 0

Теперь найдите корни неравенства как;

(x − 2) > 0 ⟹ x > 2

(x − 1) > 0 ⟹x > 1

Кривая для x ² − 3x + 2 > 0 имеет положительный y, поэтому какие значения выбрать x, при котором кривая будет выше оси x. Следовательно, решение таково: x < 1 или x > 2.

Пример 8

Решение −2x ² + 5x + 12 ≥ 0

Раствор

Multiply. + 12 ≥ 0 ⟹2x ² − 5x − 12 ≤ 0

Разложите выражение на множители, чтобы получить;

(2x + 3) (x − 4) ≤ 0.

Найдите корни;

(2x + 3) ≤ 0 ⟹ x ≤ -3/2.

(x − 4) ≤ 0 ⟹ x ≤ 4.

Применяя правило; (x – a) (x – b) ≥ 0, то a ≤ x ≤ b, мы можем удобно записать решения этого квадратного неравенства в виде:

-3/2 ≤ x ≤ 4.

Пример

x ² -x -6 <0

Solution

0
0
0
0
0
0
0
0
0
0909тели
^.
(x + 2) (x − 3) < 0
Найдите корни уравнения как;
(x + 2) (x − 3) = 0
x = −2 или x = +3
Поскольку y отрицательно для x ² − x − 6 < 0, то мы выбираем интервал, в котором кривая будет ниже оси x. Следовательно, -2 < x < 3 является решением.
Решение неравенств: обзор
Вернуться к Указатель уроков  | Делайте уроки в заказе | Подходит для печати страница
Решение Неравенства: обзор (стр. 2 из 3)
Секции: линейные неравенства, Квадратные неравенства, Другое неравенства
Предыдущие неравенства называются «линейными» неравенствами, потому что мы имеем дело с линейные выражения типа « x 2″ (« x > 2 дюйма это просто « х 2 > 0″, перед вы закончили ее решать). Когда мы имеем неравенство с » x ² » как член высшей степени, он называется «квадратичным неравенством». Способ решения сложнее.
Решить x ² 3 x + 2 > 0
Сначала я должен найти x- перехватывает связанного квадратичного, потому что точки пересечения находятся там, где г = х ² 3 x + 2 равно до нуля. Графически подобное неравенство просит меня найти, где график находится выше или ниже оси x . Проще всего найти, где на самом деле пересекает ось x , так что я начну там.
Факторинг, Я получаю х ² 3 х + 2 = ( х 2)
( х 1) = 0, поэтому x = 1 или х = 2. Тогда график пересекает ось x в 1 и 2, а числовая ось разбита на интервалы (отрицательная бесконечность, 1), (1, 2), и (2, положительная бесконечность). Между х -перехватов, график либо выше оси (и, следовательно, положителен, либо больше, чем ноль), либо ниже оси (и, следовательно, отрицательный, или меньше нуля).
Есть два разных алгебраические способы проверки этой положительности или отрицательности на интервалы. Я покажу оба.
1) Метод контрольных точек. Интервалы между x -перехватами (отрицательная бесконечность, 1), (1, 2), и (2, положительная бесконечность). Я выберу точку (любую точку) внутри каждого интервала. Я посчитаю значение и в таком случае. Каким бы ни был знак этого значения, это знак за весь этот интервал.
Для (отрицательная бесконечность, 1), скажем, я выбираю х = 0; тогда у = 0 0 + 2 = 2, что положительный. Это говорит о том, что и положительно на всем интервале (отрицательная бесконечность, 1), и этот интервал, таким образом, является частью решения (поскольку я ищу решение «больше нуля»).
Для интервала (1, 2), я выберу, скажем, х = 1,5; затем г = (1,5) ² 3(1,5) + 2 = 2,25 4,5 + 2 = 4,25 4,5 = 0,25, что отрицательно. Затем и отрицательно на всем этом интервале, и тогда этот интервал не является частью решения.
Для интервала (2, положительная бесконечность), я выберу, скажем, x = 3; затем и = (3) ² 3(3) + 2 = 99 + 2 = 2, что положителен, и тогда этот интервал является частью решения. Тогда полное решение неравенства x < 1 и x > 2. Это решение указывается по-разному:
Частное решение формат, который вы используете, будет зависеть от вашего текста, вашего учителя и вашего вкуса. Каждый формат одинаково действителен. Авторские права Элизабет Стапель 1999-2011 Все права защищены
2) Факторный метод. Факторинг, I получить у = х ² 3 x + 2 = ( х 2)( х 1). теперь буду считать каждый из этих факторов в отдельности.
Фактор x 1 положительный для х > 1; аналогично, x 2 положительно для х > 2. Оглядываясь назад когда я впервые узнал о негативных цифры, я знаю что (плюс)(плюс) = (плюс), (минус)(минус) = (плюс) и (минус)(плюс) = (минус). Итак, чтобы вычислить знак и = х ² 3 х + 2, я только очень необходимо знать знаки факторов. Тогда я смогу применить то, что знаю про умножение минусов.
Первый, Я настроил сетку, показывающую факторы и числовую линию.
Сейчас Я отмечаю интервалы, в которых каждый фактор положителен.
Где факторы не положительные, они должны быть отрицательными.
Сейчас Я умножаю столбцы, чтобы вычислить знак и . на каждом интервале.
Тогда решение x ² 3 x + 2 > 0 являются два интервала со знаком «плюс»:
(отрицательный бесконечность, 1) и (2, положительная бесконечность).
Решить 2 x ² + 5 x + 12 < 0 .
Сначала я нахожу нули, которые являются конечными точками интервалов: г = 2 х ² + 5 х + 12 =
(2 х 3)( х 4) = 0 для x = ³ / ₂ и х = 4. Таким образом, конечные точки интервалов будет ³ / ₂ и 4. Интервалы находятся между конечными точками, поэтому интервалы (отрицательные бесконечность, ³ / ₂ ], [ ³ / ₂ , 4] и [4, положительная бесконечность). (Обратите внимание, что я использую скобки для конечных точек в неравенствах «или равно» вместо скобок, потому что конечные точки будут включены в окончательное решение.)
Чтобы найти интервалы где и отрицательно по методу контрольных точек, я просто выбираю точку в каждом интервале. Я могу использовать такие точки, как х = 2, х = 0 и x = 5.
Чтобы найти интервалы где и является отрицательным по факторному методу, я просто решаю каждый фактор: 2 x 3 положительно для 2 x 3 > 0, 3 > 2 x , 3/2 > x , или x < ³/₂ ; и х 4 положительно для х 4 > 0,
x > 4. Потом заполняю сетку:

Тогда решение это неравенство равно всем x в
(отрицательный бесконечность, ³ / ₂ ] и [4, положительная бесконечность) .
<< Предыдущая Топ | 1 | 2 | 3 | Возвращаться к индексу Далее >>
Процитировать эту статью как:
Стапель, Элизабет. «Решение неравенства: обзор». Пурпурная математика . Доступно по номеру
     https://www.purplemath.com/modules/ineqsolv2.htm . Доступ [Дата] [Месяц] 2016

«Домашнее задание
» Руководство»
Опрос по обучению
Репетиторство от Purplemath
Найдите местного репетитора по математике
Solve the inequality x² — 3x -18 > 0
Expression
Equation
Inequality
Contact us
Simplify
Factor
Expand
GCF
LCM
Solve
График
Система
Решение
График
Система
Математический решатель на вашем сайте
Наши пользователи:
Большое спасибо за вашу постоянную помощь и поддержку. Ты сказал, что будешь со мной, пока не решишь проблему, и ты это сделал. Я действительно ценю твою помощь. Мне очень нравится программа, и я с нетерпением жду, чтобы изучить ее хорошо. Мои комплименты вашей компании за наличие компетентного персонала технической поддержки, который готов сделать все возможное в решении проблем с программным обеспечением.
Бриттани Питерс, Северная Каролина
Это программное обеспечение отлично помогло мне с моими фракциями. Что-то, с чем я боролся годами. Я попросил родителей о помощи, но они говорят, что вся математика сейчас выглядит иначе, чем когда они учились в школе. Теперь мне не нужно больше спрашивать, потому что программа все объясняет.
Томми Хоброкен, Вайоминг
У меня двое детей, которые являются средними учениками. Они хорошо успевают по большинству предметов, но математика всегда ставит их в тупик. Они нашли вашу программу по алгебре похожей на домашнего репетитора. Я рад сообщить, что их оценки наконец-то повысились.
Хульета Куэльяр, PN
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
г.
Поисковые фразы, использованные 03.05.2014:
вопросы по алгебре ged
mcdougal littell курс математики l (Индиана) 6 класс
решатель полиномов
сложение и вычитание целых листов
трехчлен+факторинг онлайн калькулятор
коэффициент разности математических решателей
правила алгебры в колледже
ответов для книги Glencoe McGraw-Hill California Algebra 2
дробей в степени
система двух уравнений с двумя переменными рабочий лист
год 7 орфографических листов
Предварительная алгебра Зал для учеников
ти-84 плюс эмулятор
быстро выучить алгебру в колледже
решатель упрощающих полиномов
Решение разности частных
картинок вопросов по алгебре
коэффициенты калькулятора уравнений
добавление рабочего листа 9 вычитания целых чисел0990
рабочие листы по геометрии для десятиклассников
рабочая тетрадь по математике для учеников холла номер 0130504750
процентных уравнений
дистрибутив предварительной алгебры
саксонская алгебра 1 лист
11 экзаменационных работ по математике
ПЛАН УРОКА ДЛЯ ЭКСПОНЕНТОВ
как решать уравнения в кубе
рабочих листов по алгебре с решениями
Предварительная алгебра, 5-е издание Чарльза П. МакКега
Рабочие листы по английскому языку для 6 класса
Нелинейные уравнения с использованием метода Ньютона-Рафсона в Matlab
колледж алгебра онлайн Лонг-Бич городской колледж
онлайн-программа решения задач со временем
бесплатных уроков математики для 10 класса
Алгебра 1 Иллинойсское издание Макдугал Литтел
Вступительный тест по математике для 6-го класса
векторных листов для начинающих
«решатель задач по алгебре»
уменьшите мощность и упростите
шагов в балансировке ядерных уравнений
Тестовые документы на управленческие способности
математика для чайников
определений алгебры фольги
метод преобразования процентов в дроби
как записать дроби, смешанные числа или десятичные дроби в процентах
упрощение выражения с целыми числами
«бесплатные рабочие листы для печати»+»решение неравенств»
онлайн-помощь по факторинговым полиномам
sat1 Шпаргалка по математике
распечатка рабочей тетради по биологии
множитель полиномов 3-го порядка
радикальное обозначение
вопросов по математике
как записать десятичную дробь смешанной дробью
предварительное алгебраическое моделирование
целочисленные значения миллиардов рабочий лист
найти наименьшее общее кратное
Техас графические калькуляторы онлайн
ПРЕДВАРИТЕЛЬНАЯ АЛГЕБРА И ВВОДНАЯ АЛГЕБРА МАРТИНА Л. БИТТИНГЕРА
Калькуляторы
с квадратным корнем и ключами экспоненты
план первого урока информатики первый класс
математические исследовательские проекты
год 10 экзаменов по математике
подключаемые экспоненты упрощают
clep колледж алгебра pdf
lcm прошлые работы 2 класс
нахождение абсолютного значения
Java Фаториал десятичный
саксонка проверяет домашнюю работу
алгебраические силы примеры работы
формула для соотношения?
как упростить радикальные выражения
учить себя алгебре
glencoe, Math Connects: концепции, навыки и решение задач, курс 2, ответы
вопрос о способностях+бесплатно
прентис холл алгебра 1 powerpoint
математика
glencoe алгебра глава 13 викторина ответы
добавление матриц
разделительные радикалы с переменной
преобразовать десятичную дробь в дробь Matlab
вопросов о способностях на языке Java
показатели практики алгебры
домашняя работа по тригонометрии помогите mckeague
бесплатное интерактивное обучение триггерам Gr11
построение графика предела на калькуляторе
математические тесты ks3
mcdougal littell ответы\
решить сложные нелинейные уравнения jacobian
Руководство по решениям
для CPM Algebra II
рабочий лист геометрии пиццы
Калькулятор квадратичного факторинга
Репетиторство Алегбры
учебник по перестановке и комбинации
рабочих листов с алгебраическими выражениями
линеаризованных гипербол
Предыдущий Далее
Решение неравенств | Intellecquity Math Helper
Короче говоря, решение неравенств заключается в одном: изменении знака. Найдите все точки, в которых происходит смена знака — назовем эти точки критическими значениями . Затем определите, какие из интервалов, ограниченных этими критическими значениями, если таковые имеются, приводят к решению. Решение неравенства будет состоять из множества всех точек, содержащихся в интервалах решения.
Метод решения линейных, полиномиальных или абсолютных неравенств:
Переместите все члены в одну сторону от знака неравенства , применив свойства сложения, вычитания, умножения и деления неравенств. У вас должен быть только ноль с одной стороны знака неравенства.
Решите соответствующее уравнение, используя соответствующий метод. Это решение или решения составят набор критических значений. При этих значениях в неравенстве происходит смена знака.
Нанесите критические значения на числовую прямую. Используйте закрытые кружки ∙ для ≤ и ≥ неравенств и используйте открытые кружки ο для < и > неравенств.
Проверка каждого интервала, определяемого критическими значениями. Если интервал удовлетворяет неравенству, то он является частью решения. Если оно не удовлетворяет неравенству, то оно не является частью решения.
Пример 1 (линейное неравенство): Решите 3x + 5(x + 1) ≤ 4x – 1 и нарисуйте решение
3x + 5(x + 1) ≤ 4x – 1 Дано
3x + 5x + 5 ≤ 4x – 1 Распределяющее свойство
8x + 5 ≤ 4x – 1 Объединить подобные термины
+
≤ 4x 4x с обеих сторон, добавьте 1 к обеим сторонам, используя свойства сложения и вычитания неравенства
Теперь решите 4x + 6 = 0
4x = -6 свойство сложения равенства
x = – 6/4 = -3/2 Разделение Свойство равенства
Постройте критическое значение
Проверка произвольных значений каждого интервала. Вы можете проверить значение в исходном неравенстве или его упрощенной форме.
В Интервал 1, пусть x= 1 в 4x + 6 ≤ 0.
4(1) + 6 ≤ 0 ЛОЖЬ.
В интервале 2 пусть x = -2 в 4x + 6 ≤ 0.
4(-2) + 6 ≤ 0 ИСТИНА. Таким образом, интервал 2 является решением.
Решение x ≤ – 3/2, или в интервальной записи, (- ∞, – 3/2]. График показан ниже:
Примечание. Удобнее использовать обозначение окружности для конечных точек графика, а не обозначение скобки интервала, поскольку мы не знаем, куда будут указывать скобки, пока не будут проверены интервалы неравенства.
БОРЬБА С МАТЕМАТИКОЙ? Хотите пошаговые решения с пояснениями к вопросам о неравенствах. Мы создали мобильное приложение, чтобы вы могли задать свой вопрос и получить мгновенную помощь, когда вам это нужно. Попробуйте Загрузите Intellecquity Now .
Пример 2 (полиномиальное неравенство): Решение 3x ³ + 5x ²> 4x ² и график
9 ² и график
9 ³ и граф.
3x ³ + x ²> 0 Свойства вычитания неравенства
Сейчас, решайте 3x ³ + x ² = 0
x ² = 0
x ² = 0
x ² = 0
x ² = 0
x ² = 0
x ² = 0
.0909
x ² = 0 или 3x + 1 = 0 Закон об нулевом продукте
Решение x ² = 0
x = ± √0 = 0.
3x = -1 Добавьте -1 к , используя свойство равенства сложения
x = -1/3 свойство равенства деления
Нанесите на график критические значения, x = 0 и x = -1/3. На этот раз используйте открытые круги!
Проверка произвольных значений каждого интервала. Вы можете проверить значение в исходном неравенстве или его упрощенной форме.
В интервале 1 пусть x = 1 в x ² (3x + 1) > 0.
1 ² (3∙1 + 1) > 0 ИСТИНА, поэтому интервал 1 является частью решения .
В интервале 2 пусть x=-1/4 дюйма x ² (3x + 1) > 0.
(-1/4) ² (3∙(-1/4) + 1) > 0 является ИСТИННЫМ, поскольку упрощено, мы получаем (1/16)(1/4) > 0,
, поэтому интервал 2 также является частью решения.
В интервале 3 пусть x=-1 в x ² (3x + 1) > 0,
(-1) ² (3∙(-1) + 1) > 0 является ЛОЖЬЮ, поскольку упрощено, мы получаем (1)(-2) > 0,
, поэтому интервал 3 НЕ является частью решения .
Мы затеняем Интервал 1 и Интервал 2, но не включает конечные точки.
Решение x>0 или –1/3 < x < 0.
Интервальное обозначение этого решения: (0 , ∞ ) U (-1/3, 0).
РАСПРОСТРАНЕННАЯ ОШИБКА, КОТОРУЮ НУЖНО ИЗБЕГАТЬ!
Студенты часто добираются до уравнения x ² (3x + 1) = 0, а затем разделяйте обе стороны на x ² ² ² ² 999999999999999111 0, теряя при этом нулевое решение. Всякий раз, когда вы делите обе части алгебраического уравнения на x или степень x, вы ошибочно теряете нулевое решение.
Пример: Решите ∣2x + 5∣ > 1 и нарисуйте решение
⏐ 2x + 5 ⏐ > 1 Given
Solve the related equation ⏐ 2x + 5 ⏐ = 1
Чтобы решить уравнения с абсолютной величиной, необходимо решить два случая:
2x + 5 = 1 и -(2x + 5) = 1
Решить 9009
2x = -4 Add –5 to both sides using Addition Property of Equality
x = -4/2 = -2 Division Property of Equality
Решение -(2x + 5) = 1
-2X -5 = 1 Средне до –1 с использованием Distrive Property Multiply через –1 с использованием Distribute Property . 0907 Add 5 to both sides using Addition Property of Equality
x = 6/(-2) = -3 Division Property of Equality
Plot the critical values, х = 0 и х = -1/3. Используйте открытые кружки, так как это >.
Нанесите критические значения, x = 0 и x = -1/3. Используйте открытые кружки, так как это >.
Проверка произвольных значений каждого интервала. Вы можете проверить значение в исходном неравенстве или его упрощенной форме.
In Interval 1 , let x=0 in ⏐ 2x + 5 ⏐ > 1.
⏐ 2 ∙ 0 + 5 ⏐ > 1 является ИСТИНА, поэтому интервал 1 является частью решения.
В Интервал 2 , пусть x = -2,5 в ⏐ 2x + 5 ⏐ 90 9 10 90906 ⏐ 2 ∙ (-2,5) + 5 ⏐ > 1 является ЛОЖЬ, поэтому интервал 2 НЕ является частью решения.
In Interval 3 , let x=- 4 in ⏐ 2x + 5 ⏐ > 1.
⏐ 2 ∙ (- 4) + 5 ⏐ > 1 является ИСТИННЫМ, поэтому интервал 3 является частью решения.
Мы затеняем Интервал 1 и Интервал 3, но не включаем конечные точки.
Решение x > -2 или x < -3. В интервальных обозначениях мы запишем это как
(- ∞ , -3) U (-2, ∞ ).
Метод решения рациональных неравенств:
Переместите все члены в одну сторону от знака неравенства , применяя свойства сложения, вычитания, умножения и деления неравенств. У вас должен быть только ноль с одной стороны знака неравенства.
Решите соответствующее уравнение, используя соответствующий метод. Это решение или решения составят набор критических значений. При этих значениях в неравенстве происходит смена знака.
Найдите все значения, которые приводят к делению на ноль. Это также критические значения для рациональных неравенств.
Нанесите критические значения на числовую прямую. Используйте закрытые кружки ∙ для ≤ и ≥, если значение не приводит к делению на ноль – всегда используйте открытые кружки для значений, приводящих к делению на ноль, поскольку это значение не может быть частью решения! Всегда используйте открытые кружки ο для < и > неравенств.
Проверка каждого интервала, определяемого критическими значениями. Если интервал удовлетворяет неравенству, то он является частью решения. Если оно не удовлетворяет неравенству, то оно не является частью решения.
Таким образом, единственная разница между решением рационального неравенства и полиномиального неравенства состоит в том, что существуют дополнительные критические значения, которые приводят к делению на ноль, и вы никогда не включаете эти дополнительные значения как часть решения, даже если это ≤ или ≥ неравенство.
Решите соответствующие уравнения (-2x + 10)/(x – 3) = 0 и x – 3 = 0.
(-2x + 10)/(x – 3) = 0
-2x + 10 = 0 Очистить дроби, умножив обе части = 907 2 x-9090
0
8
8 -10 Добавить –10 к обеим сторонам, используя свойство с добавлением равенства
x = -10/(2). . – 3 = 0
x = 3 Дополнение Свойство равенства
6 9 Постройте критические числа. Используйте замкнутый круг для x=5 и открытый круг для x=3.
В интервале 1, мы позволили x = 6. Это приводит к (-2 ∙ 6 + 10)/(6-3) ≤ 0 OR
909
0
0
0
0
0
0
0
r
0
0
09090— . 3 ≤ 0, что ИСТИНА. Таким образом, интервал 1 является частью решения.
В интервале 2 мы позволили x = 4. Это приводит к (-2 ∙ 4 + 10)/(4-3) ≤ 0 или
09090 0 или
909 9090 0 или
907 . ≤ 0, что ЛОЖЬ. Таким образом, интервал 2 НЕ является частью решения.
В интервале 3, мы позволили x = 2. Это приводит к (-2 ∙ 2 + 10)/(2-3) ≤ 0 или
8181
0
0
0
0
0
0
0
r
0
0
0
0
0
0
теля 0./(2-3) ≤ . (-1) ≤ 0, что ИСТИНА. Итак, интервал 3 является частью решения.
This results in a graph of
with solution x < 3 or x ≥ 5. Interval notation is (- ∞ , 3) U [5, ∞ ).
В предыдущем разделе мы решали уравнения, содержащие абсолютные значения. В этом разделе мы хотим рассмотреть неравенства, содержащие абсолютные значения. Нам нужно будет рассмотреть два отдельных случая.
Неравенства с участием < и ≤
Как и в случае с уравнениями, давайте начнем с довольно простого случая.
Это говорит о том, что независимо от значения p оно должно находиться на расстоянии не более 4 от начала координат. Это означает, что p должно быть где-то в диапазоне 91 181

. Мы могли бы иметь аналогичное неравенство с < и получить аналогичный результат.
В общем случае здесь можно использовать следующие формулы:
Пример:
На самом деле нечего делать, кроме как вставить формулу. Как и в случае с уравнениями pp просто представляет все, что находится внутри полос абсолютного значения. Итак, с этим первым у нас есть
Теперь это не более чем довольно простое двойное неравенство, которое нужно решить, так что давайте сделаем это.
Обозначение интервала для этого решения:
Неравенства, включающие > и ≥
Еще раз давайте начнем с простого числового примера.
Это говорит о том, что каким бы ни было значение p, оно должно находиться на расстоянии не менее 4 от начала координат, поэтому p должно находиться в одном из следующих двух диапазонов:
. Эти решения должны быть записаны в виде двух неравенств.
Вот общая формула для них.
Пример:
Опять же, p представляет количество внутри столбцов абсолютного значения, поэтому все, что нам нужно сделать, это подставить формулу, а затем решить два линейных неравенства.
Обозначение интервала для них:
Если у вас есть какие-либо другие вопросы, связанные с математикой, оставьте нам комментарий, и мы постараемся ответить вам или проверить, ответили ли мы уже на него для вас.
Фейсбук
Твиттер
LinkedIn
Более
Math Scene — графики неравенств и таблицы знаков
Math Scene — графики неравенств и таблицы знаков

2008 Расмус эхф
и Джанн Сак
Печать
Урок 2   Графики неравенств и таблицы знаков.
Как можем ли мы решить квадратное неравенство, такое как x ² − 1 0 ? Если решаем соответствующее квадратное уравнение, получаем два решения.
х ² — 1 = 0
    (х + 1)(х — 1) = 0
    Решения: x = 1 и х = −1.
Мы нашли точки, где выражение равно 0, теперь нам нужно найти, где меньше 0. Другими словами, мы должны выяснить, когда выражение отрицательный. Для этого рассмотрим признаки множители (x + 1) и (x − 1) . Другими словами, мы ищем интервалы, в которых они положительны или отрицательны. Для этого делаем таблицу знаков
Начнем с того, что подставим 0 в значения, где каждый из факторы равны нулю. (x+1) = 0, когда x = −1, и (x − 1) = 0
когда x = 1. Затем мы ставим + или — в зависимости от того, являются ли факторы положительный или отрицательный. Теперь мы можем использовать эту информацию для решения неравенства.
Мы знаем, что (x + 1)(x — 1) = x ² — 1.
Мы также знаем, что −∙− = + и +∙+ = +. Это означает, что выражение (x + 1)(x − 1) положительна, когда обе скобки имеют одинаковый знак, и отрицательна, когда они имеют противоположные знаки. Теперь мы можем заполнить таблицу. Мы ищем интервал, на котором x ² − 1 < 0, то есть отрицательно.
Этот интервал удовлетворяет неравенству.
−1 х 1
Теперь давайте решим неравенство без факторизации первый.
Мы просто находим корни, решая соответствующие уравнение, а затем подставьте любое значение x между этими корнями. .
Если мы выберем, например, x = 0, мы получим следующее
   Если f(x) = x ² − 1, тогда f(0) = 0 ² — 1 = -1.
Это показывает нам, что f(x) = x ² − 1 отрицательно на интервале
−1 х 1 .
Если мы попробуем любое значение x, которое меньше -1 og больше 1 мы получаем положительные значения для функции. Итак, линия реального числа будет выглядеть так:

Решение
Мы также можем найти решение, взглянув на график
f(x) = x ² — 1 . Решение x ² − 1 0 это интервал, в котором график лежит на оси x или ниже нее.
Посмотрите на график ниже.

График лежит на оси x или вокруг нее на интервале −1 х 1 (заштрихованная область графика).
Если мы перевернем знак неравенства, какое решение из
х ² – 1 0?
Глядя на график, площадь над осью x удовлетворяет этому условию. Если мы посмотрим на таблицу знаков, то там, где выражение положительное.
                  Решение: x −1 Решение: х 1
Решение неравенства х ² − 1 0 состоит из двух частей.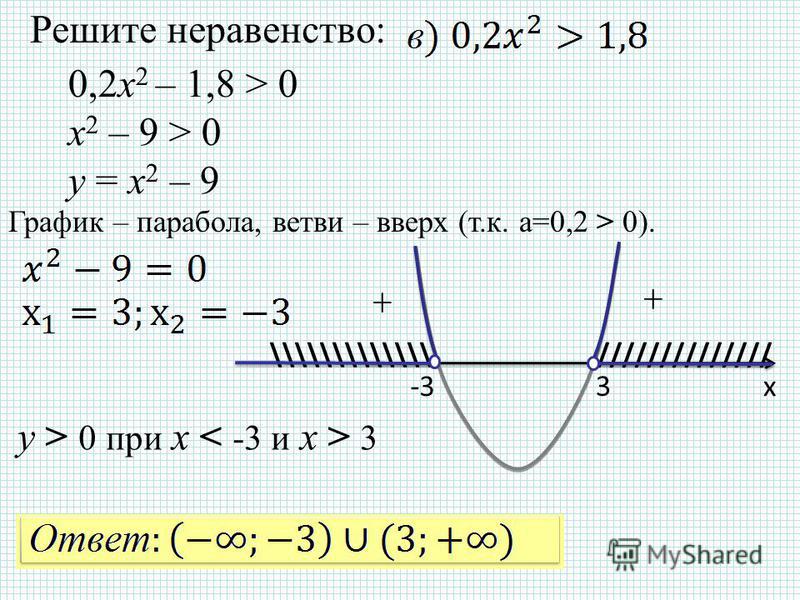
х −1 или х 1.

Пример 1
Решить неравенство x ² − 2x − 3 < x + 1,
Первый решаем соответствующее уравнение х ² — 2х — 3 = х + 1
х ² — 2х — 3 = х + 1
х ² — 3х — 4 = 0
    (х + 1)(х — 4) = 0
Решение: х = -1 и х = 4
Следующий делаем таблицу признаков.
Решение: −1 < х < 4
Если мы нарисуем два графика в одной координате система
f (х) = х ² — 2х − 3 и g(x) = x + 1, то мы ищем область, в которой f(x) ( левая часть выражения ) меньше, чем g(x) (правая часть). Это заштрихованная область графика, где x принимает значения от -1 до 4.

Пример 2
Решить неравенство
Начнем с рассмотрения знаков числителя (x + 1) и знаменатель (x − 1). Те же правила применяются для деления что касается умножения. (-/- = + и -/+ = -). Итак, если числитель и знаменатель совпадают знак, что результат положительный. Если они имеют противоположные знаки, то результат равен отрицательный

Решение
Теперь нужно позаботиться, так как x не может быть равен на 1, потому что тогда мы будем делить на 0.
Таким образом, решение равно −1 . х < 1.
Рисуем график, предварительно составив таблицу значений.
х
f(x) = ^{(x + 1)} / _{(x
— 1)}
-2
≈ 0,3
-1 0
0 -1
-3
1 асимптота
1
5
2 3
3 2
График имеет вертикальную асимптоту, когда x = 1 и лежит под осью x на интервале между −1 и 1 (заштрихованная область).
Пример 3
Решить
Начнем с перемещения 1 к другому часть уравнения, оставив там 0. Мы можем пользоваться таблицей знаков только в том случае, если правая часть равна нулю.

Мы Найдите общий знаменатель и упростите дробь.
Далее делаем таблицу знаков.

Решение х < 1
Теперь мы рисуем графики левой части и правая часть неравенства. Левая сторона такая же, как в пример 2. Правая часть g(x) = 1 (горизонтальная линия, на единицу выше x оси).
Мы видим, что график f(x) находится под графиком g(x) для всех значений x слева от вертикальная асимптота x = 1 (см. заштрихованную область). х = 1 не включены в решение, так как это означало бы, что мы делим на ноль.
Пример 4
Решить неравенство x ² < х.
Уравнение x ² = х имеет решения х = 0 и х = 1.
    x ² < х
x ² − х < 0
Упорядочить оба члена в левой части
Выберите значение x между 0 и 1, например, и введите значение в функцию.
        f(x) = x ² − х

Результат отрицательный, поэтому знак f(x) такой, как показано ниже.

не существует Решение: 0 < x < 1
Теперь посмотрите на график левой и правой руки. стороны.
График f(x) = x ² находится ниже графика g(x) = x включено интервал от 0 до 1. (см. заштрихованную область).
Пример 5
Решить неравенство ln x ln ¹ / _x .
Максимально упрощаем и переносим оба термина в левую часть уравнения.
No related posts.