Первообразная — Умскул Учебник
На этой странице вы узнаете:- Родственные связи первообразной. Как первообразная связана с производной?
- Одна функция, но много ее первообразных. Как такое происходит?
Легко догадаться, что термин “первоОбразная” происходит от двух слов: первый и образ. Первым образом у автомобиля была повозка, а у пюре — картофель.
Вернемся к математике.
Ранее мы уже рассматривали, что такое Производная и как найти её. Давайте быстро вспомним, что нахождение производной или дифференцирование — это совершение математической операции над функцией. То есть, следуя определенным правилам, любая функция может быть преобразована в новую функцию, которая и будет производной.
В обычной жизни, совершая несколько действий, мы можем преобразовать муку в тесто, а затем и в пирожки. Но разобрать готовый пирожок на муку у нас уже не получится. Зато в математике всегда можно вернуться на шаг назад: сложили два числа — вычтем обратно, возвели в степень — извлечем корень.
Но разобрать готовый пирожок на муку у нас уже не получится. Зато в математике всегда можно вернуться на шаг назад: сложили два числа — вычтем обратно, возвели в степень — извлечем корень.
Похожим образом мы можем поступить с функцией.
Возьмем любую функцию, например, f(x) = x2 и найдем для нее производную f'(x) = 2x — получилась новая функция. Теперь для того, чтобы вернуться на шаг назад, нам нужно найти первообразную от новой функции (f'(x) = 2x).
Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x).
То есть, если взять производную от первообразной какой-либо функции, получится сама эта функция. Процесс нахождения множества первообразных называется интегрированием.
F'(x) = f(x)
| Родственные связи первообразной. Как первообразная F(x) связана с функцией f(x)? Связь первообразной и функции можно рассмотреть на примере родственных связей. |
Для нахождения первообразных существует специальная таблица. В ней приведены первообразные для каждой функции. А чтобы убедиться в этом, можно найти производную от первообразной и сравнить с функцией. Они будут одинаковые.
Таблица первообразных
Где С — произвольное число
| Одна функция, но много ее первообразных. Как такое происходит? Так как нахождение первообразной — это обратное действие нахождению производной, а производная от константы всегда равна нулю, первообразная для множества функций с разными константами будет одинаковой. |
Важно: F(x) первообразная f(x) только на том промежутке, где F(x) и f(x) существуют. То есть, \(F(x) = \frac{1}{2} * ln (2x) + C\) первообразная \(f(x) = \frac{1}{2}x\) на промежутке 2х > 0 \(\rightarrow\) x > 0
Рассмотрим нахождение первообразной от следующей функции
y = 2x3
Применим правило интегрирования для степенной функции из таблицы первообразных
\(F(x) = \frac{2x^4}{4} + C\)
\(F(x) = \frac{1}{2} x^4 + C\)
Правила нахождения первообразных:
- Если нужно найти первообразную от произведения числа на функцию, то первообразной выражения будет произведение этого числа на первообразную функции.
 x}{ln2}\)
x}{ln2}\) - F(x) = ln2
- F(x) = 2
- F(x) = x2
Ответы: 1. — 4; 2. — 1; 3. — 2; 4. -1
Первообразная и неопределенный интеграл.
Функция $F(x)$ называется первообразной функции $f(x),$ заданной на некотором множестве $X,$ если $F'(x)=f(x)$ для всх $x\in X.$ Если $F(x -)$ первообразная функции $f(x),$ то $\Phi(x)$ является первообразной той же функции в том и только в том случае, когда $\Phi(x)=F(x)+C,$ где $C$ — некоторая постоянная. Совокупность всех первообразных функции $f(x)$ называется неопределенным интегралом от этой функции и обозначается символом $$\int f(x)\,dx.$$ Таким образом, по определению $$\int f(x)\,dx=F(x)+C,$$ где $F(x)$ одна из первообразных функции $f(x)$ а постоянная $C$ принимает действительные значения.
Свойства неопределенного интеграла.
1. $\left(\int f(x)\,dx\right)’=f(x).$
2. $\int f'(x)dx=f(x)+C.$
3. $\int af(x)dx=a\int f(x) dx.\,\,\,\,\,\,a\neq 0.$
4. $\int (f_1(x)+f_2(x))dx=\int f_1(x)\,dx+\int f_2(x)\, dx. 4-2 $$
4-2 $$
Найдите первообразную функции f(x) = 1\3cosx\3 + 4sin4x, график которой проходит через точку М(П;1)
Решение: Общая формула для первообразных имеет вид sin(x/3) — 4cos4x + C. Найдем С, подставив в данное выражение координаты точки М:
sin(п/3) — 4cos4п + C = 1,
(Корень из 3)/2 -4 + С = 1, откуда С = 5 — (Корень из 3)/2
Таким образом, первообразная, график которой проходит через точку М, имеет вид
sin(x/3) — 4cos4x + 5 — (Корень из 3)/2
$$ f(x)=\frac{1}{3}cos\frac{x}{3}+4sin4x\\ F(x)=sin\frac{x}{3}-cos4x+c\\ sin\frac{\pi}{3}-cos4\pi+c=1\\\frac{\sqrt3}{2}-1+c=1\\c=2-\frac{\sqrt3}{2}\\ c=\frac{4-\sqrt3}{2}\\ F(x)=sin\frac{x}{3}-cos4x+\frac{4-\sqrt3}{2} $$
Найдите ту первообразную функции f(x)=корень из 2 * cosx, график которой проходит через точку (П/4; 3)
Решение: F(x)=√2sinx+C
3=√2sinπ/4+C
C=3-√2*√2/2=3-1=2
F(x)=√2sinx+2
Найдите ту первообразную функции f(x)=корень из 2 * cosx, график которой проходит через точку (П/4; 3)
f(x)=√2cosx
F(x)=√2*sinx+C
Подставляем координаты точки в полученное выражение и находим С
3=√2*sin(π/4)+C
3=√2*√2/2+C
3=1+С
С=3-1=2
Ответ: F(x)=√2sinx+2
Найдите ту
первообразную функции f(x) = 3х – 1, для которой уравнение F(x) = 5 имеет единственный кореньРешение: $$ \int{3x-1}\, dx = \frac{3x^{2}}{2} -x $$
Чтобы это было равно 5, т. 2x}\), x∈[0;π/2), M(п/4;п/2)
2x}\), x∈[0;π/2), M(п/4;п/2)
Решение: F(x)=2x-tgx + C, x∈[0;π/2)
Подставим координаты точки М в выражение для F(x):
π/2 = 2· (π\4) — tg (π/4) + C
π/2=π/2 — 1 + С
C= 1
Ответ.F(x)=2x-tgx + 1, x∈[0;π/2)
1 2 3 > >>
Первообразная. Найти первообразную функции 2 x. Геометрический смысл первообразной. Первообразная площадь фигуры.
- Альфашкола
- Статьи
- Первообразная
Повторим, что такое функция:
функция – это зависимость одной переменной (у) от другой(х), когда для каждого значения независимой переменной (х) из множества Х, определено единственное значение зависимой переменной (у) из множества Y.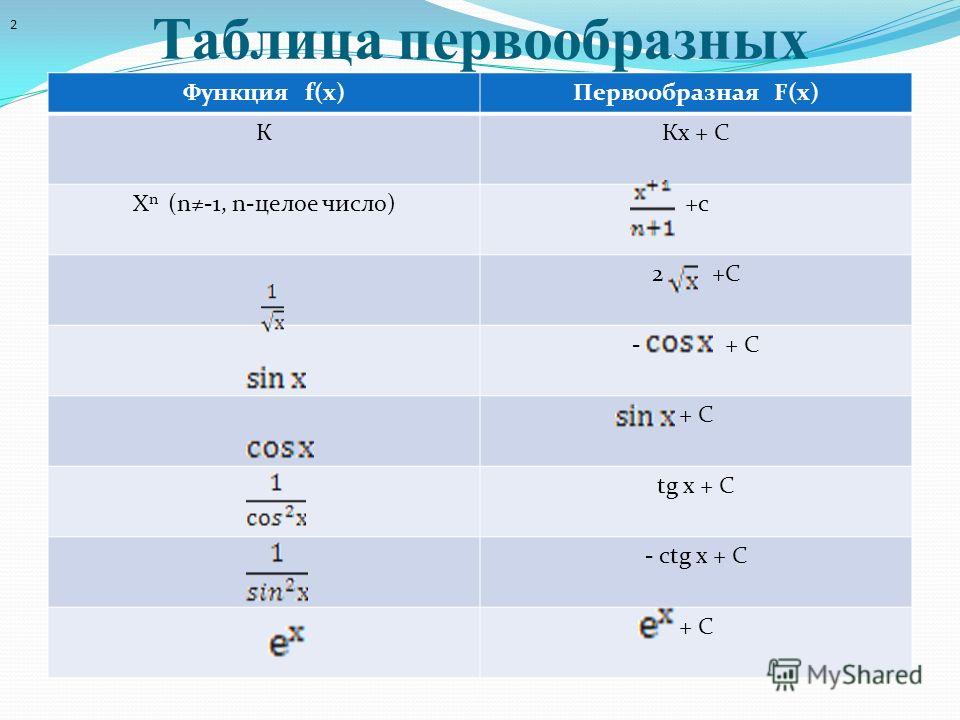
Теперь рассмотрим функцию \(y = 2x \):
Рассмотрим площади треугольников под графиком \(y = 2x.\)
Площадь треугольника равна площади \(\frac{1}{2}\) основания на высоту. Таким образом, ясно, что области под графиком:
\(S_{1} = \frac{1}{2} \times 1 \times 2 = 1\)
\(S_{2} = \frac{1}{2} \times 2 \times 4 = 4\)
\(S_{3} = \frac{1}{2} \times 3 \times 6= 9\)
Итого, можно сказать, что первообразная эквивалентна площади под функцией.
Функция может иметь несколько первообразных.
\(F(x)+C;\)
Докажем что функция может иметь несколько первообразных:
\((F(x)+C) ′ =F ′ (x)+(C) ′ =f(x)+0=f(x).\)
\((F(x)+C) ′ =f(x).\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Евгений Валентинович Грязнов
Репетитор по математике
Стаж (лет)
Образование:
Университет Иннополис
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-11 классы, (ОГЭ/ЕГЭ/олимпиады), по информатике 5-11 кл, ОГЭ, по английскому языку 1-11 классы.
Лиля Алексеевна Шевченко
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы. Подготовка к ВПР/ОГЭ, повышение успеваемости. Я люблю математику за то, что она учит логично мыслить, правильно доказывать сначала теорему, а потом и отстаивать свою точку зрения!
Подготовка к ВПР/ОГЭ, повышение успеваемости. Я люблю математику за то, что она учит логично мыслить, правильно доказывать сначала теорему, а потом и отстаивать свою точку зрения!
Татьяна Николаевна Бычкова
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Преподаватель математики в 5-9 классах, подготовка к ОГЭ и ВПР. Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Похожие статьи
- Свойства равнобедренного треугольника
- Трапеция, средняя линия трапеции
- Физфак МГУ: поступление
- Прямая пропорциональная зависимость
- Как строить графики функций с модулем из ОГЭ
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 2)
- Переезд в другой город на учебу: как освоиться в нем быстро и без стресса?
- 5 способов быстро запомнить таблицу умножения
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
| 1 | Encontre a Derivada — d/dx | логарифм непериен от x | |
| 2 | Оценщик интеграла | Непериодический интеграл логарифмического отношения x по отношению к x | |
| 3 | Encontre a Derivada — d/dx 92) | ||
| 21 | Оценщик интеграла | Intégrale de 0 à 1 de racine Cubique de 1+7x par rapport à x | |
| 22 | Encontre a Derivada — d/dx | грех(2x) | |
| 23 | Encontre a Derivada — d/dx | 9х||
| 35 | Encontre a Derivada — d/dx | непериодный логарифм 2x | |
| 36 | Encontre a Derivada — d/dx | — грех(х) | |
| 37 | Encontre a Derivada — d/dx | 4x^2-x+5 9(3x) пар раппорт à x | |
| 41 | Оценщик интеграла | Интегральная связь (2x) по отношению к | |
| 42 | Encontre a Derivada — d/dx | 1/(расин карре де х) | |
| 43 | Оценщик интеграла 9бесконечность | ||
| 45 | Encontre a Derivada — d/dx | х/2 | |
| 46 | Encontre a Derivada — d/dx | -cos(x) | |
| 47 | Encontre a Derivada — d/dx | грех(3x) | 92+1|
| 68 | Оценщик интеграла | Интегральная связь греха(х) по отношению к | |
| 69 | Encontre a Derivada — d/dx | угловой синус(х) | |
| 70 | Оценщик по лимиту | ограниченное значение x приближение 0 de (sin(x))/x 92 пар раппорта x | |
| 85 | Encontre a Derivada — d/dx | логарифм de x | |
| 86 | Encontre a Derivada — d/dx | арктан(х) | |
| 87 | Encontre a Derivada — d/dx | 92
Примитивный конек
Вероятно, в вашем браузере отключен JavaScript.
Для использования функций этого веб-сайта в вашем браузере должен быть включен JavaScript.
Быстрый просмотр
39,95 $
Быстрый просмотр
89,95 $
Быстрый просмотр
84,95 $
НОВИНКА
Быстрый просмотр
79,95 $
Быстрый просмотр
39,95 $
НОВИНКА
Быстрый просмотр
41,95 $
Быстрый просмотр
84,95 $
Быстрый просмотр
74,95 $
Быстрый просмотр
35,95 $
Быстрый просмотр
39,95 $
Быстрый просмотр
34,95 $
Быстрый просмотр
39,95 $
Быстрый просмотр
94,95 $
Быстрый просмотр
$69,99
$84,95
Купи 1, получи 1 со скидкой 50%
Быстрый просмотр
39,95 $
Быстрый просмотр
39,95 $
Быстрый просмотр
33,95 $
Быстрый просмотр
29,95 $
Быстрый просмотр
59,99 долларов США
$64,95
Купить1 Получить1 Бесплатно
Быстрый просмотр
39,95 $
НОВЫЙ
Быстрый просмотр
79,95 $
Быстрый просмотр
$74,99
$790,95
Купи 1, получи 1 со скидкой 50%
Быстрый просмотр
104,95 $
Быстрый просмотр
37,95 $
Быстрый просмотр
35,95 $
Быстрый просмотр
69,95 $
Быстрый просмотр
39,95 $
Быстрый просмотр
79,95 $
Быстрый просмотр
49,95 $
Быстрый просмотр
89,95 $
Быстрый просмотр
99,95 $
НОВИНКА
Быстрый просмотр
134,95 $
Быстрый просмотр
39 $. 95
95
Быстрый просмотр
39,95 $
Быстрый просмотр
54,95 $
Быстрый просмотр
69,95 $
Быстрый просмотр
$74,99
79,95 долларов США
Купи 1, получи 1 со скидкой 50%
Быстрый просмотр
54,95 $
Быстрый просмотр
35,95 $
Быстрый просмотр
94,95 $
Быстрый просмотр
89,95 $
Быстрый просмотр
84,95 $
Быстрый просмотр
29,95 $
Быстрый просмотр
$84,99
$890,95
Купи 1, получи 1 со скидкой 50%
Быстрый просмотр
31,95 $
Быстрый просмотр
$64,95
Купить1 Получить1 Бесплатно
Быстрый просмотр
84,95 $
Быстрый просмотр
39,95 $
Быстрый просмотр
37,95 $
Быстрый просмотр
79,99 долларов США
$84,95
Купи 1 Получи 1 Скидка 50%
Быстрый просмотр
39,95 $
Примитивный конек
Primitive Skateboarding — компания по производству товаров премиум-класса, основанная профессиональным скейтбордистом Полом Родригесом (он же P-Rod). Primitive Skate родился из глубокой страсти и любви к скейтбордингу. Они стремятся возвысить райдеров во всем мире, поощряя их продолжать творить и прогрессировать, а также предоставляя первоклассные товары для скейтбординга, чтобы помочь улучшить ваши навыки и стиль. Они получают поддержку и рекомендации от своей сильной команды райдеров, включая P-Rod, Miles Silvas, Carlos Ribeiro и Brian Peacock, которые помогают тестировать их продукты. Zumiez с гордостью предлагает широкий ассортимент продукции Primitive Skateboarding, которая поможет вам выразить себя и улучшить свои навыки. Загляните к Zumiez сегодня и ознакомьтесь с полной подборкой скейтбординга Primitive, чтобы начать выражать себя на улицах.
Primitive Skate родился из глубокой страсти и любви к скейтбордингу. Они стремятся возвысить райдеров во всем мире, поощряя их продолжать творить и прогрессировать, а также предоставляя первоклассные товары для скейтбординга, чтобы помочь улучшить ваши навыки и стиль. Они получают поддержку и рекомендации от своей сильной команды райдеров, включая P-Rod, Miles Silvas, Carlos Ribeiro и Brian Peacock, которые помогают тестировать их продукты. Zumiez с гордостью предлагает широкий ассортимент продукции Primitive Skateboarding, которая поможет вам выразить себя и улучшить свои навыки. Загляните к Zumiez сегодня и ознакомьтесь с полной подборкой скейтбординга Primitive, чтобы начать выражать себя на улицах.Альберт ван дер Сель: Примитивный интеграл.
В примечании 5 мы обнаружили, что:
Если f(x)=sin(x), то f ‘(x)=cos(x)
Если f(x)=cos(x) yhen f ‘(x)= -sin(x)
Таким образом:
∫ cos(x) dx = sin(x) + C
∫ sin(x) dx = -cos(x) + C
Пример 2:
Предположим, у нас есть f(x)=x 2 (x-√x). Что такое F(х)?
Что такое F(х)?
В общем, попробуйте переписать выражение, чтобы избавиться от «(» и «)».
Таким образом, часто проще применить одно из правил, перечисленных выше.
x 2 (x-√x)=x 2 x — x 2 √x = x 3 — x 2,5
7 Теперь мы можем применить наши правила: =1/4x 4 — 1/3,5x 3,5Это решение, но нам нужно переписать его более аккуратно:
1/4x 4 — 1/3,5x 3,5 = 1/4x 4 — 2/7x 3 √x
F(x)=(1/4) x 4 — (2/7) х 3 √х + с
Пример 3: Два примера использования «Простой замены»:
-Пример 3.1:
Предположим, нам нужно решить:
∫ (x-5) 7 dx
Call (x-5)=t.
Тогда наш интеграл примет вид:
∫ t 7 dt
Который легко решить, используя наши основные правила.
∫ t 7 dt = 1/8 t 8 + C
Подставляем (x-5)=t обратно, и наш ответ:
F(x) = 1/8 (x-5) 8 + C.
-Пример 3.2:
Решить :
∫ 2x(x 2 +1) 5 dx
Переписывание подынтегральной функции нам мало поможет, т. е. если дальше умножать слагаемые, то получается очень сложно.
В примере 2 умножение сработало, но здесь его можно сделать более хитро:
Использовать t=(x 2 +1). Тогда dt=2xdx.
∫ 2x(x 2 +1) 5 dx = ∫ t 5 dt=1/6 t 6 +C.
Замена спинки:
F(x)=1/6 (x 2 +1) 6 + C.
Пример 4: Использование цепной линейки:
Во многих случаях является альтернативой методу «подстановки», а иногда и проще.
— Предположим, у нас есть f(x)=(2x+2) 5 . Что такое F(х)? Очень похоже на
то, что мы имели в примере 3.
Обратите внимание, что «2x+2» является линейной функцией.
Как видите, что-то вроде (2x+2) 6 выводит нас на дорогу. Однако у нас все еще есть «2»
Однако у нас все еще есть «2»
из «2x», с которыми нужно иметь дело. Итак, если мы попробуем «1/12 (2x+2) 6 », сработает ли это?
Используя цепное правило для производных, мы получим «1/12 . 6 . (2x+2) 5+1 . 2″, что
действительно дает нам (2x+2) 5 снова.
Обратите внимание, что то, что находится в скобках, является линейным, то есть имеет форму ax+b. С более высокими силами
x в некоторых терминах в скобках этот метод может потребовать дополнительных соображений.
— Допустим, у нас есть:
| f(x) | = | x ——— dx (1+x 2 ) 3 |
Найдите первообраз f(x). Обратите внимание, что вы также можете записать f(x) как f(x) = x.(1+x 2 ) -3 .
Надо как-то найти формат, чтобы он подходил по цепному правилу.
Обратите внимание, что d/dx (1+x 2 ) = 2х.
Обратите внимание, что x = 1/2. 2x
2x
Обратите внимание, что примитив (…) -3 должен иметь часть (…) -2 .
Дело не в том, что мы следуем очень конкретному правилу, чтобы добраться до нашей цели, но можно
увидеть, что F(x) = -(1/4) . (1+x 2 ) -2
Если вы распознаете функцию как f ‘(g(x)).g'(x), то примитивом будет f(g(x)).
— Предположим, у нас есть f(x)=sin(2x). Что такое F(х)?
Вам всегда понадобится книга «Фокусов».
Если посмотреть на производную от cos(2x), то снова по цепному правилу имеем
-sin(2x).2 = -2sin(2x).
Таким образом:
F(x)= ∫ sin(2x)dx = -1/2 cos(2x)+c
Вот несколько важных стандартных интегралов с sin и cos:
∫ sin (ax)dx =-1/a cos(ax) + C (a — константа)
∫ cos(ax)dx = 1/a sin(ax) + C
∫ sin 2 (x)dx = (1/2)x — 1/4 sin(2x) + C = (1/2)x — (1/2) sinx cosx + C
∫ cos 2 (x)dx = (1/2)x + 1/4 sin(2x) + C = (1/2)x + (1/2) sinx cosx + C
Пример 5: Более сложный пример замены:
Предположим, у нас есть f(x)=sin 3 (x). Что такое F(х)?
Что такое F(х)?
999Во-первых, обратите внимание, что sin 3 (x)=sin(x).sin(x).sin(x)=sin(x).sin 2 (x).
В предыдущем примечании мы видели, что sin 2 (x) + cos 2 (x) = 1.
Таким образом: sin 2 (х)=1-cos 2 (х).
Итак: sin 3 (x) = (1-cos 2 (x)).sin(x).
Теперь d/dx (cos(x))=-sin(x). Таким образом, d(cos(x))=-sin(x)dx.
Таким образом:
sin 3 (x)=(1-cos 2 (x)).sin(x)=(1-cos 2 (x)).-d(cos(x) )
=(cos 2 (x) — 1)d(cos(x))
Теперь используем «трюк подстановки»: u=cos(x).
Тогда получаем:
(cos 2 (x) — 1)d(cos(x)) = (u 2 — 1) du.
∫ (U 2 — 1) DU = 1/3 U 3 -U +C
Так:
∫ SIN 3 (x) = 1/3 COS 3 9666 3 (x) = 1/3 COS 3 966696696696696696696696696696696696696696696696696696696696696696696696696696696696696966969696966969696969669696969696666969696966666 (х) -cos(х) +с
2. Примеры с e x и показательными функциями:
Примеры с e x и показательными функциями:
Пример 6:
Производная от e x равна e x . Следовательно:
∫ e x dx=e x + C
Пример 7:
Попробуем найти: ∫ e kx dx, где k — некоторая константа.
Подставим u=kx. Поэтому du=k dx. Таким образом, (1/k)du=dx.
Итак, ∫ e kx dx = ∫ e u (1/k)du = (1/k) ∫ e u 9 u du = (1 1/k 9191) 1e +C=(1/k)e kx +C.
Пример 8:
Попробуем найти: ∫ 2 х дх. (это упражнение также является моделью для x )
Если g Log(x)=y, то g y =x. Таким образом, g Log(x) =x.
Thus:
e ln(2) =2
∫ 2 x dx = ∫ (e ln(2) ) x dx = ∫ (e ln( 2) x )dx
Теперь положим u=ln(2)x. Таким образом, du=ln(2)dx. Таким образом, 1/(ln(2) du = dx.
Таким образом, du=ln(2)dx. Таким образом, 1/(ln(2) du = dx.
Подставим это: ∫ (e ln(2) x )dx=1/ln(2) ∫ e u du = 1/ln(2) e u +C.
Подставим u=ln(2)x назад:
1/ln(2) e ln(2)x +C = 1/ln(2) (e ln(2) ) x +С = 1/ln(2) 2 х +С.
Вы можете обобщить это до: ∫ a x dx = 1/ln(a) a x + C.
Таким образом, метод «подстановки» может быть весьма важным, как мы видели. в нескольких примерах выше.
3. Примеры использования метода интегрирования по частям:
Правило произведения от нахождения производной может быть полезным и при нахождении примитивной функции.
Это правило таково:
(f.g)’ = f’.g + f.g’ (обратите внимание на апострофы).
Отсюда:
f’.g = (f.g)’ — f.g’, а также f.g’ = (f.g)’ — f’.g
Это означает, что:
∫ f’.g = ∫ (f.g)’ — ∫ f.g’ = f. g — ∫ f.g’
g — ∫ f.g’
Вы можете читать это правило также как (чтобы сделать его более ясным):
∫ f.g = F.g — ∫ F.g’ , где F — примитив f, а g’ является производной от g.
Часто бывает трудно выбрать наиболее практичные «f» и «g». Давайте посмотрим несколько примеров:
Пример 9:
∫ х линкс дх = 1/2 х 2 линкс — ∫ 1/2 х 2 . 1/x dx = 1/2 x 2 lnx — 1/4 x 2 + C.
Пример 10:
∫ х sinx dx = -cosx х — ∫ -cosx . 1 dx = -xcosx — sinx + C.
Пример 11:
∫ перкс дх знак равно ∫ 1 . перкс дх знак равно Икс перкс — ∫ Икс . 1/x dx = x lnx — ∫ 1 dx = x lnx — x + C
Пример 12:
∫ xe x dx = xe x — ∫ e x . 1 дх = х.е х — е х + С.
4. Примеры с дробями:
Уже известно несколько фактов:
Если f(x)=ln(x), то
f ‘(x)= 1/x
Таким образом, если f(x)=1/x, то
F(x)=ln(|x|).
и из примера 11 мы видим, что:
∫ lnx dx = ∫ 1 . перкс дх знак равно Икс перкс — ∫ Икс . 1/x dx = x lnx — ∫ 1 dx = x lnx — x + C
Аналогично:
∫ log(x) dx = 1/ln(g) . (x lnx — x) + C
Мы могли бы использовать это в некоторых примерах.
Пример 13:
∫1/(2x+1) дх
установить t=(2x+1). Таким образом, dt=2dx. Таким образом, dx=1/2dt
∫ (1/2) 1/t dt = 1/2 ∫ 1/t dt = 1/2 ln(t) = 1/2 ln(2x+1) + C
Пример 14:
Предположим, у нас есть:
| f(x) | = | 4x 4 +4x 3 +x 2 +3 —————- 2x+1 |
Тогда ∫ f(x)dx кажется настоящей проблемой.
Есть несколько способов справиться с этим. Вы можете попробовать «хвостовой дивизион».
2x+1 / 4x 4 +4x 3 +x 2 +3 \ 2x 3 +x 2 + x
——-x—4x 6 3
——— 2x 3 +x 2
———————
—— —-2x 2 +x
с остатком «3».
Таким образом, мы имеем:
| f(x) | = | 4x 4 +4x 3 +x 2 +3 —————- 2x+1 | = | 2x 3 +x 2 +x+ | 3 —- 2x+1 |
Таким образом, мы видим, что интеграл
| ∫f(x)dx | = | ∫ ( | 4x 4 +4x 3 +x 2 +3 —————- 2x+1 | ) дх | = | ∫ ( | 2x 3 +x 2 +x+ | 3 —- 2x+1 | ) дх |
И мы знаем, как обращаться с каждым из этих терминов, включая термин 3/(2x+1) (см. пример 13).
Пример 15:
Иногда дробь можно разделить на несколько частей.
Допустим, у нас есть:
| ∫f(x)dx | = | ∫ | x 2 +3 ——— dx 2x |
Мы можем разделить это на:
| ∫ f(x)dx | = | ∫ | x 2 +3 ——— dx 2x | = | ∫ | x 2 — дх 2х | + | ∫ | 3 — дх 2х |
Где мы можем иметь дело с обоими терминами со знаниями, представленными выше.

5. Примеры более сложных вопросов:
Пример 16:
Предположим, у нас есть ванна, поверхность которой на любой высоте x определяется по формуле:
C(x)=2500x 0,5 -70x (в см 2 )
Максимальная высота ванны составляет 50 см.
Вмещает 500 литров воды? 0 p 1195 1,5 — 35x 2 ] 0 P =
(2500/1,5) P 1,5 — 35P
2 — 0 = (2500/1,5) P 1,5 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35. 2
Должен быть равен 500 л . У нас есть 1 л = 1000 см 3 . Таким образом, 500 л = 500 000 см 91 195 3 91 196 .
Таким образом (2500/1,5) p 1,5 — 35p 2 = 500000
Таким образом, p=49,9
Пример 16:
Рис. 3. Площадь, определяемая границами x=a, x=b, f(x) и g(x),
Часто на экзаменах по математике в старшей школе вы можете увидеть задачи, перечисленные ниже.
Предположим, что в области [x-a, x=b] у нас есть две функции f(x) и g(x).
Вычислите поверхность, определяемую границами x=a, x=b, осью x и лежащую между
f(x) и g(x).
В данном случае речь идет о размере зеленой зоны A Green . См. рисунок выше.
Таким образом:
А Зеленый = ∫ А b f(x) dx — ∫ a b g(x) dx
Обратите внимание, что мы всегда должны делать «верхняя область — нижняя область».
Давайте рассмотрим простой пример. Скажем, у нас есть прямая f(x)=4x+2 и парабола g(x)=x 2 +2.
У нас нет «a» и «b», поэтому мы должны сначала найти значение(я) x пересечения(й):
x 2 +2=4x+2 => x(x-4 )=0 => х=0 или х=4.
Линия находится над параболой, между x=0 и x=4, а при x>4 парабола находится над линией.
Область, которую мы должны рассчитать, заключается в интервале 0
. =
[2x 2 + 2x] 0 4 — [1/3 3 + 2x] 0 4 = 10,7.
Пример 17: Расчет объема.
Изображение функции f(x)=√x. Если вы не знаете, как «выглядит функция»,
, тогда поищите.
Теперь представим, что мы вращаем график по оси x на 2π. Создается древовидный объект
, который выглядит как трехмерная парабола с осью X в качестве центральной линии.
Если вы разрежете объект на маленькие Δx, мы получим маленькие объекты, похожие на маленькие цилиндры.
Объем такого маленького цилиндра в определенном месте x i приблизительно равен
π (f(x)) 2 . Δx i (как «π r 2 . h», для цилиндра шириной «h»).
Если вы сложите все эти маленькие цилиндры в интервале [x=a, x=b], вы получите сумму Римана
, которая является близким приближением для общий объем на интервале [x=a, x=b]
Таким образом, определенный интеграл существует, если Δx i становится бесконечно малым
Предположим, мы хотим вычислить объем в [x=0, x=4 ], имеем:
∫ 0 4 π(√x) 2 dx = 8 π
Правила интегрирования
Интеграция
Интеграцию можно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей. Он часто используется для нахождения области под графиком функции и осью X .
Он часто используется для нахождения области под графиком функции и осью X .
Первое правило, которое нужно знать, это то, что интегралы и производные противоположны!
Иногда мы можем вычислить интеграл,
, потому что мы знаем соответствующую производную.
Правила интеграции
Вот наиболее полезные правила с примерами ниже:
| Общие функции | Функция | Интеграл |
|---|---|---|
| Константа | ∫а дх | топор + С |
| Переменная | ∫x дх | x 2 /2 + С |
| Квадрат | ∫x 2 дх | x 3 /3 + С |
| Обратный | ∫(1/х) дх | лн|х| + С |
| Экспоненциальный | ∫е х дх | е х + С |
| ∫а х дх | а х /ln(а) + С | |
| ∫ln(x) дх | х пер(х) — х + С | |
| Тригонометрия (x в радианах) | ∫cos(x)dx | грех(х) + С |
| ∫sin(x) дх | -cos(x) + С | |
| ∫сек 2 (х) дх | тан(х) + С | |
| Правила | Функция | Интеграл |
| Умножение на константу | ∫cf(x)dx | c∫f(x)dx |
| Степенное правило (n≠−1) | ∫x n dx | x n+1 n+1 + C |
| Правило суммы | ∫(f + g) дх | ∫f дх + ∫g дх |
| Правило различия | ∫(е — г) дх | ∫f дх — ∫g дх |
| Интеграция по частям | См. Интеграция по частям Интеграция по частям | |
| Правило замены | См. Интеграция путем замены | |
Примеры
Пример: чему равен интеграл sin(x) ?
Из таблицы выше это указано как −cos(x) + C
Записано как:
∫sin(x) dx = −cos(x) + C
Пример: каков интеграл от 1/x ?
Из приведенной выше таблицы он указан как ln|x| + С
Записывается как:
∫(1/x) dx = ln|x| + C
Вертикальные стойки || по обе стороны от x означают абсолютное значение, потому что мы не хотим придавать отрицательные значения функции натурального логарифма ln .
Силовое правило
Пример: Что такое ∫x
3 dx ?Вопрос: «Каков интеграл от x 3 ?»
Мы можем использовать Степенное правило, где n=3:
∫x n dx = x n+1 n+1 + C
∫x 3 dx = x 4 4
33Пример: Что такое ∫√x dx ?
√x is also x 0. 5
5
We can use the Power Rule, where n=0.5:
∫x n dx = x n+1 n+1 + C
∫x 0,5 dx = x 1,5 1,5 + C
Умножение на константу
Пример: Что такое ∫6x
2 dx ?We can move the 6 outside the integral:
∫6x 2 dx = 6∫x 2 dx
And now use the Power Rule on x 2 :
= 6 x 3 3 + C
Упрощение:
= 2x 3 + C
Правило суммы
Пример. Что такое ∫(cos x + x) dx ?
Используйте правило суммы:
∫(cos x + x) dx = ∫cos x dx + ∫x dx
Вычислите интеграл каждого из них (используя таблицу выше):
= sin x + x 2 /2 + C
Правило различия
Пример: Что такое ∫(e
w − 3) dw ?Используйте правило разности:
∫(e w − 3) dw =∫e w dw − ∫3 dw
Затем вычислите интеграл каждого (используя таблицу выше):
7 = e ш — 3ш + С
Сумма, разность, постоянное умножение и правила степени
Пример: Что такое ∫(8z + 4z
3 − 6z 2 ) dz ?Используйте правило суммы и разности:
∫ (8Z + 4Z 3 — 6Z 2 ) DZ = ∫8Z DZ + ∫4Z 3 DZ — ∫6Z 2 DZ 9099 9096.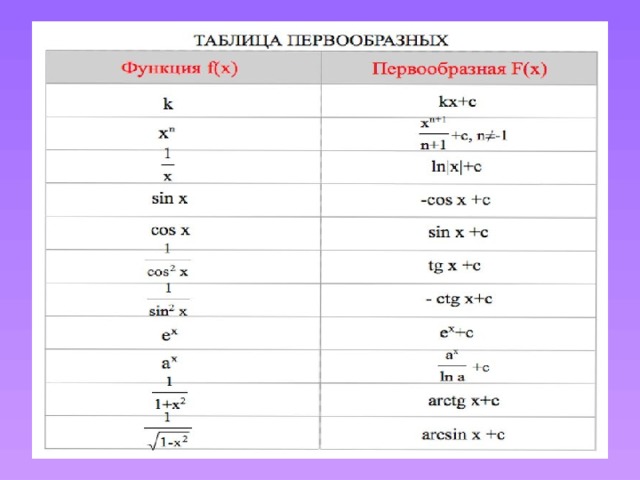
= 8∫Z DZ + 4∫Z 3 DZ — 6∫Z 2 DZ
Правило мощности:
= 8Z 2 /2 + 4Z 4 /4 — 6 + C
Упростить:
= 4z 2 + з 4 − 2з 3 + С
Интеграция по частям
См. Интеграция по частям
Правило замены
См. Интеграция путем замены
Заключительный совет
- Много практики
- Не забудьте dx (или dz и т. д.)
- Не забудьте + C
6834, 6835, 6836, 6837, 6838, 6839, 6840, 6841, 6842, 6843
509 Превышен предел пропускной способности
509 Превышен предел пропускной способности Сервер временно не может обслуживать ваши запрос из-за того, что владелец сайта достиг своего ограничение пропускной способности. Пожалуйста, попробуйте позже.
Пожалуйста, попробуйте позже..:: Список примитивных полиномов — Араш Партоу ::.
Описание
Ниже приведен список примитивные неприводимые многочлены для порождающих элементов бинарного поля расширения GF(2 m ) из базового конечного поля. Список содержит многочлены степени от 2 до 32.
Загрузки
примитивные_полиномиалы_GF2.txt
примитивные_полиномиалы_GF2_extended.zip
| Степень 02 | Степень 03 | Степень 04 | Степень 05 | Степень 06 | Степень 07 | Степень 08 | Степень 09 |
| Степень 10 | Степень 11 | Степень 12 | Степень 13 | Степень 14 | Степень 15 | Степень 16 | Степень 17 |
| Степень 18 | Степень 19 | Степень 20 | Степень 21 | Степень 22 | Степень 23 | Степень 24 | Степень 25 |
| Степень 26 | Степень 27 | Степень 28 | Степень 29 | Степень 30 | Степень 31 | Степень 32 | 91 + 1

 Мама является предшественником дочери, а первообразная — предшественник функции.
Мама является предшественником дочери, а первообразная — предшественник функции.  x}{ln2}\)
x}{ln2}\)