Дуга в окружности: Длина дуги окружности. Центральный угол окружности. Дуга большого круга.

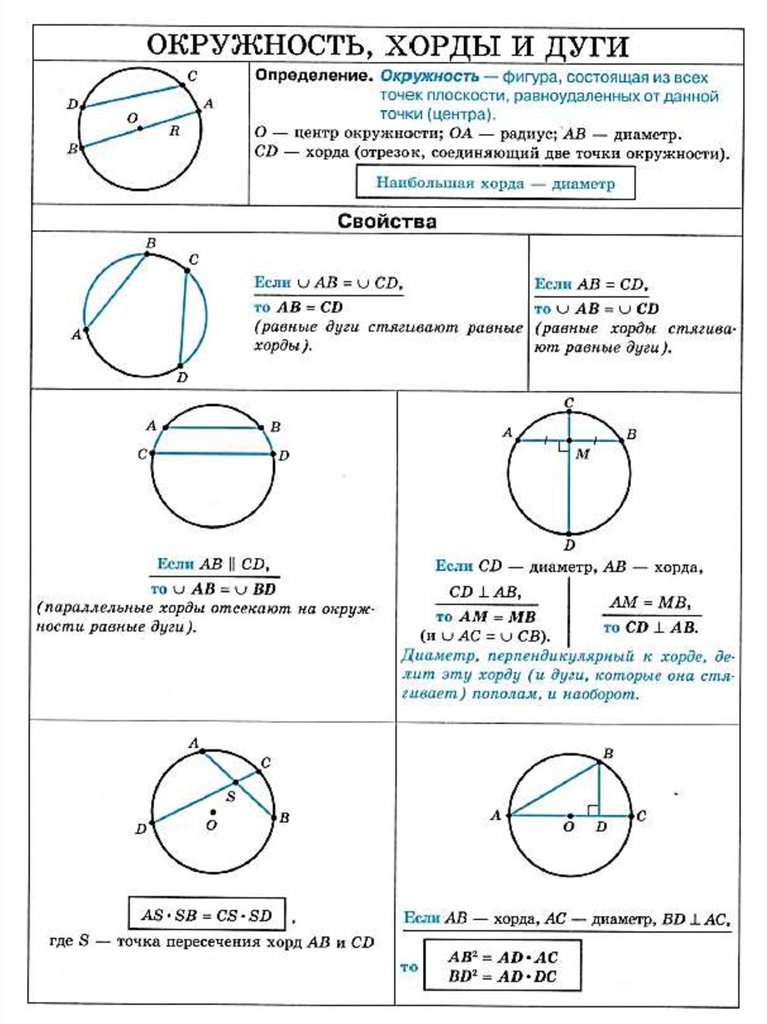
Длина дуги окружности. Центральный угол окружности. Дуга большого круга.

• Альфашкола
• Статьи
• Дуга окружности. Центральный угол

В той статье мы узнаем что такое дуга окружности, центральный угол, измерение дуги окружности.

Дуга окружности

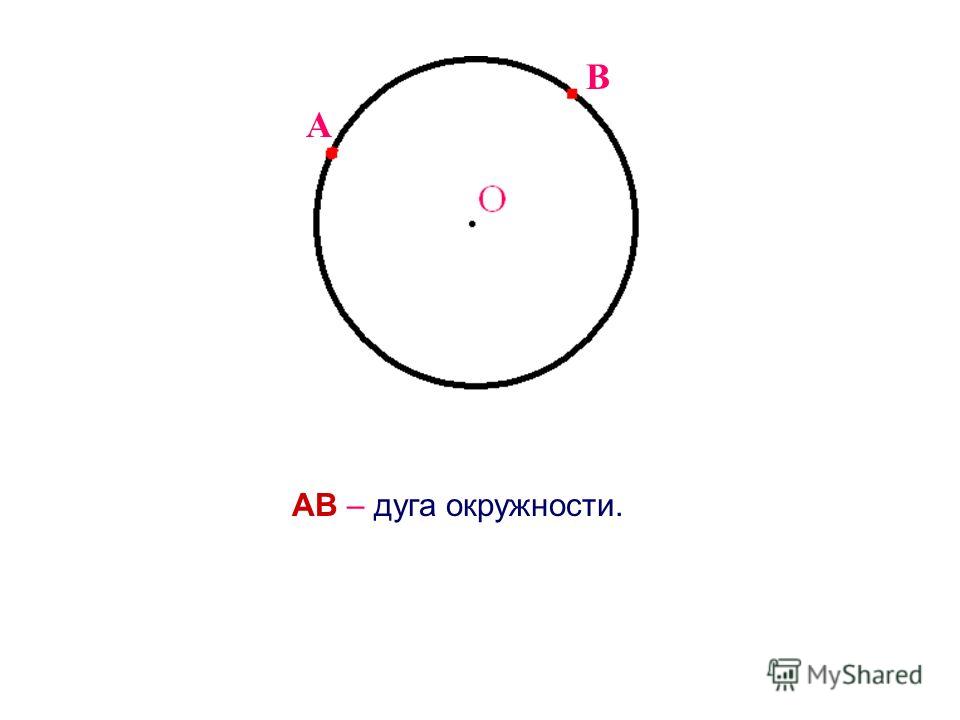
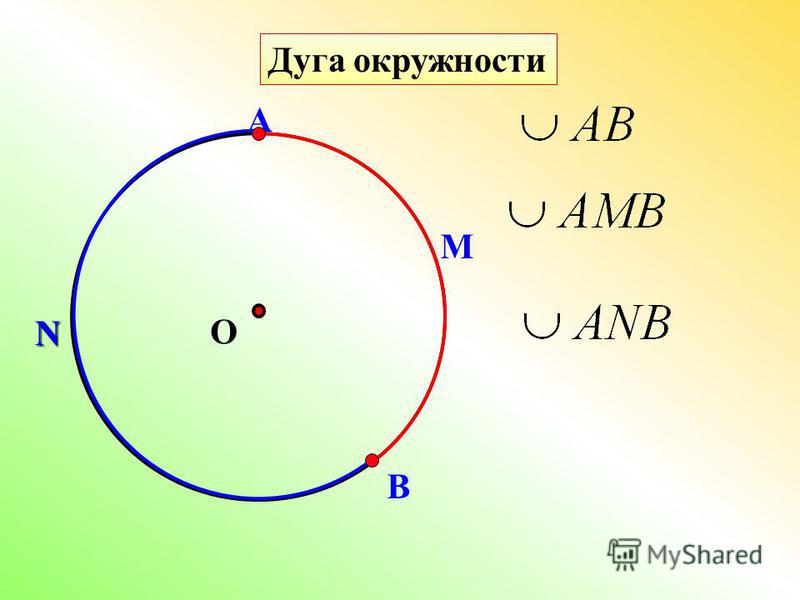
Дуга — это любая связанная часть окружности круга. На рисунке ниже часть окружности от \(M\) до \(N\) образует дугу. Она называется \(\smile\) \(MN\).

Дуга может быть малой дугой, полукругом или большой дугой. Полукруг — это дуга, равная половине круга. Малая дуга — это дуга, которая меньше полукруга. Большая дуга — это дуга, которая больше полукруга.

Центральный угол
Центральный угол — это угол, вершина которого находится в центре окружности.

Например угол \(∠NAM\):

 

Дуга круга, угол

На приведенной выше диаграмме центральный угол для дуги \(MN\) равен \(45°\).

Сумма центральных углов в любой окружности равна \(360°\). Мера полуокружности равна \(180°\).

Мера малой дуги равна мере центрального угла, который перехватывает дугу. Можно также сказать, что мера малой дуги равна мере центрального угла, который подтягивается дугой. На диаграмме ниже мера дуги \(MN\) равна \(45°\):

 

Мера главной дуги равна \(360°\).

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Мария Николаевна Орлова

Репетитор по математике

Стаж (лет)

Образование:

Оренбургский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по информатике с 5-9 класс. В наше время нельзя обойтись без знания информатики, так как компьютеры сейчас используются в любой сфере. В своей практике использую индивидуальный подход к каждому ученику. Ежегодно готовлю учеников к ОГЭ по информатике. Все ребята, которые сдавали ОГЭ имеют максимальные баллы. На своих занятиях разбираем теоретическую часть, но большее часть урока идет на развитие практических навыков решения различных типов задач. Будем разбирать такие темы: алгебра логики, система счисления, программирование, информационный объем.

Юлия Геннадьевна Газданова

Репетитор по математике

Стаж (лет)

Образование:

Актюбинский педагогический техникум

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-5 классов.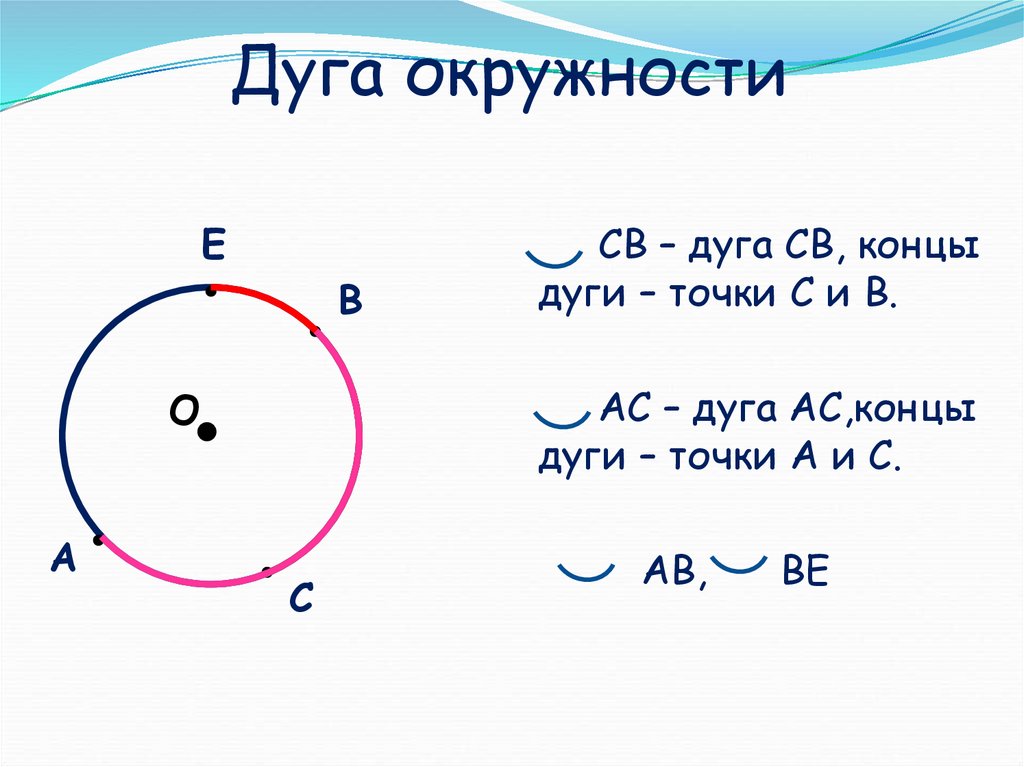 Люблю работать с детьми и умею находить с ними общий язык. Математику люблю за точность и преподаю её так, как хотела бы, чтобы учили моего ребенка. При обучении настраиваю на позитивное восприятие всего нового и непонятного. Весело и интересно объясняю сложный материал. Со мной вашим детям будет легко, занимательно и познавательно. До встречи на уроках!

Владимир Валерьевич Ковалев

Репетитор по математике

Стаж (лет)

Образование:

Пятигорский государственный педагогический институт иностранных языков

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по французскому языку для 7-11 классов.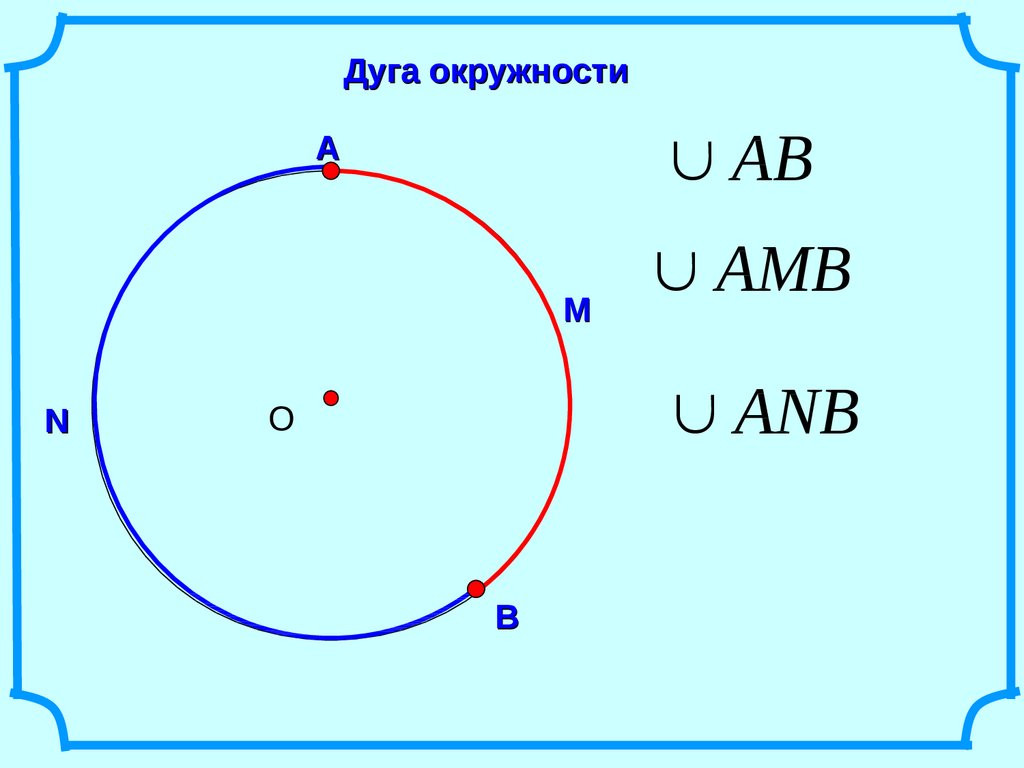 Французский язык для меня — это «любовь с первого взгляда и на всю жизнь». В нём — красота и пластичность, математическая логика и дипломатичность, простота и невероятные связи с русским. Не было ни одного дня, чтобы я не совершенствовался в нём, и всякий раз нахожу что-то новое. За 40 прошлых лет были и более 20 лет преподавания в высшей школе, и более 10 лет переводческой работы, подготовка переводчиков к Всемирной шахматной Олимпиаде, Олимпиаде в Сочи и чемпионату мира по футболу-2018. Примерно 25 лет назад во Франции была разработана методика преподавания французского, как иностранного. С тех пор я применял её, как на группах, так и индивидуально, на разных возрастных группах, и, главное — на своих детях. Во всех случаях методика била по эффективности все ВУЗовские программы. Многократно подтверждено: 350 часов занятий, и ученик понимает и говорит на любые общебытовые темы.»

Похожие статьи

• Как легко разделить на 0,25
• Как перевести квадратные километры в квадратные метры
• Скорость сближения и скорость удаления
• Факультет Менеджмента Финансового Университета: отзывы
• РУДН: факультет Экологии и Природопользования
• Задачи на движение по окружности
• Как школьнику выстроить идеальные отношения с родителями
• Топ 20 бесполезных покупок к школе

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Градусная мера дуги окружности / Окружность / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Окружность
5. Градусная мера дуги окружности

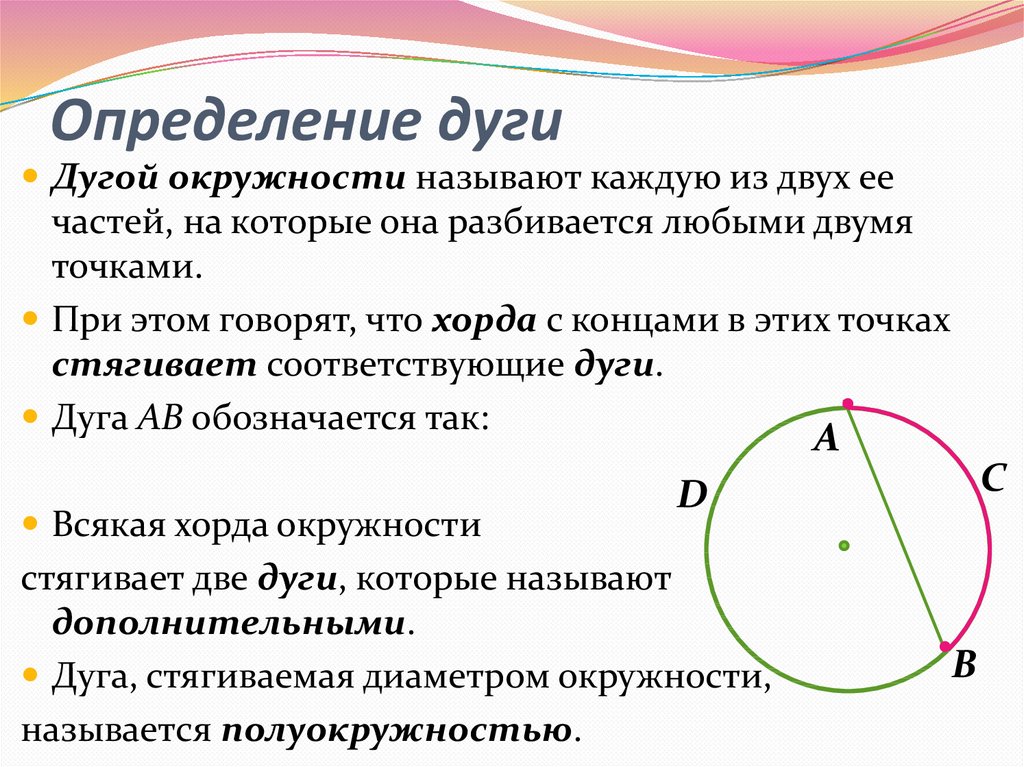
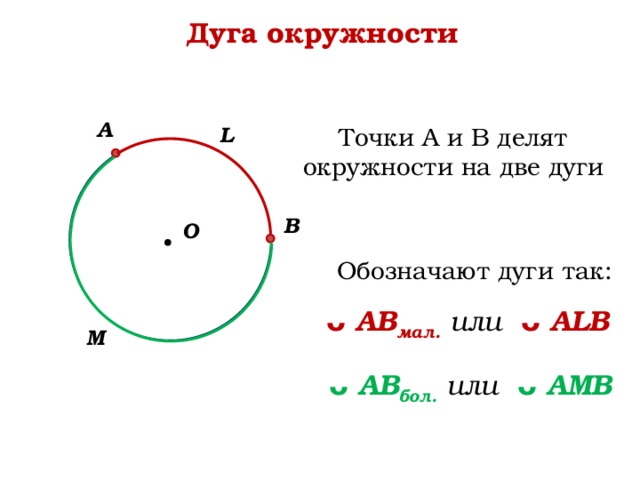
На рисунке 1 две точки А и В разделяют окружность на две дуги. На каждой дуге отмечают промежуточную точку, например L и М, для того, чтобы различать эти дуги.

Обозначают дуги так: АLB  и АМВ. Если в задаче ясно, о какой из двух дуг идет речь, то используют обозначение без промежуточной точки: АВ.

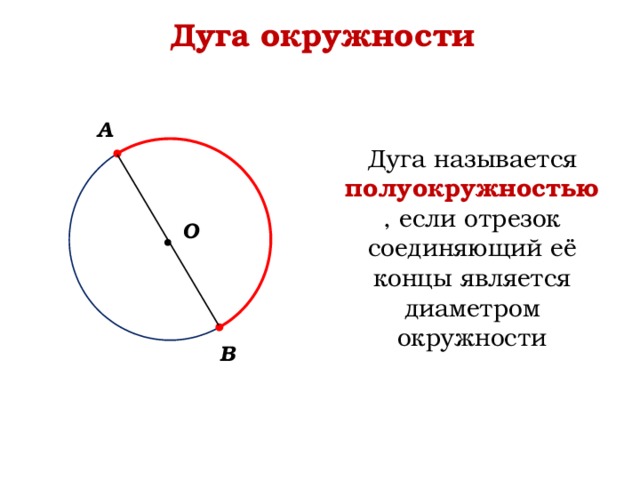
Если отрезок, соединяющий концы дуги является диаметром то, такая дуга называется полуокружностью. На рисунке 2 изображена окружность с центром О, концы диаметра АВ разделяют данную окружность на две полуокружности: АКB  и АСВ.

Центральный угол — угол с вершиной в центре окружности. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В.

Центральному углу АОВ соответствуют две дуги с концами А и В.

• Если АОВ развернутый, то ему соответствуют две полуокружности (Рис. 2).
• Если АОВ неразвернутый, то дуга АLВ, расположенная внутри этого угла, меньше полуокружности (Рис. 3, а).
• Если АОВ неразвернутый, то дуга АМВ, расположенная во внешней области этого угла, больше полуокружности (Рис. 3, б).

       

Измерение дуги окружности

Дугу окружности можно измерять в градусах

.

• Если дуга АВ окружности с центром О меньше полуокружности (Рис. 3, а) или является полуокружностью (Рис. 2), то ее градусная мера считается равной градусной мере центрального угла АОВ.
• Если дуга АВ окружности с центром О больше полуокружности (Рис. 3, б), то ее градусная мера считается равной 360⁰ — АОВ.

Сумма градусных мер двух дуг окружности с общими концами равна 3600.

Градусная мера дуги

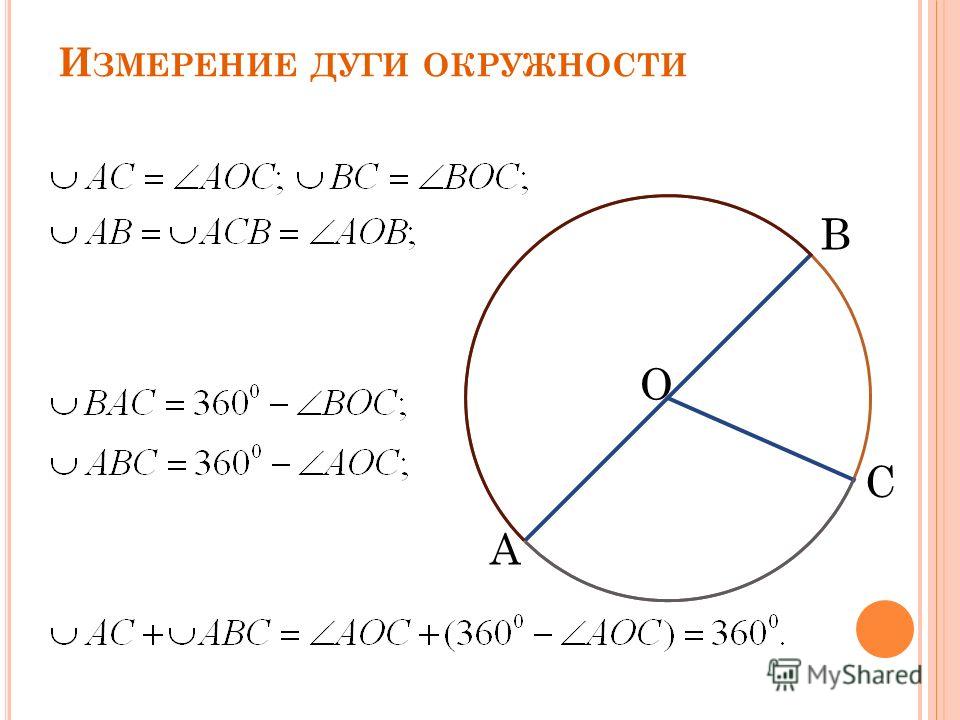
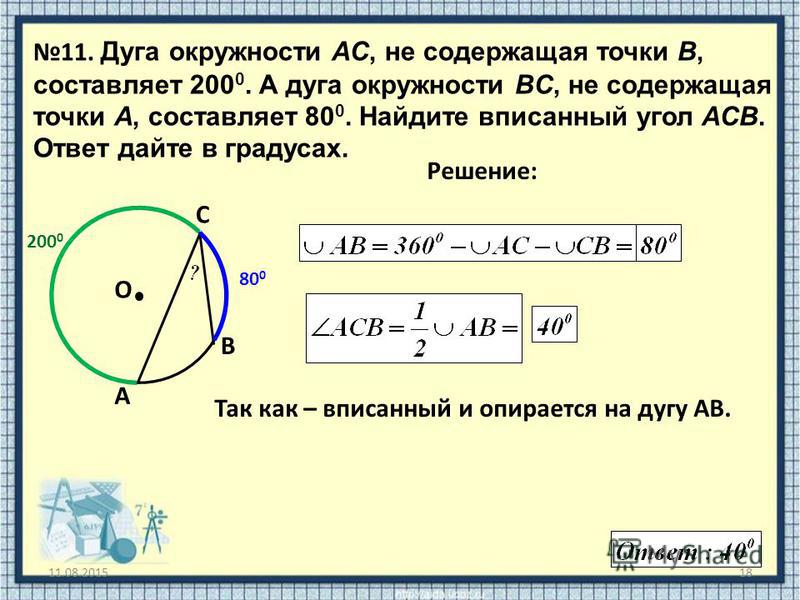АВ (дуги АLВ), как и сама дуга, обозначается символом АВ ( АLВ). На рисунке 4 градусная мера дуги САВ равна 145⁰. Обычно говорят кратко: «Дуга САВ равна 145⁰» и пишут: САВ = 145⁰. Также на рисунке 4 АDВ = 360⁰ — 115⁰ = 245⁰, СDВ = 360⁰ — 145⁰ = 215⁰, DВ = 180⁰.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Взаимное расположение прямой и окружности

Касательная к окружности

Теорема о вписанном угле

Свойство биссектрисы угла

Свойства серединного перпендикуляра к отрезку

Теорема о пересечении высот треугольника

Вписанная окружность

Описанная окружность

Окружность

Правило встречается в следующих упражнениях:

7 класс

Задание 705, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 26, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 715, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 717, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1133, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1134, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1180, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 22, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1281, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Создание дуг окружностей—ArcGIS Pro | Документация

На панели Создать объекты среди инструментов построения линейных и полигональных объектов есть метод создания дуг окружности.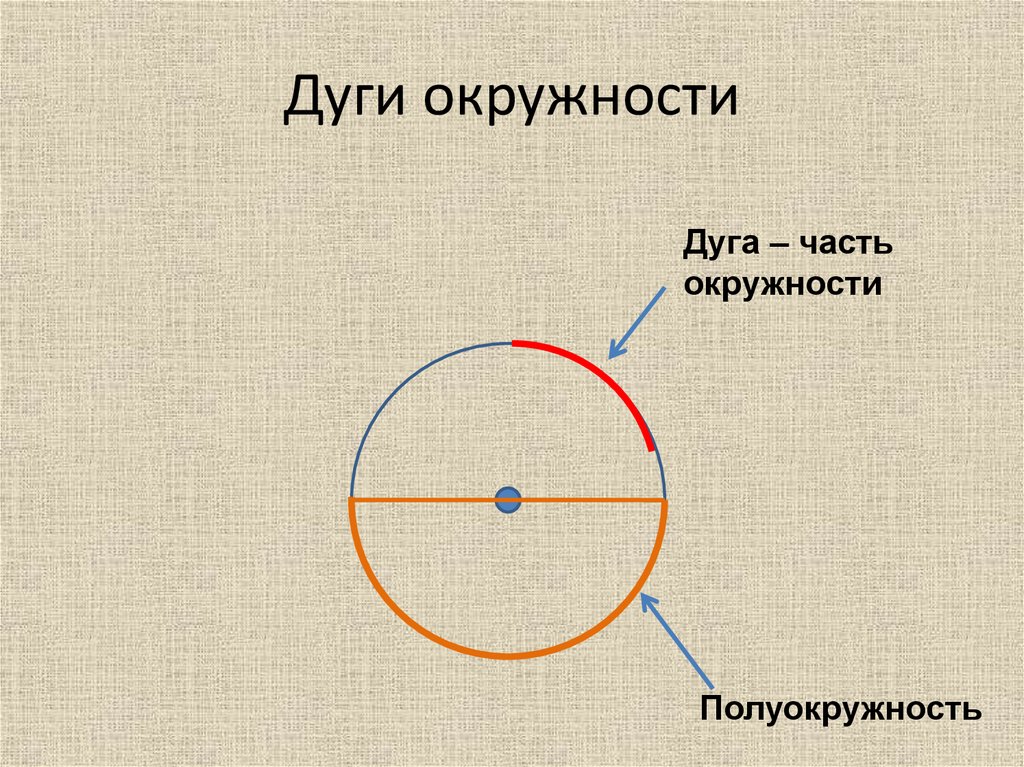 Они доступны на панели инструментов построения и в контекстном меню при создании объекта.

Дуга окружности — это часть линии круга. Геометрия задается радиусом и длиной хорды либо углом дельта. Вы можете создавать их в виде части непрерывной линии или контура полигона или как двухточечный дуговой элемент.

Шаги для получения линии или дуги из сегмента см. в разделе Изменение сегментов объектов.

Создание сегмента дуги

Сегмент дуги задается начальной точкой, точкой, через которую проходит дуга, и конечной точкой. Вы можете поставить все эти три точки, перетащить курсор либо указать радиус либо воспользоваться диалоговым окном дуги окружности, чтобы задать значения для геометрии.

1. На панели Каталог выполните следующие действия для добавления слоя полилиний к своей карте:
   • Разверните Базы данных , затем базу, содержащую ваши данные, и перетащите класс объектов на карту.
   • Щелкните правой кнопкой базу данных по умолчанию и создайте новый линейный или полигональный класс объектов.

   Перетаскивание на карту или создание класса объектов приводит к добавлению слоя на текущую карту и созданию шаблона объектов с настройками по умолчанию.

2. На закладке Редактирование в группе Замыкание задайте свои предпочтительные настройки замыкания.
3. Если вы работаете с объектами, имеющими z-значения, на вкладке Редактировать в группе Высота выберите способ добавления z-значений к объектам.

   Шаги для добавления z-значений при создании объектов с z-значениями см. в разделе Указание высоты для 3D-объектов.

4. На вкладке Редактировать в группе Объекты щелкните Создать .

   Появится панель Создать объекты.

5. На панели щелкните шаблон полилинейного или полигонального объекта.
   • Для создания вершины линии щелкните Линия .
   • Чтобы создать вершину полигона, щелкните Полигон.

   Внизу карты появляется панель инструментов Построение.

6. На панели инструментов построения щелкните инструмент Сегмент дуги .
7. Создайте начальную точку одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.
   • Начальной точкой является последняя точка предыдущего сегмента.
8. Создайте вторую точку, которая описывает путь дуги, одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.

   Путь дуги замкнется на эту новую точку.

9. Создайте конечную точку и задайте радиус, используя один из следующих способов:
   • Переместите указатель мыши, чтобы задать радиус, и снова щелкните на карте, чтобы создать конечную точку.
   • Нажмите клавишу R, введите радиус, нажмите Enter и щелкните карту, чтобы создать конечную точку.
   • Щелкните правой кнопкой, нажмите Дуга окружности , укажите радиус и другие значения геометрии и нажмите Enter, чтобы закрыть диалоговое окно и создать дугу.

     Значения геометрии по умолчанию для новой дуги основаны на расположении точек, которые вы нарисовали на карте.

10. Чтобы продолжить создание остальных сегментов дуги, используйте инструменты на панели инструментов построения.
11. На панели инструментов построения нажмите Готово или нажмите клавишу F2.

Создание дуги по конечным точкам

Сегмент дуги по конечным точкам задается начальной точкой, конечной точкой и радиусом. Вы можете поставить все эти три точки, перетащить курсор либо указать радиус, или воспользоваться диалоговым окном дуги окружности, чтобы задать значения ограничений для геометрии.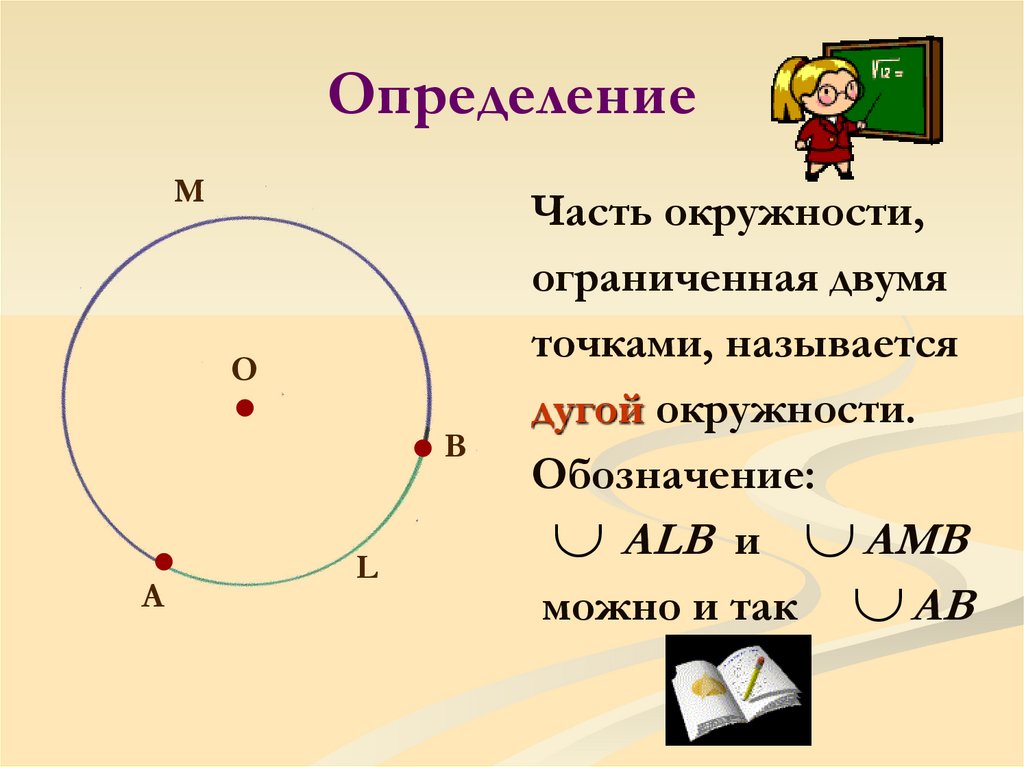

1. На панели Каталог выполните следующие действия для добавления слоя полилиний к своей карте:
   • Разверните Базы данных , затем разверните базу, содержащую ваши данные, и перетащите класс объектов на карту.
   • Щелкните правой кнопкой базу данных по умолчанию и создайте новый линейный или полигональный класс объектов.

   Перетаскивание на карту или создание класса объектов приводит к добавлению слоя на текущую карту и созданию шаблона объектов с настройками по умолчанию.

2. На закладке Редактирование в группе Замыкание задайте свои предпочтительные настройки замыкания.
3. На вкладке Редактировать в группе Объекты щелкните Создать .

   Появится панель Создать объекты.

4. На панели щелкните шаблон полилинейного или полигонального объекта.
   • Для создания вершины линии щелкните Линия .
   • Чтобы создать вершину полигона, щелкните Полигон.

   Внизу карты появляется панель инструментов Построение.

5. Если вы работаете с объектами, имеющими z-значения, на вкладке Редактировать в группе Высота выберите способ добавления z-значений к объектам.

   Шаги для добавления z-значений при создании объектов с z-значениями см. в разделе Указание высоты для 3D-объектов.

6. На панели инструментов построения щелкните инструмент Сегмент дуги конечной точки .

   Вы можете выбирать между прямыми и дуговыми сегментами в любой момент создания объекта.

7. Создайте начальную и конечную точки дуги одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.
   • Начальной точкой является последняя точка предыдущего сегмента.

   Между начальной и конечной точками будет создана дуга.

8. Создайте конечную точку и задайте радиус, используя один из следующих способов:
   • Переместите курсор, чтобы задать радиус, и щелкните на карте.
   • Нажмите клавишу R, введите радиус и нажмите Enter.
   • Щелкните правой кнопкой, нажмите Дуга окружности , укажите радиус и другие значения геометрии и нажмите Enter, чтобы закрыть диалоговое окно и создать дугу.

     Значения геометрии по умолчанию для новой дуги основаны на расположении точек, которые вы нарисовали на карте.

9. Чтобы продолжить создание остальных сегментов дуги, используйте инструменты на панели инструментов построения.
10. На панели инструментов построения нажмите Готово или нажмите клавишу F2.

Связанные разделы

---

Отзыв по этому разделу?

Вписанный и центральный угол окружности

С появлением окружности, а затем колеса  человечество сильно упростило себе жизнь.

И через много веков на ЕГЭ появились задачи по этой теме, конечно же 🙂

Зная свойства вписанного и центрального угла окружности, ты сможешь решить множество таких задач. И в этой статье мы тебе с этим поможем.

• Как измерить дуги и окружности
• Свойства вписанного угла и следствия из них
• Как выразить углы между хордами и секущими через центральный угол
• и многое другое…

Поехали!

Вписанный и центральный угол окружности — коротко о главном

Центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.

Радиус – отрезок, соединяющий центр и точку на окружности.

Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.

Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.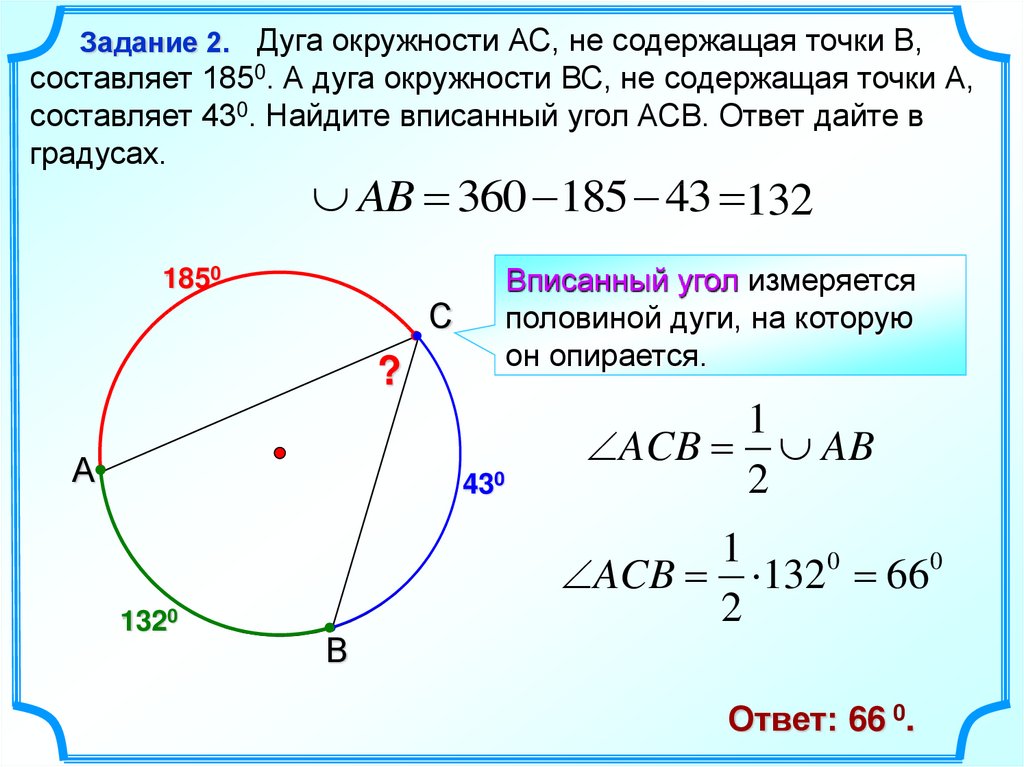

А вот что получится, если соединить две точки на окружности? Тоже отрезок? Так вот, этот отрезок называется «хорда».

Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда \( \displaystyle AB\) стягивает дугу \( \displaystyle AB\). 

А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».

Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же, 

Радиус равен половине диаметра.

Кроме хорд бывают еще и секущие.

Вспомнили самое простое?

А теперь – названия для углов.

Центральный угол – угол между двумя радиусами.

Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.

А теперь – вписанный угол.

Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.

При этом говорят, что вписанный угол \( \displaystyle ABC\) опирается на дугу (или на хорду) \( \displaystyle AC\).

Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.

Смотри на картинку:

Измерение дуг и углов окружности

Длина окружности. Дуги и углы измеряются в градусах и радианах. 

Сперва о градусах

Для углов проблем нет – нужно научиться измерять дугу в градусах.

Градусная мера (величина дуги) – это величина (в градусах) соответствующего центрального угла

Что здесь значит слово «соответствующего»? Смотрим внимательно:

Видишь две дуги \( \displaystyle AB\) и два центральных угла?

Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше \( \displaystyle 180{}^\circ \)), а меньшей дуге соответствует меньший угол.

Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.

А теперь о радианах

Что же это за зверь такой «радиан»?

Представь себе: радианы – это способ измерения угла … в радиусах!

Угол величиной \( \displaystyle 1\) радиан – такой центральный угол, длина дуги которого равна радиусу окружности.

Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?

Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?

Этим вопросом задавались учёные ещё в Древней Греции.

И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде \( \displaystyle 1,\text{ }2,\text{ }3,\frac{7}{5},\frac{2}{239}\) и т.п.

И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в \( \displaystyle 2,5\) раза или в \( \displaystyle \sqrt{17}\) раз больше радиуса!

Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву \( \displaystyle \pi \).

Итак, \( \displaystyle \pi \) – это число, выражающее отношение длины полуокружности к радиусу.

Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём \( \displaystyle \pi \) радиан. Именно оттого, что половина окружности в \( \displaystyle \pi \) раз больше радиуса.

Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число \( \displaystyle \pi \), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что

\( \displaystyle \pi \approx 3,14\)

Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна \( \displaystyle 6,28\), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква \( \displaystyle \pi \). \circ \), то есть \( \displaystyle 2\pi \)

Вписанный угол вдвое меньше центрального — доказательство

Имеет место удивительный факт:

Величина вписанного угла вдвое меньше, чем величина соответствующего центрального угла.

Посмотри, как это утверждение выглядит на картинке. «Соответствующий» центральный угол такой, у которого концы совпадают с концами вписанного угла, а вершина в центре.

И при этом «соответствующий» центральный угол должен «смотреть» на ту же хорду (\( \displaystyle AC\)), что и вписанный угол.

Почему же так? Почему вписанный угол вдвое меньше центрального?

Давай разберёмся сначала на простом случае.

Вписанный угол вдвое меньше центрального — следствия

Давай теперь сформируем два главных и очень важных следствия из утверждения о том, что вписанный угол вдвое меньше центрального:

• Все вписанные углы, опирающиеся на одну дугу, равны между собой
• Следствие 2. Угол, опирающийся на диаметр – прямой

Угол между хордами и секущими, выраженный через центральный угол

А что, если интересующий нас угол НЕ вписанный и НЕ центральный, а, например, такой:

Или такой:

Можно ли его как-то выразить всё-таки через какие-то центральные углы?

Оказывается, можно.

Угол между хордами равен полусумме угловых величин дуг, заключённых в этот угол

Нас интересует \( \displaystyle \angle ABC\).

\( \displaystyle \angle \text{ }\!\!~\!\!\text{ ABC}=\text{ }\!\!~\!\!\text{ }\angle \text{ }\!\!\alpha\!\!\text{ }+\angle \text{ }\!\!\beta\!\!\text{ }\) ( как внешний угол для \( \displaystyle \Delta ADB\)).

Но \( \displaystyle \angle \text{ }\!\!\alpha\!\!\text{ }\) — вписанный, опирается на дугу \( \displaystyle DE\) — \( \displaystyle \angle \text{ }\!\!\alpha\!\!\text{ }=\frac{1}{2}\text{ }\!\!~\!\!\text{ }\angle \text{DOE}\).

\( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }\) – вписанный, опирается на дугу \( \displaystyle AC\) — \( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }=\frac{1}{2}\text{ }\!\!~\!\!\text{ }\angle \text{AOC}\).

Значит, \( \displaystyle \angle ~ABC=\frac{1}{2}\angle \text{DOE}+\frac{1}{2}\angle \text{AOC}\).

Для красоты говорят:

Угол между хордами равен полусумме угловых величин дуг, заключённых в этот угол.

\( \displaystyle \angle \text{ }\!\!~\!\!\text{ ABC}=\frac{\text{AC}}{2}+\frac{\text{DE}}{2}\) – так пишут для краткости, но конечно, при использовании этой формулы нужно иметь в виду центральные углы.

Окружность. Длина окружности. Касательная, дуга

Общие определения

Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.

Для любой точки L, лежащей на окружности, действует равенство OL=R. (Длина отрезка OL равняется радиусу окружности). {\circ}}

Используя радианную меру: CD = \alpha R

Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой.

AN\cdot NB = CN \cdot ND

Касательная к окружности

Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.

Если же у прямой есть две общие точки, ее называют секущей.

Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.

Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.

AC = CB

Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}

\angle ADB = \angle AEB = \angle AFB

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.

Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.

\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left ( \cup DmC + \cup AlB \right )

Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.

\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left ( \cup DmC — \cup AlB \right )

Вписанная окружность

Вписанная окружность — это окружность, касающаяся сторон многоугольника.

В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.

Окружность может быть вписанной не в каждый многоугольник.

Площадь многоугольника с вписанной окружностью находится по формуле:

S = pr,

где:

p — полупериметр многоугольника,

r — радиус вписанной окружности.

Отсюда следует, что радиус вписанной окружности равен:

r = \frac{S}{p}

Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.

AB + DC = AD + BC

В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.

Радиус вписанной окружности вычисляется по формуле:

r = \frac{S}{p},

где p = \frac{a + b + c}{2}

Описанная окружность

Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника. {\circ}

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.

Радиус описанной окружности можно вычислить по формулам:

R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}

R = \frac{abc}{4 S}

где:

a, b, c — длины сторон треугольника,

S — площадь треугольника.

Теорема Птолемея

Под конец, рассмотрим теорему Птолемея.

Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.

AC \cdot BD = AB \cdot CD + BC \cdot AD

123.2. Дуга окружности

Глава 123. Пространственные кривые

Дугу окружности в пространстве можно построить следующими способами:

▼По 3 точкам,

▼По центру и радиусу,

▼По 2 точкам с направлением,

▼С касанием к кривой.

Чтобы создать дугу окружности в пространстве, вызовите команду Дуга окружности.

Выберите вариант построения дуги из списка Способ или при помощи команд контекс! тного меню. На Панели свойств появятся элементы управления построением (рис. 123.4).

Рис. 123.4. Панель свойств при построении дуги окружности по 3 точкам

Затем задайте параметры дуги и объекты, используемые при построении.

После задания одного из параметров дуги переход к следующему параметру происходит автоматически.

Во всех способах объектами построения являются точки. Точку дуги можно указать сле! дующими способами:

▼задать координаты в пространстве или указать положение мышью в окне модели;

▼связать с уже имеющимся точечным объектом;

▼создать, используя способы построения точки команды Точка, не выходя из процесса построения дуги (см. раздел 120.2 на с. 350).

Указание точечного объекта при включенной опции Ассоциировать приводит к форми! рованию ассоциативной связи точки дуги с этим объектом.

Признаком наличия связи является отображение «галочки» на кнопке Объект и наиме! нования точечного объекта в поле Объект на Панели свойств. При любом изменении по! ложения объекта точка дуги будет следовать за объектом.

Чтобы отменить ассоциативную связь с точечным объектом, следует нажать кнопку Объект. «Галочка» на кнопке исчезнет.

Для восстановления ассоциативной связи точки с точечным объектом необходимо вклю! чить опцию Ассоциировать и указать нужный объект заново.

Подробно о вводе параметров и указании объектов для каждого способа рассказано в разделах 123.2.1— 123.2.4.

Координаты точек задаются в системе координат дуги (о системе координат объекта — см. раздел 116.2 на с. 309).

363

Часть XXIII. Пространственные кривые, точки, поверхности

После задания всех необходимых данных на экране появляется фантом дуги окружнос! ти. Пока построение не завершено, вы можете изменить параметры дуги, активизировав необходимый элемент управления на Панели свойств.

При необходимости вы можете построить окружность. Для этого активизируйте пере! ключатель Окружность в группе Дуга. Такая возможность существует во всех способах построения дуги.

До завершения команды система «запоминает» параметры и объекты, указанные в каж! дом из способов построения, поэтому вы можете переключаться между способами без потери этих данных.

Чтобы сменить объекты, используемые для построения дуги окружности выбранным способом, нажмите кнопку Указать заново на Панели специального управления и пов! торите выбор объектов.

Элементы управления, расположенные на вкладке Свойства Панели свойств, позволя! ют изменить название и цвет дуги, настроить параметры ее отображения (о параметрах отображения см. раздел 123.1 на с. 361). Также на этой вкладке отображается название системы координат дуги (о системе координат объекта см. раздел 116.2.1 на с. 309).

Чтобы завершить построение, нажмите кнопку Создать объект на Панели специально! го управления.

При всех способах построения дуги окружности доступен режим автосоздания, который по умолчанию включен. Подробно об автоматическом и ручном создании объектов рас! сказано в Томе I, разделе 8. 1.10 на с. 91.

123.2.1. Построение по 3 точкам

По 3 точкам — способ построения дуги окружности по трем точкам.

Для построения дуги окружности данным способом укажите начальную точку дуги 1, за! тем конечную точку дуги 2 и промежуточную точку на дуге 3. После указания точки 1 на экране появляется фантом окружности, после указания точки 2 — фантом дуги. Указа! ние промежуточной точки 3 определяет дугу полностью.

▼Точку дуги можно указать, задав ее координаты в пространстве или связав ее с уже име! ющимся точечным объектом. Задание координат точки и связывание ее с точечным объ! ектом производится так же, как при создании точки способом По координатам (см. раздел 120.1.2 на с. 341).

▼Точку дуги можно указать, построив ее. При этом используются способы построения точки команды Точка. Подробно об этом рассказано в разделе 120.1 на с. 339.

По умолчанию дуга окружности проходит от точки 1 к точке 2 через точку 3. При этом активен переключатель Дуга по умолчанию. Чтобы построить дополняющую дугу (не проходящую через точку 3) или окружность, активизируйте нужный переключатель.

123.2.2. Построение по центру и радиусу

По центру и радиусу — способ построения дуги окружности с указанием плоскости дуги и заданием параметров: центра дуги, начального и конечного углов, радиуса.

364

Глава 123. Пространственные кривые

Плоскость дуги окружности располагается параллельно базовой плоскости. В качестве базовой плоскости может использоваться:

▼координатная или вспомогательная плоскость;

▼плоская грань;

▼плоскость эскиза.

Чтобы построить дугу, выполните следующие действия.

1.Укажите центральную точку дуги 1.

▼Точку дуги можно указать, задав ее координаты в пространстве или связав ее с уже име! ющимся точечным объектом. Задание координат точки и связывание ее с точечным объ! ектом производится так же, как при создании точки способом По координатам (см. раздел 120.1.2 на с. 341).

▼Точку дуги можно указать, построив ее. При этом используются способы построения точки команды Точка. Подробно об этом рассказано в разделе 120.1 на с. 339.

По умолчанию базовая плоскость — одна из координатных плоскостей. Система выби! рает ее автоматически в зависимости от расположения модели относительно плоскости экрана. Наименование выбранной координатной плоскости отображается в поле Базо вая плоскость.

При необходимости вы можете сменить базовую плоскость. Для этого активизируйте пе! реключатель Базовая плоскость и укажите нужный объект в Дереве или в окне модели (эскиз следует указывать в Дереве модели).

Построение дуги можно начинать с указания базовой плоскости: активизируйте пере! ключатель Базовая плоскость, выберите нужный объект, а затем укажите точку 1.

После указания точки 1 автоматически определяется положение плоскости дуги: по за! данной центральной точке и базовой плоскости. На экране появляется фантом окруж! ности дуги с центральной точкой 1.

2.Введите радиус/диаметр дуги. По умолчанию система ожидает ввода радиуса. При этом в группе Параметр активен переключатель Радиус. Чтобы ввести диаметр, активизи! руйте переключатель Диаметр. На экране появляется фантом окружности заданного размера.

3.Укажите начальную точку дуги 2, задав начальный угол дуги. Начальный угол отсчиты! вается от оси абсцисс системы координат базовой плоскости. Значение угла можно ввести с клавиатуры или связать начальную точку дуги с уже имеющимся точечным объ! ектом. На экране появляется фантом дуги с заданным начальным углом.

4.Укажите точку дуги 3, задав конечный угол. Конечный угол задается аналогично началь! ному.

После выполнения вышеописанных действий дуга определена полностью — указаны положение плоскости дуги, точка центра, начальный и конечный углы, радиус.

По умолчанию дуга окружности строится по часовой стрелке от точки 2 к 3. При этом ак!

тивен переключатель Дуга по умолчанию. Чтобы построить дополняющую дугу или окружность, активизируйте нужный переключатель.

365

Часть XXIII. Пространственные кривые, точки, поверхности

При построении полной дуги окружности после указания точки 1 система сразу перехо! дит к заданию радиуса (точки 4).

123.2.3. Построение по 2 точкам с направлением

По 2 точкам с направлением — способ построения дуги окружности по двум точкам с указанием в одной из них направления касательного вектора. Направление касательного вектора задается с помощью вектора или направляющих объектов. В качестве направля! ющих могут использоваться следующие объекты.

▼Прямолинейный объект:

▼отрезок в эскизе,

▼сегмент ломаной,

▼координатная или вспомогательная ось,

▼прямолинейное ребро.

Направление, задаваемое прямолинейным объектом — прямая, параллельная объекту.

▼Плоский объект:

▼координатная или вспомогательная плоскость,

▼плоская грань,

▼плоскость эскиза.

Направление, задаваемое плоским объектом — прямая, перпендикулярная объекту.

▼Кривая (если начальная или конечная точка дуги лежит на этой кривой).

Направление, задаваемое кривой — касательный вектор в точке касания. Таким образом можно построить дугу, сопряженную с произвольной кривой — пространственным сплайном или ломаной, ребром и др.

Чтобы построить дугу, выполните следующие действия.

1.Задайте начальную точку дуги 1.

▼Точку дуги можно указать, задав ее координаты в пространстве или связав ее с уже име! ющимся точечным объектом. Задание координат точки и связывание ее с точечным объ! ектом производится так же, как при создании точки способом По координатам (см. раздел 120.1.2 на с. 341).

▼Точку дуги можно указать, построив ее. При этом используются способы построения точки команды Точка. Подробно об этом рассказано в разделе 120.1 на с. 339.

2.Задайте конечную точку дуги 2. Точка 2 задается аналогично точке 1. После задания точ! ки 2 система переходит к выбору направления для этой точки — активизируется пере! ключатель Направление в точке, соответствующий точке 2.

3.Задайте направление. Для этого укажите нужный направляющий объект в Дереве или в окне модели (эскиз следует указывать в Дереве модели) или постройте вектор (см. главу 118).

Для создания вектора нажмите кнопку Построение вектора. Эта кнопка находится на Панели специального управления.

366

Дуга окружности – объяснение и примеры

После радиуса и диаметра другой важной частью окружности является дуга . В этой статье мы обсудим что такое дуга, найдем длину дуги и измерим длину дуги в радианах. Мы также изучим малую дугу и большую дугу.

Что такое дуга окружности?

Дуга окружности – это любая часть окружности окружности. Напомним, длина окружности — это периметр или расстояние вокруг окружности. Следовательно, можно сказать, что длина окружности — это полная дуга самой окружности.

Как найти длину дуги?

Th Формула для расчета дуги гласит:

Длина дуги = 2πr (θ/360)

Где r = радиус окружности,

π = pi = 3,14

7

7 угол ( в градусах ), опирающийся на дугу в центре окружности.

360 = угол одного полного оборота.

На приведенном выше рисунке длина дуги (обведена красным) представляет собой расстояние от точки A до точки B.

Давайте решим несколько примеров задач на длину дуги:

Пример 1 к центру окружности радиусом 7 см. Вычислите длину дуги AB.

Решение

Дано r = 7 см

θ = 40 градусов.

Замена,

Длина дуги = 2πr(θ/360)

Длина = 2 х 3,14 х 7 х 40/360

= 4,884 см.

Пример 2

Найдите длину дуги окружности, которая образует угол 120 градусов с центром окружности на расстоянии 24 см.

Решение

Длина дуги = 2πr(θ/360)

= 2 х 3,14 х 24 х 120/360

= 50,24 см.

Пример 3

Длина дуги 35 м. Найдите угол, образуемый дугой, если радиус окружности равен 14 м.

Решение

Длина дуги = 2πr(θ/360)

35 м = 2 x 3,14 x 14 x (θ/360)

35 = 87,92θ/360 6p на обе стороны

7 чтобы удалить дробь.

12600 = 87,92θ

Разделите обе стороны на 87,92

θ = 143,3 градуса.

Пример 4

Найдите радиус дуги длиной 156 см, образующей угол 150 градусов с центром окружности.

Решение

Длина дуги = 2πr (θ/360)

156 см = 2 x 3,14 x r x 150/360

156 = 2,6167 R

Разделите обе стороны на 2,6167

R = 59,62 CM.

Итак, радиус дуги равен 59,62 см.

Как найти длину дуги в радианах?

Существует связь между углом, образуемым дугой в радианах, и отношением длины дуги к радиусу окружности. В данном случае

θ = (длина дуги) / (радиус окружности).

Следовательно, длина дуги в радианах определяется как

S = r θ

, где θ = угол, образуемый дугой в радианах

S = длина дуги.

r = радиус окружности.

Один радиан — это центральный угол, опирающийся на дугу одного радиуса, т. е. s = r

Радиан — это просто еще один способ измерения величины угла. Например, чтобы преобразовать углы из градусов в радианы, умножьте угол (в градусах) на π/180.

Аналогичным образом, чтобы преобразовать радианы в градусы, умножьте угол (в радианах) на 180/π.

Пример 5

Найдите длину дуги, радиус которой равен 10 см, а образуемый угол равен 0,349 радиана.

Решение

Длина дуги = r θ

= 0,349 x 10

= 3,49 см.

Пример 6

Найдите длину дуги в радианах с радиусом 10 м и углом 2,356 радиан.

Решение

Длина дуги = r θ

= 10 м x 2,356

= 23,56 м.

Пример 7

Найдите угол, образуемый дугой длиной 10,05 мм и радиусом 8 мм.

Решение

Длина дуги = r θ

10,05 = 8 θ

Разделите обе стороны на 8.

1,2567 = θ 7

Пример 8

Вычислите радиус круга, длина дуги которого составляет 144 ярда, а угол дуги равен 3,665 радиана.

Решение

Длина дуги = r θ

144 = 3,665r

Разделите обе стороны на 3,665.

144/3,665 = r

r = 39,29 ярда.

Пример 9

Вычислите длину дуги, образующей угол 6,283 радиана с центром круга радиусом 28 см.

Решение

Длина дуги = R θ

= 28 x 6,283

= 175,93 см

Мятятная дуга (H4)

центр круга. Другими словами, малая дуга имеет размеры меньше полуокружности и представлена ​​на окружности двумя точками. Например, дуга AB в круге ниже является малой дугой.

Большая дуга (h4)

Большая дуга окружности — это дуга, образующая угол более 180 градусов с центром окружности. Большая дуга больше полуокружности и представлена ​​тремя точками на окружности.

Например, PQR — это большая дуга окружности, показанной ниже.

 

Длина дуги – Формула, Как найти длину дуги, Примеры

Длину дуги лучше определить как расстояние вдоль части окружности любой окружности или любой кривой (дуги). Любое расстояние вдоль изогнутой линии, образующей дугу, называется длиной дуги. Часть кривой или часть окружности окружности называется Дугой. Все они имеют кривую форму. Длина дуги больше, чем любое расстояние по прямой линии между ее концами (хорда).

1.	Что такое длина дуги?
2.	Формула длины дуги
3.	Как найти длину дуги кривой?
4.	Часто задаваемые вопросы о длине дуги

Что такое длина дуги?

Длина дуги определяется как промежуток между двумя точками на участке кривой. Дуга окружности – это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками прямой, соединяющими эту точку с конечными точками дуги. Например, в окружности, показанной ниже, OP — это дуга окружности с центром Q. Длина дуги этой дуги OP равна L.

Формула длины дуги

Длина дуги может быть рассчитана с использованием различных формул, основанных на единице измерения центрального угла дуги. Измерения центрального угла могут быть даны в градусах или радианах, и соответственно мы вычисляем длину дуги окружности. Для круга формула длины дуги равна θ, умноженному на радиус круга.

Формула длины дуги в радианах может быть выражена как длина дуги = θ × r, когда θ выражено в радианах. Длина дуги = θ × (π/180) × r, где θ в градусах, где

• L = длина дуги
• θ = центральный угол дуги
• r = радиус окружности

Формула длины дуги в радианах

Длину дуги окружности можно рассчитать с помощью различных формул, основанных на единице измерения центрального угла дуги. Формула длины дуги в радианах может быть выражена следующим образом:

Длина дуги = θ × r

, где

• L = длина дуги
• θ = Центральный угол дуги в радианах 903:50
• r = радиус окружности

Как найти длину дуги кривой?

Длина дуги окружности может быть рассчитана с использованием различных методов и формул на основе заданных данных. Некоторые важные случаи приведены ниже,

• найти длину дуги с радиусом и центральным углом
• найти длину дуги без радиуса
• найти длину дуги без центрального угла

Как найти длину дуги по радиусу и центральному углу?

Длину дуги окружности можно рассчитать с помощью радиуса и центрального угла, используя формулу длины дуги:

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π/180) × r, где θ выражается в градусах.

Как найти длину дуги без радиуса?

Длину дуги окружности можно рассчитать без радиуса, используя:

Центральный угол и площадь сектора:

• Умножьте площадь сектора на 2 и далее разделите результат на центральный угол в радианах.
• Найдите квадратный корень из результата деления.
• Умножьте полученный корень на центральный угол еще раз, чтобы получить длину дуги.
• Единицами расчетной длины дуги будут квадратный корень из единиц площади сектора.

Пример: Рассчитайте длину дуги кривой с площадью сектора 25 квадратных единиц и центральным углом, равным 2 радианам.

Имеем,

Площадь сектора = 25 единиц

Центральный угол = 2 радиана

• Шаг 1: Площадь сектора × 2 = 25 × 2 = 50
• Шаг 2: 50/центральный угол = 50/2 = 25
• Шаг 3: √25 = 5
• Шаг 4: 5 × центральный угол = 5 × 2 = 10 шт.

Таким образом, длина дуги = 10 единиц

Центральный угол и длина хорды:

• Разделить центральный угол в радианах на 2 и далее произвести над ним функцию синуса.
• Разделите заданную длину хорды на удвоенный результат шага 1. В результате этого вычисления вы получите радиус.
• Умножьте радиус на центральный угол, чтобы получить длину дуги.

Пример : Вычислить длину дуги кривой, концы которой касаются хорды окружности размером 5 единиц. Центральный угол, образуемый дугой, равен 2 радианам.

Имеем,

Длина хорды = 5 единиц

Центральный угол = 2 радиана

• Шаг 1: Центральный угол/2 = 2/2 = 1
• Шаг 2: Sin(1) = 0,841
• Шаг 3: Длина хорды / (2 × 0,841) = 5/ 1,682 = 2,973 единицы = радиус
• Шаг 4: Длина дуги = радиус × центральный угол = 2,973 × 2 = 5,946 единиц

Таким образом, длина дуги = 5,946 единиц

Как найти длину дуги без центрального угла?

Длину дуги окружности можно рассчитать без угла, используя:

Радиус и площадь сектора :

• Умножьте площадь сектора на 2.
• Затем разделите результат на квадрат радиуса (единицы должны быть одинаковыми), чтобы получить центральный угол в радианах.
• Умножьте центральный угол на радиус, чтобы получить длину дуги.

Пример: Рассчитайте длину дуги кривой с площадью сектора 25 квадратных единиц и радиусом 2 единицы.

Имеем,

Площадь сектора = 25 единиц

Центральный угол = 2 единицы

• Шаг 1: Площадь сектора × 2 = 25 × 2 = 50
• Шаг 2: 50/радиус ² = 50/4 = 12,5 = центральный угол (рад)
• Шаг 3: Длина дуги = радиус × центральный угол = 2 × 12,5 = 25 единиц

Таким образом, длина дуги = 25 единиц

Радиус и длина хорды:

• Разделите длину хорды на удвоенный заданный радиус.
• Найдите арксинус полученного результата.
• Удвойте результат обратного синуса, чтобы получить центральный угол в радианах.
• Умножьте центральный угол на радиус, чтобы получить длину дуги.

Пример : Вычислить длину дуги кривой, концы которой касаются хорды окружности размером 5 единиц. Радиус круга равен 2 единицам.

У нас,

Длина хорды = 5 единиц

Центральный угол = 2 единицы

• Шаг 1: Длина хорды/(2 × радиус) = 5/(2 × 2) = 1,25
• Шаг 2: Sin ^-1 (1,25) = 0,949
• Шаг 3: Центральный угол = 2 × 0,949 = 1,898 радиан
• Шаг 4: Длина дуги = радиус × центральный угол = 2 × 1,898 = 3,796 единицы

Таким образом, длина дуги = 3,796 единицы

☛ Важные примечания о длине дуги

Ниже приведены основные моменты концепции длины дуги.

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π/180) × r, где θ в градусах.

☛ Темы, связанные с длиной дуги

Ознакомьтесь с еще несколькими интересными статьями, посвященными длине дуги, чтобы лучше понять тему.

• Калькулятор длины дуги
• Центральный угол
• Что такое радиан?
• Калькулятор дуги окружности
• Радиус

 

Примеры длины дуги

1. Пример 1: Найдите длину дуги, отсеченной центральным углом 4 радиана в окружности радиусом 6 дюймов.

   Решение:

   Центральный угол, θ = 4 радиана, радиус, r = 6 дюймов . Используйте формулу длины дуги: L = θ × r = 4 × 6 = 24 дюйма. ∴ Длина дуги (PQ) = 24 дюйма

2. Вопрос 2: Радиус окружности равен 14 единицам, дуга стягивается в центре под углом 65°. Какова длина дуги?

   Решение: Мы знаем, что

   Длина окружности = 2πr

   C = 2π × 14 = 28π

   длина дуги = (θ/360) × C = (65°/360°)28π2 = ед.

3. Пример 3: Найдите длину дуги, отсеченной центральным углом θ = 40º в окружности радиусом 4 дюйма.

   Решение:

   Радиус, r = 4 дюйма, θ = 40º. Используйте формулу длины дуги: L = π × (r) × (θ/180º) = π × (4) × (40º/180º) = 2,79 дюйма. ∴ Длина дуги (P0) = 2,79 дюйма

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронировать бесплатный пробный урок

Практические вопросы по длине дуги

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о длине дуги

Что такое длина дуги окружности?

Длина дуги окружности определяется как расстояние между двумя точками на участке кривой. Дуга окружности – это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками прямой, соединяющими эту точку с конечными точками дуги.

Как найти длину дуги без радиуса?

Длину дуги окружности можно рассчитать без радиуса, используя:

Центральный угол и площадь сектора:

• Умножьте площадь сектора на 2 и далее разделите результат на центральный угол в радианах.
• Найдите квадратный корень из результата деления.
• Умножьте полученный корень на центральный угол еще раз, чтобы получить длину дуги.
• Единицами расчетной длины дуги будут квадратные корни из единиц площади сектора.

Центральный угол и длина хорды:

• Разделить центральный угол в радианах на 2 и далее произвести над ним функцию синуса.
• Разделите заданную длину хорды на удвоенный результат шага 1. В результате этого вычисления вы получите радиус.
• Умножьте радиус на центральный угол, чтобы получить длину дуги.

Что вы понимаете под уравнением длины дуги?

Есть два уравнения, связанные с длиной дуги. Ниже приведены два уравнения длины дуги.

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π/180) × r, где θ в градусах

Как найти длину дуги в радианах?

Длину дуги можно рассчитать, если центральный угол задан в радианах, по формуле: Длина дуги = θ × r, когда θ выражено в радианах.

• L = длина дуги
• θ = Центральный угол дуги
• r = радиус окружности

Должна ли длина дуги быть в радианах?

Нет, длина дуги не может быть указана в радианах. Это измерение расстояния, поэтому не может быть в радианах. Центральный угол, стягиваемый в центре, может быть выражен в радианах, градусах или угловых секундах соответственно.

Как найти длину окружности дуги?

Когда длина дуги дана с центральным углом θ, тогда длина окружности рассчитывается как длина дуги (L)/окружность = θ/360º.

Какова длина большой дуги с использованием формулы длины дуги?

Большая дуга в окружности больше, чем полуокружность. Измеряется как угол больше 180°. Используя формулу ℓ = rθ, мы можем найти длину дуги окружности, где θ в радианах.

Формула измерения дуги | Как найти меру угла дуги (видео)

Определение меры дуги

Дуга — это сегмент окружности по окружности. Дуговая мера — это угол, который образует дуга в центре окружности, тогда как длина дуги — это отрезок вдоль дуги. Эта мера угла может быть выражена в радианах или градусах, и мы можем легко преобразовать их по формуле π радианы = 180°.

Вы также можете измерить окружность или расстояние вокруг окружности. Если вы возьмете меньше полной длины вокруг окружности, ограниченной двумя радиусами, у вас будет дуги . Эта изогнутая часть круга и внутреннее пространство называется сектором , как кусок пиццы. Когда вы разрезаете круглую пиццу, корка делится на дуги.

1. Определение измерения дуги
2. Дуга окружности
3. Измерение дуги и длина дуги
4. Градусы и радианы
5. Формула измерения дуги
6. Как найти меру дуги
7. Как найти длину дуги
8. Идентификация указанного угла дуги

Дуга окружности

Если мы разрежем вкусную свежую пиццу, у нас будет две половинки, каждая из которых представляет собой дугу , измеряющую 180°. Если мы сделаем три дополнительных разреза только с одной стороны (так что мы разрезаем половину сначала на две четверти, а затем каждую четверть на две восьмых), мы получим одну сторону пиццы с одной большой дугой 180°, а другую сторону пицца с четырьмя дугами под 45° вот так:

Половина пиццы, представляющая собой один гигантский ломтик, представляет собой большую дугу , поскольку ее размер составляет 180° (или больше). Другая сторона пиццы имеет четыре малых дуги , поскольку каждая из них меньше 180°.

Измерение дуги в зависимости от длины дуги

Дуга — это часть длины окружности, которая лежит между двумя точками на окружности. Дуга имеет два измерения:

1. Длина дуги — это расстояние по окружности, измеряемое в тех же единицах, что и радиус, диаметр или вся окружность круга; эти единицы будут линейными мерами, такими как дюймы, см, м, ярды и т. д.
   
2. Измерение угла дуги , взятое в центре окружности, частью которой является дуга, измеряется в градусах (или радианах)
   

Не путайте измерение дуги (длину или угол) с расстоянием по прямой линии хорды , соединяющей две точки дуги на окружности. Длина хорды будет всегда короче длины дуги.

Градусы и радианы

Чтобы иметь возможность вычислять меру дуги, вы должны понимать измерения углов как в градусах, так и в радианах. Угол измеряется либо в градусах, либо в радианах. Круг измеряет 360 градусов, или 2π радиан, тогда как один радиан равен 180 градусам . Таким образом, градусы и радианы связаны следующими уравнениями:

360° = 2π радиан

180° = π радиан

Соотношение между радианами и градусами позволяет нам преобразовать их друг в друга с помощью простых формул. Чтобы преобразовать градусы в радианы, мы берем градусную меру, умноженную на пи, деленную на 180.

Давайте преобразуем 90 градусов в радианы, например:

90° × π180°

90π180

π2 Радианы

Теперь давайте преобразуем π3 Радиан в градусы:

π3 × 180π

180π3π

1803 = 60 °

ARC Formula

. формула, для расчета которой требуется длина дуги s и радиус окружности r.

мера дуги = радиус дуги = sr

Как найти меру дуги

Давайте рассмотрим пример, где длина дуги равна 3 см, а радиус равен 4 см, как показано на рисунке:

Начните с нашей формулы и подставьте туда все, что мы знаем:

угловая мера = sr

угловая мера = 34

Теперь мы можем преобразовать 34 радиана в градусы, умножив их на 180 и разделив на π.

34180π

42,9718 ≈ 43°

Как найти длину дуги

Чтобы рассчитать длину дуги, необходимо знать величину центрального угла, образующего дугу (угол двух радиусов). Длина дуги — это дробная часть длины окружности круга. Длина окружности любого круга находится с помощью 2πr, где r = радиус. Если у вас есть диаметр, вы также можете использовать πd, где d = диаметр.

Формула для определения длины дуги:

Длина дуги = угол дуги 360° 2πr

Давайте рассмотрим пример с этой пиццей:

Наш пирог имеет диаметр 16 дюймов, что дает радиус 8 дюймов. Мы знаем, что срез равен 60°. Таким образом, формула для этого конкретного куска пиццы:

     = 60°360° · 2·π·8

      = 16 · 16π

      ≈ 8,3775″

8 ⌢ где A и B — две точки на окружности, образующие дугу. m означает измерение, а короткая изогнутая линия над AB⌢ указывает на то, что мы имеем в виду дугу. Две точки, полученные из центрального угла (угол два радиуса, выходящие из центральной точки).

0007

Одно важное различие между длиной дуги и углом дуги заключается в том, что для двух окружностей разного диаметра секторы с одинаковым углом из каждой окружности не будут иметь одинаковую длину дуги. Длина дуги изменяется в зависимости от радиуса или диаметра круга (или пиццы).

Резюме урока

Теперь, когда вы ознакомились с этим уроком, вы можете идентифицировать и определить дугу и различать большие дуги и второстепенные дуги. Вы также можете измерить дугу в линейных единицах и градусах и использовать правильный символ mAB⌢ (где A и B — две точки на окружности), чтобы показать длину дуги. 9

Создано Bogna Szyk

Площадь сектора круга

Как найти длину дуги и площадь сектора: пример

Часто задаваемые вопросы

Этот калькулятор длины дуги представляет собой инструмент, который может рассчитать длину дуги и площадь круговой сектор. В этой статье подробно объясняется формула длины дуги и приводятся пошаговые инструкции о том, как найти длину дуги. Вы также узнаете уравнение площади сектора.

Если вы новичок в кругах, вычисление длины и площади секторов может быть немного сложным, и вам нужно начать с более простых инструментов, таких как длина круга и длина окружности и площадь круга калькуляторы.

Формула длины дуги

Длина дуги зависит от радиуса окружности и центрального угла θ . Мы знаем, что для угла, равного 360 градусам (2π), длина дуги равна длине окружности. Следовательно, поскольку пропорция между углом и длиной дуги постоянна, мы можем сказать, что:

L / θ = C / 2π

As circumference C = 2πr ,

L / θ = 2πr / 2π L / θ = r

We find out the arc length formula при умножении этого уравнения на θ:

L = r * θ

Следовательно, длина дуги равна радиусу, умноженному на центральный угол (в радианах).

Площадь сектора круга

Аналогичным образом можно найти площадь сектора круга. Мы знаем, что площадь всего круга равна πr². Из пропорций

A / θ = πr² / 2π A / θ = r² / 2

Формула площади сектора: длина дуги и площадь сектора: пример

1. Определите радиус окружности. Например, она может быть равна 15 см. (Вы также можете ввести диаметр в калькулятор длины дуги.)
2. Какой будет угол между концами дуги? Допустим, он равен 45 градусам, или π/4. 903:50
3. Рассчитайте длину дуги по приведенной выше формуле: L = r * θ = 15 * π/4 = 11,78 см .
4. Вычислите площадь сектора: A = r² * θ / 2 = 15² * π/4 / 2 = 88,36 см² .
5. Вы также можете использовать калькулятор длины дуги, чтобы найти центральный угол или радиус окружности. Просто введите любые два значения в соответствующие поля и посмотрите, как он проведет все расчеты за вас.

Не забудьте также воспользоваться калькулятором уравнения окружности!

Часто задаваемые вопросы

Как найти длину дуги без радиуса?

Чтобы вычислить длину дуги без радиуса, вам нужен центральный угол и площадь сектора :

1. Умножьте площадь на 2 и разделите результат на центральный угол в радианах.
2. Найдите квадратный корень из этого деления.
3. Умножьте этот корень на центральный угол еще раз, чтобы получить длину дуги.
4. Единицы будут квадратным корнем из единиц площади сектора.

Или центральный угол и длина хорды :

1. Разделите центральный угол в радианах на 2 и возложите на него функцию синуса.
2. Разделите длину хорды на удвоенный результат шага 1. Это вычисление даст вам радиус.
3. Умножьте радиус на центральный угол, чтобы получить длину дуги.

Как найти длину дуги в радианах?

1. Умножьте центральный угол в радианах на радиус окружности. 903:50
2. Вот оно! Результатом является просто это умножение.

Как рассчитать длину дуги без угла?

Чтобы рассчитать длину дуги без угла, вам нужен радиус и площадь сектора :

1. Умножьте площадь на 2.
2. Затем разделите результат на квадрат радиуса (убедитесь, что единицы измерения совпадают), чтобы получить центральный угол в радианах.

Или вы можете использовать радиус и длину хорды :

1. Разделите длину хорды на удвоенный радиус.
2. Найдите арксинус результата (в радианах).
3. Удвойте результат обратного синуса, чтобы получить центральный угол в радианах.
4. Получив центральный угол в радианах, умножьте его на радиус, чтобы получить длину дуги.

Должна ли длина дуги быть в радианах?

Длина дуги является мерой расстояния, поэтому она не может быть выражена в радианах . Однако центральный угол не обязательно должен быть в радианах. Это может быть любая единица измерения углов, от градусов до угловых секунд. Использование радианов , однако, намного проще для вычислений относительно длины дуги, так как найти его так же просто, как умножить угол на радиус.

Bogna Szyk

Центральный угол (θ)

Радиус (R)

Диаметр

Площадь сектора (A)

Длина хорда (C)

Длина дуги

Длина дуги (L)

Check Check. из 8 подобных калькуляторов окружностей ⭕

Площадь кругаРасчет окружности: найти c, d, a, rОкружность… 5 еще

Нахождение длины дуги окружности в радианах

Все ресурсы для предварительного исчисления

12 Диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Precalculus Help » Тригонометрические функции » Угловые меры в градусах и радианах » Найдите длину дуги окружности, используя радианы

Найдите длину дуги окружности, если радиус равен  , а угол – в радианах.

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу для нахождения длины дуги по углу в радианах.

Подставьте радиус и угол.

Сообщить об ошибке

Найдите длину дуги окружности, если радиус равен , а угол  .

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу для нахождения длины дуги по углу в радианах.

Подставьте радиус и угол, чтобы найти длину дуги.

Сообщить об ошибке

Если круг имеет радиус саженей, а сектор имеет центральный угол . Какова мера дуги?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти длину дуги, используйте следующую формулу:

Нам дан радиус, а также наш центральный угол, так что подставьте то, что мы знаем, и упростите

Итак, наш ответ: 5 морских саженей

Сообщить об ошибке

Найдите длину дуги окружности, если радиус  и угол  .

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу для длины дуги.

Подставьте известные радиус и угол.

Сообщить об ошибке

Когда ЦЕРН проектировал Большой адронный коллайдер, им нужно было проложить кабель от диспетчерской до точки    радиан   по кругу. Если радиус Большого адронного коллайдера составляет , какой длины кабель потребуется, чтобы добраться до датчика?

Возможные ответы:

Правильный ответ:

Пояснение:

Когда ЦЕРН проектировал Большой адронный коллайдер, им нужно было проложить кабель от диспетчерской до точки в радианах по кругу. Если радиус Большого адронного коллайдера составляет , какой длины кабель потребуется, чтобы добраться до датчика?

Формула длины дуги выглядит следующим образом:

Таким образом, чтобы найти меру центрального угла, мы действительно умножаем длину окружности на дробную часть интересующего нас круга. В данном случае у нас уже есть радиус и центральный угол, осталось только подключить и пыхнуть.

Итак, наш ответ:

Сообщить об ошибке

Если длина окружности равна 310 км, найдите длину дуги, связанную с центральным углом в радианах.

Возможные ответы:

Правильный ответ:

Объяснение:

Если окружность имеет длину окружности 310 км, найдите длину дуги, связанную с центральным углом  9 радиан.0004

Напомним, что длину дуги можно найти с помощью следующего:

При ближайшем рассмотрении мы видим, что формула на самом деле состоит из двух частей. Первая часть дает нам дробную площадь круга, который нас интересует. Вторая часть — это просто окружность. Это означает, что если мы умножим всю окружность на интересующую нас часть, мы просто получим длину дуги интересующей нас части.

Итак, подключите и вперед!

Выглядит беспорядочно, но мы упростим.

Итак, наш ответ: 116 км.

Сообщить об ошибке

Найдите длину дуги окружности с окружностью, которая проходит от  к  вокруг центра.

Возможные ответы:

Правильный ответ:

Объяснение:

Помните, что длина дуги окружности определяется как:

, где  это угол, полученный путем соединения радиуса с двумя концами дуги, указанный в радианах. это радиус.

Чтобы получить , мы конвертируем градусы в радианы.

Чтобы получить радиус, мы конвертируем из длины окружности

Сообщить об ошибке

Если длина  равна и , что из следующего ближе всего к длине малой дуги ?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула длины дуги окружности в радианах: , где  – длина дуги.

Затем подставьте данные:  и упростите: .

Затем округлите до нужного места: .

Следовательно, длина дуги  равна .

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы Precalculus

12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept

Математические слова: дуга окружности

Математические слова: дуга окружности

индекс: нажмите на букву индекс: предметные области
	Дуга окружности Подключенная секция окружности круга. Дуги измеряются двояко: как мера центрального угол, или как длина самой дуги. Измерение по центральному углу (градусы) Красная дуга (малая дуга) измеряет 120°. Синяя дуга (большая дуга) имеет размер 240°. Измерение по длине дуги (радианы) Формула: s = r θ s = длина дуги r = радиус окружности θ = мера центрального угла в радианах Красная дуга: r = 2 и θ = 2π/3, поэтому с = 4π/3 Синяя дуга: r = 2 и θ = 4π/3, поэтому с = 8π/3 См. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт