Тесты по математическому моделированию с ответами: Тест с ответами по теме «Математическое моделирование в биологии и медицине»

Содержание

Тест с ответами на тему: Математическое моделирование

1. Первые математические модели были созданы:
A. Ф. Кенэ*
B. К. Марксом
C. Г. Фельдманом
D. Д. Нейманом

2.Модель, представляющая собой объект, который ведет себя как
реальный объект, но не выглядит как таковой — это
A. физическая модель*
B. аналоговая модель
C. типовая модель
D. математическая модель

3.Модель, представляющая то, что исследуется с помощью увеличенного
или уменьшенного описания объекта или системы — это
A. физическая*
B. аналитическая
C. типовая
D. математическая

4.Где впервые были предложены сетевые модели?
A. США*
B. СССР
C. Англии
D. Германии

5.Какой из структурных элементов включает в себя процесс моделирования?
A. анализ*
B. модель
C. объект
D. субъект

6.Модели ПЕРТ впервые были предложены в
A. 1958 г.*
B. 1948 г.
C. 1956 г.
D. 1953 г.

7.Автоматизация процесса управления не включает в себя
A.

этап анализа*
B. этап планирования и разработки
C. этап управления ходом разработки
D. нет правильного ответа

8.Транспортная задача решается методом:
A. все ответы верны*
B. наименьших стоимостей, оптимальности
C. оптимальности, северо-западного угла
D. северо-западного угла, наименьших стоимостей

9.Мощности поставщиков определяются по формуле:
A. ui + cij*
B. vj — cij
C. (ui + cij) — vj
D. все ответы верны

10.Мощности потребителей определяются по формуле:
A. vj – cij*
B. ui + cij
C. (ui + cij) — vj
D. все ответы верны

11.Оценки матрицы перевозок (детермин.) определяются:
A. (ui + cij) – vj*
B. vj — cij
C. ui + cij
D. все ответы верны

12.Предшественниками имитационных игр были:
A. военные игры*
B. конфликтные игры
C. экономические игры
D. нет правильных ответов

13.Математической моделью конфликтных ситуаций является:
A. теория игр*

B. сетевая модель
C.

имитационная модель
D. транспортная модель

14.Какие из научных дисциплин не входят в экономико-
математические методы:
A. экспериментальное aнализ*
B. эконометрия
C. экономическая кибернетика
D. все ответы верны

15.Классификация по целевому назначению включает в себя модели
A. теоретико-аналитические, прикладные*
B. макроэкономические, микроэкономические
C. балансовые, трендовые
D. все ответы верны

16.Классификация по типу информации делится на:
A. аналитические, идентифицированные*
B. статистические, динамические
C. матричные, сетевые
D. балансовые, трендовые

17.Классификация по учету фактора неопределенности включает в себя:
A. детерминированные, стохастические*
B. статистические, динамические
C. макроэкономические, микроэкономические
D. аналитические, идентифицированные

18.Ранний срок начала работы в СГ определяется по формуле:
A. tp(i)*
B. tp(i) + t(i,j)
C. tn(j)
D.

tn(j) — t(i,j)

19.Ранний срок окончания в СГ определяется по формуле:
A. tp(i) + t(i,j)*
B. tn(j)
C. tp(i)
D. tn(j) — t(i,j)

20.Поздний срок окончания в СГ определяется по формуле:
A. tn(j)*
B. tp(i) + t(i,j)
C. tp(i)
D. tn(j) — t(i,j)

21.Поздний срок начала в СГ определяется по формуле:
A. tn(j) — t(i,j)*
B. tp(i) + t(i,j)
C. tp(i)
D. tn(j)

22.Полный резерв времени определяется как:
A. tn(j) — tp(i) — t(i,j)*
B. tp(i) + t(i,j)
C. tp(i) — tn(j)
D. tn(j)

23.При решении экономических моделей используются матрицы:
A. в теории игр, в транспортных задачах*
B. в СГ, имитационной модели
C. в транспортных задачах, в СГ
D. не используются в моделях

24.В какой из моделей используется седловая точка?

A. в теории игр*
B. в транспортной
C. в имитационной
D. в СГ

25.Материальный или мысленно представляемый объект, который
в процессе исследования замещает объект- оригинал так,
что его непосредственное изучение дает новые знания об
объекте- оригинале — это
A. модель*
B. аналогия
C. абстракция
D. гипотеза

26.Когда был принят Закон Руз «О внешнеэкономической
деятельности Республики Узбекистан».
A. 14 июня 1991г.*
B. 20 августа 1991г.
C. 15 марта 1990г.
D. 14 декабря 1993г.

27.Что относится к ведению Республики Узбекистан как субъекта ВЭД
A. всё перечисленное*
B. разработка и осуществление внешнеэкономической
политики, в т.ч. валютно-кредитной
C. заключение и исполнение международных договоров в
области ВЭД
D. установление законодательных основ организации ВЭД

28.Республика Узбекистан осуществляет внешнеэкономическую

деятельность, руководствуясь принципами:
A. все ответы веpны*
B. равенства сторон
C. невмешательства во внутренние дела партнёров по ВЭС
D. взаимовыгодности сотрудничества со всеми государствами,
иностранными юридическими и физическими лицами

29.Уполномоченные банки ВЭД Руз:
A. получившие лицензии Центробанка Руз на проведение
валютных операций*
B. акционерно-коммерческие , коммерческие и частные
банки
C. Нацбанк ВЭД РУз
D. иностранные банки

30.Резиденты во ВЭД:
A. все ответы вepны*
B. юридические лица, созданные и зарегистрированные в
соответствии с Законодательством РУз
C. дипломатические, торговые и иные официальные
представительства Руз за границей
D. физические лица, имеющие постоянное место жительства в
РУз

Поделиться с друзьями:

Adblock
detector

Тест по теме математическое моделирование | Тест по математике (6 класс) на тему:

Тест по теме: «Математическое моделирование»

1. Закончите предложение: «Объект, который используется в качестве «заместителя», представителя другого объекта с определенной целью, называется …»

моделью;
копией;
предметом;
оригиналом.

2. Закончите предложение: «Модель, по сравнению с объектом-оригиналом, содержит …»

меньше информации;
столько же информации;
больше информации.

3. Моделирование — это:

процесс замены реального объекта (процесса, явления) моделью, отражающей его существенные признаки с точки зрения достижения конкретной цели;
процесс демонстрации моделей одежды в салоне мод;
процесс неформальной постановки конкретной задачи;
процесс замены реального объекта (процесса, явления) другим материальным или идеальным объектом;
процесс выявления существенных признаков рассматриваемого объекта.

4. Процесс построения модели, как правило, предполагает:

описание всех свойств исследуемого объекта;
выделение наиболее существенных с точки зрения решаемой задачи свойств объекта;
выделение свойств объекта безотносительно к целям решаемой задачи;
описание всех пространственно-временных характеристик изучаемого объекта;
выделение не более трех существенных признаков объекта.

5. Математическая модель объекта — это:

созданная из какого-либо материала модель, точно отражающая внешние признаки объекта-оригинала;
описание в виде схемы внутренней структуры изучаемого объекта;
совокупность данных, содержащих информацию о количественных характеристиках объекта и его поведения в виде таблицы;
совокупность записанных на языке математики формул, отражающих те или иные свойства объекта-оригинала или его поведение;
последовательность электрических сигналов.

6. К числу математических моделей относится:

милицейский протокол;
правила дорожного движения;
формула нахождения корней квадратного уравнения;
кулинарный рецепт;
инструкция по сборке мебели.

7. К числу документов, представляющих собой информационную модель управления государством, можно отнести:

Конституцию РФ;
географическую карту России;
Российский словарь политических терминов;
схему Кремля;
список депутатов государственной Думы.

8. Рисунки, карты, чертежи, диаграммы, схемы, графики представляют собой:

табличные информационные модели;
математические модели;
натурные модели;
графические информационные модели;
иерархические информационные модели.

9 . Описание глобальной компьютерной сети Интернет в виде системы взаимосвязанных следует рассматривать как:

натурную модель;
табличную модель;
графическую модель;
математическую модель;
сетевую модель.

10. В биологии классификация представителей животного мира представляет собой:

иерархическую модель;
табличную модель;
графическую модель;
математическую модель;
натурную модель.

11. Информационной моделью организации занятий в школе является:

1. свод правил поведения учащихся;

2. список класса;

3. расписание уроков;

4. перечень учебников.

12. Отметьте пропущенное слово: «Географическая карта является примером … модели»

образной
знаковой
смешанной
натурной

13. Укажите пары объектов, о которых можно сказать, что они находятся в отношении «объект – модель»:

компьютер – процессор
Новосибирск – город
слякоть – насморк
автомобиль – техническое описание автомобиля
город – путеводитель по городу

14. Модель есть замещение изучаемого объекта другим объектом, который отражает:

1. все стороны данного объекта

2. некоторые стороны данного объекта

3. существенные стороны данного объекта

4. несуществующие стороны данного объекта

15. Что является моделью объекта «яблоко»?

1. муляж;

2. фрукт;

3. варенье;

4. компот.

16. Укажите примеры натурных моделей:

физическая карта
глобус
график зависимости расстояния от времени
макет здания
схема узора для вязания крючком
муляж яблока
манекен

17. Укажите примеры образных информационных моделей:

рисунок
фотография
словесное описание
формула

18. Закончите предложение: «Можно создавать и использовать …»

разные модели объекта
единственную модель объекта
только натурную модель объекта

19. Отметьте пропущенное слово: «Словесное описание горного ландшафта является примером … модели»

образной
знаковой
смешанной
натурной

20. Расписание движение поездов может рассматриваться как пример:

натурной модели;
табличной модели;
графической модели;
компьютерной модели;
математической модели.

Рекомендуемые правила при оценивании:
– за каждый правильный ответ +1 балл;
– за каждый неполный ответ +0,5 балла;
– за вопрос без ответа 0 баллов.

Рекомендуемые соотношения при выставлении оценок:
50-70% — «3»;
71-85% — «4»;
86-100% — «5».

ОТВЕТЫ:

	1
	1
	1
	2
	4
	3
	1
	4
	5
	1
	3
	3
	4,5
	1
	1
	2,4,6,7
	1,2
	1
	2
	2

Тест по дисциплине «Математическое моделирование»

Контрольные измерительные материалы

по учебной дисциплине МДК. 02.03. Математическое моделирование

1. Математическое моделирование это средство для

а) изучения свойств реальных объектов в рамках поставленной задачи

б) упрощения поставленной задачи

в) поиска физической модели

г) принятия решения в рамках поставленной задачи

2. Какой модели быть не может?

а) вещественной, физической

б) идеальной, физической

в) вещественной, математической

г) идеальной, математической

3. По поведению математических моделей во времени их разделяют на

а) детерминированные и стохастические

б) статические и динамические

в) непрерывные и дискретные

г) аналитические и имитационные

4. Как называется замещаемый моделью объект?

а) копия

б) оригинал

в) шаблон

г) макет

5. Что такое математическая модель?

а) точное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала

б) точное представление реальных объектов, процессов или систем, выраженное в физических терминах и сохраняющее существенные черты оригинала

в) приближенное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала

г) приближенное представление реальных объектов, процессов или систем, выраженное в физических терминах и сохраняющее существенные черты оригинала

6. Какие виды математических моделей получаются при разделении их по принципам построения?

а) аналитические, имитационные

б) детерминированные, стохастические

в) стохастические, аналитические

г) детерминированные, имитационные

7. На какой язык должна быть «переведена» прикладная задача для ее решения с использованием ЭВМ?

а) неформальный математический язык

б) формальный математический язык

в) формальный физический язык

г) неформальный физический язык

8. Что такое линейное программирование

а) это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием

б) раздел математического программирования, изучающий подход к решению нелинейных задач оптимизации специальной структуры

в) метод оптимизации, приспособленный, к задачам, в которых процесс принятия решения, может быть, разбит на отдельные этапы (шаги)

г) это направление математического программирования, в котором целевой функцией или ограничением является нелинейная функция

9. Какой метод относится к методам решения задач линейного программирования

а) симплекс-метод

б) метод множителей Лагранжа

в) метод хорд

г) метод половинного деления

10. Если в критериальной строке симплексной таблицы нет отрицательный коэффициентов, это означает, что

а) задача неразрешима

б) найден оптимальный план на максимум

в) найден оптимальный план на минимум

г) задача имеет бесконечно много решений

11. В каком случае задача математического программирования является линейной?

а) если ее целевая функция линейна

б) если ее ограничения линейны

в) если ее целевая функция и ограничения линейны

г) нет правильного ответа

12. Транспортная задача — это

а) математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение

б) математическая задача нелинейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение

в) математическая задача дробно-линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.

г) нет правильного ответа

13. Транспортная задача линейного программирования называется закрытой, если:

а) суммарные запасы равны суммарным потребностям

б) суммарные запасы больше суммарных потребностей

в) суммарные запасы меньше суммарных потребностей

г) целевая функция ограничена

14. В соответствии с основной теоремой теории транспортных задач всегда имеет решение

а) открытая транспортная задача

б) закрытая транспортная задача

в) транспортная задача с ограничениями типа равенств

г) транспортная задача с ограничениями типа неравенств

15. При построении опорного плана транспортной задачи методом северо-западного угла первой подлежит заполнению

а) клетка, расположенная в левом верхнем углу таблицы планирования

б) клетка, расположенная в правом верхнем углу таблицы планирования

в) клетка с минимальным значением тарифа

г) клетка с максимальным значением тарифа

16.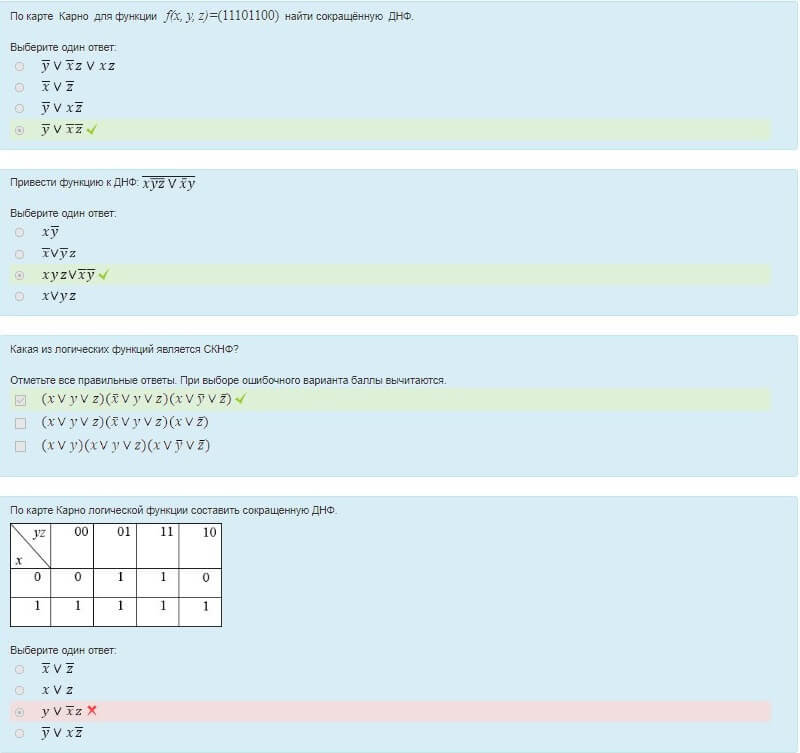 При построении опорного плана транспортной задачи на минимум методом минимального элемента первой подлежит заполнению

а) клетка, расположенная в левом верхнем углу таблицы планирования

б) клетка, расположенная в правом верхнем углу таблицы планирования

в) клетка с минимальным значением тарифа

г) клетка с максимальным значением тарифа

17. Первым шагом алгоритма метода потенциалов является:

а) нахождение первого псевдоплана

б) нахождение первого условно-оптимального плана

в) нахождение первого опорного плана

г) нахождение первого базисного решения

18. Теория динамического программирования используется:

а) для решения задач оптимизации без ограничений

б) для решения задач управления многошаговыми процессами

в) для решения задач нелинейного программирования

г) для решения задач линейного программирования

19. Для решения задачи динамического программирования используется:

а) принцип оптимальности Беллмана

б) принцип максимума Понтрягина

в) принцип симметрии

г) принцип максимума правдоподобия

20. К задачам динамического программирования относится:

а) задача планирования замены оборудования

б) задача о рационе

в) транспортная задача линейного программирования

г) задача о назначениях

21. В методе динамического программирования под управлением понимается

а) совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса;

б) совокупность решений, принимаемых на первом этапе процесса;

в) совокупность решений, принимаемых на последнем этапе процесса

г) совокупность решений, принимаемых на предпоследнем этапе процесса

22. При решении задачи динамического программирования строятся:

а) рекуррентные функциональные уравнения Беллмана

б) функции Лагранжа

в) штрафные функции

г) сечения Гомори

23. Что такое системы массового обслуживания

а) это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания

б) это совокупность математических выражений, описывающих входящий поток требований, процесс обслуживания и их взаимосвязь

в) это такие системы, в которые в определенные моменты времени поступают заявки на обслуживание

г) нет правильного ответа

24. По наличию очередей системы массового обслуживания делятся на

а) простые, сложные

б) открытые, замкнутые

в) ограниченные СМО, неограниченные СМО

г) СМО с отказами, СМО с очередью

25. По источнику требований СМО делятся на

а) простые, сложные

б) открытые, замкнутые

в) ограниченные СМО, неограниченные СМО

г) СМО с отказами, СМО с очередью

26. Как называется объект, порождающий заявки в СМО

а) очередь

б) диспетчер

в) генератор заявок

г) узел обслуживания

27. Из чего состоит узел обслуживания в СМО

а) из диспетчера и генератора заявок

б) из конечного числа каналов

в) из очереди и диспетчера

г) нет правильного ответа

28. Как называется принцип, в соответствии с которым поступающие на вход обслуживающей системы требования подключаются из очереди к процедуре обслуживания

а) дисциплина очереди

б) механизм обслуживания

в) процедура обслуживания

г) конфигурация очереди

29. Как называется дисциплина очереди, определяемая следующим правилом: «первым пришел – первый обслуживается»

а) LIFO

б) GIFO

в) FIFO

г) нет правильно ответа

30. Как называется дисциплина очереди, определяемая следующим правилом: «пришел последним – обслуживается первым»

а) LIFO

б) GIFO

в) FIFO

г) нет правильно ответа

31. Задача о замене оборудования является задачей

а) нелинейного программирования

б) динамического программирования

в) линейного программирования

г) целочисленного программирования

32. В процессе динамического программирования раньше всех планируется

а) первый шаг

б) последний шаг

в) как сказано в условии задачи

г) предпоследний шаг

33. Задача, которая возникает при необходимости максимизации дохода от реализации продукции, производимой некоторой организацией, при этом производство ограничено имеющимися сырьевыми ресурсами, называется

а) задача коммивояжера

б) задача о составлении плана производства

в) задача о назначении

г) задача о рюкзаке

34. Метод минимального элемента — это

а) один из комбинаторных методов дискретного программирования, при котором гиперплоскость, определяемая целевой функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи линейного программирования до встречи с ближайшей целочисленной точкой этого многогранника

б) один из методов отсечения, с помощью которого решаются задачи целочисленного программирования

в) один из группы методов определения первоначального опорного плана транспортной задачи

г) один из методов, упрощающий определение исходного опорного плана задачи линейного программирования и симплекс-таблицы

35. Метод потенциалов — это

а) один из методов проверки опорного плана транспортной задачи на оптимальность

б) один из комбинаторных методов дискретного программирования, при котором гиперплоскость, определяемая целевой функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи линейного программирования до встречи с ближайшей целочисленной точкой этого многогранника

в) один из методов отсечения, с помощью которого решаются задачи целочисленного программирования

г) один из группы методов определения первоначального опорного плана транспортной задачи

36. Метод северо-западного угла это

а) один из методов проверки опорного плана транспортной задачи на оптимальность

в) один из методов отсечения, с помощью которого решаются задачи целочисленного программирования

г) один из группы методов определения первоначального опорного плана транспортной задачи

37. В задачах динамического программирования шаговое управление должно выбираться

а) с учетом последствий в будущем

б) с учетом предшествующих шагов

в) наилучшим для данного шага

г) лучше, чем предыдущее

38. Метод динамического программирования применяется для решения

а) задач, которые нельзя представить в виде последовательности отдельных шагов

б) многошаговых задач

в) только задач линейного программирования

г) задач макроэкономики

39. Принцип оптимальности Беллмана состоит в том, что

а) каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придёт система в конце данного шага

б) совокупность принимаемых решений обеспечит наибольшую локальную выгоду на каждом шаге процесса

в) совокупность принимаемых решений обеспечит наибольшую локальную выгоду на последнем шаге процесса

г) нет правильного ответа

40. Часть математического программирования, задачами которой является нахождение экстремума линейной целевой функции на допустимом множестве значений аргументов называется

а) линейное программирование

б) динамическое программирование

в) квадратичное программирование

г) дискретное программирование

41.  К какому классу моделей можно отнести спичечный коробок, если представить его моделью системного блока ПК при планировании своего рабочего места?

а) это идеальная, математическая модель

б) это вещественная, натурная модель

в) это вещественная, физическая модель

г) это не является моделью

42. Какая из задач не имеет аналитической модели?

а) поиск оптимального раскроя листа фанеры

б) демодуляция аналогового сигнала

в) расчет расхода топлива по заданной формуле

г) распознавание текста

43.   Какая математическая модель не относится к стохастическим?

а) идеальный газ

б) квантовый осциллятор

в) материальная точка

г) ни одна из предложенных

44. Материальная точка это не только математическая, но и

а) натурная модель

б) физическая модель

в) наглядная модель

г) знаковая модель

45. Во время поиска лучшего результата были построены две различные математические модели: эксперимент на ЭВМ, моделирующий систему атомов, и дифференциальная система уравнений, решенная численно, от двух полученных результатов взяли среднеквадратичный. Можно ли считать такой метод моделью?

а) да, это вещественная, математическая

б) да, это идеальная, математическая

в) да, это вещественная натурная

г) нет

46. Какое максимальное количество моделей одного объекта можно составить?

а) любое количество

б) 1

в) 3

г) 7

47. Сколько классов моделей существует?

а) 4

б) 2

в) 3

г) нет правильного ответа

48. Какие модели относятся к классу вещественных моделей?

а) физические, натурные

б) идеальные, физические

в) наглядные, идеальные

г) натурные, идеальные

49. Какие модели нельзя отнести к классу мысленных моделей?

а) физические

б) натурные

в) математические

г) наглядные

50.  Какие модели входят в состав идеальных математических моделей?

а) аналитические, функциональные, имитационные, комбинированные

б) аналоговые, структурные, геометрические, графические, цифровые и кибернетические

в) символы, алфавит, языки программирования, упорядоченная запись, топологическая запись, сетевое представление

г) нет правильного ответа

51.   В чем заключается построение математической модели?

а) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста математическими величинами, и факторами, влияющими на конечный результат

б) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат

в) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно связь между теми или иными процессами и явлениями, между интересующими специалиста математическими величинами, и факторами, влияющими на конечный результат

г) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат

52.   В зависимости от характера исследуемых реальных процессов и систем, на какие группы могут быть разделены математические модели?

а) непрерывные, имитационные

б) детерминированные, стохастические

в) имитационные, детерминированные

г) стохастические, имитационные

53.  Какие группы математических моделей не являются результатом распределения моделей по их поведению во времени?

а) статические, динамические

б) динамические, изоморфные

в) изоморфные, динамические

г) непрерывные, изоморфные

54.  На какие группы можно разделить математические модели по виду входной информации?

а) статические, непрерывные

б) дискретные, непрерывные

в) динамические, непрерывные

г) динамические, статические

55. На какие группы можно разделить математические модели по степени их соответствия реальным объектам, процессам или системам?

а) стохастические, изоморфные

б) изоморфные, гомоморфные

в) детерминированные, стохастические

г) нет правильного ответа

56. Как называется модель, если между ней и реальным объектом, процессом или системой существует полное поэлементное соответствие?

а) стохастическая

б) изоморфная

в) детерминированная

г) гомоморфная

57. Как называются модели, в которых предполагается отсутствие всяких случайных воздействий и их элементы (элементы модели) достаточно точно установлены?

а) статические

б) дискретные

в) детерминированные

г) динамические

58. В каком моделировании функционирование объектов, процессов или систем описывается набором алгоритмов?

а) аппроксимационном

б) имитационном

в) аналитическом

г) нет правильного ответа

59.  Какие характеристики объекта, процесса или системы устанавливаются на этапе выбора математической модели?

а) дискретность, изоморфность

б) линейность, стационарность

в) изоморфность, линейность

г) стационарность, дискретность

60. Посредством каких конструкций, математические модели описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи?

а) логико-математических конструкций

б) статистических конструкций

в) вероятностных конструкций

г) нет правильного ответа

61.  Что не входит в предмет математического моделирования?

а) построение алгоритма, моделирующего поведение объекта (системы)

б) корректировка построенной модели

в) поиск закономерностей поведения объекта (системы)

г) построение натурной модели

62.  Какие изучаются зависимости между величинами, описывающими процессы, при их моделировании?

а) качественные и количественные

б) только качественные

в) только количественные

г) нет правильного ответа

63. В каких процессах вычислительный эксперимент является единственно возможным?

а) где натурный эксперимент может привести к очень большим объемам работ

б) где натурный эксперимент может привести к неверным результатам

в) где натурный эксперимент опасен для жизни и здоровья людей

г) нет правильного ответа

64.   С чего обычно начинается построение математической модели?

а) с построения и анализа простейшей, наиболее грубой математической модели рассматриваемого объекта, процесса или системы

б) с построения и анализа математической модели, которая наиболее полно соответствует рассматриваемому объекту, процессу или системе

в) с анализа математической модели рассматриваемого объекта

г) нет правильного ответа

65.  Какой характер носят выводы, полученные в результате исследования гипотетической модели?

а) абстрактный

б) условный

в) точный

г) нет правильного ответа

66.  Что необходимо сделать для того, чтобы проверить выводы, полученные в результате исследования гипотетической модели?

а) необходимо сопоставить результаты исследования модели на ЭВМ с результатами натурного эксперимента

б) необходимо провести повторное исследование модели и сопоставить результаты двух исследований

в) необходимо провести исследование модели несколько раз и сопоставить результаты данных исследований

г) нет правильного ответа

67.   При исследовании гипотетической модели какого характера получатся выводы?

а) абстрактного

б) условного

в) гипотетического

г) динамического

68.  Какими знаниями необходимо обладать для построения математической модели в прикладных задачах?

а) только специальными знаниями об объекте

б) только математическими знаниями

в) математическими знаниями и специальными знаниями об объекте

г) нет правильного ответа

69.  Укажите метод, неприменяемый для компьютерного моделирования:

а) численное решение

б) точное решение в виде формул

в) экспериментальный анализ

г) нет правильного ответа

70.  Численный метод предполагает решение в бесконечном цикле итераций. Когда следует прервать процесс вычисления?

а) в момент, когда решение будет меняться от итерации к итерации менее чем на 1%

б) когда будет достигнута заданная степень точности

в) в случае если число начнет расти

г) нет правильного ответа

71.   Какая задача не поддается точному решению на ЭВМ в виде формул?

а) интегральное уравнение 1-го порядка

б) дифференциально-интегральная система уравнений

в) система нелинейных уравнений

г) все указанные поддаются

72. Какой из методов имеет приближенный характер?

а) точное решение в виде формул

б) численное решение

в) оба указанных метода

г) нет правильного ответа

73.  В чем состоит суть компьютерного моделирования?

а) на основе математической модели с помощью ЭВМ проводится серия вычислительных экспериментов, т.е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, уточняется модель

б) в создании математической модели исследуемых объектов

в) посредством рассмотрения исследуемых объектов с помощью ЭВМ проводится серия вычислительных экспериментов, т. е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, и составляется математическая модель

г) в создании точной копии исследуемых объектов

74.  Какой из экспериментов наиболее выгодно применять для исследования большого числа вариантов проектируемого объекта или процесса для различных режимов его эксплуатации?

а) прогнозный

б) вычислительный

в) натурный

г) нет правильного ответа

75.  Какое преимущество имеет вычислительный эксперимент по сравнению с натурным экспериментом?

а) короткие сроки и минимальные материальные затраты

б) только короткие сроки получения результатов

в) только минимальные материальные затраты

г) нет правильного ответа

76.  Какими методами следует решать системы, состоящие из смешанных (линейных и нелинейных) уравнений?

а) точными

б) приближенными

в) оба предложенных метода годятся

г) никакими из предложенных

77.   Укажите существующие группы решения математических задач

а) численные, точные

б) приближенные, точные

в) численные, приближенные

г) алгоритмические, приближенные

78.  Какие процессы должны отражать математические модели в задачах проектирования или исследования поведения реальных объектов, процессов или систем?

а) реальные физические нелинейные процессы, протекающие в реальных объектах

б) реальные математические нелинейные процессы, протекающие в реальных объектах

в) реальные физические линейные процессы, протекающие в реальных объектах

г) реальные математические линейные процессы, протекающие в реальных объектах

79.  Для чего могут применяться результаты проверки адекватности математической модели и реального объекта, процесса или системы?

а) только для корректировки математической модели

б) только для решения вопроса о применимости построенной математической модели

в) для корректировки математической модели или для решения вопроса о применимости построенной математической модели

г) нет правильного ответа

80.   Что происходит с результатами исследований на ЭВМ при проверке адекватности математической модели и реального объекта, процесса или системы?

а) сравниваются с результатами эксперимента на опытном натурном образце

б) принимаются в качестве итоговых результатов

в) не принимаются во внимание

г) нет правильного ответа

Ключи к тестам

1. а	2. б	3. б	4. б
5. в	6. а	7. б	8. а
9. а	10. б	11. в	12. а
13. а	14. б	15. а	16. в
17. в	18. б	19. а	20. а
21. а	22. а	23. а	24. г
25. б	26. в	27. б	28. а
29. в	30. а	31. б	32. б
33. б	34. в	35. а	36. г
37. а	38. б	39. а	40. а
41. в	42. г	43. в	44. в
45. б	46. а	47. б	48. а
49. б	50. а	51. г	52. б
53. г	54. б	55. б	56. б
57. в	58. б	59. б	60. а
61. г	62. в	63. в	64. а
65. б	66. а	67. б	68. в
69. в	70. б	71. г	72. в
73. а	74. б	75. а	76. б
77. а	78. а	79. в	80. а

Ответы на тесты Интуит «Введение в математическое моделирование»

Помощь с дистанционным обучением

Получи бесплатный расчет за 15 минут

Введите контактный e-mail:

Введите номер телефона

Что требуется сделать?

Каким способом с Вами связаться?:

E-mail

Телефон

Напишем вам на вашу почту

Перезвоним вам для уточнения деталей

или напишите нам прямо сейчас

Написать в WhatsApp

В каком случае квадратурная формула называется формулой прямоугольников, а метод – методом прямоугольников?

если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени
(Правильный ответ) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т. е. прямой, параллельной оси OX
если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки

Для изучения каких систем используется аналитическое моделирование?

(Правильный ответ) сравнительно простых
любых
сложных

Какие формулы применяются в методе полярных координат для вычисления независимых нормально распределенные случайных величин x1 и x2?

(Правильный ответ)

В каком случае квадратурная формула называется формулой Симпсона, а метод – методом Симпсона?

(Правильный ответ) если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени
если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т. е. прямой, параллельной оси OX
если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки

Как выглядит формула Эйлера?

нет правильного ответа
(Правильный ответ)

Какая функция равномерного распределения существует?

(Правильный ответ) дифференциальная и интегральная функции
только интегральная функция
только дифференциальная функция

Что требуется для нахождения объективных и устойчивых характеристик процесса при статистическом моделировании?

одинарное воспроизведение процесса
многократное воспроизведение процесса, с последующей статической обработкой полученных данных
(Правильный ответ) многократное воспроизведение процесса, с последующей статистической обработкой полученных данных

Укажите более точное определение имитационных моделей:

имитационные модели имитируют разброс опытных данных
имитационные модели имитируют численное решение модели
(Правильный ответ) имитационные модели имитируют поведение реальных объектов, процессов или систем

Как называется отношение ?

разделенной разностью второго порядка
разделенной разностью нулевого порядка
(Правильный ответ) разделенной разностью первого порядка

Чем аппроксимируется искомая функция y(x) на каждом шаге интегрирования дифференциальных уравнений в методе Рунге-Кутта 4-го порядка?

(Правильный ответ) рядом Тейлора, содержащим члены ряда с h5
рядом Тейлора, содержащим члены ряда с h3
рядом Тейлора, содержащим члены ряда с h4

В градиентных методах 2-го порядка используются

наряду с первыми и значения вторых производных функции
(Правильный ответ) только значения целевой функции
значения первых производных функции

Что такое математическая модель?

точное представление реальных объектов, процессов или систем, выраженное в физических терминах и сохраняющее существенные черты оригинала
приближенное представление реальных объектов, процессов или систем, выраженное в физических терминах и сохраняющее существенные черты оригинала
(Правильный ответ) приближенное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала
точное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала

Какой закон называют нормальным законом распределения вероятностей непрерывной случайной величины?

закон распределения вероятностей непрерывной случайной величины, который описывается дифференциальной функцией , где a — среднее квадратичное отклонение нормального распределения, — математическое ожидание случайной величины
(Правильный ответ) закон распределения вероятностей непрерывной случайной величины, который описывается дифференциальной функцией , где a — математическое ожидание случайной величины, -среднее квадратичное отклонение нормального распределения
закон распределения вероятностей непрерывной случайной величины, который описывается дифференциальной функцией , где a – дисперсия случайной величины, — математическое ожидание случайной величины

Что означает сокращенное обозначение модели СДА?

стохастическая, детерминированная, аналитическая
дискретная, стохастическая, аналитическая
(Правильный ответ) стохастическая, дискретная, аналитическая

Какой из шагов не входит в состав исследования объекта, процесса или системы и составления их математического описания при математическом моделировании, но является частью математического моделирования?

выделение наиболее существенных черт и свойств реального объекта или процесса
определение внешних связей и описание их с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций
(Правильный ответ) построение алгоритма, моделирующего поведение объекта, процесса или системы
определение переменных, т. е. параметров, значения которых влияют на основные черты и свойства объекта

В сколько этапов реализуется метод Ньютона?

один
три
(Правильный ответ) два
зависит от количества уравнений

Как выглядит формула Ньютона-Лейбница?

(Правильный ответ)

Какой из способов аппроксимации данных нашел большее применение на практике?

нет правильного ответа
способ, который требует, чтобы аппроксимирующая кривая F(x), аналитический вид которой необходимо найти, не проходила ни через одну узловую точку таблицы
способ, который требует, чтобы аппроксимирующая кривая F(x), аналитический вид которой необходимо найти, проходила через все узловые точки таблицы
(Правильный ответ) способ, заключающийся в сглаживании опытных данных

Из какого количества этапов состоит метод Гаусса?

(Правильный ответ) 2
5
3
4

По какой формуле интерполяционный многочлен имеет вид:

(Правильный ответ) Лагранжа
Ньютона
Стерлинга
Бесселя

Какая модель не является плодом человеческой мысли в общем случае?

математическая
физическая
знаковая
наглядная
(Правильный ответ) натурная

В методе дихотомии, если F(x-E)<F(x+E), то для определения min выбирается отрезок

[(a+b)/2, b]
(Правильный ответ) [a, (a+b)/2]
[(a+b)/2-E, (a+b)/2+E]

это интерполяционный многочлен

(Правильный ответ) в явном виде
в форме Лагранжа
в форме Ньютона

На заданном отрезке [a,b] имеется только один корень, если

(Правильный ответ) знак производной не меняется
знак функции не меняется, но меняется знак производной
знак функции не меняется

К чему преобразуется исходная система n-го порядка в результате выполнения первого шага прямого хода метода Гаусса?

к совокупности уравнения
(Правильный ответ) к совокупности уравнения и системы линейных уравнений, порядок которой равен n-1
к системе линейных уравнений, порядок которой равен n-1

К какому способу формирования последовательности нормально распределенных случайных величин относится метод, основанный на центральной предельной теореме?

отсеивание псевдослучайных чисел из первоначальной последовательности
(Правильный ответ) моделирование условий, соответствующих центральной предельной теореме теории вероятности
прямое преобразование псевдослучайного числа
обратное преобразование псевдослучайного числа

Как добиться того чтобы результаты по методу Эйлера, модифицированному методу Эйлера и методу Рунге-Кутта 4-го порядка были почти одинаковыми

(Правильный ответ) уменьшая шаг интегрирования
увеличивая шаг интегрирования
удваивая шаг интегрирования

Какой фактор определяет использование статистической имитационной модели?

скорость процесса
(Правильный ответ) случайные воздействия
высокая требуемая точность
количество имитируемых элементов

Интерполяция — это

(Правильный ответ) нахождение значения таблично заданной функции внутри заданного интервала
восстановление функции в точках за пределами заданного интервала табличной функции
усреднение или сглаживание табличной функции

Какая величина называется непрерывной?

случайную величину, которая может принимать только одно значение из некоторого конечного или бесконечного промежутка
случайная величина, которая может принимать только одно значение из некоторого конечного и все значения бесконечного промежутка
(Правильный ответ) случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка

Как звучит постановка в численных методах задача Коши для системы y(x) с учетом двух начальных условия: y(x0)=y0, y1(x0)=(y1)0?

(Правильный ответ) найти табличные функции y(x) и (y1)(x),
нет правильного ответа
найти табличные функции y(x) и (y1)(x),

Каким количеством нелинейных уравнений описывается модель, если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы?

тремя нелинейными уравнениями
двумя нелинейными уравнениями
(Правильный ответ) одним нелинейным уравнением

К какому уравнению неприменимо отделение корней?

(Правильный ответ) применимо к обоим
трансцендентному
алгебраическому

Можно ли методом серединного квадрата генерировать натуральные числа?

нет, в любом случае
(Правильный ответ) да, в любом случае
да, если правильно подобрать первое число

Пересечение касательной к функции и осью абсцисс дает точку, используемую в методе

во всех указанных методах
простых итераций
половинного деления
(Правильный ответ) Ньютона

В чем заключается сглаживание опытных данных методом наименьших квадратов?

при сглаживании опытных данных аппроксимирующей кривую F(x) стремятся провести так, чтобы ее отклонения от табличных данных (уклонения) по всем узловым точкам были максимальными
(Правильный ответ) при сглаживании опытных данных аппроксимирующей кривую F(x) стремятся провести так, чтобы ее отклонения от табличных данных (уклонения) по всем узловым точкам были минимальными
при сглаживании опытных данных аппроксимирующей кривую F(x) стремятся провести так, чтобы ее отклонения от табличных данных (уклонения) по большинству узловых точек были максимальными
при сглаживании опытных данных аппроксимирующей кривую F(x) стремятся провести так, чтобы ее отклонения от табличных данных (уклонения) по большинству узловых точек были минимальными

К каким методам относятся численные методы по характеру результата?

нет правильного ответа
(Правильный ответ) приближенным
точным

Какое количество этапов в решении задачи моделирования случайных величин с нормальным законом распределения?

1
3
(Правильный ответ) 2
4

Сколько этапов можно выделить для решения задачи генерирования случайных чисел на ЭВМ с заданным законом распределения?

(Правильный ответ) 2
1
4
3

Дисперсия постоянной величины C равна

CD(1)
постоянной ненулевой величине
(Правильный ответ) 0
CD(0)

Как называются модели, в которых предполагается отсутствие всяких случайных воздействий и их элементы (элементы модели) достаточно точно установлены?

статические
(Правильный ответ) детерминированные
дискретные
динамические

Как еще называется метод Эйлера?

метод Рунге–Кутта второго порядка
(Правильный ответ) метод Рунге–Кутта первого порядка
метод Рунге–Кутта четвертого порядка

Отец мальчика, возвращаясь домой, заметил большое количество магазинов с колбасой и решил купить для сына килограмм, он заходил в каждый магазин и записывал цены в таблицу, однако возвращаться в магазин, где он уже был он не хочет, поэтому он решил определить вероятность того, дороже или дешевле будет колбаса в следующем магазине.

Какую математическую модель взять отцу за основу?

(Правильный ответ) СДА
СНА
ДДА
СНИ
ДНА

В каком случае уравнение f(x)=0 называется трансцендентным уравнением?

если функция f(x) имеет вид многочлена степени m,
(Правильный ответ) если функция f(x) включает в себя тригонометрические функции от некоторого аргумента x
(Правильный ответ) если функция f(x) включает в себя экспоненциальные функции от некоторого аргумента x

Какие математические модели применяются при имитационном моделировании?

с помощью которых нельзя заранее вычислить или предсказать поведение системы, а для предсказания поведения системы необходим вычислительный эксперимент (имитация) на математической модели для всех возможных исходных данных
(Правильный ответ) с помощью которых нельзя заранее вычислить или предсказать поведение системы, а для предсказания поведения системы необходим вычислительный эксперимент (имитация) на математической модели при заданных исходных данных
с помощью которых можно заранее вычислить или предсказать поведение системы, и для предсказания поведения системы нет необходимости в применении вычислительного эксперимента (имитации) на математической модели при заданных исходных данных

Математическое ожидание есть

(Правильный ответ) неслучайная величина для дискретной и непрерывной величины
неслучайная величина для дискретной величины
случайная величина для дискретной и непрерывной величины
случайная величина для дискретной величины
неслучайная величина для непрерывной величины
случайная величина для непрерывной величины

Метод «золотого сечения» является методом

градиентным методом
(Правильный ответ) прямого поиска
градиентным методом второго порядка

К какой форме представления (задания) закона распределения относится биномиальное распределение, определяемое законом Бернулли Pn(k)=Cnkpkqn-k (где k = 0, 1, 2, …, n – количество возможных появлений событий, а q = 1-p – вероятность не появления событий)?

табличное задание
графическое задание
(Правильный ответ) аналитическое задание

В простейшем случае при расчете определенного интеграла функции его представляют в виде:

(Правильный ответ) суммы значений функции
произведения значений функции
разность значений функции

Для какого из методов больше подойдет характеристика: численный метод, моделирующий на ЭВМ псевдослучайные числовые последовательности с заданными вероятностными характеристиками

метод Ньютона
метод секущих
метод хорд
линейный конгруэнтный метод
(Правильный ответ) метод Монте-Карло

В чем заключается построение математической модели?

в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат
(Правильный ответ) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат
в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно связь между теми или иными процессами и явлениями, между интересующими специалиста математическими величинами, и факторами, влияющими на конечный результат
в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста математическими величинами, и факторами, влияющими на конечный результат

Какое условие необходимо соблюдать на каждом шаге интегрирования при применении для решения системы дифференциальных уравнений тех же методов, что и для решения одного дифференциального уравнения первого порядка?

все уравнения системы необходимо решать последовательно
(Правильный ответ) все уравнения системы необходимо решать параллельно
нет правильного ответа

Какая задача не поддается точному решению на ЭВМ в виде формул?

(Правильный ответ) все указанные поддаются
дифференциально-интегральная система уравнений
интегральное уравнение 1-го порядка
дифференциальная система уравнений
система нелинейных уравнений

К каким случайным величинам применим способ описания распределения случайной величины в виде таблицы, в виде формулы или графически?

только к непрерывным
(Правильный ответ) только к дискретным
к любым

При каком условии прекращается процесс поиска корня по методу простых итераций?

(Правильный ответ)

В задаче о камне, брошенном под углом к горизонту, решенной в явном виде, как зависимость координаты от времени, была применена модель

ДДА
СДИ
СДА
(Правильный ответ) ДНА
СНИ

Как определить значение нормально распределенной случайной величины с требуемым математическим ожиданием и требуемым среднеквадратичным отклонением для двенадцати (k=12) равномерно распределенных случайных величин?

(Правильный ответ)

Какой модели быть не может?

вещественной, математической
вещественной, физической
(Правильный ответ) идеальной, физической
идеальной, математической

Какой метод называется градиентным?

(Правильный ответ) метод, в котором для нахождения корня используется значение производной
метод, в котором для нахождения корня используется нахождение значения функции в различных точках интервала изоляции
метод, в котором для нахождения корня используется нахождение значения функции на границах интервала изоляции

Укажите какого порядка будет максимальная ошибка метода Симпсона

1
4
(Правильный ответ) 3
2

Какой из методов не содержит рекуррентной формулы?

серединного квадрата
квадратичный конгруэнтный
(Правильный ответ) все указанные содержат
линейно конгруэнтный

Что необходимо сделать для построения интерполяционного многочлена в явном виде?

(Правильный ответ) получить систему уравнений:
нет правильного ответа
получить уравнение: a0x1n+ a1x1n-1+…+ an-1×1+an=yi, i= n

Укажите метод, неприменяемый для компьютерного моделирования:

(Правильный ответ) экспериментальный анализ
точное решение в виде формул
численное решение

Метод половинного деления применим для случая

алгебраического уравнения
трансцендентного уравнения
(Правильный ответ) применимо к обоим

Разделенные разности используются интерполяционным многочленом в формах

(Правильный ответ) Ньютона
Лагранжа
в явном виде

В чем состоит суть «метода середины квадрата»?

(Правильный ответ) в том, что предыдущее случайное число возводится в квадрат, а затем из результата извлекаются средние цифры
в выборе четырех «магических чисел»: x0— начальное значение, ; — множитель, ; c— приращение, ; m— модуль,

Помощь с дистанционным обучением

Получи бесплатный расчет за 15 минут

Введите контактный e-mail:

Введите номер телефона

Что требуется сделать?

Каким способом с Вами связаться?:

E-mail

Телефон

Напишем вам на вашу почту

Перезвоним вам для уточнения деталей

или напишите нам прямо сейчас

Написать в WhatsApp

Введение в математическое моделирование — тест 1

Главная / Алгоритмы и дискретные структуры / Введение в математическое моделирование / Тест 1

Упражнение 1:

Номер 1

К какому классу моделей можно отнести спичечный коробок,  если представить его моделью системного блока ПК при планировании своего рабочего места?

Ответ:

&nbsp(1) это идеальная, математическая модель&nbsp

&nbsp(2) это вещественная, натурная модель&nbsp

&nbsp(3) это вещественная, физическая модель&nbsp

&nbsp(4) это не является моделью&nbsp

Номер 2

Математическое моделирование это средство для

Ответ:

&nbsp(1) изучения свойств реальных объектов в рамках поставленной задачи&nbsp

&nbsp(2) упрощения поставленной задачи&nbsp

&nbsp(3) поиска физической модели&nbsp

Номер 3

Какая из задач не имеет аналитической модели?

Ответ:

&nbsp(1) распознавание текста&nbsp

&nbsp(2) поиск оптимального раскроя листа фанеры&nbsp

&nbsp(3) демодуляция аналогового сигнала&nbsp

&nbsp(4) расчет расхода топлива по заданной формуле&nbsp

Упражнение 2:

Номер 2

Какая математическая модель не относится к стохастическим?

Ответ:

&nbsp(1) идеальный газ&nbsp

&nbsp(2) квантовый осциллятор&nbsp

&nbsp(3) материальная точка&nbsp

&nbsp(4) ни одна из предложенных&nbsp

Упражнение 3:

Номер 1

Инженеру во сне приснился новый шпиндель для двигателя, и он хочет его испытать, какую модель ему лучше предоставить токарям, чтобы ускорить процесс его изготовления?

Ответ:

&nbsp(1) идеальную, математическую&nbsp

&nbsp(2) вещественную, математическую&nbsp

&nbsp(3) идеальную, наглядную&nbsp

&nbsp(4) вещественную, физическую&nbsp

Номер 2

Какой модели быть не может?

Ответ:

&nbsp(1) вещественной, физической&nbsp

&nbsp(2) идеальной, физической&nbsp

&nbsp(3) вещественной, математической&nbsp

&nbsp(4) идеальной, математической&nbsp

Номер 3

Какая модель не является плодом человеческой мысли в общем случае?

Ответ:

&nbsp(1) математическая&nbsp

&nbsp(2) наглядная&nbsp

&nbsp(3) натурная&nbsp

&nbsp(4) физическая&nbsp

&nbsp(5) знаковая&nbsp

Упражнение 4:

Номер 1

Материальная точка это не только математическая, но и

Ответ:

&nbsp(1) натурная модель&nbsp

&nbsp(2) физическая модель&nbsp

&nbsp(3) наглядная модель&nbsp

&nbsp(4) знаковая модель&nbsp

Номер 2

Математическая модель в общем случае представляется через

Ответ:

&nbsp(1) вектор входных переменных&nbsp

&nbsp(2) вектор выходных переменных&nbsp

&nbsp(3) вектор внешних воздействий&nbsp

&nbsp(4) все предложенное&nbsp

Номер 3

При анализе движения электронов в диодном промежутке было построено две математические модели: сперва написана программа, моделирующая взаимодействие частиц, затем выведено уравнение движения электронов из теоретических соображений.  Какие математические модели были применены в данных случаях?

Ответ:

&nbsp(1) сперва аналитическая, затем имитационная&nbsp

&nbsp(2) вначале имитационная, затем аналитическая&nbsp

&nbsp(3) две аналитические&nbsp

&nbsp(4) две имитационные&nbsp

Упражнение 5:

Номер 1

Посмотрев на набор различных математических моделей, математик сформировал четыре общих утверждения для всех математических моделей. Какое из утверждений для произвольной математической модели верно?

Ответ:

&nbsp(1) каждая модель может быть решена численно&nbsp

&nbsp(2) каждой модели соответствует реальный объект&nbsp

&nbsp(3) каждая модель имеет уравнение (систему уравнений) в явном виде&nbsp

&nbsp(4) каждая модель не может при одном и том же входном параметре иметь несколько различных решений (корней) &nbsp

&nbsp(5) все утверждения неверны&nbsp

Номер 2

Во время поиска лучшего результата были построены две различные математические модели: эксперимент на ЭВМ, моделирующий систему атомов и дифференциальная система уравнений, решенная численно, от двух полученных результатов взяли среднеквадратичный.  Можно ли считать такой метод моделью?

Ответ:

&nbsp(1) да, это вещественная, математическая&nbsp

&nbsp(2) да, это идеальная, математическая&nbsp

&nbsp(3) да, это вещественная натурная&nbsp

&nbsp(4) нет&nbsp

Номер 3

Может ли идеальный электрический контур быть моделью математического маятника?

Ответ:

&nbsp(1) да, это случай изоморфизма&nbsp

&nbsp(2) да, при отсутствии консервативных сил (гомоморфизм)&nbsp

&nbsp(3) да, при отсутствии внешнего воздействия (гомоморфизм)&nbsp

&nbsp(4) Нет, так как оба случая — уже модели&nbsp

Упражнение 6:

Номер 1

По поведению математических моделей во времени их разделяют на

Ответ:

&nbsp(1) детерминированные и стохастические&nbsp

&nbsp(2) статические и динамические&nbsp

&nbsp(3) непрерывные и дискретные&nbsp

&nbsp(4) аналитические и имитационные&nbsp

Номер 2

Для того чтобы модель была гомоморфная необходимо и достаточно в рамках поставленной задачи

Ответ:

&nbsp(1) полного соответствия между моделью и объектом&nbsp

&nbsp(2) соответствия наиболее значительных параметров модели и объекта&nbsp

&nbsp(3) какого-либо соответствия вообще между моделью и объектом&nbsp

&nbsp(4) любая модель гомоморфна любому объекту&nbsp

Номер 3

Верно ли описание: детерминированная, непрерывная, аналитическая, модель?

Ответ:

&nbsp(1) нет, т. к. модель не может быть детерминированной и непрерывной одновременно&nbsp

&nbsp(2) нет, т.к. любая аналитическая модель уже является непрерывной&nbsp

&nbsp(3) да&nbsp

Упражнение 7:

Номер 1

Как называется замещаемый моделью объект?

Ответ:

&nbsp(1) копия&nbsp

&nbsp(2) оригинал&nbsp

&nbsp(3) шаблон&nbsp

&nbsp(4) макет&nbsp

Номер 2

Какое максимальное количество моделей одного объекта можно составить?

Ответ:

&nbsp(1) любое количество&nbsp

&nbsp(2) 1&nbsp

&nbsp(3) 3&nbsp

&nbsp(4) 7&nbsp

Номер 3

Сколько классов моделей существует?

Ответ:

&nbsp(1) 4&nbsp

&nbsp(2) 2&nbsp

&nbsp(3) 3&nbsp

Упражнение 8:

Номер 1

Какие модели относятся к классу вещественных моделей?

Ответ:

&nbsp(1) физические&nbsp

&nbsp(2) идеальные&nbsp

&nbsp(3) наглядные&nbsp

&nbsp(4) натурные&nbsp

Номер 2

Какие модели нельзя отнести к классу мысленных моделей?

Ответ:

&nbsp(1) физические&nbsp

&nbsp(2) натурные&nbsp

&nbsp(3) математические&nbsp

&nbsp(4) наглядные&nbsp

Номер 3

Какие модели входят в состав идеальных математических моделей?

Ответ:

&nbsp(1) аналитические, функциональные, имитационные, комбинированные&nbsp

&nbsp(2) аналоговые, структурные, геометрические, графические, цифровые и кибернетические&nbsp

&nbsp(3) символы, алфавит, языки программирования, упорядоченная запись, топологическая запись, сетевое представление&nbsp

Упражнение 9:

Номер 1

Что такое математическая модель?

Ответ:

&nbsp(1) точное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала&nbsp

&nbsp(2) точное представление реальных объектов, процессов или систем, выраженное в физических терминах и сохраняющее существенные черты оригинала&nbsp

&nbsp(3) приближенное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала&nbsp

&nbsp(4) приближенное представление реальных объектов, процессов или систем, выраженное в физических терминах и сохраняющее существенные черты оригинала&nbsp

Номер 2

Чем является функционал "Х" в представлении математической модели в виде системы функционалов Ф_i (X,Y,Z,t)=0?

Ответ:

&nbsp(1) вектором входных переменных&nbsp

&nbsp(2) вектором выходных переменных&nbsp

&nbsp(3) вектором внешних воздействий&nbsp

&nbsp(4) координатой времени&nbsp

Номер 3

В чем заключается построение математической модели?

Ответ:

&nbsp(1) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста математическими величинами, и факторами, влияющими на конечный результат&nbsp

&nbsp(2) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат&nbsp

&nbsp(3) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно связь между теми или иными процессами и явлениями, между интересующими специалиста математическими величинами, и факторами, влияющими на конечный результат&nbsp

&nbsp(4) в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат&nbsp

Упражнение 10:

Номер 1

Какие виды математических моделей получаются при разделении их по принципам построения?

Ответ:

&nbsp(1) аналитические&nbsp

&nbsp(2) детерминированные&nbsp

&nbsp(3) стохастические&nbsp

&nbsp(4) имитационные&nbsp

Номер 2

В зависимости от характера исследуемых реальных процессов и систем, на какие группы могут быть разделены математические модели?

Ответ:

&nbsp(1) непрерывные&nbsp

&nbsp(2) детерминированные&nbsp

&nbsp(3) имитационные&nbsp

&nbsp(4) стохастические&nbsp

Номер 3

Какие группы математических моделей не являются результатом распределения моделей по их поведению во времени?

Ответ:

&nbsp(1) статические&nbsp

&nbsp(2) динамические&nbsp

&nbsp(3) изоморфные&nbsp

&nbsp(4) непрерывные&nbsp

Упражнение 11:

Номер 1

На какие группы можно разделить математические модели по виду входной информации?

Ответ:

&nbsp(1) статические&nbsp

&nbsp(2) дискретные&nbsp

&nbsp(3) непрерывные&nbsp

&nbsp(4) динамические&nbsp

Номер 2

На какие группы можно разделить математические модели по степени их соответствия реальным объектам, процессам или системам?

Ответ:

&nbsp(1) стохастические&nbsp

&nbsp(2) изоморфные&nbsp

&nbsp(3) детерминированные&nbsp

&nbsp(4) гомоморфные&nbsp

Номер 3

Как называется модель, если между ней и реальным объектом, процессом или системой существует полное поэлементное соответствие?

Ответ:

&nbsp(1) стохастическая&nbsp

&nbsp(2) изоморфная&nbsp

&nbsp(3) детерминированная&nbsp

&nbsp(4) гомоморфная&nbsp

Упражнение 12:

Номер 1

Как называются модели, в которых предполагается отсутствие всяких случайных воздействий и их элементы (элементы модели) достаточно точно установлены?

Ответ:

&nbsp(1) статические&nbsp

&nbsp(2) дискретные&nbsp

&nbsp(3) детерминированные&nbsp

&nbsp(4) динамические&nbsp

Номер 2

В каком моделировании функционирование объектов, процессов или систем описывается набором алгоритмов?

Ответ:

&nbsp(1) аппроксимационном&nbsp

&nbsp(2) имитационном&nbsp

&nbsp(3) аналитическом&nbsp

Номер 3

Что означает сокращенное обозначение модели СДА?

Ответ:

&nbsp(1) стохастическая, дискретная, аналитическая&nbsp

&nbsp(2) стохастическая, детерминированная, аналитическая&nbsp

&nbsp(3) дискретная, стохастическая, аналитическая&nbsp

Главная / Алгоритмы и дискретные структуры / Введение в математическое моделирование / Тест 1

Моделирование — тест с ответами

Информатика в настоящее время является стремительно развивающийся наукой. Многие студенты постают в технические университеты, чтобы в будущем связать свою деятельность с IT или приближенными областями. Для проверки знаний по теме Моделирование предлагаем пройти тестирование на этой странице. Обращаем ваше внимание, что в тесте правильные ответы выделены символом [+].

Могут ли разные объекты быть описаны одной моделью:

[+] а) да

[-] б) нет

[-] в) зависит от моделей

Построение модели исходных данных; построение модели результата, разработка алгоритма, разработка программы, отладка и исполнение программы, анализ и интерпретация результатов:

[-] а) анализ существующих задач

[+] б) этапы решения задачи с помощью компьютера

[-] в) процесс описания информационной модели

Процесс построения информационных моделей с помощью формальных языков называется:

[-] а) планированием

[-] б) визуализацией

[+] в) формализацией

Расписание движения поездов может рассматриваться как пример:

[+] а) табличной модели

[-] б) натурной модели

[-] в) математической модели

Математическая модель объекта:

[-] а) совокупность данных, содержащих информацию о количественных характеристиках объекта и его поведении в виде таблицы

[-] б) созданная из какого-либо материала модель, точно отражающая внешние признаки объекта-оригинала

[+] в) совокупность записанных на языке математики формул, отражающих те или иные свойства объекта-оригинала или его поведение

Натурное (материальное) моделирование:

[-] а) моделирование, при котором в модели узнается какой-либо отдельный признак объекта-оригинала

[+] б) моделирование, при котором в модели узнается моделируемый объект, то есть натурная (материальная) модель всегда имеет визуальную схожесть с объектом-оригиналом

[-] в) создание математических формул, описывающих форму или поведение объекта-оригинала

Система состоит из:

[-] а) объектов, которые называются свойствами системы

[-] б) набора отдельных элементов

[+] в) объектов, которые называются элементами системы

Может ли один объект иметь множество моделей:

[+] а) да

[-] б) нет

[-] в) да, если речь идёт о создании материальной модели объекта

Образные модели представляют собой:

[-] а) формулу

[-] б) таблицу

[+] в) зрительные образы объектов, зафиксированные на каком либо носителе информации

Какие модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме?

[-] а) табличные

[+] б) предметные

[-] в) информационные

Модель:

[+] а) материальный или абстрактный заменитель объекта, отражающий существенные с точки зрения цели исследования свойства изучаемого объекта, явления или процесса

[-] б) материальный или абстрактный заменитель объекта, отражающий его пространственно-временные характеристики

[-] в) любой объект окружающего мира

Описание глобальной компьютерной сети Интернет в виде системы взаимосвязанных следует рассматривать как:

[-] а) математическую модель

[+] б) сетевую модель

[-] в) графическую модель

Последовательность этапов моделирования:

[+] а) цель, объект, модель, метод, алгоритм, программа, эксперимент, анализ, уточнение

[-] б) объект, цель, модель, эксперимент, программа, анализ, тестирование

[-] в) цель, модель, объект, алгоритм, программа, эксперимент, уточнение выбора объекта

Моделирование:

[-] а) формальное описание процессов и явлений

[-] б) процесс выявления существенных признаков рассматриваемого объекта

[+] в) метод познания, состоящий в создании и исследовании моделей

Сколько существует основных этапов разработки и исследование моделей на компьютере:

[+] а) 5

[-] б) 4

[-] в) 6

На первом этапе исследования объекта или процесса обычно строится:

[-] а) предметная модель

[+] б) описательная информационная модель

[-] в) формализованная модель

Табличная информационная модель представляет собой:

[-] а) набор графиков, рисунков, чертежей и диаграмм

[-] б) последовательность предложений на естественном языке

[+] в) описание объектов (или их свойств)в виде совокупности значений, размещенных в таблице

Такие модели представляют объекты и процессы в образной или знаковой форме:

[-] а) материальные

[+] б) информационные

[-] в) математические

Рисунки, карты, чертежи, диаграммы, схемы, графики представляют собой:

[-] а) иерархические информационные модели

[-] б) математические модели

[+] в) графические информационные модели

Географическую карту следует рассматривать скорее всего как:

[-] а) вербальную информационную модель

[+] б) графическую информационную модель

[-] в) математическую информационную модель

В качестве примера модели поведения можно назвать:

[+] а) правила техники безопасности в компьютерном классе

[-] б) чертежи школьного здания

[-] в) план классных комнат

Какой тип моделей применяется для описания ряда объектов, обладающих одинаковыми наборами свойств:

[-] а) сетевые информационные модели

[+] б) табличные информационные модели

[-] в) иерархические сетевые модели

Информационной моделью части земной поверхности является:

[-] а) глобус

[-] б) рисунок

[+] в) картина местности

Модель отражает:

[-] а) некоторые существенные признаки объекта

[+] б) существенные признаки в соответствии с целью моделирования

[-] в) все существующие признаки объекта

При создании игрушечного корабля для ребенка трех лет существенным является:

[-] а) точность

[-] б) материал

[+] в) внешний вид

В информационной модели жилого дома, представленной в виде чертежа (общий вид), отражается его:

[-] а) стоимость

[+] б) структура

[-] в) надежность

В информационной модели облака, представленной в виде черно-белого рисунка, отражаются его:

[+] а) форма

[-] б) размер

[-] в) плотность

Модель человека в виде детской куклы создана с целью:

[-] а) познания

[-] б) продажи

[+] в) игры

Признание признака объекта существенным при построении его информационной модели зависит от:

[+] а) цели моделирования

[-] б) стоимости объекта

[-] в) размера объекта

При описании внешнего вида объекта удобнее всего использовать информационную модель следующего вида:

[-] а) структурную

[+] б) графическую

[-] в) математическую

Практические тесты по математическому моделированию

—>

Войти
Биографии репетитора
Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
Академическое обучение
репетиторство по математике
- алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все ресурсы по математическому моделированию

20 практических тестов Вопрос дня Карточки Learn by Concept

Наши совершенно бесплатные практические тесты по математическому моделированию — идеальный способ освежить свои навыки. Брать один из наших многочисленных практических тестов по математическому моделированию для прогона часто задаваемых вопросов. Ты получите невероятно подробные результаты оценки в конце практического теста по математическому моделированию, чтобы помочь вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по математическому моделированию прямо сейчас и начать!