Косинус угла онлайн. Таблица косинусов. Формула косинуса угла.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0. 7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
cos(9) = 0.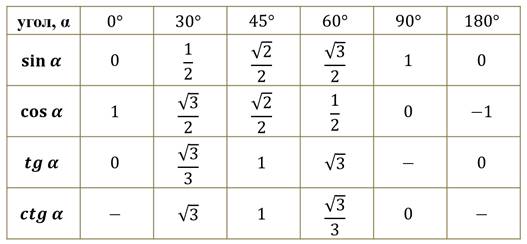 9876883406 9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.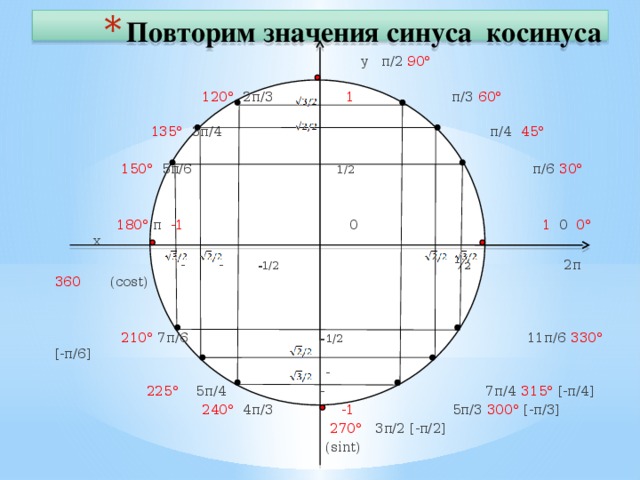 2079116908 2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.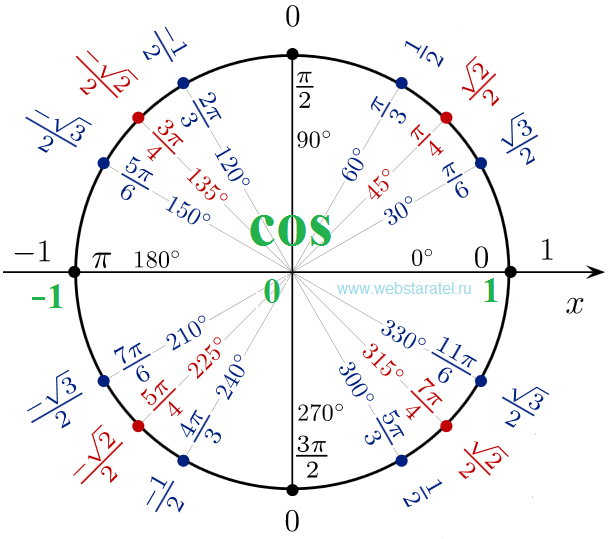 8480480962 8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
cos(38) = 0.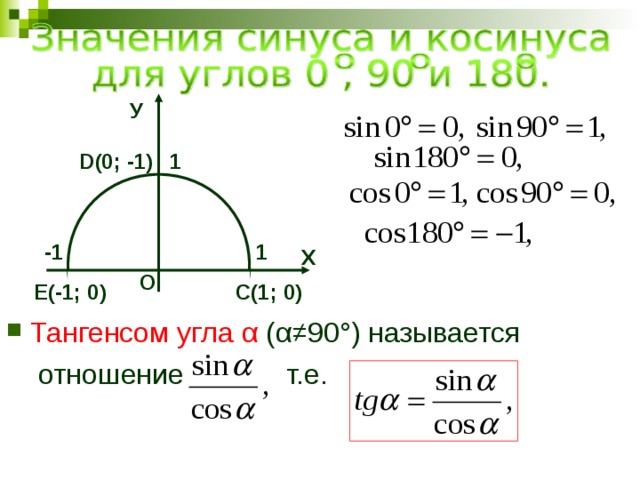 7880107536 7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.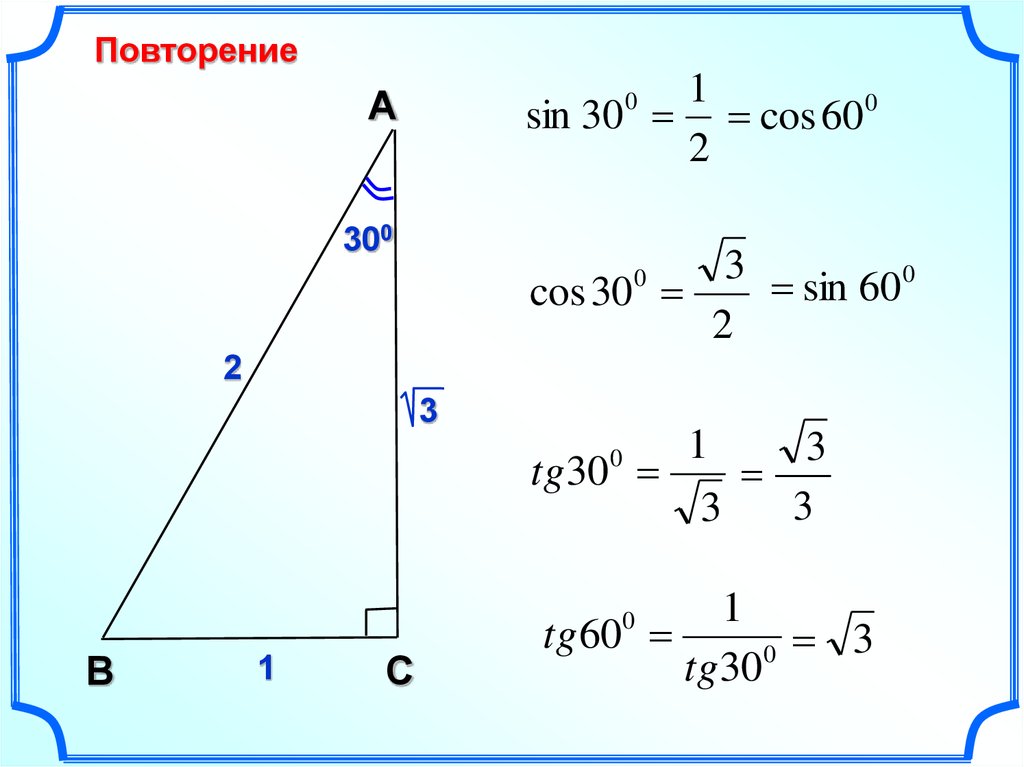 2923717047 2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.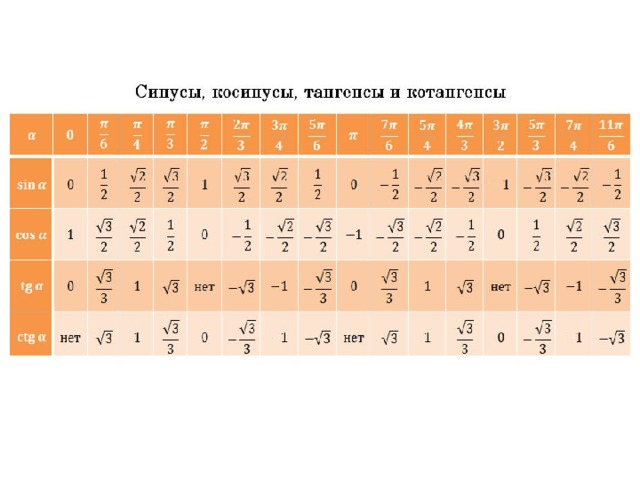 9986295348 9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.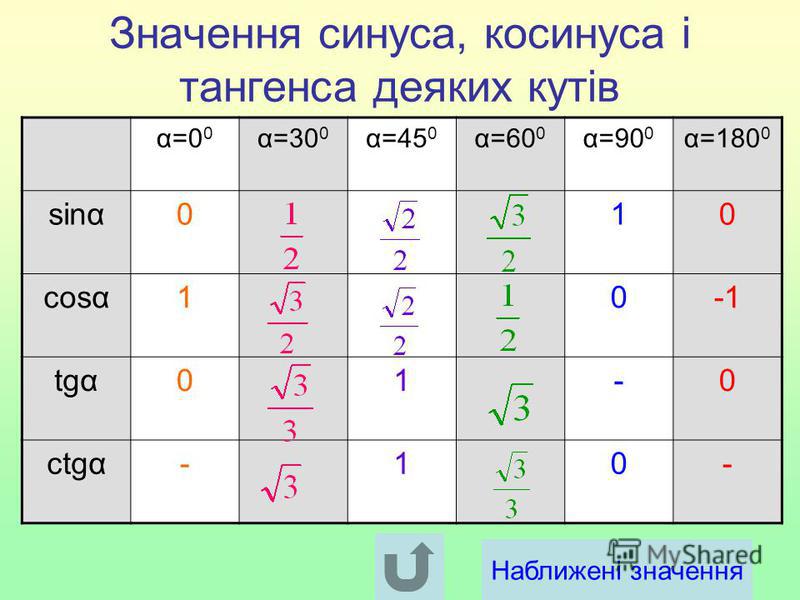 9925461516 9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
cos(77) = 0.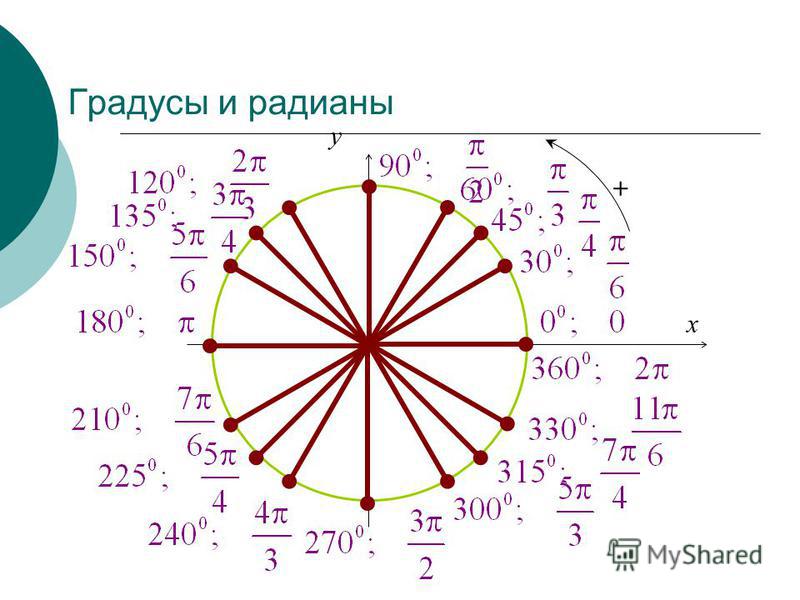 2249510543 2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0. 8290375726 8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0. 8090169944 8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
cos(106) = -0.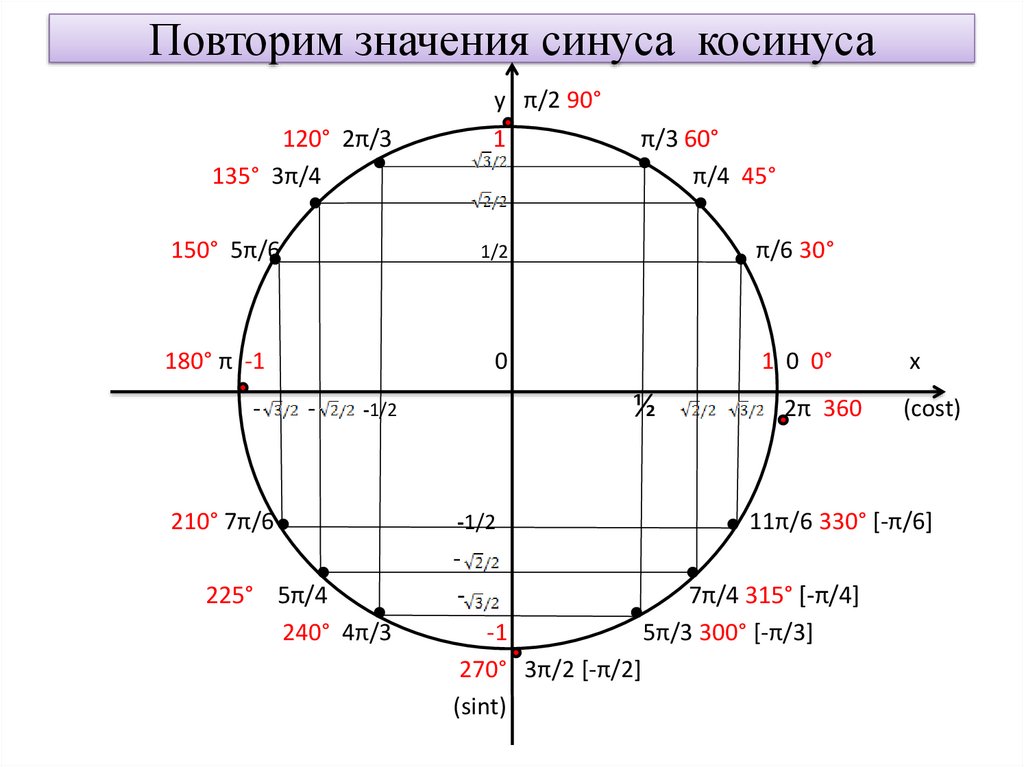 2756373558 2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0. 9961946981 9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Таблица косинусов | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Значения косинуса графически могут быть отображены в виде тригонометрической окружности, на которой угол α образует с осью прямоугольный треугольник. Из этого треугольника, спроецировав точку пересечения угла α с окружностью на ось синуса или косинуса, можно получить его приближенное значение.
Также тригонометрическая окружность показывает знак синуса и косинуса для каждого раскрытия угла α. Поскольку угол начинает раскрываться с правой стороны по оси косинусов, то значения косинуса угла α от 0° до 90° — положительны, так находятся правее нулевой точки отсчета. Угол α от 90° до 270° дает отрицательные значения косинусу, так как точка пересечения его с окружностью расположена левее оси синуса, то есть нуля. Косинус углов от 270° до 360° вновь становится положительным. Точные значения косинусов всех углов от 0° до 360° можно узнать из таблицы косинусов, приведенной ниже.
Угол α от 90° до 270° дает отрицательные значения косинусу, так как точка пересечения его с окружностью расположена левее оси синуса, то есть нуля. Косинус углов от 270° до 360° вновь становится положительным. Точные значения косинусов всех углов от 0° до 360° можно узнать из таблицы косинусов, приведенной ниже.
Найти косинус угла cos(α), зная угол
Угол α
Таблица косинусов от 0° до 180°
|
|
|
|
|
Таблица косинусов от 181° до 360°
|
|
|
|
|
Таблица косинусов, найти значения угла косинусов
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
|
|
|
|
|
|
|
|
|
|
Select rating12345
Рейтинг: 2.7 (Голосов 38)
Сообщить об ошибке
Смотрите также
Таблица косинусов углов от 0° до 360°
Таблица синусов Таблица косинусов Таблица тангенсов Таблица котангенсов Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы
Скачать таблицу косинусов
Таблица косинусов — это записанные в таблицу посчитанные значения косинусов углов от 0° до 360°. Используя таблицу косинусов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение косинуса от нужного Вам угла, достаточно найти его в таблице или вычислить с помощью калькулятора.
Калькулятор — косинус угла
cos(°) = 1
Калькулятор — арккосинус угла
arccos() = 0°
Таблица косинусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| cos α | 1 | √32 | √22 | 12 | 0 | -1 | 0 | 1 |
Таблица косинусов углов от 0° до 180°
| cos(0°) = 1 cos(1°) = 0.  999848 999848cos(2°) = 0.999391 cos(3°) = 0.99863 cos(4°) = 0.997564 cos(5°) = 0.996195 cos(6°) = 0.994522 cos(7°) = 0.992546 cos(8°) = 0.990268 cos(9°) = 0.987688 cos(10°) = 0.984808 cos(11°) = 0.981627 cos(12°) = 0.978148 cos(13°) = 0.97437 cos(14°) = 0.970296 cos(15°) = 0.965926 cos(16°) = 0.961262 cos(17°) = 0.956305 cos(18°) = 0.951057 cos(19°) = 0.945519 cos(20°) = 0.939693 cos(21°) = 0.93358 cos(22°) = 0.927184 cos(23°) = 0.920505 cos(24°) = 0.913545 cos(25°) = 0.906308 cos(26°) = 0.898794 cos(27°) = 0.891007 cos(28°) = 0.882948 cos(29°) = 0.87462 cos(30°) = 0.866025 cos(31°) = 0.857167 cos(32°) = 0.848048 cos(33°) = 0.838671 cos(34°) = 0.829038 cos(35°) = 0.819152 cos(36°) = 0.809017 cos(37°) = 0.798636 cos(38°) = 0.788011 cos(39°) = 0.777146 cos(40°) = 0.766044 cos(41°) = 0.75471 cos(42°) = 0.743145 cos(43°) = 0.731354 cos(44°) = 0.  71934 71934cos(45°) = 0.707107 | cos(46°) = 0.694658 cos(47°) = 0.681998 cos(48°) = 0.669131 cos(49°) = 0.656059 cos(50°) = 0.642788 cos(51°) = 0.62932 cos(52°) = 0.615661 cos(53°) = 0.601815 cos(54°) = 0.587785 cos(55°) = 0.573576 cos(56°) = 0.559193 cos(57°) = 0.544639 cos(58°) = 0.529919 cos(59°) = 0.515038 cos(60°) = 0.5 cos(61°) = 0.48481 cos(62°) = 0.469472 cos(63°) = 0.45399 cos(64°) = 0.438371 cos(65°) = 0.422618 cos(66°) = 0.406737 cos(67°) = 0.390731 cos(68°) = 0.374607 cos(69°) = 0.358368 cos(70°) = 0.34202 cos(71°) = 0.325568 cos(72°) = 0.309017 cos(73°) = 0.292372 cos(74°) = 0.275637 cos(75°) = 0.258819 cos(76°) = 0.241922 cos(77°) = 0.224951 cos(78°) = 0.207912 cos(79°) = 0.190809 cos(80°) = 0.173648 cos(81°) = 0.156434 cos(82°) = 0.139173 cos(83°) = 0.121869 cos(84°) = 0.104528 cos(85°) = 0.087156 cos(86°) = 0.  069756 069756cos(87°) = 0.052336 cos(88°) = 0.034899 cos(89°) = 0.017452 cos(90°) = 0 | cos(91°) = -0.017452 cos(92°) = -0.034899 cos(93°) = -0.052336 cos(94°) = -0.069756 cos(95°) = -0.087156 cos(96°) = -0.104528 cos(97°) = -0.121869 cos(98°) = -0.139173 cos(99°) = -0.156434 cos(100°) = -0.173648 cos(101°) = -0.190809 cos(102°) = -0.207912 cos(103°) = -0.224951 cos(104°) = -0.241922 cos(105°) = -0.258819 cos(106°) = -0.275637 cos(107°) = -0.292372 cos(108°) = -0.309017 cos(109°) = -0.325568 cos(110°) = -0.34202 cos(111°) = -0.358368 cos(112°) = -0.374607 cos(113°) = -0.390731 cos(114°) = -0.406737 cos(115°) = -0.422618 cos(116°) = -0.438371 cos(117°) = -0.45399 cos(118°) = -0.469472 cos(119°) = -0.48481 cos(120°) = -0.5 cos(121°) = -0.515038 cos(122°) = -0.529919 cos(123°) = -0.544639 cos(124°) = -0.559193 cos(125°) = -0.573576 cos(126°) = -0.  587785 587785cos(127°) = -0.601815 cos(128°) = -0.615661 cos(129°) = -0.62932 cos(130°) = -0.642788 cos(131°) = -0.656059 cos(132°) = -0.669131 cos(133°) = -0.681998 cos(134°) = -0.694658 cos(135°) = -0.707107 | cos(136°) = -0.71934 cos(137°) = -0.731354 cos(138°) = -0.743145 cos(139°) = -0.75471 cos(140°) = -0.766044 cos(141°) = -0.777146 cos(142°) = -0.788011 cos(143°) = -0.798636 cos(144°) = -0.809017 cos(145°) = -0.819152 cos(146°) = -0.829038 cos(147°) = -0.838671 cos(148°) = -0.848048 cos(149°) = -0.857167 cos(150°) = -0.866025 cos(151°) = -0.87462 cos(152°) = -0.882948 cos(153°) = -0.891007 cos(154°) = -0.898794 cos(155°) = -0.906308 cos(156°) = -0.913545 cos(157°) = -0.920505 cos(158°) = -0.927184 cos(159°) = -0.93358 cos(160°) = -0.939693 cos(161°) = -0.945519 cos(162°) = -0.951057 cos(163°) = -0.956305 cos(164°) = -0.961262 cos(165°) = -0.  965926 965926cos(166°) = -0.970296 cos(167°) = -0.97437 cos(168°) = -0.978148 cos(169°) = -0.981627 cos(170°) = -0.984808 cos(171°) = -0.987688 cos(172°) = -0.990268 cos(173°) = -0.992546 cos(174°) = -0.994522 cos(175°) = -0.996195 cos(176°) = -0.997564 cos(177°) = -0.99863 cos(178°) = -0.999391 cos(179°) = -0.999848 cos(180°) = -1 |
Таблица косинусов углов от 181° до 360°
| cos(181°) = -0.999848 cos(182°) = -0.999391 cos(183°) = -0.99863 cos(184°) = -0.997564 cos(185°) = -0.996195 cos(186°) = -0.994522 cos(187°) = -0.992546 cos(188°) = -0.990268 cos(189°) = -0.987688 cos(190°) = -0.984808 cos(191°) = -0.981627 cos(192°) = -0.978148 cos(193°) = -0.97437 cos(194°) = -0.970296 cos(195°) = -0.965926 cos(196°) = -0.961262 cos(197°) = -0.956305 cos(198°) = -0.951057 cos(199°) = -0.945519 cos(200°) = -0.  939693 939693cos(201°) = -0.93358 cos(202°) = -0.927184 cos(203°) = -0.920505 cos(204°) = -0.913545 cos(205°) = -0.906308 cos(206°) = -0.898794 cos(207°) = -0.891007 cos(208°) = -0.882948 cos(209°) = -0.87462 cos(210°) = -0.866025 cos(211°) = -0.857167 cos(212°) = -0.848048 cos(213°) = -0.838671 cos(214°) = -0.829038 cos(215°) = -0.819152 cos(216°) = -0.809017 cos(217°) = -0.798636 cos(218°) = -0.788011 cos(219°) = -0.777146 cos(220°) = -0.766044 cos(221°) = -0.75471 cos(222°) = -0.743145 cos(223°) = -0.731354 cos(224°) = -0.71934 cos(225°) = -0.707107 | cos(226°) = -0.694658 cos(227°) = -0.681998 cos(228°) = -0.669131 cos(229°) = -0.656059 cos(230°) = -0.642788 cos(231°) = -0.62932 cos(232°) = -0.615661 cos(233°) = -0.601815 cos(234°) = -0.587785 cos(235°) = -0.573576 cos(236°) = -0.559193 cos(237°) = -0.544639 cos(238°) = -0.529919 cos(239°) = -0.  515038 515038cos(240°) = -0.5 cos(241°) = -0.48481 cos(242°) = -0.469472 cos(243°) = -0.45399 cos(244°) = -0.438371 cos(245°) = -0.422618 cos(246°) = -0.406737 cos(247°) = -0.390731 cos(248°) = -0.374607 cos(249°) = -0.358368 cos(250°) = -0.34202 cos(251°) = -0.325568 cos(252°) = -0.309017 cos(253°) = -0.292372 cos(254°) = -0.275637 cos(255°) = -0.258819 cos(256°) = -0.241922 cos(257°) = -0.224951 cos(258°) = -0.207912 cos(259°) = -0.190809 cos(260°) = -0.173648 cos(261°) = -0.156434 cos(262°) = -0.139173 cos(263°) = -0.121869 cos(264°) = -0.104528 cos(265°) = -0.087156 cos(266°) = -0.069756 cos(267°) = -0.052336 cos(268°) = -0.034899 cos(269°) = -0.017452 cos(270°) = -0 | cos(271°) = 0.017452 cos(272°) = 0.034899 cos(273°) = 0.052336 cos(274°) = 0.069756 cos(275°) = 0.087156 cos(276°) = 0.104528 cos(277°) = 0.121869 cos(278°) = 0.139173 cos(279°) = 0.  156434 156434cos(280°) = 0.173648 cos(281°) = 0.190809 cos(282°) = 0.207912 cos(283°) = 0.224951 cos(284°) = 0.241922 cos(285°) = 0.258819 cos(286°) = 0.275637 cos(287°) = 0.292372 cos(288°) = 0.309017 cos(289°) = 0.325568 cos(290°) = 0.34202 cos(291°) = 0.358368 cos(292°) = 0.374607 cos(293°) = 0.390731 cos(294°) = 0.406737 cos(295°) = 0.422618 cos(296°) = 0.438371 cos(297°) = 0.45399 cos(298°) = 0.469472 cos(299°) = 0.48481 cos(300°) = 0.5 cos(301°) = 0.515038 cos(302°) = 0.529919 cos(303°) = 0.544639 cos(304°) = 0.559193 cos(305°) = 0.573576 cos(306°) = 0.587785 cos(307°) = 0.601815 cos(308°) = 0.615661 cos(309°) = 0.62932 cos(310°) = 0.642788 cos(311°) = 0.656059 cos(312°) = 0.669131 cos(313°) = 0.681998 cos(314°) = 0.694658 cos(315°) = 0.707107 | cos(316°) = 0.71934 cos(317°) = 0.731354 cos(318°) = 0.743145 cos(319°) = 0.75471 cos(320°) = 0.  766044 766044cos(321°) = 0.777146 cos(322°) = 0.788011 cos(323°) = 0.798636 cos(324°) = 0.809017 cos(325°) = 0.819152 cos(326°) = 0.829038 cos(327°) = 0.838671 cos(328°) = 0.848048 cos(329°) = 0.857167 cos(330°) = 0.866025 cos(331°) = 0.87462 cos(332°) = 0.882948 cos(333°) = 0.891007 cos(334°) = 0.898794 cos(335°) = 0.906308 cos(336°) = 0.913545 cos(337°) = 0.920505 cos(338°) = 0.927184 cos(339°) = 0.93358 cos(340°) = 0.939693 cos(341°) = 0.945519 cos(342°) = 0.951057 cos(343°) = 0.956305 cos(344°) = 0.961262 cos(345°) = 0.965926 cos(346°) = 0.970296 cos(347°) = 0.97437 cos(348°) = 0.978148 cos(349°) = 0.981627 cos(350°) = 0.984808 cos(351°) = 0.987688 cos(352°) = 0.990268 cos(353°) = 0.992546 cos(354°) = 0.994522 cos(355°) = 0.996195 cos(356°) = 0.997564 cos(357°) = 0.99863 cos(358°) = 0.999391 cos(359°) = 0.999848 cos(360°) = 1 |
Таблицы значений тригонометрических функций Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы Таблица синусов Таблица косинусов Таблица тангенсов Таблица котангенсов Сводная таблица тригонометрических функций
Тригонометрические формулы
Все таблицы и формулы
| cos(0) = 1 | cos(120) = -0. 5 5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0. 6427876097 6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
cos(20) = 0. 9396926208 9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0. 01745240644 01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0. 9335804265 9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
cos(49) = 0. 656059029 656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0. 4694715628 4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0. 6156614753 6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0. 9510565163 9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
cos(88) = 0. 0348994967 0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0. 9205048535 9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0. 6819983601 6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
cos(117) = -0. 2 2 |
косинусов
Как упоминалось ранее, мы обычно используем букву a для обозначения стороны, противоположной углу A, букву b для обозначения стороны, противоположной углу B, и букву c для обозначения стороны. противоположный угол C. Так как сумма углов в треугольнике равна 180°, а угол C равен 90°, то углы A и B в сумме дают 90°, то есть являются дополнительными углами. Поэтому косинус B равно синусу A. Мы видели на прошлой странице, что sin A — это сторона, противоположная гипотенузе, то есть a/c. Следовательно, cos B равно a/c. Другими словами, косинус угла прямоугольного треугольника равен прилежащему катету, деленному на гипотенузу:
Кроме того, cos A = sin B = b/c.
Тождество Пифагора для синусов и косинусов
Вспомним теорему Пифагора для прямоугольных треугольников. Он говорит, что
Он говорит, что
где c — гипотенуза. Это очень легко переводится в пифагорейское тождество синусов и косинусов. Разделите обе части на c 2 и вы получите
Но A 2 / C 2 = (SIN A ) 2 и B 2 / C 2 = (COS A ) 2 . Чтобы уменьшить количество круглых скобок, которые необходимо написать, принято соглашение, что обозначение sin 2 A является аббревиатурой для (sin A ) 2 , и аналогично для степеней другого триггера. функции. Таким образом, мы доказали, что
когда А острый угол. Мы еще не видели, какими должны быть синусы и косинусы других углов, но когда мы это увидим, мы получим для любого угла θ одно из важнейших тригонометрических тождеств, тождество Пифагора для синусов и косинусов:
Мы еще не видели, какими должны быть синусы и косинусы других углов, но когда мы это увидим, мы получим для любого угла θ одно из важнейших тригонометрических тождеств, тождество Пифагора для синусов и косинусов:
Синусы и косинусы для особых общих углов
Мы можем легко вычислить синусы и косинусы для некоторых общих углов. Рассмотрим сначала 45° угол. Он находится в равнобедренном прямоугольном треугольнике, то есть 45°-45°-9треугольник 0°. В любой прямоугольный треугольник c 2 = a 2 + b 2 , но в этом один a = b, so c 2 = 2 a 2 . Следовательно c = a √2. Следовательно, и синус, и косинус 45° равно 1/√2, что также может быть записано как √2 / 2.
Далее рассмотрим углы 30° и 60°. В диапазоне 30°-60°-90° прямоугольный треугольник, отношения
сторон равны 1 : √3 : 2. Отсюда следует, что
sin 30° = cos 60° = 1/2 и
sin 60° = cos 30° = √3 / 2.
Отсюда следует, что
sin 30° = cos 60° = 1/2 и
sin 60° = cos 30° = √3 / 2.
Эти данные заносятся в эту таблицу.
| Angle | Degrees | Radians | cosine | sine |
|---|---|---|---|---|
| 90° | π /2 | 0 | 1 | |
| 60° | π /3 | 1/2 | √3 / 2 | |
| 45° | π /4 | √2 / 2 | √2 / 2 | |
| 30° | π /6 | √3 / 2 | 1/2 | |
| 0° | 0 | 1 | 0 |
Exercises
These exercises all относятся к прямоугольным треугольникам со стандартной маркировкой.
30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. б = 6,4, в = 7,8. Найдите А и А.
36. A = 23° 15′, c = 12,15. Найти а и б.
Советы
30. Косинус числа A связывает b с гипотенузой c, , так что вы можете сначала вычислить c. Зная b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух неизвестных вам сторон, а именно а/к. Тем не менее, это дает вам уравнение для работы: 1/3 = a/c. Тогда c = 3 a. Из теоремы Пифагора следует, что а 2 + 144 = 9 а 2 . Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. c = b /cos A = 2,25/0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 дюйма, или 4’3′.
c = 3 и , что составляет 12,73 фута или 12 футов 9 дюймов.
35. cos A = b/c = 6,4/7,8 = 0,82. Следовательно, A = 34,86° = 34°52′, или около 35°.
a 2 = 7,8 2 – 6,4 2 = 19,9, поэтому a равно примерно 4,5.
36. a = c sin A = 12,15 sin 23°15′ = 4,796.
b = c cos A = 12,15 cos 23°15′ = 11,17.
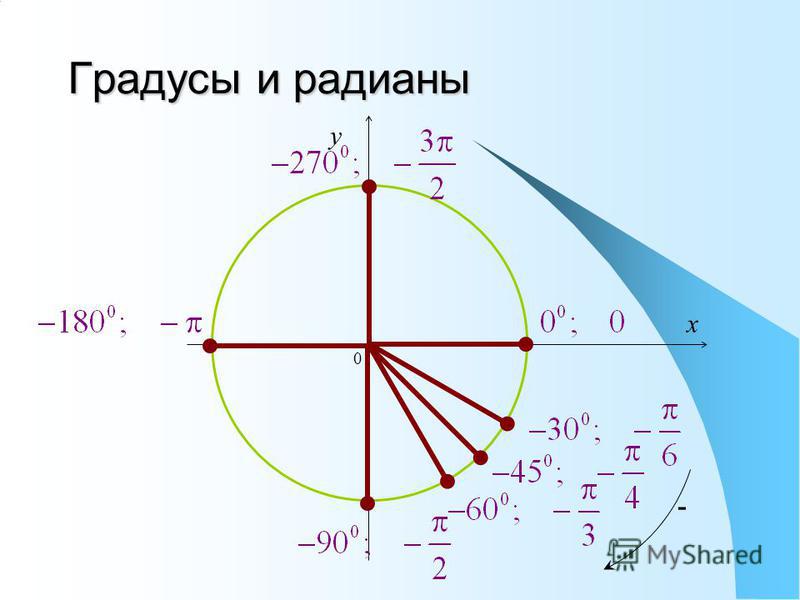
математика — Как преобразовать радианы в градусы с помощью Python?
Python конвертирует радианы в градусы или градусы в радианы:
Что такое радианы и какую проблему они решают?:
Радианы и градусы — это две отдельные единицы измерения, которые помогают людям выражать и сообщать о точных изменениях направления. В Википедии есть отличная интуиция с их инфографикой о том, как один радиан определяется по отношению к градусам:
https://en.wikipedia.org/wiki/Radian
Примеры Python с использованием библиотек, вычисляющих градусы в радианах:
>>> import math >>> math.степени(0) #0 радиан == 0 градусов 0,0 >>> math.степени(math.pi/2) #pi/2 радиана составляет 90 градусов 90,0 >>> math.степени(math.pi) #пи радиан равно 180 градусам 180,0 >>> math.степени(math.pi+(math.pi/2)) #pi+pi/2 радиан равно 270 градусов 270,0 >>> math.степени(math.pi+math.pi) #2*пи радиан это 360 градусов 360,0
Примеры Python с использованием библиотек, вычисляющих радианы из градусов:
>>> import math >>> math.radians(0) #0 градусов == 0 радиан 0,0 >>> math.radians(90) #90 градусов равно пи/2 радианам 1.5707963267948966 >>> math.radians(180) #180 градусов - пи радианы 3.141592653589793 >>> math.radians(270) #270 градусов равно пи+(пи/2) радианам 4.71238898038469 >>> math.radians(360) #360 градусов равно 2*пи радианам 6.283185307179586
Источник: https://docs.python.org/3/library/math.html#angular-conversion
Математическая запись:
Вы можете преобразовать градусы в радианы без библиотек Python:
Если вы используете собственный преобразователь градусов в радианы, вам придется написать собственный код для обработки пограничных случаев.
Ошибки здесь легко допустить, и они причинят вред точно так же, как это навредило разработчикам марсианского орбитального аппарата 1999 года, которые потратили 125 миллионов долларов на то, чтобы врезаться в Марс, из-за неинтуитивного пограничного случая.
>>> 0 * 180.0 / math.pi #0 радиан равно 0 градусов 0,0 >>> (math.pi/2) * 180.0 / math.pi #pi/2 радиана составляет 90 градусов 90,0 >>> (math.pi) * 180.0 / math.pi #pi в радианах равно 180 градусам 180,0 >>> (math.pi+(math.pi/2)) * 180.0 / math.pi #pi+(pi/2) радиан составляет 270 градусов 270,0 >>> (2 * math.pi) * 180.0 / math.pi #2*pi в радианах равно 360 градусам 360,0
Градусов в радианы:
>>> 0 * math.pi / 180.0 #0 градусов в радианах 0,0 >>> 90 * math.pi / 180.0 #90 градусов в радианах 1.5707963267948966 >>> 180 * math.pi / 180.0 #180 градусов в радианах 3.141592653589793 >>> 270 * math.pi / 180.0 #270 градусов в радианах 4.71238898038469 >>> 360 * math.pi / 180.0 #360 градусов в радианах 6.283185307179586
Выражение нескольких оборотов в градусах и радианах
Допустимые значения радиана для одного вращения находятся в диапазоне от 0 до 2*pi. Значения одного градуса вращения находятся в диапазоне от 0 до 360. Однако, если вы хотите выразить несколько вращений, допустимые значения радиана и градуса находятся в диапазоне от 0 до бесконечности.
>>> импорт математики >>> math.radians(360) #один полный оборот 6.283185307179586 >>> math.radians(360+360) #два оборота 12,566370614359172 >>> math.степени(12.566370614359172) #math.степени и математические.радианы сохраняют 720.0 #количество оборотов
Свертывание нескольких поворотов:
Вы можете свернуть несколько поворотов в градусах/радианах в один поворот, изменив значение одного поворота. Для градусов вы модифицируете на 360, для радианов — на 2*pi.
>>> импорт математики >>> math.radians(720+90) #2 полных оборота плюс 90 равно 14,14 радиана 14.137166941154069 >>> math.radians((720+90)%360) #14.1 radians приводит вас к 1.5707963267948966 #конечная точка равна 1,57 радианам. >>> math.степени((2*math.pi)+(math.pi/2)) #один оборот плюс четверть 450.0 #rotation составляет 450 градусов. >>> math.степени(((2*math.pi)+(math.pi/2))%(2*math.pi)) #один оборот плюс четверть 90.0 #rotation приводит вас к 90.
Базовое обучение по радианам и градусам
5-минутный курс повышения квалификации по тригонометрии и выражению вращения для преобразования радианов в градусы и обратно: https://youtu. be/ovLbCvq7FNA?t=31
be/ovLbCvq7FNA?t=31
Курс повышения квалификации по тригонометрии в Академии Хана, единичный круг, угловая математика для использования sin, cos, tan для описания вращения и изменений во вращении. https://www.khanacademy.org/math/алгебра2/x2ec2f6f830c9fb89:trig/x2ec2f6f830c9fb89:unit-circle/v/unit-circle-definition-of-trig-functions-1
Как найти угол с косинусом
Как найти угол с косинусом — ACT Math—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- Репетиторство ACT
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Справка по математике ACT » Тригонометрия » косинус » Как найти угол с косинусом
В приведенном выше треугольнике и . Находить .
Находить .
Возможные ответы:
Правильный ответ:
Объяснение:
Для прямоугольных треугольников мы можем использовать SOH CAH TOA для нахождения неизвестных длин сторон и углов. Для этой задачи нам даны смежная сторона и гипотенуза треугольника по отношению к углу. Имея эту информацию, мы можем использовать функцию косинуса, чтобы найти угол.
Сообщить об ошибке
Для приведенного выше треугольника и . Находить .
Возможные ответы:
Правильный ответ:
Объяснение:
Для прямоугольных треугольников мы можем использовать SOH CAH TOA для нахождения неизвестных длин сторон и углов. Для этой задачи нам даны смежная сторона и гипотенуза треугольника по отношению к углу. Имея эту информацию, мы можем использовать функцию косинуса, чтобы найти угол.
Для этой задачи нам даны смежная сторона и гипотенуза треугольника по отношению к углу. Имея эту информацию, мы можем использовать функцию косинуса, чтобы найти угол.
Сообщить об ошибке
Для приведенного выше треугольника и . Находить .
Возможные ответы:
Этот треугольник не может существовать.
Правильный ответ:
Этот треугольник не может существовать.
Объяснение:
Для прямоугольных треугольников мы можем использовать SOH CAH TOA для нахождения неизвестных длин сторон и углов. Для этой задачи нам даны смежная сторона и гипотенуза треугольника по отношению к углу. Однако, если мы подставим данные значения в формулу косинуса, мы получим:
Эта задача не имеет решения. Стороны прямоугольного треугольника должны быть короче гипотенузы. Треугольник со стороной больше гипотенузы не может существовать. Точно так же областью определения функции arccos является . В 1.3 не определяется.
Стороны прямоугольного треугольника должны быть короче гипотенузы. Треугольник со стороной больше гипотенузы не может существовать. Точно так же областью определения функции arccos является . В 1.3 не определяется.
Сообщить об ошибке
Веревка брошена со здания на землю и привязана на расстоянии от основания здания. Чему равен угол между веревкой и землей? Округлить до сотых долей градуса .
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете нарисовать свой сценарий, используя следующий прямоугольный треугольник:
Напомним, что косинус угла равен отношению прилежащей стороны к гипотенузе треугольника. Вы можете найти угол, используя функцию арккосинуса:
или градусы.
Сообщить об ошибке
Каково значение в прямоугольном треугольнике выше? Округлите до сотых долей градуса.
Возможные ответы:
Правильный ответ:
Объяснение:
Напомним, что косинус угла равен отношению прилежащей стороны к гипотенузе треугольника. Вы можете найти угол, используя функцию арккосинуса:
или .
Сообщить об ошибке
Опорная балка (контрфорс) прилегает к строящемуся зданию. Если луч имеет длину в футы и падает на здание в точке на высоте фута от стены, под каким углом луч падает на здание? Округлить до ближайшего градуса.
Возможные ответы:
Правильный ответ:
Пояснение:
Наш ответ заключается в обратных функциях. Если контрфорс имеет длину в футах и находится в футах над лестницей под нужным углом, то:
Таким образом, используя обратные функции, мы можем сказать, что
Таким образом, наш контрфорс касается здания примерно под углом.
Сообщить об ошибке
Каменный монумент служит туристической достопримечательностью. Турист хочет поймать солнце под правильным углом, чтобы «сидеть» на вершине столба. Турист ложится на землю в метрах от памятника, наводит камеру на вершину памятника, и на дисплее камеры появляется надпись «РАССТОЯНИЕ — МЕТРОВ». Под каким углом с точностью до градуса находится солнце по отношению к горизонту?
Возможные ответы:
Правильный ответ:
Пояснение:
Наш ответ заключается в обратных функциях. Если памятник находится в метрах и камера находится в метрах от вершины памятника под нужным углом, то:
Таким образом, используя обратные функции, мы можем сказать, что
Таким образом, наш контрфорс касается здания примерно под углом.
Сообщить об ошибке
Уведомление об авторских правах
Просмотр репетиторов математики ACT
Ping
Сертифицированный репетитор
Техасский университет в Далласе, бакалавр компьютерных наук. Университет Северного Техаса, магистр искусств, образование.
Университет Северного Техаса, магистр искусств, образование.
View ACT Math Tutors
Tom
Сертифицированный преподаватель
Университет Висконсин-Мэдисон, бакалавр наук, атмосферных наук и метеорологии. Embry-Riddle Aeronautical Univers…
View ACT Math Tutors
Nnang
Сертифицированный преподаватель
Колумбийский университет в городе Нью-Йорк, бакалавр экономических наук.
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учись по концепции
Cos 1, градусы — Найти значение Cos 1, градусы
LearnPracticeDownload
Значение , cos 1, градус равно 0,9998476. . . . Cos 1 градус в радианах записывается как cos (1° × π/180°), т. е. cos (0,017453…). В этой статье мы обсудим методы нахождения значения cos 1 градусов на примерах.
- Кос 1°: 0,9998476.
 . .
. . - Cos (-1 градус): 0,9998476. . .
- Cos 1° в радианах: cos (0,0174532 . . .)
Каково значение Cos 1 градусов?
Значение cos 1 градуса в десятичной системе равно 0,999847695. . .. Cos 1 градус также может быть выражен с использованием эквивалента данного угла (1 градус) в радианах (0,01745 . . .)
Мы знаем, используя преобразование градусов в радианы, θ в радианах = θ в градусах × (пи/ 180°)
⇒ 1 градус = 1° × (π/180°) рад = 0,0174. . .
∴ cos 1 ° = cos (0,0174) = 0,9998476. . .
Пояснение:
Для cos 1 градусов угол 1° лежит между 0° и 90° (первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos 1° = 0,9998476. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 1° как cos 1 градусов = cos(1° + n × 360°), n ∈ Z.
⇒ cos 1° = cos 361° = cos 721° и так далее.
Примечание: Поскольку косинус — четная функция, значение cos(-1°) = cos(1°).
Методы определения значения косинуса 1 в градусах
Функция косинуса положительна в 1-м квадранте. Значение cos 1° равно 0,99984. . .. Мы можем найти значение cos 1 градусов по:
- Используя единичный круг
- Использование тригонометрических функций
Cos 1, градусы с использованием единичной окружности
Чтобы найти значение cos 1, используя единичную окружность:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 1° с положительной осью x.
- Косвенный коэффициент 1 градуса равен координате x (0,9998) точки пересечения (0,9998, 0,0175) единичной окружности и r.
Следовательно, значение cos 1° = x = 0,9998 (приблизительно)
Cos 1° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 1 градусов как:
- ± √(1-sin² (1°))
- ± 1/√(1 + tan²(1°))
- ± раскладушка 1°/√(1 + раскладушка²(1°))
- ±√(косек²(1°) — 1)/косек 1°
- 1/сек 1°
Примечание. Поскольку 1° лежит в 1-м квадранте, окончательное значение cos 1° будет положительным.
Поскольку 1° лежит в 1-м квадранте, окончательное значение cos 1° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 1° как
- -cos(180° — 1°) = -cos 179°
- -cos(180° + 1°) = -cos 181°
- sin(90° + 1°) = sin 91°
- sin(90° — 1°) = sin 89°
☛ Также проверьте:
- cos 300 градусов
- потому что 10 градусов
- кос 45 градусов
- кос 70 градусов
- кос 22 градуса
- кос 29 градусов
Примеры использования Cos 1 градусов
Пример 1. Найдите значение 2 cos(1°)/3 sin(89°).
Решение:
Используя тригонометрические тождества, мы знаем, что cos(1°) = sin(90° — 1°) = sin 89°.
⇒ cos(1°) = sin(89°)
⇒ Значение 2 cos(1°)/3 sin(89°) = 2/3Пример 2. Найдите значение cos 1°, если sec 1° равно 1,0001.

Решение:
Так как cos 1° = 1/сек 1°
⇒ cos 1° = 1/1,0001 = 0,9998Пример 3: Найдите значение (cos² 0,5° — sin² 0,5°). [Подсказка: используйте cos 1° = 0,9998]
Решение:
Используя формулу cos 2a,
(cos² 0,5° — sin² 0,5°) = cos(2 × 0,5°) = cos 1°
∵ cos 1° = 0,9998
⇒ (cos² 0,5° — sin² 0,5°) = 0,9998
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cos 1 Degrees
Что такое Cos 1 Degrees?
Cos 1 градус — значение тригонометрической функции косинуса для угла, равного 1 градусу. Значение cos 1° равно 0,9998 (приблизительно)
Значение cos 1° равно 0,9998 (приблизительно)
Как найти Cos 1° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 1° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(1°))
- ± 1/√(1 + tan²(1°))
- ± раскладушка 1°/√(1 + раскладушка²(1°))
- ± √(косек²(1°) — 1)/косек 1°
- 1/сек 1°
☛ Также проверьте: таблицу тригонометрии
Как найти значение Cos 1 градусов?
Значение cos 1 градуса можно рассчитать, построив угол 1° с осью x и затем найдя координаты соответствующей точки (0,9998, 0,0175) на единичной окружности. Значение cos 1° равно координате x (0,9998). ∴ cos 1° = 0,9998.
Каково точное значение cos 1 в градусах?
Точное значение для cos 1 градуса может быть задано с точностью до 8 знаков после запятой как 0,99984769.
Каково значение Cos 1 в градусах относительно Tan 1°?
Мы знаем, что, используя тригонометрические тождества, мы можем записать cos 1° как 1/√(1 + tan²(1°)). Здесь значение тангенса 1° равно 0,017455.
Здесь значение тангенса 1° равно 0,017455.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный курс
| 1 | Найдите точное значение | грех(30) | |
| 2 | Найдите точное значение | грех(45) | |
| 3 | Найдите точное значение | грех(30 градусов) | |
| 4 | Найдите точное значение | грех(60 градусов) | |
| 5 | Найдите точное значение | загар (30 градусов) | |
| 6 | Найдите точное значение | угловой синус(-1) | |
| 7 | Найдите точное значение | грех(пи/6) | |
| 8 | Найдите точное значение | cos(pi/4) | |
| 9 | Найдите точное значение | грех(45 градусов) | |
| 10 | Найдите точное значение | грех(пи/3) | |
| 11 | Найдите точное значение | арктан(-1) | |
| 12 | Найдите точное значение | cos(45 градусов) | |
| 13 | Найдите точное значение | cos(30 градусов) | |
| 14 | Найдите точное значение | желто-коричневый(60) | |
| 15 | Найдите точное значение | csc(45 градусов) | |
| 16 | Найдите точное значение | загар (60 градусов) | |
| 17 | Найдите точное значение | сек(30 градусов) | |
| 18 | Найдите точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найдите точное значение | грех(60) | |
| 21 | Найдите точное значение | cos(pi/2) | |
| 22 | Найдите точное значение | загар (45 градусов) | |
| 23 | Найдите точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найдите точное значение | csc(60 градусов) | |
| 25 | Найдите точное значение | сек(45 градусов) | |
| 26 | Найдите точное значение | csc(30 градусов) | |
| 27 | Найдите точное значение | грех(0) | |
| 28 | Найдите точное значение | грех(120) | |
| 29 | Найдите точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найдите точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найдите точное значение | детская кроватка(30 градусов) | |
| 37 | Найдите точное значение | арккос(-1) | |
| 38 | Найдите точное значение | арктический(0) | |
| 39 | Найдите точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найдите точное значение | грех((5pi)/3) | |
| 43 | Найдите точное значение | грех((3pi)/4) | |
| 44 | Найдите точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найдите точное значение | грех(300) | |
| 46 | Найдите точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найдите точное значение | соз(0) | |
| 49 | Найдите точное значение | соз(135) | |
| 50 | Найдите точное значение | cos((5pi)/3) | |
| 51 | Найдите точное значение | cos(210) | |
| 52 | Найдите точное значение | сек(60 градусов) | |
| 53 | Найдите точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найдите точное значение | грех(135 градусов) | |
| 61 | Найдите точное значение | грех(150) | |
| 62 | Найдите точное значение | грех(240 градусов) | |
| 63 | Найдите точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найдите точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найдите точное значение | cos(150 градусов) | |
| 68 | Найдите точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найдите точное значение | сек(0) | |
| 71 | Найдите точное значение | cos((5pi)/6) | |
| 72 | Найдите точное значение | КСК(30) | |
| 73 | Найдите точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найдите точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найдите точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найдите точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. )/4 )/4 | |
| 79 | Найдите точное значение | грех((7pi)/4) | |
| 80 | Найдите точное значение | угловой синус(-1/2) | |
| 81 | Найдите точное значение | грех((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктангел (квадратный корень из 3) | |
| 84 | Найдите точное значение | грех(135) | |
| 85 | Найдите точное значение | грех(105) | |
| 86 | Найдите точное значение | грех(150 градусов) | |
| 87 | Найдите точное значение | грех((2pi)/3) | |
| 88 | Найдите точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найдите точное значение | грех(пи/2) | |
| 91 | Найдите точное значение | сек(45) | |
| 92 | Найдите точное значение | cos((5pi)/4) | |
| 93 | Найдите точное значение | cos((7pi)/6) | |
| 94 | Найдите точное значение | угловой синус(0) | |
| 95 | Найдите точное значение | грех(120 градусов) | |
| 96 | Найдите точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найдите точное значение | cos(270) | |
| 98 | Найдите точное значение | грех((7pi)/6) | |
| 99 | Найдите точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Функция COS в Excel (формула, примеры)
Функция COS Excel является встроенной тригонометрической функцией.
Он используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла. Здесь угол — это число в Excel. Эта функция принимает только один аргумент, который представляет собой введенное число.
Это встроенная функция MS Excel. Он относится к категории математических функций в MS Excel. Функция возвращает косинус угла, заданного в радианах. Параметр представляет собой значение угла, для которого вычисляется косинус. Угол можно рассчитать с помощью функции РАДИАНЫ или умножив на PI()/180.
Содержание
- Функция COS Excel
- Формула COS
- Как использовать функцию COS в Excel?
- Пример №1 – Расчет значения cos (0)
- Пример №2 – Расчет значения cos (30)
- Пример №3 – Расчет значения cos (45)
- Пример №4 – Расчет значения значение cos (60)
- Пример № 5. Расчет значения cos (90)
- Что нужно помнить о функции COS в Excel
- Использование функции COS в Excel VBA
- VBA Пример № 1
- VBA Пример № 2
- Рекомендуемые статьи
COSULA
COSULA
COSULA
The Formula. Excel имеет один аргумент, который является обязательным параметром.
Excel имеет один аргумент, который является обязательным параметром.
- число = Это обязательный параметр. Указывает угол, для которого должен быть рассчитан косинус.
Как использовать функцию COS в Excel?
COS можно использовать в рабочих листах Excel в качестве функции рабочего листа (WS) и Excel VBA. В качестве функции WS ее можно ввести как часть формулы COS в ячейке рабочего листа. Как функция VBAФункция VBAФункции VBA служат основной цели для выполнения определенных вычислений и возврата значения. Поэтому в VBA мы используем синтаксис для указания параметров и типа данных при определении функции. Такие функции называются пользовательскими функциями. Более того, их можно ввести в код VBA.
Вы можете скачать этот шаблон Excel для функции COS здесь — Шаблон Excel для функции COS
Обратитесь к примерам, приведенным ниже, чтобы лучше понять.
Пример №1. Вычисление значения cos (0)
В этом примере ячейка B2 содержит значение угла, для которого необходимо вычислить косинус. Ячейка C2 имеет связанную с ней формулу COS, то есть RADIANS. COS в excel присваивается ячейке D2. RADIANS(B2) равен 0. Кроме того, COS применяется к 0, что равно 1.
Ячейка C2 имеет связанную с ней формулу COS, то есть RADIANS. COS в excel присваивается ячейке D2. RADIANS(B2) равен 0. Кроме того, COS применяется к 0, что равно 1.
Следовательно, результирующая ячейка D2 имеет значение 1, так как COS(0) равен 1.
Пример №2. Вычисление значения cos (30)
В этом примере ячейка B3 содержит значение угла, для которого необходимо вычислить косинус. Ячейка C3 имеет связанную с ней формулу COS, то есть RADIANS. COS в excel присваивается ячейке D3. РАДИАНЫ (B3) равны 0,523598776. Кроме того, COS применяется к 0,523598776, что равно 0,866025404.
Следовательно, результирующая ячейка D3 имеет значение 1, так как COS (0,523598776) равен 1.
Пример №3. Вычисление значения cos (45)
В этом примере ячейка B4 содержит значение угла, для которого необходимо вычислить косинус. Ячейка C4 имеет связанную с ней формулу COS, то есть РАДИАНЫ. COS присваивается ячейке D4. РАДИАНЫ (B3) равны 0,523598776. Кроме того, COS применяется к 0,785398163, что равно 0,707106781.
Следовательно, результирующая ячейка D4 имеет значение 1, поскольку COS (0,707106781) равно 1.
Пример №4. Вычисление значения cos (60) какой косинус нужно вычислить. Ячейка C5 имеет связанную с ней формулу COS, то есть RADIANS. COS присваивается ячейке D5. РАДИАНЫ (B5) равны 1,04719.7551. Далее COS применяется к 1.047197551, что равно 0,5.
Следовательно, результирующая ячейка D5 имеет значение 0,5, поскольку COS (1,047197551) равен 0,5.
Пример № 5 – Вычисление значения cos (90)
В этом примере ячейка B6 содержит значение угла, для которого необходимо вычислить косинус. С ячейкой C6 связана формула COS, которая равна B6*PI ()/180. COS присваивается ячейке D6. 90*PI ()/180 равно 1,570796327 . Значение PI () равно 3,14159. Итак, это 90 * (3,14159/180) = 1,570796327. Далее COS применяется к 1.570796327, что равно 6.12574E-17 .
Следовательно, результирующая ячейка D6 имеет 6,12574E-17, поскольку COS (1,570796327) равен 6,12574E-17.
- COS в Excel всегда предполагает радианы в качестве параметра, для которого вычисляется косинус.
- Если угол выражен в градусах, его необходимо вычислить с помощью функции РАДИАНЫ или умножить угол на PI ()/180.
COS в Excel можно использовать в Excel VBA следующим образом. Во-первых, он служит той же цели: получить значение косинуса предоставленного угла.
| Синтаксис : COS (число) |
Пример VBA #1 знач1 = потому что ( 0 ) знач1 :
1Здесь знач1 — это переменная. Он объявлен как Double, что указывает на то, что он может хранить данные с типом данных double. Косинус 0 равен 1. Следовательно, val1 имеет значение 1.
Пример VBA № 2
Const pi = 3,1415 Dim val As Double ' Преобразование 45 градусов в радианы путем умножения на число пи/180.

 9703
9703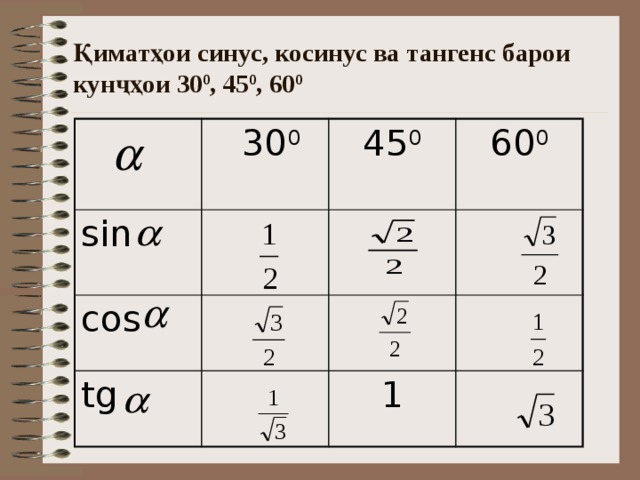 788
788 454
454 0523
0523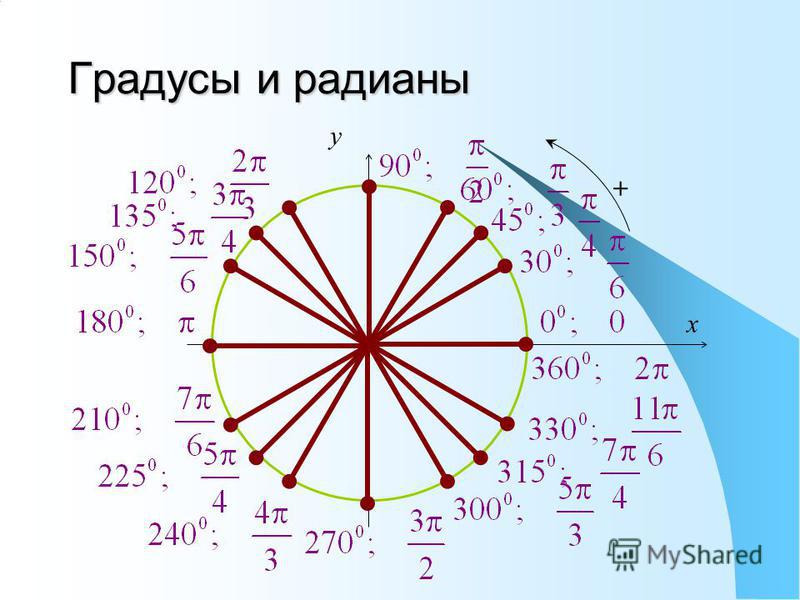 342
342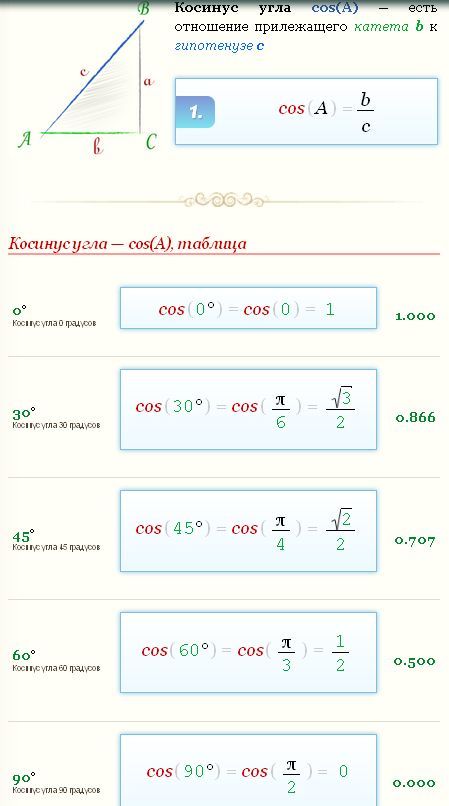 6947
6947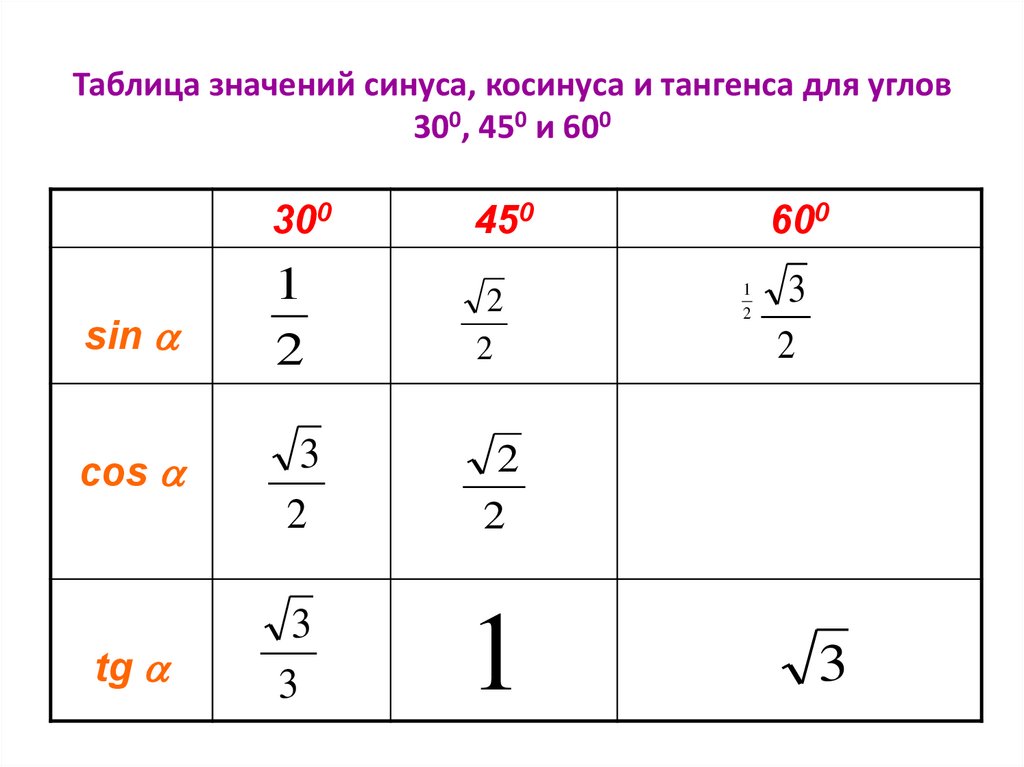 9205
9205 9998
9998
 6691
6691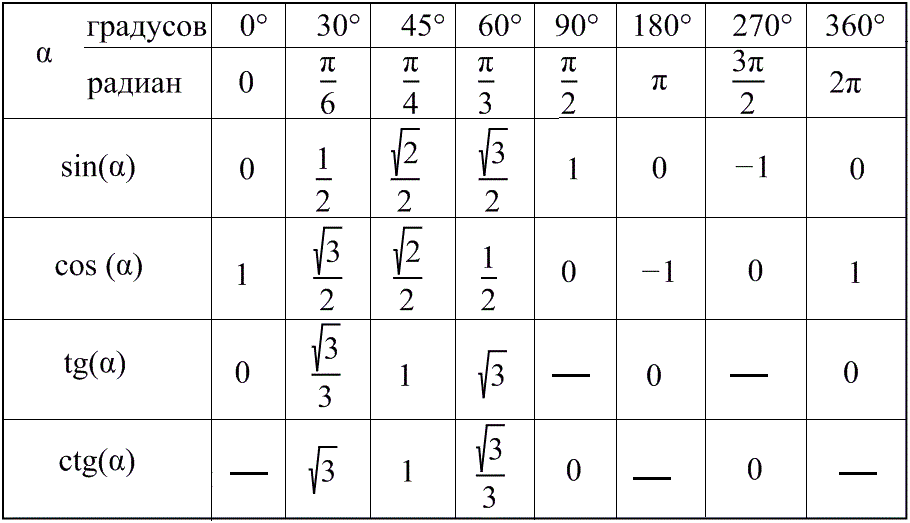 309
309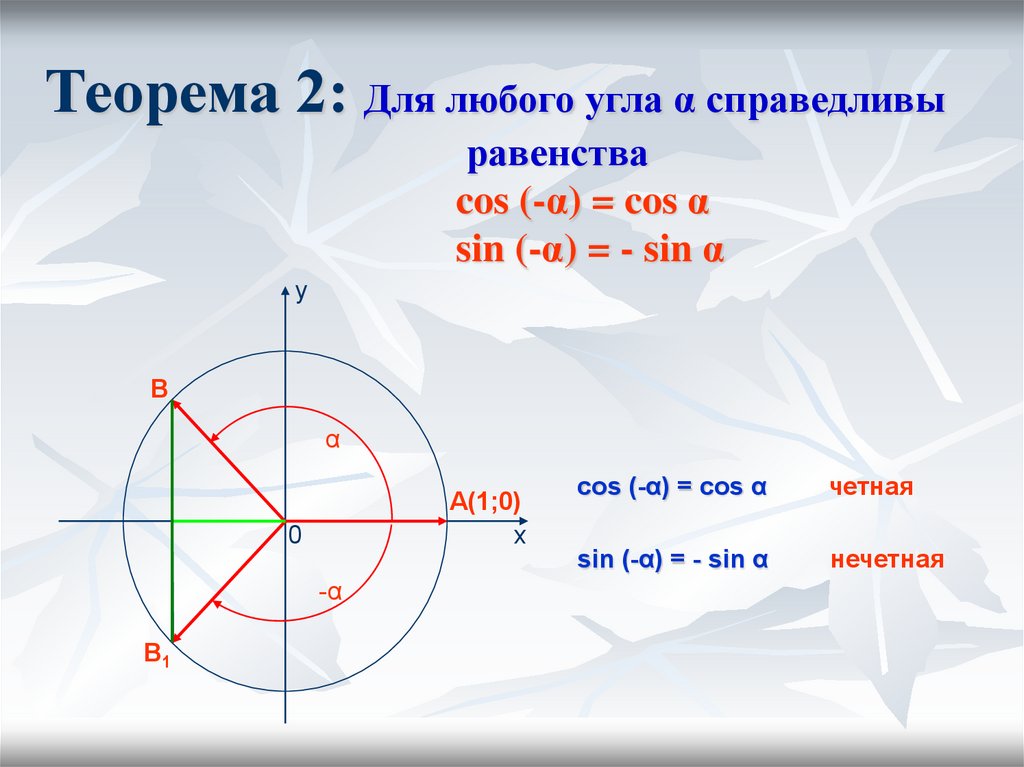 0872
0872