ЕГЭ. Задача 4. Теория вероятностей
Подготовка к единому государственному экзамену по математике. Полезные материалы и видеоразборы задач по теории вероятностей.
Полезные материалы
- Теория вероятностей (Фоксфорд.Учебник)
Видеоразборы задач
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
В Волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня 28 марта, погода в Волшебной стране хорошая. Найдите вероятность того, что 1 апреля в Волшебной стране будет отличная погода.
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 8 прыгунов из России и 10 прыгунов из Мексики. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что пятнадцатым будет выступать прыгун из России.
Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что пятнадцатым будет выступать прыгун из России.
На рисунке изображен лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому еще не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придет к выходу D.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Подборка задач
- В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
- В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии.
 Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции. - Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
- В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: $$1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.$$ Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
- Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями.
 Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора Максимова окажется запланированным на последний день конференции?
Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора Максимова окажется запланированным на последний день конференции? - В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
- Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
- Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
- В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орел, а во второй — решка.
- В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

- В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки.
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
- На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
- В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
- В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
- Стрелок стреляет по мишени один раз.
 В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом). - Если гроссмейстер Антонов играет белыми, то он выигрывает у гроссмейстера Борисова с вероятностью 0,52. Если Антонов играет черными, то Антонов выигрывает у Борисова с вероятностью 0,3. Гроссмейстеры Антонов и Борисов играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что Антонов выиграет оба раза.
- В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
- Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука.
 На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе? - При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
- Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
- Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
- Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнет игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.

- В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
- По отзывам покупателей Иван Иванович оценил надежность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
- Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых
- Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

- На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятость того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
- Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Вероятность того, что на тесте по биологии учащийся О.
 верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. - Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
- В Волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
- В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами.
 Артем хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Артем пойдет в магазин?
Артем хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Артем пойдет в магазин? - Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трех предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трех предметов — математика, русский язык и обществознание. Вероятность того, что Петров получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что Петров сможет поступить хотя бы на одну из двух упомянутых специальностей
- При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6.

Теория вероятностей. Задачи повышенной сложности (Математика 11 класс) доклад, проект
Теория вероятностей.
Задачи повышенного и высокого уровней сложности
Математика 11 класс
МБОУ СШ №12
Учитель: Шудраков Николай Николаевич
Несовместные события
Два события А и В называются несовместными, если отсутствуют исходы, благоприятные одновременно как событию А, так и событию В.
ПРИМЕР:
Бросают кубик. События «выпало число 3» и «выпало четное число» несовместны.
При этом события «выпало число больше 3» и выпало четное число» совместны.
Объединение событий
Пусть событие С означает, что произошло хотя бы одно из событий А и В. Тогда событие С называют объединением (суммой) событий А и В.
Тогда событие С называют объединением (суммой) событий А и В.
С = А U В
Вероятность несовместных событий
Если события А и В несовместны, то вероятность их объединения равна сумме вероятностей событий А и В.
Р(А U В) = Р(А) + Р(В)
Независимые события
Два события А и В называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события
ПРИМЕР:
Выполнили два подбрасывания монеты. События «при первом подбрасывании выпала решка» и «привтором подбрасывании выпал орел» независимы.
В урне 2 белых и 2 черных шара. Событие «первый извлеченный шар белый» и «второй извлеченный шар черный — зависимые.
Пересечение событий
Пусть событие С означает, что произошло как событие А, так и В. Тогда событие С называют пересечением (произведением) событий А и В.
С = А ∩ В
Вероятность независимых событий
Если события А и В независимы, то вероятность их пересечения равна произведению вероятностей событий А и В.
Р(А ∩ В) = Р(А) ∙ Р(В)
Частота события
Частотой события А называют отношение m / n, где n – общее число испытаний, m – число появления события А.
ПРИМЕР:
Мы подбросили монету 100 раз, орел выпал 47 раз. Частота выполнения орла равна 47/100=0,47
Задачи об объединении несовместных событий
1. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Ромб», равна 0,1. Вероятность того, что это вопрос на тему «Окружность», равна 0,15. Вопросов, относящихся одновременно к этим двум темам, нет.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задачи об объединении несовместных событий
2. Вероятность, что новая кофемолка прослужит больше года , равна 0,93.
Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Задачи об объединении несовместных событий
3. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 25 пассажиров, равна 0,91. Вероятность того, что окажется меньше 18 пассажиров, равна 0,39. Найдите вероятность того, что число пассажиров будет от 18 до 25.
Задачи о пересечении независимых событий
1. Если гроссмейстер К. играет белыми, то он выигрывает у гроссмейстера Н. с вероятностью 0,45. Если К. играет черными, то он выигрывает с вероятностью 0,4. Гроссмейстеры К. и Н. играют две шахматные партии, причем во второй партии меняют цвет фигур.
Гроссмейстеры К. и Н. играют две шахматные партии, причем во второй партии меняют цвет фигур.
Найдите вероятность того, что К. выиграет оба раза.
Задачи о пересечении независимых событий
2. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,4. Найдите вероятность того, что в случайный момент времени все три продавца заняты (клиенты заходят независимо друг от друга).
Задачи о пересечении независимых событий
3. В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Задачи о пересечении независимых событий
4. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые два раза попал в мишени, а последние три – промахнулся. Результат округлите до сотых.
Найдите вероятность того, что биатлонист первые два раза попал в мишени, а последние три – промахнулся. Результат округлите до сотых.
Задачи о пересечении независимых событий
5. Мышка заползает в лабиринт в точке «Вход». Развернуться и идти назад мышка не может, поэтому на каждом
разветвлении мышка
выбирает один из
путей. Считая, что
выбор дальнейшего
пути чисто случайный,
определите, с какой
вероятностью мышка
выйдет к выходу В.
Задачи об объединении пересечений событий
1. Ковбой Билл попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Билл стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,25. На столе лежат 5 револьверов, из них 2 пристрелянные. Ковбой Билл видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху.
Найдите вероятность того, что Билл попадет в муху.
Задачи об объединении пересечений событий
2. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,98. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,08.
Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Задачи об объединении пересечений событий
3. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стёкол, вторая 40%. Первая фабрика выпускает 4% бракованных стёкол, а вторая 3%.
Найдите вероятность того, что случайно купленное стекло окажется бракованным.
Задачи об объединении пересечений событий
4. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятность выигрыша и проигрыша одинаковы и равны 0,3.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятность выигрыша и проигрыша одинаковы и равны 0,3.
Урок 33. вероятность события. сложение вероятностей — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Глоссарий по теме
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Равновозможные события — такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
180-188.
Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9. сс.242-261.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Рассмотрим пример:
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
Варианты ответов:
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Определение.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
- Процесс доставания предмета из коробки является испытанием.
- Результат доставания предмета из корзины является событием.

- Событие «вынутый предмет окажется клубком» является достоверным событием.
- События «вынутый предмет не окажется клубком» или «вынутый предмет окажется красным клубком» являются невозможными событиями.
- Событие «вынутый предмет окажется зеленым клубком» является вероятным событием.
А={вынутый предмет оказался клубком}.
В={вынутый предмет не оказался клубком.
С={вынутый предмет оказался зеленым клубком}.
D ={вынутый предмет оказался красным клубком}.
2. Определим еще несколько важных понятий теории вероятностей
Определение
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω= {w 1, w 2, w 3, w 4, w 5, w6}, где wi— выпадение i очков.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Например:
- A – сдал экзамен по математике;
- Ᾱ – не сдал экзамен по математике.
Определение.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Пример .
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпало два «орла»
— Выпало две «решки»
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Определение.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Пример.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
2 .Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Например:
- Пусть А — идет дождь, B — идет снег, тогда А + В – «идет снег или дождь»
- При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 — «произошло не больше двух попаданий»
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅D — из урны вынули два белых шара
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅- из урны вынули два шара: белый и не белый
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Решение:
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
Карта сайта
Муниципальное автономное общеобразовательное учреждение «Средняя образовательная школа № 5 имени дважды Героя Советского Союза Ивана Даниловича Черняховского»
Калининградская область, г. Черняховск, ул, Ленинградская, 18/2
-
О школе
- Антикоррупционная деятельность
- Сведения об образовательной организации
- Публичный отчёт
- История
- Наши достижения
- Коллектив
- Структура школы
- Сотрудничество с вузами
- Охрана здоровья, безопасность
- Охрана труда
- Контакты
- Задать вопрос
- Качество условий оказания услуг
- ФГОС
- Поступающим
-
Школьная жизнь
- Инновационная площадка.
 Самбо в школу
Самбо в школу - Школьный спортивный клуб «Энергия»
- Фотогалерея
- Видеогалерея
- «Пятёрочка» школьная газета
- Поезд памяти 2020
- «Знамя Победы»
- «Бессмертный полк школы»
- К 75-летию Победы в Великой Отечественной войне
- Медиация
- История школы в истории Калининградской области
- Выпускники МАОУ «СОШ № 5 им.И.Д.
 Черняховского»
Черняховского»
- Инновационная площадка.
-
Ученикам
- Личный кабинет
- Дорожная безопасность
- Детский телефон доверия 8-800-2000-122
- Информационная безопасность
- Профориентация
- Библиотека
- Безопасность детей в быту
- ВЕРСИЯ ДЛЯ СЛАБОВИДЯЩИХ ВВЕРХУ Аа
- Учителям
-
Родителям
- Личный кабинет
- Дорожная безопасность
- Сертификат ПФДО
- Карта возможностей особого ребенка
- ДОМ И СЕМЬЯ
- ПРОКУРОР РАЗЪЯСНЯЕТ
- !!! Реализация начального общего, основного общего и среднего общего образования с применением электронного обучения, дистанционных образовательных технологий
-
Учебные материалы
- Для учеников
- Для родителей
- Для учителей
- Результаты олимпиад
- Учебники
- Методические и иные документы
- Новости
- ВПР
-
Итоговая аттестация
- ЕГЭ-11
- Итоговое сочинение
- ГИА-9
- Итоговое собеседование
- ВПР
- Функциональная грамотность
- «Антитеррор»
- Независимая оценка качества образования
- Программа развития школы и проекты
- Центр «Точка роста»
- 2022-2023 УЧЕБНЫЙ ГОД
- Организация питания
- (ЦОС) Цифровая образовательная среда
- Главная страница
- ›
- Документы
Личный кабинет
Выйти
Презентация «Задачи по теории вероятностей»
#9 класс #10 класс #11 класс #Алгебра #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование
Задачи по теории вероятностей
Выполнила:
учитель математики
МБОУ СШ №6
г. Камышина
Киселева Г.М.
Камышина
Киселева Г.М.
Задача 1 На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет меньше 4? Решение: 4 цифры – количество благоприятных исходов (0, 1, 2, 3) 2) 10 цифр – количество всевозможных исходов 3) Р = = 0,4 Ответ: 0,4
Задача 2 На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест. Решение: 1) 12 + 18 = 30 удобных мест – количество благоприятных исходов 2) 300 – количество всевозможных исходов 3) Р = = = 0,1 Ответ: 0,1
Задача 3
Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение:
1) 100 сумок – количество благоприятных исходов
2) 100 + 8 = 108 сумок – количество всевозможных исходов
3) Р = = ≈ 0,9259 ≈ 0,93
Ответ: 0,93
В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение:
1) 100 сумок – количество благоприятных исходов
2) 100 + 8 = 108 сумок – количество всевозможных исходов
3) Р = = ≈ 0,9259 ≈ 0,93
Ответ: 0,93
Задача 4 Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Решение: 1) (75 – 3 · 17) : 2 = 12 (докладов) – количество благоприятных исходов 2) 75 – количество всевозможных исходов 3) Р = = = 0,16 Ответ: 0,16
Задача 5
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение:
5 — благоприятные события
(2;6) (6;2) (3;5) (5;3) (4;4)
2) 36 – количество всевозможных исходов
3) Р = ≈ 0,1388 ≈ 0,14
Ответ: 0,14
Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение:
5 — благоприятные события
(2;6) (6;2) (3;5) (5;3) (4;4)
2) 36 – количество всевозможных исходов
3) Р = ≈ 0,1388 ≈ 0,14
Ответ: 0,14
Задача 6 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз. Решение: 1) 2 – количество благоприятных исходов (ОР И РО) 4 – количество всевозможных исходов (ОР, ОО, РО, РР) 3) Р = = 0,5 Ответ: 0,5
Задача 7 В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу. Решение: 1) 1 – количество благоприятных исходов (РРР) 8 – количество всевозможных исходов (ООО, РОО, ОРО, ООР, РРО, РОР, ОРР, РРР) 3) Р = = 0,125 Ответ: 0,125
Задача 8
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение:
1) 4 – количество благоприятных, т.е. с номером 2, исходов.
2) 16 – количество
всевозможных исходов
3) Р = = = 0,25
Ответ: 0,25
С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение:
1) 4 – количество благоприятных, т.е. с номером 2, исходов.
2) 16 – количество
всевозможных исходов
3) Р = = = 0,25
Ответ: 0,25
Задача 9 В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе. Решение: 1) Пусть один из друзей, например, Вадим находится в некоторой группе. В каждой группе – 7 учащихся. Значит, вариантов попасть в эту группу Олегу – 6. 2) 6 – количество благоприятных исходов 3) 20 – количество всевозможных Исходов 4) Р = = = 0,3 Ответ: 0,3
Задача 10
Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,096. В некотором городе из 1000 проданных блендеров в течение года в гарантийную мастерскую поступило 102 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение:
1) 102 – количество благоприятных исходов
2) 1000 — количество всевозможных исходов
3) Р = = 0,102
4) 0,102 – 0,096 = 0,006
Ответ: 0,006
В некотором городе из 1000 проданных блендеров в течение года в гарантийную мастерскую поступило 102 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение:
1) 102 – количество благоприятных исходов
2) 1000 — количество всевозможных исходов
3) Р = = 0,102
4) 0,102 – 0,096 = 0,006
Ответ: 0,006
Правило сложения вероятностей Если события А и В не могут наступить одновременно в ходе одного и того же опыта, то такие события называют несовместными если A и В несовместимые события, то вероятность того, что наступит хотя бы одно из двух событий А или В, равна сумме их вероятностей Р(А+В) = Р(А)+Р(В), Р(А) – вероятность события А, Р(В) – вероятность события В.
Задача 11
На экзамене по геометрии школьнику достаётся один вопрос. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
1) Событие A: вопрос о вписанной окружности
Событие В: вопрос о параллелограмме.
В условии задачи сказано, что нет вопросов, которые одновременно относятся и к А и к В. События А и В являются несовместными.
Значит, применим правило сложения вероятностей
2) 0,2 + 0,15 = 0,35
Ответ: 0,35
Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
1) Событие A: вопрос о вписанной окружности
Событие В: вопрос о параллелограмме.
В условии задачи сказано, что нет вопросов, которые одновременно относятся и к А и к В. События А и В являются несовместными.
Значит, применим правило сложения вероятностей
2) 0,2 + 0,15 = 0,35
Ответ: 0,35
Задача 12 Магазин получил продукцию в ящиках с четырех оптовых складов: четыре с 1-го, пять со 2-го, семь с 3-го и четыре с 4-го. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада Решение: 1) 4 + 5 + 7 + 4 = 20 ящ – количество всевозм. исходов 2) Р1 = = 0,2 — вероятность того, что для продажи будет выбран ящик с 1-го склада; 3) Р1 = = 0,35 — вероятность того, что для продажи будет выбран ящик с 3-го склада; 4) По правилу сложения несовместных событий: 0,2 + 0,35 = 0,55 Ответ: 0,55
Правило умножения вероятностей
Если события А и В не могут наступить одновременно в ходе одного и того же опыта, то такие события называют несовместными
Если A и В независимые события, то вероятность одновременного наступления обоих событий А и В, равна произведению их вероятностей. Р(А·В) = Р(А)·Р(В),
Р(А) – вероятность события А,
Р(В) – вероятность события В.
Р(А·В) = Р(А)·Р(В),
Р(А) – вероятность события А,
Р(В) – вероятность события В.
Задача 13 Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение: 1) Событие Н: гроссмейстер А. играет белыми и выигрывает Событие К: гроссмейстер А. играет белыми и выигрывает 2) События Н и К независимые события. Вероятность того, что гроссмейстер А. выиграет оба раза равна произведению вероятностей Р(Н) и Р(К). Применим правило умножения вероятностей 0,52 · 0,3 = 0,156 Ответ: 0,156
Задача 14
Двое военнослужащих на учениях независимо друг от друга проходят полосу препятствий. Для первого вероятность пройти ее равна 0,8, а для второго 0,5. Найдите вероятность того, что они оба не пройдут это испытание.
Решение:
1 — 0,8 = 0,2 — вероятность того, что первый не пройдёт препятствие
1 — 0,5 = 0,5 — вероятность того, что
первый не пройдёт препятствие
3) Так как эти события независимы
друг от друга, то применим
правило умножения
вероятностей Р = 0,2 ∙ 0,5 = 0,1
Ответ: 0,1
Найдите вероятность того, что они оба не пройдут это испытание.
Решение:
1 — 0,8 = 0,2 — вероятность того, что первый не пройдёт препятствие
1 — 0,5 = 0,5 — вероятность того, что
первый не пройдёт препятствие
3) Так как эти события независимы
друг от друга, то применим
правило умножения
вероятностей Р = 0,2 ∙ 0,5 = 0,1
Ответ: 0,1
Вероятностные задачи, методы решений в 11 классе
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Простейшие вероятностные задачи (PPTX)
Ребята, сегодня мы переходим к изучению элементов теории вероятностей. Что же такое «теория вероятности»? Теория вероятности – раздел математики занимающийся поиском закономерностей случайностей. Теория вероятности, как раздел математики сформировался не так давно, до начала ХХ века он считался разделом физики.
Теория вероятности, как раздел математики сформировался не так давно, до начала ХХ века он считался разделом физики.
Различного рода случайности встречаются нам повсюду. Начиная с подбрасывания монетки, заканчивая гораздо более сложными вещами. Например, давайте вспомним знаменитый роман М. А. Булгакова «Мастер и Маргарита» и его «Аннушку с маслицем» и Берлиозом. На первый взгляд, все произошло случайно. Но зная все подробности, начинаешь в этом сомневаться. Так вот, нет ничего более стабильного, постоянного или, как говорят во взрослой математике «детерминированного», чем теория вероятности. В рамках математической задачи мы предполагаем, что все возможные исходы описаны и никакие случайности невозможны.
Давайте рассмотрим самый простой пример с подбрасыванием монетки.
В реальной жизни при подбрасывании монетки может произойти все, что угодно: монетка может упасть ребром, например, в траву, может и вовсе не упасть — кто-нибудь поймает и унесет ее с собой. На процесс могут повлиять и другие факторы, которые принято называть случайными. При построении математической задачи подбрасывания монеты мы строго оговариваем условия нашего эксперимента. Мы договариваемся, что монетка симметричная и может упасть только орлом и решкой, падает на идеально ровную поверхность. Существуют и многие другие моменты, которые также должны быть оговорены. Если добавить «усложнения» к нашей задаче, то она, скорее всего, станет не решаемой в рамках школьной математики.
При построении математической задачи подбрасывания монеты мы строго оговариваем условия нашего эксперимента. Мы договариваемся, что монетка симметричная и может упасть только орлом и решкой, падает на идеально ровную поверхность. Существуют и многие другие моменты, которые также должны быть оговорены. Если добавить «усложнения» к нашей задаче, то она, скорее всего, станет не решаемой в рамках школьной математики.
Теория вероятности нашла свое применение практически во всех науках: квантовой физике, медицине, биологии, астрономии и многих других.
Как подсчитывать вероятность того или иного события?
Обратимся к классическому определению вероятности.
При проведении некоторого эксперимента вероятностью события А называют отношение количества тех событий, когда А произошло к количеству всех проведенных испытаний данного эксперимента.
Проще говоря:
Вероятность события, как известно, обозначается буквой Р, тогда математически классическое определение вероятности запишется:
$P(A)=\frac{m}{n}$,
где n – количество всевозможных исходов испытания, m – количество благоприятных исходов.
При решении задач нам следует выполнить следующие действия:
- Определить все возможные исходы и подсчитать их количество, то о чем мы говорили ранее.
- Определить благоприятные нам исходы и подсчитать их количество.
- Найти отношение благоприятных исходов к общему количеству исходов.
Классическое определение вероятности, можно применять только в том случае, если исходы всех событий являются равновозможными.
Теория вероятности — интересный предмет. Как вы думаете, какова вероятность, выйдя на улицу встретить динозавра? Здравый смысл говорит, что это не возможно, то есть нулевая вероятность. Но мы можем построить математическую интерпретацию этой задачи так, что ответ будет 0,5. Мы либо встретим динозавра, либо нет. Но мы все таки живем в реальном мире и старайтесь решать задачи в рамках здравого смысла.
Пример.
Петя подбрасывает игральный кубик, найти вероятность того, что у него выпадет:
а) три очка;
б) нечетное число очков;
в) число очков большее четырех.
Решение.
Первое, что нам надо сделать — найти количество всех исходов. Кубик имеет шесть граней, на каждой из которой написано число. При подбрасывании кубика возможно выпадение шести чисел, значит имеется 6 возможных исходов.
а) При одном броске три очка или тройка может выпасть только один раз, значит благоприятных исходов только один. Согласно классическому определению вероятность будет равна — 1/6.
б) Нечетных чисел может выпасть три: 1, 3, 5. Тогда благоприятных исходов — 3. Вероятность выпадения нечетного числа очков — 3/6=1/2.
в) Число очков большее 4 мы получим, если выпадут цифры 5 или 6. Значит возможны два благоприятных исхода. Вероятность: 2/6=1/3.
Вспомним правило умножения:
Для двух независимо проведенных испытаний А и В, число всех возможных исходов равно произведению количества исходов события А на количество исходов события В.
Пример.
Петя дважды подбрасывает кубик. Найдите вероятность того, что у него в сумме выпадет 7 очков.
Решение.
Кубик подбрасывается дважды — это два события, притом независимых: сколько очков выпадет второй раз ни как не зависит, от того сколько выпало в первый раз. Воспользуемся правилом умножения. Всего исходов получается: 6*6=36.
Найдем благоприятные нам исходы, 7 очков может выпасть при таких комбинациях: (1;6), (6;1), (2;5), (5;2), (3;4), (4;3). Всего 6 благоприятных исходов.
Используем классическое определение: 6/36=1/6.
Вспомним еще пару определений теории вероятности:
Невозможное событие – это событие, которое в рамках нашей задачи произойти не может. Например, при подбрасывании двух кубиков, выпасть больше 12 очков не может. Вероятность невозможного события равна нулю.
Достоверное событие — событие, которое в рамках задачи, происходит всегда. При подбрасывании двух кубиков – сумма очков всегда будет больше одного. Вероятность достоверного события равна единице.
Противоположное событие – событие, обратное интересующему нас событию.
В некоторых задачах проще найти противоположное событие. Противоположное событие событию А обозначается как ¯А, при чем: $P(A)+P(¯A)=1$.
Пример.
В нашем алфавите 33 буквы: 10 гласных, 21 согласная и 2 особенные буквы. Выбирается две буквы, независимо друг от друга. Найти вероятности:
а) выбраны разные буквы,
б) выбраны буквы: ь и ъ,
в) среди выбранных букв есть согласные,
г) выбраны соседние буквы.
Решение:
а) Первый раз мы можем выбрать любую букву алфавита, чтобы выбрать другую букву у нас остается 32 варианта. Тогда вероятность выбора разных букв: 32/33.
б) Требуемые буквы – особенные (их всего две). В условии не оговорено, что они должны быть разными, тогда одна и таже буква может быть выбрана дважды. Выбор буквы независим, тогда всего у нас исходов 33*33. Благоприятных исходов получается — 2*2 так, как и первого, так и второго благоприятны всего два исхода.
Ответ: 4/1089.
в) В данном примере нам будет проще найти вероятность того, что среди выбранных букв нет согласных. Вероятность того, что оба раза выберут не согласную букву — 12*12/33*33 (по аналогии пункту б).
Вероятность того, что оба раза выберут не согласную букву — 12*12/33*33 (по аналогии пункту б).
Тогда вероятность появления согласной буквы — 1-144/1089=945/1089≈0,87.
г) Для каждой буквы (кроме А и Я) есть сосед слева и справа, тогда букв с соседями: $33*2-2=64$. (Вычитаем 2 комбинации, так как у буквы «А» нет соседа слева, а у буквы «Я» нет соседа справа.)
Тогда вероятность: 64/1089≈0,06.
Задачи для самостоятельного решения
1. Петя подбрасывает игральный кубик. Найдите вероятность того, что у него выпадет:
а) четыре очка,
б) четное число очков,
в) число очков меньше четырех,
г) число очков не меньше трех.
2. Петя дважды подбрасывает кубик. Найти вероятность:
а) в сумме выпадет 10 очков,
б) в сумме выпадет больше 11 очков,
в) произведение, выпавших очков, равно 8,
г) произведение, выпавших очков, меньше либо равно 12.
3. Иван выучил 25 вопросов к экзамену по математике. Всего 30 вопросов. Найти вероятность того, что Ивану не попадется выученный вопрос.
4. В урне 5 красных и 3 белых шара. Найти вероятность того, что наугад вытащенный шар будет белым. Найдите вероятность, что первый вытащенный шар — красный, а второй вытащенный шар — белый.
MBF3C Математика для 11 класса колледжа | Основы математики
MBF3C 11 класс Колледж Описание курса
Этот курс позволяет учащимся расширить свое понимание математики как инструмента решения задач в реальном мире. Студенты расширят свое понимание квадратичных отношений; исследовать ситуации, связанные с экспоненциальным ростом; решать проблемы со сложными процентами; решить финансовые проблемы, связанные с владением транспортным средством; развивать способность рассуждать, собирая, анализируя и оценивая данные, включающие одну переменную; связать вероятность и статистику; и решать задачи по геометрии и тригонометрии. Учащиеся будут укреплять свои математические навыки, решая задачи и
сообщают о своих мыслях.
Предварительные требования: Основы математики, 10 класс, прикладные
MBF3C 11 класс Реальные задачи по математике для колледжа
Доступ к 3 актам математических задач, связанных с курсом математики колледжа MBF3C для 11 класса.
3 Act Math Tasks
MBF3C Заметки и раздаточные материалы по математике для 11 класса
MBF3C – Блок 1 – Тригонометрия| сек. 1.2 – Решение задач с использованием тригонометрических соотношений Стр. 21-23 #1-6, 12, 13 |
| сек. 1.3 – Закон синусов стр. 32-33 #1-6, 8 |
| сек. 1.4 – Закон косинусов стр. 39-41 #1-3, 5-7, 9 |
| сек. 1.5 – Принятие решений с использованием тригонометрии Страница 48-51 #1-10 |
| сек. 2.1 – Вероятностные эксперименты Стр. 66-67 #1-7 |
| сек. 2.2 – Теоретическая вероятность Страница 73-74 #1-9 |
| сек. 2.3 – Сравнение экспериментальных и теоретических вероятностей Стр.  82-83 #1-6, 8a 82-83 #1-6, 8a |
| сек. 2.4 – Интерпретация информации, связанной с вероятностью Стр. 90-92 #1-8 |
| сек. 3.1 – Методы отбора проб Стр. 106-109 #1-5, 7-10 |
| сек. 3.2 – Сбор и анализ данных Страница 114-116 #1-10 |
| сек. 3.3 – Отображение данных (день 1) Стр. 125-127 #1-3,6 |
| сек. 3.3 – Отображение данных (день 2) стр. 125-128 #4, 5, 7, 9, 11 |
| сек. 3.4 – Меры центральной тенденции Стр. 136-139 #1-3, 6-8 |
| сек. 3.5 – Меры распространения (День 1) стр. 145-147 #5, 6, 7ab, 8, 10, 11 |
| сек. 3.5 – Показатели распространения (День 2) Страница 145-147 #1-4, 9, 12 |
| сек. 3.6 – Типы распределений Страница 153-155 #1-7 |
Разд. 4.1 – Моделирование с помощью квадратичных уравнений (Часть 1) 4.1 – Моделирование с помощью квадратичных уравнений (Часть 1) Стр. 174-175 #1, 3, 6 |
| сек. 4.1 – Моделирование с помощью квадратичных уравнений (часть 2) стр. 174-176 #2, 4, 7, 9 |
| сек. 4.2 – Квадратное соотношение y = ax 2 + k Страница 190-193 #1-3, 4(a,c,e,g), 7(a,c,e), 8 |
| сек. 4.3 – Квадратичная зависимость y = a(x – h) 2 Страница 200-203 #1-4, 5(a,c), 7 |
| сек. 4.4 – Квадратное соотношение y = a(x – h) 2 + k Страница 212-217 #1, 2(a,c,e,g), 6 |
| сек. 4.5 – Интерпретация графиков квадратичных отношений стр. 222-225 #1(a,c,e,g), 2, 4, 5 |
| сек. 4.6 – Графическое построение квадратичных уравнений в форме вершин Полные раздаточные материалы |
Разд. 5.1 – Расширение биномов 5.1 – Расширение биномов Страница 238-241 #1, 2, 3-7(a,c,e) |
| сек. 5.2 – Переход от вершинной формы к стандартной форме Страница 245-247 #1-4(a,c,e), 6, 7 |
| Страница 253-255 #1-3 |
| сек. 5.4 — Факторные трехчлены формы y = ax 2 + bx + c Страница 259-263 #1-7(a,c,e) |
| сек. 5.5 – Х-пересечения квадратного отношения Страница 271-275 #1-2, 3-5(a,c,e), 6, 7(a,c,e) |
| Сек. 7.1 – Правила экспоненты Стр. 360-363 #1-5, 9, 10 |
| сек. 7.2 – Нулевые и отрицательные экспоненты Страница 367-371 #1-3, 6-7(a,c,e), 8 |
| сек. 7.3 – Исследование экспоненциальных зависимостей Страница 377-381 #1-3, 6, 7 |
| сек. 7.4 – Экспоненциальные соотношения Стр. 390-394 #1-4, 6 |
сек. 7. 5 – Экспоненциальный рост и спад 5 – Экспоненциальный рост и спад Стр. 401-405 #1(b,c,d), 2(b,c), 5(a,b), 6 |
| сек. 7.6 – Решение проблем, связанных с экспоненциальным ростом и спадом Страница 410-413 #1-7 |
| Страница 428-429 #1-7 |
| Страница 432-435 #1-9 |
| Страница 439-441 #1, 2-3(a,b), 4, 5, 8, 9 |
| Страница 450-453 #3-10 |
| Страница 465-467 #2-5, 7-9 |
| Стр. 472-473 #2, 3, 6, 7, 8, 10 |
| Страница 479-481 #1, 2, 4-8 |
| Стр. 486-487 #1, 5, 6, 8 |
| Страница 493-495 #1-9 |
MBF3C 11 класс Колледж Математика
Направления и общие ожидания
Математические модели
- MM1 – установить связи между числовыми, графическими представлениями и алгебраическими задачами
- MM2 — продемонстрировать понимание показателей и установить связи между числовыми, графическими и алгебраическими представлениями экспоненциальных отношений;
- MM3 — описывать и представлять экспоненциальные отношения, а также решать проблемы, связанные с экспоненциальными отношениями, возникающие в реальных приложениях.

Личные финансы
- PF1 – сравнение простых и сложных процентов, связь сложных процентов с экспоненциальным ростом и решение задач, связанных со сложными процентами;
- PF2 — сравнить услуги, доступные в финансовых учреждениях, и решить проблемы, связанные со стоимостью совершения покупок в кредит;
- PF3 — интерпретировать информацию о владении и эксплуатации транспортного средства и решать проблемы, связанные с сопутствующими расходами.
Геометрия и тригонометрия
- GT1 – различные способы представления двухмерных форм и трехмерных фигур, возникающих в реальных приложениях, и решение задач проектирования;
- GT2 — решение задач, связанных с тригонометрией в остроугольных треугольниках, с использованием закона синуса и закона косинуса, включая задачи, возникающие в реальных приложениях.
Управление данными
- DM1 – решать задачи, связанные с данными с одной переменной, путем сбора, организации, анализа и оценки данных;
- DM2 — определить и представить вероятность, а также определить и интерпретировать ее приложения.

7 лучших вероятностных ресурсов и занятий по математике KS4
SecondaryMaths
Каковы шансы, что каждый ученик вашего класса освоит теорию вероятности? Что ж, эти ресурсы, безусловно, улучшат эти шансы
- по Ллойд Берджесс
Одна из критических замечаний, высказанных в адрес математики неэнтузиастами, состоит в том, что некоторые вещи, которые они узнали в школе, не имели никакого отношения к их жизни.
Не все из нас ежедневно пользуются программой Pythagoras, вычисление площади трехмерной фигуры не всегда необходимо , и вот что Cracked. com сказал о делении в длину:
com сказал о делении в длину:
Но на самом деле вероятность — это то, что окружает нас повсюду, особенно когда речь идет о финансах, риске и вознаграждении. В конце концов, кто-то всегда пытается убедить вас, что их продукт определенно стоит ваших инвестиций:
Надеюсь, эти ресурсы помогут им в пути.
1 | Серый слон в Дании
Этот старый каштан — отличный способ познакомить учащихся с вероятностью.
Сначала им нужно придумать число, выполнить некоторые простые математические вычисления, а затем (после того, как они неизбежно останутся с числом четыре) придумать страну, начинающуюся с соответствующей буквы этого числа (если A=1, B=2 так далее).
Большинство людей инстинктивно выбирают Данию, поэтому, когда их просят подумать о животном, начинающемся со второй буквы названия страны, на ум приходит слон.
А когда их спросят, какого цвета это животное, если только они не пробовали шампанское в духе Дамбо, они скажут, что они серые.
После того, как вы получите результаты, страница разберет факторы вероятности, связанные с тем, почему она смогла предсказать, казалось бы, маловероятного серого слона из Дании, о котором подумали многие студенты.
Более того, вы испытываете огромное удовлетворение, когда получаете коричневую выдру из Доминиканской Республики, и она говорит вам, что вы уникальный человек.
Попробуйте сами здесь.
2 | В коробке
Это не только отличное небольшое упражнение, вы также можете посмотреть на этого очаровательного котенка на плакате в формате PDF, который можно распечатать.
Здесь есть множество других вероятностных задач NRICH для KS4.
Но именно этот вы найдете здесь.
3 | Закономерности в случайных событиях
Это задание позволяет учащимся создать свою собственную игру в стиле ярмарочной площади, чтобы исследовать относительную частоту выброшенных случайным образом фишек, приземляющихся на определенные участки доски.
Учащиеся тестируют игру, подсчитывают свои результаты и представляют их в наиболее подходящей форме.
Это позволяет им исследовать вероятность с помощью честного тестирования и выяснить, какой размер выборки вам нужен, чтобы делать выводы на основе случайных результатов.
Загрузите PDF-файл для печати здесь.
4 | Камень, ножницы, бумага древовидные диаграммы
Это упражнение включает в себя классическую игру «Камень, ножницы, бумага» для ознакомления с древовидными диаграммами.
Ученики играют парами 30 раз. Каждая игра записывается в простую таблицу подсчета, отмечая, выигрывает ли игрок А, выигрывает игрок Б или ничья.
Затем они могут посмотреть на относительную частоту своих результатов, а также на результаты всего класса, что приведет к обсуждению теоретической вероятности, ожидания и относительной частоты.
Вы можете скачать план урока PowerPoint здесь.
Или вы можете просмотреть полный пост (включая ссылку для скачивания PowerPoint) здесь.
5 | Прогнозы Hi-Low
Это задание основано на старой карточной игре из телешоу Цена правильная .
Только, вместо ужасной моды 80-х и 90-х и толпы людей, кричащих вам «выше» или «ниже», вы должны действительно потратить время, чтобы вычислить вероятность того, что каждая карта окажется выше или ниже, чем предыдущая .
И хотя вы не играете в азартные игры на настоящие деньги (это было бы плохо), он хранит счет воображаемых финансов, на которые вы можете делать ставки, поэтому вы можете легко устроить соревнование в группах или в классе, чтобы узнать больше о риске. и вознаграждение.
Дайте вашим урокам бонус Брюси с этим заданием здесь.
6 | Глава вероятности OUP
Если вам нужна целая глава по обучению теории вероятностей бесплатно, OUP вам поможет.
Этот 32-страничный PDF-файл наполнен информацией, идеями и действиями.
Просто нажмите здесь, и вы можете скачать, распечатать и использовать.
7 | Оценка вероятностных утверждений
В этом ресурсе отдела стандартов DfE учащиеся обсуждают и разъясняют некоторые распространенные заблуждения о вероятности.
Это включает в себя обсуждение концепций равновероятных событий, случайности и размеров выборки.
Они также научатся рассуждать и объяснять. На этом занятии предполагается, что учащиеся уже сталкивались с вероятностью раньше.
Найдите этот ресурс здесь.
Вероятность в реальной жизни | Применение вероятности
Содержание| 1. | Введение |
| 2. | Что такое вероятность? |
| 3. | Вероятность в математике |
| 4. | Примеры вероятности из реальной жизни |
5. | Резюме |
| 6. | Часто задаваемые вопросы |
При подбрасывании монеты выпадет либо вперед, либо решка, результат легко предсказуем. Но что, если вы подбросите две монеты одновременно? Результатом может быть комбинация головы и хвоста. В последнем случае правильный ответ получить невозможно, поэтому можно только предсказать возможность результата. Это предсказание известно как Вероятность. Вероятность широко используется во всех сферах повседневной жизни, таких как спорт, сводки погоды, образцы крови, предсказание пола ребенка в утробе матери, врожденные дефекты, статика и многое другое. В этой теме мы подробно узнаем о вероятности.
Вероятность в реальной жизни
Вот вероятность в PDF, которая объясняет, что вероятность как-то связана со шансом. Это изучение вещей, которые могут произойти или не произойти. Мы используем его большую часть времени, обычно не задумываясь об этом. Изучите вероятность в реальной жизни, нажав на ссылку для загрузки ниже:
Изучите вероятность в реальной жизни, нажав на ссылку для загрузки ниже:
| 📥 | Вероятность в реальной жизни | Скачать |
Что такое вероятность?
Вероятность наступления любого события можно назвать Вероятностью.
Применение вероятностиНекоторые приложения вероятности предсказывают результат, когда вы:
- Подбрасываете монету.
- Выбор карты из колоды.
- Бросание игральной кости.
- Вытащить зеленую конфету из мешка с красными конфетами.
- Выигрыш в лотерею 1 из многих миллионов.
Вероятность в математике
Аль-Халил, математик с Ближнего Востока, написал «Книгу криптографических сообщений», в которой демонстрируется первое использование перестановок и комбинаций для перечисления всех арабских слов с гласными или без них. Это была самая ранняя форма вероятности и статистики.
Это была самая ранняя форма вероятности и статистики.
Вероятность Раздел математики, связанный с численной иллюстрацией вероятности того, что событие может существовать. Вероятность возникновения любого события представляет собой число от 0 до 1, где 0 указывает на невозможность события, а 1 на его достоверность.
Теория вероятностей широко используется в таких областях, как статистика, финансы, азартные игры, искусственный интеллект, машинное обучение, информатика, теория игр и философия.
Формула для расчета вероятности
Примеры реальной вероятности Планирование погоды: записывать риски, связанные с погодой. Метеорологи всего мира используют различные приборы и инструменты для прогнозирования изменений погоды. Они собирают базу данных прогноза погоды со всего мира, чтобы оценить изменения температуры и вероятные погодные условия для определенного часа, дня, недели и месяца.

| Пример |
Если вероятность дождя составляет 40 %, то погодные условия таковы, что 40 дней из 100 идет дождь.
Спортивные стратегии:В спорте анализы проводятся с помощью вероятности, чтобы понять сильные и слабые стороны конкретной команды или игрока. Аналитики используют вероятность и шансы, чтобы предсказать результаты в отношении результатов команды и участников в спорте.
Тренеры используют вероятность как инструмент, чтобы определить, в каких областях их команда достаточно сильна и во всех областях им нужно работать, чтобы добиться победы. Тренеры даже используют вероятность, чтобы оценить способности конкретного игрока в его команде, а также когда разрешить ему играть и против кого.
| Пример |
Тренер по крикету оценивает способности игрока отбивать мяч и играть в боулинг, оценивая его средние результаты в предыдущих матчах, прежде чем включить его в состав.
страховые компании используют теорию вероятности или теоретическую вероятность для оформления полиса или его оформления по премиальной ставке. Теория вероятности — это статистический метод, используемый для предсказания возможности будущих результатов.
| Пример |
Оформление медицинской страховки для алкоголика, вероятно, дороже, чем для здорового человека. Статистический анализ показывает высокие риски для здоровья обычного алкоголика, гарантируя, что они представляют собой большой финансовый риск, учитывая более высокую вероятность серьезного заболевания и, следовательно, подачи заявки на получение премиальных денег.
В играх: Блэкджек, покер, азартные игры, все виды спорта, настольные игры, видеоигры используют вероятность, чтобы узнать, насколько велики шансы команды или человека на победу.
| Пример |
При одновременном броске двух игральных костей результаты будут следующими:
Теория игр:Он имеет приложения в социальных науках, логике, системных науках и информатике. В 1944 года Джон фон Нейман опубликовал статью «Теория игр и экономическое поведение». Он доказал теорему Брауэра о неподвижной точке о непрерывном отображении в компактные выпуклые множества, стандартный метод теории игр.
Применение переносимости в теории игр: 1. Экономика и бизнес: экономисты используют теорию игр в качестве инструмента для анализа экономической конкуренции и таких явлений, как торги, теория голосования, аукцион, проектирование механизмов. Руководители, инвесторы и менеджеры в деловом мире используют стратегию теории игр для инвестиций, запуска новых продуктов или входа в новый бизнес. Модели теории игр заставляют каждого игрока учитывать действия своего конкурента и планировать следующую стратегию.
Модели теории игр заставляют каждого игрока учитывать действия своего конкурента и планировать следующую стратегию.
2. В политике. Дипломаты и политики используют теорию игр для анализа любой конфликтной ситуации между отдельными людьми, компаниями, государствами и политическими партиями. Он также используется в военных стратегиях, политическом голосовании и политических делах.
3. В философии: философы используют теорию игр в различных аспектах философии.
4. В биологии: применяется для анализа аномальных природных явлений в биологии.
Сводка
Вероятность играет жизненно важную роль в повседневной жизни. В прогнозе погоды, спортивных и игровых стратегиях, покупке или продаже страховки, онлайн-покупках и онлайн-играх, определении групп крови и анализе политических стратегий.
Написано Нетравати С., учителем Куэмата
Часто задаваемые вопросы Что такое определение вероятности?
Вероятность в математике можно определить как количество возможных исходов события.
| Пример 1 |
Подбрасывание монеты: У монеты две лицевые стороны: орел и решка. Когда он перевернут, вероятность получения орла на выходе равна ½, а вероятность получения решки на выходе равна ½.
Как рассчитать вероятность?Вероятность = количество благоприятных исходов/количество возможных исходов
Как вероятность используется в повседневной жизни?- Прогноз погоды
- Расчет среднего показателя в крикете.
- С какой вероятностью можно выиграть лотерейный билет.
- Игральные карты
- Стратегия голосования в политике
- Бросание игральной кости.
- Вытаскивание черных носков из ящика с белыми носками.
- Покупка или продажа страховки.
- Теоретическая вероятность
- Экспериментальная вероятность
- Аксиоматическая вероятность
- Правило 1: Для любого события «А» вероятность возможных исходов равна 0 или 1, где 0 — событие, которое никогда не произойдет, а 1 — событие обязательно произойдет
P(A) = [0 < P(A) < 1]
- Правило 2: Сумма вероятностей всех возможных исходов равна 1,
если S является выборочным пространством в модели , тогда P(S) = 1
- Правило 3: Если A и B два взаимоисключающих события, то
P (A или B) = P (A∪ B) = P (A) + P (B).
Это правило добавления для непересекающихся событий.
- Правило 4: Дополнением любого события A является событие, состоящее из всех исходов, не входящих в A.
- Правило 5: Если и A, и B независимы, то условная вероятность того, что событие B произойдет, при условии, что событие A уже произошло.
P ( A и B) = P (A) P (B | A). Это называется общим правилом умножения.
Концепции вероятности и статистики для средней школы – Time4Learning
Посмотрите наши демонстрации уроков!
Курс«Концепции вероятности и статистики» — это факультативный курс для старших классов средней школы, цель которого — помочь учащимся применять идеи статистики в реальных ситуациях. Он идеально подходит для студентов, которым нужен альтернативный зачет по математике, но которые могут не захотеть изучать более продвинутые математические курсы, такие как алгебра II и предварительное исчисление.
На этой странице представлена информация об онлайн-курсе Time4Learning по статистике и вероятности, о том, почему важно понимать вероятность и статистику, а также о том, что вы можете ожидать от старшеклассника на этом двухсеместровом факультативе.
- Зачем изучать теории вероятности и статистики в старшей школе?
- Чему вы научитесь на уроках вероятности и статистики?
- Вероятность и статистика в средней школе Объем и последовательность курса
- Почему стоит выбрать учебную программу Time4Learning по теории вероятностей и статистике для старших классов?
- Дополнительные предметы по выбору
Зачем изучать теории вероятности и статистики в старшей школе?
Часто, сами того не осознавая, мы все ежедневно пользуемся статистикой и вероятностью. От сводок погоды до результатов медицинских анализов, от опросов на выборах до данных переписи населения, вероятностный и статистический язык и концепции наполняют все аспекты жизни нашего общества. Введение в вероятность и статистику дает старшеклассникам возможность судить о том, верны ли выводы, сделанные на основе данных.
Успешная учебная программа по статистике в старших классах поможет учащимся стать информированными, критически настроенными пользователями данных, которые смогут осмысленно применять их в своей повседневной жизни. В эпоху, когда граждан бомбардируют аргументами за и против всего, от политических позиций до медицинских вмешательств, те, кто прошел курс статистики и вероятностей для средней школы, могут лучше судить об обоснованности утверждений каждой стороны.
В эпоху, когда граждан бомбардируют аргументами за и против всего, от политических позиций до медицинских вмешательств, те, кто прошел курс статистики и вероятностей для средней школы, могут лучше судить об обоснованности утверждений каждой стороны.
Чему вы научитесь на уроках вероятности и статистики?
Курс Time4Learning по вероятности и статистике для старшей школы начинается с углубленного изучения вероятности с упором на концептуальное понимание. Затем учащиеся переходят к исследованию выборки и сравнению населения.
На протяжении всего курса статистики учащиеся будут стремиться к достижению следующих целей:
- Понимание концепций вероятности, включая разницу между теоретической вероятностью и экспериментальными результатами.
- Выразите вероятность одного или нескольких событий численно.
- Понимать процедуры выборки и делать выводы о совокупностях на основе соответствующих выборок.
- Вычисление и интерпретация описательных статистических данных о выборках, включая меры центра и меры изменчивости.

- Графическое представление данных содержательными способами, включая точечные диаграммы, гистограммы и диаграммы.
- Представление и интерпретация взаимосвязи между двумя переменными с помощью диаграмм рассеяния и регрессии.
- Применять понимание нормально распределенных данных для выдвижения и проверки гипотез.
- Применяйте концепции вероятности к различным ситуациям.
Курс вероятности и статистики в старших классах Объем и последовательность курса
Глава 1: «Основы вероятности»
Глава 2: «Вероятность»
Глава 3: «Применение вероятности»
Глава 4: «Распределение данных
.
Глава 5. «Выборка и сравнение популяций»
Глава 6: «Анализ данных»
Глава 7: «Строительство рассеянных графиков»
Глава 8: «Анализ рассеянных партий»
ГЛАВ 9: «Двух». Статистика»
Почему стоит выбрать учебную программу Time4Learning по теории вероятностей и статистике для старших классов?
Учебная программа Time4Learning по статистике на дому использует уникальные упражнения и материалы, чтобы помочь старшеклассникам связать данные с текущими реальными дилеммами. Этот курс подготовки к колледжу учит их абстрактно и количественно рассуждать и принимать обоснованные решения.
Этот курс подготовки к колледжу учит их абстрактно и количественно рассуждать и принимать обоснованные решения.
Если ваш школьник ищет факультатив по практической математике, это введение в вероятность и статистику предлагает:
- 9 глав и более 350 заданий, охватывающих все: от анализа данных до построения диаграмм рассеяния.
- Содержание и задания соответствуют государственным стандартам содержания, чтобы дать учащимся всестороннее представление о статистике и вероятности для старших классов средней школы.
- Занятия, которые вовлекают учащихся в активное обучение, включая визуальную поддержку, руководства и инструменты для создания заметок.
- Онлайн-обучение для самостоятельного обучения, в котором используются видео, печатные материалы и виртуальная поддержка для вовлечения разных типов учащихся.
- Интерактивные уроки, в которых используются таланты опытных учителей для вовлечения, поддержки и поощрения.
- Постоянные, разнообразные и частые оценки для проверки усвоения материала учащимися.

- Доступ родителей к инструментам планирования и ведения документации для более эффективного и результативного обучения на дому.
- Обслуживание клиентов и поддержка не имеют себе равных в любом другом онлайн-курсе статистики домашнего обучения.
Дополнительные предметы по выбору
- Обзор списка предметов по выбору
- Экология
- Социология
- Введение в общение и речь
- История искусства I
- Психология
- Введение в искусство
- Современное здоровье
- Основы личного здоровья
- Пожизненный фитнес
- Стратегии академического успеха
- Здоровый образ жизни
- Экономика
- Личные финансы
- Компьютерные приложения — Office 2019
Диаграмма Венна
Что такое диаграмма Венна?
Диаграмма Венна — это иллюстрация, которая использует круги, чтобы показать отношения между вещами или конечными группами вещей. Круги, которые перекрываются, имеют общие черты, в то время как круги, которые не перекрываются, не разделяют эти черты.
Круги, которые перекрываются, имеют общие черты, в то время как круги, которые не перекрываются, не разделяют эти черты.
Диаграммы Венна помогают визуально представить сходства и различия между двумя концепциями. Они давно признаны за их полезность в качестве образовательных инструментов. С середины 20-го века диаграммы Венна использовались как часть вводной учебной программы по логике и в образовательных планах начального уровня по всему миру.
Ключевые выводы
- На диаграмме Венна используются круги, которые перекрываются или не перекрываются, чтобы показать общие черты и различия между вещами или группами вещей.
- Вещи, которые имеют общие черты, показаны как перекрывающиеся круги, в то время как вещи, которые различаются, стоят отдельно.
- Диаграммы Венна теперь используются в качестве иллюстраций в бизнесе и во многих академических областях.
Понимание диаграмм Венна
Диаграммы Венна полезны для иллюстрации того, как различные концепции или факторы пересекаются друг с другом. Они могут с первого взгляда показать, чем вещи похожи или различаются, а также где и как они пересекаются. Часто центр диаграммы Венна (пересечение двух или более кругов) представляет собой некую связь или основную идею, которую можно разложить на различные другие круги с метками на внешних частях, более общими и отдельными идеями, чем те, что ближе к центру.
Они могут с первого взгляда показать, чем вещи похожи или различаются, а также где и как они пересекаются. Часто центр диаграммы Венна (пересечение двух или более кругов) представляет собой некую связь или основную идею, которую можно разложить на различные другие круги с метками на внешних частях, более общими и отдельными идеями, чем те, что ближе к центру.
Перекрывающиеся области также можно использовать, чтобы показать, где два разных контекста имеют общие черты. Например, на диаграмме ниже мы видим, что, хотя городской и сельский контексты различаются своим собственным набором действий, они также имеют общие спортивные события.
Диаграмма Венна (нажмите, чтобы увеличить). Грейс ФлемингКомпоненты диаграммы Венна
Хотя существует множество способов организовать диаграмму Венна, чаще всего они состоят из перекрывающихся кругов. Каждый круг сам по себе представляет , , которые могут включать идеи, концепции, числа или объекты.
Когда круги перекрываются или пересекаются, те подмножества, которые являются общими, известны как объединение или пересечение . Области, которые не перекрываются, показывают различия между наборами, а дополнительный набор относится ко всему, что не является общим для определенного набора или подмножества.
Области, которые не перекрываются, показывают различия между наборами, а дополнительный набор относится ко всему, что не является общим для определенного набора или подмножества.
История и происхождение диаграмм Венна
Английский логик Джон Венн популяризировал диаграмму в 1880-х годах. Он назвал их эйлеровыми кругами в честь швейцарского математика Леонарда Эйлера, создавшего подобные диаграммы в 1700-х годах.
Термин «диаграмма Венна» не появлялся до 1918 года, когда Кларенс Льюис, американский академический философ и в конечном итоге основатель концептуального прагматизма, назвал круговое изображение диаграммой Венна в своей книге «Обзор символической логики» .
Венн изучал и преподавал логику и теорию вероятностей в Кембриджском университете, где разработал свой метод использования диаграмм для иллюстрации раздела математики, известного как теория множеств. Он опубликовал работу, создающую прецедент, Логика случая , которая объясняет частотную теорию вероятностей. В нем он утверждал, что вероятность, вопреки распространенному предположению, должна устанавливаться на основе регулярности, с которой предсказывается что-то. В другой книге, Symbolic Logic, Venn , были построены и развиты теории математика Джорджа Буля по алгебре. Эта работа помогла ему разработать диаграмму Венна.
В нем он утверждал, что вероятность, вопреки распространенному предположению, должна устанавливаться на основе регулярности, с которой предсказывается что-то. В другой книге, Symbolic Logic, Venn , были построены и развиты теории математика Джорджа Буля по алгебре. Эта работа помогла ему разработать диаграмму Венна.
Диаграммы Венна использовались с середины 20-го века в классах от начальной школы до вводной логики.
Приложения для диаграмм Венна
Диаграммы Венна используются для изображения того, как элементы соотносятся друг с другом на общем фоне, вселенной, наборе данных или среде. Диаграмму Венна можно использовать, например, для сравнения двух компаний в одной отрасли, иллюстрируя продукты, предлагаемые обеими компаниями (где круги перекрываются), и продукты, которые являются эксклюзивными для каждой компании (внешние круги).
Диаграммы Венна на базовом уровне представляют собой простые графические изображения взаимосвязей, существующих между двумя наборами вещей. Однако они могут быть гораздо более сложными. Тем не менее, упрощенное назначение диаграммы Венна для иллюстрации понятий и групп привело к их популяризации во многих областях, включая статистику, лингвистику, логику, образование, информатику и бизнес.
Однако они могут быть гораздо более сложными. Тем не менее, упрощенное назначение диаграммы Венна для иллюстрации понятий и групп привело к их популяризации во многих областях, включая статистику, лингвистику, логику, образование, информатику и бизнес.
Примеры диаграмм Венна
Диаграмму Венна можно нарисовать, чтобы проиллюстрировать фрукты красного или оранжевого цвета. Ниже мы видим, что есть оранжевые фрукты (круг B), такие как хурма и мандарины, а яблоки и вишни (круг A) окрашены в красный цвет. Перец и помидоры бывают как красного, так и оранжевого цвета, о чем свидетельствует перекрывающаяся область двух кругов.
Изображение Джули Бэнг © Investopedia 2020Вы также можете нарисовать диаграмму Венна, чтобы решить, какую из двух машин купить. На диаграмме Венна показаны функции, присущие только каждой машине, и функции, которыми обладают обе машины.
Ниже мы видим, что автомобиль A — это седан, работающий на бензине и расходующий 20 миль на галлон, а автомобиль B — гибрид, расходующий 40 миль на галлон и являющийся хэтчбеком.
Заштрихованная область, где два круга перекрываются, показывает общие черты обоих автомобилей, в том числе радио, четыре двери, Bluetooth и подушки безопасности.
Диаграмма Венна графически отображает сходства и различия между двумя автомобилями, чтобы помочь решить, какой из них купить.
Что такое диаграмма Венна в математике?
Диаграмма Венна в математике используется в теории логики и теории множеств для отображения различных наборов или данных и их связи друг с другом.
Как читать диаграмму Венна?
Диаграмма Венна читается путем наблюдения за всеми кругами, составляющими всю диаграмму. Каждый круг — это отдельный элемент или набор данных. Части кругов, которые перекрываются, указывают области, которые являются общими среди различных элементов, тогда как части, которые не перекрываются, указывают на уникальные черты элемента или набора данных, представленного кружком.
Почему они называются диаграммами Венна?
Их называют диаграммами Венна, потому что диаграмма была разработана английским логиком Джоном Венном.
Как называется середина диаграммы Венна?
Середина диаграммы Венна, где два или более набора перекрываются, называется пересечением.
Всегда ли в диаграмме Венна используются 2 или 3 круга?
Хотя часто используется пара или тройка кругов, диаграмма Венна может использовать любое количество кругов (или любую другую форму), чтобы показать различия и пересечения различных наборов.
1.1 Определения статистики, вероятности и ключевых терминов
ВведениеСтатистические моделиВероятностьКлючевые термины
Введение
Статистическая наука занимается сбором, анализом, интерпретацией и представлением данных. Мы видим и используем данные в нашей повседневной жизни.
В этом курсе вы научитесь систематизировать и обобщать данные. Организация и обобщение данных называется описательной статистикой. Два способа суммировать данные — это графическое изображение и использование чисел, например, нахождение среднего значения. После того, как вы изучили вероятности и распределения вероятностей, вы будете использовать формальные методы для получения выводов из хороших данных. Формальные методы называются статистикой вывода. Статистический вывод использует вероятность, чтобы определить, насколько мы можем быть уверены в правильности наших выводов.
После того, как вы изучили вероятности и распределения вероятностей, вы будете использовать формальные методы для получения выводов из хороших данных. Формальные методы называются статистикой вывода. Статистический вывод использует вероятность, чтобы определить, насколько мы можем быть уверены в правильности наших выводов.
Эффективная интерпретация данных или вывод основан на хороших процедурах получения данных и вдумчивом изучении данных. Вы столкнетесь с тем, что вам покажется слишком много математических формул для интерпретации данных. Цель статистики не в том, чтобы выполнять многочисленные расчеты по формулам, а в том, чтобы получить представление о ваших данных. Расчеты можно производить с помощью калькулятора или компьютера. Понимание должно исходить от вас. Если вы сможете досконально понять основы статистики, вы будете более уверены в решениях, которые принимаете в жизни.
Статистические модели
Статистика, как и все другие разделы математики, использует математические модели для описания явлений, происходящих в реальном мире. Некоторые математические модели являются детерминированными. Эти модели можно использовать, когда одно значение точно определяется из другого значения. Примерами детерминированных моделей являются квадратные уравнения, описывающие ускорение автомобиля из состояния покоя, или дифференциальные уравнения, описывающие передачу тепла от плиты к кастрюле. Эти модели достаточно точны и могут использоваться для ответов на вопросы и прогнозирования с высокой степенью точности. Космические агентства, например, используют детерминированные модели, чтобы предсказать точную величину тяги, которая необходима ракете, чтобы оторваться от гравитации Земли и выйти на орбиту.
Некоторые математические модели являются детерминированными. Эти модели можно использовать, когда одно значение точно определяется из другого значения. Примерами детерминированных моделей являются квадратные уравнения, описывающие ускорение автомобиля из состояния покоя, или дифференциальные уравнения, описывающие передачу тепла от плиты к кастрюле. Эти модели достаточно точны и могут использоваться для ответов на вопросы и прогнозирования с высокой степенью точности. Космические агентства, например, используют детерминированные модели, чтобы предсказать точную величину тяги, которая необходима ракете, чтобы оторваться от гравитации Земли и выйти на орбиту.
Однако жизнь не всегда точна. Хотя ученые могут с точностью до минуты предсказать время восхода солнца, они не могут точно сказать, где ураган обрушится на сушу. Статистические модели можно использовать для прогнозирования наиболее неопределен- ных жизненных ситуаций. Эти специальные формы математических моделей или функций основаны на идее, что одно значение влияет на другое значение. Некоторые статистические модели представляют собой более точные математические функции: один набор значений может предсказывать или определять другой набор значений. Или некоторые статистические модели представляют собой математические функции, в которых набор значений точно не определяет другие значения. Статистические модели очень полезны, поскольку они могут описывать вероятность или вероятность возникновения события и предоставлять альтернативные результаты, если событие не произойдет. Например, прогнозы погоды являются примерами статистических моделей. Метеорологи не могут с уверенностью предсказать завтрашнюю погоду. Однако они часто используют статистические модели, чтобы определить вероятность дождя в любой момент времени, и вы можете подготовиться, основываясь на этой вероятности.
Некоторые статистические модели представляют собой более точные математические функции: один набор значений может предсказывать или определять другой набор значений. Или некоторые статистические модели представляют собой математические функции, в которых набор значений точно не определяет другие значения. Статистические модели очень полезны, поскольку они могут описывать вероятность или вероятность возникновения события и предоставлять альтернативные результаты, если событие не произойдет. Например, прогнозы погоды являются примерами статистических моделей. Метеорологи не могут с уверенностью предсказать завтрашнюю погоду. Однако они часто используют статистические модели, чтобы определить вероятность дождя в любой момент времени, и вы можете подготовиться, основываясь на этой вероятности.
Вероятность
Вероятность — это математический инструмент, используемый для изучения случайности. Он имеет дело с вероятностью возникновения события. Например, если вы подбрасываете монету четыре раза, результаты не могут быть двумя орлами и двумя решками. Однако, если вы подбросите одну и ту же монету 4000 раз, результаты будут близки к половине орла и полурешки. Ожидаемая теоретическая вероятность выпадения орла при одном броске составляет 1212 или 0,5. Несмотря на то, что результаты нескольких повторений неопределенны, существует регулярная картина результатов при большом количестве повторений. Прочитав об английском статистике Карле Пирсоне, который подбросил монету 24 000 раз и выпало 12 012 орлов, один из авторов подбросил монету 2 000 раз. Результатов было 996 голов. Дробь 9962 0009962 000 равна 0,498, что очень близко к 0,5, ожидаемой вероятности.
Однако, если вы подбросите одну и ту же монету 4000 раз, результаты будут близки к половине орла и полурешки. Ожидаемая теоретическая вероятность выпадения орла при одном броске составляет 1212 или 0,5. Несмотря на то, что результаты нескольких повторений неопределенны, существует регулярная картина результатов при большом количестве повторений. Прочитав об английском статистике Карле Пирсоне, который подбросил монету 24 000 раз и выпало 12 012 орлов, один из авторов подбросил монету 2 000 раз. Результатов было 996 голов. Дробь 9962 0009962 000 равна 0,498, что очень близко к 0,5, ожидаемой вероятности.
Теория вероятности началась с изучения азартных игр, таких как покер. Прогнозы принимают форму вероятностей. Чтобы предсказать вероятность землетрясения, дождя или того, получите ли вы A в этом курсе, мы используем вероятности. Врачи используют вероятность, чтобы определить вероятность того, что прививка вызовет болезнь, которую вакцинация должна предотвратить. Биржевой маклер использует вероятность для определения нормы прибыли на инвестиции клиента.
Биржевой маклер использует вероятность для определения нормы прибыли на инвестиции клиента.
Ключевые термины
В статистике мы обычно изучаем население. Вы можете думать о населении как о наборе изучаемых лиц, вещей или объектов. Для изучения совокупности мы отбираем выборку. Идея выборки состоит в том, чтобы выбрать часть или подмножество большей совокупности и изучить эту часть — выборку — для получения информации о совокупности. Данные являются результатом выборки из населения.
Поскольку обследование всего населения требует много времени и денег, выборка является очень практичным методом. Если вы хотите рассчитать общий средний балл в вашей школе, имеет смысл выбрать выборку учащихся, посещающих школу. Данные, собранные из выборки, будут средними баллами учащихся. На президентских выборах берется выборка общественного мнения в 1000–2000 человек. Опрос общественного мнения должен отражать взгляды жителей всей страны. Производители банок с газированными напитками берут пробы, чтобы определить, содержит ли банка на 16 унций 16 унций газированного напитка.
Из выборочных данных мы можем рассчитать статистику. Статистика — это число, представляющее свойство выборки. Например, если мы рассматриваем один математический класс как выборку из 91 124 всех 90 369 математических классов, то среднее количество баллов, набранных учащимися в этом одном математическом классе в конце семестра, является примером статистики. Поскольку у нас нет данных по всем математическим классам, эта статистика является нашей наилучшей оценкой среднего значения для всей совокупности математических классов. Если у нас есть данные для все математических классов, мы можем найти параметр населения. Параметр — это числовая характеристика всего населения, которую можно оценить с помощью статистики. Поскольку мы считали все математические классы генеральной совокупностью, то среднее количество баллов, заработанных одним учащимся по всем математическим классам, является примером параметра.
Одной из основных проблем в области статистики является то, насколько точно статистика оценивает параметр. Чтобы иметь точную выборку, она должна содержать характеристики населения, чтобы быть репрезентативной выборкой. Нас интересует как статистика выборки, так и параметр совокупности в статистике вывода. В одной из последующих глав мы будем использовать выборочную статистику для проверки достоверности установленного параметра генеральной совокупности.
Переменная, обычно обозначаемая заглавными буквами, например X и Y , представляет собой характеристику или измерение, которое можно определить для каждого члена совокупности. Переменные могут описывать такие значения, как вес в фунтах или любимый предмет в школе. Числовые переменные принимают значения с одинаковыми единицами измерения, например, вес в фунтах и время в часах. Категориальные переменные помещают человека или вещь в категорию. Если мы допустим, что X равно количеству баллов, набранных одним студентом-математиком в конце семестра, то X — это числовая переменная. Если мы допустим, что Y является партийной принадлежностью человека, то некоторые примеры Y включают республиканцев, демократов и независимых. Y — категориальная переменная. Мы могли бы произвести некоторые математические действия со значениями X — вычислить среднее количество заработанных очков, например, — но нет смысла делать математические действия со значениями Y — вычисление средней партийной принадлежности не имеет смысла.
Если мы допустим, что Y является партийной принадлежностью человека, то некоторые примеры Y включают республиканцев, демократов и независимых. Y — категориальная переменная. Мы могли бы произвести некоторые математические действия со значениями X — вычислить среднее количество заработанных очков, например, — но нет смысла делать математические действия со значениями Y — вычисление средней партийной принадлежности не имеет смысла.
Данные — это фактические значения переменной. Это могут быть числа или слова. Datum — одно значение.
В статистике часто встречаются два слова: означает и пропорционально . Если бы вы сдали три экзамена на уроках математики и получили 86, 75 и 92 балла, вы бы рассчитали свой средний балл, сложив три экзаменационных балла и разделив их на три. Ваш средний балл будет 84,3 с точностью до одного десятичного знака. Если в вашем математическом классе 40 учеников, из них 22 мальчика и 18 девочек, то доля учащихся-мужчин составляет 22402240, а доля учащихся-женщин — 18401840. Среднее значение и пропорция обсуждаются более подробно в последующих главах.
Ваш средний балл будет 84,3 с точностью до одного десятичного знака. Если в вашем математическом классе 40 учеников, из них 22 мальчика и 18 девочек, то доля учащихся-мужчин составляет 22402240, а доля учащихся-женщин — 18401840. Среднее значение и пропорция обсуждаются более подробно в последующих главах.
ПРИМЕЧАНИЕ
Слова означают , а — среднее , часто используются как синонимы. В этой книге мы используем термин среднее арифметическое для обозначения среднего.
Пример 1.1
Определите, какие совокупность, выборка, параметр, статистика, переменная и данные используются в следующем исследовании:
Мы хотим узнать среднее количество внеклассных мероприятий, в которых участвуют старшеклассники. Мы случайным образом опросили 100 старшеклассников. Трое из этих студентов участвовали во 2, 5 и 7 внеклассных мероприятиях соответственно.
Решение 1. 1
1
Население состоит из старшеклассников.
Выборка — это 100 опрошенных старшеклассников.
Параметр — это среднее количество внеклассных занятий, в которых участвуют все старшеклассники.
Статистический показатель – это среднее количество внеклассных мероприятий, в которых участвует выборка старшеклассников.
Переменная может быть количеством внеклассных занятий на одного старшеклассника. Пусть X = количество внеклассных занятий одного старшеклассника.
Данные — это количество внеклассных мероприятий, в которых участвуют старшеклассники. Примеры данных: 2, 5, 7.
Пример 1.2
Определите, к чему относятся ключевые термины в следующем исследовании:
В местной средней школе было проведено исследование для анализа среднего совокупного среднего балла учащихся, окончивших школу в прошлом году. Вставьте букву фразы, которая лучше всего описывает каждый из пунктов ниже.
Вставьте букву фразы, которая лучше всего описывает каждый из пунктов ниже.
1. Население ____ 2. Статистика ____ 3. Параметр ____ 4. Выборка ____ 5. Переменная ____ 6. Данные ____
a) все учащиеся, посещавшие среднюю школу в прошлом году
b) совокупный средний балл одного учащегося, окончили среднюю школу в прошлом году
в) 3,65, 2,80, 1,50, 3,90
г) группа учащихся, окончивших среднюю школу в прошлом году, выбранная случайным образом
д) средний совокупный средний балл учащихся, окончивших старшая школа в прошлом году
f) все учащиеся, окончившие среднюю школу в прошлом году
g) средний совокупный средний балл учащихся, окончивших среднюю школу в прошлом году
Решение 1.2
1. f, 2. g, 3 е, 4. г, 5. б, 6. в
Пример 1.3
Определите, какие совокупность, выборка, параметр, статистика, переменная и данные упоминаются в следующем исследовании:
В рамках исследования, предназначенного для проверки безопасности автомобилей, Национальный совет по безопасности на транспорте собрал и рассмотрел данные о влиянии автомобильной аварии на испытательные манекены (The Data and Story Library, nd). Вот какой критерий они использовали.
Вот какой критерий они использовали.
| Скорость, с которой автомобили разбивались | Местонахождение Водителя (т. е. манекена) |
| 35 миль/час | Переднее сиденье |
Таблица 1.1
Автомобили с манекенами на передних сиденьях врезались в стену на скорости 35 миль в час. Мы хотим знать долю манекенов на водительском сиденье, у которых были бы травмы головы, если бы они были настоящими водителями. Начнем с простой случайной выборки из 75 автомобилей.
Решение 1.3
Население — это все автомобили с манекенами на переднем сиденье.
Выборка — это 75 автомобилей, выбранных методом простой случайной выборки.
Параметр представляет собой долю фиктивных водителей, если бы они были реальными людьми, которые получили бы травмы головы среди населения.
Статистика — это доля манекенов водителей — если бы они были реальными людьми — которые получили бы травмы головы в выборке.
Переменная X = количество манекенов водителей, если бы они были реальными людьми, которые получили бы травмы головы.
Данные : да, травма головы; или нет, не сделал.
Пример 1.4
Определите совокупность, выборку, параметр, статистику, переменную и данные, упомянутые в следующем исследовании:
Страховая компания хотела бы определить долю всех врачей, принимавших участие в судебные иски о злоупотреблении служебным положением. Компания случайным образом отбирает 500 врачей из профессионального каталога и определяет число в выборке, которые были вовлечены в судебный процесс о злоупотреблении служебным положением.
Решение 1.4
Население — это все врачи, перечисленные в профессиональном справочнике.

 Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.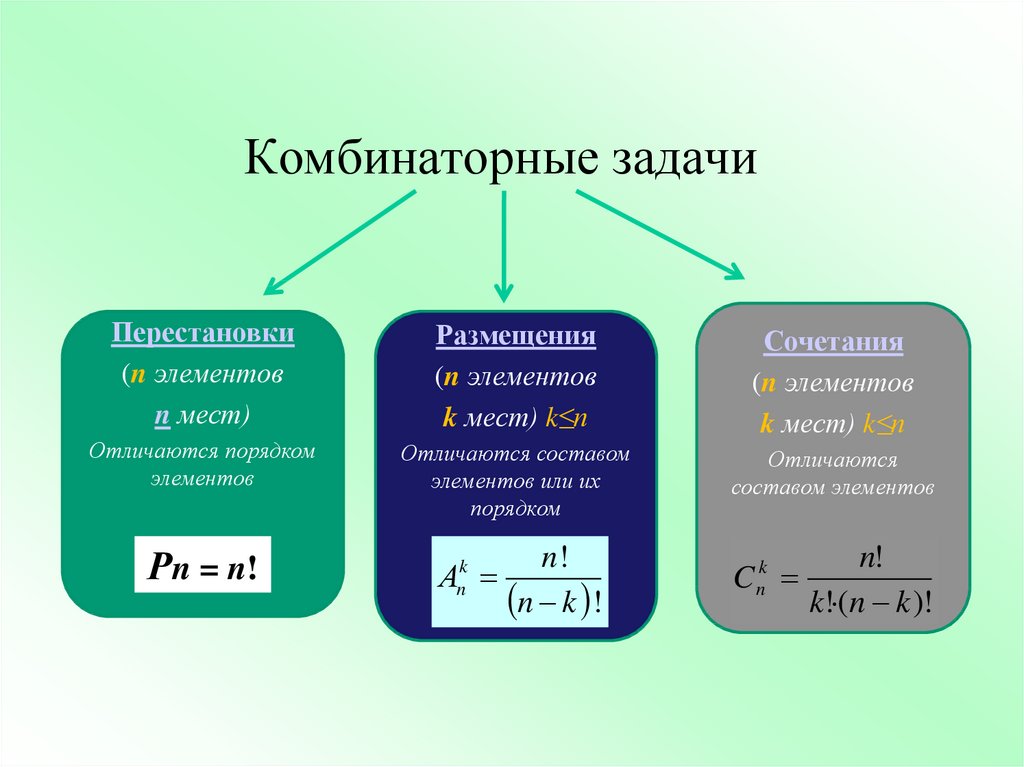 Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора Максимова окажется запланированным на последний день конференции?
Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора Максимова окажется запланированным на последний день конференции?
 В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом). На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

 верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. Артем хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Артем пойдет в магазин?
Артем хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Артем пойдет в магазин?

 Самбо в школу
Самбо в школу Черняховского»
Черняховского»