Презентация на тему: «Новосёлово Решением данной системы уравнений Х+У = 2 3х – 2у =6 является пара чисел: 1)(- 6; 8 ) 1)(- 6; 8 ) 2) ( 0; — 3 ) 3) (2; 0 )2) ( 0;
1 Новосёлово Решением данной системы уравнений Х+У = 2 3х – 2у =6 является пара чисел: 1)(- 6; 8 ) 1)(- 6; 8 ) 2) ( 0; — 3 ) 3) (2; 0 )2) ( 0; — 3 ) 3) (2; 0 )
2
Швейцария Выберите из предложенных систем ту, которая имеет бесконечное множество решений.
3 Германия Уравнения системы 2х – 3у =1 умножили почленно на такие множители 5х + 2у = 0 что коэффициент при х в первом уравнении стал равен 10, а во втором – ( — 10 ). Сложив полученные уравнения, получили: 1) – 19у = 5 2) — 11у = 5 3) — 19у = 1
4
Лондон Составьте систему уравнений по условию задачи: « Одна сторона прямоугольника меньше другой на 5 см, периметр прямоугольника равен 38 см.
Найти стороны этого прямоугольника.» 1) х – у = 5 х + у = 38 2)х + у =5х + у =5 2( х + у) = 38 3)х – у = 5х – у = 5 2( х + у) = 38
5 Шотландия Известно, что прямая х + ву = 2 проходит через точку А ( 1 ; — 1), а прямая ах – у = 3 проходит через точку В ( 1 ; — 4). Найдите координаты точек пересечения этих прямых. 1)( — 0,5 ; 2,5)( — 0,5 ; 2,5) 2)(- 0,5 ; — 2,5)(- 0,5 ; — 2,5) 3)( 1,5 ; 0,5)( 1,5 ; 0,5)
6 Италия При каком значении Р график функции у + рх = 0 пройдет через точку пересечения прямых у = х – 16 и у = х + 5 ? 1) 1) — 2) 3) — 2) 3)
7 Молодец За решение заданий Вы получаете оценку « хорошо» Далее
8 Прекрасно За решение заданий Вы получаете оценку « отлично» Далее
9
Есть успехи За решение заданий Вы получаете оценку «удовлетворительно».
10 Мало правильно решенных заданий Для получения положительной оценки Вам нужно ещё поработать над этой темой. Домой ДомойДомой
11
Предлагаем посетить наше заведение и проверить свою удачу.
12
Игровой зал Организаторы состязания попросили зрителей высказать их предположения. Четыре человека назвали следующие числа : 196 кг, 163 кг, 178 кг, и 185 кг. Впоследствии оказалось, что все ошиблись. Кто-то ошибся на 1 кг, кто-то — на 6 кг, еще один на 16 кг и еще один — на 17 кг.
14
Берн Берн Укажите взаимное расположение прямых 2х – у = 4 и 3х – у = 6.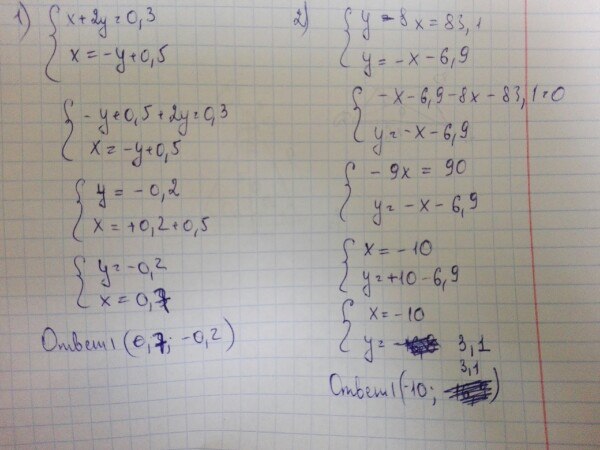
15 Цюрих Составьте систему уравнений по условию задачи: « В туристический поход ребята взяли двухместные и трёхместные палатки. Сколько человек разместилось в трехместных палатках, если на 26 человек ребята взяли 10 палаток? 1)х + у = 10 х + у = 10х + у = 10 2х +3у = 26 2х +3у = 26 2)х – у = 10 х – у = 10х – у = 10 2х + 3у = 26 2х + 3у = 26 3) х + у = 10 х + у = 10х + у = 10 2х – 3у = 26 2х – 3у = 26
16 Лугано Система уравнений 2х +3у =1 равносильна системе уравнений: 4х + у = 0 4х + у = 0 1)4х + 6у =1 4х + 6у =14х + 6у =1 4х +у = 0 4х +у = 0 2)- 4х + 3у = 1 — 4х + 3у = 1- 4х + 3у = 1 4х + у = 0 4х + у = 0 3)-4х – 6у = -2 -4х – 6у = -2-4х – 6у = -2 4х +у = 0 4х +у = 0
17 Люцерн Решите систему уравнений: 2х – 3у = — 4 5х + 2у = 9 5х + 2у = 9 1) ( 2 ; 1 )1) ( 2 ; 1 ) 2) ( 1; 2 ) 3) ( — 1 ; — 2) 2) ( 1; 2 )3) ( — 1 ; — 2) 1) ( 2 ; 1 )2) ( 1; 2 )3) ( — 1 ; — 2)
18 Давос Укажите взаимное расположение прямых 2х – у = 3 и х – у = 2 х – у = 2 1)Совпадают 2) Пересекаются Совпадают2) ПересекаютсяСовпадают2) Пересекаются 3) Параллельны 3) Параллельны3) Параллельны3) Параллельны
19
Санкт – Мориц Санкт – Мориц Составьте систему уравнений по условию задачи: « Одна сторона прямоугольника на 4 см больше другой.
Если меньшую сторону увеличить в 2 раза, а большую оставить без изменения, то периметр нового прямоугольника будет равен 56 см.Найдите стороны данного прямоугольника.» 1)х – у = 4 х – у = 4х – у = 4 х + 2у = 56 х + 2у = 56 2)х – у = 4 х – у = 4х – у = 4 (2х + у)× 2 = 56 (2х + у)× 2 = 56 3)х – у = 4 х – у = 4х – у = 4 (х + 2у) × 2 =56 (х + 2у) × 2 =56
20 Ароза Система уравнений х + 2у = 1 равносильна системе уравнений: 3х – у = 0 3х – у = 0 1)- 3х – 6у = х – 6у = х – 6у = — 3 3х –у = 0 3х –у = 0 2)- 3х – 6у = 1 — 3х – 6у = 1- 3х – 6у = 1 3х – у = 0 3х – у = 0 3)3х + 6у = 1 3х + 6у = 13х + 6у = 1 3х – у = 0 3х – у = 0
21 Вербье Вербье Решите систему уравнений: 3х – 2 у = 4 Решите систему уравнений: 3х – 2 у = 4 2х + 3у = 7 2х + 3у = 7 1) (1 ; 2)1) (1 ; 2) 2) ( 2 ; 1) 3) ( 2 ; — 1 ) 2) ( 2 ; 1)3) ( 2 ; — 1 ) 1) (1 ; 2) ( 2 ; 1)3) ( 2 ; — 1 )
22 Красноярск Реши систему методом подстановки: 5у – х = 6 5у – х = 6 3х – 4у = 4 3х – 4у = 4 1) (2; 4) 1) (2; 4) 2) (- 4 ; — 2) 3) ( 4 ; 2 ) 2) (- 4 ; — 2)3) ( 4 ; 2 ) 1) (2; 4) 2) (- 4 ; — 2)3) ( 4 ; 2 )
23 Суздаль Найти координаты точки пересечения прямых: у = 10 х + 30 и у = — 12 х ) (11; 140 )1) (11; 140 ) 2) ( -11; ) 3) ( 140; 11 ) 2) ( -11; )3) ( 140; 11 ) 1) (11; 140 )2) ( -11; )3) ( 140; 11 )
24 Истра Решить систему методом сложения: 4 х + 5 у = 1 4 х + 5 у = 1 5 х + 7 у = 5 5 х + 7 у = 5 1) ( 6; — 5 )1) ( 6; — 5 ) 2) ( 5 ; 6 ) 3) ( — 6 ; 5 ) 2) ( 5 ; 6 )3) ( — 6 ; 5 ) 1) ( 6; — 5 )2) ( 5 ; 6 )3) ( — 6 ; 5 )
25
Казань Составьте систему уравнений по условию задачи: Периметр прямоугольника равен 48 см.
Если одну его сторону увеличить в 2 раза, а другую уменьшить на 6см, то периметр нового прямоугольника будет равен 64 см. Найдите стороны данного прямоугольника. 1) х + у = 48 2 х + у – 6 = 64 2) 2 ( х – у ) = 482 ( х – у ) = 48 2 ( 2 х + у – 6 ) = 64 3) 2 ( х + у ) = 482 ( х + у ) = 48 2 ( 2 х + у – 6 ) = 64
26 Псков Вычислить сумму абсциссы и ординаты точки пересечения графиков функций у = — 7х – 19 и у = 14 х )111) 11)11) 1) 12 2)2) 2) 13 3) 14
27 красноярск Реши систему методом сложения: 2 х — 3 у = 9 2 х — 3 у = 9 х +2 у = 1 х +2 у = 1 1) ( 3 ; — 1 ) 1) ( 3 ; — 1 ) 2) ( — 3 ; 1) 3) ( — 1 ; 3 ) 2) ( — 3 ; 1)3) ( — 1 ; 3 ) 1) ( 3 ; — 1 ) 2) ( — 3 ; 1)3) ( — 1 ; 3 )
28 Енисейск Решить систему методом подстановки: х = 4 у х = 4 у х + 5 у = 99 х + 5 у = 99 1) ( 16; 4 )1) ( 16; 4 ) 2) ( 4 ; 16 ) 3) ( -4 ; — 16 😉 2) ( 4 ; 16 )3) ( -4 ; — 16 😉 1) ( 16; 4 )2) ( 4 ; 16 )3) ( -4 ; — 16 😉
29 Канск Решить систему методом сложения: х + у = 49 х + у = 49 — х + у = 17 — х + у = 17 1) ( 33 ; 16 )1) ( 33 ; 16 ) 2) ( — 33 ; — 16 ) 3) (16; 33) 2) ( — 33 ; — 16 )3) (16; 33) 1) ( 33 ; 16 )2) ( — 33 ; — 16 )3) (16; 33)
30 Ачинск Какое уравнение получится при почленном сложении уравнений системы х – у = 2 2 х + у = х + у = — 3 1) 3х + 2у = 1) 3х + 2у = -1 2) 3 х = -1 3) 3 х = 5 2) 3 х = 3) 3 х = 5 1) 3х + 2у = 2) 3 х = 3) 3 х = 5
31 Зеленогорск Если система двух линейных уравнений с двумя переменными имеет бесконечное множество решений, графики уравнений этой системы 1) Пересекаются 2) параллельны Пересекаются2) параллельны Пересекаются2) параллельны 3) совпадают 3) совпадают3) совпадают3) совпадают
32
Свято –Покровский кафедральный собор в г.
Красноярске Решить методом сложения: х + у =45 х + у =45 х – у = 13 х – у = 13 1) ( — 29; 16 )1) ( — 29; 16 ) 2) (29; — 16) 3) ( 29 ; 16 ) 2) (29; — 16)3) ( 29 ; 16 ) 1) ( — 29; 16 )2) (29; — 16)3) ( 29 ; 16 )
33 Римско – Католический костёл в г. Красноярске Какое уравнение получится при почленном сложении уравнений системы х + у = -1 х + у = -1 3 х – у = 2 3 х – у = 2 1 ) 4 х = 11 ) 4 х = 1 2) 4 х – 2 у = 1 3) 4 х + 2у = 1 2) 4 х – 2 у = 13) 4 х + 2у = 1 ) 4 х = 12) 4 х – 2 у = 13) 4 х + 2у = 1
34
Свято –Никольский Храм в г.
Красноярске Если графики уравнений системы линейных уравнений – параллельные прямые, то эта система 1) Неопределённая 2) несовместная Неопределённая2) несовместная Неопределённая2) несовместная 3) не существует 3) не существует3) не существует3) не существует
35 Дом молитвы в г. Красноярске Решить систему методом сложения х + у = 5 х + у = 5 х – у = 7 х – у = 7 1) ( 6; — 1 )1) ( 6; — 1 ) 2) ( — 6; — 1) 3) ( — 6 ; 1) 2) ( — 6; — 1)3) ( — 6 ; 1) ( 6; — 1 )2) ( — 6; — 1)3) ( — 6 ; 1)
36
Часовня Св.
Великомученицы Параскевы Пятницы в г. Красноярске Решить систему методом подстановки: у = 6 х у = 6 х 4 х + у = х + у = 150 1) ( 90 ; 15 )1) ( 90 ; 15 ) 2) ( — 90 ; — 15 ) 3) ( 15 ; 90 ) 2) ( — 90 ; — 15 )3) ( 15 ; 90 ) 1) ( 90 ; 15 )2) ( — 90 ; — 15 )3) ( 15 ; 90 )
37 Храм Аристратига Михаила и Чуда его в Хонех в г. Красноярске Решить систему методом сложения х + у = 9 х + у = 9 х – у = 3 х – у = 3 1) (6; 3)1) (6; 3) 2) ( 3; 6) 3) (- 6 ; 3) 2) ( 3; 6)3) (- 6 ; 3) 1) (6; 3)2) ( 3; 6)3) (- 6 ; 3)
38 Необитаемый остров Решить систему уравнений методом подстановки 15 х – 4 у = х + у = 1 1) (4; 13)1) (4; 13) 2) ( 13; 4) 3) ( 1,3; 4)2) ( 13; 4)3) ( 1,3; 4)
39 Зыбучие пески Решить систему методом подстановки у = 3 х – 1 х + 2 у = 5 1) (1; — 2)1) (1; — 2) 2) (- 1; 2) 3) (1 ; 2)2) (- 1; 2)3) (1 ; 2)
40 Замок вампиров Решить систему методом подстановки у = 3 х – 1 2 х + 3 у = 8 1) (2; 1)1) (2; 1) 2) (1; 2) 3) (- 1; — 2)2) (1; 2)3) (- 1; — 2)
Презентации к урокам алгебры в 7 классе по теме «Системы линейных уравнений с двумя неизвестными».
| Презентация к уроку по алгебре (7 класс):Слайд 1
Системы двух уравнений с двумя неизвестными
Слайд 2
Урок 1 Уравнения первой степени с двумя неизвестными. Системы уравнений Цели : ввести понятие линейного уравнения с двумя неизвестными, системы линейных уравнений с двумя неизвестными; способствовать усвоению определения решения системы уравнений с двумя неизвестными.
Слайд 3
Уравнение и его свойства Определение Уравнение – это равенство, содержащее одну или несколько переменных ax=b Линейное уравнение с одной переменной Л ин ейное уравнение с двумя переменными ax+by =c а x + b y = c , где а, b, c – заданные числа. Коэффициенты Свободный член
Слайд 4
Из истории уравнений Уравнение с двумя неизвестными выражает зависимость между двумя величинами , имеет бесчисленное множество реше — ний и является неопределенным. Решением таких уравнений занимались в древности китайцы, греки и индийцы. В «Арифметике» Диофанта приведено много задач, решаемых им с помощью неопределенных уравнений.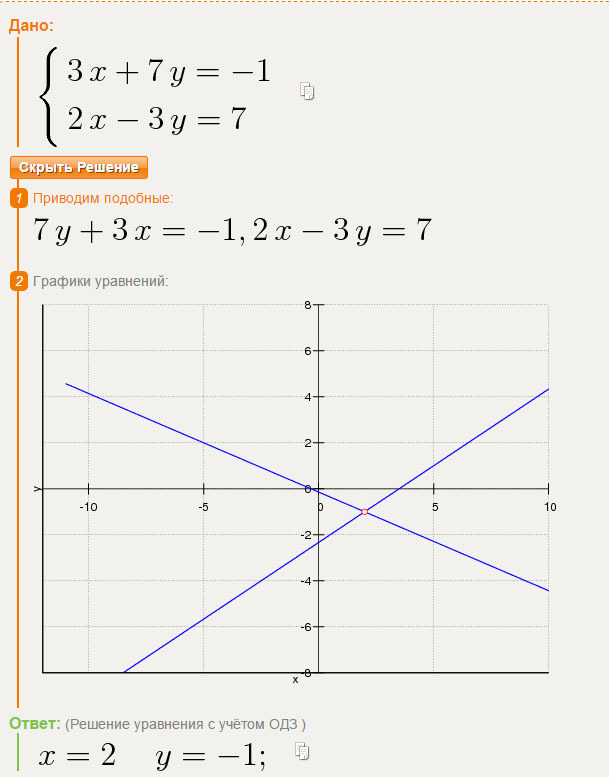
Диофант из Александрии ( 3 век )
Слайд 5
Свойства уравнений если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному 12х – 5у = 12х – 7 = 5у если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному 9х + 15у = 3 Ι 🙁 — 3 ) -3х — 5у = — 1 7
Слайд 6
Задание 1. 1.1. Из линейного уравнения с двумя неизвестными 2х – 8у = — 10 выразите переменную х: 1.2. Из линейного уравнения с двумя неизвестными 3х – 2у = 5 выразите переменную у: 3х – 5 = 2у Ι : 2 2х = 8у – 10 Ι : 2, Х = 4у — 5 3х — 5 2 = у
Слайд 7
Решением уравнения с двумя неизвестными х и у называется упорядоченна я пара чисел ( х ; у ), при подстановке которых в это уравнение получается верное числовое равенство.
Слайд 8
Задание 2 Найдите все пары ( х ; у ) натуральных чисел, которые являются решениями уравнения. 2.1. 13х + 4у =55 Ответ: ( 3 ; 4) 2.
2. 5х + 7у =59 Ответ: (2 ; 7) (9 ; 2)
Слайд 9
Система уравнений и её решение Определение Системой двух линейных уравнений с двумя неизвестными называются два уравнения, объединенные фигурной скобкой. Фигурная скобка означает, что эти уравнения должны быть решены одновременно. а 1 х + b 1 y = c 1, а 2 х + b 2 y = c 2 ; В общем виде систему двух линейных уравнений с двумя неизвестными записывают так : где а 1 , b 1 , c 1 , а 2 , b 2 , c 2 — Заданные числа, а х и у — неизвестные
Слайд 10
Из истории систем уравнений Задачи на составление и решение систем уравнений встречаются в вавилонских и египетских текстах II тыся — челетия до н. э., в трудах древнегреческих, китайских и индийских ученых. Нижние индексы при буквах впервые употребил в 1675 г. немецкий математик Лейбниц Лейбниц Готфрид Вильгельм ( 1646 – 1716 )
Слайд 11
Например, в системе а 1 = 1, b 1 = -1, с 1 = 2; а 2 = 3, b 2 = -2, с 2 = 9. Задание 3. (Устно.) Проверьте, являются ли числа х = 4 , у = 3 решениями системы Решение: х – у = 2, 3х – 2у = 9.
2,5 ·4 – 3 · 3 =1, 5·4 – 6 · 3 = 2. 2,5х – 3у = 1, 5х – 6у = 2. Ответ: числа х = 4 , у = 3 являются решениями системы
Слайд 12
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство Решить систему уравнений — это значит найти все её решения или установить, что их нет
Слайд 13
Задание 4. Если в системе уравнений 6х – 21 у = 9, 6х + 2у = 4. 2х – 7у = 3, 3х + у = 2. уравнять модули коэффициентов при х , то система примет вид 2х – 7у = 3 Ι · 3 , 3х + у = 2 Ι · 2 . 2 · 3х – 7 · 3у = 3 · 3, 3 · 2х + 2у = 2 · 2; 6х – 21 у = 9, 6х + 2у = 4. РЕШЕНИЕ
Слайд 14
Домашнее задание 1. Учебник «Алгебра 7», авторы Ш.А.Алимов и др. § 33 № 615(1), 616(1), 617(1), 619(1). 2. Рабочая тетрадь по алгебре, 7, авторы Ю.М.Колягин и др. § 33, № 3, 4(1), 5(1), 14(1). 3. Дополнительно: Дидактические материалы «Алгебра 7», авторы М.В.Ткачева и др. § 33 ( стр. 90) № 4(1), 7.
Слайд 15
Спасибо всем за работу
| 1 | Найдите количество возможностей | 7 выбрать 3 | |
| 2 | Найдите количество возможностей | 8 выбрать 3 | |
| 3 | Найдите количество возможностей | 5 выбрать 2 | |
| 4 | Найдите количество возможностей | 4 выбрать 2 | |
| 5 | Найдите количество возможностей | 8 выбрать 4 | |
| 6 | Найдите количество возможностей | 10 выбрать 3 | |
| 7 | Найдите количество возможностей | 7 выбрать 4 | |
| 8 | Найдите количество возможностей | 6 выбрать 3 | |
| 9 | Найдите количество возможностей | 9 выбрать 3 | |
| 10 | Найдите количество возможностей | 3 выбрать 2 | |
| 11 | Найдите количество возможностей | 6 выбрать 4 | |
| 12 | Найдите количество возможностей | 5 выбрать 4 | |
| 13 | Найдите количество возможностей | 7 переставить 3 | |
| 14 | Найдите количество возможностей | 7 выбрать 2 | |
| 15 | Найдите количество возможностей | 10 выбрать 5 | |
| 16 | Найдите количество возможностей | 10 выбрать 6 | |
| 17 | Найдите количество возможностей | 13 выбрать 5 | |
| 18 | Найдите количество возможностей | 3 выбрать 3 | |
| 19 | Найдите количество возможностей | 4 выбрать 1 | |
| 20 | Найдите количество возможностей | 4 выбрать 4 | |
| 21 | Найдите количество возможностей | 5 выбрать 1 | |
| 22 | Найдите количество возможностей | 6 переставить 3 | |
| 23 | Найдите количество возможностей | 8 выбрать 5 | |
| 24 | Найдите количество возможностей | 9переставить 4 | |
| 25 | Найдите количество возможностей | 13 выбрать 3 | |
| 26 | Найдите количество возможностей | 12 выбрать 2 | |
| 27 | Найдите количество возможностей | 12 выбрать 4 | |
| 28 | Найдите количество возможностей | 12 выбрать 3 | |
| 29 | Найдите количество возможностей | 9 выбрать 5 | |
| 30 | Найдите количество возможностей | 9 выбрать 2 | |
| 31 | Найдите количество возможностей | 7 выбрать 5 | |
| 32 | Найдите количество возможностей | 6 переставить 6 | |
| 33 | Найдите количество возможностей | 8 переставить 5 | |
| 34 | Найдите количество возможностей | 8 переставить 3 | |
| 35 | Найдите количество возможностей | 7 переставить 5 | |
| 36 | Найдите количество возможностей | 52 выбрать 5 | |
| 37 | Найдите количество возможностей | 5 переставить 3 | |
| 38 | Найдите количество возможностей | 12 выбрать 5 | |
| 39 | Найдите количество возможностей | 3 выбрать 1 | |
| 40 | Найдите количество возможностей | 11 выбрать 5 | |
| 41 | Найдите количество возможностей | 10 выбрать 2 | |
| 42 | Найдите количество возможностей | 15 выбрать 3 | |
| 43 | Найдите количество возможностей | 52 выбрать 4 | |
| 44 | Найдите количество возможностей | 9 выбрать 4 | |
| 45 | Найдите количество возможностей | 9 переставить 3 | |
| 46 | Найдите количество возможностей | 7 переставить 4 | |
| 47 | Найдите количество возможностей | 7 переставить 2 | |
| 48 | Найдите количество возможностей | 11 выбрать 4 | |
| 49 | Найдите количество возможностей | 11 выбрать 2 | |
| 50 | Найдите количество возможностей | 11 выбрать 3 | |
| 51 | Найдите количество возможностей | 10 переставить 5 | |
| 52 | Найдите количество возможностей | 5 выбрать 5 | |
| 53 | Найдите количество возможностей | 6 выбрать 1 | |
| 54 | Найдите количество возможностей | 8 переставить 4 | |
| 55 | Найдите количество возможностей | 8 выбрать 6 | |
| 56 | Найдите количество возможностей | 13 выбрать 4 | |
| 57 | Оценить | и | |
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найдите количество возможностей | 13 выбрать 2 | |
| 60 | Найдите количество возможностей | 10 переставить 2 | |
| 61 | Найдите количество возможностей | 10 переставить 3 | |
| 62 | Найдите количество возможностей | 10 выбрать 7 | |
| 63 | Найдите количество возможностей | 20 выбрать 4 | |
| 64 | Найдите количество возможностей | 6 переставить 4 | |
| 65 | Найдите количество возможностей | 5 переставить 4 | |
| 66 | Найдите количество возможностей | 6 выбрать 5 | |
| 67 | Найдите количество возможностей | 52 выбрать 3 | |
| 68 | Найдите количество возможностей | 4 выбрать 0 | |
| 69 | Найдите количество возможностей | 9переставить 7 | |
| 70 | Найдите количество возможностей | 6 выбрать 2 | |
| 71 | Найдите количество возможностей | 5 переставить 5 | |
| 72 | Найдите количество возможностей | 5 переставить 2 | |
| 73 | Найдите количество возможностей | 6 выбрать 6 | |
| 74 | Найдите количество возможностей | 7 выбрать 6 | |
| 75 | Найдите количество возможностей | 8 переставить 6 | |
| 76 | Найдите количество возможностей | 7 переставить 7 | |
| 77 | Найдите количество возможностей | 9 переставить 5 | |
| 78 | Найдите количество возможностей | 2 переставить 2 | |
| 79 | Найдите количество возможностей | 10 выбрать 8 | |
| 80 | Найдите количество возможностей | 12 выбрать 7 | |
| 81 | Найдите количество возможностей | 15 выбрать 5 | |
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Найти диапазон | 1/4x-7 | |
| 84 | Найдите количество возможностей | 10 переставить 7 | |
| 85 | Найдите количество возможностей | 12 выбрать 6 | |
| 86 | Найдите количество возможностей | 2 выбрать 1 | |
| 87 | Найдите количество возможностей | 30 выбрать 3 | |
| 88 | Найдите количество возможностей | 9 выбрать 6 | |
| 89 | Найдите количество возможностей | 8 переставить 2 | |
| 90 | Найдите количество возможностей | 7 выбрать 1 | |
| 91 | Найдите количество возможностей | 6 перестановка 2 | |
| 92 | Найдите количество возможностей | 4 переставить 2 | |
| 93 | Найдите количество возможностей | 4 переставить 3 | |
| 94 | Найдите количество возможностей | 3 переставить 3 | |
| 95 | Найдите количество возможностей | 46 выбрать 6 | |
| 96 | Найдите количество возможностей | 5 переставить 1 | |
| 97 | Найдите количество возможностей | 52 выбрать 7 | |
| 98 | Найдите количество возможностей | 52 переставить 5 | |
| 99 | Найдите количество возможностей | 9выбрать 1 | |
| 100 | Найдите количество возможностей | 9 переставить 6 |
Каково решение 3x + 2y = 7 и 2x + 3y = 1
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяУкажите эту страницу следующим образом:
«Каково решение 3x + 2y = 7 и 2x + 3y = 1» eNotes Editorial , 20 мая 2012 г.
, https://www.enotes.com/homework-help/what-solution-3x-2y-7 -2x-3y-1-339292.
По состоянию на 12 февраля 2023 г.
Вот более подходящий метод решения одновременных уравнений, чем простая подстановка.
`3x + 2y = 7`
`2x + 3y = 1`
Умножьте 1-е уравнение на 2 и умножьте второе уравнение на 3 и вычтите их.
`2(3x + 2y) -3(2x + 3y) = 2 xx 7 — 3 xx 1`
`6x+4y-6x-9y = 14-3`
`-5y = 11` `y = -11/5`
Вы можете использовать это во втором уравнении,
`2x+3(-11/5) = 1`
`2x — 33/5 = 1`
`2x = 1+33/5`
`2x = (5+33)/5`
`2x = 38/5`
`x = 19/5`
Это дает `x = 19/5` и `y = -11/5`
Утверждено редакцией eNotes
Необходимо решить систему линейных уравнений 3x + 2y = 7 и 2x + 3y = 1.
3x + 2y = 7
=> `x = (7 — 2y)/3`
заменить в 2x + 3y = 1
=> `(2/3)*(7 — 2y) + 3y = 1`
=> `2(7 — 2y) = 3(1-3y)`
=> 14 — 4y = 3 — 9y
=> 5y = -11
=> y = -11/5
x = `(7 + 22/5)/3 = 57/15 = 19/5`
Решением системы уравнений является x = `19/5` и y = `-11/5`
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г.
в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 Ответы воспитателя
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ преподавателя
Математика
Последний ответ опубликован 15 мая 2012 г. в 7:13:43.
Как записать sin x через cos x?
1 Ответ учителя
Математика
Последний ответ опубликован 16 мая 2012 г.