Алгебра Построение графика квадратичной функции
Материалы к уроку
Конспект урока
Квадратичная функция имеет вид игрек равно а икс квадрат плюс бэ икс плюс цэ. Запишем эту формулу в виде игрек равно а умноженное на квадрат разности икс и эм плюс эн.
Выделим из трехчлена а икс в квадрате плюс бэ икс плюс це… квадрат двучлена. В итоге получим разность, уменьшаемым которого является произведение а на квадрат суммы икс и бэ деленного на два а, а вычитаемым – дробь, числителем которой является разность между бэ квадрат и четыре а цэ, а знаменателем – четыре а.
Пусть минус бэ деленное на два а будет равно эм; а эн примет значение отрицательного отношения разности бэ квадрат и четыре а це.. к четырем а. Тогда игрек будет равен а умноженному на квадрат разности икс и эм.. плюс эн.
Значит графиком функции игрек равно а икс квадрат плюс бэ икс плюс цэ является парабола, которую можно получить из графика функции игрек равно а икс квадрат с помощью двух параллельных переносов – сдвига вдоль оси икс и сдвига вдоль оси игрек.
Осью симметрии параболы является прямая икс равная эм, параллельная оси игрек. Если а больше нуля, ветви параболы направлены вверх, если а меньше нуля – вниз.
Для построения графика квадратичной функции необходимо:
- Найти координаты вершины параболы и отметить ее в координатной плоскости;
- Построить несколько точек, принадлежащих параболе;
- Соединить отмеченные точки плавной линией.
Абсциссу эм можно находить по формуле эм равно минус бэ деленное на два а. Ординату эн – подставив найденное значение абсциссы в формулу игрек равно а икс квадрат плюс бэ икс плюс цэ, так как при икс равном эм оно обращается в эн.
Рассмотрим примеры на построение графиков квадратичных функций.
Построим график функции игрек равно ноль целых две десятые икс квадрат плюс четыре икс плюс один.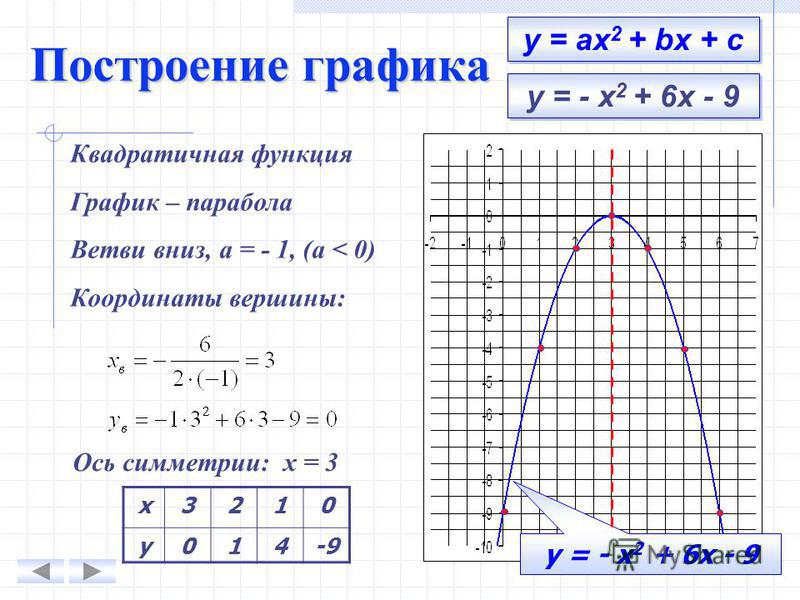
Его графиком является парабола, ветви которой направлены вверх, так как коэффициент а больше нуля. Найдем координаты вершины параболы… Координата эм будет равна минус десяти, координата эн – минус девятнадцати. Таким образом, вершиной параболы является точка с координатами минус десять, минус девятнадцать.
Составим таблицу значений функции…, отметим точки на координатной плоскости… и соединим их плавной линией. Получим график функции игрек равно две десятые икс квадрат плюс четыре икс плюс один.
При составлении таблицы и построении графика не забываем, что прямая икс, равная минус десяти, является осью симметрии параболы.
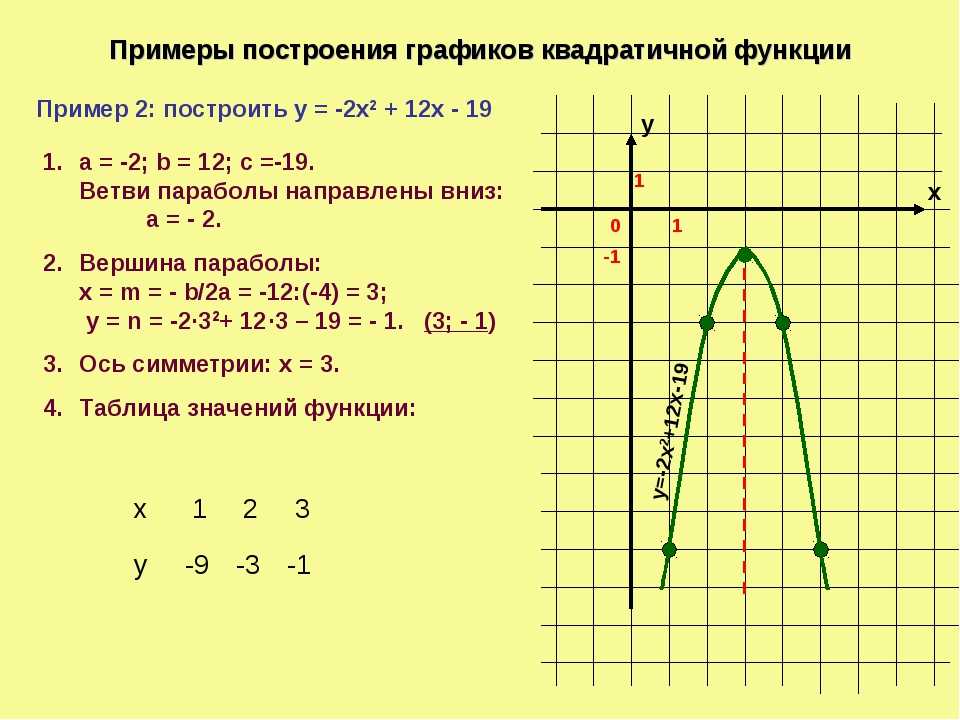
Построим график функции игрек равно минус три икс квадрат плюс двенадцать икс минус одиннадцать.
Графиком функции является парабола, ветви которой направлены вниз, так как коэффициент а меньше нуля. Найдем координаты вершины параболы. Это будет точка два, один.
Вычислим координаты еще нескольких точек с помощью таблицы…., отметим их на координатной плоскости….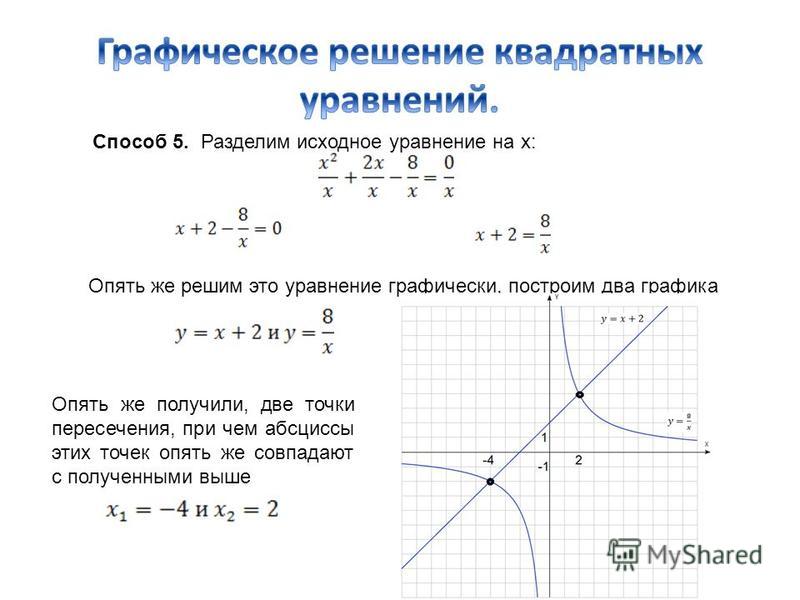 . и соединим плавной линией.
. и соединим плавной линией.
Получим график функции игрек равно минус три икс квадрат плюс двенадцать икс минус одиннадцать.
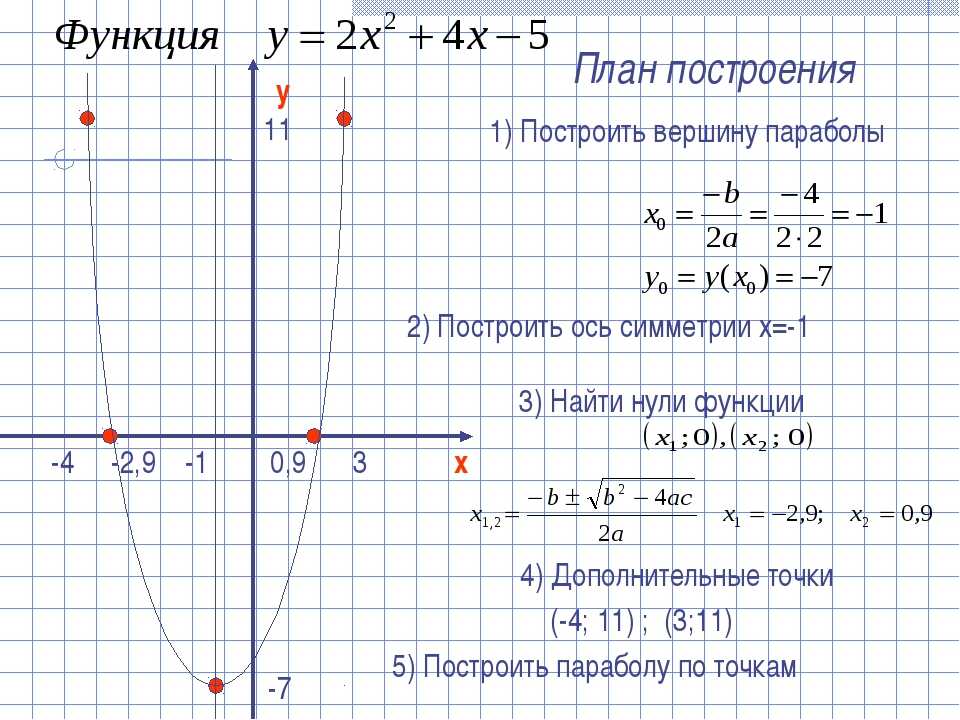
Построим график функции игрек равно одна третья икс квадрат плюс два икс плюс три.
Графиком функции является парабола, ветви которой направлены вверх. Координаты вершины параболы будут равны минус три и нуль… Найдем еще несколько точек с помощью таблицы…., отметим их на координатной плоскости…. и соединим плавной линией. Получим график функции игрек равно одна третья икс квадрат плюс два икс плюс три.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
График функции x 2 3. Как построить график функции. Построение графика сложной функции
Камни
20. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.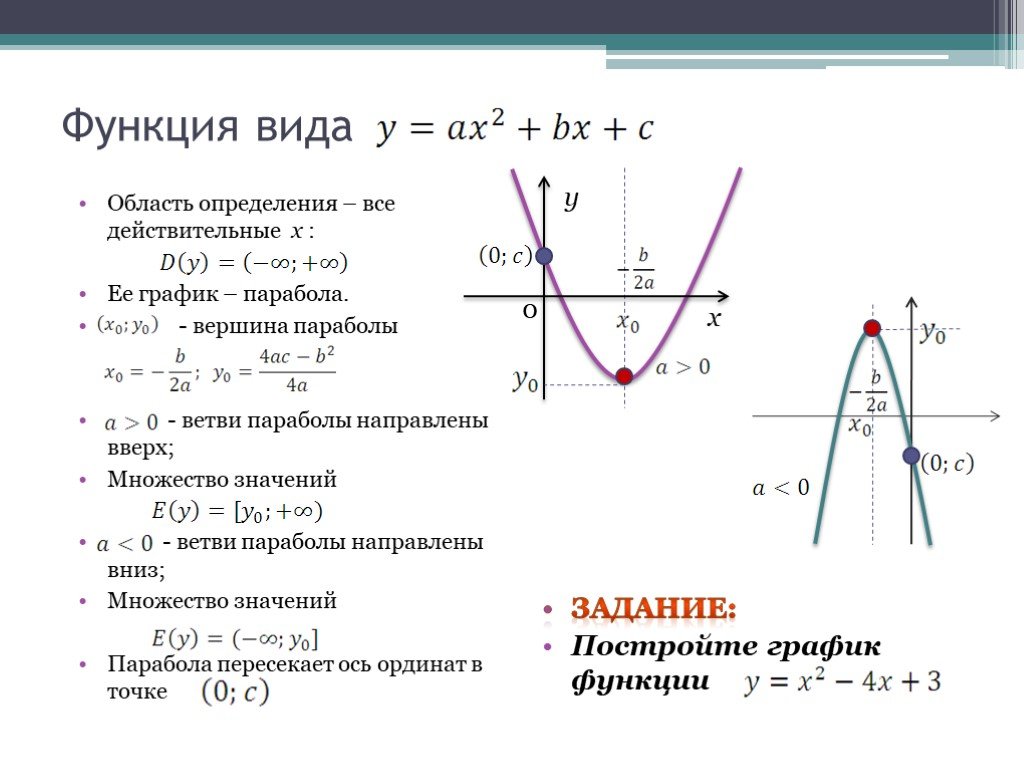
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Денежная удача
Исполнение желаний
Обереги
Обереги
2023-02-20 01:34:54
Красота
2023-02-20 01:34:54
Красота
2023-02-09 03:20:12
Денежная удача
2023-02-09 03:20:12
Построение квадратичных диаграмм — GCSE Maths
ВведениеКак построить квадратичный график
Рабочий лист построения квадратичных графиков
Распространенные заблуждения
Практика построения квадратичных графиков вопросы
Построение квадратичных графиков Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Как построить квадратичный график
Рабочий лист построения квадратичных графиков
Распространенные заблуждения
Практика построения квадратичных графиков вопросы
Построение квадратичных графиков Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о построении квадратичных графиков , в том числе о том, как подставлять значения для создания таблицы, а затем рисовать график квадратичной функции из этой таблицы.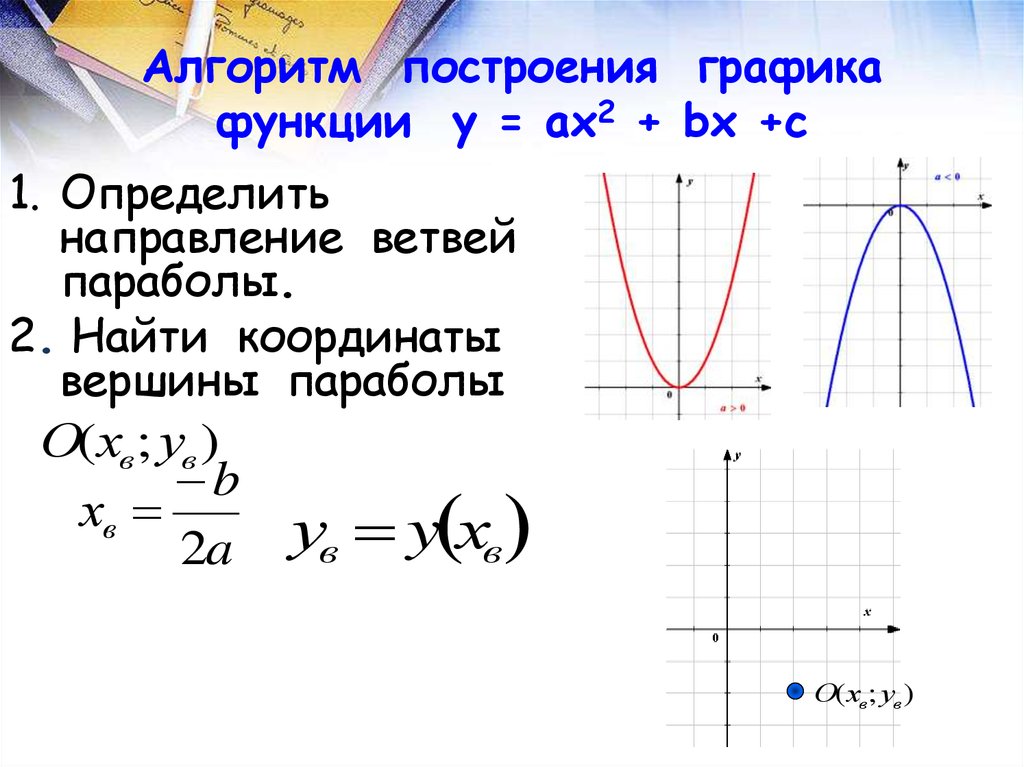
Существуют также рабочие листы с квадратичными графиками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое построение квадратичных графиков? 9{2}+2 x+5 , таблица значений от x=-3 до x=2 будет выглядеть так:
\begin{align} &x \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2 \\ &y \quad \quad \quad 8 \quad \quad\quad 5 \quad \quad \quad 4 \quad \quad \quad 5 \quad \quad \quad 8 \quad \quad \quad 13 \end{align}
и график будет выглядеть так:
Фигура, образованная графиком квадратичной функции, называется парабола и симметрична.
Что такое построение квадратичных графиков?
Как построить квадратичный график
Чтобы построить график квадратичной функции:
- Нарисуйте таблицу значений и подставьте значения x, чтобы найти соответствующие значения y.

- Нанесите эти пары координат на график.
- Соедините точки плавной кривой.
Объясните, как построить квадратичный график
Рабочий лист для построения квадратичных графиков
Получите бесплатный рабочий лист для построения квадратичных графиков, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист для построения квадратичных графиков
Получите бесплатный рабочий лист для построения квадратичных графиков, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Связанные уроки по квадратичным графикам
Построение квадратичных графиков является частью нашей серии уроков, посвященных пересмотру типов графиков . Возможно, вам будет полезно начать с основного урока по квадратичным графикам , чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства, приведенные ниже, для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
Возможно, вам будет полезно начать с основного урока по квадратичным графикам , чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства, приведенные ниже, для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
- Типы графиков
- Квадратичные графы
- Рисование квадратичных графиков 9{2}
- Нарисуйте таблицу значений и подставьте значения x , чтобы найти соответствующие значения y .
Обычно вам будет дан диапазон значений для x . Иногда это может быть записано как «от -3 до 3», или вы можете увидеть его символически написанным как -3 ≤ x ≤ 3.
\begin{align} &x \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \ четверка 3 \\ &y \четверка \четверка \четверка 9{2}-4
Нарисуйте таблицу значений и подставьте x значений, чтобы найти соответствующие y значения .

\begin{align} &x \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad \; 0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \quad 3 \\ &y \quad \quad \quad 5 \quad \quad\quad 0 \quad \quad -3 \quad \quad \ ; -4 \quad \quad -3 \quad \quad \quad 0 \quad \quad \quad 5 \end{align} 9{2}+3x
Нарисуйте таблицу значений и подставьте x значений, чтобы найти соответствующие y значения .
\begin{align} &x \quad \quad -5 \quad \quad -4 \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \\ &у \четырехъядерный \четырехъядерный \;\; 10 \quad \quad\quad 4 \quad \quad \quad 0 \quad \quad -2 \quad \quad -2 \quad \quad \quad 0 \quad \quad \quad 4 \end{align} 92 \quad \quad 25 \quad \quad \;\;\;16 \quad \quad \;\;\; 9 \quad \quad \quad 4 \quad \quad \quad1 \quad \quad \quad 0 \quad \quad \quad 1 \\ + 3&x \quad \;\; -15 \квадрат\;\; -12 \квадратный\;\;\; -9 \quad \quad -6 \quad \quad -3 \quad \quad +0 \quad \quad+3 \\ &y \quad \quad \;\; 10 \quad \quad\quad 4 \quad \quad \quad 0 \quad \quad -2 \quad \quad -2 \quad \quad \quad 0 \quad \quad \quad 4 \end{align}
Plot эти пары координат на графике .
9{2}+3x+2
Нарисуйте таблицу значений и подставьте x значений, чтобы найти соответствующие y значения .
\begin{align} &x \quad \quad -5 \quad \quad -4 \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2\\ &y \quad \quad \;\;12 \quad \quad\quad 6 \quad \quad \quad 2 \quad \quad \quad 0 \quad \quad \quad 0 \quad \ quad \quad 2 \quad \quad \quad 6 \quad \quad \;\; 12 \конец{выровнено} 9{2}+3(-3)+2=9-9+2=2 \end{align}
И так далее…
Возможно, вам будет полезно добавить в таблицу дополнительные строки для обработки этих замен. Разбейте функцию на составные части, как показано в заштрихованных строках таблицы. Чтобы получить значение y, просто просуммируйте заштрихованные части.
\begin{align} &x \quad \quad -5 \quad \quad -4 \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \ quad \quad 1 \quad \quad \quad 2 \\ &x^2 \quad \quad 25 \quad \quad \;\;16 \quad \quad \quad 9\quad \quad \quad 4 \quad \quad \quad1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 4\\ + 3&x \quad \;\; -15 \квадрат\;\; -12 \квадратный\;\;\; -9 \quad \quad -6 \quad \quad -3 \quad \quad +0 \quad \quad+3 \quad \quad+6 \\ + &2 \quad \quad +2 \quad \quad +2 \quad \quad +2\quad \quad +2\quad \quad +2\quad \quad +2\quad \quad +2\quad \quad +2 \\ &y \quad \quad \;\;12 \quad \quad \quad 6 \quad \quad \quad 2 \quad \quad \quad 0 \quad \quad \quad 0 \quad \quad \quad 2 \quad \quad \quad 6 \quad \quad \;\;12 \end{ выровнено} 9{2}-2x+4Нарисуйте таблицу значений и подставьте x значений, чтобы найти соответствующие y значения .

\begin{align} &x \quad \quad -2 \quad \quad -1 \quad \quad \quad0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \quad 3 \quad \quad \ quad 4 \\ &y \quad \quad \;\; 12 \quad \quad \quad 7 \quad \quad \quad 4 \quad \quad \quad 3 \quad \quad \quad 4 \quad \quad \quad 7 \quad \quad \quad 12 \end{align} 92 \четверка \четверка \;\; 4 \quad \quad \quad 1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad4 \quad \quad \quad 9 \quad \quad \;\; 16 \\ -2&x \quad \;\; +14 \квадратный \;\;\; +2 \четверка \четверка\: -0 \четверка \четверка -2 \четверка \четверка -4 \четверка \четверка -6 \четверка \четверка -8 \\ + &4 \четверка \четверка +4 \четверка \четверка +4 \quad \quad +4\quad \quad +4\quad \quad +4\quad \quad+4\quad \quad +4 \\ &y \;\; \quad \quad 12 \quad \quad \quad 7 \quad \quad \quad 4 \quad \quad \quad 3 \quad \quad \quad 4 \quad \quad \quad 7 \quad \quad \quad 12 \end{ выровнено} 9{2}+3x-5
Нарисуйте таблицу значений и подставьте x значений, чтобы найти соответствующие y значения .

\begin{align} &x \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad \; 0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \quad 3 \\ &y \quad \quad \quad 4 \quad \quad -3 \quad \quad -6 \quad \quad \; -5 \quad \quad \quad0 \quad \quad \quad 9 \quad \quad \;\; 22 \конец{выровнено} 92 \quad \quad 18 \quad \quad \quad 8 \quad \quad \quad 2 \quad \quad \, \quad 0 \quad \quad \quad 2 \quad \quad \quad 8 \quad \quad \;\ ; 18 \+3&x \четверка \четверка-9 \четверка \четверка -6 \четверка \четверка -3 \четверка \четверка +0 \четверка \четверка +3 \четверка \четверка +6 \четверка \четверка+9 \\ — &5 \четверка \четверка -5 \четверка \четверка -5 \четверка \четверка-5\четверка \четверка -5\четверка \четверка -5\четверка \четверка-5 \четверка \четверка -5 \\ &y \четверка \четверка \quad 4 \quad \quad -3 \quad \quad -6 \quad \quad -5 \quad \quad \quad0 \quad \quad \quad 9 \quad \quad \;\; 22 \конец{выровнено} 9{2}-4x+3
Нарисуйте таблицу значений и подставьте x значений, чтобы найти соответствующие y значения .

\begin{align} &x \quad \quad -4 \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2\\ &y \quad \;\; -13 \quad \quad -3 \quad \quad \quad 3 \quad \quad \quad 5 \quad \quad \quad3 \quad \;\;\, -3 \quad \;\; -13 \конец{выровнено} 92 \квадратный \;\; -32 \квадратный\;\; -18 \квадратный\;\; -8 \quad \;\;\;-2 \quad \quad \quad \,0 \quad \quad -2 \quad \;\;\;-8 \\ -4&x \quad \quad +16 \quad \ ;\; +12 \квадрат\;\; +8 \quad \;\;\, +4 \quad \quad \; -0 \quad \quad -4 \quad \quad -8 \\ + &3 \quad \quad \, +3 \quad \quad +3 \quad \quad +3\quad \;\;\; +3 \четверка \четверка \; +3 \quad \quad+3 \quad \quad +3 \\ &y \quad \quad-13 \quad \;\; -3 \quad \quad \quad \, 3 \quad \quad \;\;\; 5 \quad \quad \quad\: 3 \quad \quad -3 \quad \quad -13 \end{align}
Нанесите эти пары координат на график .
Соедините точки плавной кривой .
Распространенные заблуждения
- Рисование заостренной вершины
Убедитесь, что вершина графика представляет собой гладкую кривую, а не заостренную:
- Ошибки при работе с отрицательными x значениями, особенно при возведении в квадрат 9{2}+4x-2 для значений x от -6 до 1 .
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18865
- OpenStax
- OpenStax 9{2}=1\)
-
Рисунок 9. 7.67
7.67 - Правила сдвига функций, применяемые к квадратичным функциям
- Изменение квадратичной формы из стандартной формы в вершинную
- Использование преобразований для графических квадратичных функций
- Нахождение квадратного уравнения в форме вершины из графика 9{2}+k\) форма.
- Определите, направлена ли парабола вверх, \(a>0\), или вниз, \(a<0\).


(4 балла)
Показать ответ
(a)
\begin{выровнено} &x \quad \quad -6 \quad \quad -5 \quad \quad -4 \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1\\\\ &у \четырехъядерный \четырехъядерный\;\; 10 \quad \quad \quad 3 \quad \quad -2 \quad \quad -5 \quad \quad -6 \quad \quad -5 \quad \quad -2 \quad \quad 3 \end{выровнено} 9{2} для значений x от -2 до 5 .
(4 балла)
Показать ответ
(a)
\begin{выровнено} &x \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \quad 3 \quad \quad \quad 4 \quad \четырехъядерные \четырехъядерные 5\\\\ &y \quad \quad -8 \quad \quad -2 \quad \quad \quad 2 \quad \quad \quad 4 \quad \quad \quad 4 \quad \quad \quad 2 \quad \quad -2 \quad \ четверка -8 \end{выровнено} 9{2}+x-5 для значений x от -3 до 2 .

(4 балла)
Показать ответ
(a)
\begin{выровнено} &x \quad \quad -3 \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2 \\\\ &у \четырехъядерный \четырехъядерный \;\; 10 \quad \quad \quad 1 \quad \quad -4 \quad \quad -5 \quad \quad -2 \quad \quad \quad 5 \end{выровнено}
(2)
(b)
(2)
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта.
 Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять
Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять9.8: Графики квадратичных функций с использованием преобразований
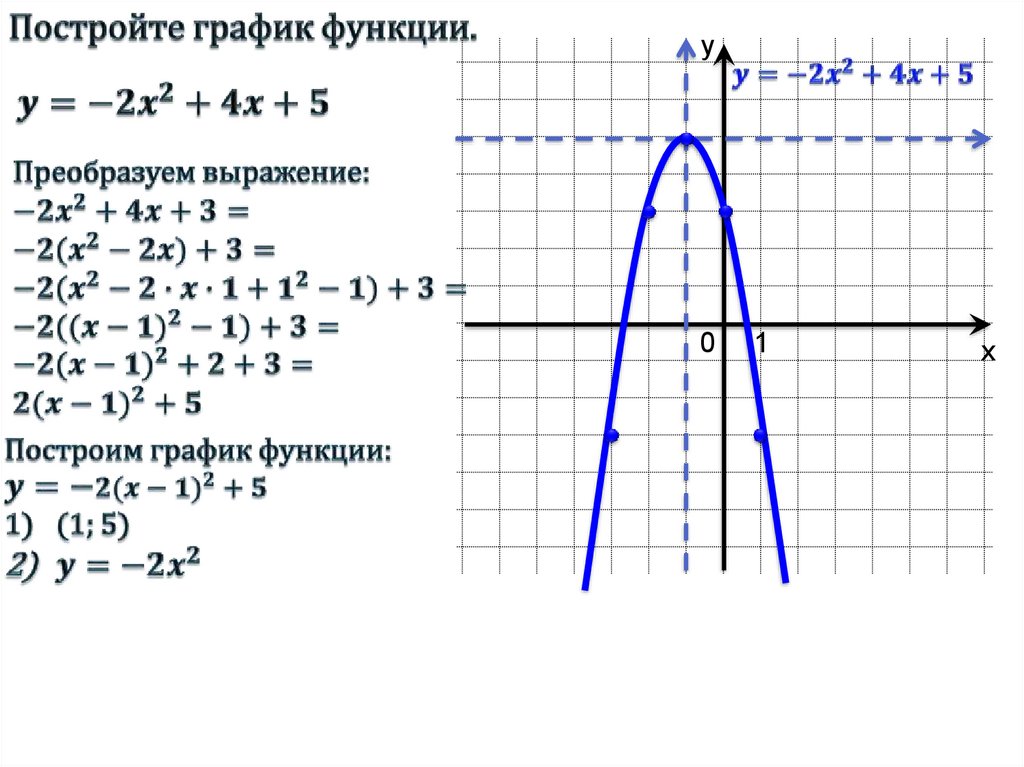
Константа \(1\) дополняет квадрат в скобках, но скобки умножаются на \(-3\). Таким образом, мы действительно добавляем \(-3\). Затем мы должны добавить \(3\), чтобы не изменить значение функции. Перепишите трехчлен в виде квадрата и вычтите константы.  { 2}+к\) форма 9{2}+3\)
{ 2}+к\) форма 9{2}+3\)Определите константы \(a, h, k\). \(а=2 ч=-1 к=3\) Так как \(a=2\), парабола открывается вверх. Ось симметрии \(x=h\). Ось симметрии равна \(x=-1\). Вершина \((h,k)\). Вершина равна \((-1,3)\). 9{2}+4 \cdot 0+5\) \(f(0)=5\) \(y\)-перехват \((0,5)\) Найдите точку, симметричную относительно \((0,5)\) относительно оси симметрии. \((-2,5)\) Найдите \(x\)-перехваты. Дискриминант отрицателен, поэтому \(x\)-перехватов нет. Нарисуйте параболу. 9{2}+1\)Найти квадратичную функцию по ее графику
До сих пор мы начинали с функции, а затем нашли ее график.
Теперь обратимся к процессу. Начав с графика, найдем функцию.
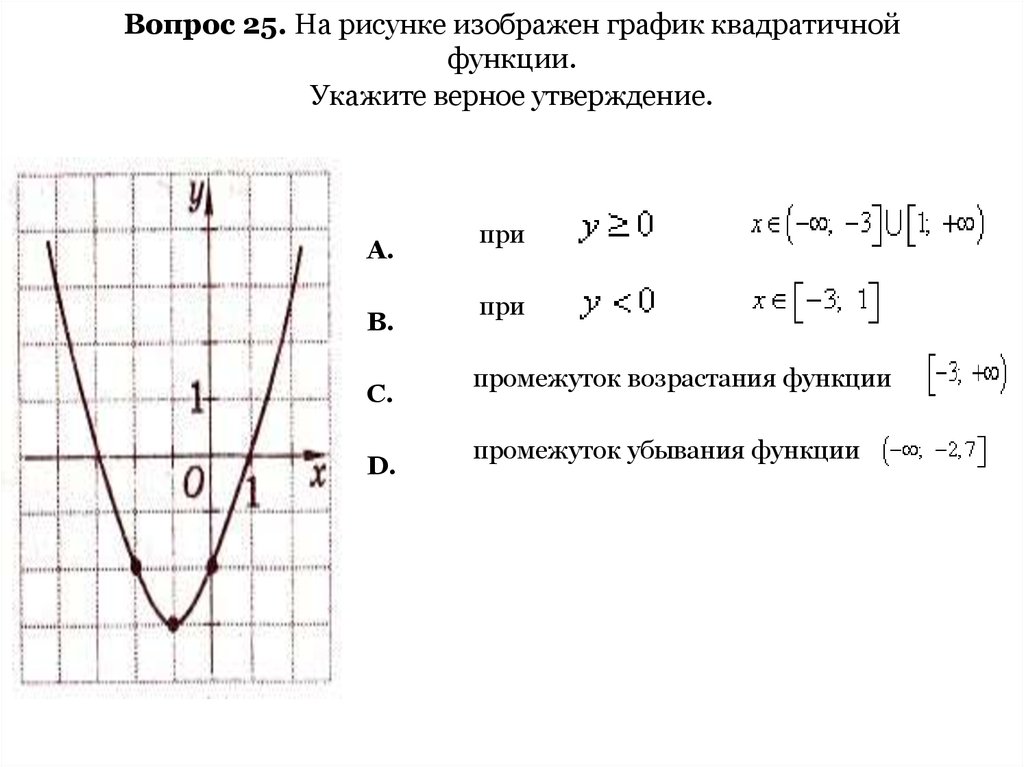
Пример \(\PageIndex{11}\)
Определите квадратичную функцию, график которой показан.
Рисунок 9.7.68Решение 9{2}-1\)
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики построения графиков квадратичных функций с использованием преобразований.





 Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять
Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять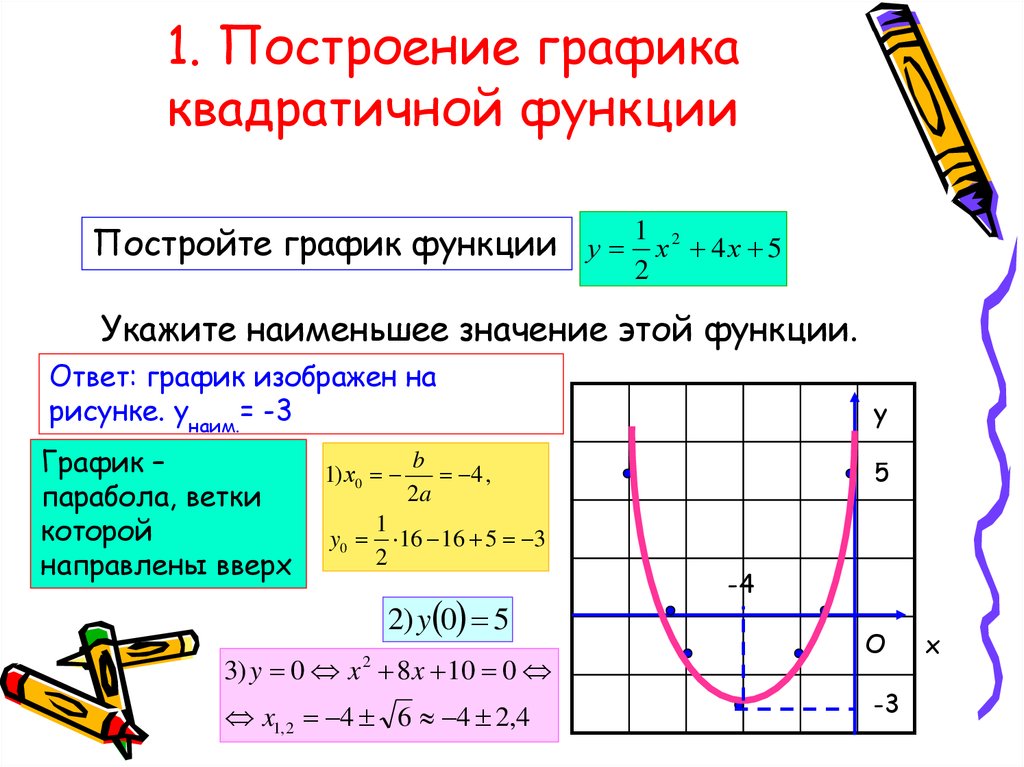 { 2}+к\) форма 9{2}+3\)
{ 2}+к\) форма 9{2}+3\) 7.67
7.67 