Решите систему уравнений x y 2y x y 2x: Решить систему уравнения: (x-y)²-x+y=0 x²y²-xy-2=0

Содержание

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения

Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например,

уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию. 2-… — Учеба и наука

Лучший ответ по мнению автора

22.

11.15

Лучший ответ по мнению автора

Михаил Александров

Читать ответы

Евгений

Читать ответы

Андрей Андреевич

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

В «Детском мире» продавали двухколесные и трехколесные велосипеды. Коля пересчитал все рули и колеса.Получилось 11 рулей и 29 колес.Сколько трехколесных велосипедов продавали в «Детском мире»?

Коля, Дима и Саша собрали…

в магазине продавали велосипеды 2х и 3х колесные известно что рулей-12,колес-27 вопрос сколько трехколесных велосипедов? ответ-3 велосипеда подскажите как правильно оформить решение

Оксана На олимпийских играх встретились четыре спортсмена: конькобежец, биатлонист, хоккеист и фигурист. Каждый владеет двумя языками из четырёх :…

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Пользуйтесь нашим приложением

Контрольная работа по алгебре 7 класс по теме: «Системы уравнений»

Контрольная работа по теме: «Системы уравнений»

Вариант 1

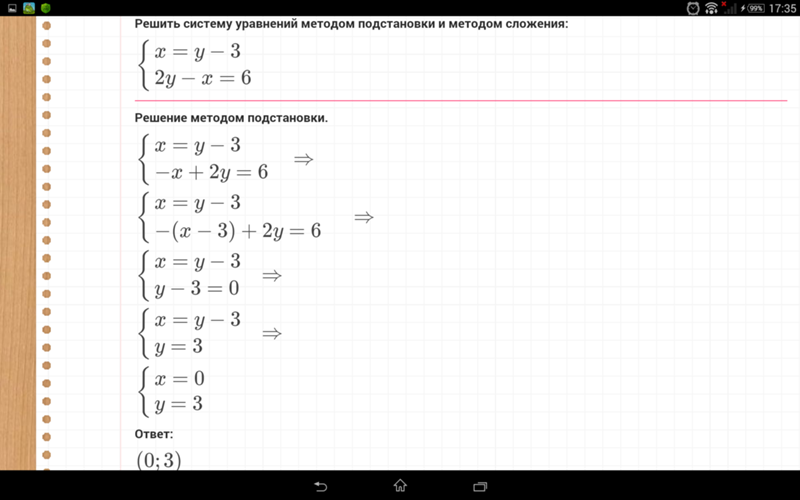
1. Решите методом подстановки систему уравнений:

х-3у = 8,

2х — у = 6.

2. Решите методом сложения систему уравнений:

4x — 5y = -83,

2х + 5у = 29.

3. Решите графически систему уравнений:

х — у = 5,

х + 2у = -1.

4. Из двух сёл, расстояние между которыми равно 20 км, одновременно вышли навстречу друг другу два пешехода и встретились через 2 ч после начала движения. Найдите скорость каждого пешехода, если известно, что первый пешеход проходит за 4 ч на 12 км больше, чем второй за 3 ч.

5. Решите систему уравнений:

7х + 5у = 19, 3х — 2у = 6,

4х- 3у= 5; 12х-8у = 20.

Контрольная работа по теме: «Системы уравнений»

Вариант 2

1. Решите методом подстановки систему уравнений:

х+4у = -6,

3х — у = 8.

2. Решите методом сложения систему уравнений:

7x + 3y = 43,

4х -3у = 67.

3. Решите графически систему уравнений:

х + у = 3,

2х — у = 3.

4. Из двух городов, расстояние между которыми равно 52 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Найдите скорость каждого велосипедиста, если известно, что первый велосипедист проезжает за 3 ч на 18 км больше, чем второй за 2 ч.

5. Решите систему уравнений:

3х — 2у = 5, 5х — 4у = 8,

11х+ 3у= 39; 15х-12у = 18.

Контрольная работа по теме: «Системы уравнений»

Вариант 3

1. Решите методом подстановки систему уравнений:

5у-х = 8,

5х — 4у = 23.

2. Решите методом сложения систему уравнений:

2x +у = -11,

3х -у = 9.

3. Решите графически систему уравнений:

3х-2у=12,

х + 2у = -1.

4. За 5 ручек и 4 карандаша заплатили 96 р. Сколько стоит ручка и сколько карандаш, если 3 ручки дороже, чем 2 карандаша, на 18р.?

5.Решите систему уравнений:

3х — у = 3, 2х — 3у = 1,

3х- 2у= 0; 3х+ у = 7.

Контрольная работа по теме: «Системы уравнений»

Вариант 4

1. Решите методом подстановки систему уравнений:

2х+у = 10,

4х — 7у = 2.

2. Решите методом сложения систему уравнений:

x — 3y = 4,

-х + у =-8.

3. Решите графически систему уравнений:

х — 3у = 8,

2х -3у = 10.

4. Моторная лодка за 2 ч движения по течению реки и 5 ч против течения проходит 120 км. Найдите скорость по течению и её скорость против течения, если за 7 ч движения против течения она проходит на 52 км больше, чем за 3 ч движения по течению.

5. Решите систему уравнений:

2х + у = 1, х + у = 6,

5х+2у= 0; 5х-2у = 9.

Контрольная работа по теме: «Системы уравнений»

Вариант 5

1. Решите методом подстановки систему уравнений:

5х-3у = 14,

2х + у = 10.

2. Решите методом сложения систему уравнений:

4x +11y = 15,

10х -11у = 9.

3. Решите графически систему уравнений:

2х + у = 1,

2х +у =3.

4. Петя с Димой собирают марки. Если Петя отдаст Диме 10 своих марок, то у мальчиков станет поровну. Если же Петя отдаст Диме 50 марок, то у него останется в 5 раз меньше марок, чем станет у Димы. Сколько марок в коллекции у каждого мальчика?

5. Решите систему уравнений:

х +5у = 7, х + у = 7,

3х+2у= -5; 5х-7у = 11.

Контрольная работа по теме: «Системы уравнений»

Вариант 6

1. Решите методом подстановки систему уравнений:

х + 5у= 35,

3х +2у = 27.

2. Решите методом сложения систему уравнений:

9y+13х = 35,

29у-13х = 3.

3. Решите графически систему уравнений:

х — 3у = 2,

2х -6у = 4.

4. За 7 тетрадей и 4 ручки заплатили 130 р. После того как тетради подешевели на 40 %, а ручки — 20 %, одна ручка стала дороже одной тетради на 6 р. Сколько стоила ручка и тетрадь первоначально?

5. Решите систему уравнений:

4х -3 у =- 1, х + 2у = -2,

Х-5у= 4; 3х-у = 8.

Контрольная работа по теме: «Системы уравнений»

Вариант 7

1. Решите методом подстановки систему уравнений:

2х — у= 2,

3х — 2у = 3.

2. Решите методом сложения систему уравнений:

х -6у= 17,

5х +6у=1 3.

3. Решите графически систему уравнений:

х + у = -5,

3х -у = -7.

4. За 7 кг апельсинов и 4 кг лимонов заплатили 700 р. Сколько стоит 1 кг апельсинов и сколько 1 кг лимонов, если 5 кг апельсинов дороже, чем 2 кг лимонов, на 160 р.?

5. Решите систему уравнений:

2х -5 у = -7, х — у = 3,

Х -3у= -5; 3х+ 4у = 2.

Контрольная работа по теме: «Системы уравнений»

Вариант 8

1. Решите методом подстановки систему уравнений:

5у -х= 6,

3х — 4у = 4.

2. Решите методом сложения систему уравнений:

9х -7у= 19,

-9х -4у=25.

3. Решите графически систему уравнений:

х — 2у = 7,

3х +2у = 5.

4. Лодка за 3 ч движения по течению реки и 4 ч против течения проходит 114 км. Найдите скорость лодки по течению и её скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.

5. Решите систему уравнений:

3х -5 у = 16, 2х +3 у = -7,

2х+у= 2; х-у = 4.

Контрольная работа по теме: «Системы уравнений»

Вариант 9

1. Решите методом подстановки систему уравнений:

7х — 2у= 15,

2х +у = 9.

2. Решите методом сложения систему уравнений:

х +у= 7,

х -3у=-5.

3. Решите графически систему уравнений:

х — 2у = 1,

у-х = 1.

4. В двух ящиках лежат яблоки. Если из первого ящика переложить во второй 45 яблок, то в ящиках их станет поровну. Если же из второго ящика переложить в первый 20 яблок, то в первом станет в 3 раза больше яблок, чем во втором. Сколько яблок лежит в каждом ящике?

5. Решите систему уравнений:

2х + 5у = -7, х -3 у = 8,

3х- у= 15; 2х-у = 6.

Контрольная работа по теме: «Системы уравнений»

Вариант 10

1. Решите методом подстановки систему уравнений:

х + 3у= 2,

2х +3у = 7.

2. Решите методом сложения систему уравнений:

4х -у= 3,

х — у=6.

3. Решите графически систему уравнений:

х — 2у = 7,

3х +2у = 5.

4. Известно, что 2 стола и 6 стульев стоили 7 600 р. После того как столы подешевели на 10 %, а стулья — на 20 % , стол и два стула стали стоить 2 760 р. Какова была начальная цена одного стола и одного стула?

5. Решите систему уравнений:

2х -3 у = 5, х -4 у = -1,

Х-6у= -2; 3х-у = 8.

Контрольная работа по теме: «Системы уравнений»

Вариант 11

1. Решите методом подстановки систему уравнений:

3х + 4у= 55,

7х -у = 56.

2. Решите методом сложения систему уравнений:

4х -7у= 17,

4х -5у=90.

3. Решите графически систему уравнений:

х +у = -2,

2х -у = -4.

4. Один металлический слиток содержит 30 % меди, второй — 70 % меди. Сколько килограммов каждого слитка надо взять, чтобы получить 120 кг сплава, содержащего 40 % меди?

5. Решите систему уравнений:

5х -4 у = 12, 6х + у = 5,

Х-5у= -6; 2х-3у = -5.

Контрольная работа по теме: «Системы уравнений»

Вариант 12

1. Решите методом подстановки систему уравнений:

4у -х= 11,

6у-2х = 13.

2. Решите методом сложения систему уравнений:

3х -6у= 12,

3х +5у=100.

3. Решите графически систему уравнений:

х — у = 1,

х +2у = 7.

4. Сумма цифр двузначного числа равна 8. Если поменять местами его цифры, то получим число, которое больше данного на 18. Найдите данное число.

5. Решите систему уравнений:

2х -3у = 11, х -6 у = -2,

5х+у= 2; 2х+3у = 11.

Контрольная работа по теме: «Системы уравнений»

Вариант 13

1. Решите методом подстановки систему уравнений:

15 -х = 2у,

4х — 3у = 27.

2. Решите методом сложения систему уравнений:

-5х +7у= 6,

2х +7у=76.

3. Решите графически систему уравнений:

х +у = 0,

3х -у = 4.

4. Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения — за 5 ч. Найдите собственную скорость лодки и скорость течения реки.

5. Решите систему уравнений:

3х -2у = 16, 2х + 3у = 3,

4х+у= 3; 5х+6у = 9.

Контрольная работа по теме: «Системы уравнений»

Вариант 14

1. Решите методом подстановки систему уравнений:

5х -у= 6,2,

0,8х +3у = 13.

2. Решите методом сложения систему уравнений:

-3х +5у= -11,

8х +5у=11.

3. Решите графически систему уравнений:

х + у = -5,

4х -у = -5.

4. Два пешехода отправились одновременно навстречу друг другу из пунктов М и N, расстояние между которыми 38 км. Через 4 ч расстояние между ними сократилось до 2 км, а еще через 3 ч первому пешеходу осталось пройти до пункта N на 7 км меньше, чем второму до М. Найдите скорости пешеходов.

5. Решите систему уравнений:

4х -2 у = -6, 3х + 2у = 8,

6х+у= 11; 2х+6у = 10.

Контрольная работа по теме: «Системы уравнений»

Вариант 15

1. Решите методом подстановки систему уравнений:

4х + у= 12,

7х +2у = 20.

2. Решите методом сложения систему уравнений:

-6х +у= 16,

6х +4у=34.

3. Решите графически систему уравнений:

2х+ 3у = 6,

2х -у = 9.

4. Из пунктов А и В, расстояние между которыми 30 км, навстречу друг другу одновременно вышли два пешехода и встретились через 3 ч 20 мин. Если бы первый вышел на 2 ч раньше второго, то встреча произошла бы через 2,5 ч после выхода второго. Найдите скорости пешеходов.

5. Решите систему уравнений:

5х + у = 14, 3х -2 у = 5,

3х-2у= -2; 2х+5у = 16.

Контрольная работа по теме: «Системы уравнений»

Вариант 16

1. Решите методом подстановки систему уравнений:

х — 2у= 5,

3х +8у = 1.

2. Решите методом сложения систему уравнений:

3х +у= 14,

5х — у=10.

3. Решите графически систему уравнений:

2х+ у = 8,

2х -у = 0.

4. Катер за 4 ч по течению реки проплывает на 10 км меньше, чем за 6 ч против течения. Найдите собственную скорость катера, если плот по этой реке за 15 ч проплывает такое же расстояние, что и катер за 2 ч по озеру.

5. Решите систему уравнений:

х + 4у = 7, 2х — 3у = 5,

х -2у= -5; 3х+ 2у = 14.

Контрольная работа по теме: «Системы уравнений»

Вариант 17

1. Решите методом подстановки систему уравнений:

4у -х= 11,

5х — 2у = 17.

2. Решите методом сложения систему уравнений:

2х -9у= 11,

7х +9у=25.

3. Решите графически систему уравнений:

7х — 3у = -26,

У-2х = 8.

4. Теплоход 120 км проходит за 5 ч против течения реки и 180 км за 6 ч по течению. Найдите скорость течения реки и собственную скорость теплохода.

5. Решите систему уравнений:

х -2у = 7, 4х -6 у =2 6,

х+2у= -1; 5х+3у = 1.

Контрольная работа по теме: «Системы уравнений»

Вариант 18

1. Решите методом подстановки систему уравнений:

6х — у= -1,

2х -3у = -11.

2. Решите методом сложения систему уравнений:

8х +у= 8,

12х +у=4.

3. Решите графически систему уравнений:

х +2у = 0,

5х + у = -18.

4. По течению реки лодка за 3 ч 20 мин проходит расстояние 30 км, а против течения за 4 ч — расстояние 28 км. Какое расстояние по озеру пройдет лодка за 1,5 ч?

5. Решите систему уравнений:

х + 3у = 7, 8х + 3у = -21,

х+2у= 5; 4х+5у = -7.

Контрольная работа по теме: «Системы уравнений»

Вариант 19

1. Решите методом подстановки систему уравнений:

х + у= 7,

9у-2х = -25.

2. Решите методом сложения систему уравнений:

7х -5у= 29,

7х +8у=-10.

3. Решите графически систему уравнений:

2х — 5у = 10,

4х -у = 2.

4. Найдите два числа, если известно, что утроенная разность этих чисел на 6 больше их суммы, а удвоенная разность этих чисел на 9 больше их суммы.

5. Решите систему уравнений:

х -2 у = 8, 8х + 2у = 11,

х -3у= 6; 6х-4у = 11.

Контрольная работа по теме: «Системы уравнений»

Вариант 20

1. Решите методом подстановки систему уравнений:

2х -у= 8,

3х +2у = 5.

2. Решите методом сложения систему уравнений:

4х -у= 20,

4х +у=12.

3. Решите графически систему уравнений:

х — 2у = 1,

у -х = 2.

4. Два тракториста вспахали вместе 678 га. Первый тракторист работал 8 дней, а второй — 11 дней. Сколько гектаров вспахивал за день каждый тракторист, если первый тракторист за каждые 3 дня вспахивал на 22 га меньше, чем второй за 4 дня?

5. Решите систему уравнений:

2х — у = 13, 7х + 3у = 1,

2х+3у= 9; 2х-6у = -10.

Контрольная работа по теме: «Системы уравнений»

Вариант 21

1. Решите методом подстановки систему уравнений:

х-3у = 8,

2х — у = 6.

2. Решите методом сложения систему уравнений:

9х +17у= 52,

26х -17у=18.

3. Решите графически систему уравнений:

х +у = 0,

4х +у = 6.

4. Две бригады работали на уборке картофеля. В первый день одна бригада работала 2 ч, а вторая — 3 ч, причем ими было собрано 23 ц картофеля. Во второй день первая бригада за 3 ч работы собрала на 2 ц больше, чем вторая за 2 ч. Сколько центнеров картофеля собирала каждая бригада за 1 ч работы?

5. Решите систему уравнений:

2х + 3у = 10, 3х -2 у = 5,

Х-2у= -9; 5х+4у = 1.

Контрольная работа по теме: «Системы уравнений»

Вариант 22

1. Решите методом подстановки систему уравнений:

х+4у = -6,

3х — у = 8.

2. Решите методом сложения систему уравнений:

-5х +7у= 2,

8х +7у=15.

3. Решите графически систему уравнений:

у-х = 2,

2у -2х = 5.

4. Зерно перевозилось на двух автомашинах различной грузоподъемности. В первый день было вывезено 27 т зерна, причем одна машина сделала 4 рейса, а другая — 3 рейса. На следующий день вторая машина за 4 рейса перевезла на 11 т зерна больше, чем первая машина за 3 рейса. Сколько тонн зерна перевозили на каждой машине за один рейс?

5. Решите систему уравнений:

2х + у = -5, 2х + 3у = 1,

Х-3у= -6; 6х-2у = 14.

Контрольная работа по теме: «Системы уравнений»

Вариант 23

1. Решите методом подстановки систему уравнений:

5у-х = 8,

5х — 4у = 23.

2. Решите методом сложения систему уравнений:

9х -6у= 24,

9х +8у=10.

3. Решите графически систему уравнений:

х +у = 0,

2х +у = -3.

4. Для перевозки руды из карьера были отправлены пятитонные и трехтонные самосвалы. За 1 рейс пятитонные самосвалы перевозят руды на 18 т больше, чем трехтонные. За рабочий день пятитонные самосвалы совершили 4 рейса, а трехтонные — 6 рейсов, и всего ими перевезено за день 192 т руды. Сколько самосвалов каждой грузоподъемности перевозили руду?

5. Решите систему уравнений:

5х + у = 7, 6х -5у = 23,

7х -4у= -1; 2х-7у = 13.

Контрольная работа по теме: «Системы уравнений»

Вариант 24

1. Решите методом подстановки систему уравнений:

2х+у = 10,

4х — 7у = 2.

2. Решите методом сложения систему уравнений:

х -3у= 5,

4х +9у=41.

3. 3. Решите графически систему уравнений:

х +у = -1,

3х +3у = -2.

4. На рынке было закуплено 84 кг черешни и вишни, причем черешни куплено на 3 ящика меньше, чем вишни. Сколько ящиков черешни и вишни закуплено по отдельности, если в 1 ящике черешни 8 кг, а вишни 10 кг?

5. Решите систему уравнений:

5х -2у = 16, 5х -4у = 10,

8х+3у= 38; 2х-3у = -3.

Контрольная работа по теме: «Системы уравнений»

Вариант 25

1. Решите методом подстановки систему уравнений:

5х-3у = 14,

2х + у = 10.

2. Решите методом сложения систему уравнений:

3х -2у= 1,

12х +7у=-26.

3. Решите графически систему уравнений:

х +у = -3,

х -у = -1

4. Двое рабочих изготовили 162 детали. Первый работал 8 дней, а второй — 15 дней. Сколько деталей изготовил каждый рабочий, если первый изготовил за 5 дней на 3 детали больше, чем второй за 7 дней?

5. Решите систему уравнений:

4х +6у = 9, 9х -13 у = 22,

3х -5у= 2; 2х +3у = -1.

Контрольная работа по теме: «Системы уравнений»

Вариант 26

1. Решите методом подстановки систему уравнений:

х + 5у= 35,

3х +2у = 27.

2. Решите методом сложения систему уравнений:

10х +2у= 12,

-5х +4у=-6.

3. Решите графически систему уравнений:

х — у = 5,

х + 2у = -1.

5. Решите систему уравнений:

4х -3у = 15, 2х -3у = 2,

3х -4у= 6; 5х+2у = 24.

Контрольная работа по теме: «Системы уравнений»

Вариант 27

1. Решите методом подстановки систему уравнений:

2х — у= 2,

3х — 2у = 3.

2. Решите методом сложения систему уравнений:

3х -2у= 1,

12х +7у=-26.

3. Решите графически систему уравнений:

х + у = 6,

2х -у = -2.

5. Решите систему уравнений:

5у-6х = 4, 4х +5 у = 1,

7х -4у= -1; 8х-2у = 38.

Контрольная работа по теме: «Системы уравнений»

Вариант 28

1. Решите методом подстановки систему уравнений:

5у -х= 6,

3х — 4у = 4.

2. Решите методом сложения систему уравнений:

40х +3у= -10,

20х -7у=-5.

3. Решите графически систему уравнений:

х + у = 3,

2х -у = 3.

5. Решите систему уравнений:

5х -4у = 3, 8х -2 у = 11,

2х -3у= 11; 9х +4у = 8.

Контрольная работа по теме: «Системы уравнений»

Вариант 29

1. Решите методом подстановки систему уравнений:

7х — 2у= 15,

2х +у = 9.

2. Решите методом сложения систему уравнений:

3х +8у= 13,

5х -16у=7.

3. Решите графически систему уравнений:

3х-2у=12,

х + 2у = -1.

5. Решите систему уравнений:

5х + 2у = 15, 7х + 4у = 5,

8х+3у= 20; 3х+2у = 3.

Контрольная работа по теме: «Системы уравнений»

Вариант 30

1. Решите методом подстановки систему уравнений:

х + 3у= 2,

2х +3у = 7.

2. Решите методом сложения систему уравнений:

5х +2у= 1,

15х +3у=3.

3. Решите графически систему уравнений:

х — 3у = 8,

2х -3у = 10.

4.Леша с Димой собирают марки. Если Леша отдаст Диме 10 своих марок, то у мальчиков станет поровну. Если же Леша отдаст Диме 50 марок, то у него останется в 5 раз меньше марок, чем станет у Димы. Сколько марок в коллекции у каждого мальчика?

5. Решите систему уравнений:

8х -5у = -11, 6х -5у = -38,

5х -4у= -6; 2х +7у = 22.

3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.

92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Однородные дифференциальные уравнения

Дифференциальное уравнение – это уравнение с функцией и одной или несколькими ее производными:

Пример: уравнение с функцией y и ее производная dy dx

Здесь мы рассмотрим специальный метод решения «Однородных дифференциальных уравнений»

Дифференциальное уравнение первого порядка равно Однородный если он может быть в такой форме:

dy dx = F( y x )

Мы можем решить это с помощью разделения переменных, но сначала создадим новую переменную v = y x

v = y x , что также равно y = vx

И dy dx = d (vx) dx = v dx dx + x dv dx (по Правилу продукта)

, который можно упростить до dy dx = v + x dv dx

Используя y = vx и dy dx = v + x dv dx , мы можем решить дифференциальное уравнение.

Пример покажет, как это все делается:

Пример: Решите

dy dx = x ² + y ² xy

Можем ли мы получить это в стиле F ( y x )?

Start with: x ² + y ² xy

Separate terms: x ² xy + y ² xy

Simplify: x y + y x

Обратная величина первого члена:( y x ) ^-1 + y x

Да, у нас есть функция y x .

So let’s go:

Start with: dy dx = ( y x ) ^-1 + y x

y = vx and dy dx = v + x dv dx :v + x dv dx = v ^-1 + v

Вычитание V с обеих сторон: x DV DX = V ^-1

Теперь используйте разделение переменных:

Отдельные переменные

. Поставьте перед ним знак интеграла: ∫v dv = ∫ 1 x dx

Интегрируем: v ² 2 = ln(x) + C

) : v ² 2 = ln(x) + ln(k)

Объединить ln: v ² 2 = ln(kx)

Упростить:v = ±√(2 ln(kx))

Теперь заменить обратно v = y x

Замена v = y x : y x = ±√(2 ln(kx))

))

И у нас есть решение.

Положительная часть выглядит так:

Другой пример:

Пример: Решите

dy dx = y(x−y) x ²

Можем ли мы получить это в стиле F( y x )?

Start with: y(x−y) x ²

Separate terms: xy x ² − y ² x ²

Simplify: г х − ( г х ) ²

Да! So let’s go:

Start with: dy dx = y x − ( y x ) ²

y = vx and dy dx = V + x DV DX V + X DV DX = V — V ²

SORTRART V от SHIDES: x ^{909. 909. 9099. 9099. ^{. ^{15 DA ^{9999999999999999999999999999999999999999. ^{999999999999999999999. ^{9999999999999999999999999999999.}}}}}}

5 ^{15 DV.16 = −v ²}

Теперь используйте разделение переменных:

Отдельные переменные: — 1 V ² DV = 1 x DV = 1 x DX = 1 x DX = 1 x DX = 1 . — 1 V ² DV = ∫ 1 x DX

Integrate: 1 V = LN (X) + C V = LN (X) + C V = LN (X) + C V = LN (x) + C V . : 1 v = ln(x) + ln(k)

Combine LN: 1 V = LN (KX)

Упрощение: V = 1 LN (KX)

Теперь. Заднее v =

. Y x : Y x = 1 LN (KX)

Упрощение: Y = x LN (KX)
0
0
0
0
09090

.
Вот некоторые примеры значений k:
И последний пример:
Пример: решить
dy dx = x−y x+y
Можем ли мы получить это в стиле F( y x )?
Начать с: x−y x+y
Разделить на x: x/x−y/x x/x+y/x
Упростить: 1−y/y/x 1+y/x
Да! Итак, приступим:
Начните с: dy dx = 1−y/x 1+y/x
y = vx and dy dx = v + x dv dx v + x dv dx = 1−v 1+v
Subtract v from both sides:x dv dx = 1−v 1+v − v
Then:x dv dx = 1−v 1+v − V+V ² 1+V
Упрощение: x DV DX = 1–2V -V ² 6 1-2V -V ² 6 1-2V -V ² 1 -2V -V -V ² 6 1 -й. Разделите переменные: 1+v 1−2v−v ² dv = 1 x dx
Поставьте перед ним знак интеграла: 2 dv = ∫ 1 x dx
Интегрируем: − 1 2 ln(1−2v−v ² ) = ln(x) + C
Тогда получаем C = ln(k) :− 1 2 ( −v ² ) = ln(x) + ln(k)
Объединить ln:(1−2v−v ² ) ^-½ = kx
Квадрат и обратный: 1−2v−v ² = 1 k ² x ²
Теперь подставьте обратно v = y x
Подставьте v3 =
15 x :1−2( y x )−( y x ) ² = 1 k ² x ²
Multiply through by x ² 😡 ² −2xy−y ² = 1 k ²
Мы почти у цели. .. хотя приятно отделить y!
Мы можем попытаться разложить на множители x ² −2xy−y ², но сначала мы должны сделать некоторую перестановку:
Change signs:y ² +2xy−x ² = − 1 k ²
Replace − 1 k ² by c:y ² +2xy− x ² = C
Добавить 2x ² к обеим сторонам: Y ² +2xy +x ² = 2x ² +C
Фактор: (Y +X) ² +2x ^{9906: (Y +X) ² = 2x}
6
6: (Y +X) 9099 2 = 2x
6
. 2 +c
Квадратный корень: y+x = ±√(2x ² +c)
Вычесть x с обеих сторон: y = ±√(2x ² +c) − x
И у нас есть решение.
Положительная часть выглядит так:

Решите для x и y: x + y/xy = 5, 3x + 2y/xy = 13 — Sarthaks eConnect
← Предыдущий вопрос Следующий вопрос →
Пожалуйста, войдите или зарегистрируйтесь, чтобы ответить на этот вопрос.
1 ответ
0 голосов
ответил 12 июня 2021 г. по Зафаа (30,4 тыс. баллов)
У нас есть
x + y = 5xy
и 3x + 2y = 13xy
, где x≠0 и y≠0
Давайте упростим эти уравнения.
x + y = 5xy
Разделив уравнение на xy,
Приняв p = 1/y и q = 1/x, получим
p + q = 5 …(i)
Также , 3x + 2y = 13xy
Разделив уравнение на xy,
Предполагая p = 1/y и q = 1/x, получаем
⇒ 3p + 2q = 13 …(ii)
Чтобы решить эти уравнения, нам нужно сделать так, чтобы одна из переменных (в обоих уравнениях) имела одинаковый коэффициент.
Умножим уравнение (i) на 2, чтобы переменная q в обоих уравнениях имела одинаковый коэффициент.
Recalling equations (i) & (ii),
p + q = 5 [×2]
3p + 2q = 13
⇒ — p = — 3
⇒ p = 3
Подставьте p = 3 в уравнение (i)/уравнение (ii) в соответствии с удобством решения.
Таким образом, подставляя в уравнение (i), мы получаем
3 + q = 5
⇒ q = 5 – 3
⇒ q = 2
Таким образом, p = 3 и q = 2
Поскольку q = 1/x,
⇒
= 1/x,
⇒ x = 1/2
И p = 1/y
⇒ 3 = 1/y
⇒ y = 1/3
Отсюда имеем x = 1/2 и y = 1/3
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
Решите каждую из следующих систем уравнений методом перекрестного умножения: (x+y)/xy = 2, (x — y)/xy = 6
спросил 27 апр. 2021 г. в линейных уравнениях по Гарги01 (50,8 тыс. баллов)
пара линейных уравнений с двумя переменными
класс-10
Решите следующую систему уравнений: 2/x + 3/y = 9/xy 4/x + 9/y = 21/xy
спросил 25 фев. 2020 г. в линейных уравнениях по ШасиРадж (62,8 тыс. баллов)
пара линейных уравнений с двумя переменными
класс-10
Решите следующие системы уравнений: (7x — 2y)/xy = 5 (8x + 7y)/xy = 15
спросил 26 апр. 2021 г. в линейных уравнениях по Хайфа (52,3 тыс. баллов)
пара линейных уравнений с двумя переменными
класс-10
Решите следующие системы уравнений: x + y = 2xy (x — y)/xy = 6, x ≠ 0, y ≠ 0
спросил 26 апр. 2021 г. в линейных уравнениях по Хайфа (52,3 тыс. баллов)
пара линейных уравнений с двумя переменными
класс-10
Решите следующие системы уравнений: (x+y)/xy = 2 (x — y)/xy = 6
спросил 26 апр. 2021 г. в статистике по Хайфа (52,3 тыс. баллов)
пара линейных уравнений с двумя переменными
класс-10
Категории
Все категории
JEE (28,1к)
NEET (8,5к)
Наука (739к)
Математика (240к)
Система счисления (9,7к)
Множества, отношения и функции (5,5к)
Алгебра (35,3к)
Алгебраические выражения (2,2к)
г.
Полиномы (2,4к)
Линейные уравнения (4.1к)
Квадратные уравнения (3,5к)
Арифметическая прогрессия (2,6к)
Геометрические прогрессии (485)
Биномиальная теорема (1,9к)
Перестановки (873)
Комбинации (411)
Комплексные числа (1,5к)
Матрицы (3,5к)
Детерминанты (1,9к)
Математическая индукция (543)
Линейные неравенства (356)
г.
Экспоненты (803)
Квадраты и квадратные корни (748)
Кубы и кубические корни (254)
Факторизация (871)
Расстояние, время и скорость (877)
Логарифм (1,1к)
Коммерческая математика (7,4к)
Координатная геометрия (10,0 к)
Геометрия (11,7к)
Тригонометрия (10,7к)
Измерение (6,8к)
Статистика (4,8к)
Вероятность (5,3к)
г.
Векторы (2,8к)
Исчисление (19,6к)
Линейное программирование (902)
Статистика (2,2к)
Наука об окружающей среде (3,6к)
Биотехнология (536)
коммерция (61,0к)
Электроника (3,7к)
Компьютер (14,9к)
Искусственный интеллект (ИИ) (1,4к)
Информационные технологии (13,2к)
Программирование (8. 6к)
Политическая наука (6,4к)
г.
Домашняя наука (3,5к)
Психология (3,3к)
Социология (5,5к)
Английский (55,7к)
хинди (18,1к)
Способность (23,7к)
Рассуждение (14,6к)
ГК (25,7к)
Олимпиада (527)
Советы по навыкам (72)
CBSE (710)
РБСЭ (49,1к)
Общий (56,7к)
МСБШСЭ (1,8к)
Совет Тамилнаду (59,3к)
Совет Кералы (24,5к)
г.
Как найти решение системы уравнений
Все математические ресурсы SAT
16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 Следующая →
SAT Math Help » Алгебра » Уравнения / Неравенства » Системы уравнений » Как найти решение системы уравнений
Пусть f(x) = 2x ² – 3x + 1, и пусть g(x) = 13 – x. Каково расстояние между точками пересечения f(x) и g(x)?
Возможные ответы:
5√2
√26
5
5√26
2чина
5√26
2чина
. Пояснение:
Сначала нам нужно найти точки пересечения между f(x) и g(x), приравняв их друг к другу и решив.
f(x) = g(x)
2x ² — 3x + 1 = 13 – x
Прибавьте x к обеим сторонам.
2x ² – 2x + 1 = 13
Вычтите 13 с обеих сторон.
2x ² – 2x – 12 = 0.
Разделите на два, чтобы упростить работу с коэффициентами.
x ² – x 6 = 0
Коэффициент.
(x – 3)(x + 2) = 0
Приравняйте каждый из множителей к нулю, а затем решите.
х – 3 = 0
x = 3
x + 2 = 0
x = –2
Две функции пересекаются, где x = –2 и где x = 3.
Задача состоит в том, чтобы найти расстояние между точками пересечения . Следовательно, нам потребуется найти y-координаты точек пересечения при x = –2 и при x = 3.
При x = –2 f(–2) = g(–2) = 13 – ( –2) = 15,
При x = 3 f(3) = g(3) = 13 – 3 = 10,
Таким образом, точками пересечения являются (–2, 15) и (3, 10) .
Теперь мы можем использовать приведенную ниже формулу расстояния.
Ответ: 5√2
Сообщить об ошибке
Какова сумма x и y при решении следующей системы уравнений:
x – 3y = –5
2x + 5y = 12
Возможные ответы:
Правильный ответ:
3
Пояснение:
Мы можем решить эту систему уравнений с помощью подстановки. Переписывая первое уравнение, получаем x = –5 + 3y. Это уравнение подставляется во второе уравнение, затем решается для y. Как только мы узнаем, что такое y, мы можем подставить значение в первое уравнение, чтобы найти x. В этом случае x = 1 и y = 2,
Сообщить об ошибке
Сэмми пересчитывает деньги, когда замечает, что у него на две четверти больше, чем десятицентовиков, а количество пятаков равно сумме четвертаков и десятицентовиков. Общая сумма наличных денег, которые у него есть на руках, составляет 1,05 доллара. Сколько у него четвертей?
Возможные ответы:
Правильный ответ:
3
Объяснение:
Определите переменные как
x = количество десятицентовиков
x + 2 = количество четвертей
х + х + 2 = количество пятицентовых монет
В общем, формула денежных проблем в V ₁ N ₁ + V ₂ N ₂ + V ₃ N _{8 $ 2 = _{8 всего}}
0,10x + 0,25(x + 2) + 0,05(2x + 2) = 1,05
Решая уравнение, мы видим, что есть один цент, три четверти и четыре пятака.
Сообщить об ошибке
Если x ² – y ² = 20, а x + y = 10, то каково произведение x и y?
Possible Answers:
6
–64
24
–24
–4
Correct answer:
24
Пояснение:
В этой задаче используется система двух уравнений. Первое уравнение имеет вид x ² – y ² = 20, а второе уравнение имеет вид x + y = 10. Решим второе уравнение относительно y, а затем подставим это значение в первое уравнение.
x + y = 10
Вычесть y с обеих сторон.
x = 10 – y
Подставьте 10 — y вместо x в первое уравнение.
x ² — Y ² = 20
(10 — Y) ² — Y ² = 20
Мы можем использовать метод Фольга, чтобы найти (10 — Y) ².
(10 – у) ² = (10 – у)(10 – у) = 10(10) – 10у – 10у + у ² = 100 –20у + у ² .
Теперь мы можем вернуться к исходному уравнению и заменить (10 – y) ² с 100 — 20y + y ^2.
(100 — 20y + y ²) — Y ² = 20
100 — 20y = 20
Subtract 100 от обоих СИД -СИДИС.
–20y = –80
Разделите обе части на –20.
y = 4.
Теперь, когда мы знаем, что y = 4, мы можем использовать любое из наших исходных двух уравнений, чтобы найти x. Использование уравнения x + y = 10, вероятно, проще.
х + у = 10
х + 4 = 10
х = 6,
Исходный вопрос требует произведения x и y, которое будет 4(6), что равняется 24.
Ответ: 24.
Сообщить об ошибке
Если x – 4 = y и 2x + 4y = 16, каково значение x?
Possible Answers:
5 ¹ / ₃

0
8
7 ¹ / ₅
6
Correct answer:
5 ¹ / ₃

Объяснение:
Правильный ответ: 5 ¹ / ₃ . Проблема решается заменой. Первый шаг — подставить x – 4 во второе уравнение. Тогда у нас есть 2x + 4(x – 4) = 16. Следующий шаг 2x + 4x – 16 = 16. Тогда 6x = 32. Затем мы делим 32 на 6 для X и получаем 5 ¹ / ₃ .
Сообщить об ошибке
Если x + 2y + z = 5, а y – 2z = 6, то что такое –x – 5z?
Possible Answers:
cannot be determined
7
–7
0
–5
Correct answer:
7
Объяснение:
В этом вопросе нам предлагается найти значение –x – 5z, которое не включает никаких членов y. Следовательно, нам нужно исключить y членов из наших уравнений. Один из способов сделать это — найти y во втором уравнении и подставить это значение в первое.
г – 2z = 6
Добавьте по 2z с обеих сторон.
y = 6 + 2z
Теперь возьмем 6 + 2z и подставим это вместо y в первое уравнение.
х + 2(6 + 2z) + z = 5
Распределить.
х + 12 + 4z + z = 5
х + 5z + 12 = 5
Вычесть 12 с обеих сторон.
x + 5z = –7
В исходном вопросе требуется указать значение –x – 5z, равное –1(x + 5z). Умножим обе части уравнения x + 5z = –7 на минус единицу.
–1(x + 5z) = –7
–x – 5z = 7
Ответ: 7.
Сообщить об ошибке
Шесть лет назад Том был вдвое старше Сьюзан. Тринадцать лет назад Том был в три раза старше Сьюзен. На сколько лет Том старше Сьюзен?
Possible Answers:
21
34
7
14
20
Correct answer:
14
Объяснение:
909:06 Пусть t и s обозначают текущий возраст Тома и Сьюзан соответственно.
Нам говорят, что шесть лет назад возраст Тома был в два раза больше возраста Сьюзан. Мы могли бы представить возраст Тома шесть лет назад как t – 6, а возраст Сьюзан – как s – 6. Поскольку t – 6 в два раза больше, чем s – 6, мы могли бы написать следующее уравнение:
t – 6 = 2 (s – 6)
Кроме того, нам говорят, что тринадцать лет назад Том был в три раза старше Сьюзен. Тринадцать лет назад возраст Тома был бы t – 13, а возраст Сьюзен – s – 13. Тогда мы можем написать следующее уравнение:
t – 13 = 3(s – 13)
Теперь у нас есть два уравнения и два неизвестных. Чтобы решить эту систему уравнений, мы могли бы найти t в первом уравнении и подставить это значение во второе уравнение.
t – 6 = 2(s – 6)
Распределить.
t – 6 = 2s – 12
Прибавьте шесть к обеим сторонам.
t = 2s – 6
Далее подставим 2s — 6 во второе уравнение.
(2с – 6) – 13 = 3(с – 13)
Распределить.
2 с – 6 – 13 = 3 с – 39
Объединение констант.
2 с – 19 = 3 с – 39
Вычтите 2 с с обеих сторон.
–19 = s – 39
Прибавьте 39 к обеим сторонам.
s = 20
Так как t = 2s – 6, t = 2(20) – 6 = 34
Это означает, что Тому сейчас 34 года, а Сьюзен сейчас 20. Вопрос спрашивает нас, на сколько лет старше Том. чем у Сьюзен, которая составляет 34 — 20 = 14 лет.
Ответ 14.
Сообщить об ошибке
Если (x ² + y ² ) ^(1/2) = 4 и 4xy = 4, каково значение (x-y) ² .
Возможные ответы:
4
18
14
2
16
Правильный Ответ:
9099
9
9
9
9909
0
чем Пояснение:
Нас просят найти (x – y) ² . Разложим (x – y) ², используя метод FOIL.
(x – y) ² = (x – y)(x – y) = x(x) – x(y) – y(x) + y(y) = x ² – 2xy + y ²
Другими словами, нам нужно найти значение x ² – 2xy + y ² . Мы можем использовать данную информацию, чтобы найти значения x ² + y ² и –2xy. Тогда, если объединить значения x ² + y ² и –2xy, мы получим значение x ² – 2xy +y ² , равное (x – y) ² .
В задаче указано, что (x ² + y ² ) ^(1/2) = 4. Если бы мы возвели в квадрат обе части уравнения, мы могли бы найти значение x ² + y ² .
((x ² + y ² ) ^(1/2) ) ² = 4 ² = 16
^C = A ^{до н.э.}, затем ((x ² + Y ²) ^(1/2)) ² становится (x ² + у ²) ^{2 (1/1999 + у ²) 2)} = х ² + у ² .
Таким образом, x ² + y ² = 16.
Вторая часть данной информации утверждает, что 4xy = 4. Если мы разделим обе части уравнения на -2, мы получим -2xy слева сторона.
4xy = 4
Разделите обе части на –2.
–2xy = –2
Наконец, мы добавим x ² + y ² + –2xy.
x ² + y ² + –2xy = 16 + –2 = 14
Ответ составляет 14.
Отчет о ошибке
IF ( x + y ) ² = 15 и x ^{2 271000 + y} 2 + y ^{9999999999999999999999999999999,99999999999999999999999999999999999, 271000 + y ^{9999999999999999999999999999999,99999999999999999. из x ² у ² ?}}
Possible Answers:
12
–12
–6
144
36
Correct answer:
36
Объяснение:
Сначала расширим ( x + y ) ², используя метод FOIL.
( x + y ) ² = ( x + y )( x + y )
According to the FOIL method, we will multiply the first terms of the binomials , затем внешние члены, затем внутренние члены, а затем последние члены. Затем мы добавим эти четыре продукта вместе.
( x + y )( x + y )= x ( x ) + x ( y ) + y ( x ) + y ( y ) = x ² + 2 XY + Y ²
Нам говорят, что ( x + y ) ² = 15. Let’s Replicat х ² + 2 ху + у ² .
x ² + 2 xy + y ² = 15
Перебросы, мы можем написать уравнение следующим образом:
x
x
x
x
x
x
. 2 xy = 15
The second part of the problem tells us that x ² + y ² = 27. Thus, we can replace x ² + y ² с 27.
27 + 2 xy = 15
Вычтите 27 с обеих сторон.
2 xy = –12
Разделить на два.
xy = –6
Вопрос требует от нас x ² y ² . Согласно одному из свойств экспонент, ( xy ) ² = x ² y ² . Таким образом, возведя в квадрат обе части уравнения xy = –6, мы получим значение x ² у ² .
( xy ) ² = (–6) ²
x ² y ² = 36
The answer is 36.
Report an Error
In triangle ABC , точки A и B расположены в точках пересечения графиков y = 9 – x ² и y = 3 – x 0914 , а точка C находится в точке ( p ,0), где p < 0. Каким должно быть число p , чтобы площадь треугольника ABC была равна 50?
Possible Answers:
–21
–13
–9
–5
–17
Correct answer:
–17
Пояснение:
Сначала нам нужно найти точки A и B, которые, как нам сказали, образуют точки пересечения графиков y = 9 – x ² и y = 3 – x . Чтобы решить эти два уравнения, мы можем установить значение y в первом уравнении равным значению y во втором, а затем найти х .
9 – x ² = 3 – x
Добавьте x ² с обеих сторон.
9 = 3 – x + x ²
Вычесть 9с обеих сторон. Затем переставьте так, чтобы степени x располагались в порядке убывания.
-6 — x + x ² = x ² — x -6 = 0
Фактор x -6 = 0
Фактор x -6 = 0
Фактор x -6 = 0
. которые умножают, чтобы дать -6 и добавляют, чтобы дать -1. Эти два числа равны –3 и 2.
x ² – x – 6 = ( x – 3)( x + 2) = 0
Приравняйте каждый множитель к нулю и решите.
x — 3 = 0
x = 3
x + 2 = 0
x = –2
. 3. Мы можем найти y значений точек пересечения, подставив –2 и 3 в любое уравнение. Давайте воспользуемся уравнением y = 3 – x .
При x = –2, y = 3 – (–2) = 5. Одна точка пересечения – (–2,5).
Когда x = 3, y = 3 – 3 = 0. Другой точкой пересечения является (3,0).
Предположим, что точка A находится в точке (–2,5), а B находится в точке (3,0). Нам говорят, что C находится в точке ( p ,0), где p < 0. Давайте нарисуем треугольник ABC , используя информацию, которая у нас есть.
На рисунке выше оранжевая линия представляет высоту со стороны г. до н.э. по А .
Площадь любого треугольника равна (1/2) bh , где b — длина основания, а h — длина высоты. Мы будем использовать BC для обозначения основания и оранжевую линию для обозначения высоты.
Длина до н.э. будет равна 3 – p , так как обе точки лежат на оси x . Длина оранжевой линии — это расстояние от CB до точки 9.0913 A , что равно 5. Теперь мы можем найти формулу для площади и установить ее равной 50.
Площадь ABC = (1/2)(3 — p )(5) = 50
Умножьте обе части на 2.
(3 – p )(5) = 100
Разделите на 5.
3 – p = 20
Вычтите 3 из обеих сторон.
–p = 17
Умножьте обе части на –1.
р = –17.
Ответ: –17.
Сообщить об ошибке
← Назад 1 2 3 4 5 6 7 8 9 Далее →
Уведомление об авторских правах
Все математические ресурсы SAT
16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Learn by Concept
Решите x y 14 и x y 4 линейных уравнений методом подстановки и найдите x и y…
Перейти к
Пара линейных уравнений с двумя переменными — упражнение 3.1
г.
Пара линейных уравнений с двумя переменными — упражнение 3.2
Пара линейных уравнений с двумя переменными — упражнение 3. 3
Пара линейных уравнений с двумя переменными — упражнение 3.4
г.
Пара линейных уравнений с двумя переменными — упражнение 3.5
Пара линейных уравнений с двумя переменными — упражнение 3.6
Пара линейных уравнений с двумя переменными — упражнение 3.7
г.
Вещественные числа
Полиномы
Пара линейных уравнений с двумя переменными
г. Квадратные уравнения
Арифметические прогрессии
Треугольники
г. Координатная геометрия
Введение в тригонометрию
Некоторые приложения тригонометрии
г. Круги
Конструкции
Области, связанные с кругами
г. Площади поверхности и объемы
Статистика
Вероятность
Главная > Решения НЦЭРТ Класс 10 Математика > Глава 3. Пара линейных уравнений с двумя переменными > Пара линейных уравнений с двумя переменными — упражнение 3.3 > Вопрос 4
Вопрос 4. Пара линейных уравнений с двумя переменными. Упражнение 3.3
Решите x + y = 14 и x – y = 4 линейных уравнений методом подстановки и найдите x и y.
Ответ:
Дано,
x + y = 14 и x – y = 4 являются двумя уравнениями.
Из уравнения 1 ^st получаем
x = 14 – y
Теперь подставим значение x во второе уравнение, чтобы получить
(14 – y) – y = 4
14 – 2y = 4
2y = 10
Или y = 5
По значению y мы теперь можем найти точное значение x;
∵ x = 14 – y
∴ x = 14 – 5
Или x = 9
Следовательно, x = 9 и y = 5.
Связанные вопросы
** Тренер команды по крикету покупает 7 бит и 6 мячей за 3800 рупий. Позже она покупает 3 биты и 5 мячей…
**Разница между двумя числами составляет 26, и одно число в три раза больше другого. Найдите х и у.**
**Решите 2x + 3y = 11 и 2x – 4y = – 24 и, следовательно, найдите значение «m», для которого y = mx + 3.**
Решить 0,2x + 0,3y = 1,3 и 0,4x + 0,5y = 2,3 линейных уравнений методом подстановки и найти…
**Больший из двух дополнительных углов больше меньшего на 18 градусов. Найдите х и у.**
**Стоимость такси в городе состоит из фиксированной платы вместе с платой за проезд в…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Пара линейных уравнений с двумя переменными — Упражнение 3.
No related posts.

заказ решений на аукционе за минимальную цену с максимальным качеством

Объединение сервисов в одну систему

Принцип работы

За счет чего будет развиваться сервис

Преимущества для заказчиков

Преимущества для решающих задания

Преимущества для владельца сервиса

Что необходимо для создания сервиса

Лучший ответ по мнению автора

Михаил Александров

Евгений

Андрей Андреевич

Контрольная работа по алгебре 7 класс по теме: «Системы уравнений»

Однородные дифференциальные уравнения

Пример: Решите

Пример: Решите

Пример: решить

Решите для x и y: x + y/xy = 5, 3x + 2y/xy = 13 — Sarthaks eConnect

Пожалуйста, войдите или зарегистрируйтесь, чтобы ответить на этот вопрос.

1 ответ

Похожие вопросы

Категории

Как найти решение системы уравнений

Все математические ресурсы SAT

Все математические ресурсы SAT

Решите x y 14 и x y 4 линейных уравнений методом подстановки и найдите x и y…

Добавить комментарий Отменить ответ