Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .
Решено
Вася проходит серию тестов, за каждый из которых он может получить от 0 до 100 баллов. Перед выполнением последнего теста Вася подсчитал, что если он…
Решено
Среди сорока чиновников Министерства важных дел некоторой Страны есть как честные чиновники, так и жулики. Известно, что из любых шести чиновников…
Решено
Чему равно наименьшее натуральное число N, обладающих следующим свойством: 10N является квадратом некоторого натурального числа, а 15N — кубом?
Решено
Два грузовика едут по шоссе со скоростью 75 км/ч, расстояние между ними — 300 метров. Когда грузовик сворачивает на проселочную дорогу, его скорость снижается до 25 км/ч. Сколько метров будет между гр
Пользуйтесь нашим приложением
Решите уравнение 1 3х 2х 1.
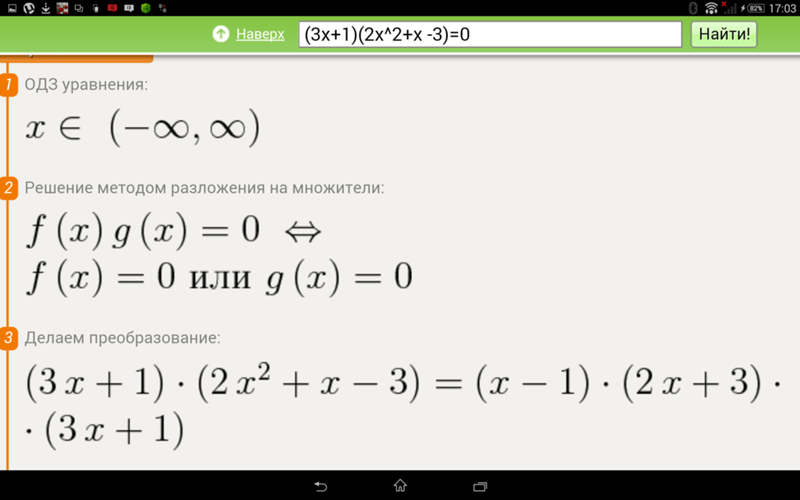 2-4\cdot \:5\cdot \:9}<0\)
2-4\cdot \:5\cdot \:9}<0\)нет решений
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анжелика Альбертовна Макаренко
Репетитор по математике
Стаж (лет)
Образование:
Московский государственный областной университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 3-9 классов и по информатике для 5-9 классов. Цифры нас окружают всегда — хочу научить любить и понимать этот важный аспект нашей жизни. Уверена, что любой предмет можно подать интересно, могу привить интерес к математике и научить основам и деталям. С каждым учеником стараюсь найти общий язык, учитывать сильные и слабые стороны. Всегда отвечаю на вопросы, веду диалог, объясняю непонятные моменты. Разбираемся вместе с учеником в задачах, которые вызывают трудности. Буду рада видеть на своих занятиях!
Цифры нас окружают всегда — хочу научить любить и понимать этот важный аспект нашей жизни. Уверена, что любой предмет можно подать интересно, могу привить интерес к математике и научить основам и деталям. С каждым учеником стараюсь найти общий язык, учитывать сильные и слабые стороны. Всегда отвечаю на вопросы, веду диалог, объясняю непонятные моменты. Разбираемся вместе с учеником в задачах, которые вызывают трудности. Буду рада видеть на своих занятиях!
Виктория Анатольевна Шилова
Репетитор по математике
Стаж (лет)
Образование:
Северо-Казахстанский государственный университет имени Козыбаева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку 5-11 классов, подготовка к ОГЭ и ЕГЭ.
Жанна Игоревна Стефанович
Репетитор по математике
Стаж (лет)
Образование:
Гродненский государственный университет им. Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии 7, 8 классов и биология до 9 класса включительно. Меня завораживает мир молекул и химических реакций. Химия имеет свою красоту. Когда смешиваешь два бесцветных раствора и получается ярко-красный или когда что-то взрывается мы все в восторге. В химии наряду с этой красотой существует своя глубокая логика. Если Вы ее познаете, то поймете химию. Красота всегда рождает интерес.
Меня завораживает мир молекул и химических реакций. Химия имеет свою красоту. Когда смешиваешь два бесцветных раствора и получается ярко-красный или когда что-то взрывается мы все в восторге. В химии наряду с этой красотой существует своя глубокая логика. Если Вы ее познаете, то поймете химию. Красота всегда рождает интерес.
Похожие статьи
- Система линейных уравнений
- Соответственные углы
- Как перевести килограммы в тонны?
- Задачи на координатной решетке. Задание №3 из ЕГЭ прошлых лет
- Решаем задачи из ЕГЭ. Профильный уровень. Задание №5
- Чем ребенку заняться на даче? 10 способов нескучно провести время в деревне
- Традиции и приметы на Хэллоуин: празднуем «страшный» праздник по всем правилам
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Тренажер по решению линейных уравнений.
 | Тест по алгебре (7 класс) по теме:
| Тест по алгебре (7 класс) по теме:Опубликовано 02.10.2016 — 1:24 — Егорова Раушания Леонидовна
Тренажер «Решение линейных уравнений»
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
Тренажер по теме «Решение линейных уравнений»
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель |
Образец: 2х=10 х=10:2 х=5 |
Решите уравнение по образцу:
- 5х=10
- 10х=90
- 13у=78
- 25m=375
- 2х=-12
- -3к=15
- -12у=-36
- 31в=-93
- -4х=1,2
- 6у=-0,36
- -12к=-1,44
- -0,2х=-1,2
- 1.
 7у=-0,34
7у=-0,34 - -7,4m=-1,48
- 3х=1
- 7r =-4
- 13у=-10
- -10v=-7
- х=4
- у=6
- к=-.
- х=-1
- а=-1
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный. |
Образец: х+5=10 х=10-5 х=5 | Образец: х-4=10 х=10+4 х=6 |
Решите уравнения:
- Х+6=10.
- У+14=19,
- а+41=60,
- 2х+3=13,
- 3у+14=77,
- 5х+13=73,
- Х-4,5=10,
- 5-у=4,
- 10-х=6,
- х -7,8=1,2,
- 2х-3=16,
- 100-5х=17,
- 0,2х+3=-1,5,
- -1,2у-4,7=-3,5,
- 4х+х=-15,
- 3у-5у=7,
- -4х-3у=-49,
- Х+4=3х,
- -3у+7=2у.
- 5а-1,5=2а.
- -0,2х+7=-1,6х,
- t+5=t-7,
- 2у=7у,
- -3к+8=-3к+9,
- 6,9-9n=-5n-33,1,
Образец: 3х+6=4х-1 3х-4х=-1-6 -х=-7 х=7 |
Решить уравнения:
- 2х+8=6х-2,
- 10у+3=2у-1,
- -4+3к=8к+5.

- 9+4а=8а-9,
- 3в+9=8в+2,
- 6-2с=3с-10,
- 5-2у=8у+9,
- -4х+3=4х-5,
- 4а+4=-6а-5.
- 3у+3=-2-7у.
- -10х+3=-1-8х,
- 9-4х=-4-9х,
- -8а+9=3-4а,
- с+3=с+5,
- t-t+2=t-3,
- x+x+5=x,
- 0,2f+2,3=0,7f-3,2,
- -0,4x-14=0,3x,
- -40·(-7x+5)=-1600,
- (-20t-50)·2=100,
- 2,1·(4-6e)=-42,
- -3·(2-15k)=-6,
- -20·(x-13)=-220,
- (30-7r)·8=352,
- (2,8-0,1h)·3,7=7,4,
- (3x-1,2)·7=10,5,
- x-=.
Образец: 2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5. |
Решить уравнение.
- 5·(у-9)=-2.
- 3=4·(к+2),
- 5·(с+5)=-7,
- 7·(а-1)=3а.
- 7·(-3+2х)=-6х-1,
- 2·(7+9к)=-6к+2,
- 6·(5-3с)=-8с-7,
- 4·(2-3х)=-7х+10,
- -4·(-к+7)=к+17,
- -5·(0,8t-1,2)=-t+7,2,
- -5·(3а+1)-11=-16,
- -3,2n+4,8=-2·(1,2n+2,4),
- -5·(0,8f-1,4)=-f+7,
- 5·(r-7)=3·(r-4)-27,
- 8-7·(c-2)=2·(2c-3)+3c,
- 4·(x-3)-16=5·(x-5),
- 5·(y-3)+27=4y+3·(2y-5),
- -4·(3-5z)=18z-7,
- 1,2-2·(1,3y+1)=5,6y-27,04,
- 8·(2f-6)=2·(4f+3),
- -3·(2,1m-1)+4,8=-6,7m+9,4,
- 6·(2c-3)+2·(4-3c)=5,
- h+- =2-h+2h,
- 1-1x+3x=1x-2x+2,5,
- 2·(z+1)+3=4-·(z-1).

Образец: =, 9х=5·4 9х=20 х=, х=2, |
Решить уравнения.
- =,
- = ,
- =,
- = ,
- = ,
- = ,
- = ,
- =4,
- =7,
- = ,
- = ,
- = ,
- = ,
- = ,
Образец: |
Решите уравнения:
Предварительный просмотр:
Тренажер по теме «Решение линейных уравнений»
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель |
Образец: 2х=10 х=10:2 х=5 |
Решите уравнение по образцу:
- 5х=10
- 10х=90
- 13у=78
- 25m=375
- 2х=-12
- -3к=15
- -12у=-36
- 31в=-93
- -4х=1,2
- 6у=-0,36
- -12к=-1,44
- -0,2х=-1,2
- 1.
 7у=-0,34
7у=-0,34 - -7,4m=-1,48
- 3х=1
- 7r =-4
- 13у=-10
- -10v=-7
- х=4
- у=6
- к=-.
- х=-1
- а=-1
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный. |
Образец: х+5=10 х=10-5 х=5 | Образец: х-4=10 х=10+4 х=6 |
Решите уравнения:
- Х+6=10.
- У+14=19,
- а+41=60,
- 2х+3=13,
- 3у+14=77,
- 5х+13=73,
- Х-4,5=10,
- 5-у=4,
- 10-х=6,
- х -7,8=1,2,
- 2х-3=16,
- 100-5х=17,
- 0,2х+3=-1,5,
- -1,2у-4,7=-3,5,
- 4х+х=-15,
- 3у-5у=7,
- -4х-3у=-49,
- Х+4=3х,
- -3у+7=2у.
- 5а-1,5=2а.
- -0,2х+7=-1,6х,
- t+5=t-7,
- 2у=7у,
- -3к+8=-3к+9,
- 6,9-9n=-5n-33,1,
Образец: 3х+6=4х-1 3х-4х=-1-6 -х=-7 х=7 |
Решить уравнения:
- 2х+8=6х-2,
- 10у+3=2у-1,
- -4+3к=8к+5.

- 9+4а=8а-9,
- 3в+9=8в+2,
- 6-2с=3с-10,
- 5-2у=8у+9,
- -4х+3=4х-5,
- 4а+4=-6а-5.
- 3у+3=-2-7у.
- -10х+3=-1-8х,
- 9-4х=-4-9х,
- -8а+9=3-4а,
- с+3=с+5,
- t-t+2=t-3,
- x+x+5=x,
- 0,2f+2,3=0,7f-3,2,
- -0,4x-14=0,3x,
- -40·(-7x+5)=-1600,
- (-20t-50)·2=100,
- 2,1·(4-6e)=-42,
- -3·(2-15k)=-6,
- -20·(x-13)=-220,
- (30-7r)·8=352,
- (2,8-0,1h)·3,7=7,4,
- (3x-1,2)·7=10,5,
- x-=.
Образец: 2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5. |
Решить уравнение.
- 5·(у-9)=-2.
- 3=4·(к+2),
- 5·(с+5)=-7,
- 7·(а-1)=3а.
- 7·(-3+2х)=-6х-1,
- 2·(7+9к)=-6к+2,
- 6·(5-3с)=-8с-7,
- 4·(2-3х)=-7х+10,
- -4·(-к+7)=к+17,
- -5·(0,8t-1,2)=-t+7,2,
- -5·(3а+1)-11=-16,
- -3,2n+4,8=-2·(1,2n+2,4),
- -5·(0,8f-1,4)=-f+7,
- 5·(r-7)=3·(r-4)-27,
- 8-7·(c-2)=2·(2c-3)+3c,
- 4·(x-3)-16=5·(x-5),
- 5·(y-3)+27=4y+3·(2y-5),
- -4·(3-5z)=18z-7,
- 1,2-2·(1,3y+1)=5,6y-27,04,
- 8·(2f-6)=2·(4f+3),
- -3·(2,1m-1)+4,8=-6,7m+9,4,
- 6·(2c-3)+2·(4-3c)=5,
- h+- =2-h+2h,
- 1-1x+3x=1x-2x+2,5,
- 2·(z+1)+3=4-·(z-1).

Образец: =, 9х=5·4 9х=20 х=, х=2, |
Решить уравнения.
- =,
- = ,
- =,
- = ,
- = ,
- = ,
- = ,
- =4,
- =7,
- = ,
- = ,
- = ,
- = ,
- = ,
Образец: |
Решите уравнения:
По теме: методические разработки, презентации и конспекты
Открытый урок по математике в 6 классе «Решение линейных уравнений»
здесь представлен план — конспект урока по математике в 6 классе «Решение линейных уравнений» с применением ЭОР….
Проект по теме «Решение линейных уравнений с параметрами»
Проект по теме «Решение линейных уравнений с параметрами». ..
..
Разработка методических рекомендаций решения линейных уравнений с параметрами.
Разработка методических рекомендаций решения линейных уравнений с параметрами….
Функционально-графический подход к решению линейных уравнений с параметром и модулем
План-конспект урока с использованием ЦОР для обобщающих уроков по теме «Линейные уравнения с параметром и модулем» для учащихся 7-9 классов и для подготовки к ГИА (презентация к уроку)…
Презентация:»Решение линейных уравнений»
Презентация по алгебре «Решение линейных уравнений».Данная презентация может быть использована на уроке алгебры в 7 классе при изучении темы: «Линейное уравнение с одной переменной». Данная тема изуча…
Задание по теме «Решение линейных уравнений», составление фигуры «Танграм»
Задания по теме решение линейных уравнений для 6, 7 классов. Задания комбинированные. Вначале решить все уравнения, а затем составить фигуру танграм….
Тематический тренажер для подготовки к ГИА в 2014 г.
 по математике 9 класс. Тематические тренировочные задания. Отработка заданий: модуль «Алгебра» Тема№2 «Решение линейных уравнений»
по математике 9 класс. Тематические тренировочные задания. Отработка заданий: модуль «Алгебра» Тема№2 «Решение линейных уравнений»Представляю вашему вниманию очередной тематический тренажер для подготовки к ГИА в 2014г по алгебре по теме «Решение линейных уравнений». Подобраны упражнения, которые соответствуют типовым заданиям К…
Поделиться:
Реши уравнение относительно n. Уравнения онлайн. Возможные решения задач
Решить уравнение — это значит найти такие значения неизвестного, при которых равенство будет верным.
Решение уравнения
- Представим уравнение в следующем виде:
2х * х — 3 * х = 0.
- Видим, что члены уравнения в левой части имеют общий множитель х. Вынесем его за скобки и запишем:
х * (2х — 3) = 0.
- Полученное выражение является произведением множителей х и (2х — 3). Вспомним, что произведение равно 0 в том случае, если хотя бы один из множителей равен 0.
 Значит, можно записать равенства:
Значит, можно записать равенства:
х = 0 или 2х — 3 = 0.
- Значит одним из корней исходного уравнения является х 1 = 0.
- Найдем второй корень, решив уравнение 2х — 3 = 0.
В этом выражении 2х — уменьшаемое, 3 — вычитаемое, 0 — разность. Чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое:
В последнем выражении 2 и х — множители, 3 — произведение. Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:
Таким образом, мы нашли второй корень уравнения: х 2 = 1,5.
Проверка правильности решения
Для того, чтобы узнать, правильно ли решено уравнение, необходимо подставить в него числовые значения х и выполнить необходимые арифметические действия. Если в результате вычислений получится, что левая и правая части выражения имеют одинаковое значение, то уравнение решено правильно.
Выполним проверку:
- Вычислим значение исходного выражения при х 1 = 0 и получим:
2 * 0 2 — 3 * 0 = 0,
0 = 0, верно.
- Вычислим значение выражения при х 2 = 0 и получим:
2 * 1,5 2 — 3 * 1,5 = 0,
2 * 2,25 — 4,5 = 0,
0 = 0, верно.
- Значит, уравнение решено правильно.
Ответ: х 1 = 0, х 2 = 1,5.
В этой статье мы будем учиться решать биквадратные уравнения.
Итак, уравнения какого вида называются биквадратными?
Все уравнения вида ах 4 + bx 2 + c = 0 , гдеа ≠ 0 , являющиеся квадратными относительно х 2 , и называются биквадратными уравнениями. Как видите, эта запись очень похожа на запись квадратного уравнения, поэтому и решать биквадратные уравнения будем используя формулы, которые мы применяли при решении квадратного уравнения.
Только нам необходимо будет ввести новую переменную, то есть обозначим х 2 другой переменной, например, у или t (или же любой другой буквой латинского алфавита).
Например, решим уравнение х 4 + 4х 2 ‒ 5 = 0.
Обозначим х 2 через у (х 2 = у ) и получим уравнение у 2 + 4у – 5 = 0.
Как видите, такие уравнения вы уже умеете решать.
Решаем полученное уравнение:
D = 4 2 – 4 (‒ 5) = 16 + 20 = 36, √D = √36 = 6.
у 1 = (‒ 4 – 6)/2= ‒ 10 /2 = ‒ 5,
у 2 = (‒ 4 + 6)/2= 2 /2 = 1.
Вернемся к нашей переменной х.
Получили, что х 2 = ‒ 5 и х 2 = 1.
Замечаем, что первое уравнение решений не имеет, а второе дает два решения: х 1 = 1 и х 2 = ‒1. Будьте внимательны, не потеряйте отрицательный корень (чаще всего получают ответ х = 1, а это не правильно).
Ответ: — 1 и 1.
Для лучшего усвоения темы разберем несколько примеров.
Пример 1. Решите уравнение 2х 4 ‒ 5 х 2 + 3 = 0.
Пусть х 2 = у, тогда 2у 2 ‒ 5у + 3 =0.
D = (‒ 5) 2 – 4· 2 · 3 = 25 ‒ 24 = 1, √D = √1 = 1.
у 1 = (5 – 1)/(2· 2) = 4 /4 =1, у 2 = (5 + 1)/(2· 2) = 6 /4 =1,5.
Тогда х 2 = 1 и х 2 = 1,5.
Получаем х 1 = ‒1, х 2 = 1, х 3 = ‒ √1,5 , х 4 = √1,5.
Ответ: ‒1; 1; ‒ √1,5; √1,5.
Пример 2. Решите уравнение 2х 4 + 5 х 2 + 2 = 0.
2у 2 + 5у + 2 =0.
D = 5 2 – 4 · 2 · 2 = 25 ‒ 16 = 9, √D = √9 = 3.
у 1 = (‒ 5 – 3)/(2 · 2) = ‒ 8 /4 = ‒2, у 2 = (‒5 + 3)/(2 · 2) = ‒ 2 /4 = ‒ 0,5.
Тогда х 2 = ‒ 2 и х 2 = ‒ 0,5. Обратите внимание, ни одно из этих уравнений не имеет решения.
Ответ: решений нет.
Неполные биквадратные уравнения — это когда b = 0 (ах 4 + c = 0) или же c = 0
(ах 4 + bx 2 = 0) решают как и неполные квадратные уравнения.
Пример 3. Решить уравнение х 4 ‒ 25х 2 = 0
Разложим на множители, вынесем х 2 за скобки и тогда х 2 (х 2 ‒ 25) = 0.
Получим х 2 = 0 или х 2 ‒ 25 = 0, х 2 = 25.
Тогда имеем корни 0; 5 и – 5.
Ответ: 0; 5; – 5.
Пример 4. Решить уравнение 5х 4 ‒ 45 = 0 .
Решить уравнение 5х 4 ‒ 45 = 0 .
х 2 = ‒ √9 (решений не имеет)
х 2 = √9, х 1 = ‒ 3, х 2 = 3.
Как видите, умея решать квадратные уравнения, вы сможете справиться и с биквадратными.
Если же у вас остались вопросы, записывайтесь на мои уроки. Репетиор Валентина Галиневская.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решите уравнение х 2 +(1-х) 2 =х
Докажите, что нет целых чисел, которые от перестановки начальной цифры в конец, увеличиваются в 5 раз.
В некотором царстве каждые двое – либо друзья, либо враги. Каждый человек может в некоторый момент поссориться со всеми друзьями и помириться со всеми врагами. Оказалось, что каждые три человека могут таким образом стать друзьями. Докажите, что тогда и все люди в этом царстве могут стать друзьями.
В треугольнике одна из медиан перпендикулярна одной из биссектрис. Докажите, что одна из сторон этого треугольника вдвое больше другой.
Докажите, что одна из сторон этого треугольника вдвое больше другой.
Задания для проведения районной (городской) олимпиады школьников по математике.
По стрельбе из мишени спортсмен выбивал только по 8,9 и 10 очков. Всего он, сделав более 11 выстрелов, выбил ровно 100 очков. Сколько выстрелов сделал спортсмен, и какие были попадания?
Докажите истинность неравенства:
3. Решите уравнение:
Найдите трехзначное число, которое уменьшается в 7 раз после зачеркивания в нем средней цифры.
В треугольнике АВС проведены биссектрисы из вершин А и В. Затем из вершины С проведены прямые, параллельные этим биссектрисам. Точки Д и Е пересечения этих прямых с биссектрисами соединены. Оказалось, что прямые ДЕ и АВ параллельны. Докажите, что треугольник АВС – равнобедренный.
Задания для проведения районной (городской) олимпиады школьников по математике.
Решите систему уравнений:
На сторонах АВ и АД параллелограмма АВСД взяты соответственно точки Е и К так, что отрезок ЕК параллелен диагонали ВД. Докажите, что площади треугольников ВСЕ и СДК равны.
Докажите, что площади треугольников ВСЕ и СДК равны.
Группу туристов решили рассадить по автобусам так, чтобы в каждом автобусе было одинаковое число пассажиров. Сначала в каждый автобус сажали по 22 человека, однако оказалось, что при этом не удается посадить одного туриста. Когда же один автобус уехал пустым, то в оставшиеся автобусы все туристы сели поровну. Сколько первоначально было автобусов и сколько туристов в группе, если известно, что в каждый автобус помещается не более 32 человек?
Задания для проведения районной (городской) олимпиады школьников по математике.
Решите систему уравнений:
Докажите, что четыре расстояния от точки окружности до вершины вписанного в нее квадрата не могут одновременно быть рациональными числами.
Возможные решения задач
1. Ответ: х=1, х=0,5
От перестановки начальной цифры в конец значность числа не изменится. При этом, по условию задачи, должны получить число, в 5 раз большее первого числа. Следовательно, первая цифра искомого числа должна равняться 1 и только 1. (т.к. если первая цифра будет 2 или больше, то изменится значность, 2*5=10). При перестановке 1 в конец, полученное число оканчивается на 1, следовательно на 5 не делится.
Следовательно, первая цифра искомого числа должна равняться 1 и только 1. (т.к. если первая цифра будет 2 или больше, то изменится значность, 2*5=10). При перестановке 1 в конец, полученное число оканчивается на 1, следовательно на 5 не делится.
Из условия следует, что если А и В – друзья, то С либо их общий враг, либо общий друг (иначе им троим не примириться). Возьмем всех друзей человека А. Из сказанного следует, что все они дружны между собой и враждуют с остальными. Пусть теперь А и его друзья по очереди ссорятся с друзьями и мирятся с врагами. После этого все окажутся друзьями.
Действительно, пусть А первым поссорился со своими друзьями и помирился со своими врагами, но тогда каждый их его бывших друзей будет с ним мириться, а бывшие враги останутся друзьями. Итак, все люди оказываются друзьями А, а следовательно, и друзьями между собой.
Число 111 делится на 37, поэтому на 37 делится и названная сумма.
По условию, число делится на 37, поэтому и сумма
Делится на 37.
Заметим, что указанные медиана и биссектриса не могут выходить из одной вершины, так как в противном случае угол при этой вершине был бы больше 180 0 . Пусть теперь в треугольнике АВС биссектриса АD и медиана СЕ пересекаются в точке F. Тогда AF – биссектриса и высота в треугольнике АСЕ, значит этот треугольник равнобедренный (АС=АЕ), а так как СЕ – медиана, то АВ = 2АЕ и, следовательно, АВ =2АС.
Возможные решения задач
1. Ответ: 9 выстрелов по 8 очков,
2 выстрела по 9 очков,
1 выстрел по 10 очков.
Пусть x выстрелов сделал спортсмен, выбивая по 8 очков, y выстрелов по 9 очков, z выстрелов по 10 очков. Тогда можно составить систему:
Используя первое уравнение системы, запишем:
Из этой системы следует, что x + y + z =12
Умножим второе уравнение на (-8) и сложим с первым. Получим, что y +2 z =4 , откуда y =4-2 z , y =2(2- z ) . Следовательно, у – четное число, т.е. y=2t , где .
Следовательно, у – четное число, т.е. y=2t , где .
Следовательно,
3. Ответ: х = -1/2, х = -4
После приведения дробей к одному знаменателю получаем
4. Ответ: 105
Обозначим через x , y , z соответственно первую, вторую и третью цифру искомого трехзначного числа. Тогда его можно записать в виде . После вычеркивания средней цифры получится двузначное число . По условию задачи , т.е. неизвестные цифры x , y , z удовлетворяют уравнению
7(10 x + z )=100 x +10 y + x , которое после приведения подобных членов и сокращений принимает вид 3 z =15 x +5 y .
Из этого уравнения следует, что z должно делиться на 5 и должно быть положительным, так как по условию . Поэтому z =5, а цифры х, у удовлетворяют уравнению 3=3х + у, которое в силу условия имеет единственное решение х =1, у = 0. Следовательно, условию задачи удовлетворяет единственное число 105.
Следовательно, условию задачи удовлетворяет единственное число 105.
Обозначим буквой F точку, в которой пересекаются прямые АВ и СЕ. Так как прямые DB и CF параллельны, то . Ввиду того, что BD – биссектриса угла АВС, заключаем, что . Отсюда следует, что , т.е. треугольник BCF равнобедренный и BC=BF. Но из условия следует, что четырехугольник BDEF – параллелограмм. Поэтому BF = DE, и, значит ВС = DE. Аналогично доказывается, что АС = DE. Это приводит к требуемому равенству.
Возможные решения задач
1.
Отсюда (х + у) 2 = 1 , т.е. х + у = 1 или х + у = -1 .
Рассмотрим два случая.
а) х + у = 1 . Подставив х = 1 – у
б) х + у = -1 . После подстановки х = -1-у
Итак, решениями системы могут быть лишь следующие четыре пары чисел: (0;1), (2;-1), (-1;0), (1;-2). Подстановкой в уравнения исходной системы убеждаемся, что каждая из этих четырех пар является решением системы.
Треугольники CDF и BDF имеют общее основание FD и равные высоты, так как прямые ВС и AD параллельны. Следовательно, их площади равны. Аналогично, равны площади треугольников BDF и BDE, так как прямая BD параллельна прямой EF. И равны площади треугольников BDE и BCE, так как АВ параллельна CD. Отсюда и следует требуемое равенство площадей треугольников CDF и BCE.
Учитывая область определения функции, построим график.
Используя формулу выполним дальнейшие преобразования
Применяя формулы сложения и выполняя дальнейшие преобразования, получим
5. Ответ: 24 автобуса, 529 туристов.
Обозначим через k первоначальное число автобусов. Из условия задачи следует, чтои что число всех туристов равно 22 k +1 . После отъезда одного автобуса всех туристов удалось рассадить в оставшиеся (k-1) автобусов. Следовательно, число 22 k +1 должно делиться на k-1 . Таким образом, задача свелась к определению всех целых , для которых число
Является целым и удовлетворяет неравенству (число n равно числу туристов, посаженных в каждый автобус, а по условию задачи автобус вмещает не более 32 пассажиров).
Число будет целым только тогда, когда число будет целым. Последнее возможно только при k =2 и при k =24 .
Если k =2 , то n=45.
А если k =24 , то n=23.
Отсюда и из условия получаем, что только k =24 удовлетворяет всем условиям задачи.
Следовательно, первоначально было 24 автобуса, а число всех туристов равно n(k-1)=23*23=529
Возможные решения задач
1. Ответ:
Тогда уравнение примет вид:
Получили квадратное уравнение относительно р .
2. Ответ: (0;1), (2;-1), (-1;0), (1;-2)
Сложив уравнения системы, получим , или
Отсюда (х + у) 2 = 1 , т.е. х + у = 1 или х + у = -1 .
Рассмотрим два случая.
а) х + у = 1 . Подставив х = 1 – у в первое уравнение системы, получим
б) х + у = -1 . После подстановки х = -1-у в первое уравнение системы, получим или
3-8 Последнее невозможно, так как разность этих множителей по модулю $3$ равна $\pm 1$, поэтому решения в точности
$c = \mp 1, \mp 3$. Последовательная подстановка этих четырех решений в наши уравнения для $b, a, x$ дает все решения исходного уравнения: $$x \equiv 13, 57, 139, 183 ,$$
что согласуется с решением liones99a, полученным с использованием W.A.
Последнее невозможно, так как разность этих множителей по модулю $3$ равна $\pm 1$, поэтому решения в точности
$c = \mp 1, \mp 3$. Последовательная подстановка этих четырех решений в наши уравнения для $b, a, x$ дает все решения исходного уравнения: $$x \equiv 13, 57, 139, 183 ,$$
что согласуется с решением liones99a, полученным с использованием W.A.. $\endgroup$ 92$, поэтому мы можем сказать, что $y\equiv14$ является решением. Следовательно, мы также можем сказать, что $y\equiv-14\mod198\equiv184$ также является решением
Итак, мы нашли два значения для $x$: $x\in\{13,183\}$
Мы можем использовать WolframAlpha, чтобы найти еще два решения для $y$: $y\equiv58$ и $y\equiv-58\mod 198\equiv140$, однако я не совсем уверен, как их вычислить без использования ошибка
Это дает нам последние два значения для $x$: $x\in\{13,57,139,183\}$
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Комментарий résoudre l’équation 2x 3 0 ?
Примеры алгебры
Добавление 3 aux deux côtés de l’ équation . Diviser Chaque Terme пар 2 и упрощение. Diviser chaque terme dans 2x = 3 2 x = 3 пар 2 2 . Éliminer le facteur commun de 2 2 .
Ensuite, Комментарий résoudre 3x 5 ?
плюс Комментарий найти решение équation ? Пример. Soit l’ équation « 2x + y = 12 » не содержит переменных x et y и не определяет ансамбль E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Пара (5, 2) оценивается как , решение по этому уравнению , puisque «2 × 5 + 2 = 12». L’ensemble solution de cette équation est donc : {(1, 10), (2, 8), (3, 6), (4, 4), (5, 2), (6, 0) }.
Комментарий résoudre une équation en 3eme ? Rechercher pour quelles valeurs de l’inconnue x , l’égalité 3x+7=1 3 x + 7 = 1 est verifiee s’appelle résoudre l’ équation . Номер −2 является решением уравнения .0998 . Propriété 1 : Часть равноправия, при обязательном равноправии, эквивалентном аджуте или при возврате мема номбре в чаке члена.
Номер −2 является решением уравнения .0998 . Propriété 1 : Часть равноправия, при обязательном равноправии, эквивалентном аджуте или при возврате мема номбре в чаке члена.
Или Комментарий résoudre une équation 0 ?
Налейте , получив результат по уравнению , по формуле A×B= 0 ⇔A= 0o uB= 0 . В результате уравнений A = 0 и B = 0 разделены. Les Solutions obtenues en résolvant ces deux équations sont celles de l’ , уравнение , инициал.
Table des matières
Комментарий Faire une équation mathématique ? Какое уравнение равно 0 ? L’ уравнение (x + 2) (3 – x) = 0 оценка и уравнение produit nul. Or si un produit de facteur est nul alors l’un au moins des facteurs est nul. L’ équation produit nul (x + 2)(3 – x) = 0 admet deux решения: -2 et 3. Si un produit de facteur est nul alors l’un au moins des facteurs est nul.
L’ équation produit nul (x + 2)(3 – x) = 0 admet deux решения: -2 et 3. Si un produit de facteur est nul alors l’un au moins des facteurs est nul.
4x² = 5x 4x² – 5x = 0 На случай множителя 1-го члена x(4x – 5) = 0 На множитель 1-го члена, Si un produit est nul , alors l’un au moins des facteurs est nul .
Комментарий Преобразователь ип problème en équation ?Первые шаги по мизе по номеру , уравнение :
Резолюция по уравнению : По результатам по уравнению creée avec la méthodehavuelle. Вывод: на вопрос posée dans l’énonce par une фраза en français. Проверка: Les valeurs trouvées dans la troisieme étape, doivent être des Solutions du probleme de départ.
Комментарий savoir si une équation est produit nul ? com/embed/APj1WPPNUgo» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″> Qu’est-ce qu’un facteur non nul ?Qu ‘ est ce qu ‘un nombre relatif non – nul ? C’ est un nombre positif ou négatif mais pas zero.
Комментарий fonctionne une équation ?Dans une équation , les deux côtés du signe égal doivent être égaux, toujours ! Nous pouvons déplacer des termes d’un côté à l’autre du signe égal, mais toujours de façon que l’égalité des deux membres de l’ équation reste vraie.
Комментарий факторизатор по уравнению продукта ? 1 ère Метод: Залить факторизатором , на cherche un facteur commun. Une équation est dite du second degré lorsque que l’inconnue est à la puissance 2 dans l’ équation . а) уравнение « произведений » : ( 2x – 8 ) ( x + 3 ) = 0 оценка уравнение произведения .
Шесть х 1 et x 2 sont les racines d’un polynôme du second degré ax 2 + bx + c, alors ilse factorise sous la forme a(x − x 8) 91×16 х 2 ). Si x 0 является уникальным расом полинома второй степени ax 2 + bx + c, кроме того, что факторизуется sous la forme a(x − x 0 ) 8 9.147 8.
Комментарий Как найти решение для решения сложной проблемы?Не начинайте работу с номером по номеру le problème . Essayez d’abord de comprendre son origine. Используйте вопросы для générer des idées visant à résoudre le problème . Изучите проблем précédents pour trouver les réponses aux nouveaux problèmes .
Комментарий к fait pour résoudre un problème ?- Дефинир ле проблема предатель.
 La première étape est de bien intégrer les tenants et aboutissants de la problematique à résoudre . …
La première étape est de bien intégrer les tenants et aboutissants de la problematique à résoudre . … - Файл идентификаторов причин. …
- Единый раствор. …
- Lancer les action : Метр в творчестве ла решения retenue. …
- Suivre l’efficacité de la solution et de sa mise en oeuvre.
Évaluez вос решения.
Posez-vous quelques questions qui peuvent vous aider à décider de privilégier une approche par rapport aux autres. Требуемый пример X Источник из поиск : си ла решение ва vraiment résoudre votre problème . это решение является эффективным в терминах временных ресурсов и необходимых ресурсов.
C’est quoi un nombre non nul ? Un nombre négatif est un nombre réel inférieur ou égal à 0 : donc 0 ; et par example -1, -2… Les nombres négatifs non nuls sont resentés avec un signe – placé à gauche. Le nombre zéro est à la fois positif et négatif.
Le nombre zéro est à la fois positif et négatif.
Un Nombre Réel est un nombre qui peut s’écrire sous la forme d’un entier suivi d’un nombre fini ou infini de decimales (chiffres après la virgule). Les nombres entiers, Les Fractions sont des nombres réels . Пример: Pi est un nombre réel .
Qu’est-ce qu’un entier naturel non nul ?Un nombre entier naturel (или simplement un naturel ) est un nombre qui permet de dénombrer des objets. Премьеры naturalls s’écrivent selon la notation decimale comme suit : 0, 1, 2, 3… L’ensemble des naturels se note N, et celui des naturels non nuls se note N0 ou N∗.
Комментарий факторизатора une expression littérale 3eme ?Залейте факторизатором и литтеральным выражением :
- Идентифицируйте продукты.

- О repère un facteur commun.
- S’il n’y a pas de facteur commun, при использовании 3 identités remarquables ci-dessous:
Si un полином P de градус 3 добавленный расин réelle α , кроме того полином est факторизуемая часть (x-α). по алору: P(x) = (x −α)×Q(x) или Q(x) определяется полиномом степени 2. Использование: Le полиномом P(x) = x3 −4×2 − 7x +10 admet comme racine évidente le nombre 1.
Comment factoriser une inéquation ?Théorème: Lorsque le diversant est nul, on peut факторизатор ax²+bx+c sous la forme a(x-x1)² où x1 является уникальным расовым числом полиномов. Значение имени ax²+bx+c=a(x-x1)² является положительным или нулевым; ce nombre est nul lorsque x=x1.
Комментарий trouver la forme factoriser ? Pour passer de la form factorisée à la form générale, il suffit de développer de développer de façon algébrique l’équation de la fonction.

 7у=-0,34
7у=-0,34

 7у=-0,34
7у=-0,34

 Значит, можно записать равенства:
Значит, можно записать равенства: