14. Что обозначает римская прописная буква с или римская цифра II, нанесенная на панели прибора?
Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита тем больше значения допускаемой абсолютной погрешности. Буквенное обозначение принято для мер с аддитивной погрешностью, цифра ΙΙΙ для мер с обоими оставляющими погрешности
15. Какое обозначение принято для приборов с существенно неравномерной шкалой?
Для приборов с существенно неравномерной шкалой нормирующее значение устанавливается равным длине шкалы или ее части, соответствующей диапазону измерений. В этом случае предел абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на шкалу прибора наносится обозначение класса точности в виде цифры под которой находится знак .
Например,
обозначение класса точности означает, что для данного прибора
установлен предел допускаемой погрешности,
составляющей 2,5% от длины шкалы,
действительное значение измеряемой
величины должно находиться в пределах
±2,5% от длины шкалы, отсчитанных от
установившегося положения стрелки.
Обозначения классов точности в документах и на приборах приведены в табл. 2.
Таблица 2
16. Привести алгоритм статистической обработки результатов многократных измерений фв.
Правила обработки прямых многократных измерений учитывают следующие факторы:
обрабатываются результаты конечной серии из n измерений физической величины Х;
результаты измерений Хi могут содержать как случайную, так и систематическую погрешности;
в серии могут встречаться грубые ошибки или промахи;
распределение случайных погрешностей может отличаться от нормального
Обработка результатов многократных измерений должна осуществляться по следующему алгоритму:
1.
Исключить известные систематические
погрешности (например методическую
погрешность) из результатов измерений
(введением поправки).
2. Вычислить среднее арифметическое из исправленных результатов измерений, принимаемое за действительное значение измеряемой величины.
3. Вычислить среднеквадратичное отклонение (СКО) результатов измерений σ.
4. Проверить наличие в группе наблюдений грубых погрешностей (промахов), исходя из того, что при нормальном законе распределения f(Δ) ни одна абсолютная погрешность = —случайного характера с вероятностью Р=0,997 не может выйти за пределы ±3σ. Наблюдения, не удовлетворяющие этому критерию, исключаются из группы и снова повторяют вычисления и σ.
5. Вычислить оценку по формуле (7).
6. Проверить гипотезу о том, что результаты измерений , а также абсолютная погрешность принадлежат нормальному распределению.
П
риближенно
это можно сделать по критерию
,
или построив гистограмму. Строго это
определяется с использованием критериев
Пирсона, Мизеса-Смирнова и др. При n<15
нормальность распределения не проверяется (распределение Стьюдента).
При n<15
нормальность распределения не проверяется (распределение Стьюдента).
7. Вычислить доверительные границы случайной погрешности результата измерения при заданной доверительной вероятности Р, =± , где коэффициент Стьюдента.
8. Вычислить границы, суммарной неисключенной систематической погрешности (НСП) средства измерений, которая складывается из основной и дополнительных.
9. Вычислить доверительные границы погрешности результата измерений для случаев
Кто придумал первые цифры?
Прежде всего, нужно напомнить, что цифры и числа – не одно и то же. Цифрами мы называем особые знаки, которые обозначают числа.
Ответ на вопрос, кто придумал такие значки, и кто стал ими впервые пользоваться, не так прост. Очевидно, что человек сначала научился считать, то есть усвоил, что в мире все можно измерить, всему присвоить числовое значение. Изобретя письменность, люди задумались и над тем, чтобы обозначить числа какими-то особыми знаками.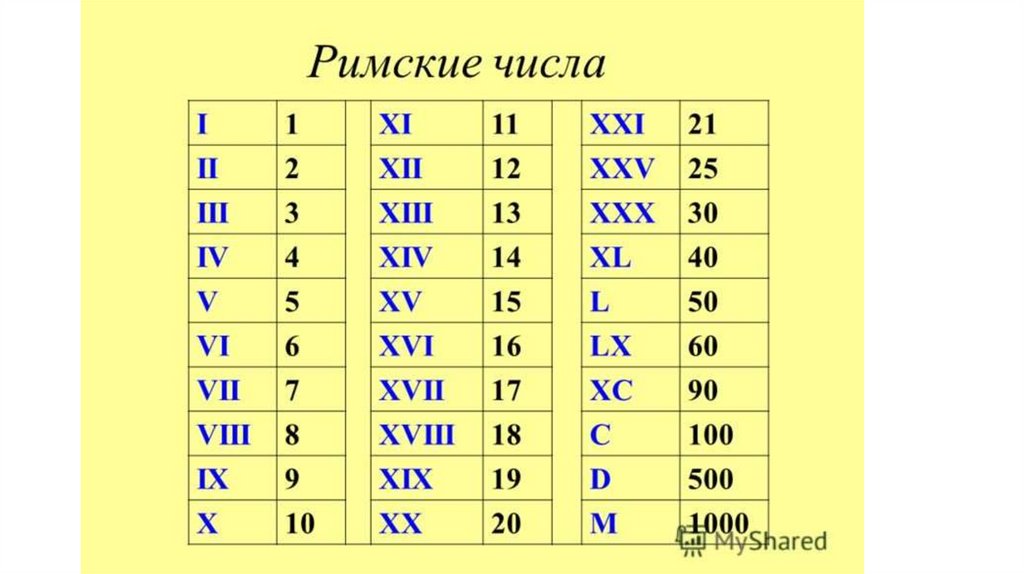
Самая первая числовая символика
Изначально это были засечки, которые делались палочкой на мягком материале, или вырезались. Одна засечка – число 1, две – 2 и так далее. Причем в самых древних сохранившихся документах количество засечек соответствовало тому числу, которое выражалось – например, тысяча. Прошло немало столетий, прежде чем люди додумались до того, что числам нужно присвоить разряды и обозначать крупные величины отдельными знаками. Это значительно упростило запись,
Считается, что самые первые численные обозначения появились в Древнем Египте и в древнем Вавилоне. Египтяне разработали иероглифическое письмо, в котором числа обозначались черточками, а разряды – особыми символами. Начиная со ста, это было стилизованное изображение священного египетского животного – кошки.
Огромный скачок в обозначении чисел сделали древние вавилоняне. Они изобрели позиционную запись, в которой имеет значение место знака в последовательности. В Вавилоне пользовались шестидесятиричной системой счисления, которой мы пользуемся и по сей день, определяя время (наш час разделен на 60 минут, минута – на 60 секунд).
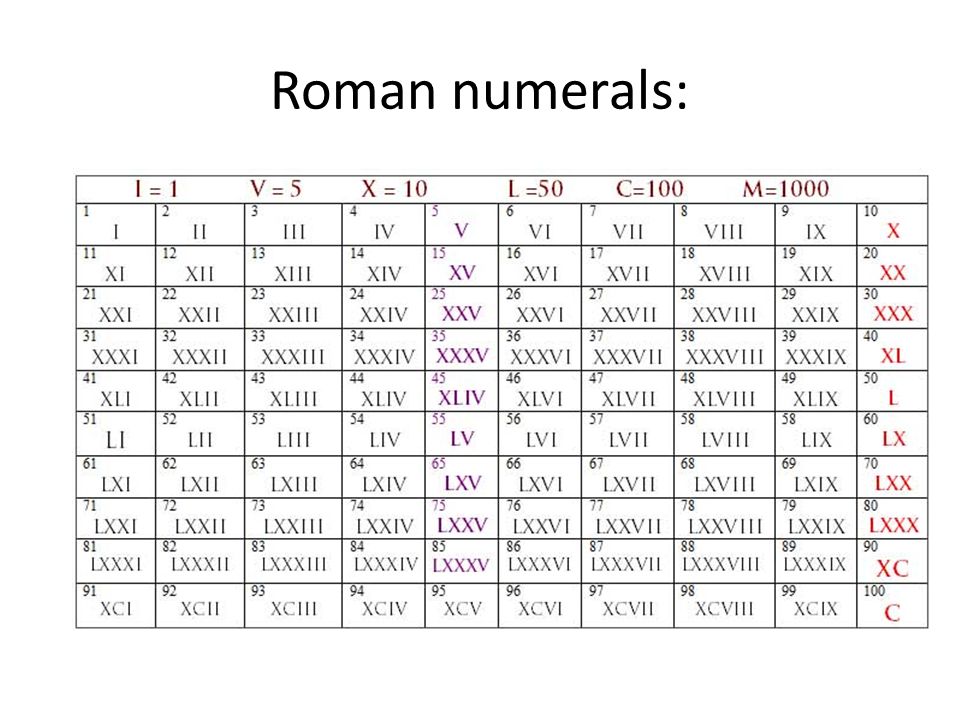
Древние римляне придумали свои цифры. Римские цифры в ходу до сих пор, но сфера их применения строго ограничена. Римскими цифрами обозначают, например, столетия и номера глав в книге. Взглянув на эти знаки, можно сразу понять, что и они ведут свою историю от простейших зарубок – полосок.
Римская цифровая запись не позиционная: понять, какое число обозначено цифрами, можно совершив определенные арифметические действия – сложить или вычесть числа по определенному алгоритму. Записать римскими цифрами большие числа очень сложно, а использовать эти записи для вычислений практически невозможно.
Откуда взялись современные цифры?
Заслуга изобретения современных цифр (а именно их можно считать настоящими цифрами) принадлежит индусам. В пятом веке нашей эры они сделали важнейшее открытие: ввели в математический обиход понятие ноля и придумали для него знак – пустоту, обведенную в кружок. Насколько открытие ноля было важным, говорит тот факт, что в переводе с арабского само слово «Сыфр» (от которого произошло наше «цифра») обозначает именно ноль. Остальные цифры от 1 до 9 индийцы записывали с помощью простейших символов, похожих на те, которыми мы пользуемся сейчас.
Остальные цифры от 1 до 9 индийцы записывали с помощью простейших символов, похожих на те, которыми мы пользуемся сейчас.
Индусы стали представлять числа позиционным способом, когда число десятков, сотен, тысяч и других разрядов обозначается одной цифрой, стоящей на определенной позиции. Эту традицию они переняли у вавилонян. Стало возможным не просто записывать любые числа от нуля до бесконечности, но и проводить с ними математические операции.
А как индийские цифры попали в Европу и почему мы называем их арабскими? Арабы тесно контактировали с индийцами, вели оживленную торговлю. Кроме того, в арабских странах того времени активно развивались науки, культура и бизнес, а для этого было совершенно необходимо заниматься математикой. Арабы восприняли индийские цифры, начали ими пользоваться.
Известно имя человека, который впервые применил десятичную позиционную запись чисел по индийской методике и популяризировал данную идею в арабском мире. Это был персидский ученый Мухаммед ибн Муса аль-Хорезми, написавший свой знаменитый трактат по арифметике. В книге он изложил основы индийского счета и цифровой записи.
В книге он изложил основы индийского счета и цифровой записи.
Это произошло в 9-м веке нашей эры. Новая система быстро распространилась на Ближнем Востоке, а в 10-13 веках попала и в Европу. В европейских странах арабские цифры изначально использовались при чеканке монет, затем – при нумерации страниц в книгах, в документах и т.д.
Арабская система цифровой записи позволила человечеству сделать огромный скачок в науке, экономике, образовании. Эту систему способен усвоить любой дошкольник, она стала привычной, и мы редко задумываемся о том, что когда-то для записи больших чисел людям приходилось рисовать множество палочек или изображать на папирусе кошку!
Amazon.com: римская цифра 36 XXXVI Рубашка: одежда, обувь и украшения
Узнать больше
Видно краткое содержание, дважды нажмите, чтобы прочитать полное содержание.
Отображается полный контент, дважды нажмите, чтобы прочитать краткий контент.
Обновлены другие варианты на основе этого выбора
Посмотреть все 5 вариантов
Мужчины
4
40003
Молодежь
Обновлены другие варианты на основе этого выбора
Посмотреть все 3 варианта
-
Маленький
Средний
Большой
Большой
ХХ-большой
3X-большой
2T
См.
 доступные варианты
доступные варианты3T
См. доступные варианты
4Т
См. доступные опции
X-Small
См. доступные варианты
Обновлены другие параметры на основе этого выбора
Просмотреть все 10 вариантов
Римские цифры: 36 = XXXVI
« 3537 »
Преобразовать римские цифры
арабские цифры:
Римские цифры:
Конвертер позволяет перейти от арабских цифр к римским и наоборот.
Чтобы легко преобразовать римские и арабские цифры, вы можете использовать таблицу выше. Ключ состоит в том, чтобы обрабатывать по одной арабской цифре за раз и переводить ее в правильное римское число, где нули становятся пустыми. Используйте конвертер и наблюдайте, как таблица показывает решение в реальном времени!
Текущая дата и время римскими цифрами
| 2023-01-30 | 20:45:06 |
| MMXXIII-I-XXX | ХХ:XLV:VI |
Здесь текущая дата и время написаны римскими цифрами. Поскольку в римской системе счисления нет нуля, час, минута и секунда в метках времени иногда становятся пустыми.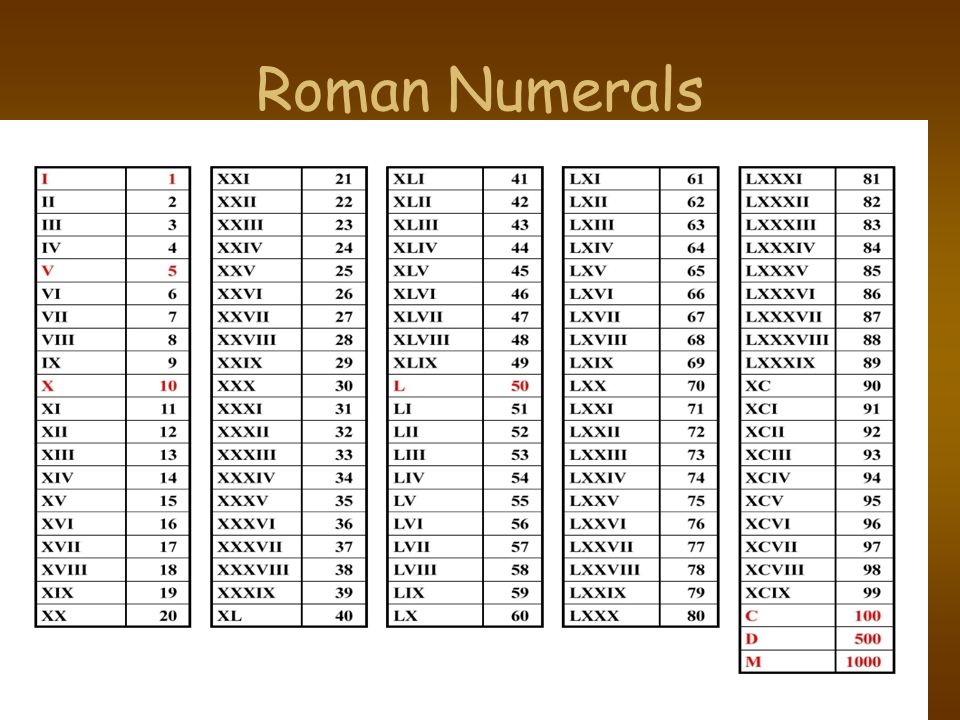
Год 36
Здесь вы можете прочитать больше о том, что произошло в 36 году.
Число 36
Число 36 делится на 2, 3, 4, 6, 9, 12 и 18 и может быть разложено на простые множители как 2 2 × 3 2 .
36 в виде двоичного числа: 100100
36 в виде восьмеричного числа: 44
36 в виде шестнадцатеричного числа: 24
Химическим элементом с атомным номером 36 является криптон (Kr).
Номера близкие к 36
Ниже приведены числа от 33 до 39, которые близки к 36. В правой колонке показано, как каждая римская цифра составляет общую сумму.
| 33 | = | XXXIII | 10 + 10 + 10 + 1 + 1 + 1 | |||||||||||
| 34 | = | XXXIV | = | 10 + 10 + 10 + 5 − 1 | ||||||||||
| 35 | = | XXXV | = | 10 + 10 + 10 + 5 | ||||||||||
| 36 | = | XXXVI | = | 10 + 10 + 10 + 5 + 1 | ||||||||||
| 37 | = | XXXVII | = | 10 + 10 + 10 + 5 + 1 + 1 | ||||||||||
| 38 | = | XXXVIII | = | 10 + 10 + 10 + 5 1 + 1 | = | 10 + 10 + 5 1 + 1 | = | 10 + 10 + 5 1 + 1 | = | 10 + 10 + 1 + 1 | .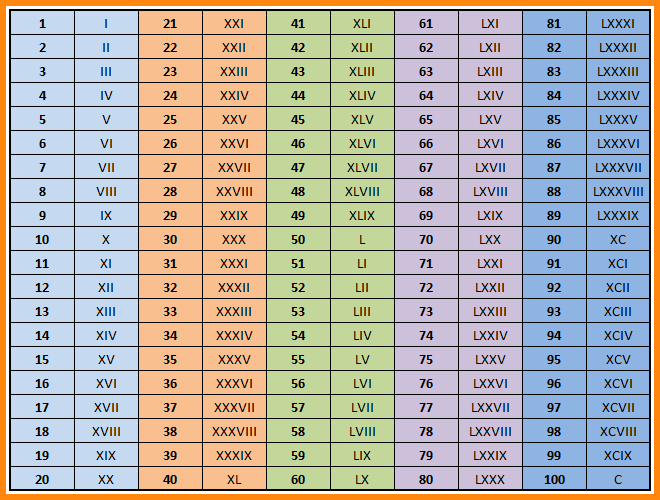 | XXXIX | = | 10 + 10 + 10 + 10 — 1 |
О римских цифрах
Римские цифры происходят, как следует из названия, из Древней Римской империи. В отличие от нашей позиционной системы с основанием 10, римская система основана на сложении (а иногда и вычитании) семи различных значений. Это символы, используемые для представления этих значений:
| Символ | Значение |
| I | 1 |
| В0129 | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Например, чтобы выразить число 737 римскими цифрами, вы пишете DCCXXXVII, то есть 500 + 100 + 100 + 10 + 10 + 10 + 5 + 1 + 1. Однако для чисел 4 и 9 вместо сложения используется вычитание. , и меньшее число записывается перед большим числом: например.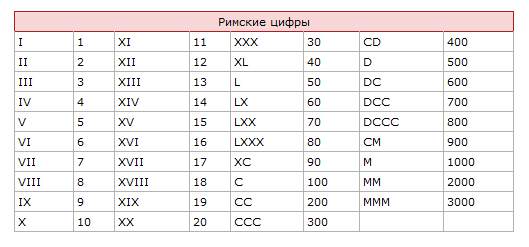

 доступные варианты
доступные варианты