Рівнобедрена трапеція: Рівнобедрена трапеція — урок. Геометрія, 8 клас.

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Навигация по странице: Определение равнобедренной трапеции Признаки равнобедренной трапеции Основные свойства равнобедренной трапеции Стороны равнобедренной трапеции Средняя линия равнобедренной трапеции Высота равнобедренной трапеции Диагонали равнобедренной трапеции Площадь равнобедренной трапеции Окружность описанная вокруг равнобедренной трапеции

Формулы и свойства трапеции

Определение.

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

Рис.1

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можно описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h²

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h² = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC² + BD² = AB² + CD² + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC, HF ┴ AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD — BC
	2

10. Также смотрите свойства трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a — 2h ctg α = a — 2c cos α

c =	h	=	a — b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d12 — c2	b =	d12 — c2	c = √d12 — ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b      b =	2S	— a
	h		h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	(a + b) sin α

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a — h ctg α = b + h ctg α = a — √c² — h² = b + √c² — h²

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1.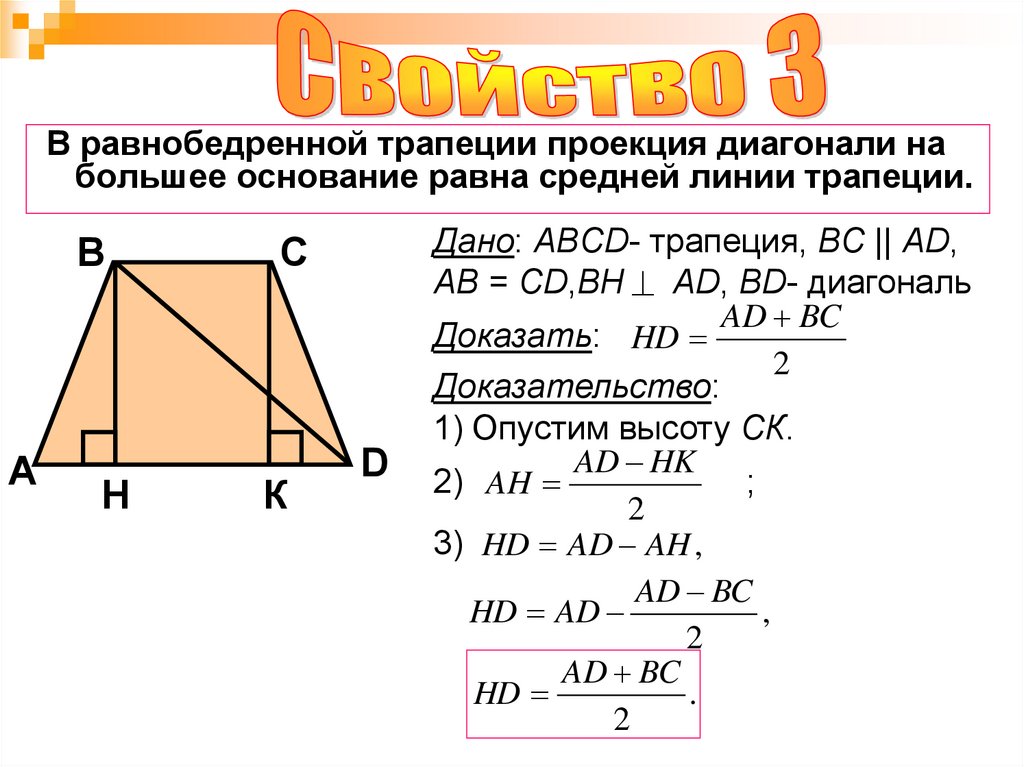 Формула высоты через стороны:

h =	1	√4c2 — (a — b)2
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
	2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с² + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a² + c² — 2ac cos α

d₁ = √b² + c² — 2bc cos β

3.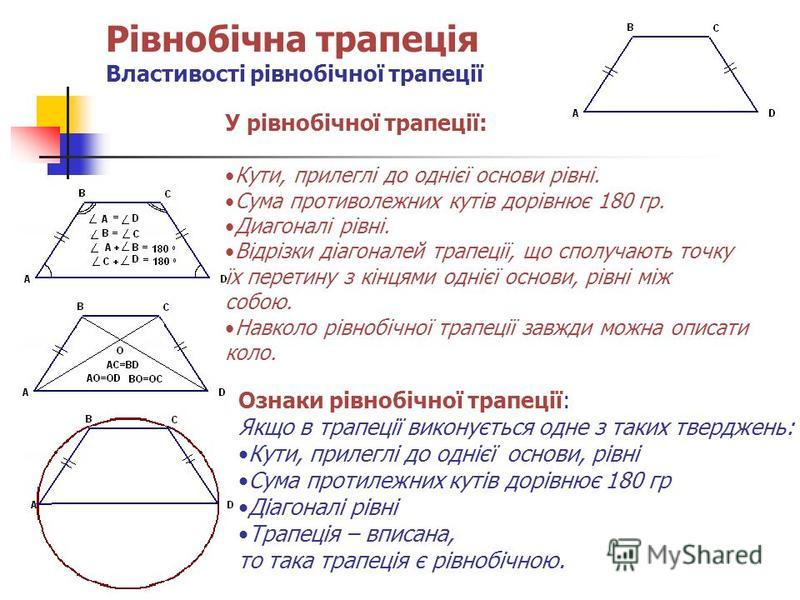 Формула длины диагонали через высоту и среднюю линию:

d₁ = √h² + m²

4. Формула длины диагонали через высоту и основания:

d1 =	1	√4h2 + (a + b)2
	2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c2 — (a — b)2
	4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a — c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
	sin α		sin β

4. Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площади через диагонали и угол между ними:

S =	d12	· sin γ	=	d12	· sin δ
	2			2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

S =	a + b	· h
	2

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d 1
	2

a — большее основание

Все таблицы и формулы

Рівнобедрена трапеція: властивості, співвідношення та формули, приклади — Наука

Відеоролик: Площа трапеції. Формула. Задача

Зміст

• Властивості
• Ексклюзивна для рівнобедреної трапеції
• Для всіх трапецій
• Відносини та формули
• Унікальні стосунки рівнобедреної трапеції
• Відносини для будь-якої трапеції
• Відносини для рівнобедреної трапеції з вписаним колом
• Формули для визначення однієї сторони, знання інших та кута
• Визначення однієї сторони, знання інших та діагоналі
• Основа по висоті, площі та іншій основі
• Відомі бічні основи, площа та кут
• Відомі бічні медіана, площа та кут
• Відома висота бортів
• Відома висота кута і двох сторін
• Відомі діагоналі всіх сторін, або дві сторони та кут
• Периметр рівнобедреного трикутника
• Площа рівнобедреної трапеції
• -Якщо сторони відомі
• -Коли у вас є дві сторони та кут
• -Якщо відомі радіус вписаного кола та кут
• -Коли основи та кут відомі
• -Якщо на трапецію можна вписати окружність
• -Знайти діагоналі та кут, який вони утворюють між собою
• -Коли у вас є бічні, медіана та кут
• Радіус описаного кола
• Приклади використання рівнобедреної трапеції
• В архітектурі та будівництві
• У дизайні
• Розв’язані вправи
• — Вправа 1
• Рішення для
• Рішення б
• Рішення c
• Рішення d
• — Вправа 2
• Рішення для
• Рішення б
• Рішення c
• Рішення d
• Список літератури

A трапеціярівнобедренийє чотирикутником, у якому дві зі сторін паралельні одна одній, а також два кути, що прилягають до однієї з цих паралельних сторін, мають однакову міру.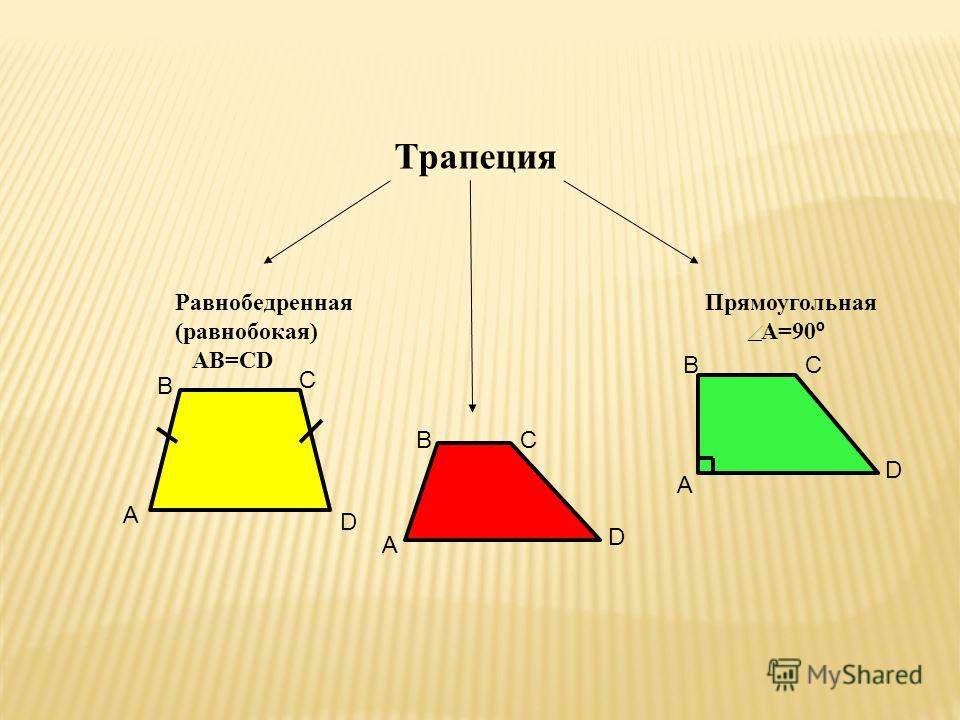

На малюнку 1 ми маємо чотирикутник ABCD, у якому сторони AD і BC паралельні. Крім того, кути ∠DAB і ∠ADC, прилеглі до паралельної сторони AD, мають однакову міру α.

Отже, цей чотирикутник, або чотиригранний многокутник, насправді є рівнобедреною трапецією.

У трапеції називаються паралельні сторони бази і називаються непаралелі бічні. Ще однією важливою особливістю є висота, що становить відстань, що розділяє паралельні сторони.

Крім рівнобедреної трапеції існують і інші типи трапеції:

-Тморська морська риба, який має всі різні кути та сторони.

-Тпрямокутник рибалка, у яких бічний бік має прямі суміжні кути.

Трапецієвидна форма поширена в різних областях дизайну, архітектури, електроніки, розрахунків та багатьох інших, як це буде видно пізніше. Звідси важливість ознайомлення з його властивостями.

Властивості

Ексклюзивна для рівнобедреної трапеції

Якщо трапеція рівнобедрена, то вона має такі характерні властивості:

1.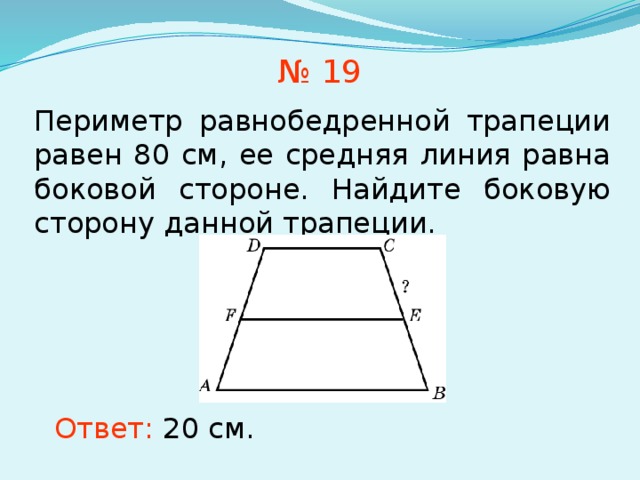 — Сторони мають однакові виміри.

2.- Кути, прилеглі до основ, рівні.

3. — Протилежні кути є додатковими.

4. — Діагоналі мають однакову довжину, два відрізки, які приєднуються до протилежних вершин, однакові.

5. — Кут, утворений між основами та діагоналями, однаковий.

6. — Він має обмежену окружність.

І навпаки, якщо трапеція відповідає будь-якому з вищезазначених властивостей, то це рівнобедрена трапеція.

Якщо в рівнобедреній трапеції один із кутів є правильним (90º), то всі інші кути також будуть прямими, утворюючи прямокутник. Тобто, прямокутник — це приватний випадок рівнобедреної трапеції.

Для всіх трапецій

Наступний набір властивостей дійсний для будь-якої трапеції:

7. — The медіана трапеції, тобто відрізок, який приєднується до середин його непаралельних сторін, паралельний будь-якій з основ.

8. — Довжина медіани дорівнює півсуму (сума, поділена на 2) довжини її основ.

9. — Медіана трапеції обрізає її діагоналі в середній точці.

10.- Діагоналі трапеції перетинаються в точці, яка ділить їх на два перерізи, пропорційні часткам основ.

11.- Сума квадратів діагоналей трапеції дорівнює сумі квадратів її сторін плюс подвійний добуток її основ.

12. — Відрізок, який приєднується до середніх точок діагоналей, має довжину, рівну напіввідмінності основ.

13. — Кути, прилеглі до бічних, є додатковими.

14.- Трапеція має вписану окружність тоді і тільки тоді, коли сума її основ дорівнює сумі її сторін.

15. — Якщо трапеція має вписану окружність, то кути з вершиною в центрі згаданої окружності та сторони, що проходять через кінці тієї ж сторони, є прямими кутами.

Відносини та формули

Наступний набір взаємозв’язків та формул відноситься до фігури 3, де на додаток до рівнобедреної трапеції показані інші важливі вже згадані сегменти, такі як діагоналі, висота та медіана.

Унікальні стосунки рівнобедреної трапеції

1. — AB = DC = c = d

2. — ∡DAB = ∡CDA і ∡ABC = ∡BCD

3. — ∡DAB + ∡BCD = 180º та ∡CDA + ∡ABC = 180º

4. — BD = AC

5. — ADCAD = ∡BDA = ∡CBD = ∡BCA = α₁

6. — A, B, C і D належать до описаної окружності.

Відносини для будь-якої трапеції

1. Якщо AK = KB і DL = LC ⇒ KL || AD та KL || Е

8. — KL = (AD + BC) / 2

9. — AM = MC = AC / 2 і DN = NB = DB / 2

10.- AO / OC = AD / BC і DO / OB = AD / BC

11. — змінного струму² + БД² = AB² + Постійний струм² + 2⋅AD⋅ до н.е.

12. — MN = (AD — BC) / 2

13.- ∡DAB + ∡ABC = 180º та ∡CDA + ∡BCD = 180º

14. — Якщо AD + BC = AB + DC ⇒ ∃ R, ніж рівновіддалені від AD, BC, AB та DC

15. — Якщо ∃ R рівновіддалене від AD, BC, AB і DC, то:

∡BRA = ∡DRC = 90º

Відносини для рівнобедреної трапеції з вписаним колом

Якщо в рівнобедреній трапеції сума основ дорівнює подвійному бічному, то вписана окружність існує.

Наступні властивості застосовуються, коли рівнобедрена трапеція має вписану окружність (див. Малюнок 4 вище):

16. — KL = AB = DC = (AD + BC) / 2

17.- Діагоналі перетинаються під прямим кутом: AC ⊥ BD

18. — Висота вимірюється так само, як і медіана: HF = KL, тобто h = m.

19.- Квадрат висоти дорівнює добутку основ: h² = BC⋅AD

20. — За цих конкретних умов площа трапеції дорівнює квадрату висоти або добутку основ: Площа = h² = BC⋅AD.

Формули для визначення однієї сторони, знання інших та кута

Знаючи основу, бічний та кут, іншу основу можна визначити за:

a = b + 2c Cos α

b = a — 2c Cos α

Якщо довжину основ і кут навести як відомі дані, то довжини обох сторін:

c = (a — b) / (2 Cos α)

Визначення однієї сторони, знання інших та діагоналі

a = (d₁² — c²) / b;

b = (d₁² — c²) / до

c = √ (d₁² — a⋅b)

Де d₁ — довжина діагоналей.

Основа по висоті, площі та іншій основі

a = (2 A) / год — b

b = (2 A) / год — a

Відомі бічні основи, площа та кут

c = (2A) / [(a + b) sin α]

Відомі бічні медіана, площа та кут

c = A / (m sin α)

Відома висота бортів

h = √ [4 c² — (а — б)²]

Відома висота кута і двох сторін

h = tg α⋅ (a — b) / 2 = c. гріх α

Відомі діагоналі всіх сторін, або дві сторони та кут

d₁ = √ (c²+ а б)

d₁ = √ (а²+ c² — 2 a c Cos α)

d₁ = √ (b² + c²— 2 b c Cos β)

Периметр рівнобедреного трикутника

P = a + b + 2c

Площа рівнобедреної трапеції

Існує кілька формул для обчислення площі залежно від відомих даних. Наступне є найбільш відомим, залежно від підстав та висоти:

A = h⋅ (a + b) / 2

А також ви можете використовувати такі інші:

-Якщо сторони відомі

A = [(a + b) / 4] √ [4c² — (а — б)²]

-Коли у вас є дві сторони та кут

A = (b + c Cos α) c Sen α = (a — c Cos α) c Sen α

-Якщо відомі радіус вписаного кола та кут

A = 4 r² / Sen α = 4 r² / Сен β

-Коли основи та кут відомі

A = a⋅b / Sen α = a⋅b / Sen β

-Якщо на трапецію можна вписати окружність

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2

-Знайти діагоналі та кут, який вони утворюють між собою

A = (d₁²/ 2) Sen γ = (d₁² / 2) Сен δ

-Коли у вас є бічні, медіана та кут

A = mc.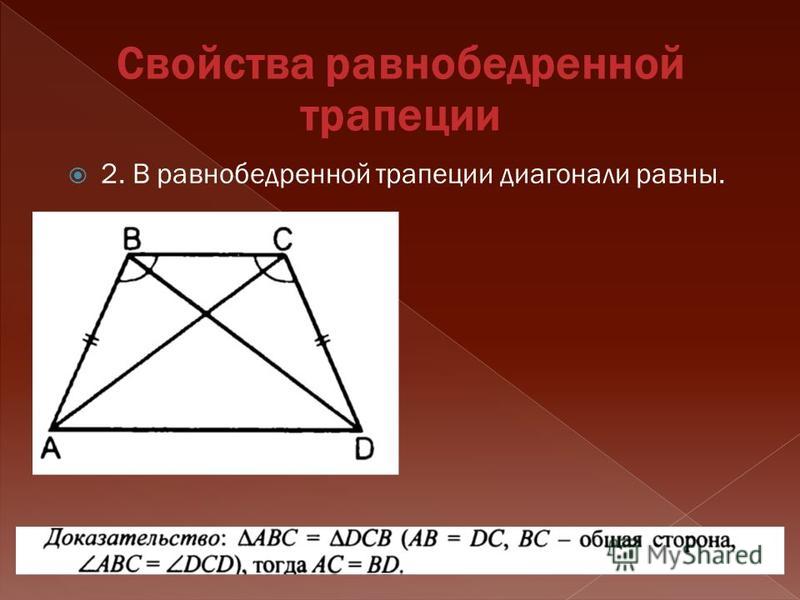 sen α = mc.sen β

Радіус описаного кола

Тільки рівнобедрені трапеції мають обмежену окружність. Якщо більша основа a, відомі бічні c і діагональ d₁, то радіус R кола, що проходить через чотири вершини трапеції, дорівнює:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p — d₁)]

Де p = (a + c + d₁) / 2

Приклади використання рівнобедреної трапеції

Рівнобедрена трапеція з’являється в галузі дизайну, як видно на малюнку 2. І ось кілька додаткових прикладів:

В архітектурі та будівництві

Древні інки знали рівнобедрену трапецію і використовували її як будівельний елемент у цьому вікні в Куско, Перу:

І тут у дзвінку знову з’являється трапеція трапецієподібний лист, матеріал, який часто використовується в будівництві:

У дизайні

Ми вже бачили, що рівнобедрена трапеція з’являється у повсякденних предметах, включаючи такі продукти, як ця плитка шоколаду:

Розв’язані вправи

— Вправа 1

Рівнобедрена трапеція має основу більше 9 см, основу менше 3 см, а діагоналі — 8 см кожна. Обчислити:

а) Бічні

б) Висота

в) Периметр

г) Площа

Рішення для

Нанесено висоту CP = h, де підніжжя висоти визначає сегменти:

PD = x = (a-b) / 2 y

AP = a — x = a — a / 2 + b / 2 = (a + b) / 2.

Використовуючи теорему Піфагора до прямокутного трикутника DPC:

c² = h² + (а — б)² /4

А також до прямокутного трикутника APC:

d² = h² + AP² = h² + (a + b)² /4

Нарешті, член за членом, друге рівняння віднімається від першого та спрощується:

d² — c² = ¼ [(a + b)² — (a-b)²] = ¼ [(a + b + a-b) (a + b-a + b)]

d² — c² = ¼ [2a 2b] = a b

c²= d² — a b ⇒ c = √ (d² — a b) = √ (8² — 9⋅3) = √37 = 6,08 см

Рішення б

h² = d² — (a + b)² /4= 8² – (12² / 2² )= 8² – 6² = 28

h = 2 √7 = 5,29 см

Рішення c

Периметр = a + b + 2 c = 9 + 3 + 2⋅6. 083 = 24.166 см

Рішення d

Площа = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 см

— Вправа 2

Існує рівнобедрена трапеція, більша основа якої вдвічі менша, а менша основа дорівнює висоті, яка дорівнює 6 см. Вирішіть:

а) Довжина бічного

б) Периметр

в) Площа

г) Кути

Рішення для

Дані: a = 12, b = a / 2 = 6 і h = b = 6

Поступаємо так: малюється висота h і застосовується теорема Піфагора до гіпотенузного трикутника “c” та катетів h і x:

c² = h²+ xc²

Потім вам потрібно обчислити значення висоти за даними (h = b) та значення катету x:

a = b + 2 x ⇒ x = (a-b) / 2

Підставивши попередні вирази, ми маємо:

c² = b²+ (a-b)²/2²

Тепер введені числові значення, і це спрощено:

c² = 62+(12-6)2/4

c² = 62(1+¼)= 62(5/4)

Отримання:

c = 3√5 = 6,71 см

Рішення б

Периметр P = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 см

Рішення c

Площа як функція висоти та довжини основ становить:

A = h⋅ (a + b) / 2 = 6⋅ (12 + 6) / 2 = 54 см²

Рішення d

Кут α, який утворює поперек з більшою основою, отримується тригонометрією:

Загар (α) = h / x = 6/3 = 2

α = ArcTan (2) = 63,44º

Інший кут, той, який утворює бічний бік з меншою основою, це β, який доповнює α:

β = 180º – α = 180º – 63,44º= 116,56º

Список літератури

1. Е. А. 2003. Елементи геометрії: з вправами та геометрією компаса. Університет Медельїна.
2. Кампос, Ф. 2014. Математика 2. Grupo Editorial Patria.
3. Фрід, К. 2007. Відкрийте багатокутники. Бенчмарк освітня компанія.
4. Хендрік, В. 2013. Узагальнені багатокутники. Біркхейзер.
5. ІГЕР. Математика Перший семестр Такана. ІГЕР.
6. Геометрія-молодший. 2014. Багатокутники. Lulu Press, Inc.
7. Міллер, Хірен та Хорнсбі. 2006. Математика: міркування та застосування. 10-й. Видання. Пірсон Освіта.
8. Патіньо, М. 2006. Математика 5. Редакційне прогресо.
9. Вікіпедія. Трапеція. Відновлено з: es.wikipedia.com

Рівнобедрена трапеція

В Евклідова геометрія, ан рівнобедрена трапеція (рівнобедрена трапеція в Британська англійська мова ) є опуклі чотирикутник з рядком симетрія ділення навпіл однієї пари протилежних сторін. Це приватний випадок трапеція. Як варіант, його можна визначити як a трапеція при якому обидві ніжки та обидва базові кути мають однакову міру. ^[1] Зверніть увагу, що не прямокутний паралелограм не є рівнобедреною трапецією через другу умову або тому, що не має лінії симетрії. У будь-якої рівнобедреної трапеції є дві протилежні сторони (основи) паралельний, а дві інші сторони (катети) мають однакову довжину (властивості, спільні з паралелограм ). Діагоналі також мають однакову довжину. Базові кути рівнобедреної трапеції рівні за мірою (насправді є дві пари рівних базових кутів, де один базовий кут є додатковий кут кута основи на іншій основі).

Зміст

• 1 Особливі випадки
  • 1.1 Самоперетинання
• 2 Характеристика
• 3 Кути
• 4 Діагоналі та висота
• 5 Площа
• 6 Циркумрадіус
• 7 Дивитися також
• 8 Список літератури
• 9 зовнішні посилання

Особливі випадки

Особливі випадки рівнобедрених трапеції

Прямокутники і квадрати зазвичай вважаються особливими випадками рівнобедрених трапецій, хоча деякі джерела їх виключають. ^[2]

Інший особливий випадок — 3-рівна бічна трапеція, іноді відомий як a тристороння трапеція^[3] або a тристоскові трапеції.^[4] Їх також можна побачити у розрізі правильні многокутники з 5 сторін або більше як усічення 4 послідовних вершин.

Самоперетинання

Будь-який несамостійний перехід чотирикутник з рівно однією віссю симетрії повинна бути рівнобедрена трапеція або a змій.^[5] Однак, якщо дозволено перетинання, набір симетричних чотирикутників повинен бути розширений, включаючи також перехрещені рівнобедрені трапеції, перехрещені чотирикутники, у яких перехрещені сторони мають однакову довжину, а інші сторони паралельні, а антипаралелограми, перехрещені чотирикутники, у яких протилежні сторони мають однакову довжину.

Кожен антипаралелограма має рівнобедрену трапецію опуклий корпус, і може утворюватися з діагоналей та непаралельних сторін рівнобедреної трапеції.^[6]

Опуклий рівнобедрений трапеція	Перехрещений рівнобедрений трапеція	антипаралелограма

Характеристика

Якщо відомо, що чотирикутник є трапеція, Це є ні достатньо лише перевірити, що ніжки мають однакову довжину, щоб знати, що це рівнобедрена трапеція, оскільки ромб є особливим випадком трапеції з катетами однакової довжини, але не є рівнобедреною трапецією, оскільки їй бракує лінії симетрії через середини протилежних сторін.

Будь-яка з наступних властивостей відрізняє рівнобедрену трапецію від інших трапецій:

• Діагоналі мають однакову довжину.
• Базові кути мають однакову міру.
• Відрізок, який приєднується до середин паралельних сторін, перпендикулярний до них.
• Протилежні кути є додатковими, що, в свою чергу, означає, що рівнобедрені трапеції є циклічні чотирикутники.
• Діагоналі ділять один одного на відрізки, довжини яких попарно рівні; з точки зору малюнка нижче, AE = DE, БУТИ = CE (і AE ≠ CE якщо хочеться виключити прямокутники).

Кути

У рівнобедреній трапеції базові кути мають однакову міру попарно. На малюнку нижче кути ∠ABC та ∠DCB є тупий кути однакової міри, тоді як кути ∠БАД та ∠CDA є гострі кути, також тієї ж міри.

Оскільки лінії Н.е. і Е паралельні, кути, прилеглі до протилежних основ додаткові, тобто кути ∠ABC + ∠БАД = 180°.

Діагоналі та висота

Ще одна рівнобедрена трапеція. {2}}}.}

Відстань від точки Е на базу Н.е. задається

d=aha+b{ displaystyle d = { frac {ah} {a + b}}}

де a і b — довжини паралельних сторін Н.е. і Е, і h — висота трапеції.

Площа

Площа рівнобедреної (або будь-якої) трапеції дорівнює середньому довжини основи та верху (паралельні сторони), помножений на висоту. На сусідній діаграмі, якщо ми пишемо Н.е. = a, і Е = b, і висота h — довжина відрізка між Н.е. і Е тобто перпендикулярно до них, тоді площа К дається наступним чином:

К=h3(a+b).{ displaystyle K = { frac {h} {2}} ліворуч (a + b праворуч).}

Якщо замість висоти трапеції, загальна довжина ніг AB =CD = c відомо, тоді площа може бути обчислена за допомогою Формула Брахмагупти для площі циклічного чотирикутника, який з двома сторонами, рівними спрощується до

К=(s−a)(s−b)(s−c)2,{ displaystyle K = { sqrt {(s-a) (s-b) (s-c) ^ {2}}},}

-де s=12(a+b+2c){ displaystyle s = { tfrac {1} {2}} (a + b + 2c)} — напівпериметр трапеції. Трапеція на Math34.net: Формули та таблиці [1] Доступ 1 липня 2014 року.

зовнішні посилання

• Деякі інженерні формули із залученням рівнобедрених трапецій

Синус гострого кута трапеції. Кути рівнобедреної трапеції

На просте запитання «Як знайти висоту трапеції?» Існує кілька відповідей, і всі тому, що можуть бути різні вихідні величини. Тому й формули відрізнятимуться.

Ці формули можна запам’ятати, але вони легко виводяться. Потрібно лише застосовувати раніше вивчені теореми.

Прийняті у формулах позначення

У всіх наведених нижче математичних записах вірні такі прочитання букв.

У вихідних даних: всі сторони

Для того, щоб знайти висоту трапеції в загальному випадку потрібно скористатися такою формулою:

н = √(з 2 — (((а — в) 2 + з 2 — d 2)/(2(а — в))) 2).Номер 1.

Не найкоротша, але й зустрічається у завданнях досить рідко. Зазвичай можна скористатися іншими даними.

Формула, яка підкаже, як знайти висоту рівнобедреної трапеції в тій самій ситуації, набагато коротша:

н = √(з 2 — (а — в) 2/4).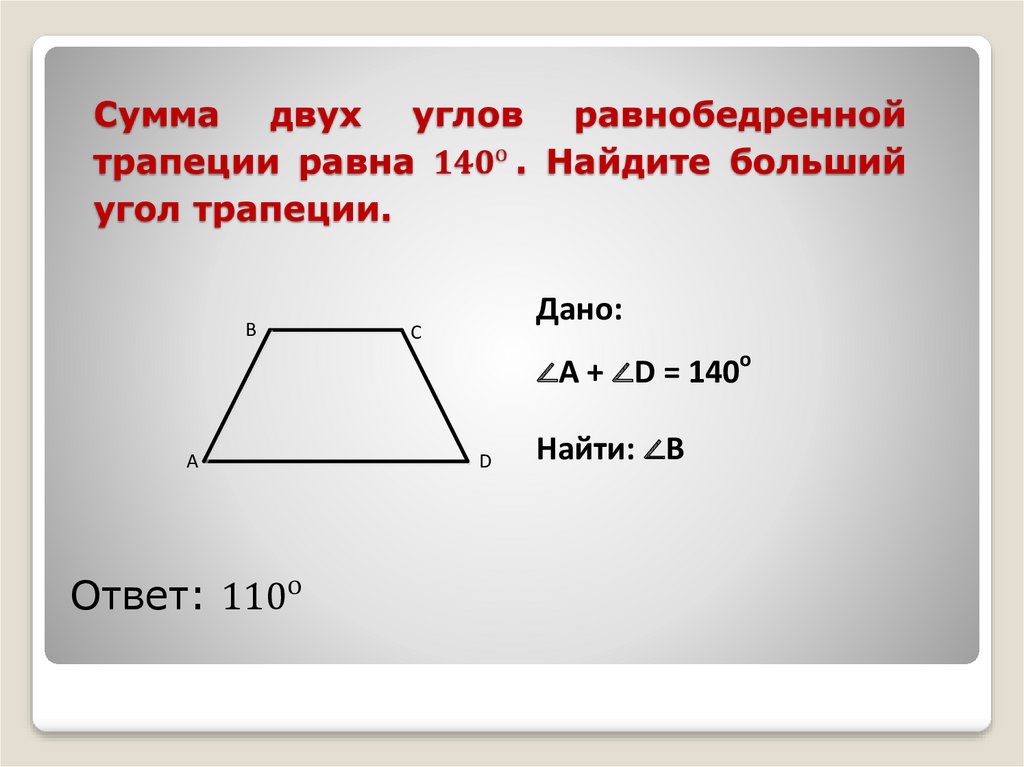 Номер 2.

У задачі дано: бічні сторони та кути при нижній підставі

Приймають, що кут прилягає до бічної сторони з позначенням «с», відповідно кут до сторони d. Тоді формула для того, як знайти висоту трапеції, загалом буде такою:

н = с * sin α = d * sin β.Номер 3.

Якщо фігура рівнобедрена, то можна скористатися таким варіантом:

н = с * sin α = ((а — в) / 2) * tg α.Номер 4.

Відомі: діагоналі та кути між ними

Зазвичай до цих даних приєднуються ще відомі величини. Наприклад, основи або середня лінія. Якщо дані підстави, то відповіді питанням, як знайти висоту трапеції, знадобиться така формула:

н = (d 1 * d 2 * sin γ) / (а + в) або н = (d 1 * d 2 * sin δ) / (а + в).Номер 5.

Це для загального вигляду постаті. Якщо дана рівнобедрена, то запис перетвориться так:

н = (d 1 2 * sin γ) / (а + в) або н = (d 1 2 * sin δ) / (а + в).Номер 6.

Коли в задачі йдеться про середню лінію трапеції, то формули для пошуку її висоти стають такими:

н = (d 1 * d 2 * sin γ) / 2m або н = (d 1 * d 2 * sin δ) / 2m. Номер 5а.

н = (d 1 2 * sin γ) / 2m або н = (d 1 2 * sin δ) / 2m.Номер 6а.

Серед відомих величин: площа з основами або середньою лінією

Це, мабуть, найкоротші і найпростіші формули того, як знайти висоту трапеції. Для довільної фігури вона буде такою:

н = 2S/(а+в).Номер 7.

Вона ж, але із відомою середньою лінією:

н = S/m.Номер 7а.

Як не дивно, але для рівнобедреної трапеції формули виглядатимуть так само.

Завдання

№1. На визначення кутів за нижньої підстави трапеції.

Умова.Дана рівнобедрена трапеція, бічна сторона якої 5 см. Її основи дорівнюють 6 і 12 см. Потрібно знайти синус гострого кута.

Рішення.Для зручності слід ввести позначення. Нехай ліва нижня вершина буде А, решта за годинниковою стрілкою: В, С, Д. Таким чином, нижня основа буде позначена АТ, верхня — ВС.

Потрібно провести висоти з вершин В і С. Точки, які вкажуть кінці висот, будуть позначені Н 1 і Н 2 відповідно.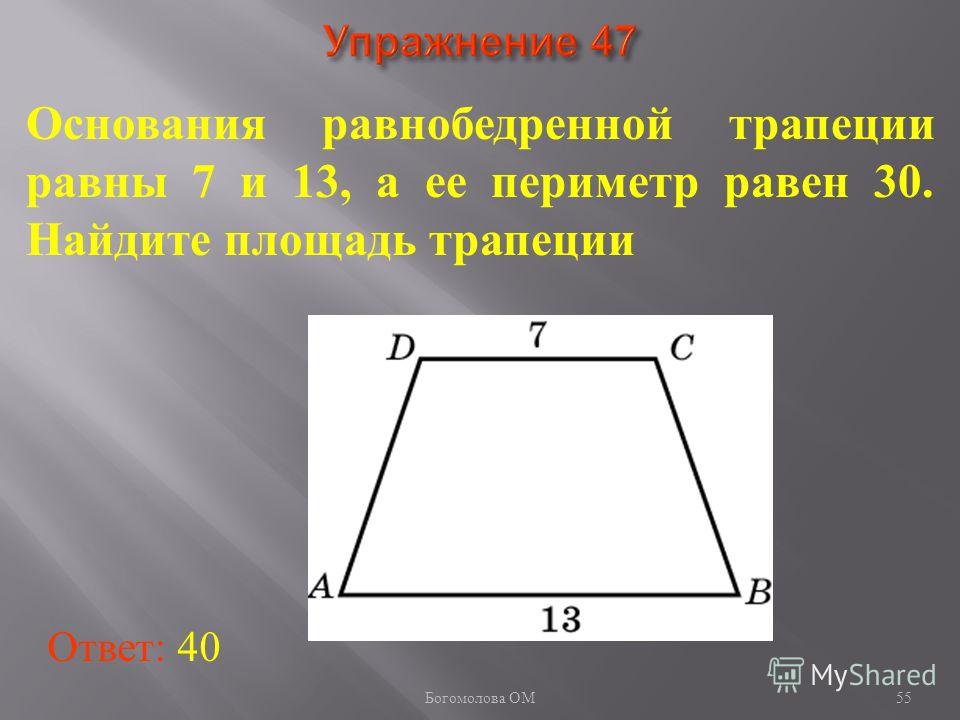 Оскільки у фігурі ВСН 1 Н 2 усі кути прямі, вона є прямокутником. Це означає, що відрізок Н1Н2 дорівнює 6 см.

Тепер потрібно розглянути два трикутники. Вони рівні, оскільки є прямокутними з однаковими гіпотенузами та вертикальними катетами. Звідси випливає, що й менші катети вони рівні. Тому їх можна визначити як окреме від різниці. Остання вийде від віднімання з нижньої основи верхньої. Ділитись воно буде на 2. Тобто 12 – 6 потрібно поділити на 2. АН 1 = Н 2 Д = 3 (см).

Тепер із теореми Піфагора потрібно знайти висоту трапеції. Вона необхідна перебування синуса кута. ВН 1 = √ (52 — 32) = 4 (см).

Скориставшись знанням про те, як знаходиться синус гострого кута в трикутнику з прямим кутом, можна записати такий вираз: sin = ВН 1 / АВ = 0,8.

Відповідь.Шуканий синус дорівнює 0,8.

№2. На перебування висоти трапеції за відомим тангенсом.

Умова.У рівнобедреної трапеції слід обчислити висоту. Відомо, що її підстави дорівнюють 15 і 28 см. Даний тангенс гострого кута: 11/13.

Рішення.

Позначення вершин таке саме, як у попередньому завданні. Знову потрібно провести дві висоти із верхніх кутів. За аналогією з рішенням першого завдання потрібно знайти АН 1 = Н 2 Д, які визначаться як різницю 28 та 15, поділена на два. Після підрахунків виходить: 6,5 див.

Оскільки тангенс — це відношення двох катетів, можна записати таку рівність: tg α= АН 1 / ВН 1 . Причому це відношення дорівнює 11/13 (за умовою). Оскільки АН 1 відомий, можна обчислити висоту: ВН 1 = (11 * 6,5) / 13. Прості розрахунки дають результат 5,5 див.

Відповідь.Шукана висота дорівнює 5,5 см.

№3. На обчислення висоти за відомими діагоналями.

Умова.Про трапецію відомо, що її діагоналі дорівнюють 13 і 3 см. Потрібно дізнатися про її висоту, якщо сума підстав становить 14 см.

Рішення.Нехай позначення фігури буде таким самим, як раніше. Припустимо, що АС менша діагональ. З вершини З потрібно провести висоту, що шукається, і позначити її СН.

Тепер потрібно виконати додаткову побудову. З кута З потрібно провести пряму, паралельну більшій діагоналі та знайти точку її перетину з продовженням сторони АТ. Це буде Д1. Вийшла нова трапеція, усередині якої накреслено трикутник АСД 1 . Він і потрібен для подальшого вирішення задачі.

Шукана висота виявиться ще й їй у трикутнику. Тому можна скористатися формулами, вивченими в іншій темі. Висота трикутника визначається як добуток числа 2 та площі, ділене на бік, до якої вона проведена. А сторона виявляється дорівнює сумі підстав вихідної трапеції. Це виходить із правила, яким виконано додаткове побудова.

У розглянутому трикутнику всі сторони відомі. Для зручності введемо позначення х = 3 см, у = 13 см, z = 14 см.

Тепер можна порахувати площу, скориставшись теоремою Герона. Напівпериметр дорівнюватиме р = (х + у + z) / 2 = (3 + 13 + 14) / 2 = 15 (см). Тоді формула для площі після підстановки значень буде виглядати так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см 2).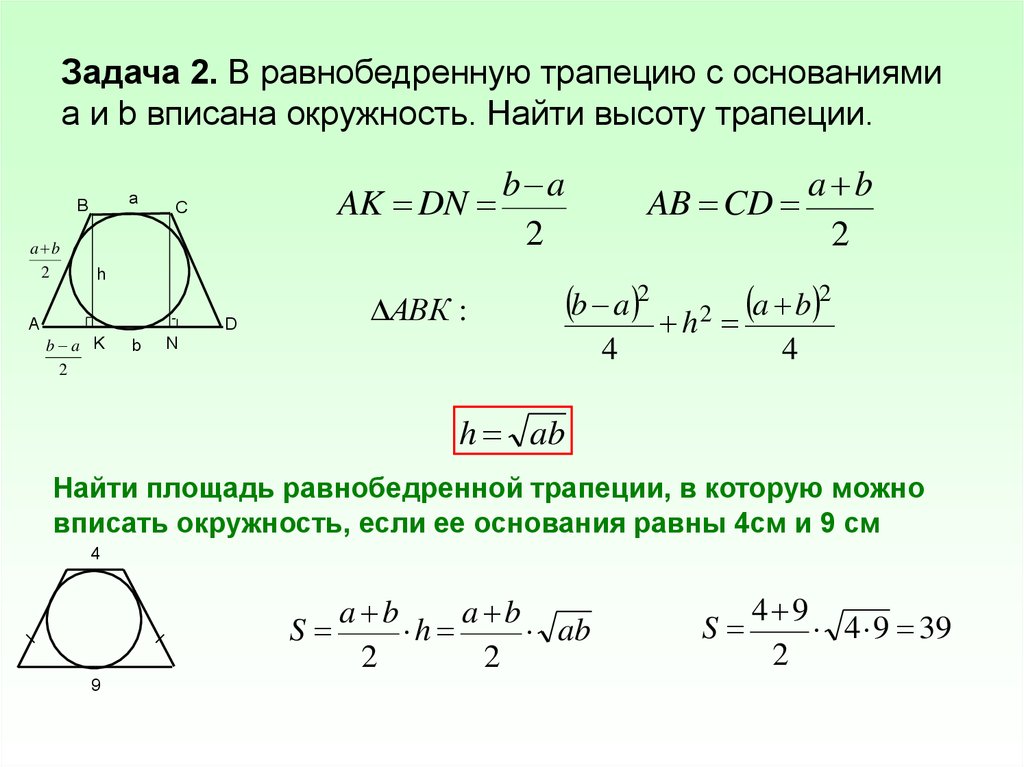

Відповідь.Висота дорівнює 6√10/7 см.

№4. Для пошуку висоти на всі боки.

Умова.Дана трапеція, три сторони якої дорівнюють 10 см, а четверта 24 см. Потрібно дізнатися про її висоту.

Рішення.Оскільки фігура рівнобедрена, то знадобиться формула під номером 2. У неї потрібно просто підставити всі значення та порахувати. Це буде виглядати так:

н = √(10 2 — (10 — 24) 2/4) = √51 (см).

Відповідь.н = √51 см.

Примітка. Це частина уроку із завданнями з геометрії (розділ прямокутна трапеція). Якщо Вам необхідно вирішити задачу геометрії, якої тут немає — пишіть про це у форумі. У задачах замість символу «квадратний корінь» застосовується функція sqrt(), у якій sqrt — символ квадратного кореня, а дужках зазначено підкорене вираз. Для простих підкорених виразів може використовуватися знак «√»

Властивості прямокутної трапеції

• У прямокутної трапеціі два кути обов’язково прямі
• Обидва прямі кутипрямокутної трапеції обов’язково належать суміжним вершинам
• Обидва прямі кутиу прямокутній трапеції обов’язково належать до однієї і тієї ж бічної сторони
• Діагоналі прямокутної трапеціїутворюють з одного з боків прямокутний трикутник
• Довжина бокової сторонитрапеції, перпендикулярній основам дорівнює її висоті
• У прямокутної трапеції основи паралельні, одна бічна сторона перпендикулярна до підстав, а друга бічна сторона — похила до підстав
• У прямокутної трапеції два кути прямі, а два інших – гострий і тупий

Завдання

В прямокутної трапеціївелика бічна сторона дорівнює сумі основ, висота дорівнює 12 см. Знайдіть площу прямокутника, сторони якого рівні основ трапеції.

Рішення.
Позначимо трапецію як ABCD. Позначимо довжини основ трапеції як a (більша основа AD) та b (менша основа BC). Нехай прямим кутом буде

∠A.

Площа прямокутника, сторони якого рівні підстав трапеції, дорівнюватиме
S = ab

З вершини C верхньої основи трапеції ABCD опустимо на нижню основу висоту CK. Висота трапеції відома за умовою завдання. Тоді, за теоремою Піфагора
CK 2+KD

2 = CD 2

Оскільки велика бічна сторона трапеції за умовою дорівнює сумі підстав, то CD = a + b
Оскільки трапеція прямокутна, то висота, проведена з верхньої основи трапеції, розбиває нижню основу на два відрізки.

AD=AK+KD. Величина першого відрізка дорівнює меншому підставі трапеції, так як висота утворила прямокутник ABCK, тобто BC = AK = b, отже, KD дорівнюватиме різниці довжин основ прямокутної трапеції KD = a — b.
тобто
12 2 + (a — b) 2 = (a + b) 2
звідки
144 + a 2 — 2ab + b 2 = a 2 + 2ab + b 2
144 = 4ab

Оскільки площа прямокутника S = ab (див. вище), то
144 = 4S
S = 144/4 = 36

Відповідь: 36 см

2 .

Інструкція

Якщо відомі довжини обох основ (b і c) і однакових за визначенням бічних сторін (a) рівнобедреної, то для обчислення величини одного з її гострих кутів (γ) можна використовувати прямокутний трикутник. Для цього опустіть висоту з будь-якого кута, що прилягає до короткої основи. Прямокутний трикутник буде утворений висотою (), бічною стороною (гіпотенуза) та відрізком довгої основи між висотою та ближньою бічною стороною (другий катет). Довжину цього відрізка можна знайти, відібравши від довжини більшої основи довжину меншого та поділивши результат навпіл: (c-b)/2.

Отримавши значення довжин двох суміжних сторін прямокутного трикутника, переходьте до обчислення кута між ними. Відношення довжини гіпотенузи (a) до довжини катета ((c-b)/2) дає значення косинуса цього кута (cos(γ)), ​​а функція арккосинус допоможе перетворити його на величину кута в градусах: γ=arccos(2*a/(c-b) )). Так ви отримаєте величину одного з гострих, а оскільки вона рівнобедрена, то і другий гострий кут матиме таку саму величину. Сума всіх кутів повинна становити 360°, а це , що сума двох кутів дорівнюватиме різниці між цим і подвоєною величиною гострого кута. Оскільки обидва тупі кути теж будуть однакові, то для знаходження величини кожного з них (α) цю різницю треба поділити навпіл: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)) . Тепер у вас є обчислення всіх кутів рівнобедреної трапеції за відомими довжинами її сторін.

Якщо довжини бічних сторін фігури невідомі, але дано її висота (h), то діяти потрібно за такою ж схемою. В цьому випадку в прямокутному трикутнику, складеному з бокової сторони і короткого відрізка довгої основи, вам будуть відомі довжини двох катетів. Їхнє співвідношення визначає тангенс потрібного вам кута, а ця тригонометрична функція теж має свого антипода, що перетворює значення тангенса на величину кута — арктангенс. Отримані у попередньому кроці формули гострого та тупого кутів трансформуйте відповідним чином: γ=arctg(2*h/(c-b)) та α = 180°-arctg(2*h/(c-b)).

Для вирішення цього завдання методами векторної алгебри вам необхідно знати такі поняття: геометрична векторна сума і скалярний добуток векторів, а також слід пам’ятати властивість суми внутрішніх кутів чотирикутника.

Вам знадобиться

• — папір;
• — ручка;
• — Лінійка.

Інструкція

Вектор – це спрямований відрізок, тобто величина, що вважається заданою повністю, якщо задана його довжина та напрямок (кут) до заданої осі. Положення вектора більше не обмежене. Рівними вважаються два вектори, що володіють довжинами та одним напрямком. Тому з використанням координат вектори зображують радіус-векторами точок його кінця (початок початку координат).

За визначенням: результуючим вектором геометричної суми векторів називається вектор, що виходить з початку першого і має кінець другого, за умови, що кінець першого суміщений з початком другого. Це можна продовжувати і далі, будуючи ланцюжок аналогічно розташованих векторів.
Зобразіть заданий ABCD векторами a, b, c та d у рис. 2)).

Кути рівнобедреної трапеції. Доброго дня! У цій статті мова піде про розв’язання задач із трапецією. Ця група завдань входить до складу іспиту, завдання прості. Обчислюватимемо кути трапеції, основи та висоти. Рішення низки завдань зводиться до розв’язання, як кажуть: куди ми без теореми Піфагора?

Працюватимемо з рівнобедреною трапецією. У неї рівні бічні сторони та кути при підставах. Про трапецію є стаття на блозі.

Зазначимо невеликий та важливий нюанс, який у процесі вирішення самих завдань докладно не розписуватимемо. Подивіться, якщо у нас дано дві основи, то більша основа висотами, опущеними до неї, розбивається на три відрізки – один дорівнює меншій основі (це протилежні сторони прямокутника), дві інші рівні один одному (це катети рівних прямокутних трикутників):

Простий приклад: дано дві основи рівнобедреної трапеції 25 і 65. Більша основа розбивається на відрізки таким чином:

*І ще! У завданнях не введено літерних позначень. Це зроблено навмисне, щоб не перевантажувати рішення алгебраїчними вишукуваннями. Згоден, що це математично неписьменно, але мета донести суть. А позначення вершин та інших елементів ви завжди можете зробити самі та записати математично коректне рішення.

Розглянемо завдання:

27439. Основи рівнобедреної трапеції дорівнюють 51 і 65. Бічні сторони дорівнюють 25. Знайдіть синус гострого кута трапеції.

Щоб знайти кут необхідно побудувати висоти. На ескізі позначимо дані за умови величини. Нижня основа дорівнює 65, висотами воно розбивається на відрізки 7, 51 і 7:

У прямокутному трикутнику нам відома гіпотенуза та катет, можемо знайти другий катет (висота трапеції) і далі вже обчислити синус кута.

По теоремі Піфагора зазначений катет дорівнює:

Таким чином:

Відповідь: 0,96

27440. Основи рівнобедреної трапеції дорівнюють 43 і 73. Косинус гострого кута трапеції дорівнює 5/7. Знайдіть бічну сторону.

Побудуємо висоти та відзначимо дані в умові величини, нижня основа розбивається на відрізки 15, 43 та 15:

27441. Більша основа рівнобедреної трапеції дорівнює 34. Бічна сторона дорівнює 14. Синус гострого кута дорівнює (2√10)/7. Знайдіть меншу основу.

Збудуємо висоти. Для того щоб знайти меншу основу нам необхідно знайти чому дорівнює відрізок, що є катетом у прямокутному трикутнику (позначений синім):

Можемо обчислити висоту трапеції, а потім знайти катет:

По теоремі Піфагора обчислюємо катет:

Таким чином, менша основа дорівнює:

27442. Підстави рівнобедреної трапеції дорівнюють 7 і 51. Тангенс гострого кута дорівнює 5/11. Знайдіть висоту трапеції.

Побудуємо висоти та відзначимо дані за умови величини. Нижня основа розбивається на відрізки:

Що робити? Виражаємо тангенс відомого нам кута при основі у прямокутному трикутнику:

27443. Менша основа рівнобедреної трапеції дорівнює 23. Висота трапеції дорівнює 39. Тангенс гострого кута дорівнює 13/8. Знайдіть більшу основу.

Будуємо висоти і обчислюємо чому дорівнює катет:

Таким чином більша основа дорівнюватиме:

27444. Основи рівнобедреної трапеції дорівнюють 17 і 87. Висота трапеції дорівнює 14. Знайдіть тангенс гострого кута.

Будуємо висоти та відзначаємо відомі величини на ескізі. Нижня основа розбивається на відрізки 35, 17, 35:

За визначенням тангенсу:

77152. Основи рівнобедреної трапеції дорівнюють 6 і 12. Синус гострого кута трапеції дорівнює 0,8. Знайдіть бічну сторону.

Побудуємо ескіз, побудуємо висоти та відзначимо відомі величини, більша основа розбивається на відрізки 3, 6 та 3:

Виразимо гіпотенузу позначену як х через косинус:

З основної тригонометричної тотожності знайдемо cosα

Таким чином:

27818. Чому дорівнює більший кут рівнобедреної трапеції, якщо відомо, що різниця протилежних кутів дорівнює 500? Відповідь дайте у градусах.

З курсу геометрії нам відомо, що якщо маємо дві паралельні прямі та січну, що сума внутрішніх односторонніх кутів дорівнює 180 0 . У нашому випадку це

З умовою сказано, що різниця протилежних кутів дорівнює 50 0 тобто

З точок D і C опустимо дві висоти:

Як уже сказано вище, вони розбивають більшу основу на три відрізки: один дорівнює меншій основі, дві інші рівні один одному.

У разі вони рівні 3, 9 і 3 (у сумі 15). Крім того, зазначимо, що висотами відсікаються прямокутні трикутники, причому вони є рівнобедреними, тому що кути при підставі дорівнюють 45 0 . Звідси випливає, що висота трапеції дорівнюватиме 3.

На цьому все! Успіху вам!

З повагою, Олександр.

скільки ліній симетрії має трапеція

Скільки ліній симетрії має трапеція?

Трапеція має щойно один рядок симетрії.

Скільки ліній симетрії мають трапеції?

1 рядок З усіх випадків, згаданих вище, можна сказати, що тільки для трапецій 1 лінія симетрії можливо. Отже, правильна відповідь «Варіант А». Примітка. У наведеному вище розв’язанні ми виявили, що трапеція має лише одну лінію симетрії, але чи знаєте ви, що таке трапеція?

Дивіться також, що означає це поняття

Чи повинна трапеція мати одну лінію симетрії?

Ні, трапеція не може мати двох ліній симетрії, оскільки у чотирикутнику рівні лише одна пара паралельних сторін.

Що таке симетрія трапеції?

Трапеція не має осей симетрії відбиття. Трапеція не має обертальної симетрії (1-й порядок). Примітка: відсутність симетрії обертання означає, що фігуру потрібно повернути на 360º, щоб знову з’явитися у вихідному положенні.

Чи має трапеція 4 лінії симетрії?

Скільки прямих симетрії має трапеція?

Що таке трапеція з однією лінією симетрії?

Трапеція. Деякі трапеції мають одну лінію симетрії. Вони називаються рівнобедрені трапеції оскільки у них дві рівні сторони, як у рівнобедрених трикутників.

Чи має трапеція симетрію з медіаною?

Трапеція не має симетрії щодо медіани трапеції. Медіана ділить трапецію на дві менші трапеції, кожна з яких має половину висоти вихідної.

Яка фігура не має лінії симетрії?

А розгорнутий трикутник, паралелограм, і трапеція — це три приклади фігур без лінії симетрії.

Скільки ліній симетрії має ромб?

Ромб/Лінія симетрії

Лінія симетрії — це уявна вісь, що проходить через центр об’єкта і ділиться на дві рівні половини. Оскільки всі чотири сторони алмаза рівні, він має дві лінії симетрії.

Скільки ліній симетрії має фігура?

Фігура може мати більше однієї лінії симетрії. Таким чином, прямокутник має дві лінії симетрії, рівносторонній трикутник має три лінії симетрії, а квадрат — чотири. Коло має нескінченну кількість ліній симетрії, оскільки його можна скласти за будь-яким діаметром.

Скільки прямих симетрії має рівнобедрена трапеція?

Трапеція має 2 рядки рефлексійної симетрії.

Які фігури мають лінію симетрії?

Правильні багатокутники

Рівносторонній трикутник (3 сторони) має 3 лінії симетрії
Правильний п’ятикутник (5 сторін) має 5 ліній симетрії
	Правильний шестикутник (6 сторін) має 6 ліній симетрії
Правильний семикутник (7 сторін) має 7 ліній симетрії
	Правильний восьмикутник (8 сторін) має 8 ліній симетрії

Чи є трапеція симетричною?

Трапеція має лише вертикальну лінію симетрії. Паралелограм не має ліній симетрії, і, як і з прямокутником, учні повинні поекспериментувати зі згинанням копії, щоб побачити, що відбувається з лініями, що проходять через діагоналі, а також горизонтальними та вертикальними лініями.

Дивіться також, як виглядає вода під мікроскопом

Скільки кутів має трапеція?

чотири кути

Трапеція є чотирикутником, тобто має чотири сторони. Дві сторони повинні бути паралельні одна одній, щоб вона була трапецією. Трапеція також має чотири кути.

Скільки паралельних сторін має трапеція?

два А трапеція має одна пара паралельних сторін а паралелограм має дві пари паралельних сторін.

Чи може трапеція мати 3 рівні сторони?

Трапеція з 3 сторонами дорівнює рівнобедреної трапеції, що має принаймні три рівні сторони. Нижче наведено зображення трапеції з 3 сторонами. У деяких діалектах англійської мови (наприклад, британська англійська) цю фігуру називають трапецією з 3 сторонами.

Чи рівні сторони трапеції?

Трапеція — квадрат, якщо обидві пари її протилежних сторін паралельні; всі його сторони мають однакову довжину і під прямим кутом один до одного.

Скільки осей симетрії має трапеція?

Повний порядок симетрії

Форма	Осі симетрії	Повний порядок симетрії
Трапеція		1
Рівнобедрена трапеція	1	2
Паралелограм		2
ромб	2	4

Що з наведеного є медіаною трапеції?

Медіана трапеції є відрізок, що з’єднує середини непаралельних сторін (катетів). Теорема: Медіана трапеції паралельна кожній основі, а довжина медіани дорівнює половині суми довжин двох основ.

Як знайти сторони трапеції?

Оскільки ця задача забезпечує довжину обох основ, а також загальний периметр, відсутні сторони можна знайти за допомогою такої формули: Периметр= Основа один Основа два (нога), де довжина «катета» є однією з двох еквівалентних непаралельних сторін.

Чи має трапеція прямі кути?

Трапеція має два прямих кута.

Які існують 4 види симетрії?

Типи симетрій бувають симетрія обертання, симетрія відбиття, симетрія трансляції та симетрія відбиття ковзання. Ці чотири типи симетрії є прикладами різних типів симетрії на плоскій поверхні, які називаються площинною симетрією.

Чи має трикутник лінійну симетрію?

Поділ трикутників на розгорнуті, рівнобедрені та рівносторонні можна уявити через лінії симетрії. А Розширений трикутник — це трикутник без ліній симетрії тоді як рівнобедрений трикутник має принаймні одну лінію симетрії, а рівносторонній трикутник має три лінії симетрії.

Дивіться також Як утворюються руди?

Яка фігура має рівно 3 лінії симетрії?

рівносторонній трикутник Рівносторонній трикутник має три лінії симетрії. Має обертальну симетрію порядку 3. Має три рівні сторони.

Скільки ліній симетрії має овал?

дві лінії симетрії Загалом, еліпс має дві лінії симетрії.

Скільки прямих симетрії має п’ятикутник?

5

Скільки прямих симетрії має шестикутник?

6

Скільки ліній симетрії має нонакутник?

9

Скільки прямих симетрії має ця рівнобедрена трапеція?

Рівнобедрені трапеції мають один рядок симетрії, що утворює бісектрису перпендикуляру з паралельними сторонами.

Що з наведеного нижче найкраще описує симетрію трапеції?

Відповідь: Покрокове пояснення: Трапеція — це двовимірна фігура з двома паралельними сторонами. Симетрична трапеція повинні мати рівні дві непаралельні сторони.

Чи має рівнобедрена трапеція точкову симетрію?

В евклідовій геометрії рівнобедреної трапеції (рівнобедреної трапеції в британській англійській мові) є опуклий чотирикутник з лінія симетрії, що розділяє одну пару протилежних сторін навпіл.

…

Рівнобедрена трапеція
Тип	чотирикутник, трапеція
Ребра і вершини	4
Група симетрії	Діх2, [ ], (*), порядок 2
Подвійний багатокутник	Змій

Яка фігура має 4 сторони і 1 лінію симетрії?

Змій. Повітряний змій є чотирикутником з однією віссю симетрії.

Як знайти лінію симетрії?

Скільки прямих у трапеції?

одна пряма Трапеція має щойно один рядок симетрії.

Лінії симетрії рівнобедреної трапеції

Скільки прямих симетрії має паралелограм

Симетрія рівнобедреної трапеції

ЯК ВИГЛЯДАЄ ТРАПЕЦІЯ?

Як знайти площу рівнобедреної трапеції :: площа трапеції рівнобедреної :: математика :: neprostoguru.ru: як просто зробити все

Рівнобедрена трапеція — це трапеція, у якої протилежні непаралельних сторони рівні. Ряд формул дозволяють знайти площу трапеції через її боку, кути, висоту і.т.д. Для випадку рівнобедрених трапецій ці формули можуть кілька спрощуватися.

Зміст

• Вам знадобиться
• Інструкція
• Відео: У рівнобедреної трапеції основи дорівнюють 2 і 8 … | ОГЕ 2017 | ЗАВДАННЯ 11 | ШКОЛА ПІФАГОРА
• Відео: Урок 4 Завдання про площу рівнобедреної трапеції
• Відео: Математика Урок 9 Площа трапеції
• Інструкція

Вам знадобиться

• Формули для площі звичайної трапеції

Інструкція

1

Найпоширеніша формула для обчислення площі трапеції — S = (a + b) h / 2. Для випадку рівнобедреної трапеції вона явно не зміниться. Можна лише відзначити, що у рівнобедреної трапеції кути при будь-якому з підстав дорівнюватимуть (DAB = CDA = x). Так як її бічні сторони теж рівні (AB = CD = с), то і висоту h можна порахувати за формулою h = с * sin (x).

Тоді S = (a + b) * с * sin (x) / 2.

Відео: У рівнобедреної трапеції основи дорівнюють 2 і 8 .

2).

Чотирикутник, у якого пара протилежних сторін паралельна, називають трапецією. В трапеції визначають підстави, сторони, діагоналі, висоту, середню лінію. Знаючи різні елементи трапеції, можна знайти її площа.

Відео: Математика Урок 9 Площа трапеції

Інструкція

1

Знайдіть площа трапеції за формулою S = 0,5 (a + b) -h, якщо відомі a і b — довжини підстав трапеції, тобто паралельні сторони чотирикутника, і h — висота трапеції (Найменша відстань між основами). Наприклад, нехай дана трапеція з основами a = 3 см, b = 4 см і висотою h = 7 см. Тоді її площа буде дорівнює S = 0,5 (3 + 4) -7 = 24,5 смsup2-.

2

Скористайтеся наступною формулою для обчислення площі трапеції: S = 0,5-AC-BD-sin (beta-), де AC і BD — діагоналі трапеції, а beta- — кут між цими діагоналями. Наприклад, задана трапеція з діагоналями AC = 4 см і BD = 6 см і кутом beta- = 52 °, тоді sin (52 °) asymp-0,79. Підставте значення в формулу S = 0,5-4-6-0,79asymp-9,5 смsup2-.

3

порахуйте площа трапеції, коли відомі її m — середня лінія (відрізок, що з`єднує середини сторін трапеції) І h — висота. В цьому випадку площа буде дорівнює S = m-h. Наприклад, нехай у трапеції середня лінія m = 10 см, а висота h = 4 см. У цьому випадку виходить, що площа заданої трапеції дорівнює S = 10-4 = 40 смsup2-.

4

Обчисліть площа трапеції, в разі коли дані довжини її бічних сторін і підстав за формулою: S = 0,5 (a + b) -radic- (csup2 — (((ba) sup2- + csup2 — dsup2-) divide- (2 (ba))) sup2-), де a і b — підстави трапеції, а c і ​​d — її бічні сторони. Наприклад, нехай дана трапеція з основами 40 см і 14 см і бічними сторонами 17 см і 25 см. За вищевказаною формулою S = 0,5 (40 + 14) -radic- (17sup2 — (((14-40) sup2 — + 17sup2—25sup2-) divide- (2- (14-40))) sup2-) asymp-423,7 смsup2-.

5

Розрахуйте площа рівнобедреної (равнобокой) трапеції, тобто трапеції у якій бічні сторони рівні, якщо в неї вписана окружність за формулою: S = (4-rsup2-) divide-sin (alpha-), де r — радіус вписаного кола, alpha- — кут при підставі трапеції. У рівнобедреної трапеції кути при основі рівні. Наприклад, нехай в трапецію вписано коло радіусом r = 3 см, а кут при підставі alpha- = 30 °, тоді sin (30 °) = 0,5. Підставте значення в формулу: S = (4-3sup2-) divide-0,5 = 72 смsup2-.

Поділися в соціальних мережах:

Схожі

• Як розрахувати площу трапеції
• Як знайти середню лінію рівнобедреної трапеції
• Як знайти підставу трапеції, якщо відома сторона і кут
• Як знайти бічні сторони рівнобедреної трапеції
• Як знайти периметр рівнобедреної трапеції
• Як знайти менше підставу трапеції
• Як довести, що діагоналі рівнобедреної трапеції дорівнюють
• Як знайти площу трапеції, якщо відомі підстави
• Як знайти площу трапеції по вписаного кола
• Як знайти довжину діагоналей трапеції
• Як визначити площу трапеції
• Як знайти висоту трапеції, якщо відома площа
• Як знайти кути рівнобедреної трапеції
• Як знайти периметр прямокутної трапеції
• Як знайти висоту рівнобедреної трапеції
• Як знайти підстави прямокутної трапеції
• Як дізнатися площа трапеції
• Як знаходити периметр трапеції
• Як обчислити площу чотирикутника
• Як знайти висоту в трапеції, якщо відомі всі сторони
• Як знайти висоту трапеції формула

იცოდე кути трапеции якщо відомі ორი კუტი.

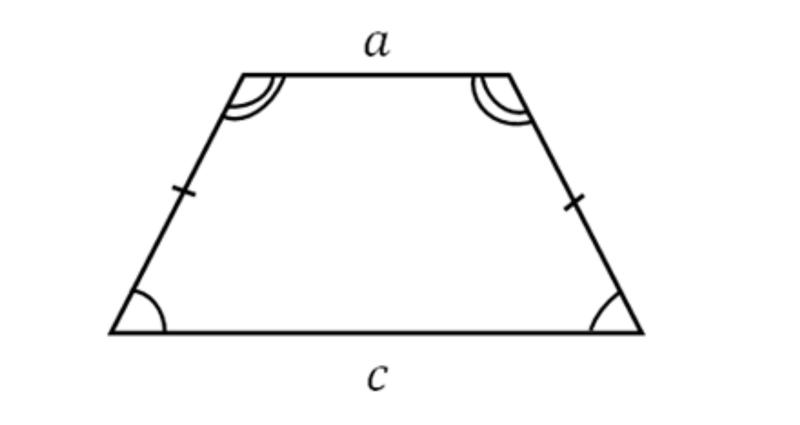
როგორ გავიგოთ კუტი ტრაპეციაზე

ტრაპეცია — ცე ბრტყელი ჭოტირი კოსინეც , რომელსაც აქვს ორი პარალელური გვერდი. სუნებს ქვესადგურებს უწოდებენ ტრაპეცია , და ორი სხვა მხარე — გვერდითი მხარეები ტრაპეცია .

ინსტრუქცია

1. გარკვეული მნიშვნელობის მენეჯერი ტრაპეცია საკმარისი რაოდენობის დამატებითი მონაცემების გულისთვის. ჩვენ ვუყურებთ კონდახს, რომელშიც ძირში არის ორუ კრუ კრიუ0003 ტრაპეცია . მოდით წავიდეთ კუტი ∠BAD та ∠CDA, მოდით წავიდეთ კუტი ∠ABC та. ტრაპეციას შეიძლება ჰქონდეს სიმძლავრე, რომ კუტივის ჯამი, თუ ეს გზის იგივე მხარეა, იყოს 180 °. შემდეგ ∠ABC = 180°-∠BAD და ∠BCD = 180°-∠CDA.

2. სხვა შეიძლება დაინიშნოს მხარეთა თანასწორობა თანასწორობა ტრაპეცია და Be-yaki Dodatkovi kuti. ვთქვათ, პატარას მსგავსად, ხედავთ, რომ ab, bc და CD გვერდები ტოლია და დიაგონალი ქვედა ფუძის ჭრილით Ϫcad = α. კოსინეც ABC, ровнофемори, რომ AB = BC. შემდეგ ∠BAC = ∠BCA. მნიშვნელოვნად x არის სტილი, და ∠ABC არის y.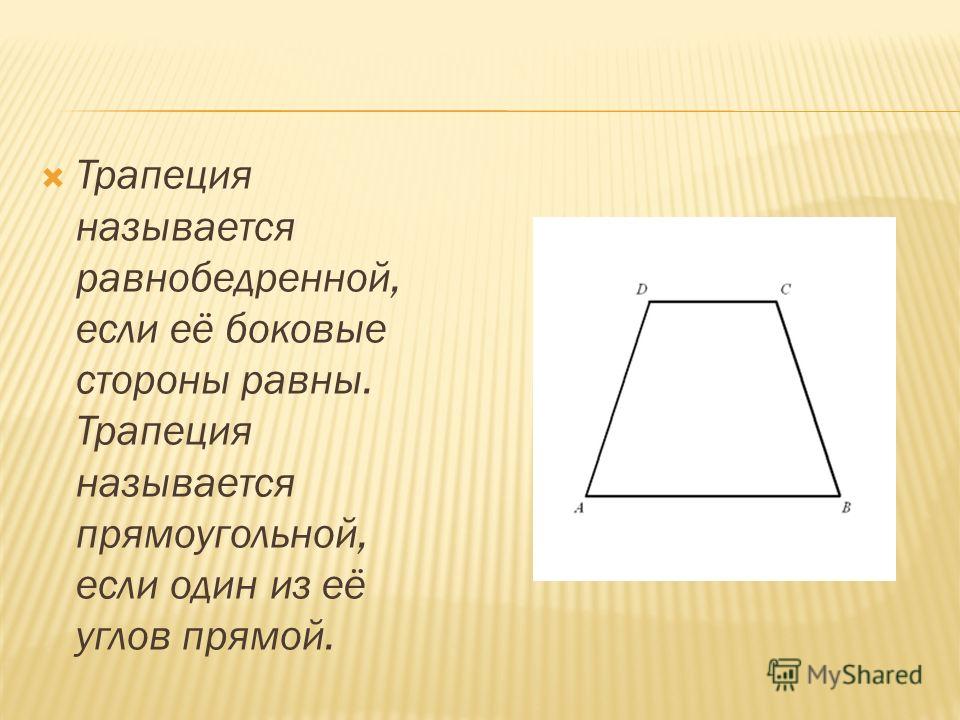 სუმა კუტივი ყოველ სამში კოსინეც და Dorivnyuє 180 °, საიდანაც ნათელია, Scho 2x + y \ u003d 180 °, შემდეგ y \ u003d 180 ° — 2x. Водноча из власти ტრაპეცია : y + x + α = 180° и відтак 180° — 2x + x + α = 180°. ასევე, х = α. ორი კუტი ვაჩვენეთ ტრაპეცია : ∠BAC = 2x = 2α i ∠ABC = y = 180° – 2α. ვინაიდან ab \ u003d CD გონების უკან, მაშინ ტრაპეცია არის თანაბარი ან თანაბარი ბარძაყის. Отже, დიაგონალური ровні й ровні кути під ч основы. ამ თანმიმდევრობით, ∠CDA = 2α, და ∠BCD = 180° — 2α.

ბაგატოს დიაგონალი კოსინცია — Vhidgrok, ის, რომელიც ფიგურის ორი წვერის უკან, რომელიც არ იკვეთება თავისთავად (მაშინ წვეროები არის შემაჯამებელი შემაჯამებელი არ დევს მდიდრების მხარეს მხარეს) კოსინცია ). პარალელოგრამზე, დიაგონალების სიგრძისა გვერდების სიგრძის ცოდნით ცოდნით, შეგიძლიათ გახსნათ კუტი დიაგონალები .

ინსტრუქცია

1. ინფორმაციის კომფორტისთვის კომფორტისთვის, თაღოვან მოათავსეთ სრული პარალელოგრამი პარალელოგრამი abcd (პარალელოგრამი არის ჭოტირიკუტნიკი, რომლის გვერდები წყვილში ტოლი და და პარალელურია).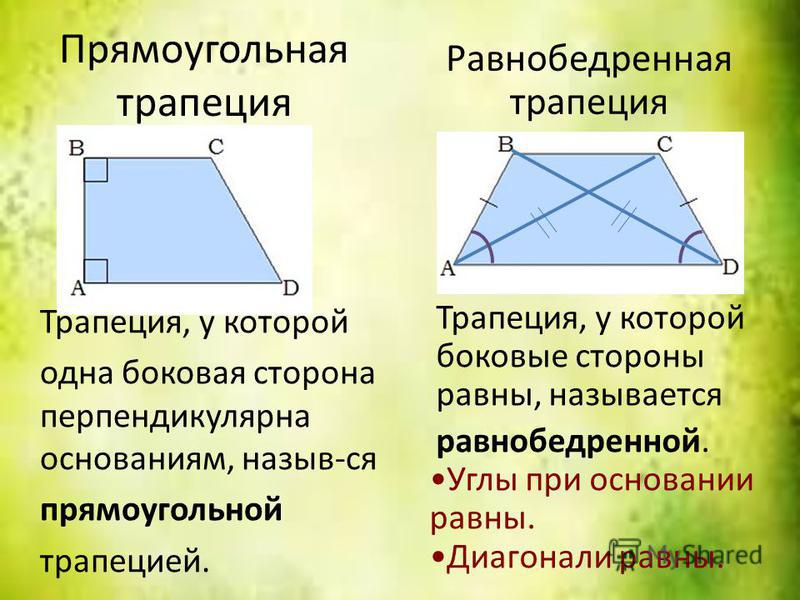 შეაერთეთ პროტილის წვერები ნეკნებით. ამოიღეთ AC და BD — დიაგონალები. დანიშნეთ დიაგონალების გადაკვეთის წერტილი O ასთ᝝. აუცილებელია გამოვლინდეს კუტი BOC (AOD) და COD (AOB).

2. პარალელოგრამს ჰქონდეს დაბალი მათემატიკური სიმკვრივე: — პარალელოგრამის დიაგონალი გავყოთ ორ პარალელურად კოსინცია ; — პარალელოგრამის ყველა კიდეების ჯამი არის 360 გრადუსი, — კიდეების ჯამი, რომლებიც პარალელოგრამის ერთ მხარეს, არის 180 გრადუსამდე;

3. შჩობ კუტი მიჟ დიაგონალები , დააჩქარეთ კოსინუსების თეორემა გეომეტრიის თეორიიდან თეორიიდან (ევკლიდური). ვიდპოვიდნო კოსინუსის თეორემამდე, ტრის კვადრატი კვადრატი კოსინცია (a) შეგიძლიათ აიღოთ მე -2 გვერდების კვადრატების (b და c) კვადრატების და ორი მხარის ქვედაკეცვის ქვედაკეცვის (b და c) ჯამის აღებით მათ შორის ჭრილის კოსინუსით.

4. ასჯერ ტრიკოტის Boc პარალელოგრამზე abcd, კოსინუსების თეორემა გამოიყურება შეტევითი რანგის სახით: კვადრატი bc \ u003d კვადრატი Bo + კვადრატი OS — 2 * vo * os * cos kuta boc zv_dsi cos kuta boc \ u003d (კვადრატი bc — კვადრატი bo — კვადრატული oc) / / (2*ВО*ОС)

5. კუტას BOC (AOD) ღირებულების ჩვენების შემდეგ, ადვილია გამოვთვალოთ სხვა კუტას მნიშვნელობა დიაგონალები — ХПК (АОБ). 180 გრადუსიანი ხედისთვის გასათვალისწინებელია Bos ჭრის (ATD) მნიშვნელობა. მთლიანი ჭრების ჯამი აღწევს 180 გრადუსს, ხოლო ჭრები ჭრები Boc და Cod და ჭრები aod და aob არის ჯამები.

ვიდეო თემაზე

ამ გადასაჭრელად ვექტორული ალგებრის გამოყენებით, თქვენ უნდა იცოდეთ შემდეგი გამოვლინება: გეომეტრიული ჯამი და ვექტორების სკალარული დამატება, ასევე ქოტირიკუტნიკის შიდა ჭრილების ჯამის მეხსიერება.

შენ გჭირდება

• — ქაღალდი;
• — კალამი;
• — ხაზი.

ინსტრუქცია

1. ვექტორი სწორი ხაზების ხაზი, ეს არის მნიშვნელობა, რომელიც მნიშვნელოვანია მოცემული ხაზისთვის, რადგან მანძილი პირდაპირ პირდაპირ (გაჭრა) მოცემულ ღერძამდე. ვექტორის რაზტაშუვანია არაფერზე დიდი არ არის. თანაბრად вважаются ორი ვექტორი, що водіют іденичными довжина რომ ერთი სწორი. ასევე, როდესაც ფიქსირდება, ვექტორები წარმოადგენენ მესამე წერტილის წერტილს რადიუს-ვექტორებით (სვლა კოორდინატების კუბზე კუბზე).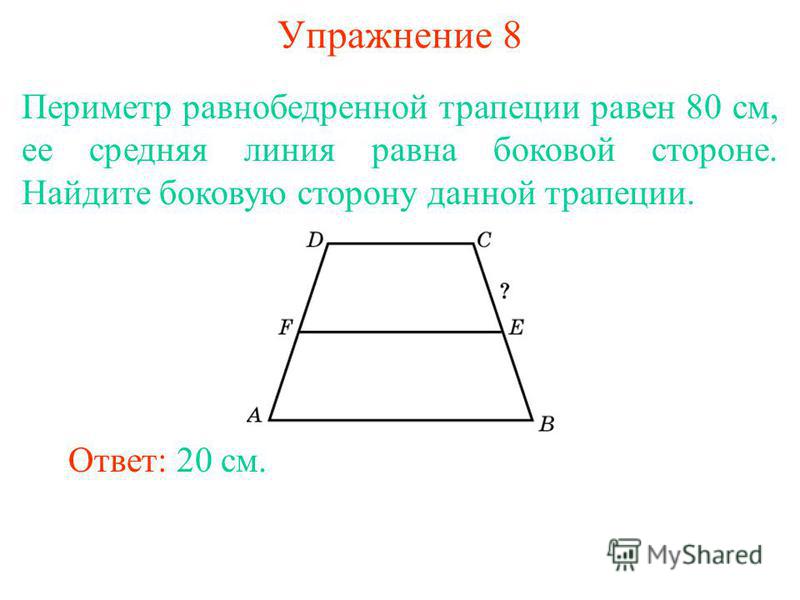

2. მიზნებისთვის: ვექტორთა ჯამის შედეგად მიღებული ვექტორი არის ვექტორი, რომელიც მიდის კობიდან და შეიძლება მეორეს მსგავსად, გონებისთვის, რომ პირველი დაბნეულობის დასასრული მეორის კობიდან. შესაძლებელია გაგრძელდეს გაგრძელდეს გაგრძელდეს, როგორც ლანცეტი, ხელით დახატული ვექტორების მსგავსი. გამოსახეთ მთელი ABCD a, b, c და d ვექტორებით, ისევე როგორგორგორთ 1. შესაძლოა, ასეთი გავრცელებით, მიღებული ვექტორი იყოს d = a+b+c.

3. 92)).

4. ვექტორული ძირითადი გამოვლინებები დაკისრებულ ამოცანასთან მიმართებაში იწვევს იმ ფაქტს, რომ მოცემული ცალსახა ფორმულირებისთვის აუცილებელია 3 ვექტორის შესრულება შესრულება, გავრცელება, შესაძლებელია, ab, bc yd, შემდეგ ა, ბ, გ. საბოლოოდ შეგიძლიათ დააყენოთ a, b, c, d წერტილების კოორდინატები და შემდეგ მეთოდი ზედმეტია (4 პარამეტრი ცვლის 3-ს).

5. კონდახი. ჩოტიროხკუტნიკი ABCD ამოცანები იოგო მხარეების ვექტორებით AB, BC, CD A (1,0), B (1,1), C (-1,2). აჩვენეთ კუტი იოგას წვეულებებს შორის. გამოსავალი. ზემოაღნიშნულთან დაკავშირებით მე -4 ვექტორი (ad- სთვის) d (dx, dy) = a+b+c = (ax+bx+cx, ay+by+cy) = (1,3).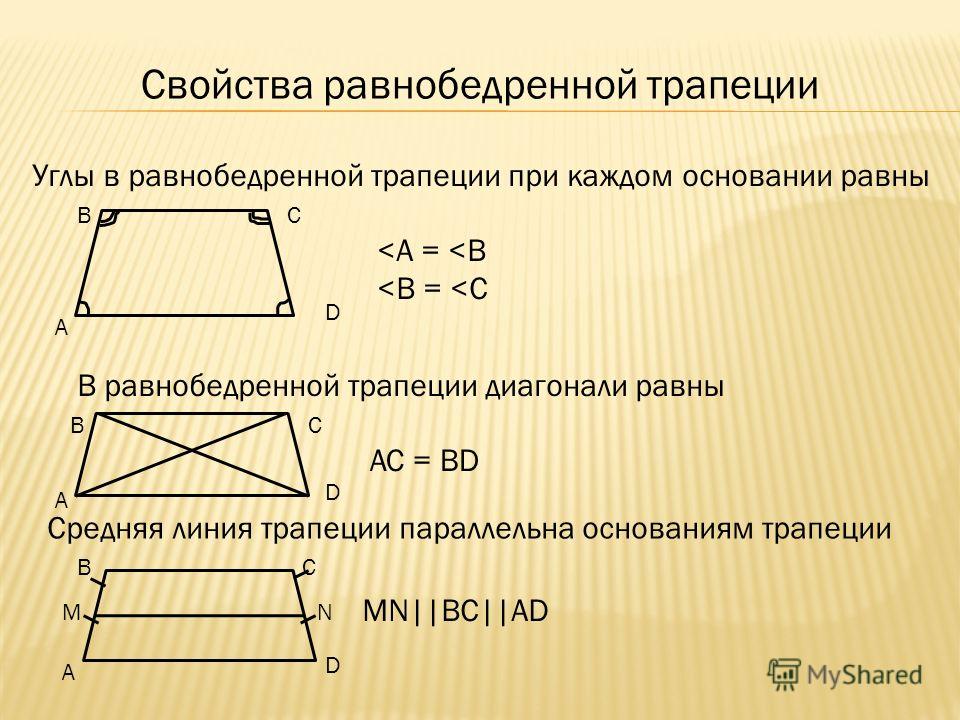 2))=1/(sqrt2sqrt5), f3=arcos( -1/кв.(10))=p-f1. Видповидно до затравки 2 — f4=2п-f1 — f2-f3=п/4.

ვიდეო თემაზე

მიიღეთ პატივისაTH
შენიშვნა 1. სკალარული შექმნის დანიშნულება არის სტაგნაცია ვექტორებს შორის. აი, ვთქვათ, f2 — ცე კუთ მიჟ AB და BC და მიჟ ა და ბ დანს კუფ-ტ კუფტ კუფტ cos(p-f2)=- cosf2. f3-ის მსგავსი. 2р. ასევე f4 = 2p-f1 — f2-f3.

ტრაპეციის არ არის დასაკეცი ბოძების ბოლოში, რომლებიც ადრე იყო ნაქარგი. იაკ ოკრემი ვიპადოკიჩანს სწორხაზოვანი ტრაპეცია. და როცა ითხოვთ კვადრატებს, უმჯობესია გატეხოთ її ორზე, თქვენ უკვე იცით: სწორი და ტრიკუტი ტრიკუტი. ცოტა დაფიქრდი და იპოვე გამოსავალი ენის შესახეეე.

მართკუთხა აღნიშვნა და її დომინირება დომინირება

საკმაოდ ტრაპეციაში ფუძეები პარალელურია და გვერდების გვერდებს შეიძლება ჰქონდეთ საკმარისი მათ წინაშე არსებული ჭრილებისთვის. თუ მართკუთხა უყურებთ უყურებთ, მაშინ მასში ერთ-ერთი მხარე ყოველთვის საძირკვლის პერპენდიკულარულია. Тобто ორი кути в ний дорівнюватимут 90 გრადუსი. უფრო მეტიც, სუნი ყოველთვის იყოს მწვერვალებზე, წინააღმდეგ შემთხვევაში, როგორც ჩანს, ბრძოლის ერთ მხარეს.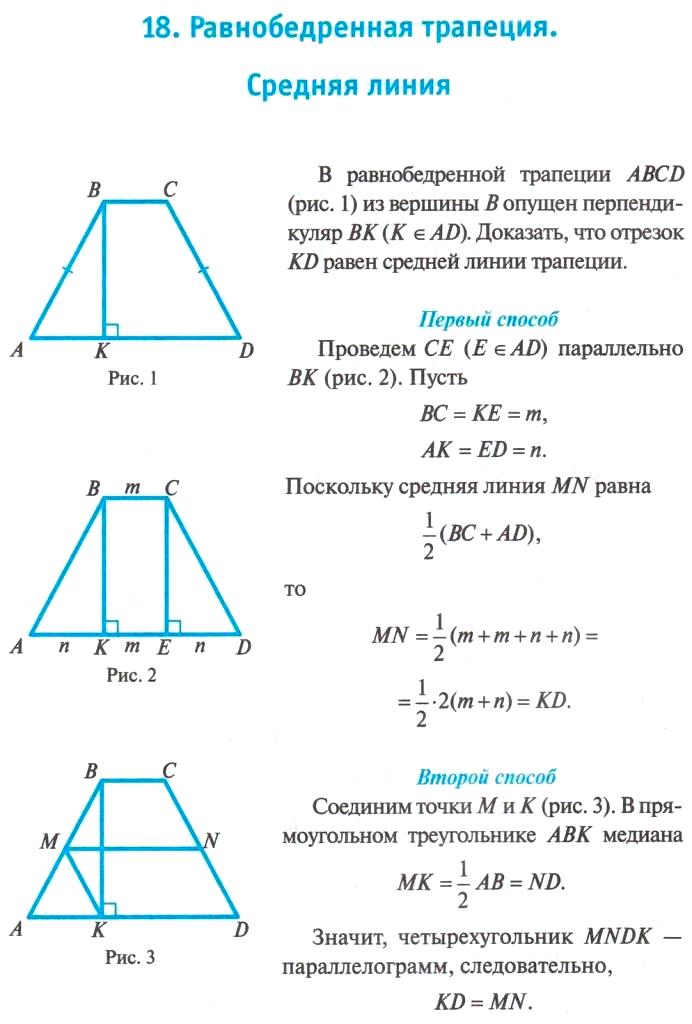

სხვა სწორხაზოვან ტრაპეციაში ტრაპეციაში — ცე ზავჟდი ჰოსტრია და სულელი. უფრო მეტიც, ფულის ჯამი ყოველთვის 180 გრადუსზე მეტმეტტ.

კანის დიაგონალი სწორხაზოვან ტრიკუტნიკს პატარა გვერდით გვერდით. ხოლო სიმაღლე, ზემოდან დახატული კუტით კუტით, ყოფს ფიგურას ორად. ერთი მათგანი სწორი ჭრილი, ხოლო მეორე არის სწორი ჭრილი. გამოსვლამდე ეს ყოველთვის იქნება ტრაპეციის სიმაღლე.

როგორ მიღებული მნიშვნელობები მოცემულ მოცემულ ფორმულებში?

ყველა მნიშვნელობა, რომელიც სხვადასხვა სხვადასხვა ვირაზებში, თითქოს ისინი აღწერენ ტრაპეციას, შეგიძლიათ გაარკვიოთ ეს გადასახადი მაგიდაზე:

ფორმულები, რომლებიც მართკუთხა ტრაპეციის ელემენტებს

მათგან აჩვენებს სიმაღლეს და პატარა მხარეს მხარეს:

მეტი მართკუთხა ტრაპეციის ცენტრალური მხარისთვის:

C \ U003D D * SINα;

с = (а — б) * თან α;

с = √(d 2 — (a — b) 2).

პერშა ცახცახებს პირდაპირ მოჭრილი ტრიკუტნიკიდან. მე ვსაუბრობ მათზე, ვინც ანიჭებს პროტიგუული კუტის სინუსს სინუსს.

იგივე ორი ფუნდამენტის კარის განსხვავებული ფეხი აქვს აქვს. ეს სამართლიანია მტკიცება მტკიცება, თითქოს იყოს კუტას ტანგენსი კათეტერების გაფართოებაზე გაფართოებაზე.

ამავე შეგიძლიათ შეიყვანოთ ფორმულა პითაგორას თეორემის ცოდნაზე დაყრდნობით დაყრდნობით. ცე მესამე ჩანაწერი ვირაზ.

შეგიძლიათ დაწეროთ ფორმულები მეორე მხარისთვის. ასევე არის სამი:

d = (a — b) /cosα;

d = c/sinα;

d = √ (c 2 + (a — b) 2).

პირველი კვლავ ერთდროულად ჩნდება მხარეთა თანამშრომლობიდან სწორი ნაქსოვი, ხოლო მეორე მომდინარეობს პითაგორას თეორემიდან.

რა შეიძლება გამოითვალოს როზრაჰუნკას როზრაჰუნკას ფართობისთვის?

თუმცა, школа მოცემულია გრძელი ტრაპეციისთვის. საჭიროა მხოლოდ vrahuvat, რომ სიმაღლე არის პერპენდიკულარული პერპენდიკულარული ფონდები.

S = (a + b) * h/2.

Ци სიდიდე який завжди მოცემულია ცალსახად. ამისთვის, მართკუთხა ტრაპეციის გამოსათვლელად, აუცილებელია მათემატიკური ცხრილების ვისკონირება.

როგორ მაგრამ, როგორ არის საჭირო დიაგონალების დანიშვნა?

ამგვარად სიმღერა სიმღერა, რომ სუნმა დააკმაყოფილოს ორი სწორი ტრიუკი. მამაო, პითაგორას თეორემით ყოველთვის შᩔგიძლაეაა შᩔგიძლაიაა ა მაშინ პირველი შეიძლება გამოიხატოს შემდეგნაირად:

D1 \ U003D √ (H 2 + B 2)

ან სხვაგვარად, შეცვალეთ «C» «H»-ით:

D1 = √ (H 2 + B 2).

ანალოგიური წესრიგი არის ფორმულები სხვა დიაგონალისთვის:

D2 \ U003D √ (H 2 + B 2) ან დ 2 \ U003D √ (H 2 + A 2).

მენეჯერი No1

უმოვი . სახლისა და კარის მართკუთხა ტრაპეციის კვადმატᘛატᘏ Її სიმაღლე შეიძლება იყოს 8 დმ. აუცილებელია ტრაპეციის ყველა მხარის შემობრუნეა. Додатковой умовой є ვისაც აქვს ერთი ბაზა ნაკლები 6 дм.

გამოსავალი. ოსკელკის სწორი ტრაპეცია, იაკის ვიდომის სიმაღლეზე, მაშინვე შეგვიძლია ვთქვათ მათზე, რომ ერთ-ერთი უფრო ძვირია 8 დმ, ეს არის პატარა მხარე.

ახლა თქვენ შეგიძლიათ იზრუნოთ інсшу-ზე: d = √ (s 2+ (a — b) ). უფრო მეტიც, აქ მოცემულია მხარე და მოცემულია განსხვავება განსხვავება. დანარჩენი ერთი 6 დმ, გაითვალისწინეთ. იგივე d უდრის z- ის კვადრატულ ფესვს (64 + 36), შემდეგ z 100. ასე რომ, ნაპოვნია კიდევ გვერდი გვერდი, რომელიც არის 10 დმ.

სუბსტავის ჯამი იხილოთ ფართობის ფართობის ფორმულიდან. ის უფრო ღირებულია, ვიდრე დაყოფილი ტერიტორიის ორმაგი ღირებულება ღირებულება. Yakscho rahuvati, მერე გამოდი 240/8. Кроме того, сумма подставок — 30 дм.м. მეორე მხარეს დღეს საცალო ფასი 6 დმ. გაერთიანებული ці вняння, შესაძლებელია შეურაცხყოფცს ვაის ვაის ვაის ვ

A + B = 30 და A — B = 6.

შეგიძლიათ იაკობოთ (B + 6), ჩადეთ ისინი პირველ თანაბარობაში. Тоді вийде, шо 2б довнюватиме 24. ეს მხოლოდ б გამოჩნდება 12 дм.

მაშინ დანარჩენი მხარე არის 18 დმ.

ვიდპოვიდი. მართკუთხა ტრაპეციის გვერდები: а = 18 дм, b = 12 дм, = 8 дм, d = 10 дм.

მენეჯერი No2

უმოვი. მოცემულია მართკუთხა ტრაპეცია. Її დიდია ძვირადღირებული თანხის მხარე. Її სიმაღლე შეიძლება იყოს 12 სმ. აუცილებელია ამ მართკუთხედის ფართობის გამოთვლთვლის.

გამოსავალი. უმეტესად ხუმრობისთვის ეს აუცილებელია. აუცილებელია დასახელდეს ტერიტორია დობუტოკ a და b. დანაშაულები უცნობია.

 

ერთმა აიძულა გამაგრებული გონება: d = a + b. საჭიროა მეორე მესამე ფორმულის დაჩქარება, რადგან ის უფრო მაღალია. Weide: D 2 \ U003D S 2 + (A — B) 2 ან (A + B) 2 \ U003D S 2 + (A — B) 2.

აუცილებელია ტრანსფორმაციის ჩანაცვლება მნიშვნელობის შემცვლელით — 12. მშვილდების გახსნის მსგავსი მსგავსი დამატებების გამოტანის შემდეგ 144 = 4 აბ.

კობზე გადაწყვეტილება ის ის, ვინც a *b აძლევს შუკანს კვადრატს. ამისთვის დანარჩენ შეგიძლიათ შეცვალოთ ტვირი S- ით. S = 36 სმ2.

ვიდპოვიდი. შუკანა ფართობი 36 სმ 2.

მენეჯერი No3

უუუუუ 900. მართკუთხა ტრაპეციის ფართობია 150√3 სმ². Гострий кут дорівнює 60 გრადუსი. იგივე მნიშვნელობა მოიძებნოს პატარა ფუძესა და პატარა დიაგონალს შორის. საჭიროა პატარა დიაგონალის შეცვლა.

გამოსავალი. ტრაპეციის კაპოტიდან გამოვიდეს გამოვიდეს, ეს ბლაგვი კუტი კარგია 120º. Todi დიაგონალური Podinhlyaє Yogo მდინარეზე, კიდევ ერთი იოგო ნაწილი უკვე 60 გრადუსია. Тоді кут між цією დიაგონალი და სხვა საფუძველი теж 60 გრადუსი. Tobto არის მატყუარა, დამზადებული საძირკვლით საძირკვლით, სუსტი გვერდით პატარა დიაგონალით, є ტოლგვერდა. ამ თანმიმდევრობით, шукана დიაგონალი არის доривнюватиме а, як и бічна მხაააი

ახლა მოდით შევხედოთ სწორი ჭრის ტრიკოტს. ახალ მესამე კვარტალში მაგარი 30 გრადუსია. Otzhe, ფეხი, Scho მოტყუება ახალი ახალი, ჯანსაღი ნახევარი ჰიპოტენზია. ასე რომ, ტრაპეციის უფრო ფუძე არის შუკანოს დიაგონალის ძველი ნახევარი: b = a/2. ახალი ჭიდან ვიცოდეთ სიმაღლე, მხარის თანაბარი მხარე, საძირკველზე პერპენდიკულარული. მხარე აქ ქვემოთაა. პითაგორას თეორემიდან:

ч = (а/2) * √3.

ახლა აღარ არის საკმარისი ფართობის ფორმულის ფორმულის ყველა მნიშვნელობის მიწოდება:

150 адрес = (A + A/2)*(A/2*√3)/2.

Вер_шення цгого рывняна მისცეს root 20

ვიდპოვიდი. ყველაზე პატარა დიაგონალი 20 სმ სიგრძისაა.

ტრაპეცია — წე ფიგურა ფიგურა, Chotirikutnik, რომელიც შეიძლება იყოს პარალელური ხაზი ხაზი. დანარჩენი ორი არ შეიძლება იყოს პარალელური, ამავე დროს ისინი უნდა იყოს ორ პარალელოგრამი.

იხილეთ ტრაპეცია

ტრაპეცია სახისაა სახისაა: მართკუთხაა, თუ ტრაპეცია ტრაპეცია 90 გრადუსზეა დაკეცილი; ტოლგვერდა, який ორი бічні линії ровни; разнообразна, дебичні ხაზები и вії разної дожина.

ივარჯიშეთ ტრაპეციონებით, შეგიძლიათ როგორ გამოთვალოთ მათი ფართობი, სიმაღლე, ხაზის და ასევე გაიგოთ როგორ უნდა მოჭრათ ტრაპეცია.

მართკუთხა ტრაპეცია

მართკუთხა ტრაპეციას შეიძლება ჰქონდეს 90 გრადუსიანი ორი ჭრილი. ორი ჭრის ამოხსნის ჯამი არის 180 გრადუსი. არსებობს გზა, როგორ სწორი ჭრის ტრაპეციის ჭრილები, იცოდეთ ერთ-ერთი ჭრილის გაფართოება. ნება მიეცით გამოვიდეს, მაგალითად, 26 გრადუსით. საჭიროა მხოლოდ მხოლოდ მხოლოდ მხოლოდ ის ის ჯამის ნახვა ნახვა — 360 გრადუსი — შეხედეთ kutі kutw- ის ჯამს ჯამს ჯამს ჯამს. 360-(90+90+26) = 154. შუკან კუტი ხდება 154 გრადუსი. თქვენ შეგიძლიათ გაამარტივოთ: ორი ნატეხი სწორია, მაშინ მთლიანი სუნი ხდება 180 გრადუსი, ეს ნახევარი ნახევარი 360; არაპირდაპირი KUTIV- ის ასევე უფრო ძვირია ვიდრე ვიდრე 180, ასე რომ თქვენ უფრო მარტივი და გახადოთ გახადოთ 180 -26 = 154.

რივნოფემორალური ტრაპეცია

Ривнофеморал. Є ფორმულები, როგორ ავხსნათ, როგორ გავიგოთ ბარძაყის ტრაპეციის თანაბარი კუტი.

როზრაჰუნოკი 1

სუნები ასოებით ასოებით a, ხოლო c: a — გვერდითი გვერდების ზომები, I — ძირის ზომები, უფრო პატარა და დიდი. ტრაპეციას უნდა ეწოდოს ABCD. გამოსათვლელად აუცილებელია h- ის სიმაღლე კუტა კუტა v- დან. სწორი ჭრის ტრიკუტნიკი BHA, de AH და BH — ფეხები, AB — ჰიპოტეზნუუი ახლა თქვენ შეგიძლიათ მიუთითოთ розмір ფეხი АН. აქედან გამომდინარე, აუცილებელია უფრო დიდი ფუძე აიღოს პატარა და გაიყოს ტობტო. (გ-ბ)/2.

იმისათვის, რომ ვიცოდეთ ტრიკოტის მასპინძელი, აუცილებელია მოიგოთ ფუნქცია cos. შუკან კუტის (β) უფრო ძვირი იქნება a/((c-b)/2). იმისათვის რომ ვიცოდეთ კუტა β- ის გაფართოების შესახებ, აუცილებელია არკოსების ფუნქციის დაჩქარება. β = arcos 2а/с-b. იმიტომ რომ ორი თანაბარი ტრაპეციული რივნი რივნი, შემდეგ სუნი ხდება: კუტ Bad = კუტ SDA = arcos 2A/c-B.

Розрахунок 2. როგორც ხარკი розміри ქვეშ трапеция.

მაიუჩის მნიშვნელობა Supav Trapezium — I B, შეიძლება დაჩქარდეს იმავე მეთოდით, რომელიც არის ხსნარის წინ. ქუთადან აუცილებელია სიმაღლის დაწევა h. Mayuchi Razmiri DVH KateIw choyno შექმნილი trikutnik, შეგიძლიათ მსგავსი ტრიგონომეტრიული ფუნქციამხოლოდ მომავალში იქნებით ტგ ტგ ტგ ტგ ტგ ტგ ტგ ტგ ტგ ტგ ჭრის შესაცვლელად და მისაღებად აუცილებელია arctg ფუნქციის დაჩქარება. 3 ფორმულა, OTRIMUёMO ROZMIRI SHUKANIH KUTIW:

β = არქტანი 2 სთ/ს-ბ და α α = 180-არქტანი 2 სთ/ს-ბ/

Zvichayna rhznobhina Trapeziya

არ გზა გზა როგორ გავიგოთ ტრაპეციის უფრო დიდი ჭრილი ჭრილი ჭრილი ჭრილი ჭრილი ჭრილი ჭრილი ჭრილი ჭრილი ჭრილი ვისთვისაც აუცილებელია სტუმართმოყვარე კუტივს შორის განსხვავება. ვიცი їх їх, I ვიცი, რომ ჯამი ტრაპეციების უნდა უნდა თუ არა არა 180 გრადუსი, Робимо Вишновок, რომ კუტის ხმაური იკეცება 180 -დან — ცხელი კუტის ზომა. თქვენ ასევე იცოდეთ ტრაპეციის სხვა სულელური ჭრილი.

ქუტის თანაბარბარძაყის ტრაპეცია. Მე ვცხოვრობ! ამ სტატიაში, Pova Pide ტრაპეციიდან ამოცანების შემუშავების შესახებ. Tya ჯგუფი შევიდეს საწყობში და დაიძინოს, მენეჯერი მარტივია. კუტის ტრაპეციის დათვლა, საძირკვლები და სიმეეილაღლაღლაღლაღლაღლაღლაღლაღლაღლაელრკვლები გადაწყვეტილებები დაბალია Zavdan Zvoditsya to Rozvyazannya, როგორც ჩანს: სად პითაგორას თეორემის

ივარჯიშეთ ровнобедренную трапецию. მას აქვს თანაბარი მხარეები და კუტი საყრდენებიებიეთ. ტრაპეციის შესახებ, არის სტატია ბლუზაზე.

საგრძნობლად და მნიშვნელოვანი ნიუანსია ნიუანსია, რომელსაც თავად პროცესი არ წერს. გასაოცრად, რადგან ძირი მოგვცეს, შემდეგ უფრო დიდი ფუძე სიმაღლით, ახალზე დაშვებული, იყოფა ნაწილად — ერთ პატარა ძირად (ეს არის რექტო ჭრის მხარეები მხარეები), დანარჩენი უდრის ერთს. (ეს არის თანაბარი სწორკუთხა ფეხები):

მარტივი კონდახი: მოცემულია rivnofemoral Trapeze 25 და 65 ორი ძირი.

*Მე უფრო! ზავდანნიას არ ჰქონდა პირდაპირი აღნიშვნა. ყველაფერი ნავმისად დაშლილი დაშლილი, რათა გამოსავალი იდეებით არ არ გადაიტვირთოს. ვარგისი, რომელიც არადაწერილია არადაწერილია, მაგრამ მეტა არსის გადმოსაცემად. და სხვა მწვერვალების განსაზღვრა ყოველთვის შეგიძლიათ თავად შეიმუშაოთ და ჩაწეროთ მათემატიკურად სწორი ამოხსნა.

მოდით შევხედოთ დავალებას:

27439. ბარძაყის თანაბარი ფუძეები სწორია 51 და 65. გვერდითი მხარეები სწორია 25. იპოვეთ ტრაპეციის მკვეთრი ჭრილის სინუსი.

 

ესკიზზე ეს მნიშვნელოვანი მონაცემები გონების ღირებულებებისთვის. ქვედა ბაზა არის 65, იგი დაყოფილია სიმაღლეებით 7, 51 და 7 ტოტებად:

სწორი ჭრის ტრიკაუტში ჩვენ დავინახოთ ჰიპოტენუზა და ფეხი, შეგვიძლია ვიცოდეთ მეორე ფეხი (ტრაპეციის სიმაღლე) და გამოვთვალოთ ჭრილის სინუსი სინუსი.

პითაგორას თეორემის თანახმად, ფეხების მნიშვნელობა უფრო მეტია:

ამ გზით:

სიგანე: 0,96

27440. ტოლბარძაყის ტრაპეციის ფუძეები კარგია 43 და 73. ტრაპეციის ჭრილის კოსინუსი კარგია 5/7. იცოდე ბოროტი მხარე.

თუ მნიშვნელოვანია და მოცემულია მნიშვნელობების გათვალისწინებით გათვალისწინებით გათვალისწინებით, ქვედა საყრდენი იყოფა 15, 43 და 15 ნაწილებად:

27441. ტოლ-ბარძაყის ტრაპეციის ფუძე ჯანმრთელია 34. გვერდითი მხარე 14. მწვავე კუტას სინუსი (2√10) /7. იპოვნეთ პატარა ბაზა.

დაივიწყე სიმაღლეები. იმისათვის, რომ უფრო მცირე საფუძველი, ჩვენ უნდა ვიცოდეთ, რატომ არის ის ძვირი ძვირი, რა სწორი მოჭრილი ტრიკოს ფეხი (ლურჯი მნიშვნელობები):

ჩვენ გამოვთვალოთ ტრაპეციის სიმაღლე და შემდეგ გავიგოთ ფეხი ფეხი:

პითაგორას თეორემის მიხედვით, ფეხები გამოითვლება:

ამ უფრო მნიშვნელოვანია ნაკლები საფუძველი:

27442. . იპოვეთ ტრაპეციის სიმაღლე.

მოდით მონაცემების სიმაღლეზე და მნიშვნელობაზე მნიშვნელობაზე გონებამახვილობისთვის. ქვედა ბაზა დაყოფილია ნეკნებში:

რა სუაშოაშო? ჩვენ შეგვიძლია კუტის ტანგენსი, რომელიც ჩვენ ვიცით სწორი ჭრის ტრიკაუტის ფუძეზე:

27443. ტოლი ბარძაყის ტრაპეციის ქვედა ფუძე კარგია 23. ტრაპეციის სიმაღლე კარგია 39. მკვეთრი ტანგენსი ტანგენსი კარგია 13/8. შეიტყვეთ მეტი საფუძვლები.

მაღალი და ჩვენ გამოვთვლით რატომ არის კარგი კათეტიკისთვის კათეტიკისთვის:

ამ რანგში, დორივნუვატემეს უფრო დიდი საფუძველია:

27444. ბარძაყის ტრაპეციის ფუძეებია 17 და 87. ტრაპეციის 14. იპოვეთ ბასრი ტანგენსი ტანგენსი.

Будємо სიმაღლე და виднаємо відомі ზომა ესკიზზე. ქვედა ბაზა დაყოფილია ნეკნებზე 35, 17, 35:

ტანგენტის მიზნისთვის:

77152. ბარძაყის თანაბარი ტრაპეციის ფუძეები ნორმალურია 6 და 12. ტრაპეციის მწვავე სინუსი ნორმალურია 0,8. იცოდე ბოროტი მხარე.

მოდით ესკიზი ესკიზი, ვიფიქროთ სიმაღლეზე და მნიშვნელოვან ზომაზე, უფრო დიდი იყოფა იყოფა 3, 6 და 3 განყოფილებებად:

ვირაზიმო აღინიშნება როგორც x კოსინუსის მეშვეობით:

ძირითადი იდენტობიდან ჩვენ ვიცით COSα

ამ გზით:

27818. რატომ ტოლ ტოლ ტრაპეციის უფრო დიდი ჭრილი, როგორც ჩანს, რომ სხვაობა საპირისპირო შორის არის არის 500? მიეცით მტკიცებულება გრადუსით.

გეომეტრიის ჩვენ ვიცით ვიცით, რომ შესაძლებელია ორი ხაზი იყოს სწორი, რომ შიდა ცალმხრივი ჭრების ჯამი უფრო ძვირია 180 0. ჩვენი გონება არის

გონებიდან ნათქვამია, რომ მიმდებარე ფასი კარგია კარგია 50 0 Tobto

ტრაპეცია — ცე ბრტყელი ჭოტირი კოსინეც სუნს საფუძვლებს უწოდებენ ტრაპეცია , და ორი სხვა მხარე — გვერდითი მხარეები ტრაპეცია .

ინსტრუქცია

გარკვეული კუტის მნიშვნელობის მენეჯერი ტრაპეცია მე მოვითხოვ საკმარისი რაოდენობის დამატებით ხარკს. ვნახოთ კონდახი, რომელსაც სადგამზე ორი აქვს აქვს ტრაპეცია . შეგვატყობინეთ кути &ang-BAD და &ang-CDA, ჩვენ ვიცით kuti &ang-ABC და &ang-BCD. ტრაპეციას აქვს ისეთი ძალა, რომ კუტივების გვერდით გვერდით კანზე არის 180 ° -. შემდეგ &ang-ABC = 180°—&ang-BAD და &ang-BCD = 180°—&ang-CDA.

Trapezoid «Data-lightbox =» article-image «>

სხვა შეიძლება დაინიშნოს მხარეთა თანასწორობა თანასწორობა თანასწორობა ტრაპეცია და yakis dodatkovi kuti. მაგალითად, ბავშვის, ხედავთ, რომ ab, bc და ტოლია, ქვედა ფუძით kut ang-cad = α-. მოდი ვნახოთ ვნახოთ კოსინეც ABC, riwnofemori, რომ ab = bc. შემდეგ & ang-bac = & ang-bca. მნიშვნელოვნად yogo x სტილისთვის და ang-abc-y. კოსინეც და Dorivnyuє 180 ° -, საიდანაც შეგიძლიათ ნახოთ, Scho 2x + y \ u003d 180 ° -, შემდეგ y \ u003d 180 ° — — 2x. Водноча із власти ტრაპეცია : y + x + α- = 180° — მე ასევე 180° — — 2x + x + α- = 180° -. ასევე, х = α-. ორი კუტი ვიცოდი ტრაპეცია : &ang-BAC = 2x = 2α- და &ang-ABC = y = 180°- — 2α-. Oskilki ab \ u003d cd გონების უკან, მაშინ ტრაპეცია არის თანაბარი ან ბარძაყის ბარძაყის. ანუ,

Что значит включить трикутник на чоли. Тату трикутник

Смысл татуировки трикотаж винятково разноманитне, осколки там фигурируют в разных человеческих культурах, а в каменистой остаются этот рисунок все чаще и чаще выбирают среди других эскизов и фото в тату-салонах. У нее аура таинственности и святости, как будто она порабощена мудростью.

Открывая окно

Початок маленький на колосе, что на картинке трико символизирует невнятное единство основных початков народа:

• души;
• розум;
• физическое тело.

Часть татуировки вальники віводят ёма в другое значение:

Загальное между цими обозначенными теми що вонью повязані с процессом перетыкания одного сегмента в другой.

О людях и женщинах

Человеческая татуировка опирается на мудрость и силу, а женская — на три основных этапа жизни. Романтические закоханы часто висят на увази под трикутник, нападение на гнев и единение двух людей. В таких ситуациях девушка может носить намного больше за один тату-проект. Христианам воспевать у кого символы своей троицы, масонам — своей.

Как меняется смысл

Те, что означают трикутник, заключаются не только в состоянии ношения и в його высоких помыслов, но и в месте расташування, во вхождении в фигуру бэ-яку інша, или включение товаров на склад трикотажа. Какая икота, спутанные фигуры чудесным образом смотрятся на части тела.

Равностенные трикотажные изделия здебильных надеваются на запястье, хомилки на тильную сторону рук (как способ обхода головокружений), а девушкам больше нравится самый простой рисунок с тремя линиями. Этим зловонием удары размазываются по передним плечам, лопаткам, плечам, ступням, поперек. Цикаво, что середина криминального трикутника трактуется двояко: как вираз бездыханной глухой куты и тотальное отсутствие побега, а также жаль, что я пошел по кривой дорожке.

Преимущество геометрических фигур заключается в том, что запах универсален, не затаиться в часовой и весенней моде, красиво смотреться на коже любого цвета, на человеке, любого возраста и состояния. До этого трикоутник вариативен: можно вырастить кутью во фронтах лучших или тупых, соорудить верхушку, приподнятую в гору или опущенную. Нет особого смысла, в котором нет ничего, что вам подходит.

Navit Ринофеморальный трикотаж в целом можно перевернуть. А если вписать йогу в квадрат, то вы увидите растяжку по низу небесных и земных початков. Цвет подбирайте сами, здесь нет ежедневных правил.

Тату Трикутник позволяет изображать на тили как мужчину, так и женщину. Головне, поставь новую сенсацию, которая будет говорить о тех, для кого рисуется сам эскиз, такой стиль, конкретно

colori. Женщины могут имитировать с таким малышом три жизненных цикла, что означает юность, материнство и старость, или мудрость, силу и красоту. Важное место, разложить изображение. Варианты значение татуировки «трикутник» безликий:

• символизирует мицную школу;
• судьбы сошлись;
• круговорот людей-жизни-смерти;
• единство тела, души и разума;
• полное здоровье;
• триплет в одном.

Вы можете знать, как расшифровывать, как подписывать значение татуировки трикутник , и они могут быть правдой во всем. Варто вряд ли назначат, такой набросок будущей матери Володара.

Кого грабить трикутник тату

Такие знаки привлекают людей, как и символика, и внушают религиозно-философские особенности. Так что не обходят стороной такие татуировки и любители мистики и загадочности.

Малыш может расташоваться де завгодно. Це ложитесь в бажан будущего власника. Самые популярные места – зона между лопатками у девочек, на груди и локтях – у мальчиков. Вывернутый трикотаж больше подходит для слабого состояния, то есть женского початка. Поместить фигуру в квадрат — значит представить себе ментальное и астральное, небесное и земное.

Формы трикутника также можно корректировать, экспериментируя с навершием, основанием, навязчивостью. Вы можете разместиться в середине фигуры, как ребенок или принт. Головне, приукрашивая татуировку, не «стирают» того ощущения, которое хотелось бы передать.

Значение татуировки трикутник Большое разнообразие маленьких тату включает в себя и геометрические фигуры. Фигура обманщика больше всего почитается стариком, который является одним из первых человеческих малышей. Эти маленькие в стиле унисекс, вы можете выбрать быть человеком. Есть ощущение того, что человек вносит в тело образа. Для женщин он может стать символом трех жизненных циклов: девственности, материнства, старости. У людей разное значение татуировки — мудрость, сила, красота. Первый ребенок тела, введенный для маленького, также усиливает смысл, на который надеются. Значение тату в облике трикотажа может быть безличными вариациями. Для кого ты станешь символом того слубу, того міцного, что основано на единстве тела, духа, того разума. Такой образ более актуален как для молодых людей, как будто дали обіцянку баты разом на горе радости, так за то, за плечами таких давних дней, на час не легких, а счастливых судеб спящая жизнь. Такая татуировка может стать парной для мужчины и женщины. В остальном значение татуировки трикутник связано и с другими значениями: люди-жизнь-смерть, или даже больше жизнь-смерть-новая жизнь. Цикличность человеческой жизни отчетливо видна в фигуре трикутника, которая привлекает философов, умных мыслить людей. Также популярен трикутник как символ единства трех складских людей – тела, разума, души. Трикутник с подобными значениями людям, как будто они считают себя особенными, что они возвысились, что они живут в гармонии с собой. Но самое популярное значение татуировки Трикутник пришло к нам из христианской религии. Здесь трикутник является символом Отца, Греха, Святого Духа. У евреев издавна це означает совершенство. Для членов масонской ложи трико изображает сущность космоса — свет, ночь, час. Евреи наделяли три стороны трикутника значениями правильной мысли, правильной словесной подвески, правильной виконнанны. Культура кожи имеет свои символы трикутника. Значение символа изменено, но зловоние основано на случайной основе. Также возможно использование другой формы трикотажа, завяки увеличенного размера или изменение основы кутива. Маленький может быть с вершиной, не закрученной в гору, а с другой стороны, приплюснутой. Подобные образы встречаются редко, как бы так, что смысл давно забыт. Самый большой в доме применяется ровнобедренный трикутник. Однако вина могут быть написаны в звуковом разрезе или вершиной вниз, а три вязаных трикотажа символизируют полноту здоровья. Два трикутника, что смешались, означают огонь и воду, преодолею духовное над физическим. Зустричается трикутник среднего кола, это символ триединства в одном, причем под триединством можно понимать разные значения, принятые в религии людей. Трикутник в середине квадрата также означает два протяженных значения: небесное и земное, духовное и материальное, божественное и человеческое. Особое значение имеет трикутник, пофарбованный у любого цвета. Значение цвета выбирает сам человек.

Среди татуировок с геометрическими фигурами особой популярностью пользуется трикутник. Лаконичный на вид и богатый на правду, он чудесным образом подходит как для маленького ребенка, так и для кадра окружающих. Так что клиенты тату-салонов могут выбрать как минималистичные самодельные гексорамы и пентограммы, так и различные изображения в трикотажных рамках.

Трикутник — богатый символ. Среди основных трактовок: божество, творческая сила, солнце, духовный мир, вода, огонь, родство, гармония, сила, кохання, истина, схождение, мудрость, устойчивость, твердость строения, жизнь, дерево, холод, сердце.

Знак неуступчивости религиозного значения: трикутник знать, как знак Троицы. Вин говорит с духами других многообразных триад – буддийского Будда-Дхарма-Сангха, триединая природа мироздания, «мать-отец-ребенок», «человек-земля-небо», а также гармония духа, разума и любовь.

Трикутник — один час человеческий и женский знак. Он по-своему использует идею Великой Матери. Це «материнское чрево космоса» — женский початок. А пока я заставляю человека создавать силу.

Форма Трикутну может иметь богатую символику. Татуировка с греческой дельтой – это знак жизни космоса. Гексограмма — день мужчины и женщины. Тригон с поднятыми мечами — символ обновления, родины Китая. Инструмент или стул пифагорейского трикутника означает мудрость.

Знак В_домы — Око Гора — те же подсказки на основе геометрической фигуры. Вин — индийский третий глаз Будды, древнегреческий глаз Юпитера, глаз Великого духа того Люцифера среди просветителей. Это знак всеприсутствия, мудрости, света, духовного творчества, святости, сна, единства и ревности. Похож на глаз, спрятанный в трикотажнике. На некоторых татуировках геометрическая фигура окружена сверкающим колом. В это время тату имеет еще одно значение – неумолимость святости.

При татуировке трикутником — тугой амулет. Стоит как Всевидящее Око, так и другие родные малютки, у которых такая геометрическая фигура. Наколку целесообразно выбрать захисту, чтобы отдать дань уважения трикстеру, разместить рядом с пентаклем. На ритуально-магической практике необходимо стоять победоносно, как талисман. Постройку связывают с оторванностью власника от священства и прочих малозначительных притоков.

 

සමමිතික අක්ෂය. සියලු සමමිතිය ඇති කරන රූප

අක්ෂ සමමිතිය — සමමිතිය සෑම විටම සෘජු වේ.

දාන දෙයක් කෙලින් වෙන්න දෙන්න г .

සරල රේඛාවක් වැනි a ලක්ෂ්‍යයට සමමිතික සමමිතික ලක්ෂ්‍යයක් ප්‍රේරණය කිරීමට G , අවශ්ය:

1) A ලක්ෂයේ සිට රේඛාවකට අඳින්න අඳින්න G ලම්බක AO.

2) සරල රේඛාවේ අනෙක් දිගු කළ කළ ලම්බක මත G OA1 හි පංතිය පංතිය, AO: OA1 = AO ට මිල අධිකය.

OTRIMAN ලක්ෂ්‍යය A1 සරල රේඛාවක් ඔස්සේ A ලක්ෂ්‍යයට සමමිතික වේ G .

කෙලින්ම г සියලු සමමිතිය ලෙස හැඳින්වේ.

එවැනි ආකාරයෙන්, ලකුණු a සහ a1 g රේඛා මෙන් සමමිතික වේ, එබැවින් ඒවා රේඛා වේ කපන ලද AA1 මැද හරහා ගමන් කරන අතර නව එකට ලම්බක වේ 9000ේ 9000ේ

a ලක්ෂ්‍යය g රේඛාව මත තිබේ තිබේ නම්, ලක්ෂ්‍යය є ලක්ෂ්‍යය a වේ.

දී රේඛාවට සමමිතිකව සම ලක්ෂ්‍යය ලක්ෂ්‍යය a1 ලක්ෂ්‍යයට පරිවර්තනය වන විට, f රූපය f1 රූපය බවට පරිවර්තනය කිරීම G , සරල වැනි සමමිතිය පරිවර්තනයක් ලෙස හැඳින්වේ G .

F සහ F1 රූප සරල රේඛාවකට සමමිතික රූප ලෙස හැඳි඀්඀5 g ි඀්ක

ට්‍රයිකුට්නික් කිරීමට, මෙම ෂෝඩෝ සරල රේඛාවට වේ වේ G , ත්‍රිකෝණයේ මුදුන් සහ ඒවායේ පිටුපසට ලක්ෂ්‍ය ප්‍රේරණය කිරීම ප්‍රමාණවත් වේ.

උදාහරණයක් ලෙස, ට්‍රයිකොට් ABC සහ A1B1C1 අවම වශයෙන් ලෙස සමමිතික වේ වේ G .

සමමිතිය වගේ වගේ, සරල වගේ වගේ G රූපයක් පරිවර්තනය කරන්න, එවිට එවැනි රූපයක් සමමිතික සරල රේඛාවක් ලෙස හැඳින්වේ г , නමුත් කෙළින්ම г її සියලු සමමිතිය ෽ෙස හැස හැස හැස

රූපය වන අතර එහි බර සමමිතිය සමාන කොටස් දෙකකට බෙදා ඇත. කඩදාසි මත රූපයක් අඳින්නේ කෙසේද, එය දෙස බැලීමට සහ සමමිතියේ අක්ෂය දිගේ නැමීමට නැමීමට, අර්ධ නැවී ඇත.

අවම වශයෙන් සමමිතික රූප යොදන්න.

1) සෘජුකෝණාස්රය.

සෘජුකෝණාස්‍රයක අක්ෂ 2 ක් තිබිය හැක: කෙළින්ම, පැතිවලට සමාන්තරව හරස් ලක්ෂ්‍යය හරහා ගමන් කිරීමට.

රොම්බස් හට සමමිතික අක්ෂ දෙකක් තිබිය හැක:

යෝග විකර්ණ ඇති සරල රේඛා.

3) Ромб සහ සෘජුකෝණාස්රය චතුරස්රයක් චතුරස්රයක්, සමමිතික අක්ෂ තිබිය යුතුය: සරල රේඛා, විකර්ණ පළිගැනීමට සහ සරල රේඛා, පැතිවලට සමාන්තරව විකර්ණවල ලක්ෂ්යය හරහා ගමන් කිරීමට.

4) කවය.

පරිධිය පුද්ගල නොවන අක්ෂ විය හැක හැක:

සෘජු, විෂ්කම්භය පළිගැනීමට, є කණුවේ සියලු සමමිතිය.

සරල සමමිතියේ පුද්ගල නොවන අක්ෂ ද විය හැකිය: එය සමමිතියේ දී ඇති සරල රේඛාවක් සඳහා සරල ලම්බක වේ ද ද යන්න.

6) Ривнобедренная трапеция.

Rivnostegnova Trapezium — රූපයක්, සරල සමමිතික සමමිතික, පාදවලට සහ ඒවායේ මධ්යස්ථාන හරහා ගමන් කිරීම කිරීම.

7) Ровностегновый трикотаж.

Rivnofemoral ට්‍රයිකොට් සම්පූර්ණ සම්පූර්ණ සමමිතියක් තිබිය හැක:

උස ගමන් කිරීමට සරල රේඛාවක් (මධ්‍යන්‍ය, බයිසෙක්ට්‍රික්ස්), පාදම වෙත ඇද ඇත.

8) Ровносторонний трикутник.

Ровенский трикотажник має සමමිතික අක්ෂ තුනක්:

кут යනු යෝග පළිගැනීම සඳහා සෘජු වුවත් සමමිතික රූපයකි රූපයකි.

අක්ෂ සමමිතිය යනු චලනයකි.

සමමිතිය

පුරාණ කාලයේ සිටම තමන් වටා ලෝකය සංවිධානය කිරීමට පටන් ගෙන ඇත. එබැවින් එය තුළට ඇතුල් විය හැකි නමුත් එය වැඩි නොවේ. සෞන්දර්යාත්මක දෘෂ්ටි කෝණයෙන්, රන්වන් රිදී කැපීම් මෙන්ම, සංවේදීව, සමමිතිය හුරුපුරුදු දසුනක් ලෙස පෙනේ. මෙම පදය Maє ග්රීක Pohodzhennya වන අතර එහි වචනාර්ථයෙන් «සමානුපාතිකත්වය» යන්නයි. Зрозуміло, цією ලකුණ සඳහා збіг ගැන වගේ යන්න, සහ අනෙකුත් අය අතර й. සංවේදී හැඟීම ඇත ඇත — එවැනි බලය බලය, නිහඬ chi inshih utvorni ප්රතිඵලයක් ප්රතිඵලය වඩා ගෞරවනීය වේ වේ. Tse zustrichaetsya ජීවමාන, ඒ අජීවී ස්වභාවය ස්වභාවය, මෙන්ම මිනිසුන් විසින් කැඩී වස්තූන් තුළ තුළ.

දැනට, «සමමිතිය» යන ජ්‍යාමිතියට ජ්‍යාමිතියට පුරුදු වී ඇත, නමුත් පොහොසත් විද්‍යාත්මක ක්ෂේත්‍රවල සිරවී ඇති බව ගැනීමට සහ එහි අර්ථය දැවෙන නොනවතින පිළිස්සීම් වලින් යටපත් ඇත ඇත. එය විට විට විට විට විට විට විට හා හා vvazhaєtsya tswhavim අවසන් වටිනවා වටිනවා කැබලි yogo විශේෂ වෙනස් වෙනස්, සහ මූලද්රව්ය ගෙන. Vikoristannya simetrї එසේ එසේ එසේ එය ස්වභාව ධර්මයේ නොව නොව, රෙදිපිළි ආභරණ ආභරණ, දේශසීමා අනෙකුත් මිනිසා විසින් සාදන ලද වස්තූන්ගේ ධනය මත වුවද. වර්ටෝ විස්තර දෙස බලන්න, දාරයේ ඇති කැබලි ගොරෝසු ྲྀු ྲྀ.

වෙනත් සඟරාවල සඟරාවල යෙදුම හඳුන්වාදීම

ජ්‍යාමිතියේ සමමිතිය බලමු බලමු, Prote Varto අනුමාන කරන්න ජයග්‍රාහී වචනය පමණක් නොවේ නොවේ. ජීව විද්‍යාව, වෛරස් විද්‍යාව, රසායන විද්‍යාව, භෞතික විද්‍යාව, ස්ඵටික විද්‍යාව — මෙම විවිධ පැතිවලින් සහ රට තුළ වන වන වල එකම ලැයිස්තුවකි ලැයිස්තුවකි. විවිධ සිත්. මීට අමතරව, මෙම පදය කිරීමට කුමන විද්යාවටද, තැබීමට, උදාහරණයක් ලෙස, වර්ගීකරණය. ඒ නිසා, මම ප්රධාන ක්රියා, සමහර විට, නොවැළැක්විය හැකි скрипки පිරී ඇතත්, බරපතල වෙනස් වෙනස් tipi ගියා.

වර්ගීකරණය

ප්‍රධාන හාල්මැස්සන් වෙන්කර හඳුනා ගන්න ගන්න, ඒවායින් තුනක් විට විට භාවිතා වේ:

ඊට අමතරව, ඔවුන් එවැනි වර්ග වෙන්කර හඳුනා ගනී, දුර්ගන්ධය බොහෝ සෙයින් කැපී පෙනේ, නමුත් වලට වඩා අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු අඩු ගනී ගනී ගනී දුර්ගන්ධය බොහෝ සෙයින් පෙනේ පෙනේ පෙනේ පෙනේ ව්යාජය ව්යාජය ව්යාජය බොහෝ බොහෝ සෙයින් පෙනේ පෙනේ පෙනේ පෙනේ පෙනේ ;

ප්‍රකාශිත;

තිත;

ප්රගතිශීලී;

ඉස්කුරුප්පු ඇණ;

ඛණ්ඩනය;

සහ ආදිය.

ජීව විද්‍යාවේදී, සියලුම වෙනත් ආකාරයකින් ආකාරයකින් ලෙස හැඳින්වේ හැඳින්වේ, නමුත් දී ඒවා සමාන විය හැකිය. ті чи інші කණ්ඩායම් выделяется මත Підрозділ підставі наивности чи відсутности මත, සහ колкости дейків элементов, එවායම් підрозділ підставі наивністи чи відсутности මත, සහ колкости дейків элементов, එවායමි підців цэнтрив, підців цэнтри. අපි ඒවා වඩාත් විස්තරාත්මකව සලකා බලමු.

මූලික අංග

Yavishchi දී සහල් රූප බලන්න, එම Obov’yazkovo є එකක්. එබැවින් මූලික නම්වලට ගුවන් යානා, මධ්‍යස්ථාන සහ සමමිතික අක්ෂ ඇතුළත් වේ. ඒවායේ පැහැදිලි බව, පැවැත්ම වර්ගයෙහි ප්රමාණය තීරණය කරනු ලබන්නේ වඩාත්ම පැහැදිලිය පැහැදිලිය.

සමමිතියේ රූපයේ මැද ලක්ෂ්‍යයක් හෝ ස්ඵටිකයක් ලෙස හැඳින්වේ, එහි අභිසාරී වන අතර එමඟින් සියලුම යුගල එක පැත්තකට සමාන වේ. මට තේරුණා, වයින් පටන් ගන්න එපා කියලා. පැති තිබේ නම්, සමාන්තර නැත නැත, එවිට එවැනි කරුණක් දැන ගැනීමට ය ය, කැබලි නොමැත. නිසැකවම, සමමිතියේ ඔබට තනිවම නැගී සිටිය හැකි බව පැහැදිලිය. බට් може бути, උදාහරණයක් ලෙස, මැද අසල තිත අසල. මෙම මූලද්රව්යය C ලෙස නම් කර ඇත.

සමමිතියේ සංවේදී සංවේදී, පැහැදිලි ය, නමුත් රූපය සමාන කොටස් දෙකකට බෙදිය නොහැක. ඔබට පැති හෝ කිහිපයක් හරහා යා හැකිය, නමුත් එයට සමාන්තරව හෝ ඒවා කළ හැකිය. එක හා සංඛ්‍යාවක් සඳහා, ඔබට සමතලා ස්ප්‍රැට් එකක් භාවිතා කළ හැකිය. Ци මූලද්‍රව්‍ය P වැනි ශබ්දයක්.

එහෙත්, සමහර විට, සමමිතිය අක්ෂ ලෙස හඳුන්වන අය බොහෝ විට භාවිතා වේ. කිසියම් හේතුවක් නිසා, ප්‍රකාශනයක් සහ ස්වභාවධර්මයේ මෙන් චලනය විය හැකිය. මට දර්ශනය දෙස බැලීමට නොහැකි වනු ඇත.

අක්ෂය

බොහෝ මූලද්‍රව්‍යයක් මූලද්‍රව්‍යයක්, එම සමමිතික ලෙස හැඳින්විය හැක,

කෙලින්ම чи відрізок කතා කරන්න. ඕනෑම වපඩ්කා සඳහා, එය ලක්ෂ්යයක් සහ පැතලි එකකොගගැ් ගැ් ගැ් ඔවුන් රූපවල සමමිතියේ අක්ෂ දෙස බලයි. ඔබ ඊටත් පොහොසත් විය හැකි අතර, දුගඳ හමන හොඳ දෙයක් විය හැකිය: පැති බෙදන්න, නැතහොත් සමාන්තරව සමාන්තරව, කුටි සකස් කරන්න, නැතහොත් එය වැඩ නොකරන්න. L වැනි සමමිතික අක්ෂ ශබ්ද කරයි.

බට් ровнобедренный සහ ровносторонний трикутник විය හැක. පළමු පේළියේ, සියලු සමමිතිය අතට අතට, පැතිවල, පැතිවල, එය සමාන මුහුණු වලට වනු ඇත, සහ රේඛාවේදී රේඛාවේදී, උඩු බයිසෙක්ට්රික්ස් බයිසෙක්ට්රික්ස්, මධ්යන්ය සම කැපීම සහ Zbі බවට පත් කරනු ලැබේ ලැබේ. සහ උස. Звичайне හොඳින් трикутникс ඇය හදන්න එපා.

අවම කිවහොත් කිවහොත්, ස්ඵටික සහ සහ ඇති ඇති සියලුම දිව්‍යමය එකතුව සමමිතික උපාධිය ලෙස හැඳින්වේ. Цей показник අක්ෂ, පැතලි හා මධ්යස්ථාන සංඛ්යාව බොරු කිරීමන.

ජ්යාමිතිය අයදුම් කරන්න කරන්න

මානසිකව, ඔබට සියලුම අපද්‍රව්‍ය සියලු සමමිතිය ගැන සිතිය හැකි ස්ථාන බෙදිය හැකිය, නමුත් කළ කළ නොහැක. පළමු කාණ්ඩයේ, ඔවුන් නිවැරදි නිවැරදි Bagatokutniki, Cola, овалы, මෙන්ම okremi vipadki සහිත ස්වයංක්‍රීයව පරිභෝජනය කරයි, එසේ නොමැති නම් මිතුරෙකුගෙන් කණ්ඩායමක් පරිභෝජනය කරයි.

එය මෙන් මෙන්, එය ත්‍රිකෝණාකාරයේ සියලුම සමමිතිය ගැන නම්, මෙම මූලද්‍රව්‍යය මූලද්‍රව්‍යය මූලද්‍රව්‍යය මූලද්‍රව්‍යය සඳහා භාවිතා නොකරන්න නොකරන්න. චතුරස්රයක් සඳහා, සෘජුකෝණාස්රයක්, රොම්බස් සමාන්තර චලිතයක් චලිතයක් චලිතයක් є, සහ අක්රමවත් රූපයක් සඳහා, පැහැදිලිවම, නොවේ. කොටස් සඳහා, සමමිතියේ පුද්ගල නොවන සරල රේඛා වේ, як_ її කේන්ද්‍රය ගමන් කිරීමට.

එපමණක් නොව, බැලූ සාමාන්‍ය සාමාන්‍ය පෝස්ට් එක දෙස බලන්න. ක්‍රිමියාවේ සමමිතියේ බරක් ඇති කිරීමට මම කැමතියි නිවැරදි බගටොකුට්නිකිව් සහ සිසිලස වොලොඩිටි ඩෙයාකි මෙන්ම පිරමිඩ, සමාන්තර චලිත සහ ඩීකි ඉංෂි. окремо පෙනුම සඳහා සම випадок ලිස්සා ගියේය.

ස්වභාවධර්මයට යොදන්න

ජීවිතයේ දර්පණ සමමිතිය ලෙස හැඳින්වේ හැඳින්වේ, එය උච්චාරණය උච්චාරණය වේ
බොහෝ විට. ඒ පස්සට මිනිසෙක්, පොහොසත් සත්වයෙක් වෙන්න. අක්ෂය රේඩියල් හඳුන්වනු ලබන අතර, රීතියක් ලෙස, වඩාත් පොහොසත් ලෙස කඩුල්ලේ වර්ධනය ලෝකය ලෝකය. ඒ වුණත් ඒවා ගඳ ගහනවා. උදාහරණයක් ලෙස, ඒ සිතන්න සිතන්න, ඔබට අක්ෂ අක්ෂ කීයක් දැකිය හැකිද, ඒවා වූයේ වූයේ ඇයි? තේරුම් ගත පරිදි පරිදි, අපි කරන්නේ මුහුදු බෑගර් ගැන මිස තාරකා විද්‍යාත්මක පුහුණුව පිළිබඳ විෂය නොවේ. නිවැරදි පිළිතුර වගේ වනු ඇත: තරු වෙනස් වන ප්‍රමාණයේ වැතිර සිටීම හොඳය, උදාහරණයක් ලෙස, එය පහක්, එය පහක් වැනි ය.

මීට අමතරව, පොහොසත් වල රේඩියල් රේඩියල් සමමිතිය නිරීක්ෂණය කරනු ලැබේ: ромашка, හිසකෙස්, ඩෝමවුස් සහ යනාදිය.

අරිතිමියාව

මෙම පදය, සෑම දෙයකටම පළමුවැන්න, වෛද්‍ය සහ හෘද විද්‍යාව ගැන වැඩිපුර අනුමාන කරයි, අනෙක් ප්‍රෝටියෝ වයින්, එයට තේරුමක් නැත නැත. සමහර අවස්ථාවලදී, එය «අසමමිතිය» සමග වනු ඇත ඇත, එනම්, අනෙකාගේ නිත්යභාවය ඇති බව පෙනේ. Її එය vipadkovist ලෙස කිරීමට හැකි වන අතර, සමහර විට එය උපක්රමයක් බවට පත් විය හැකිය, උදාහරණයක් ලෙස, ගෘහ නිර්මාණ ශිල්පය වැනි ඇඳුමකින්. Aje සමමිතික Budvel ඊටත් පොහොසත් පොහොසත්, ප්රසිද්ධ ප්රසිද්ධ ප්රසිද්ධ ප්රසිද්ධ ප්රසිද්ධ ප්රසිද්ධ නමුත් තිබුණද නමුත් නමුත් තවමත් බට් සොයා ගන්න. එය එසේ випадково වූ බව පෙනේ, නමුත් тсома දී එය එහි ම අලංකාරය ඇත.

ඊට අමතරව, මිනිසුන්ගේ සහ ශරීරය ශරීරය එම එම සත්වයා සමමිතික නොවන බව පැහැදිලිය. පසු විපරම් සිදු කරන ලදී, සමහර «නිවැරදි» පුද්ගලයන්ගේ ප්රතිඵල අනුව, ඔවුන් අජීවී, සරලව නොහැකි ලෙස හඳුනාගෙන හඳුනාගෙන ඇත. සියල්ලටම සමානව, සමමිතිය ගෙන අතර පෙනුමම පුදුම සහගතය සහගතය, සහ යුද්ධය අවසන් වන තුරු, නමුත් Цикава අද්දරට.

ජ්යාමිතික සමමිතිය

ජ්‍යාමිතික රූපයක් නැගී සහ සමමිතිය යන්නෙන් අදහස් වන්නේ කෙනෙකුට පරිවර්තනය කළ හැකි බවයි — උදාහරණයක් ලෙස, හැරවීම — බලයේ උපස්ථායකයන් හිරිවැටීමට.

එවැනි සඳහා ඇති හැකියාව රූපයෙන් රූපයට වෙනස් වේ වේ. උදාහරණයක් ලෙස, ලක්ෂ්යය තිත් වටා එතීමට හැකි නම්, මධ්යයේ තැන්පත් කර ඇති අතර, එය නැති විය හැකි නම්, ඔහුට කිසිවක් වෙනස් නොවනු ඇත.

සමමිතිය සංකල්පය වැඩි දුර නොගොස් පැහැදිලි කළ හැකිය හැකිය. කණුවේ කේන්ද්‍රය සරල රේඛාවක් ඇඳීම සහ රවුමේ ලක්ෂ්‍ය දෙකක් සම්බන්ධ කරන ලම්බක තිබේද යන්න ප්‍රේරණය කිරීම ප්‍රමාණවත් වේ. සරල රේඛාව හරස් රේඛාවේ ලක්ෂ්යය ඉළ ඇට එකකට එකක් මෙන් කොටස් දෙකකට බෙදා ඇත.

වෙනත් වලින් කිවහොත් කිවහොත්, ඇය කෙලින්ම රූපය සමාන කොටස් දෙකකට බෙදා ඇත. රූපයේ කොටස්වල ලක්ෂ්ය, දමස් ලම්බකව සරල රේඛා මත රළු කර ඇති අතර, එය සරල රේඛාවක් මත පිහිටා ඇත ඇත. අක්ෂය සෘජු වන අතර සියලු සමමිතිය ලෙස හැඳින්වේ. මේ ආකාරයේ සමමිතිය — සෘජු නම් — අක්ෂීය සමමිතිය ලෙස හැඳින්වේ.

සමමිතික ගණන ගණන

විවිධ රූපවල, සමමිතියේ ගණන වෙනස් වේ වේ. නිදසුනක් වශයෙන්, එවැනි පරදුවට තැබීම සහ සිසිල් වීම පුද්ගල නොවේ. සමපාර්ශ්වික ට්‍රයිකට්නික්ට ලම්බක, පැතිවල මත අතපසුවීම් ඇත, නමුත් අක්ෂ තුනක් තිබිය හැකිය. චතුරස්රයේ සහ සෘජුකෝණාස්රයේ, කෙනෙකුට අක්ෂ කිහිපයක් ඇඳිය ​​හැකිය හැකිය. ඒවායින් දෙකක් පැතිවලට ලම්බක වන අතර අනෙක් ඒවා විකර්ණ වේ. සමාන- бедренная трикотаж වල ඇත්තේ එකම සමමිතියක් පමණක් වන අතර එය සමාන පැති පැතිර ඇත ඇත.

අක්ෂ සමමිතිය ස්වභාවයෙන්ම තියුණු වේ. ඔබට විකල්ප දෙකක් පරීක්ෂා කළ හැකිය.

පළමු රේඩියල් සමමිතිය වන අතර එය බහු අක්ෂ ඇති බව ප්‍රකාශ කරයි. උදාහරණයක් ලෙස, සාගර තරු සඳහා Vaughn සාමාන්ය වේ. ශරීරය කොටස් බෙදන තනි බරක් සහිත ද්විපාර්ශ්වික හෝ ද්විපාර්ශ්වික සමමිතිය මගින් වඩාත් දියුණු ආධිපත්‍යය දරයි.

මිනිස් ටමාන් ද්විපාර්ශ්වික සමමිතියක් ඇත, නමුත් එය පරමාදර්ශය නම් කළ නොහැක. සමමිතික ලෙස කකුල් කකුල්, අත්, ඇස්, කකුල්, නමුත් හදවත, අක්මාව සහ ප්ලීහාව නොවේ. ද්විපාර්ශ්වික සමමිතිය දැනුවත්භාවය ඇමතීමට මතක තබා ගන්න. නිදසුනක් වශයෙන්, පුද්ගලයෙකුට දෙකෙහිම එකම උපත් සලකුණු ඇති බව කලාතුරකින් සිදු වේ.

දසුන් දෙකක සමමිතිය: මධ්‍යම එක අක්ෂයයි. මධ්‍යම සමමිතිය සමඟ, සෘජු වන්න, රූපයේ හරහා හරහා ඇද, එය සමානව සමමිතික පරම සමාන කොටස් දෙකකට බෙදන්න. සරල වචන වලින් කිවහොත්, තනි තනිව දර්පණ රූපවල ගඳ. එවැනි සරල වල පරදුවට තැබීමේදී, කෙනෙකුට පුද්ගල චරිතයක් ඇඳිය, සුළු දුර්ගන්ධයක් විට විට, එය සමමිතික කොටස් දෙකකට බෙදන්න.

සියලු සමමිතිය

බොහෝ ජ්යාමිතික රූපවල එවැනි ලක්ෂණ නොමැත. ඔවුන්ට සිදු හැක්කේ සියලු සමමිතිය පමණක් වන අතර සියල්ලටම වඩා දුරින්. Віс — це ද සෘජු ය, රූපය සමමිතික කොටස් වලට බෙදීම වැනි ය. නමුත් සමමිතියේ සඳහා සඳහා, කුණු වැඩි ඉඩක් නොමැති නම්, ඔබ ටිකක් වෙනස් කළත්, සමමිතිය කඩා වැටෙනු ඇත.

සම් එහි සියලු පැති සමාන වුවත් සම් අංශක අනූවක් වුවද එයට සියලු තිබිය හැකි බව තර්කානුකූල ය ය. Трикутники වෙනස්. වෙනසෙහි පැති ට්‍රයිකුට්නික් සියල්ලන්ගේම මව හෝ සමමිතියේ කේන්ද්‍රය විය නොහැක. සහ සමාන-бедренные трикотажные изделия අක්ෂය සියලු සමමිතිය ඇද ගත හැක. පාදම — තුන්වන වැටී ඇති සමාන පැති දෙකක් සහ සමාන නැමීම් දෙකක් සහිත යැයි අනුමාන කරමු. ඉරට්ටේ-කෙළිකාවක් සඳහා, වැස්ම වනු ඇත ඇත, එය මුදුනේ මුදුනේ සිට දක්වා ගමන් කරයි. මෙම දිශාවට, එය එකවරම සෘජු ඇත සහ මධ්යස්ථ මධ්යස්ථ, සහ bisectrix, එහි කැබලි, තුන්වන මැදට ඒකාකාරව ඒකාකාරව kut Navpil සහ diide බෙදනු ඇත. ඔබ මෙම රේඛාව දිගේ ට්‍රයිකට්නික් නැමුවහොත්, ඔබ දැක ඇති සංඛ්‍යා, මම එකකින් එකක් පිටපත් කරමි. කෙසේ වෙතත්, සමාන- бедренная ත්‍රිකෝණයට සියලු සමමිතිය ඇත, නමුත් එකක් පමණි. ඔබ її හරහා සරල රේඛාවක් අඳින්නේ නම්, ඔබ එය සමමිතික කොටස් දෙකකට බෙදන්නේ නැත.

විශේෂ trioutnik

අද්විතීය ¾ සමපාර්ශ්වික ට්‍රයිඒඒ Це විශේෂ පෙනුම трикутников, සමාන-бедренный ද වේ. ඇත්තම කිව්වොත්, අලුත් සමේ පැත්ත පදනම විය හැකි අතර අතර, සියලු පැති වන අතර, සම හැටක් හැටක් පත් පත් විය හැකිය. එසේම, සමාන පාර්ශ්වීය ඇඳුමේ, සමමිතික අක්ෂ තුනක් ඇත. Ци කෙලින්ම tricutnik මධ්‍යයේ එක් ස්ථානයක අභිසාරී වේ. නමුත් එවැනි නිර්මාණය කිරීම සඳහා රූපයේ ඇති සමාන-පාර්ශ්වික ත්‍රිකෝණය කේන්ද්‍රීය සමමිතියෙන් පරිවර්තනය නොවේ. සමමිතියේ කේන්ද්‍රය පාර්ශ්වීය ගෙතුම් ඇඳුමකින් සොයාගත නොහැක, නම් කරන ලද ලක්ෂ්‍යයක් හරහා කැබලි සමාන කොටස් මත රූපය බෙදීමට සරල තුනක් පමණි පමණි. ඔබට වෙනත් රේඛාවකින් සරල රේඛාවක් ඇඳීමට අවශ්‍ය නම්, එවිට තවදුරටත් ට්‍රයිකොට් මාටිමා ඇති නොවේ නොවේ. එයින් අදහස් සංඛ්‍යා සංඛ්‍යා අඩු අක්ෂීය සමමිතික විය හැකි බවයි.

මිනිසුන්ගේ ජීවිතය වඩාත් සමමිතික වේ. එය පහසු, ලස්සනයි, එය නව ප්රමිතීන් සෑදීමට අවශ්ය අවශ්ය අවශ්ය එය පහසු. නමුත් එය වශයෙන්ම කුමක්ද සහ එවැනි ගාර්නා ස්වභාවයක් ඇත්තේ ඇයි, ගරු කිරීම වන්නේ කෙසේද කෙසේද?

සමමිතිය

පුරාණ සිටම සිටම තමන් වටා ලෝකය සංවිධානය කිරීමට පටන් ගෙන ඇත. එබැවින් එය තුළට ඇතුල් විය හැකි නමුත් එය වැඩි නොවේ. සෞන්දර්යාත්මක දෘෂ්ටි කෝණයෙන්, රන්වන් රිදී කැපීම් මෙන්ම, සංවේදීව, සමමිතිය හුරුපුරුදු දසුනක් ලෙස පෙනේ. මෙම පදය ග්රීක Pohodzhennya විය අතර වචනාර්ථයෙන් වචනාර්ථයෙන් «සමානුපාතිකත්වය» යන්නයි. Зрозуміло, цією ලකුණ සඳහා збіг ගැන වගේ යන්න, සහ අනෙකුත් අය අතර й. සංවේදී හැඟීම ඇත ඇත — එවැනි බලය බලය, නිහඬ chi inshih utvorni ප්රතිඵලයක් ප්රතිඵලය වඩා ගෞරවනීය වේ වේ. Tse zustrichaetsya ජීවමාන, ඒ අජීවී ස්වභාවය ස්වභාවය, මෙන්ම මිනිසුන් විසින් කැඩී වස්තූන් තුළ තුළ.

අපට, «සමමිතිය» යන පදය ජ්‍යාමිතිය සඳහා භාවිතා වේ, නමුත් පොහොසත් විද්‍යාත්මක ක්ෂේත්‍රවල සිරවී ඇති බව ගැනීමට සහ එහි අර්ථය බොහෝ දුරට නොවෙනස්ව පවතී. එය බොහෝ සිදු කිරීමට අවශ්ය වන අතර, එය නාද කිරීම වැදගත් වේ, කැබලි නැඟිටුවනු ලබන අතර, මූලද්රව්ය ගෙන ඒම. Vikoristannya simetrї එසේ එසේ එසේ එය ස්වභාව ධර්මයේ නොව නොව, රෙදිපිළි ආභරණ ආභරණ, දේශසීමා අනෙකුත් මිනිසා විසින් සාදන ලද වස්තූන්ගේ ධනය මත වුවද. වර්ටෝ විස්තර දෙස බලන්න, දාරයේ ඇති කැබලි ගොරෝසු ྲྀු ྲྀ.

වෙනත් විද්‍යාත්මක සඟරාවල යෙදුම හඳුන්වාදීද

ජ්‍යාමිතියේ සමමිතිය බලමු බලමු බලමු, Prote varto අනුමාන කරන්න වචනය මෙහි පමණක් නොවේ. ජීව විද්‍යාව, වෛරස් විද්‍යාව, රසායන විද්‍යාව, භෞතික විද්‍යාව, ස්ඵටික විද්‍යාව — මෙම විවිධ පැතිවලින් සහ විවිධ මනස්වලින් විකෘති ඇති ප්‍රදේශ වල එකම ලැයිස්තුවකි ලැයිස්තුවකි. මීට අමතරව, මෙම පදය කිරීමට කුමන විද්යාවටද, තැබීමට, උදාහරණයක් ලෙස, වර්ගීකරණය. ඒ නිසා, මම ප්රධාන ක්රියා, සමහර විට, නොවැළැක්විය හැකි скрипки පිරී ඇතත්, බරපතල වෙනස් වෙනස් tipi ගියා.

වර්ගීකරණය

ප්‍රධාන හාල්මැස්සන් වෙන්කර හඳුනා ගන්න, ඒවායින් තුනක් විට විට භාවිතා වේ:

ඊට අමතරව, ජ්‍යාමිතියේදී ඔවුන් එවැනි වර්ග වෙන්කර හඳුනා ගනී, දුර්ගන්ධය බොහෝ කැපී පෙනේ පෙනේ, නමුත් Cicavi වලට වඩා නොවේ නොවේ:

• ව්යාජය;
• ප්‍රකාශිත;
• තිත;
• ප්රගතිශීලී;
• ඉස්කුරුප්පු ඇණ;
• ඛණ්ඩනය;
• සහ ආදිය.

ජීව විද්‍යාවේදී, සියලුම වෙනත් ආකාරයකින් ආකාරයකින් ලෙස හැඳින්වේ හැඳින්වේ, නමුත් දී ඒවා සමාන විය හැකිය. ті чи інші කණ්ඩායම් выделяется මත Підрозділ підставі наивности чи відсутности මත, සහ колкости дейків элементов, එවායම් підрозділ підставі наивністи чи відсутности මත, සහ колкости дейків элементов, එවායමි підців цэнтрив, підців цэнтри. අපි ඒවා වඩාත් විස්තරාත්මකව සලකා බලමු.

මූලික අංග

Yavishchi දී සහල් රූප බලන්න, එම Obov’yazkovo є එකක්. එබැවින් මූලික නම්වලට ගුවන් යානා, මධ්‍යස්ථාන සහ සමමිතික අක්ෂ ඇතුළත් වේ. ඒවායේ පැහැදිලි බව, පැවැත්ම වර්ගයෙහි ප්රමාණය තීරණය කරනු ලබන්නේ වඩාත්ම පැහැදිලිය පැහැදිලිය.

සමමිතියේ රූපයේ මැද ලක්ෂ්‍යයක් හෝ ස්ඵටිකයක් ලෙස හැඳින්වේ, එහි අභිසාරී වන අතර එමඟින් සියලුම යුගල එක පැත්තකට සමාන වේ. මට තේරුණා, වයින් පටන් ගන්න එපා කියලා. පැති තිබේ නම්, සමාන්තර නැත නැත, එවිට එවැනි කරුණක් දැන ගැනීමට ය ය, කැබලි නොමැත. පැහැදිලිවම, සමමිතියේ රූපය තමා මත ප්‍රදර්ශනය කළ හැකි එකක් බව පැහැදිලිය. බට් може бути, උදාහරණයක් ලෙස, මැද අසල තිත අසල. මෙම මූලද්රව්යය C ලෙස නම් කර ඇත.

සමමිතියේ සංවේදී සංවේදී, පැහැදිලි ය, නමුත් රූපය සමාන කොටස් දෙකකට බෙදිය නොහැක. ඔබට පැති හෝ කිහිපයක් හරහා යා හැකිය, නමුත් එයට සමාන්තරව හෝ ඒවා කළ හැකිය. එක හා සංඛ්‍යාවක් සඳහා, ඔබට සමතලා ස්ප්‍රැට් එකක් භාවිතා කළ හැකිය. Ци මූලද්‍රව්‍ය P වැනි ශබ්දයක්.

එහෙත්, සමහර විට, «සමමිතියේ අක්ෂ» ලෙස හඳුන්වන අය විට උගුලට හසු වේ. කිසියම් හේතුවක් නිසා, ප්‍රකාශනයක් සහ ස්වභාවධර්මයේ මෙන් චලනය විය හැකිය. මට දර්ශනය දෙස බැලීමට නොහැකි වනු ඇත.

අක්ෂය

බොහෝ මූලද්‍රව්‍යයක් මූලද්‍රව්‍යයක්, එම රූපය සමමිතික ලෙස හැඳින්විය හැක,

කෙලින්ම Chi Vhirzok කතා කරන්න කරන්න කරන්න. ඕනෑම වපඩ්කා සඳහා, එය ලක්ෂ්යයක් සහ පැතලි එකකොගගැ් ගැ් ගැ් එතකොට ඒ අය පෝස්ට් බලනවා. ඔබ ඊටත් පොහොසත් විය හැකි අතර, දුගඳ හමන හොඳ දෙයක් විය හැකිය: පැති බෙදන්න, හෝ සමාන්තරව සමාන්තරව, කුටි සකස් කරන්න, නැතහොත් එය වැඩ නොකරන්න. L වැනි සමමිතික අක්ෂ ශබ්ද කරයි.

බට් සමාන-femoral විය හැකි අතර පළමු එක සිරස් සියලු සමමිතිය ඇත, දෙපැත්තේ සිට එය සමාන මුහුණු මෙන් පෙනේ, පසුව අනෙක් රේඛාව සම කපා ඇති අතර bisectrixes, medians සහ උස යන නැඹුරුව සමඟ zbіgatisya ඇත. Звичайне හොඳින් трикутникс ඇය හදන්න එපා.

අවම කිවහොත් කිවහොත්, ස්ඵටික සහ සහ ඇති ඇති සියලුම දිව්‍යමය එකතුව සමමිතික උපාධිය ලෙස හැඳින්වේ. Цей показник අක්ෂ, පැතලි හා මධ්යස්ථාන සංඛ්යාව බොරු කිරීමන.

ජ්යාමිතිය අයදුම් කරන්න කරන්න

මානසිකව, ඔබට පුද්ගල නොවන වස්තූන් එම ස්ථානයේ වෙන් කළ හැකිය, ඔබට සමමිතිය ගැන සිතිය හැකිය, එබැවින්, як її її. පළමු කාණ්ඩයේ, ඔවුන් ස්වයංක්‍රීයව රැවුල රැවුල, ඕවලාකාර මෙන්ම මෙන්ම මෙන්ම මෙන්ම කණ්ඩායම කණ්ඩායම පරිභෝජනය කරයි කරයි.

එය මෙන් මෙන්, එය ත්‍රිකෝණාකාරයේ සියලුම සමමිතිය ගැන නම්, මෙම මූලද්‍රව්‍යය මූලද්‍රව්‍යය මූලද්‍රව්‍යය මූලද්‍රව්‍යය සඳහා භාවිතා නොකරන්න නොකරන්න. චතුරස්රයක් සඳහා, සෘජුකෝණාස්රයක්, රොම්බස් සමාන්තර චලිතයක් චලිතයක් චලිතයක් є, සහ අක්රමවත් රූපයක් සඳහා, පැහැදිලිවම, නොවේ. සමමිතියෙහි කොටස් අක්ෂය සඳහා — ce පුද්ගල නොවන රේඛා රේඛා, як_ її කේන්ද්‍රය ගමන් කරන්න කරන්න.

එපමණක් නොව, බැලූ සාමාන්‍ය සාමාන්‍ය පෝස්ට් එක දෙස බලන්න. ක්‍රිමියාවේ සමමිතියේ බරක් ඇති කිරීමට මම කැමතියි නිවැරදි බගටොකුට්නිකිව් සහ සිසිලස වොලොඩිටි ඩෙයාකි මෙන්ම පිරමිඩ, සමාන්තර චලිත සහ ඩීකි ඉංෂි. окремо පෙනුම සඳහා සම випадок ලිස්සා ගියේය.

ස්වභාවධර්මයට යොදන්න

ජීවිතයේ දී එය ලෙස හැඳින්වේ හැඳින්වේ, එය උච්චාරණය උච්චාරණය වේ
බොහෝ විට. ඒ පස්සට මිනිසෙක්, පොහොසත් සත්වයෙක් වෙන්න. අක්ෂය රේඩියල් හඳුන්වනු ලබන අතර, රීතියක් ලෙස, පිනි සහිත ආලෝකයේ දී පොහොසත් ලෙස ඝන වී ඇත. ඒ වුණත් ඒවා ගඳ ගහනවා. උදාහරණයක් ලෙස, ඒ සිතන්න සිතන්න, ඔබට අක්ෂ අක්ෂ කීයක් දැකිය හැකිද, ඒවා වූයේ වූයේ ඇයි? තේරුම් ගත පරිදි පරිදි, අපි කරන්නේ මුහුදු බෑගර් ගැන මිස තාරකා විද්‍යාත්මක පුහුණුව පිළිබඳ විෂය නොවේ. නිවැරදි පිළිතුර වගේ වනු ඇත: තරු වෙනස් වන ප්‍රමාණයේ වැතිර සිටීම හොඳය, උදාහරණයක් ලෙස, එය පහක්, එය පහක් වැනි ය.

මීට අමතරව, පොහොසත් වල රේඩියල් රේඩියල් සමමිතිය නිරීක්ෂණය කරනු ලැබේ: ромашка, හිසකෙස්, ඩෝමවුස් සහ යනාදිය.

අරිතිමියාව

මෙම, සෑම දෙයකටම පළමුවැන්න, වෛද්‍ය විද්‍යාව හෘද විද්‍යාව ගැන අනුමාන කරයි, අනෙක් අතට වයින්, එයට වැඩි තේරුමක් ඒ අතරම, එය «අසමමිතිය» සමඟ වනු ඇත ඇත, එයින් අදහස් වන්නේ කෙනෙකුගේ නිතිපතා බාධාවක් ඇති බවයි. Її එය vipadkovist ලෙස කිරීමට හැකි වන අතර, සමහර විට එය උපක්රමයක් බවට පත් විය හැකිය, උදාහරණයක් ලෙස, ගෘහ නිර්මාණ ශිල්පය වැනි ඇඳුමකින්. Aje සමමිතික Budvel ඊටත් පොහොසත් පොහොසත්, නමුත් Трохивы nachilen සඳහා ප්රසිද්ධ, සහ එකකට වඩා තිබේ නම්, නමුත් තවමත් බට් සොයා සොයා. එය එසේ випадково වූ බව පෙනේ, නමුත් тсома දී එය එහි ම අලංකාරය ඇත.

ඊට අමතරව, මිනිසුන්ගේ සහ ශරීරය ශරීරය එම එම සත්වයා සමමිතික නොවන බව පැහැදිලිය. පසු විපරම් සිදු කරන ලදී, සමහර «නිවැරදි» පුද්ගලයන්ගේ ප්රතිඵල මත පදනම්ව, ඔවුන් අජීවී, සරලව නොහැකි නොහැකි ලෙස හඳුනාගෙන ඇත. සියල්ලටම සමානව, සමමිතිය ගෙන අතර පෙනුමම පුදුම සහගතය සහගතය, සහ යුද්ධය අවසන් වන තුරු, නමුත් Цикава අද්දරට.

Qile:

• ආලෝකය සපයන:
  • සමමිතිය ගැන ප්රකාශයක් දෙන්න;
  • ප්රදේශයේ විවෘත අවකාශයේ ප්රධාන සමමිතිය ගැන ඉගෙන ගන්න;
  • виробити міцні навички будови සමමිතික රූප;
  • VIDMODY POSTAI, බලධාරීන්ගේ සංජානනය, Po’yazanih і පිළිබඳ දැනුම පුළුල්;
  • දිනය වේලාවේදී ජයග්‍රාහී සමමිතියක ශක්‍යතාව පෙන්වන්න;
  • දැනුම වසා දමන්න;
• හිස සිට හිස:
  • pratsyuvati පුහුණු වීමට ඔනටම උග඀්඀්්;
  • ඔබ සහ පක්ෂය සමඟ පාලනය තබා ගැනීමට ඉගෙන ගන්න;
  • පක්ෂයට අනුව susіda බව ඔබම ඇගයීමට ඉගෙන ගන්න;
• සංවර්ධනය වෙමින්:
  • ස්වයං ක්රියාකාරිත්වය සක්රිය කරන්න;
  • දැනුම ක්රියාකාරිත්වය වර්ධනය කිරීම;
  • ඔට්රිමානා තොරතුරු කියවීම සහ ක්රමවත් කිරීම;
• අවට:
  • учнів «почутья උරහිස» තුළ виховувати;
  • вести коммуникативность;
  • спілкування සංස්කෘතිය щепотка.

සැඟවුණු පාඩම

සමේ පිහිය පිහි සහ අර්කුෂ් කඩදාසි වැතිර සිටී.

හිස 1 (3 л.с.).

— අපි අර්කුෂ් කඩදාසි ගන්නෙමු, අපි මෙන් යෝග සහ vir_zhemo නාස්ති කළෙමු. දැන් අපි කොළය පුළුස්සා මරණ රේඛාව ගැන පුදුම වෙමු.

බල සැපයුම: මෙම රේඛාවේ කාර්යය කුමක්ද?

පෙරෙඩ්බචුවනා විඩ්පොවිඩ්: රූපය Navpil බෙදීමට tya රේඛාව.

බල සැපයුම: රූ දෙකේ තියෙන තිත් ඔක්කොම තියෙන්නේ කොහොමද, මොනවද දැක්කේ?

Количество номеров: අර්ධවල රැවුලේ ස්ථාන වංගු රේඛාව දිගේ සරල රේඛාවක් සහ එක් සරල මත පිහිටා ඇත ඇත.

— Otzhe, එම රූප Navpil බෙදීමට මරණය රේඛාව එම 1 අර්ධ පිටපත් 2 අර්ධ, පසුව. මෙම රේඛාව සරල නැත, එය ආශ්චර්යමත් ඇත ඇත (ලකුණු වල උඩු රැවුල රේඛාවකින් සොයාගත හැකිය), මෙම රේඛාව සියලු සමමිතිය වේ.

කළමනාකරු 2 (2 хв).

— කුඩා කැබැල්ලක් බලන්න, සියලු සමමිතිය දැනගන්න, එය ගුනාංගීකරනය කරන්න.

කළමනාකරු 3 (විනාඩි 5).

— зошить коло එකක හරස් කරන්න.

බල සැපයුම: ඔබ සියලු සමමිතිය හරහා යන්නේ නේ නේ නේ

පෙරෙඩ්බචුවනා විඩ්පොවිඩ්: විවිධ අනුව.

බල සැපයුම: සමමිතියේ අක්ෂ කීයකේ තිබිය හ඄?

Номер телефона: номер телефона.

— ඒක හරි, සමමිතියේ පුද්ගල නොවන අක්ෂ ඇති විට. එවැනි ආශ්චර්යමත් රූපයක් є Куля (අභ්යවකාශ රූපය)

බල සැපයුම: ඔබට සමමිතිය එකකට වඩා පළ කළ හැක්කේ කෙසේද කෙසේද?

පෙරෙඩ්බචුවනා විඩ්පොවිඩ්: හතරැස්, සෘජුකෝණාස්‍රය, සමපාර්ශ්වික සහ සමපාර්ශ්වික ත්‍රිකෝණය.

— අපි හැඩතල දෙස බලමු: ඝනකයක්, පිරමීඩයක්, කේතුවක්, තුනී සිලින්ඩරයක්. රූප සංඛ්‍යා මගින් ද සියලු සමමිතිය පිළිබිඹු කහ හහ රූප සංඛ්‍යා චතුරස්රයක්, සෘජුකෝණාස්රයක්, සමාන-පාර්ශ්වික ත්‍රිකෝණයක් සහ පරිමාමිතික රූප රූප සමමිතික සමමිතික අක්ෂ කීයක් තිබේද?

මම ප්ලාස්ටික් වලින් වලින් ලද ලද රූප භාගයක් බෙදා හරිමි.

ප්‍රධාන කාර්යාලය 4 (3 хв).

— මම තොරතුරු රැගෙන යන්නෙමි, රූපයේ නැතිවූ කොටස එකතු කරන්න.

Номер: රූපය පැතලි හා පරිමාමිතික විය හැකිය. විද්යාඥයන් සියලු හරහා ගමන් කරන ආකාරය තීරණය කිරීම වැදගත් වන අතර, ප්රතික්ෂේප ලද මූලද්රව්යය එකතු කරන ලදී. vikonannya හි බව පාර්ශවය විසින් suswid තීරණය කරයි, රොබෝවරයා කොපමණ ජයග්‍රාහී ලෙස නිවැරදිව තක්සේරු කරයි කරයි.

වැඩ මේසය මත මත පාට ලේස් ලේස් තුනක් රේඛාවක් (වසා, විවෘත, ස්වයං-හරස් කිරීමකින් තොරව, ස්වයං-හරස් කිරීමකින් තොරව) තැබීය.

ප් ‍රධාන කාර්යාලය 5

— සියලුම සමමිතිය සහ වෙනත් ලේස් එකකින් එය වෙනත් කොටසකට ලබා ගන්නේ කෙසේද දෘශ්‍යමය වශයෙන් පෙන්වන්න පෙන්වන්න.

දුෂ්ට නිවැරදි නිවැරදි බව තීරණය වන්නේ ඉගැන්වීම් මගිනි.

සිසුන් ඉදිරිපිට, කුඩා දරුවන්ගේ අංග ඉදිරිපත් කරනු ලැබේ

ප්‍රධාන කාර්යාලය 6 (2 HV).

— මෙම කුඩා දරුවන්ගේ සමමිතික කොටස් සොයා ගන.

සම්මත ලද ද්රව්ය ඒකාබද්ධ කිරීම සඳහා සඳහා, ඊළඟ 15 වන මාරු කරන ලදී.

ට්‍රයිකොට් Kor සහ Com හි අවශ්‍ය සමාන මූලද්‍රව්‍ය නම් කරන්න. මොන වගේ трикутников ද?

2. සෙ.මී. 6ක් දිග ඇඹුල් පාදයක සිට зошит හි рівнобедренные трикотаны килька එකක් තබන්න.

3. හරස් AB. А.Б. කටර් acbd ab රේඛාව සමමිතික වන පරිදි එය මත c සහ d ලකුණු නම් කරන්න.

— ආකෘතිය පිළිබඳ පළමු ප්රකාශයන් පුරාණ ශිලා ශතවර්ෂයේ ඈත අතීතයට ආපසු යා හැක — පැලියොලිතික්. අවුරුදු සිය ගණනක් තිස්සේ මිනිසුන් ජීවත් වූයේ ගුහාවල, ජීවිතයේ සුළු සතුටක් ලැබූ මනසෙහි ය ය. මිනිසුන් එකිනෙකා සමඟ znaryaddya polyuvannya සහ ribalstvo, virobralyali mova splkuvannya සූදානම් කළ අතර, pizny Paleolithic යුගය ඔවුන්ගේම අත්තිවාරමක් අලංකාර කර, mystekstva, රූප සහ කුඩා අය නිර්මාණය කර, ආශ්චර්යමත් ආකාර පෙනෙන සේ පෙනේ.
සරල සිට සක්‍රීය වගාව දක්වා, මසුන් ඇල්ලීමේ සිට ගොවිතැන දක්වා තිබේ නම්, මිනිසුන් නව ගල් යුගයකට, නව ශිලා යුගයට ඇතුළු වේ.
නව යුගයේ මිනිසුන් පාහේ ජ්‍යාමිතික හැඩතල සඳහා කුඩා වේ. මැටි භාජන කිරීම සහ සහ rozfarbuvannya, දළ සටහන් පැදුරු, Koshikiv, රෙදිපිළි කිරීම කිරීම, සහ පසුව — ලෝහ සැකසීම රූපවල පැතලි බව විස්තාරය ප්රකාශනයන් කම්පනය. නව ශිලා ආභරණ ඇස වසා, සමානාත්මතාවය සහ සමමිතිය හෙළි කරයි.
— Как узнать больше?

Количество номеров: හිම කුණාටු පියාපත්, කුරුමිණියන්, ගස් කොළ.

— ගෘහ නිර්මාණ ශිල්පයේ සමමිතිය නිරීක්ෂණය කළ හැකිය. Будівництво, будільники පැහැදිලිව доримуются සමමිතිය.

එබැවින් සමමිතිය යනු මිනිසෙකි, ජීවියෙකි.

ගෙදර වැඩ:

1. ඔබේම ආභරණයක් අඳින්න, A4 ආකෘතියෙන් මත යෝගෝ අඳින්න (ඔබට පෙනෙන විට ඇඳිය ​​හැකිය හැකිය).
2. හිම කුණාටු ආලේප කිරීම සඳහා, දර්ශක, සමමිතික මූලද්රව්ය.

Chotirikutnik මෙන්, සියලු කැපුම් කෙළින්ම, යෝගෝ කැපුමක් ලෙස හැඳින්වේ හැඳින්වේ.

කුඩා 125 හි, ABCD සෘජුකෝණාස්රයක් නිරූපණය කෙරේ.

AB සහ BC පැති B කොනේ ශීර්ෂය අඳින්න. නම x අධිකරණ ABCD සෘජුකෝණාස්රයේ පැති. එයම සත්‍ය වේ, උදාහරණයක් ලෙස, පැති BC සහ CD.

සෘජුකෝණාස්රයක සුසිඩ්නි යෝගෝ ලෙස හැඳින්වේ හැඳින්වේ Dozhina I පුළුල් .

පැති AB සහ CD ද්විත්ව සිරස් තිබිය නොහැක. Їх සෘජුකෝණාස්රයේ ABCD හි ප්රතිවිරුද්ධ පැති ලෙස හැඳ්. එසේම ප්රතිවිරුද්ධ පැති ක්රි.පූ සහ ක්රි.ව.

සෘජුකෝණාස්රයේ протилежні පැති සමාන වේ.

ළදරුවෙකු සඳහා 125 AB = CD, BC = AD. සෘජුකෝණාස්‍රයේ දිග a ට දිගු නම් සහ පළල B නම්, පරිමිතිය ගණනය කරනු ලබන්නේ දැනටමත් දන්නා සූත්‍රය භාවිතා කරමිනි:

p = 2a + 2b

සියලුම සමාන වන සෘජුකෝණාස්රයක් ලෙස හැඳින්වේ හතරැස් (රූපය 126).

No related posts.