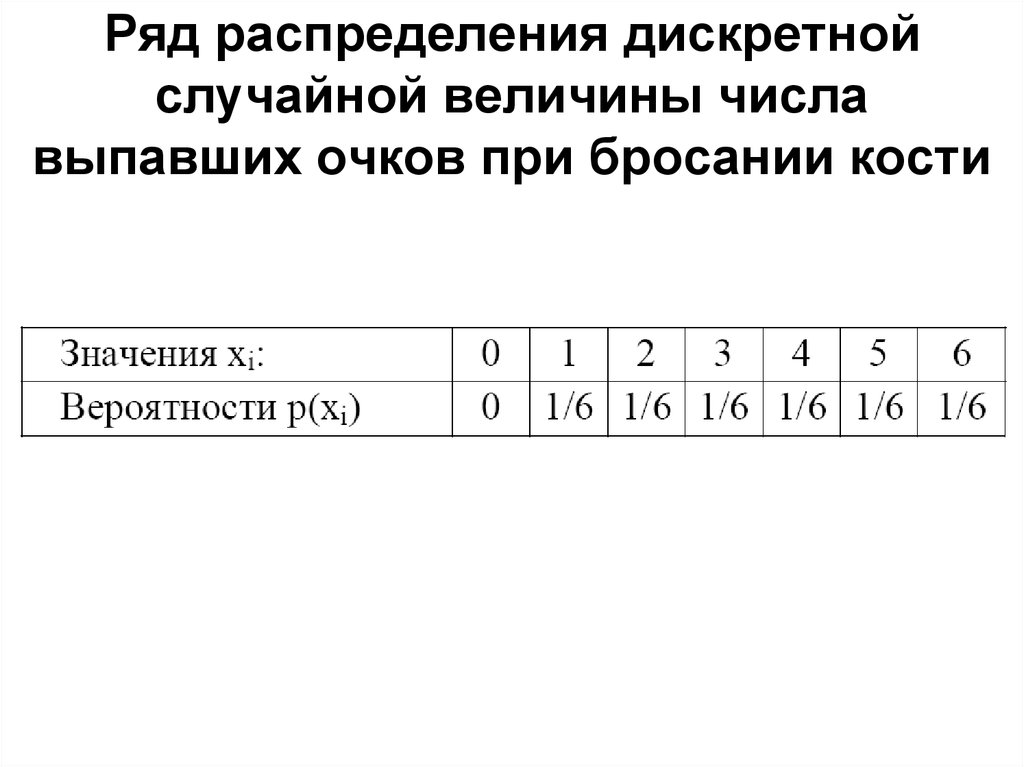
16. Дискретная случайная величина, ряд распределения, многоугольник и функция распределения
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Определение . Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:F (x) = p (X < x).
17.
Мат. Ожидание дсв, его интерпретация и свойстваОпределение
7.1. Математическим ожиданием дискретной
случайной величины называ-ется сумма
произведений ее возможных значений на
соответствующие им вероятности: М(Х)
= х
Е сли число возможных значений случайной величины бесконечно, то , если полученный ряд сходится абсолютно.
Cвойства математического ожидания.
Математическое ожидание постоянной равно самой постоянной: М(С) = С. (7.2)
Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С·1 = С.
Постоянный множитель можно выносит за знак математического ожидании М(СХ) = С М(Х). (7.3)
Доказательство. Если случайная величина Х задана рядом распределения
xi | x 1 | x2 | … | xn |
pi | p1 | p2 | … | pn |
то ряд распределения для СХ имеет вид:
Сxi | Сx1 | Сx2 | … | Сxn |
pi | p1 | p2 | … | pn |
Тогда
М(СХ) = Сх1р1 + Сх2р2 + … + Схпрп = С( х1р1 + х2р2 + … + хпрп)
= СМ(Х).
18.Дисперсия и ее свойства. Среднее квадратическое отклонение.
Определение . Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания:D(X) = M (X – M(X))²
Свойства дисперсии.
1) Дисперсия постоянной величины С равна нулю:D (C) =0
2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D(CX) = C²D(X)
3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:D(X + Y) = D(X) + D(Y)
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X – Y) = D(X) + (Y)
Дисперсия
дает среднее значение квадрата отклонения
случайной величины от среднего; для
оценки самого отклонения служит величина,
называемая средним квадратическим
отклонением.
Определение. Средним
квадратическим отклонением σ случайной
величины Х называется квадратный корень
из дисперсии:
Случайная величина дискретная — Энциклопедия по экономике
Ложная регрессия 218 Математическое ожидание случайной величины дискретной 26, 27 [c.301]Информация первого типа имеет в основном объективный характер, ее подготовка должна предшествовать проведению численных расчетов на ЭВМ. Все количественно выражаемые параметры исходной информации, учитывая прежде всего способ их представления в задаче, разделим на два класса детерминированные, неоднозначные. К детерминированным отнесем все параметры исходной информации, точные однозначные значения которых априорно можно считать известными. У неоднозначных параметров точные значения неизвестны, вследствие чего в исходной информации задачи каждый такой параметр не может быть представлен единым числовым значением. Его целесообразно рассматривать либо в виде некоторого числового интервала (от—до), либо как некоторый набор дискретных возможных значений, либо как случайную величину (дискретную или непрерывную, чаще всего заданную на ограниченном интервале возможных значений).
Различают дискретные и непрерывные случайные величины. Случайная величина дискретна, если результаты наблюдений представляют собой конечный или счетный набор возможных чисел. Случайная величина непрерывна, если ее значения могут лежать в некотором континууме возможных значений. (Это предполагает, что их нельзя пересчитать, ставя в соответствие им натуральные числа 1, 2,….) Значения непрерывной случайной величины могут лежать на отрезке, интервале, луче и т. д. [c.252]
Можно выделить два класса случайных величин — дискретные и непрерывные. Случайная величина X называется дискретной, если множество ее значений конечно или счетно. Несмотря на то что функция распределения универсальным образом описывает вероятностный характер случайной величины, дискретную случайную величину удобно представлять в виде таблицы
[c.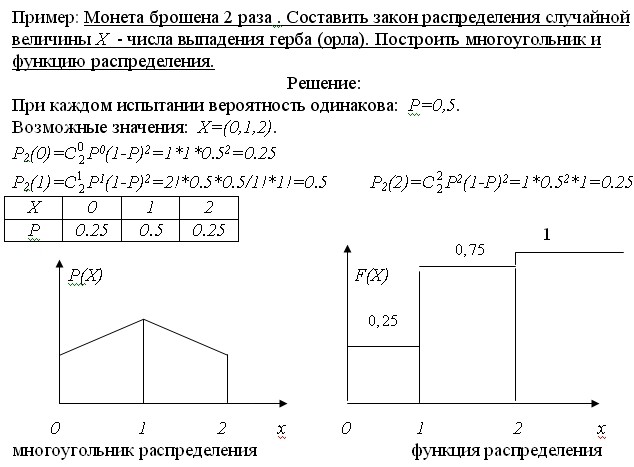
В преодолении некоторых из отмеченных выше трудностей могут помочь более строгие статистические методы в случае взаимозависимых случайных величин можно применять, например, условные вероятности и правило Байеса, а для решения проблемы дискретности оценок — закон нормального распределения и предназначенные для него инструменты анализа. Детальное рассмотрение подобных методов выходит за рамки данной книги, но сделать два замечания по их поводу имеет смысл. [c.423]
Дискретные случайные величины — это величины, которые в отличие от непрерывных изменяются скачкообразно, и каждому такому значению соответствует определенная вероятность. Число возможных значений дискретной случайной величины может быть конечно или бесконечно. [c.43]
Законом распределения дискретной случайной величины называют перечень всех возможных ее значений и их вероятностей. Сумма вероятностей этих событий равна единице. Например, в табл. 4.1 приведена экспертная оценка потока денежных средств от реализации инвестиционного проекта, которая представляет эмпирическое распределение дискретной случайной величины.
Числовые характеристики дискретных случайных величин. Часто закон распределения неизвестен и приходится оперировать только с основными числовыми характеристиками случайной величины. [c.43]
Математическое ожидание, как известно, представляет собой наиболее вероятное ожидаемое значение этой величины. Математическое ожидание дискретной случайной величины равно сумме произведений всех ее возможных значений на их вероятности [c.43]
М(х) — математическое ожидание величины х SD(x) — среднеквадратическое отклонение величины х. Кроме того, напомним, что математическое ожидание и среднеквадратическое отклонение определяются следующим образом. Математическое ожидание дискретной случайной величины подсчитывается как [c.120]
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от математического ожидания.
При заданном законе распределения дисперсия дискретной случайной величины определяется как [c.121]
Необходимость сочетания формализованных и неформализованных процедур принятия управленческого решения накладывает естественный отпечаток и на процесс подготовки аналитических документов они не могут быть раз и навсегда жестко заданными, напротив, будут корректироваться как по форме, так и по существу, а дискретность такой корректировки — случайная величина. Именно текущая корректировка аналитических процедур и их результатов, которую необходимо выполнить в определенные сроки, по ряду объективных и субъективных причин не всегда может быть реализована в полном объеме в цепочке руководитель — аналитик . [c.216]
Случайной величиной называется такая, которая в результате испытания принимает определенное значение при повторных испытаниях значения случайной величины могут изменяться. Случайные величины могут быть дискретными и непрерывными. [c.261]
Чтобы задать дискретную случайную величину, необходимо перечислить ее возможные значения и вероятности, с которыми они достигаются (табл.
5.2).
[c.262]
| Таблица 5.2 Дискретная случайная величина X |
Здесь X, Y — дискретные случайные величины, a Z — непрерывная случайная величина. [c.25]
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. [c.25]
Такая таблица называется рядом распределения дискретной случайной величины. [c.25]
Для любой дискретной случайной величины [c.25]
Закон (ряд) распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной.
Однако такой закон (ряд) распределения бывает трудно обозримым, не всегда удобным (и даже необходимым) для анализа.
[c.26]
Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности [c.26]
Если случайная величина X — дискретная с конечным числом значений, то [c.27]
Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения О, 1, 2,…, т,…, п с вероятностями [c.33]
Дискретная случайная величина X имеет закон распределения [c.33]
Пусть введенная дискретная случайная величина k (t0,t) представляет собой приращение стохастического процесса Пуассона k (t) [c.180]
Предполагая, 4to к моменту времени t счет не ликвидирован, введем случайную величину a.(n(tu,t)), представляющую собой случайный коэффициент изменения величины начального вклада х0 к моменту времени t (после случайного числа n(t0,t) операций с депозитом).
Используя формулу полной вероятности, функцию распределения F(a a(n(t0,t))) случайной величины a(n(t0,t)) можно представить как дискретную смесь
[c.184]
Для этого вначале обработаем опытные данные по закачке нефтепродуктов в резервуарные емкости пункта перевалки. Полученный статистический материал позволяет для каждого объекта (для каждого наблюдения) найти дискретную случайную величину х, которая может принимать значения [c.107]
Случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить, называют дискретными случайными величинами. [c.16]
Закон распределения дискретной случайной величины может быть задан аналитически, численно, графически. [c.16]
Численно закон распределения дискретной величины задается в виде таблицы распределения, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. [c.17]
Составить таблицу распределения или построить многоугольник для непрерывной случайной величины невозможно, так как отдельные ее значения имеют вероятности, стремящиеся к нулю.
В то же время при решении ряда практических задач и при переходе к обобщениям пользуются понятием как непрерывной, так и дискретной случайной величины.
[c.18]
Поэтому возникает необходимость такого задания функции распределения, которое подходило бы для непрерывных и дискретных случайных величин. С этой целью удобно иметь дело с вероятностью события Хзаконе распределения дискретных случайных величин. [c.18]
Теоретические распределения характеризуются величиной своих основных параметров математическим ожиданием М (X) — центром группирования и дисперсией D(X) — величиной рассеивания. Для дискретной случайной величины [c.19]
Случайной величиной называется такая величина, которая принимает те или иные значения с определенными вероятностями. Случайные величины могут быть дискретными и непрерывными. [c.14]
Дискретной случайной величиной называется такая величина, все возможные значения которой образуют конечную или [c.14]
Случайные величины делятся на дискретные (прерывные) и непрерывные.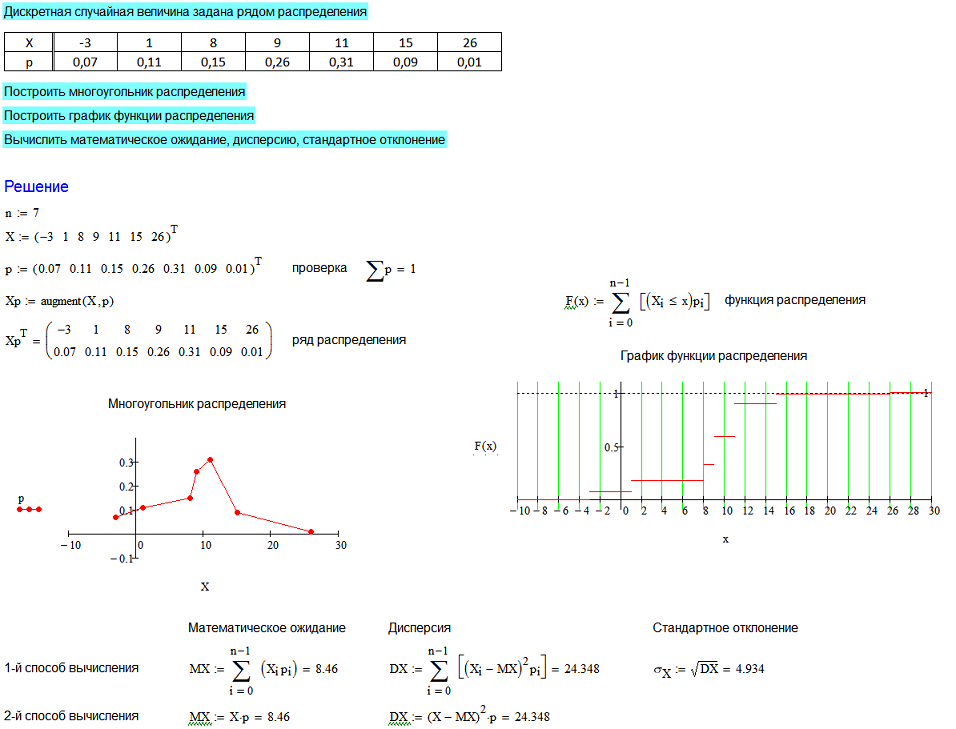
[c.130]
Дискретные случайные величины — это величины, могущие принимать лишь отдельные изолированные значения, которые можно заранее предусмотреть, перечислить. Например, ожидаемое количество единиц продукции ноль, один, два. Больше никаких значений оно принимать не может. [c.130]
При этом распределение дискретной случайной величины х будет [c.131]
Закон применим для дискретных случайных величин, вероятность каждой из которых очень мала. Поэтому закон Пуассона называют законом распределения редких событий (рис. 3.8). [c.136]
Третий метод основан на использовании некоторой части оперативной памяти ЭВМ для уменьшения количества необходимых расчетов, т. е. экономии машинного времени. Этот метод обычно применяется для генерирования дискретных случайных величин. Обратим внимание, что реализация формулы (5.2) требует значительного машинного времени, особенно если число N достаточно велико. Вместо этого предлагается следующий метод. Пусть оеро-ятности pk заданы числами с тремя цифрами после десятичной точки, т.
е. pk = 0, a k» а ь а Р, гдеа — цифры. Тогда выделим в оперативной памяти ЭВМ 1000 ячеек, причем в a k а ь с43 ячеек запишем число X(k , k =1,…, N.
[c.273]
Случайные величины могут быть либо дискретными, либо непре- [c.41]
3.1 — Распределения вероятностей: дискретные случайные величины
Для дискретной случайной величины ее распределение вероятностей (также называемое функцией распределения вероятностей) представляет собой любую таблицу, график или формулу, которые дают каждое возможное значение и вероятность этого значения. Примечание : Сумма всех вероятностей в распределении должна быть равна 1, а каждая отдельная вероятность должна быть между 0 и 1 включительно.
Пример s:
| Головки | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Вероятность | 1/16 | 4/16 | 6/16 | 4/16 | 1/16 |
Это можно найти, перечислив все 16 возможных последовательностей орла и решки для четырех бросков, а затем подсчитав, сколько последовательностей есть для каждого возможного количества орлов.
| Татуировки | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Вероятность | 0,850 | 0,120 | 0,015 | 0,010 | 0,005 |
Это можно найти при переписи большого количества студентов.
Кумулятивные вероятности
Часто нам нужно знать вероятность того, что переменная меньше или равна некоторому значению. Это называется кумулятивной вероятностью , потому что, чтобы найти ответ, мы просто добавляем вероятности для всех значений, квалифицируемых как «меньше или равных» указанному значению.
Пример: Предположим, мы хотим узнать вероятность того, что количество орлов в четырех бросках равно 1 или меньше. Уточняющие значения — 0 и 1, поэтому мы добавляем вероятности для этих двух возможностей.
\( P(X<2)=P(X \leq 1 )=P(X=0)+P(X=1)=(1/16)+(4/16)=5/16 \)
кумулятивное распределение представляет собой список всех возможных значений, а также Пример совокупной вероятности для каждого значения
Пример S:
| Головки | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Вероятность | 1/16 | 4/16 | 6/16 | 4/16 | 1/16 |
| Суммарная вероятность | 1/16 | 5/16 | 16/11 | 15/16 | 1 |
Каждая кумулятивная вероятность была найдена путем сложения вероятностей (во второй строке) до определенного столбца таблицы.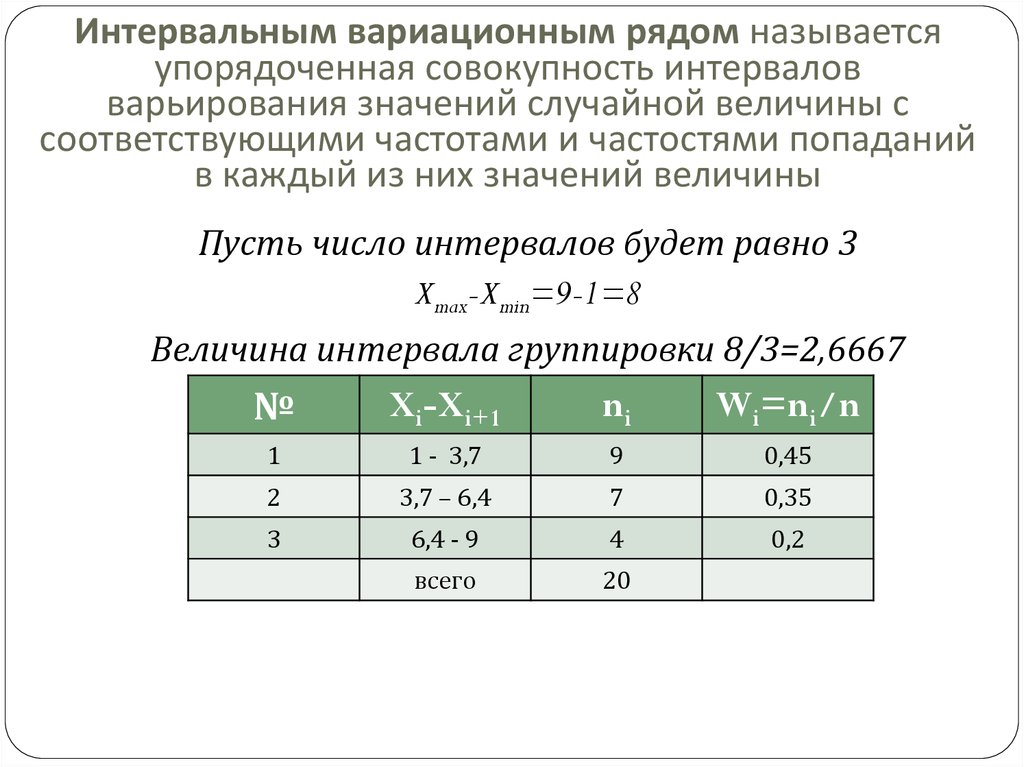
Например, для 2 орлов мы складываем вероятности для 0, 1 и 2 орлов, чтобы получить 11/16. Это вероятность того, что количество решек равно двум или меньше.
| Татуировки | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Вероятность | 0,850 | 0,120 | 0,015 | 0,010 | 0,005 |
| Суммарная вероятность | 0,850 | 0,970 | 0,985 | 0,995 | 1 |
Например, вероятность того, что случайно выбранный студент имеет 2 или меньше татуировок = 0,985 (рассчитывается как 0,850 + 0,120 + 0,015).
Общие дискретные функции вероятности
Этот сайт является частью учебных объектов JavaScript E-labs для принятия решений. Другой JavaScript в этой серии классифицируется по разным областям. приложения в МЕНЮ раздел на этой странице.Профессор Хоссейн Аршам
Следующий JavaScript вычисляет функцию массы вероятности (p) и кумулятивную функцию распределения (F) для широко используемой дискретной случайной величины.
Дискретные случайные величины: Дискретная случайная величина используется для моделирования случайного результата с конечным или счетным числом возможных результатов. То есть дискретная случайная величина — это та, которая может принимать только счетное число различных значений. Если случайная величина может принимать только конечное число различных значений, то она должна быть дискретной. Примерами могут служить количество пациентов в кабинете врача, количество неисправных лампочек в коробке из десяти штук.
Функция массы вероятности: Функция массы вероятности дискретной случайной величины представляет собой список вероятностей, связанных с каждым из ее возможных значений. Ее также иногда называют функцией вероятности или функцией массы вероятности, т. е. p = P (X = x).
Кумулятивная функция распределения: Кумулятивная функция распределения случайной величины — это функция, определяющая вероятность того, что случайная величина X меньше или равна x для каждого значения x, т. е. F = P(X £ x)
МЕНЮ
- Биномиальный
- Отрицательно-биномиальный
- Геометрический
- Пуассон
- Гипергеометрический
Биномиальная вероятность
Введите параметры (n) и (p) и (k), затем нажмите кнопки Compute , чтобы получить P = P(X = k) и F = P(X £ k).
п | р | к | ||||||||
| Р = | Ф = | |||||||||
Для получения технических деталей вернитесь к:
Биномиальная вероятность
Отрицательно-биномиальная вероятность
Введите параметры (r) и (p) и (k), затем нажмите
кнопки Compute , чтобы получить P = P(X = k) и F = P(X £ k).
р | р | к | ||||||||
| Р = | Ф = | |||||||||
Для получения технических подробностей вернитесь к:
Отрицательно-биномиальная вероятность
Геометрическая вероятность
Введите параметры (p) и (k), затем нажмите Вычислить кнопок, чтобы получить P = P(X = k) и F = P(X £ k).
р | к | |||||||||
| Р = | Ф = | |||||||||
Для получения технических деталей вернуться к:
Геометрическая вероятность
Вероятность Пуассона
Введите параметры (l) и (k), затем нажмите
кнопки Compute , чтобы получить P = P(X = k) и F = P(X £ k).
л | к | ||||||||
| Р = | Ф = | ||||||||
Для получения технических деталей вернуться к:
Вероятность Пуассона
Гипергеометрическая вероятность
Введите параметры (n) и (p) и (k), затем нажмите кнопки Compute , чтобы получить P = P(X = k) и F = P(X £ k).
М | Н | п | к |
| Р = | Ф = | ||
Для получения технических подробностей вернитесь к:
Гипергеометрическая вероятность
Вернуться к:
Статистическое мышление для принятия решенийПожалуйста, отправьте ваши комментарии по адресу:
Профессор Хоссейн Аршам
|
|
Заявление об авторских правах.
