Ряд тейлора с: Недопустимое название | Математика | Fandom

Ряды (Математический анализ)

Ряды (Математический анализ)

Виленкин Н.Я., Куницкая Е.С., Мордкович А.Г. Ряды. Математический анализ. Учебное пособие для студентов-заочников III курса физико-математических факультетов педагогических институтов. — М.: Просвещение, 1982. — 160 с. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА 2. Сумма ряда. Сходящиеся и расходящиеся ряды. § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ 1. Необходимый признак сходимости ряда. Остаток ряда. § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ § 4. ФОРМУЛА ТЕЙЛОРА § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА 1. а, где |x| 7. Разложение других элементарных функций. ЗАКЛЮЧЕНИЕ ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 2. Признаки сходимости Даламбера и Коши. 3. Интегральный признак сходимости Коши. 4. Примеры исследования рядов на сходимость. § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 1. Перестановка членов ряда с неотрицательными членами. 2. Группировка членов и умножение рядов с неотрицательными членами. § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ 2. Абсолютно сходящиеся ряды. 3. Свойства абсолютно сходящихся рядов. 4. Свойства условно сходящихся рядов. § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ 2. Чебышевское расстояние между функциями. 3. Равномерно сходящиеся функциональные последовательности. 4. Равномерно сходящиеся ряды. Признак Вейерштрасса. 5. Сохранение свойства непрерывности в случае равномерной сходимости. § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ 1. Почленное интегрирование функциональных рядов. 2. Почленное дифференцирование функциональных рядов. § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 1. Функции комплексного переменного. 2. Дифференцирование функций комплексного переменного. 3. Функциональные последовательности и ряды в комплексной области. ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА 2. Область сходимости степенного ряда. Круг и радиус сходимости. 3. Равномерная сходимость и непрерывность суммы степенного ряда. § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ 1. Интегрирование и дифференцирование степенных рядов в действительной области. 2. Почленное дифференцирование рядов в комплексной области. 3. Единственность разложения функции в степенной ряд. § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ 1. Показательная функция в комплексной области. 2. Тригонометрические функции в комплексной области. Формулы Эйлера. § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ 1. Вычисление значений функций и интегралов. 2. Вычисление пределов. 3. Метод последовательных приближений. ГЛАВА V. РЯДЫ ФУРЬЕ § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ 2. Скалярное произведение функций. 3. Ортонормированные системы функций. § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ 2. Коэффициенты Фурье для тригонометрических систем функций. § 20. ЛЕММА РИМАНА 1. Кусочно гладкие функции. 2. Лемма Римана. § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ 1. Формула для частичных сумм ряда Фурье. 2. Сходимость разложения кусочно гладких функций в ряды Фурье. 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье. 4. Разложение четных и нечетных функций в ряды Фурье. 5. Примеры разложения функций в ряды Фурье. Ответы к упражнениям

Ряд Тейлора.

2}&\text{при }x\neq0\\0&\text{при } x=0\end{cases}\tag{6}f(x)={e−1/x20​при x=0при x=0​(6)бесконечно дифференцируема на всей действительной оси, не равна тождественно нулю ни в какой окрестности нуля, а все коэффициенты её ряда Тейлора в нуле равны нулю.

Если функция раскладывается в некоторой окрестности данной точки в степенной ряд, то такой ряд единствен и является её рядом Тейлора в этой точке. Однако один и тот же степенной ряд может являться рядом Тейлора для разных действительных функций. Так, степенной ряд, у которого все коэффициенты равны нулю, является рядом Тейлора как для функции, тождественно равной нулю на всей действительной оси, так и рядом Тейлора для функции (6) в точке x0=0x_0= 0x0​=0.

Достаточным условием сходимости ряда Тейлора (1) к действительной функции fff на интервале (x0−h,x0+h)(x_0-h, x_0+h)(x0​−h,x0​+h) является ограниченность в совокупности всех её производных на этом интервале.

Ряд (1) опубликовал Б. Тейлор (1715), ряд, сводящийся к (1) простым преобразованием, – И. Бернулли (1694).

Редакция математических наук

Дата публикации:  30 мая 2022 г. в 12:14 (GMT+3)

Искусство решения проблем

Полином Тейлора степени функции about является уникальным полиномом степени, значение и первые производные которой совпадают со значением и первыми производными функции at .

Формула для полинома степени-Тейлора приблизительно равна В приведенной выше формуле обозначает производную по порядку от .

Полиномы Тейлора часто используются для аппроксимации неполиномиальных функций, которые не могут быть точно вычислены, таких как тригонометрические функции, экспоненциальные функции и логарифмы.

Содержание

• 1 Вывод формулы
• 2 Особые случаи
  • 2.1 Полином Маклорена
  • 2.2 Касательная аппроксимация
• 3 Привязка ошибки
• 4 серии Тейлора
  • 4.1 Конвергенция

Вывод формулы

Мы хотим, чтобы полином Тейлора имел -ую производную при . Правило мощности для производных дает, что производная для всех положительных целых чисел и для (потому что, когда функция является константой). Здесь Цепное правило используется неявно с тем, что имеет производную для всех .

Для степень-член в имеет th производную , потому что после дифференцирования степень члена будет достигнута и тогда по крайней мере еще одно дифференцирование гарантирует, что член будет исключен.

Для степень-член в имеет th производную при , потому что дифференцирования оставляют член с положительной степенью , который равен нулю в .

Степень-член подвергается дифференцированию, оставляя постоянный член и накапливая все множители для . Таким образом, его th производная умножается на исходный коэффициент для всех , поэтому коэффициент должен быть определен как .

Особые случаи

Полином Маклорена

A Полином Маклорена представляет собой ряд Тейлора с . Установка несколько упрощает внешний вид полинома, так как каждый экземпляр в формуле заменяется на .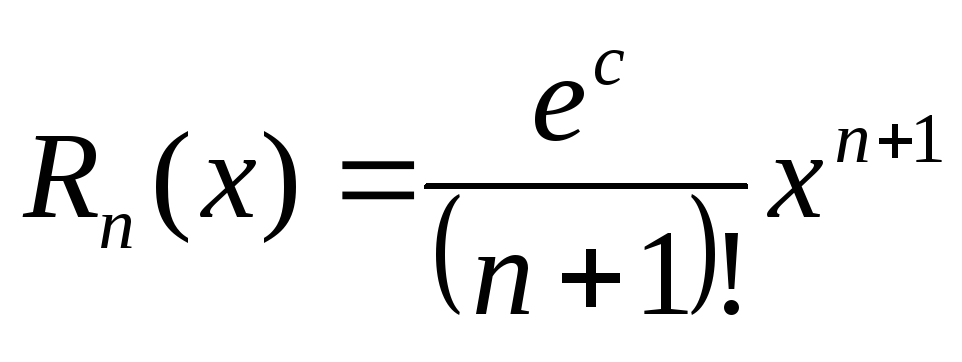

Для некоторых функций, таких как и , полиномы Маклорена обычно эффективны во всей области (хотя использование другого значения может обеспечить большую точность при том же выборе степени). Однако для таких функций, как полиномы Маклорена не могут быть определены, поскольку функция и ее производные не определены при . Для других функций можно определить полиномы Маклорена, но в целом они плохо аппроксимируют функцию (см. Ряд Тейлора), поэтому необходимо выбрать значение, более близкое к -значению желаемой аппроксимации.

Касательная аппроксимация

Касательная аппроксимация представляет собой полином Тейлора первой степени, определяемый формулой . Название «аппроксимация касательной линии» происходит от того факта, что график является линией, касательной к графику при . Аппроксимации касательной используются в методе Эйлера и методе Ньютона.

Граница ошибки

Позволяя быть полиномом Тейлора степени примерно , Граница ошибки Лагранжа утверждает, что если определено и имеет абсолютное значение не более чем на всем интервале, если или если .

Граница ошибки Лагранжа ограничивает истинное значение как выше, так и ниже.

Ряд Тейлора

Ряд Тейлора бесконечно дифференцируемой функции является бесконечным рядом. Частичные суммы ряда Тейлора представляют собой полиномы Тейлора приблизительно каждой степени.

Серия Maclaurin — это серия Taylor, выбранная с . Частичные суммы ряда Маклорена представляют собой полиномы Маклорена каждой степени.

Конвергенция

Если предел ошибки Лагранжа, указанный выше, стремится к бесконечности, то ряд Тейлора должен сходиться к функции. Из-за быстрорастущего факторного члена в знаменателе границы ошибки ряды Тейлора часто сходятся для всех . Например, все ряды Тейлора для , и сходятся к соответствующим функциям для всех .

Однако, если производные последовательных порядков растут достаточно быстро, то ряд Тейлора может сходиться только достаточно близко к .

Рассмотрим ряд Тейлора около . По и степенное правило для производных, для . Поскольку функции с отрицательной степенью строго убывают и положительны для положительных , максимальное абсолютное значение на интервале равно , поэтому максимальное абсолютное значение на равно . Следовательно, для оценка ошибки Лагранжа оценивается как Если , то предел приведенного выше выражения при стремлении к бесконечности равен , поэтому ряд Тейлора должен фактически сходиться к ; но для ряда Тейлора не гарантируется сходимость к . На самом деле, ряд Тейлора для примерно равен , который по критерию отношений вообще не сходится для .

Также возможно, что ряд Тейлора сходится, но не к значению функции, которую он должен аппроксимировать. Для хорошо известного примера все производные функции равны нулю в , поэтому ряд Маклорена сходится к для всех . Однако если , то ряд Маклорена сходится к другому значению, чем для всех .

Серия Тейлор | Определение, формула и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.

  No related posts.