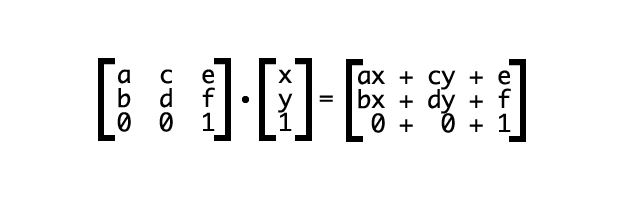С умножение матрицы на вектор: C# .Net: Умножение матрицы на вектор

28.9. Умножение матрицы на вектор и матрицы на матрицу

← 28.8. Алгоритмы упорядочивания элементов в…

28.10. Возведение квадратной матрицы в целую… →

Алгоритмы умножения матрицы на вектор и матрицы на матрицу реализуют основные операции матричной алгебры. Они достаточно просты, но очень наглядно иллюстрируют применение циклов при работе с массивами.

В результате умножения матрицы A состоящей из m строк и n столбцов на вектор X, со-держащий n компонентов, получается вектор Y, состоящий из m компонентов:

Y = A x X.

Каждый компонент результирующего вектора Y находится по формуле:

; ( i = 1, 2, 3, … , m )

Из этой формулы следует внешний цикл по индексу i. В теле этого цикла происходит накопление суммы. Обычно специальной переменной для суммы не используют, а накапливают ее в

i-том компоненте вектора Y. Перед накоплением суммы Y_i обнуляется, а затем организуется цикл по индексу суммирования j. Блок-схема этого алгоритма приведена на рис. 28.19 а.

В результате умножения матрицы A из m строк и n столбцов на матрицу B из n строк и p столбцов получается матрица C, состоящая из m строк и p столбцов:

C = A x B

Каждый элемент матрицы-результата рассчитывается по формуле:

( i = 1, 2, 3, … , m; j = 1, 2, 3, … , p )

Блок-схема алгоритма перемножения матриц приведена на рис. 28.19 б. Он очень похож на предыдущий, но только элементы результирующей матрицы рассчитываются в двойном цикле по индексу строки i и индексу столбца j. Накопление суммы выполняется в цикле по переменной

k.

← 28.8. Алгоритмы упорядочивания элементов в…

28.10. Возведение квадратной матрицы в целую… →

← 28.9. Умножение матрицы на вектор и матрицы на…

28.11. Исключение элементов массивов →

Операция перемножения матриц дает возможность путем повторного умножения реализовать операцию возведения квадратной матрицы в целую степень. Это, в свою очередь, позволяет вычислять матричные степенные ряды, через которые выражаются матричные функции матричного аргумента. Рассмотрим алгоритм возведения квадратной матрицы

A, содержащей n строк и n столбцов в степень m. Результирующую матрицу будем именовать B.

 B = A^m = E x A x A x…x A ,

где E – единичная матрица. Операция умножения выполняется m раз.

Блок-схема этого алгоритма представлена на рис. 28.20. Она представлена на двух уровнях детализации. На первом уровне (изображение слева) основные блоки представлены укрупненно. На изображении справа первый и последний блоки детализированы до основных алгоритмических конструкций. Блок умножения матрицы на матрицу не детализирован, т.к. он рассмотрен в предыдущем подразделе и предполагается, что в данном алгоритме он реализован как вызов вспомогательного алгоритма.

В основе алгоритма лежит цикл повторного умножения (по переменной k), который выполняется m раз. До начала цикла в выходной матрице B формируется единичная матрица. В теле основного цикла вызовом вспомогательного алгоритма выполняется умножение матрицы B на возводимую матрицу A, результатом является матрица C. Второй фрагмент тела цикла заключается в передаче данных от матрицы С матрице B. Детализации первого и третьего блока просты и не требуют особых пояснений.

← 28.9. Умножение матрицы на вектор и матрицы на…

28.11. Исключение элементов массивов →

НОУ ИНТУИТ | Лекция | Параллельные методы умножения матрицы на вектор

< Лекция 12 || Лекция 6: 1234567

Аннотация: В лекции рассматривается задача умножения матрицы на вектор. Приводится постановка задачи и последовательный алгоритм ее решения. Описываются методы разделения матрицы между процессорами вычислительной системы, которые необходимы для параллельной реализации матричных операций. Далее излагаются три возможных подхода к параллельной реализации алгоритма умножения матрицы на вектор

Ключевые слова: операции, матричные вычисления, математика, структуры хранения, метод матричных вычислений, перемножение матриц, параллелизм по данным, параллельные алгоритмы матричных вычислений, скалярное умножение, MPI, эффективность, ускорение, операции передачи данных, вычислительный эксперимент, EM64T, computer cluster, частичный результат, каскадная схема, программная реализация

intuit.ru/2010/edi»>Матрицы и матричные операции широко используются при математическом моделировании самых разнообразных процессов, явлений и систем. Матричные вычисления составляют основу многих научных и инженерных расчетов – среди областей приложений могут быть указаны вычислительная математика, физика, экономика и др.

С учетом значимости эффективного выполнения матричных расчетов многие стандартные библиотеки программ содержат процедуры для различных матричных операций. Объем программного обеспечения для обработки матриц постоянно увеличивается – разрабатываются новые экономные структуры хранения для матриц специального типа (треугольных, ленточных, разреженных и т.п.), создаются различные высокоэффективные машинно-зависимые реализации алгоритмов, проводятся теоретические исследования для поиска более быстрых методов матричных вычислений.

Являясь вычислительно трудоемкими, матричные вычисления представляют собой классическую область применения параллельных вычислений. С одной стороны, использование высокопроизводительных многопроцессорных систем позволяет существенно повысить сложность решаемых задач. С другой стороны, в силу своей достаточно простой формулировки матричные операции предоставляют прекрасную возможность для демонстрации многих приемов и методов параллельного программирования.

В данной лекции обсуждаются методы параллельных вычислений для операции матрично-векторного умножения, в следующей лекции ( «Параллельные методы матричного умножения» ) излагается более общий случай – задача перемножения матриц. Важный вид матричных вычислений – решение систем линейных уравнений – представлен в «Решение систем линейных уравнений» . Общий для всех перечисленных задач вопрос разделения обрабатываемых матриц между параллельно работающими процессорами рассматривается в первом подразделе лекции 6.

При изложении следующего материала будем полагать, что рассматриваемые матрицы являются плотными ( dense ), то есть число нулевых элементов в них незначительно по сравнению с общим количеством элементов матриц.

6.1. Принципы распараллеливания

Для многих методов матричных вычислений характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Данное свойство свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов, и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами используемой вычислительной системы. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений; существование разных схем распределения данных порождает целый ряд параллельных алгоритмов матричных вычислений.

Наиболее общие и широко используемые способы разделения матриц состоят в разбиении данных на полосы (по вертикали или горизонтали) или на прямоугольные фрагменты ( блоки ).

1. Ленточное разбиение матрицы. При ленточном ( block-striped ) разбиении каждому процессору выделяется то или иное подмножество строк ( rowwise или горизонтальное разбиение ) или столбцов ( columnwise или вертикальное разбиение ) матрицы (рис. 6.1). Разделение строк и столбцов на полосы в большинстве случаев происходит на

непрерывной ( последовательной ) основе. При таком подходе для горизонтального разбиения по строкам, например, матрица A представляется в виде (см. рис. 6.1)

( 6.1)

где a_i=(a_i1,a_i2,…,a_in), 0<=i<m, есть i -я строка матрицы A (предполагается, что количество строк m кратно числу процессоров p, т. е. m = kxp ). Во всех алгоритмах матричного умножения и умножения матрицы на вектор, которые будут рассмотрены в этой и следующей лекциях, применяется разделение данных на непрерывной основе.

Другой возможный подход к формированию полос состоит в применении той или иной схемы чередования ( цикличности ) строк или столбцов. Как правило, для чередования используется число процессоров p – в этом случае при горизонтальном разбиении матрица A принимает вид

( 6.2)

Циклическая схема формирования полос может оказаться полезной для лучшей балансировки вычислительной нагрузки процессоров (например, при решении системы линейных уравнений с использованием метода Гаусса – см.

«Решение систем линейных уравнений» ).

2. Блочное разбиение матрицы. При блочном ( chessboard block ) разделении матрица делится на прямоугольные наборы элементов – при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p = sxq, количество строк матрицы является кратным s, а количество столбцов – кратным q, то есть m = kxs и n = lxq. Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:

где A_ij — блок матрицы, состоящий из элементов:

( 6.3)

При таком подходе целесообразно, чтобы вычислительная система имела физическую или, по крайней мере, логическую топологию процессорной решетки из s строк и q столбцов. В этом случае при разделении данных на непрерывной основе процессоры, соседние в структуре решетки, обрабатывают смежные блоки исходной матрицы. Следует отметить, однако, что и для блочной схемы может быть применено циклическое чередование строк и столбцов.

В данной лекции рассматриваются три параллельных алгоритма для умножения квадратной матрицы на вектор. Каждый подход основан на разном типе распределения исходных данных (элементов матрицы и вектора) между процессорами. Разделение данных меняет схему взаимодействия процессоров, поэтому каждый из представленных методов существенным образом отличается от двух остальных.

Рис. 6.1. Способы распределения элементов матрицы между процессорами вычислительной системы

Дальше >>

< Лекция 12 || Лекция 6: 1234567

линейная алгебра — Как умножить вектор слева на матрицу?

спросил 6 лет, 11 месяцев назад

Изменено 1 год, 10 месяцев назад

Просмотрено 26 тысяч раз

$\begingroup$

Я всегда имел дело с умножением вектор-матрица, где вектор является правым множимым, но я не уверен, как применить произведение между матрицей и вектором, когда вектор является левым множимым.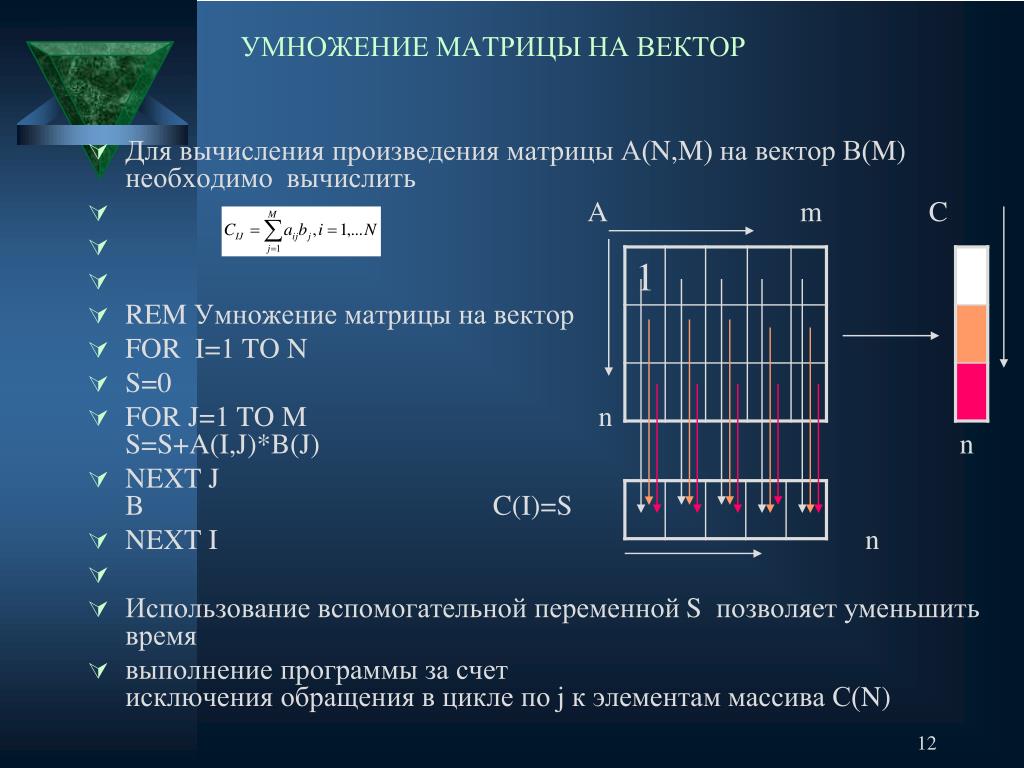 9{2 \times 2}$$

Каков алгоритм умножения $\beta \cdot A$? Конечно, результатом является вектор-строка $1 \times 2$.

• линейная алгебра
• матрицы
• векторы
• произведения

$\endgroup$

3

$\begingroup$

Таким образом, вы хотите вычислить: $$ \begin{pmatrix} \бета_0&\бета_1 \end{pматрица} \begin{pmatrix} а_{11}&а_{12}\\ а_{21}&а_{22} \end{pmatrix}.$$ Это равно следующему: $$\begin{pматрица} а_{11}\бета_0+а_{21}\бета_1&а_{12}\бета_0+а_{22}\бета_1 \end{pmatrix} . $$ Надеюсь, понятно, как работает умножение. 9T$, а операция, переводящая матрицу в ее транспонирование, является самообратной.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Как умножить матрицу на вектор в R?

Когда мы умножаем матрицу на вектор, на выходе получается вектор. Предположим, у нас есть матрица M и вектор V, тогда их можно перемножить как M%*%V. Чтобы понять пошаговое умножение, мы можем умножить каждое значение в векторе на значения строки в матрице и найти сумму этого умножения.

Пример 1

 Демонстрация в реальном времени

 M1<-matrix(1:25,nrow=5)
M1 

Выход

    [1] [2] [3] [4] [5]
[1,] 1     6   11   16   21
[2,] 2     7   12   17   22
[3,] 3     8   13   18   23
[4,] 4      9   14   19   24
[5,] 5   10   15   20   25 

Пример

 V1<-1:5
V1
[1] 1 2 3 4 5
M1%*%V1 

Выход

     [1]
[1,] 215
[2,] 230
[3,] 245
[4,] 260
[5,] 275 

Пример 2

 Живая демонстрация

 M2<-matrix(1:100,nrow=10)
М2 

Выход

     [1] [2] [3] [4] [5] [6] [7] [8] [9] [10]
[1,] 1 11 21 31 41 51 61 71 81 91
[2,] 2 12 22 32 42 52 62 72 82 92
[3,] 3 13 23 33 43 53 63 73 83 93
[4,] 4 14 24 34 44 54 64 74 84 94
[5,] 5 15 25 35 45 55 65 75 85 95
[6,] 6 16 26 36 46 56 66 76 86 96
[7,] 7 17 27 37 47 57 67 77 87 97
[8,] 8 18 28 38 48 58 68 78 88 98
[9,] 9   1929 39 49 59 69 79 89 99
[10,] 10 20 30 40 50 60 70 80 90 100 

Пример

 V2<-1:10
V2
[1] 1 2 3 4 5 6 7 8 9 10
M2%*%V2 

Выход

    [1]
[1,] 3355
[2,] 3410
[3,] 3465
[4,] 3520
[5,] 3575
[6,] 3630
[7,] 3685
[8,] 3740
[9,] 3795
[10,] 3850 

Пример 3

 Живая демонстрация

 M3<-matrix(rnorm(36,5,1),nrow=18)
M3 

Выход

        [1]     [2]
[1,] 3,627929 6,929146
[2,] 3,363237 4,400114
[3,] 4.
No related posts.