Параллельные прямые — Геометрия — Презентации
Определение.
Две прямые на плоскости
называются параллельными,
если они не пересекаются.
Признаки параллельности прямых
c
а
1
Если при пересечении двух прямых
секущей накрест лежащие углы равны ,
то прямые параллельны.
2
b
c
а
1
Если при пересечении двух прямых
секущей соответственные углы равны ,
то прямые параллельны.
b
2
c
а
Если при пересечении двух прямых секущей сумма односторонних углов равна 180 0 , то прямые параллельны.
1
2
b
Аксиома параллельности и следствия из неё.
Через точку, не лежащую на данной
прямой, проходит только одна прямая, параллельная данной.
b
А
c
Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
a II b , c b ⇒ c a
а
Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.
a II с , b II с ⇒ a II b
с
а
b
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Дано: a II b , MN — секущая.
Доказать: 1= 2 (НЛУ)
Доказательство:
способ от противного.
Допустим, что 1 2.
Р
M
а
1
b
2
N
Отложим от луча М N угол N МР, равный углу 2.
По построению накрест лежащие углы N МР= 2
РМ II b .
Получили, что через точку М проходит две прямые (а и МР), параллельные прямой b !!! Это противоречит аксиоме параллельных прямых. Значит наше допущение неверно!!!
1= 2.
Теорема доказана.
Теорема об односторонних углах, образованных при пересечении двух параллельных прямых секущей.
две параллельные прямые пересечены секущей,
сумма односторонних углов равна 180 0 .
Если
условие
то
заключение теоремы
c
а
3
Дано: а II b, c- секущая.
Доказать: O У 1 + 2=180 0 .
2
1
b
Доказательство:
3+ 2 =180 0 , т. к. они смежные.
1= 3, т. к. это НЛУ при а II b
3 + 2 =180
1
Теорема доказана.
х+30 0
х
х
Если MN II AB, а угол 2 больше угла 1 на 30 0 , то угол 2 равен…
Задача
Решение:
1= х,
2= х+30
1= ВОС,
они вертикальные.
В
N
М
2= х+30
180 0 , т.к. ОУ при а II b
ВОА=х,
Составь уравнение…
Найди сам угол.
2
О
B
A
1
B
С
Теорема о соответственных углах, образованных при пересечении двух параллельных прямых секущей.
Если
две параллельные прямые пересечены секущей,
соответственные углы равны.
условие
то
заключение теоремы
c
2
а
Дано: а II b, c- секущая.
Доказать: СУ 1 = 2.
3
b
1
Доказательство:
2 = 3, т. к. они вертикальные.
3 = 1, т. к. это НЛУ при а II b
1
2
1 = 3 = 2
Теорема доказана.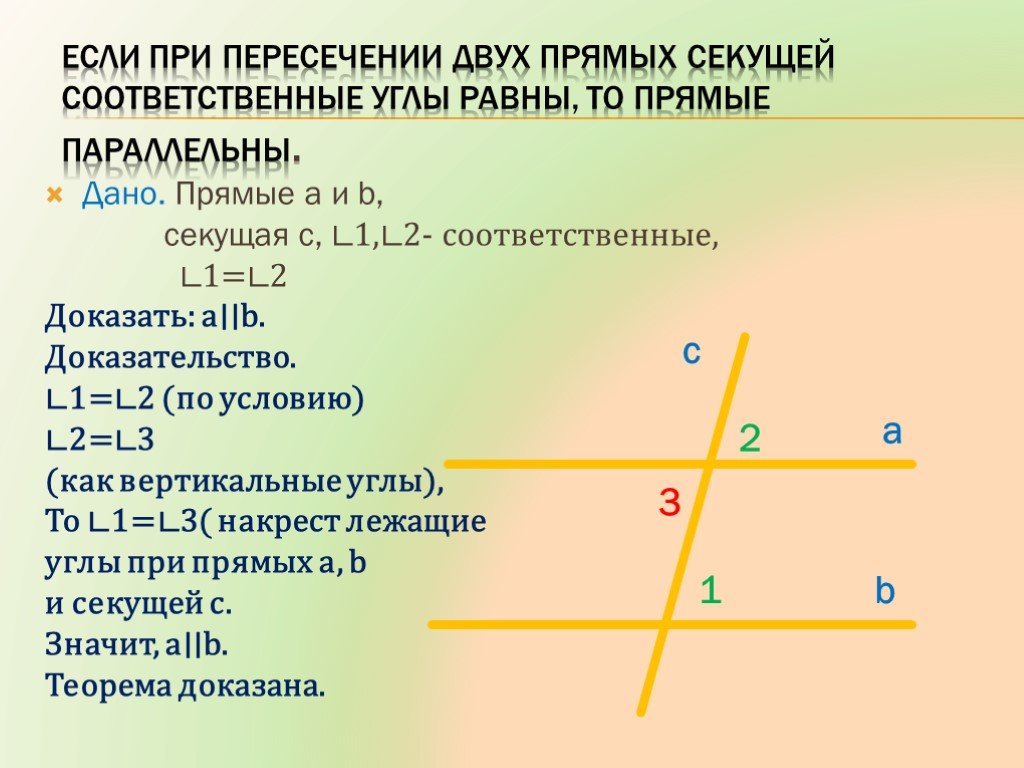
Свойства углов при параллельных прямых. Дано: a II b .
136
a
a
a II b
a II b
1=
1 34 0
1=
34 0
2 =
2 =
b
b
2
2
1
1
Сумма углов 1 и 2 равна 76 0 .
a
a II b
1=
1: 2 = 4 : 5.
2
a
a II b
3 =
2
b
1
3
b
1
1=
a
2 =
2
44 0
1=
b
1
2 =
44
0Дано: а II b, c – секущая.
Один из односторонних углов на
20% меньше другого.
Найти: все углы.
Задача
c
6
7
а
8
Решение:
2=х,
1 на 20% меньше, т.е. 80%
1=0,8х
2=х
180 0 , т.к. ОУ при 1=0,8х а II b
Составь уравнение…
Найди сам все углы…
2
3
1
b
4
5
5
5=
1=
6=
2=
3=
7=
4=
8=
Тренировочные упражнения
Дано: а II b , с – секущая
1 = 4 2
Найдите: 1 и 2
c
а
4х
1
Угол 1 в 4 раза больше угла 2
х
b
2
С.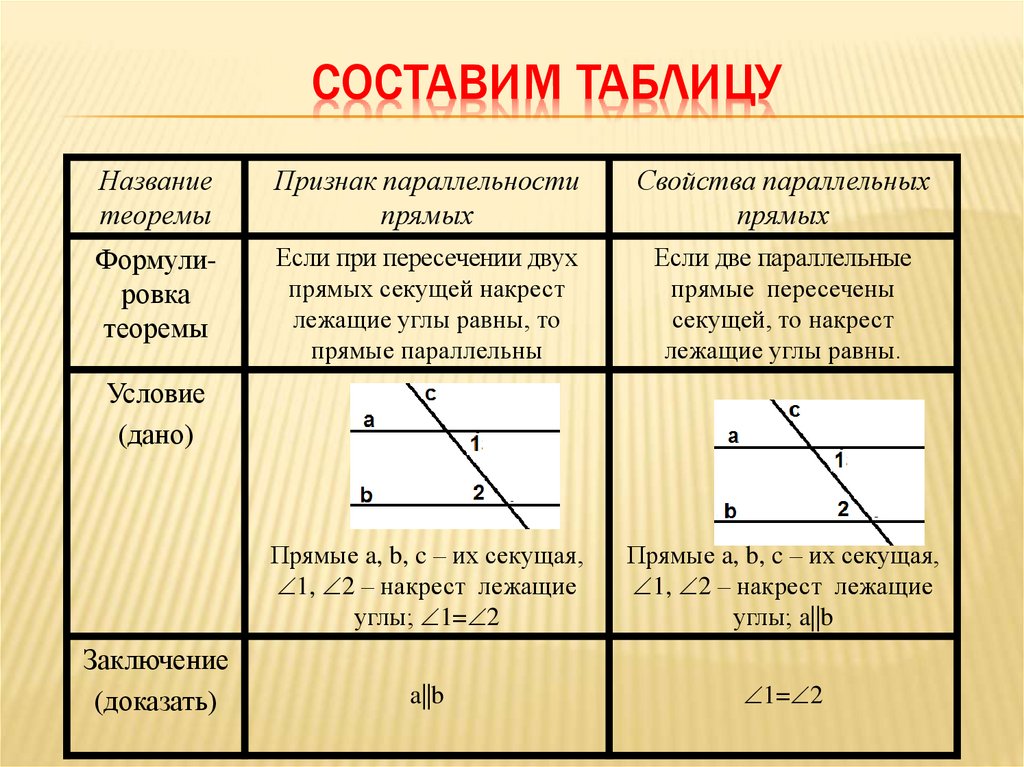
М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»
Тренировочные упражнения
Дано: а II b , с – секущая
1 – 2 = 30 0
Найдите: 1 и 2
Угол 1 на 30 0 больше угла 2
c
а
х+30
1
х
b
2
С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»
Тренировочные упражнения
Дано: а II b , с – секущая
2 = 0,8 1
Найдите: 1 и 2
c
а
х1
0,8х
b
2
С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах». Как еще можно «расшифровать» условие? Угол 2 составляет 80% угла 1. Угол 2 на 20% меньше угла 1.
Угол 2 составляет 0,8 части угла 1
Тренировочные упражнения
Дано: а II b , с – секущая
1 : 2 = 5 : 4
Найдите: 1 и 2
Пусть х – 1 часть
c
а
5х
1
4х
b
2
С.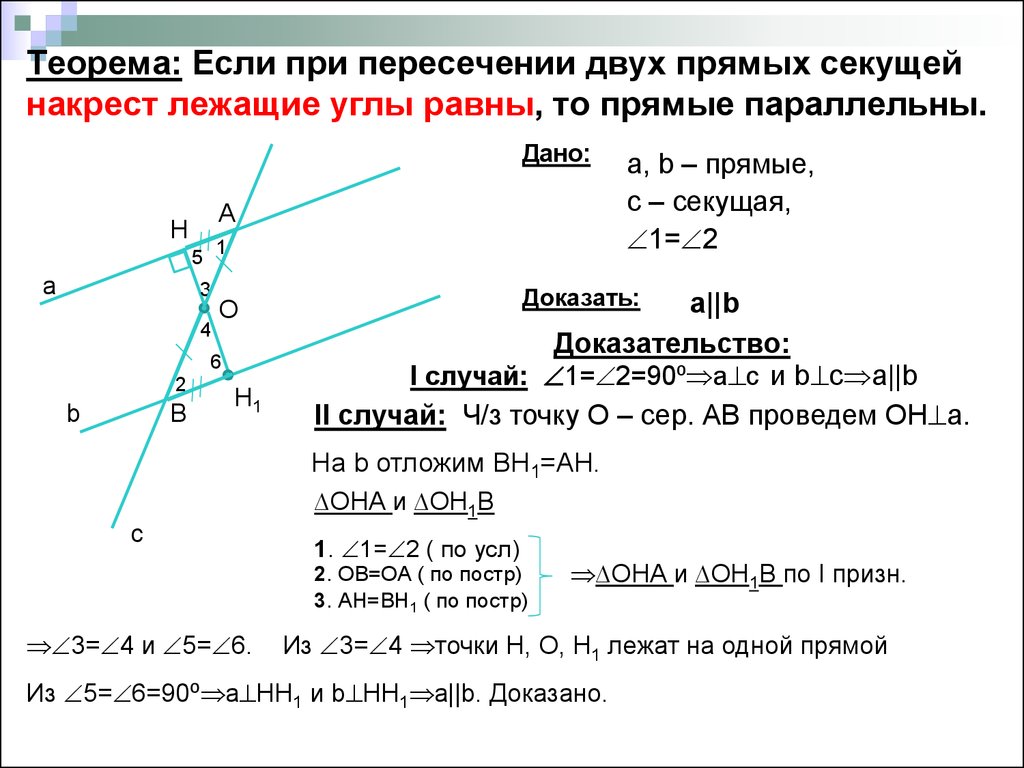
М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»
Тренировочные упражнения
Дано: а II b , с – секущая
2 составляет 80% от 1
Найдите: 1 и 2
c
а
х
1
0,8х
b
2
С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»
биссектриса
AB = BC, A=60 0 ,
CD – биссектриса угла ВСЕ.
Докажите, что АВ II CD .
Дано: а II b , с – секущая
1 : 2 = 5 : 4
Найдите: 1 и 2
c
Пусть х – 1 часть
B
D
а
5х
1
4х
b
2
120 0
60 0
С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»
60 0
60 0
60 0
E
С
A
Используя данные рисунка, найдите углы 1, 2 и 3.
с
d
а
120 0
20 0
1
2
160 0
b
3
Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»
Может ли еще один из семи остальных углов, образованных при пересечении прямых a и b с прямой d , быть равен 110 0 ? 60 0 ? Почему?
d
m
а
11 0 0
11 0 0
11 0 0
4 0 0
b
11 0 0
Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»
4 0 0
4 0 0
На рисунке АС II В D и АС = АВ, МАС = 40 0 .
Найдите СВ D.
M
40 0
A
С
2
3
1
B
D
Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»
На рисунке АВ II Е D .
Докажите, что ВС D = B + D
Подсказка
A
B
1
N
C
Построим CN II AB
2
3
Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»
4
D
E
На рисунке АВ II Е D . C ВА = 140 0 , С DE = 130 0
Докажите, что ВС С D
Подсказка
B
A
40 0
140 0
N
C
Построим CN II AB
Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»
130 0
50 0
D
E
5 ,8 см
На рисунке a II b , c – секущая, DM и DN – биссектрисы смежных углов, образованных прямыми a и c . DE = 5 ,8 см
Найдите MN.
с
40 0
а
D
2
4
3
6
5
1
b
П.
И. Алтынов «Геометрия. Тесты. 7-9 кл.»
E
N
M
?
На рисунке АВ ED и KM ED, ABE = 34 0
MN – биссектриса КМС
Найдите EMN.
D
K
N
A
146 0
П. И. Алтынов «Геометрия. Тесты. 7-9 кл.»
73 0
?
73 0
C
E
3 4 0
3 4 0
M
B
На рисунке АС II BD и KC II MD, ACK = 48 0
CDK в 3 раза больше EDM
Найдите К DE.
A
B
K
48 0
48 0
48 0
C
M
3x
П. И. Алтынов «Геометрия. Тесты. 7-9 кл.»
x
D
E
Свойства углов, образованных двумя параллельными прямыми и секущей.Задачи на признаки параллельности
12+
4 месяца назад
Математика от Баканчиковой252 подписчика
Геометрия 7 класс.
Есть ли у признаков параллельности прямых обратные теоремы? Как решать задачи на свойства углов, образованных двумя параллельными прямыми и секущей, и признаки параллельности прямых? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Признаки параллельности прямых», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. А чтобы Вы лучше и быстрее запомнили новый материал, сначала мы напомним Вам, что такое обратная теорема и пять признаков параллельности прямых. Мы обратим Ваше внимание, что у всех признаков параллельности прямых есть обратные теоремы — свойства углов, образованных двумя параллельными прямыми и секущей. Затем на примере двух задач мы покажем Вам, как применяются свойства углов, образованных двумя параллельными прямыми и секущей, вместе с признаками параллельности прямых. Первая задача — №211 (а) из учебника «Геометрия 7-9 класс» Л.С.Атанасяна, вторая задача – типовая задача для ОГЭ или ЕГЭ. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:26 Вспомним пять признаков параллельности прямых, и что такое обратная теорема.
02:39 Свойства углов, образованных двумя параллельными прямыми и секущей.
04:31 Задача 1 (№211 а из учебника «Геометрия 7-9 класс» Л.С.Атанасяна).
11:45 Задача 2.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки по геометрии, то рекомендуем Вам посмотреть следующие видео:
Свойства углов, образованных двумя параллельными прямыми и секущей. Задачи на признаки параллельности прямых. Геометрия 7 класс. https://youtu.be/ZJh5RT92k14
Задачи на признаки параллельности прямых. Часть 2. Как найти признаки параллельности прямых в задачах. Геометрия 7 класс. https://rutube.ru/video/015e68bc452f983888ae2fea6c7a06bd/
Задачи на признаки параллельности прямых. Часть 1. Как кратко и грамотно оформить завершение задачи. Геометрия 7 класс. https://rutube.ru/video/712982cb449bc656fd17a0c54574cb12/
Признаки параллельности прямых. Геометрия 7 класс. https://rutube.ru/video/1dc208d378dc0bbf4675dcd5296ae074/
Углы, образованные при пересечении двух прямых секущей (третьей прямой).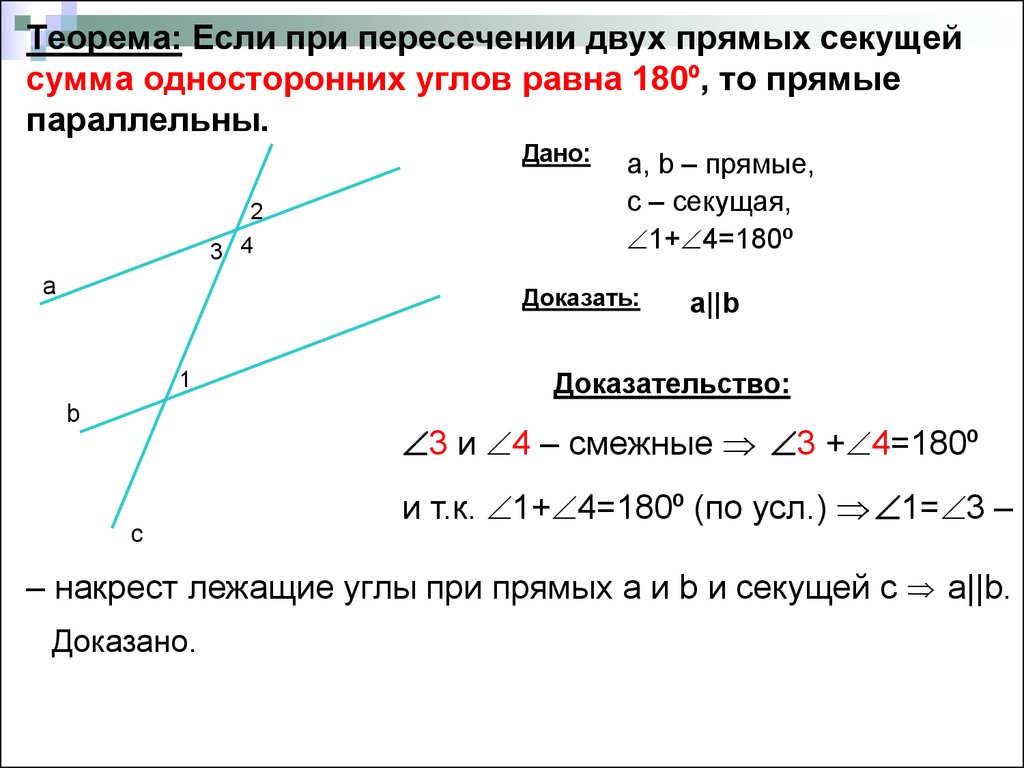
Геометрия 7 класс. https://rutube.ru/video/88af7c90cdc9fb725219d1d299acaa8d/
Геометрия 7 класс. Основные понятия и фигуры геометрии. Их компоненты. https://rutube.ru/video/321ccc54b501c6dbc235d9b52b266abb/
Геометрия 7 класс. Взаимное расположение прямых на плоскости. Перпендикулярные прямые. Примеры построения перпендикулярных прямых. https://rutube.ru/video/c46955ce83ccef0dee45f4c72fc2583e/
Свойства биссектрисы равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника. Геометрия 7 класс. https://rutube.ru/video/2a2b7dfc5b44830f209dc9cc4e28d2f7/
Геометрия 7 класс. Треугольники. Признаки равенства треугольников. Урок 3. https://rutube.ru/video/0339e0588490b1b5ca732547aac3ec06/
Геометрия 7 класс. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач на свойства медианы и биссектрисы. Урок 5.
https://rutube.ru/video/3c88c497ce7a312249ea9e2b770fb8b1/
Геометрия 7 класс. Треугольники. Высота треугольника. Определение, свойства, точки пересечения высот.
Примеры построения. Урок 6. https://rutube.ru/video/575bead43e6717ec773788d15e7380c1/
Геометрия 7 класс. Вертикальные углы. Определение. Доказательство теоремы о свойстве вертикальных углов. Виды углов урок 3. https://rutube.ru/video/10ca7111475a4f1a6dbe6b67fd71588c/
Геометрия 7 класс. Смежные углы. Определение. Свойства. Примеры задач на свойство смежных углов. Виды углов урок 2. https://rutube.ru/video/f12d3379fb0751e037c1f1bede88805f/
Что такое обратная и прямая теоремы. Примеры обратных и прямых теорем. Геометрия 7 класс. https://rutube.ru/video/f72250e5edd8eeed8948bd0664a23692/
Доказательство теорем методом «от противного». Параллельность прямых на плоскости. Геометрия 7 класс. https://rutube.ru/video/d4f7b6c064dd143c73b738ebe92373dd/
#задачинапризнакипараллельностипрямых #свойстваугловприпараллельныхпрямых #свойстваодностороннихуглов #задачинапризнакипараллельностипрямых7класс #признакипараллельностипрямыхзадачи #задачиначертежахпризнакипараллельностипрямых #свойстванакрестлежащихуглов #накрестлежащиеуглыравны #задачинапризнакипараллельностипрямыхАтанасян #параллельныепрямыенакрестлежащие #еслинакрестлежащиеуглыравнытопрямые #сумманакрестлежащих #суммадвухнакрестлежащих #суммаодностороннихугловравна #суммаодностороннихуглов #соответственныеуглыравны #свойствасоответственныхуглов #еслисоответственныеуглыравнытопрямые #суммадвухсоответственныхуглов #суммасоответственныхугловравна180 #двепрямыепараллельныеслисумма #доказатьпараллельностьпрямых #МатематикаОтБаканчиковой
Геометрия 7 класс, задачи на признаки параллельности прямых 7 класс, задачи на признаки параллельности прямых, задачи на чертежах признаки параллельности прямых, признаки параллельности прямых задачи, накрест лежащие углы равны, сумма накрест лежащих, сумма односторонних углов равна, сумма одн
Теорема о среднем значении
Теорема о среднем значении Секущая — это линия, проведенная через две
точки на кривой.
Теорема о среднем значении связывает наклон секущей с наклон касательной.
Теорема. (Среднее значение Теорема) Если f непрерывна на и дифференцируема на , то существует число c такое, что
Я не буду приводить здесь доказательства, но на рисунке ниже показано, почему это делает смысл. Я провел секущую через точки и . Среднее значение Теорема утверждает, что где-то между a и b есть точка c на кривая, где касательная имеет тот же наклон, что и секущая линия.
Прямые с одинаковым наклоном параллельны. Чтобы найти точку, где касательная параллельна секущей, возьмите секущую и «сдвиньте» его (не меняя наклона), пока он не станет касательной к кривой.
Если вы поэкспериментируете с некоторыми кривыми, вы обнаружите, что всегда это возможно (при условии, что кривая непрерывна и дифференцируема, как указано в теореме).
Пример. Для функции на интервале найти число (или числа), удовлетворяющее
заключение теоремы о среднем значении.
Поскольку f полином, f непрерывен на и дифференцируем на . Более того,
Следовательно, существует число c — может быть больше одного — между -5 и 1 такой, что . Я постараюсь найти один.
, так . Приравняйте к 9 и решите для с:
, а не в интервале — это конечная точка — но есть. число, удовлетворяющее заключение теоремы о среднем значении.
Примечание. Математики часто говорят «есть номер» как сокращение от «есть по крайней мере одно число». Таким образом, теорему о среднем значении следует интерпретировать как означают «существует хотя бы одно число c», удовлетворяющее заключение теоремы. Там может быть много номеров, которые работают — даже бесконечное их количество!
Кроме того, найти значение с, которое работает, может быть сложно. Но
теорема гарантирует только то, что такое c существует , а не то, что
вы сможете найти его.
Пример. Рассмотрим на интервале . Затем
Однако , и не имеет решения. Почему это не противоречит теореме о среднем значении? Это не противоречит среднему Теорема о ценности, потому что f не определено в точке , которая находится в середине интервала .
Пример. Кэлвин Баттербол бежит 100 ярдов рывок за 20 секунд. Предположим, что функция, задающая его положение относительно начального линия непрерывна и дифференцируема. Покажите, что Кальвин должен иметь бегал со скоростью 5 ярдов в секунду во время своего бега.
Когда , он на стартовой линии, так что . Когда , он на финише, так что . Применение теоремы о среднем значении к s для , я нахожу, что есть точка c между 0 и 20 таких, что
То есть скорость Кальвина была равна 5 ярдам в секунду. Во-вторых, это то, что я хотел показать.
Вы знаете, что производная константы равна нулю.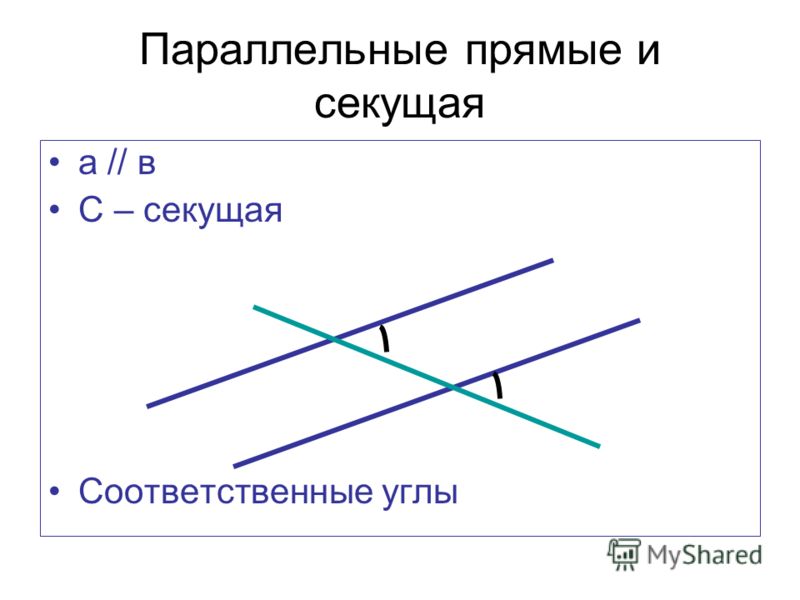
Среднее значение
Теорему можно использовать, чтобы показать, что верно и обратное.
Теорема. Если f непрерывна на замкнутом интервал и для всех x в открытом интервале, то f постоянна на закрытом интервале.
Доказательство. Пусть d будет любым числом таким, что . Теорема о среднем значении применяется к f на интервале , значит, существует число c такое, что и
По предположению, . Поэтому,
Поскольку d было произвольным числом таким, что , следует, что для всех x в . Это означает, что f постоянна на интервал.
Мы воспользуемся этой идеей, когда будем обсуждать . первопроизводные . Вот набросок идеи.
я знаю это
Если любая другая функция такая, что , то
По теореме , где c — константа. Поэтому, . Другими словами, единственный функции, производные которых являются функциями типа
Когда я буду обсуждать первообразные, я буду выражать этот факт, написав
Следствие.
( Ролль
Теорема ) Пусть f непрерывна на и дифференцируема на и, кроме того, что . Тогда существует число c такое, что
Доказательство. Примените теорему о среднем значении, чтобы получить
Но, значит, и левая сторона равна 0 — что дает заключение теоремы Ролля.
Частным случаем, когда гипотеза верна, является случай, когда a и b являются корнями f, так как тогда
В этой ситуации теорема Ролля говорит, что существует по крайней мере один горизонтальная касательная между каждой парой корней.
На рисунке выше есть три критические точки между корни в a и b.
Пример. По теореме о среднем значении функция имеет критическое значение точки — места, где — от 0 до 20, от 20 до 200 и от 200 до 2000.
Пример. Докажите, что функция имеет ровно один корень.
Шаг 1.
Так как и , и
поскольку f непрерывно, из теоремы о промежуточном значении следует, что
есть корень между -10 и 10. Таким образом, f имеет по крайней мере один корень.
Шаг 2. Предположим, что f имеет более одного корня. Предположим, в частности, что a и b — два корня f.
По теореме Ролля f должна иметь горизонтальную касательную между a и b. То есть для .
Однако производная есть. Поскольку четные степени неотрицательны, для всех x. Это противоречит.
Это противоречие показывает, что двух корней быть не может, поэтому не может быть более одного корня.
Шаг 1 показывает, что есть хотя бы один корень. Шаг 2 показывает, что не может быть больше одного. Следовательно, должен быть ровно один корень.
Определение. Функция f равна строго увеличивая на интервале, если для всех p и q таких, что ,
Если последнее неравенство заменить на , то f будет увеличение .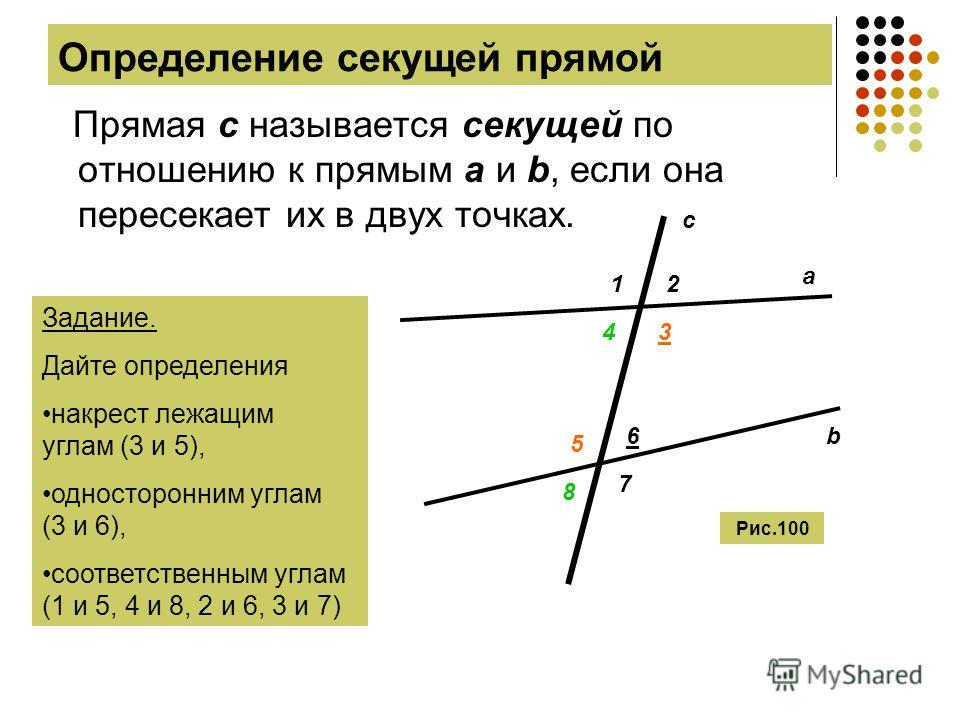
Функция f есть , строго убывающая на интервал, если для всех p и q таких, что ,
Если последнее неравенство заменить на , то f будет уменьшение .
Предложение. Предположим, что f дифференцируема на .
(a) Если на , то f есть строго возрастает на .
(б) Если на , то f есть строго убывает на .
Доказательство. Возьмите p и q между a и b; сказать . Я хочу показать . По теореме о среднем значении существует число c, такое это и
Но так
Это доказывает, что f строго возрастает на отрезке.
Доказательство (b) аналогично.
Примечание. В (а) если вместо этого предположить, что на , то то же самое доказательство показывает, что f возрастает на . Аналогично, в (b), если вы предполагаете, что на , то f равно уменьшается на .
Пример.
Докажите, что если , то
Примените теорему о среднем значении к интервал , где . Тогда для некоторого c между 0 и k
Теперь и так
Изображение, которое иллюстрирует это (не в масштабе):
Кривая — это график, а линия — это . Вы можете видеть, что кривая лежит выше линия.
Пример. ( Использование среднего Теорема о значении для оценки значения функции ) Предположим, что f является дифференцируемая функция,
Докажи это .
Примените теорему о среднем значении к f на интервале:
Затем, так как у меня есть
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2018 Брюс Икенага
Раздел 7.6: Касательные и секущие
Секция_7_6 7.6
Касательные и секущие
Начнем с некоторых вопросов о параллельных прямых и
круги.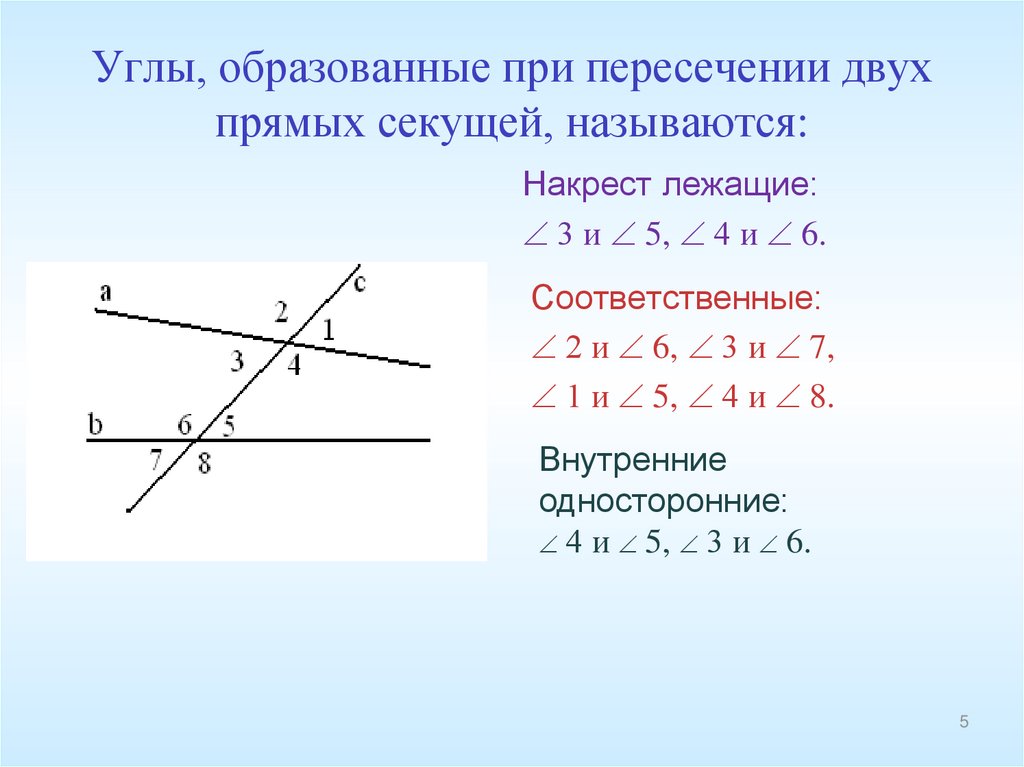
- Теорема 7.14:
Параллельные секущие пересекают конгруэнтные дуги между собой на окружности.
| Дано:
$\overleftrightarrow{AB}\parallel \overleftrightarrow{CD}$ Докажите: $\overparen{AC}\cong\overparen{BD}$ Доказательство: Нарисуйте аккорд $\overline{BC}$. Поскольку $\overleftrightarrow{AB}\parallel \overleftrightarrow{CD}$, у нас есть $\angle 1\cong \angle 2$. С $m\overparen{AC}=2\cdot m\угол 1$ и $m\overparen{BD}=2\cdot m\угол 2$, то имеем $m\overparen{AC}=m\overparen{BD}$, так что $\overparen{AC}\cong\overparen{BD}$. | |
- Теорема 7.15:
Если секущая и касательная к окружности параллельны, то они пересекают
конгруэнтные дуги между ними на окружности.
Дано:
$\overleftrightarrow{AT}$ касается $\odot P$ в точке $T$.
$\overleftrightarrow{BC}\parallel \overleftrightarrow{AT}$.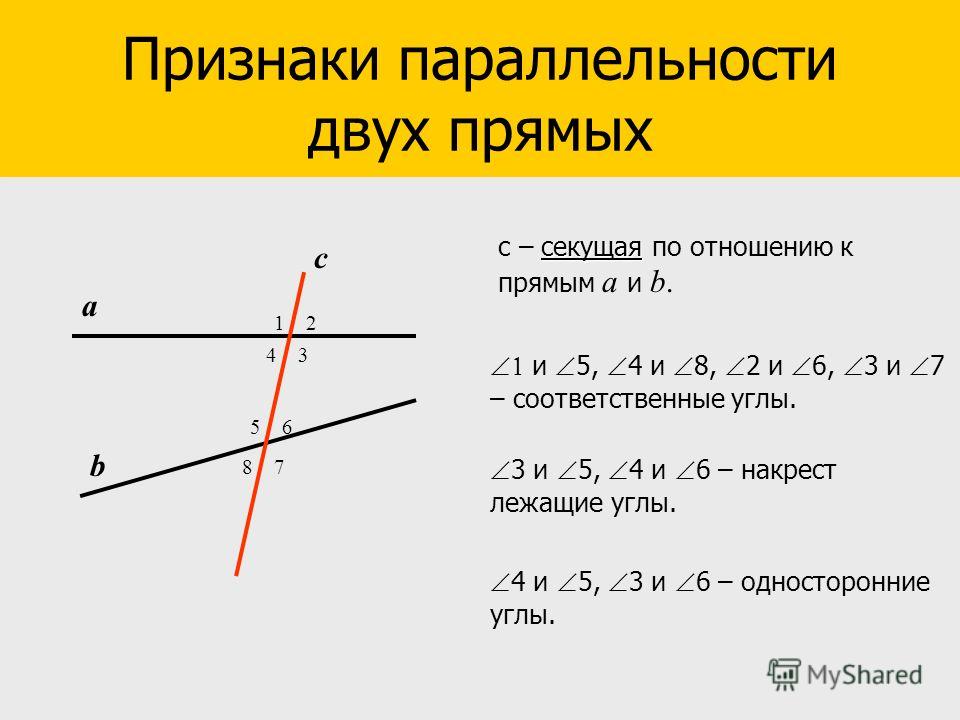 Доказать: $\overparen{BT}\cong\overparen{CT}$ Доказательство: мы рисовать диаметр $\overline{TQ}$. Этот диаметр перпендикулярен касательная $\overleftrightarrow{AT}$. Так как касательная и секущая $\overleftrightarrow{BC}$ параллельны, диаметр перпендикулярен также для аккорда $\overline{BC}$. Но такой диаметр перпендикуляр хорде делит хорду и ее дуги пополам. Поэтому $m\overparen{BQ}=m\overparen{CQ}$. Две дуги $\overparen{TBQ}$ и $\overparen{TCQ}$ — полуокружности. Использование добавления дуги Постулат, тогда мы знаем, что $\overparen{BT}\cong\overparen{CT}$. | |
- Теорема 7.16:
Параллельные касательные к окружности пересекают конгруэнтные дуги между собой.
Дано:
$\overleftrightarrow{AT}$ и $\overleftrightarrow{BQ}$ касаются
$\odot P$ в $T$ и $Q$ соответственно.
$\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$.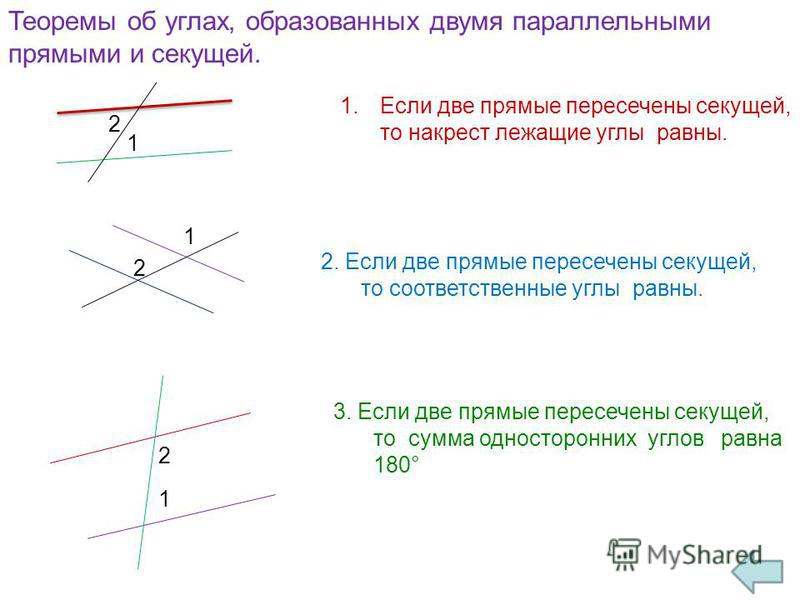 Доказать: $\overparen{TXQ}\cong\overparen{TYQ}$ | |
Доказательство: это все слишком заманчиво предположить (из-за картинки), что $\overleftrightarrow{PT}$ и $\overleftrightarrow{PQ}$ одинаковы линия. Они есть, но это требует некоторого объяснения. $\overleftrightarrow{PT}\perp \overleftrightarrow{AT}$ в $T$. Любая линия, перпендикулярная $\overleftrightarrow{AT}$, будет также перпендикулярно $\overleftrightarrow{BQ}$, так как $\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$. Поэтому $\overleftrightarrow{PT}\perp\overleftrightarrow{BQ}$. Мы знаем также, что $\overleftrightarrow{PQ}\perp\overleftrightarrow{BQ}$, так как это радиус, проведенный к точке касания. Здесь только один перпендикуляр к $\overleftrightarrow{BQ}$, проведенный через точку $P$, поэтому $\overleftrightarrow{PT}$ и $\overleftrightarrow{PQ}$ должны быть та же линия. Тогда $\overparen{TXQ} и $\overparen{TYQ} оба полуокружности, значит, они равны.
Все это приводит к теореме о мере
угла, образованного касательной и хордой.
- Теорема 7.17:
Теорема о касательной хорде
Мера угла, образованного касательным отрезком а хорда, проведенная к точке касания, равна половине меры перехваченная дуга.
| Дано:
$\overline{AT}$ касается окружности в точке $T$. Доказать: $m\angle ATB=\dfrac{1}{2}m\overparen{TB}$ Анализ: Есть три случая: $\angle ATB$ прямой, $\angle ATB$ острый и $\угол ATB$ тупой. Мы разберемся с первыми двумя и оставим третий для упражнений. | |
Случай 1. Если $\angle ATB$ — прямой угол, тогда $\overline{TB}$ — диаметр и дуга $\overparen{TB}$ — полуокружность. Мера угла 90, в то время как мера дуги равна 180. Мера угла действительно, половина меры пересекаемой дуги.
| Вариант 2:
Если $\угол ATB$ острый, то проведем хорду $\overline{BC}$, параллельную
касательная $\overleftrightarrow{AT}$. $м\угол 1=м\угол 2$;
$м\угол
2=\frac{1}{2}m\overparen{TC}$; $m\overparen{TC}=m\overparen{TB}$ (поскольку
$\overline{BC}\parallel\overleftrightarrow{AT}$), поэтому
$\frac{1}{2}m\overparen{TC}=\frac{1}{2}m\overparen{TB}$. Затем
$м\угол
ATB=\frac{1}{2}m\overparen{TB}$. | |
Мы рассмотрели углы, образованные линиями, которые пересекаются внутри круга и по (специальным) линиям, которые пересекаются на круг. Теперь рассмотрим прямые, которые пересекаются вне круга.
- Теорема 7.18:
Мера угла, образованного двумя секущими, секущей и тангенсом,
или две касательные, пересекающиеся в точке вне круга, составляют половину
разница перехваченных дуг.
Опять же, есть три случая для рассмотрения. Докажем первое один, а два других оставьте для упражнений.
Данный: $\overline{ABC}$ и $\overline{ADE}$ — секущие окружности.
Докажите: $m\угол A=\frac{1}{2}\left(m\overparen{CE}-m\overparen{BD}\right)$
Доказательство:
Теорема о внешнем угле, $m\угол 2=m\угол 1+m\угол A$.