Параллелограмм
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
На Рис.1 изображен параллелограмм поскольку \( \small AB \ || \ CD, \;\; AD \ || \ BC .\)
Свойства параллелограмма
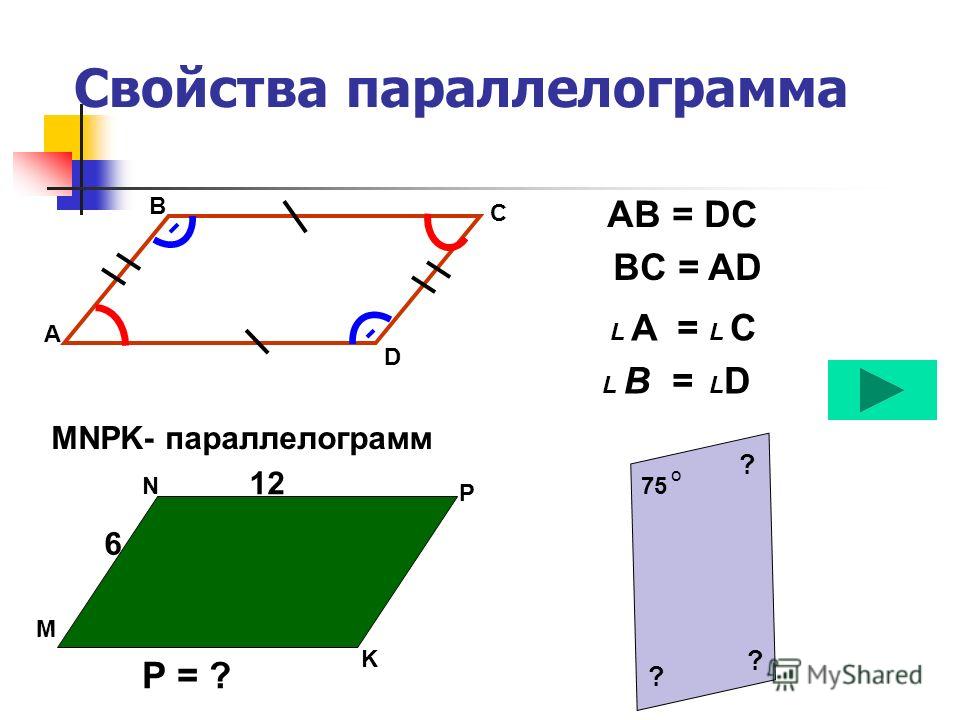
Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).
Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, \( \small \angle 1=\angle 2 \), \( \small \angle 3=\angle 4 \) (см.
статью Треугольники. Признаки равенства треугольников). Поэтому \( \small AB=CD, \;\; AD=BC, \;\; \angle B=\angle D. \)
Из рисунка Рис.2 имеем: \( \small \angle A=\angle 1+\angle 3, \;\; \angle C=\angle 2+\angle 4. \) Учитывая, что \( \small \angle 1=\angle 2 \) и \( \small \angle 3=\angle 4 \), получим: \( \small \angle A=\angle C. \)
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам.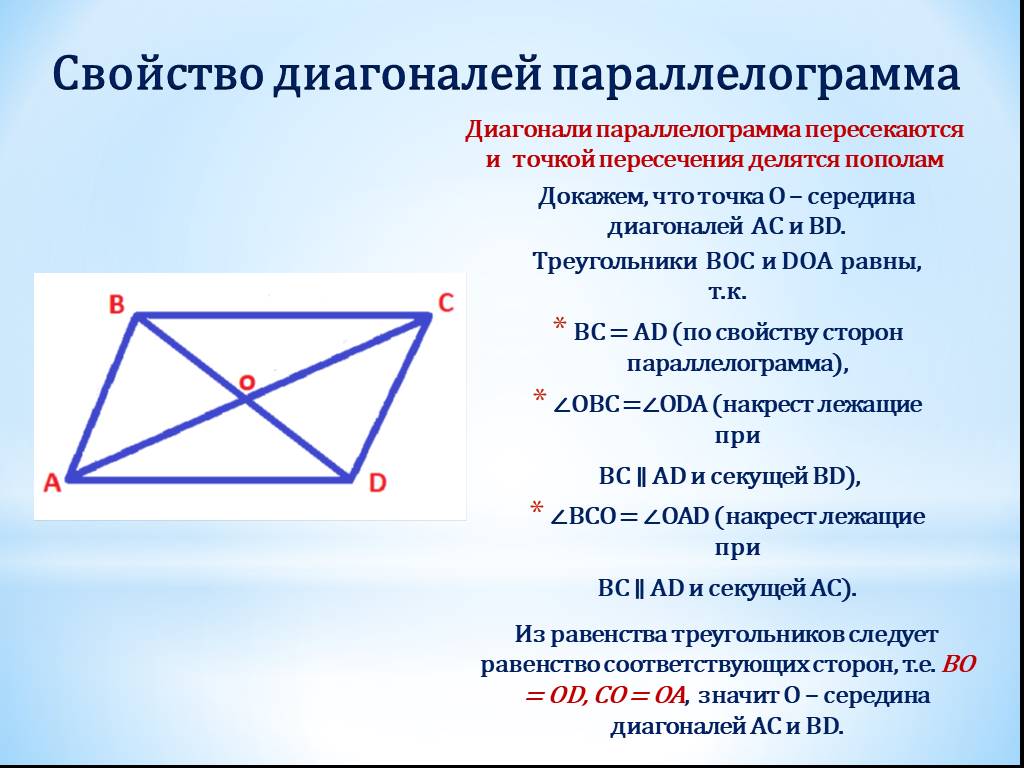
Тогда AO=OC и BO=OD.
Признаки параллелограмма
Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.
Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то \( \small \angle 1=\angle 2 \) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона \( \small \angle 1=\angle 2 \). Но тогда \( \small \angle 3=\angle 4. \) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку \( \small \angle 3 \) и \( \small \angle 4 \) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.
Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда \( \small \angle 1=\angle 2 \). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.
Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:
Углы AOB и COD вертикальные, следовательно \( \small \angle AOB=\angle COD \).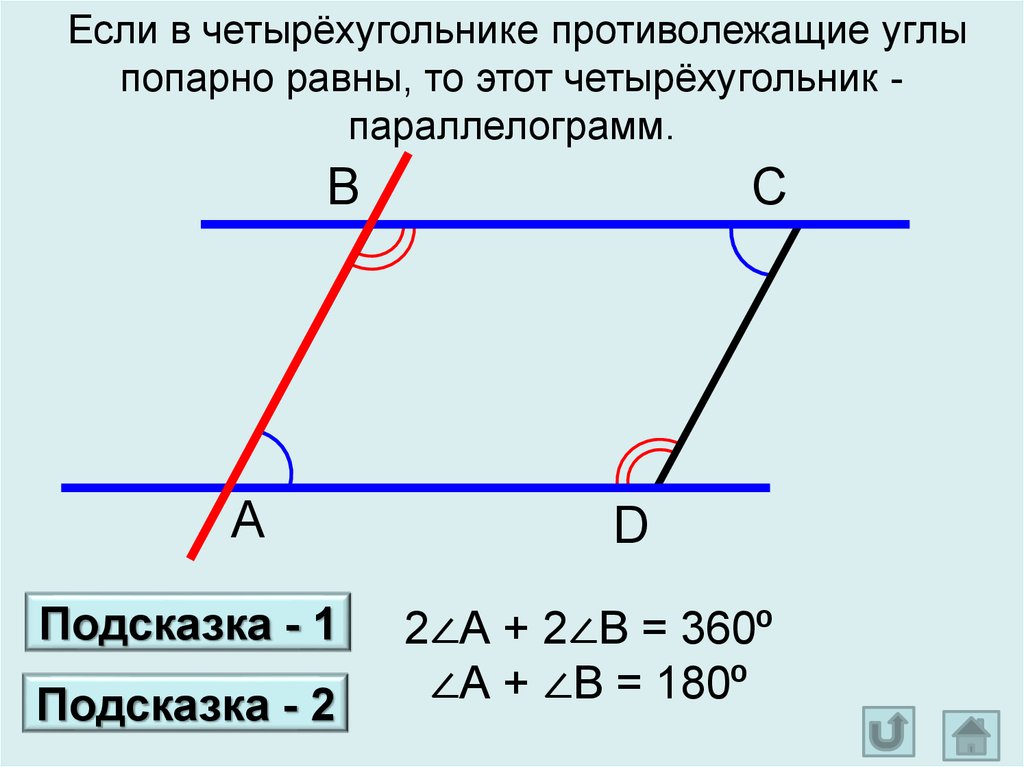
Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:
Тогда AB = CD и \( \small \angle 1=\angle 2 \). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:
и, по признаку 1 четырехугольник ABCD − параллелограмм.
Параллелограмм / Четырехугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Параллелограмм
Параллелограмм — выпуклый четырехугольник, у которого противоположные стороны попарно параллельны. На рисунке 1 изображен параллелограмм АВСD, противоположные стороны АВ и DC, АD и ВС параллельны, т.
е. АВDC, АDВС.
Свойства параллелограмма:
| 10. В параллелограмме противоположные стороны равны |
Доказательство:
Дано: АВСD — параллелограмм.
Доказать: АВ = DC, АD = ВС, А =C, В =D.
Доказательство:
1. Проведем в параллелограмме АВСD диагональ АС.
2. Рассмотрим АВС и АDС: АС — общая, 1 =3 и 2 =4 (т.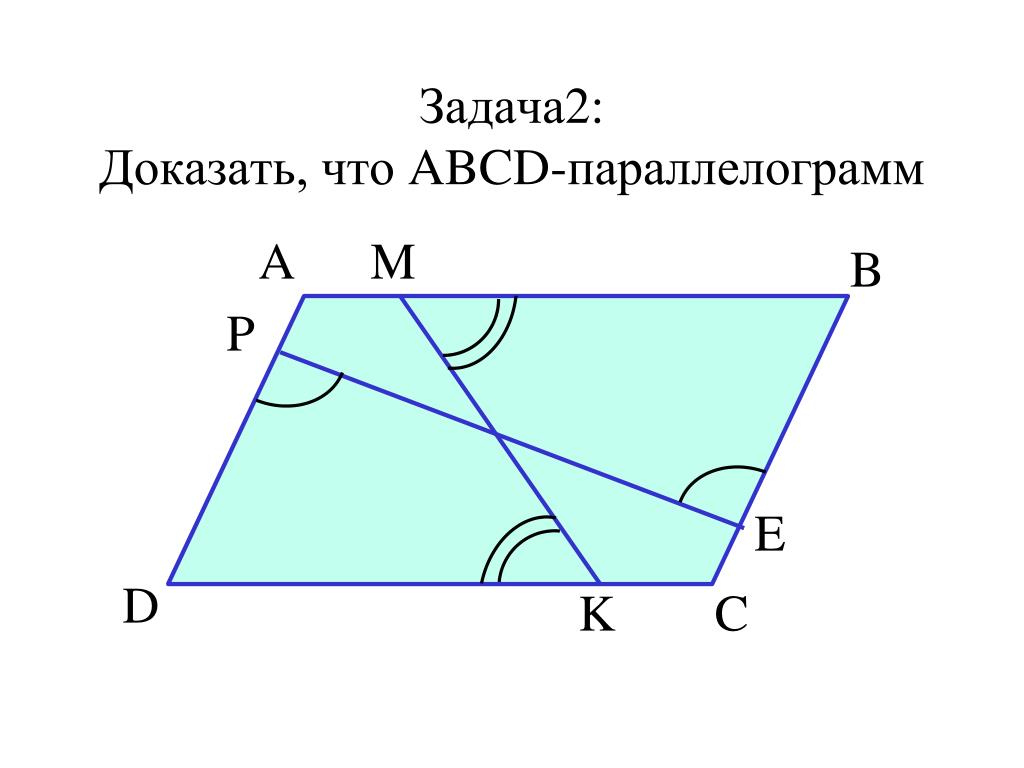
к. по условию АВСD — параллелограмм, АВDC, 1 и 3, 2 и 4 накрест лежащие углы при пересечении параллельных прямых АВ и DC секущей АС), АВС =АDС (по стороне и двум прилежащим к ней углам), АВ = DC, АD = ВС и В =D.
3. А =1 +2, C =3 +4, при этом 1 =3 и 2 =4, А =C. Что и требовалось доказать.
Иллюстрация свойства
1020. Диагонали параллелограмма точкой пересечения делятся пополам. |
Доказательство:
Дано: АВСD — параллелограмм, АС и DВ — диагонали, АСDВ = О.
Доказать: АО = ОС, DО = ОВ.
Доказательство:
Рассмотрим АОD и ВОС: АD = ВС (как противоположные стороны параллелограмма), 1 =4 и 2 =3 (т.к. по условию АВСD — параллелограмм, АDВС, 1 и 4, 2 и 3 накрест лежащие углы при пересечении параллельных прямых АD и ВС секущими АС и DВ соответственно), АОD =ВОС (по стороне и двум прилежащим к ней углам), АО = ОС, DО = ОВ.
Что и требовалось доказать.
Иллюстрация свойства
20Советуем посмотреть:
Многоугольник
Выпуклый многоугольник
Четырехугольник
Признаки параллелограмма
Трапеция
Прямоугольник
Ромб и квадрат
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 384, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 385, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 432, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 551, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 770, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1021, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1030, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1178, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сексуальные и касательные линии
Мастер 7 столбов школьного успеха
Улучшить свои оценки и снизить стресс
Связанные участки Секретные линии
Геометрия Геометрия.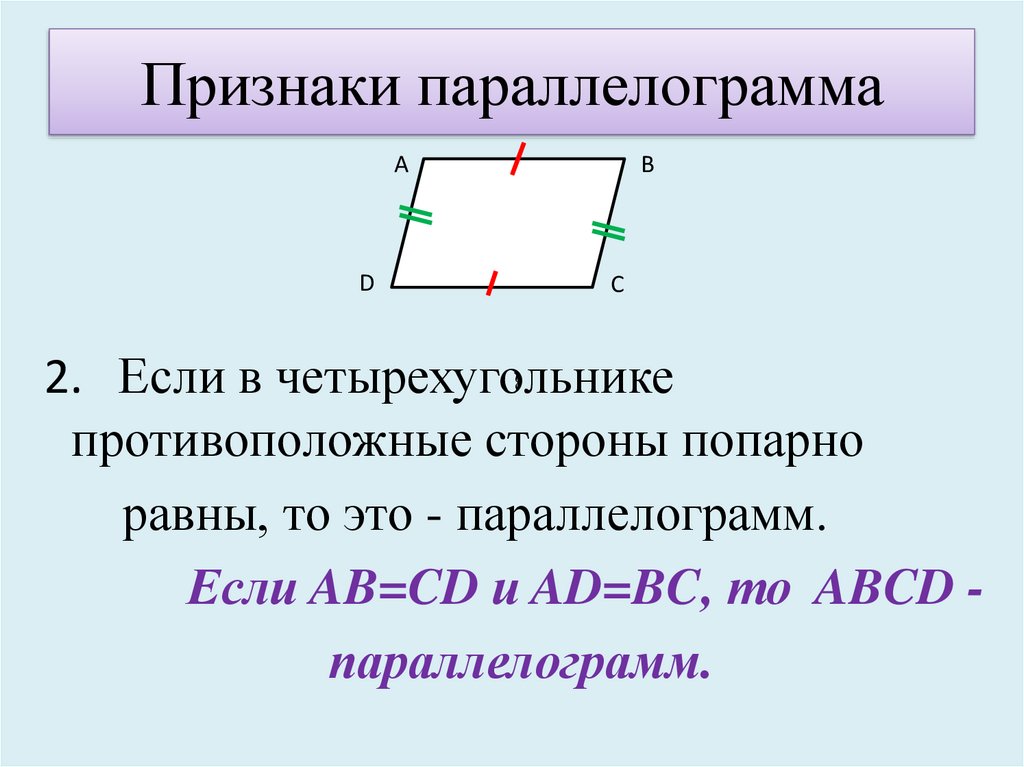
Sparknotes На этом сайте рассматриваются касательные и секущие линии, а также изображения. Sparknotes делает все возможное, чтобы определения и объяснения этих терминов геометрии были краткими и легкими для понимания. Окружности: секущие и касательные На этой странице, созданной AlgebraLAB , объясняется, как измерять и определять углы, образованные касательными и секущими линиями в круге.
Правила работы с хордами, секущими и касательными в окружностях На этой странице, созданной Regents, рассматриваются три правила, которые используются при работе с секущими и касательными к окружностям.
A s линия эканта — это линия, которая пересекает кривую или окружность и проходит через нее в двух или более точках.
A касательная это линия, пересекающая кривую или окружность в одной точке.
Точка касания — это точка, в которой кривая или окружность пересекает касательную.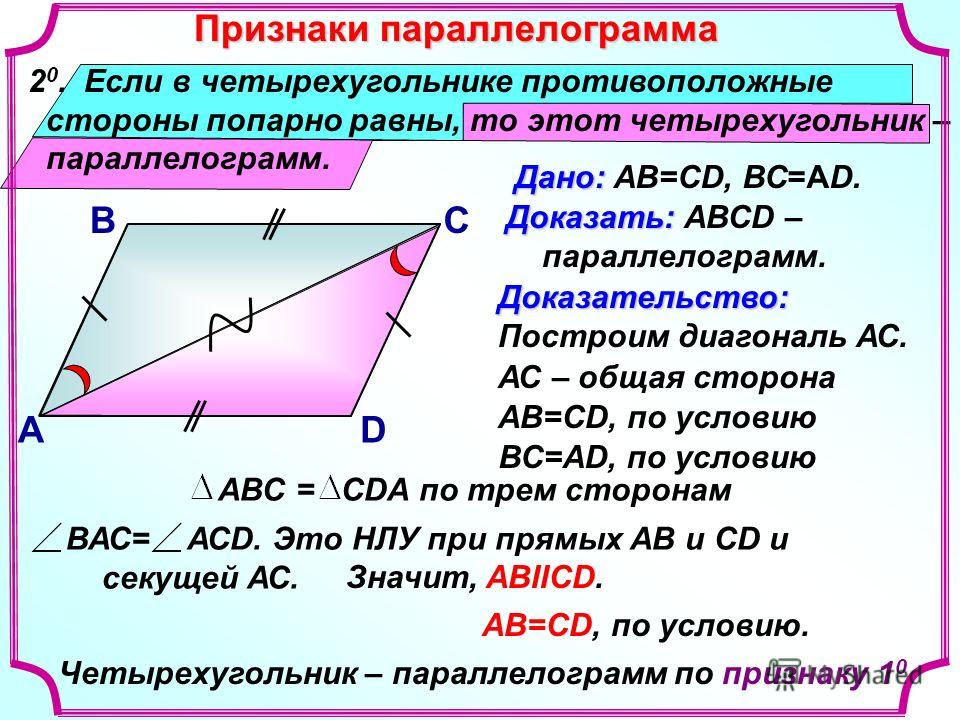
Шаг 1. Измерение большой дуги будет от wx на рисунке, а малой дуги от yz
(большая дуга-малая дуга) ⁄ 2
(80°-20°) ⁄ 2
(60°) ⁄ 2 = 30°
Стенограмма
Привет! Добро пожаловать в MooMooMath. Сегодня мы рассмотрим углы, созданные секансами. Ищем секансов . Теперь секанс – это линия, проходящая через окружность в двух местах. Итак, у нас есть эта линия (указывает на линию A Y) — это секущий отрезок
Итак, давайте подставим некоторые числа. Большая дуга равна 120, меньшая дуга равна сороку. Я собираюсь вычесть их, чтобы получить 80, и я собираюсь разделить на два. Этот угол А равен сороку градусам. Теперь этот угол просто оказался таким же, как дуга. Это нетипично, поэтому не думайте, что вы просто берете дугу и прикрепляете ее туда. Вы должны вычесть и разделить на два, но именно так вы найдете угол. Давайте посмотрим на правила нахождения углов, созданные сек. . Возьмите большую дугу минус малая дуга и разделите на два, чтобы получить меру угла. Вот второй тому пример. Мы возьмем дугу WX большую дугу минус YZ маленькую дугу и разделим на два. Я заменил WX на 80 минус 20 и разделил на два. Так что разделите 60 на два, тогда угол 1 здесь равен 30 градусам. Надеюсь, это видео было полезным Угол А
Большая дуга проходит от W до X и имеет размеры 80 градусов
Небольшая дуга от Z до Y и угол равен 20 градусам
youtube.com/embed/yCvoDSYcqbk?autoplay=0&color1=0x999999&color2=0xe8e8e8&wmode=transparent» allowfullscreen=»»> Давайте рассмотрим пример задачи.
Найдите величину внешнего угла А, образованного двумя секущими, если большая дуга равна 80 градусов, а малая — 20 градусов. Пример 2 измеряет 40 градусов.
Шаг 1. Используйте формулу (Большая дуга – Малая дуга) ⁄ 2
Шаг 2. Подставьте свои числа (120°-40°) ⁄ 2
Шаг 3. Решите 80° ⁄ 2 = 40 ° = Угол A
Вы также можете использовать
Окружности
Касательная
Углы, образованные секущими
Объяснение углов, образованных секущими
Секущие линии
Проверьте себя, является ли изображение секущей линией или касательной? Наведите курсор на картинку, чтобы получить ответ.
Когда две секущие пересекаются вне круга, они образуют угол на внешней стороне круга. Чтобы найти меру внешнего угла, вам нужно знать меру двух пересекаемых дуг. Эти дуги попадают между двумя секущими. Один большой и один маленький. Чтобы найти внешний угол, используйте формулу Big Arc-небольшая дуга, разделенная на 2.
Предальгебра/Экспрессии, уравнения, целые числа
Pre-Algebra/Frection
математические калькуляторы
Геометрия/формы
Геометрия/SAT
Геометрия/Плоскость
Хорошие привычки исследования
Геометрия/Основы
SEGRIN0162
Правило секущих секущих: Используя одну и ту же внешнюю точку, если проведены два секущих сегмента, сумма одного секущего сегмента и его внешней части равна сумме другого секущего сегмента и его внешней части
A *B = C *D
ВСЕГО СЕКАНТ * Внешняя часть = ВСЕ СЕКСОНТ * Внешняя часть
Секвенту секущий отрезок, а его внешняя часть равна квадрату касательного отрезка.
92
вся секущая* внешняя часть = тангенс в квадрате
геометрия — Площадь окружности, проходящей через две вершины параллелограмма и касающейся одной стороны.
Задавать вопрос
спросил
Изменено 1 год, 1 месяц назад 9\circ$ и $\angle CDO$.
Пусть $M$ — середина стороны $CD$, тогда, учитывая $\треугольник ODM$, $OD$, или радиус окружности равен $2\sqrt3$.
Следовательно, площадь круга равна $12\pi$.
$\endgroup$
0
$\begingroup$
Центр $(x,y)$ окружности имеет очевидное значение $x=10$; ордината $y$ задается пересечением прямых $x=10$ и перпендикуляра к отрезку $DC$ в его середине (а эта ордината, очевидно, является радиусом и по касанию).