Как найти координаты середины отрезка: формулы, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение координат середины отрезка
В данной публикации мы рассмотрим, что такое середина отрезка, по какой формуле считаются ее координаты (в плоскости и пространстве). Также разберем примеры решения задач по этой теме.
- Расчет координат середины отрезка
- Примеры задач
Расчет координат середины отрезка
Серединой называется точка, лежащая на отрезке и находящаяся на одинаковом расстоянии от его концов.
AC = CB
Если концы отрезка A (xa, ya) и B (xb, yb) расположены в одной плоскости, то координаты его середины (точки C) считаются по формуле:
Если отрезок с концами A (xa, ya, za) и B (xb, yb, zb) находится в трехмерном пространстве, координаты его середины рассчитываются следующим образом:
Примеры задач
Задание 1
Вычислим координаты точки C, которая является серединой отрезка AB, образованного точками A (5, -2) и B (11, 10).
Решение:
В данном случае нам подойдут формулы для плоскости:
xc = (5 + 11) / 2 = 8
yc = (-2 + 10) / 2 = 4
Таким образом, точка C имеет координаты (8, 4).
Задание 2
Найдем координаты точки B, являющейся одним из концов отрезка AB. При этом известны координаты точки A (7, 13) и середины отрезка – C (4, -3).
Решение:
Нужные нам формулы можно вывести из выражений для расчета координат середины отрезка:
xb = 2xc – xa = 2 · 4 – 7 = 1
yb = 2yc – ya = 2 · (-3) – 13 = -19
Следовательно, координаты B – (1, -19).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Как найти длину зная координаты точек.
Нахождение координат середины отрезка: примеры, решенияОтрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 .
Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат.
Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y .
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно.
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 .
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая.
В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.Пускай у вас сейчас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность.Координаты вектора r, видимо, будут следующими: x1-x2, y1-y2, z1-z2. Тогда модуль вектора r либо расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)).
2))
Видео по теме
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками.
Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
MathScene — Векторы — Урок 3
MathScene — Векторы — Урок 32008 Расмус Эф и Джанн Сак |
Урок 3
Векторы в системе координат
Пример 1
точка А имеет координаты (2, 2), а точка В — координаты (6, 5) (см. схему). Координаты вектора
Мы
можно использовать формулу расстояния между двумя точками, чтобы найти расстояние
между A и B, то есть длина вектора
(см. Правило Пифагора в уроке 2). Формула выглядит следующим образом:
Подставляя заданные координаты в формулу получаем:
Мы видим, что числа под квадратным корнем — это просто координаты
вектор. Это, конечно, потому, что длина вектора — это просто
гипотенуза в прямоугольном треугольнике с более короткими сторонами 3 и 4.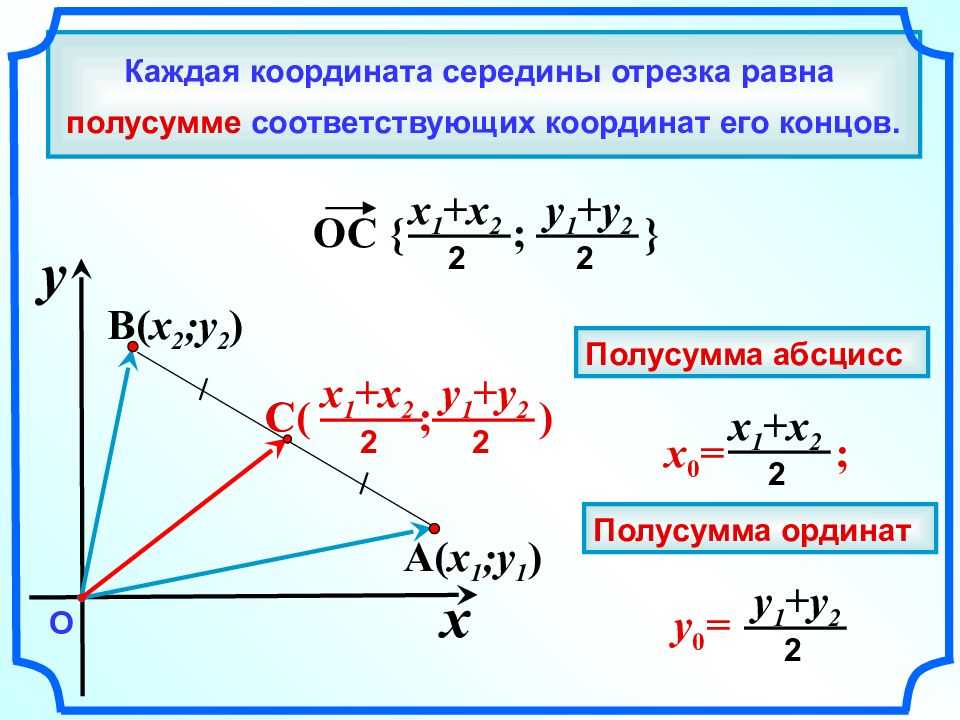
Формула длины вектора, начинающегося в точке
A = (x 1 , y 1 ) и заканчивается на B = (x 2 ,
у 2 ) равно:
Если координаты вектора то имеем следующее правило:
Пример 2
Найдите вектор что параллельно и который имеет длину 2 единицы (видеть диаграмму).
Два треугольника на диаграмме подобны, поэтому соответствующие
стороны находятся в одинаковом соотношении.
||
= т∙||. Число t есть отношение между соответствующими сторонами. Отношение такое.
Мы можем найти координаты как
следует:
Если векторы и являются параллельно, то существует число t такое, что:
= т∙ |
Пример 3
Какие из следующих векторов параллельны и
.
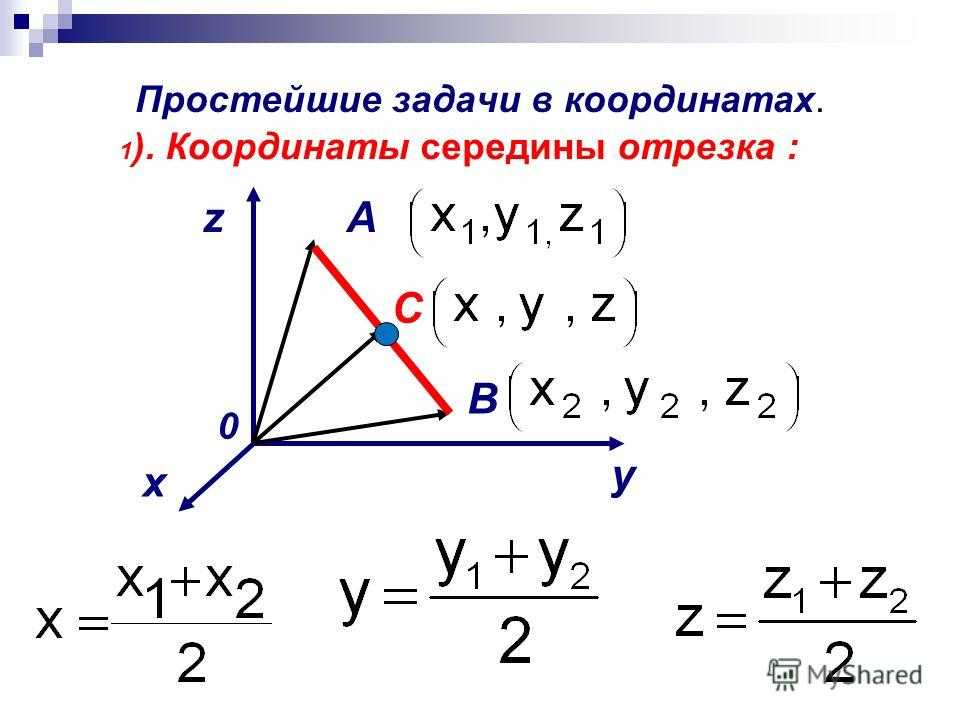
Если векторы и являются параллельно, то существует число t такое, что = т∙. Если векторы и являются параллельно существует число r такое, что «=» р∙.
Мы можно найти числа t и r, используя координаты x, а затем проверить, чтобы увидеть найдены ли те же значения, когда мы используем координаты y.
= т∙
3 = t∙13 дает t = 3/13 = 2/9
4 = t∙18 также дает t = 4/18 = 2/9
векторы и есть параллель .
= р∙
3 = r∙6 дает r =
4 = r∙9 дает r = 4/9
векторы и есть не параллельно (Это значит, что и являются тоже не параллельно).
Вектор на диаграмме имеет координаты
. вектор начинается в точке (0, 0) и заканчивается в (3, 2), поэтому координаты
конечная точка совпадает с координатами самого вектора. Это относится к
все векторы, которые начинаются в начале системы координат, то есть в
точка (0, 0).
Вектор, который начинается в точке (0, 0), имеет те же координаты, что и его конечная точка. Этот вектор называется вектором положения для A. |
Каждая точка в системе координат может быть представлена своим вектором положения. Координаты точки и вектор ее положения совпадают. Это может быть очень полезно при просмотре переводов в системе координат.
Пример 4
Треугольник, показанный на диаграмме, должен быть переведен вектором .
Мы используем векторы положения вершинных точек (−3, 0),
(2, −2) и (3, 1) и добавляем вектор
каждому из них.
Это дает нам новый вектор положения каждой вершины. Диаграмма ниже показывает перевод.
Пример 5
Теперь мы будем использовать векторы положения, чтобы найти середину отрезка AB, если А = (1, 2) и В = (4, 3).
Как обычно, точка O является началом системы координат.
Если M середина
AB тогда:
«=» + ∙
Вектор является вектор положения точки M и, следовательно, имеет те же координаты, что и точку М, которую мы хотим вычислить. Вектор – это вектор положения A. Чтобы достичь середины M, нам нужно добавить половину вектор . Нарисуйте схему, чтобы увидеть это.
Сначала нам нужно найти вектор .
Теперь мы можем найти .
«=» + ∙
Координаты M такие же, как у вектора положения или (2, 2) .
Легко найти формулу, по которой можно найти координаты точки. середина отрезка АВ.
Из диаграммы видно, что в середину М можно попасть из двух направлениях, от O через A до M и от O через B до M. Таким образом, мы можем написать два векторных уравнения для . «=» + ∙ «=» — ∙ Складывая эти два уравнения вместе, мы получаем |
2 = + ∙ + — ∙
Мы видим, что вектор положения середины отрезка представляет собой своего рода
среднее значение векторов положения конечных точек.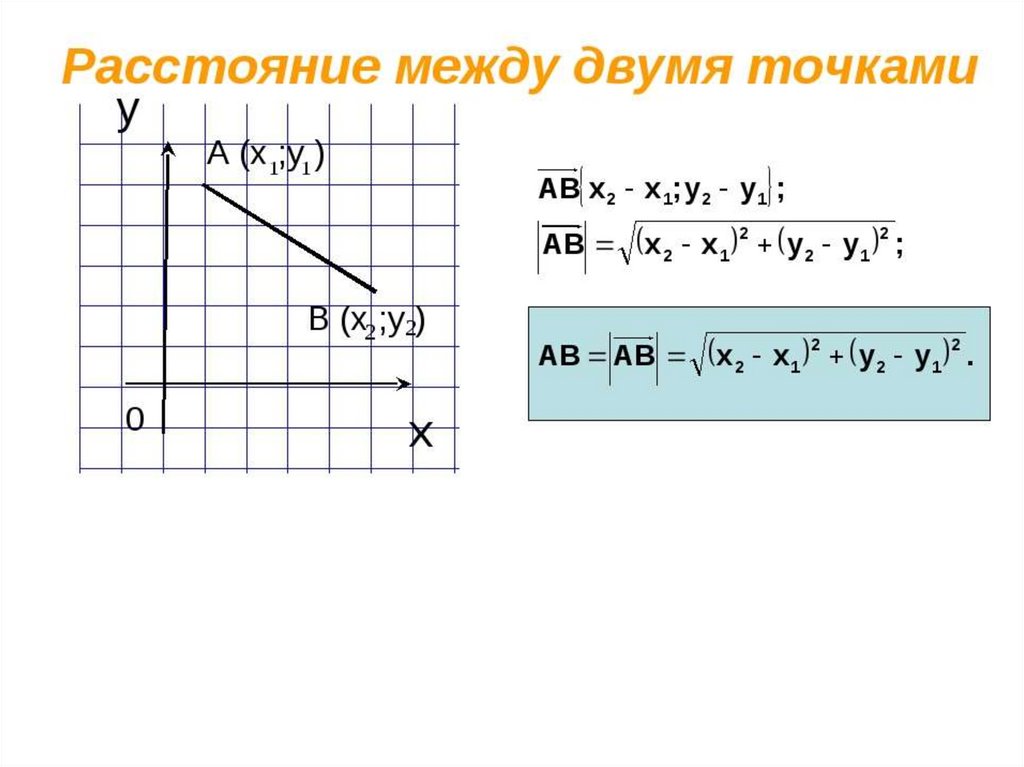
Поэтому мы можем найти
координаты средней точки, найдя среднее значение координат x и y
координаты соответственно.
Это приводит нас к правилу, которое мы называем правилом средней точки.
Середина M отрезка AB задается правилом: При использовании координат правило: |
Пример 6
Вершинами треугольника ABC являются A = (1, 2), B = (4, 3) и C = (3, 0).
Найдите длину прямой, проведенной от А до середины стороны ВС (медиану стороны ВС). треугольник АВС).
Мы начнем с нахождения середины BC, используя приведенное выше правило.
Назовем середину M и найдем ее вектор положения (видеть схему).
= ∙ + ∙ |
Следовательно, M, середина ВС, имеет координаты
М = (3, 1).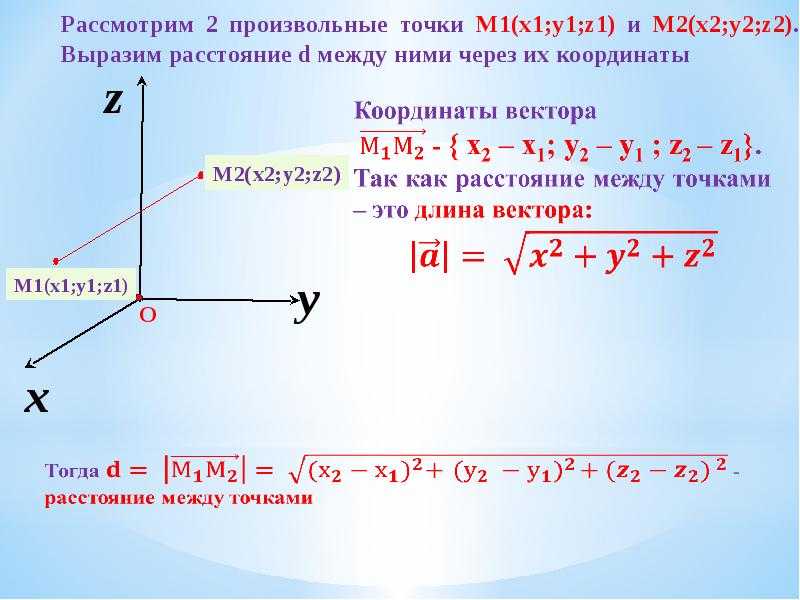
Далее находим координаты вектора .
Наконец, мы можем найти длину вектора как необходимый.
≈ 2,55
Три медианы треугольника пересекаются в одной точке, называемой центр треугольника (обозначен Т на диаграмме). Если мы знаем координаты вершин треугольника можно найти координаты T по простой формуле. Эта формула находится аналогично Правило средней точки. Мы можем достичь T через все три вершины треугольника, тогда мы добавляем три векторных выражения вместе. |
В уроке 2 о треугольниках мы видели, что все медианы пересекаются в одной точке. точки, делящие друг друга в соотношении 2:1 или 2/1. Отсюда мы знаем, что длина вектора в два раза больше, чем и поэтому
«=» ∙ и «=» −∙. Используя это, мы можем написать три уравнения:
= + ∙
= + ∙ — ∙
= — ∙ — ∙
Когда мы сложим их вместе, выходит и мы получаем:
3= + +
Чтобы найти координаты T, мы берем среднее значение x
и y координаты вершин соответственно. |
Таким образом, мы находим точку пересечения T медиан треугольника путем нахождения своего рода среднего векторов положения вершины. Таким образом, это правило является расширением правила средней точки.
Пример 7
Найдите точку пересечения Т медиан треугольника АВС ( центр ) при условии, что A = (1, 2), B = (4, 3) и C = (3, 0) (см. схему). |
Центр Т = (2, 1) .
Попробуйте Викторина
3
на Векторы.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Координаты точки, компоненты вектора и середины отрезка
Координаты точки на плоскости
Давайте посмотрим, как векторы используются для присвоения координат точкам на плоскости.
Рассмотрим фиксированную точку на плоскости $$O$$ (известную как начало координат) и базис $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$ $$V_2$ $ (пространственный вектор размерности $$2$$).
Напомним, что в основе $$V_2$$ лежат два линейно независимых вектора. Множество, образованное $$O$$ и $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, образует систему отсчета на плоскости, поскольку позволяет определить положение любых других точки на плоскости.
Это связано с тем, что любые другие точки $$P$$ на плоскости вместе с точкой $$O$$ определяют вектор $$\overrightarrow{OP}$$. Пусть $$(p_1,p_2)$$ — компоненты вектора в базисе $$B$$. Тогда $$(p_1,p_2)$$ — это координаты точки $$P$$ в системе отсчета $$R=\{O;\overrightarrow{u}, \overrightarrow{v}\}$$, и мы пишем $$P=(p_1,p_2)$$.
Процедура нахождения координат точки $$P$$ в заданной системе отсчета следующая:
Из точек $$O$$ и $$P$$ определяем вектор $$\overrightarrow{OP}$$
Выразим вектор $$\overrightarrow{OP}$$ в виде линейной комбинации векторов базиса $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, т.
е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$- $$P=(p_1,p_2)$$
е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$Выразите точку $$P$$ чертежа в системе отсчета $$R =\{O;\overrightarrow {u}, \overrightarrow{v}\}$$.
- Рисуем вектор $$\overrightarrow{OP}$$:
- Выразим вектор $$\overrightarrow{OP}$$ в виде линейной комбинации векторов базиса $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$:
- Получаем $$\overrightarrow{OP}=\overrightarrow{u}+2\overrightarrow{v}$$ и, следовательно, координаты точки $$P$$ равны $$P = (1 , 2 )$$
В дальнейшем в качестве системы отсчета $$R$$ будем рассматривать систему, образованную началом координат $$O = (0, 0)$$ и каноническим базисом $$V_2$$ $$B =\{\overrightarrow{i},\overrightarrow{j}\}$$.
Компоненты вектора, определяемого двумя точками
Теперь посмотрим, как определить компоненты вектора, если известны координаты его концов:
Пусть $$P =(p_1,p_2)$$ и $$ Q = (q_1,q_2)$$ — две точки плоскости, а $$\overrightarrow{PQ}$$ — вектор, идущий из $$P$$ в $$Q$$.
Тогда компоненты вектора $$\overrightarrow{PQ}$$ равны $$\overrightarrow{PQ}=(q_1-p_1,q_2-p_2)$$.
Даны $$P = (2, 6)$$ и $$Q = (-3, 9)$$. Компоненты вектора $$\overrightarrow{PQ}$$ таковы: $$\overrightarrow{PQ}= (-3 — 2, 9- 6) = (-5, 3)$$
Применение вектора к точке
Для данной точки $$P$$ и вектора $$\overrightarrow{v}$$ результат применения вектора к точка — это новая точка $$Q$$, расположенная в направлении $$\overrightarrow{v}$$ и на расстоянии $$|\overrightarrow{v}|$$. (модуль вектора $$\overrightarrow{v}$$)
Координаты этой новой точки $$Q$$ вычисляются из координат $$P =(p_1,p_2)$$ и $$\overrightarrow{ v}=(v_1,v_2)$$ таким образом $$$Q = P +\overrightarrow{v}=(p_1+v_1,p_2+v_2)$$$
ПРИМЕЧАНИЕ. Очень важно помнить, что эта операция сложения имеет смысл только между точкой и вектором. Мы никогда не должны складывать две точки, а результатом сложения двух векторов будет другой вектор, а не точка!
Рассмотрев следующий рисунок, определите координаты точки $$P$$ рисунка, полученного приложением вектора $$\overrightarrow{v}$$ к точке $$A$$.