Шаблон параболы у 2х в квадрате: Используя шаблон параболы у = хˆ2, постройте график функции: а) у = (х — 2)ˆ2 + 3; б) у = -(х

Содержание

С помощью шаблона параболы построить график функции. Упр. 617, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Поделитесь кому не жалко чертежами
С помощью шаблона параболы у=х

2 построить график функции:
1) у = (х + 2)²; 2) у = (х-3)²;
3) у= х² — 2; 4) у = -х² + 1;
5) y = -(x-l)²— 3; 6) у = (х + 2)² + 1.

Лучший ответ

Вообще не жалко

еще ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Психология

ЕГЭ

10 класс

9 класс

похожие вопросы 5

Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство

Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)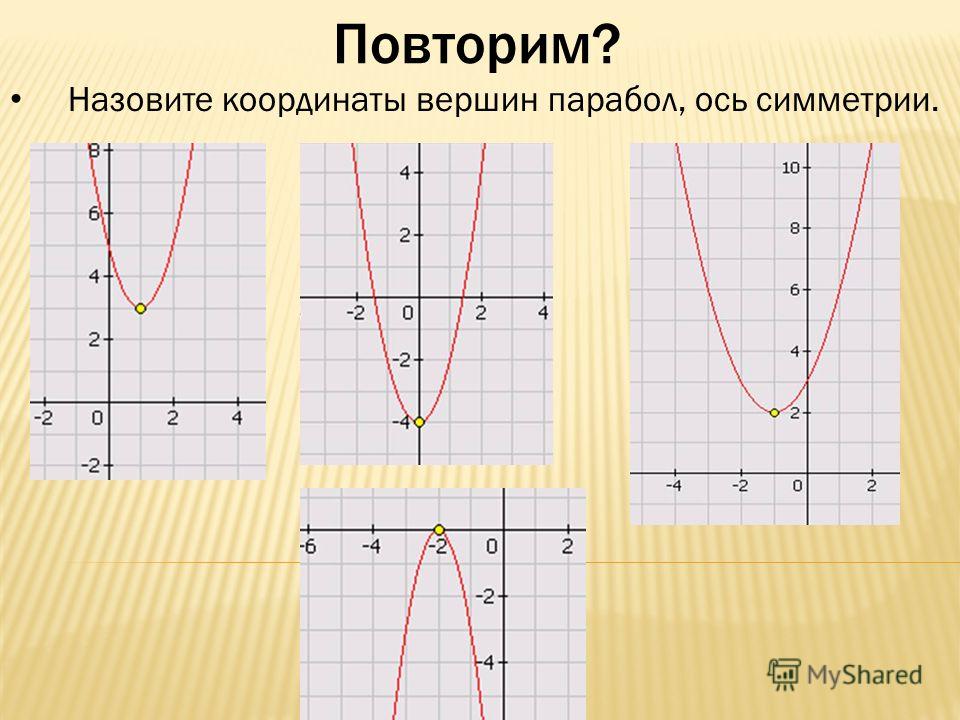

ГДЗ11 классКолмогоров А.Н.Алгебра

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Функция вида у=а(х-m)2+n, её свойства и график » Мир учителя

Казахстан, Западно-Казахстанская область, с. Володарское

Володарская СОШ

Учитель математики и физики I категории

Савосина В.С.

Цели урока:

1) обобщить и систематизировать знания, умения и навыки учащихся в построении графиков квадратичной функции вида у=а(х-m)

2 и у=ах²+n если известен график функции у= ах² , научить строить график функции вида у=а(х-m)²+n.

2) развитие исследовательской и познавательной деятельности, самостоятельности и творческой активности, пространственного воображения и логического мышления.

Тип урока: формирование знаний.

Ожидаемый результат: результатом деятельности учащихся на уроке является понимание сути построения графиков квадратичных функций видау=а(х-m)²+n описание её свойств.

Оборудование:

Презентация урока, карточки – задания для самостоятельной работы, чертёжные инструменты, координатная плоскость, шаблон параболы, листы самоконтроля.

План урока

Организационный момент.
Устная работа.
Алгоритм построения графиков квадратичной функции вида

у=а(х-m)²+n

Тренировочные упражнения.
Итог урока.
Домашнее задание.

Ход урока

I. Организационный момент.

Сегодня на уроке мы повторим алгоритмы разложения квадратного трёхчлена на множители, построения графика квадратичной функции вида у=а(х-m)² и у=ах²+n, продолжим формирование умений применять эти свойства при выполнении практических заданий.

Загадка: Кто знаком со мною, тот знает мой каприз:

Мои ветви смотрят то вверх, а то и вниз.

То есть пересечения с осями, то их нет.

В вершине моей максимум, а минимума нет,

А иногда бывает всё наоборот.

Но кто меня узнает, тот сразу всё поймёт.

(квадратичная функция, парабола).

II. Устная работа.

1. Что является графиком функции у = аx².
2. Как зависит график функции у = аx² от коэффициента а.
3. Вспомни алгоритм построения графиков функций вида у=а(х-m)² и у=ах²+n , если известен график функции у= ах².
4. Выдели полный квадрат: x² — 4х + 5

III. Изучение нового материала.

1) График функции у=а(х-m)²+n можно получить из графика функции у = аx² последовательно выполняя преобразования, которые мы выполняли на предыдущих уроках

2) Отработать умение учащихся по графику описывать свойства квадратичной функции на готовых графиках-тренажёрах:

-Множество значений функции

-Ось симметрии квадратичной функции

-Промежутки убывания функции

-Промежутки возрастания функции

— наименьшее или наибольшее значение функции.

Пример 1. Построить график функции у = (х — 2)² — 3.
Решение. Выполним построение данного графика по этапам.
Способ построения графика функции у = (х — 2)² — 3
1) Построим график функции у = х² (пунктирная линия).
2) Сдвинув параболу у = х², на 2 единицы вправо, получим график функции у = (х — 2)².
3) Сдвинув параболу у=(х — 2)² на 3 единицы вниз, получим график функции у=(х — 2)² — 3 .

Опишите свойства функции у = (х — 2)² – 3 по графику.

— Область определения функции – это…

-Множество значений функции – это…

-Ось симметрии квадратичной функции

-Промежутки убывания функции — …

-Промежутки возрастания функции — …

— наименьшее значение функции …

IV. Тренировочные упражнения.

Закрепление темы в процессе работы по карточкам-тренажёрам. Отработка навыков чтения графика квадратичной функции, описание свойств квадратичной функции на готовых графиках-тренажёрах.

Самостоятельная работа учащихся по карточкам, с проверкой на доске на координатной плоскости.

2. Записать в нижней строке таблицы уравнение параболы, полученной из параболы у=3х² сдвигом вдоль одной из координатных осей.

Вдоль оси Ох на 4 ед. вправо.	Вдоль оси Ох на 1,5 ед. влево.	Вдоль оси Оу на 2 ед. вниз.	Вдоль оси Оу на 5 ед. вверх.
	у=3(х+1,5)²

3. Записать в нижней строке таблицы уравнение параболы, полученной из параболы у=-2х² сдвигом вдоль одной из координатных осей.

Вдоль оси Ох на 3 ед. влево и вдоль оси Оу на 0,5 ед. вниз.	Вдоль оси Ох на 2 ед.вправо и вдоль оси Оу на 4 ед. вверх.	Вдоль оси Ох на 5 ед.влево и вдоль оси Оу на 2 ед. вверх.	Вдоль оси Ох на 4 ед.вправо и вдоль оси Оу на 2 ед. вниз.
	у=-2(х-2)² +4

4. На одной и той же координатной плоскости построить графики функций у=2х² , у=2(х+3)² и у=2(х+3)² -1 , используя шаблон параболы у=2х².

5. 1) Назовите промежутки, в которых у>0, у<0.

2) Назовите промежутки возрастания и убывании функции.

V. Итоги урока.

Карта учета работы учащихся на уроке (ученики заполняют по ходу урока)

№	Ф. И ученика	Д/З	устно	№1	№2	№3	оценка

VI.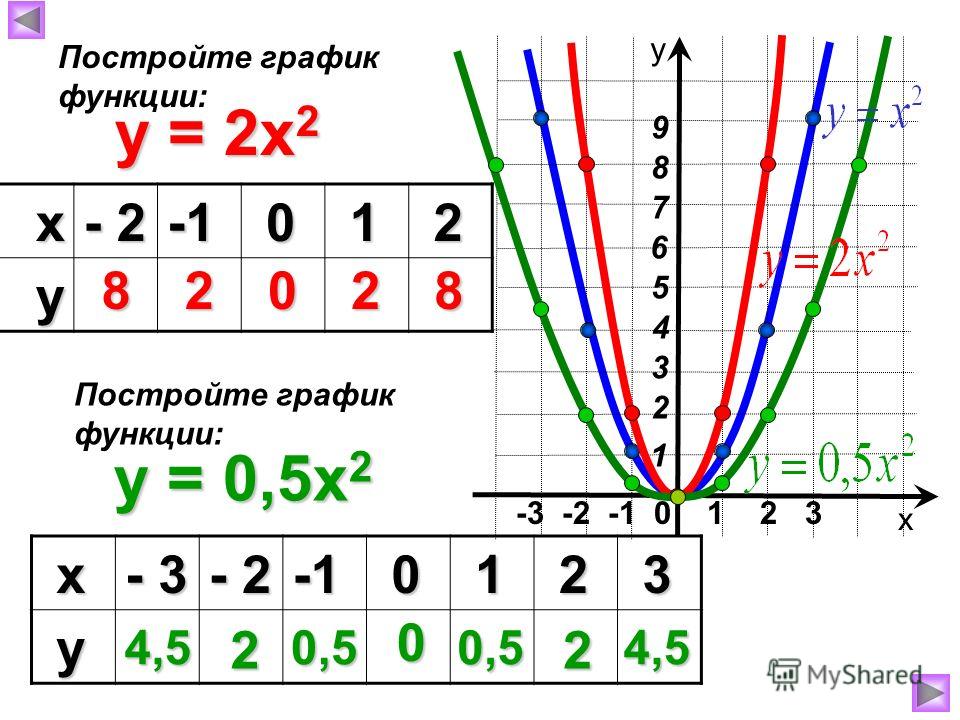 Домашнее задание

§14, с.86-88, №264(1,2).

ВЕРШИННАЯ ФОРМА | квадратика

Ось симметрии (K=h)

Что такое ось симметрии? Ось симметрии параболы — это вертикальная линия, которая делит параболу на две соответствующие половины. Ось симметрии всегда проходит через вершину параболы. Это координата X вершины. Х=ч.

Оптимальное значение (y=k)

Оптимальное значение — это самая высокая или самая низкая точка параболы. Оптимальное значение, также известное как вершина параболы, будет максимальным, если только парабола раскрывает слова вниз. Одно открытие вверх имеет минимальное значение. Это «Y» координата вершины. 9Для этого уравнения вершина параболы будет (1,1). следовательно, осью симметрии является прямая x=1

Пример;

y=k

Ex;

y=a(x-h)²+k

y=-3(x+2)+27

y=27

Следовательно, оптимальное значение для уравнения

y=-3(x+2) ²+27 is y=27

Ступенчатый шаблон определяет, какие точки пересекает парабола. Это шаблон, за которым следует число в квадрате, начиная с 1. Например, уравнение, в котором «а» равно 2, пройдет через 1, увеличится на 2, затем на 2, увеличится на 8. Это было найдено с помощью «а», умноженного на шаг шаблон один.

Больше 1, больше 1

Больше 2, больше 4

Больше 3, больше 9

Больше 4, больше 16 » в этом квадратном уравнении представляет собой горизонтальный перенос. это означает, насколько далеко влево или вправо график сдвинут от точки x=0, также известной как начало координат. если значение «H» положительное, число будет отрицательным. Если «H» является отрицательным числом, число будет преобразовано в положительное. Поэтому происходит переключение знаков. 92 + 8, значение h равно 4, а k равно 8.

«К» в этом уравнении представляет вертикальный сдвиг, то есть насколько вверх или вниз график смещается от x=0 или начала координат. В случае выяснения, куда идет «К», вам просто нужно знать, что если значение отрицательное, оно останется отрицательным, а если число положительное, число будет положительным. значение «K».

«a» в этом уравнении указывает на растяжение/сжатие (растяжение или сжатие будет умножать вертикулярную часть ступенчатого паттерна. Это также показывает, открывается ли квадратик вверх или вниз. Вы могли бы сказать, открывается ли он вниз или вверх, положительное «а» рисует смайлик, а отрицательное «а» рисует хмурый. откроется. Если значение «а» отрицательное, то оно упадет.

Х-пересечения или нули

Чтобы выяснить, что такое пересечение «x», вам нужно заменить «y» на нули. у=0. 92+k

Используйте таблицу значений для построения графика точек

Давайте сделаем пример

Используйте ШАБЛОН для построения точек или используйте информацию, полученную из графика

5 9 с обеих сторон, и поскольку левая сторона может быть разделена поровну на два положительных и два отрицательных значения, их можно использовать для определения пересечений по оси x

Как это связано с построением графика?

Это связано с построением графиков, потому что дает понимание построения парабол не только одним, но и тремя способами, с более точными расчетами.

Вот видео, показывающее, как найти

нули или точки пересечения x

Примеры словесных задач

y=a(x-h)²+k

Майк бросает мяч с высоты 1 м над землей. Через 2 секунды мяч достигает максимальной высоты 5 м.

а) Напишите уравнение в вершинной форме для квадратичной функции, выражающей высоту и время полета мяча.

y=a(x-h)²+k

1=a(x-2)²+5

1=a(0-2)²+5

1=a(-2)²+5

1=a(4)+5

1-5=a(4)

-4=a(4)

-1=a

b) Найдите точки пересечения y и x этого уравнения. или

2.2+2=x

4.2=x

Следовательно, точка пересечения x для уравнения y=-(x-2)²+5 равна x=4,2 и x=-0,2.

y=-(0-2)²+5

y=-(4)+5

y=1

Следовательно, точка пересечения y этого уравнения равна y=1.

Форма вершины — Причудливая квадратичная форма

Форма вершины

Как только вы узнаете, как каждая часть формы вершины влияет на параболу, будет намного проще решать или находить части параболы, такие как направление раскрытия и преобразований.

Щелкните здесь, чтобы увидеть обзор частей вершинной формы.

Ступенчатый рисунок 92, когда число возводится в квадрат, чтобы получить значение «у». В вершинной форме, когда «а» равно , а не , это означает, что будет затронут ступенчатый шаблон и изменится парабола.

Это видео включает в себя объяснение того, как работает пошаговый паттерн и как он соотносится с графикой с некоторыми примерами.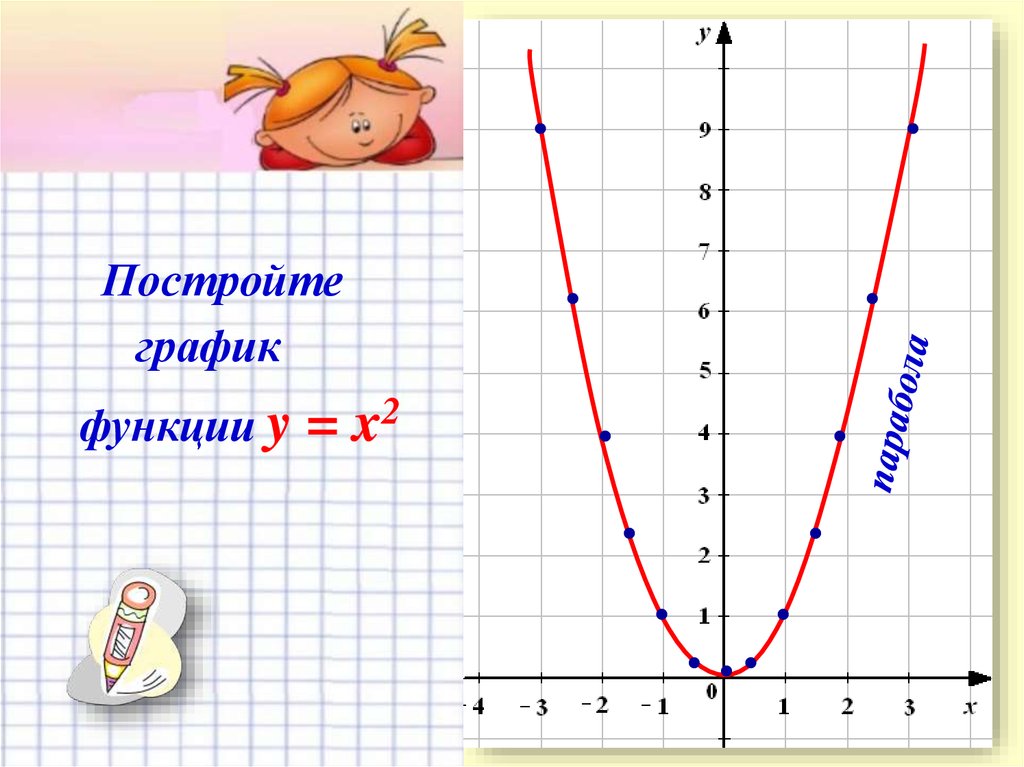

Щелкните здесь, чтобы просмотреть урок по построению графиков в вершинной форме.
Теперь, когда вы узнали, как найти аспекты параболы в форме вершины, вы также можете начать строить их графики и находить квадратные уравнения, используя вершину.
Построение графика из вершинной формы
При построении графика вершинную форму легко использовать, если вы знаете, как каждая часть уравнения влияет на параболу. Например, когда вы понимаете, как найти такие вещи, как вершина, как умножить шаблон шага на «а» с его отношением к базовой параболе и как «h» или «k» перемещают параболу, вы можете легко посмотреть на уравнение и начертите его.
Части формы вершины (краткое описание)
Ось симметрии 92+k (в котором есть «-h»), «h» в уравнении всегда будет одним и тем же числом, но
противоположным символом.
Помня о том, как каждая часть уравнения вершины преобразует параболу, вы также можете решить, чтобы найти уравнения, даже если некоторые части отсутствуют. Например, если «а» в уравнении формы вершины отсутствует, но у нас есть вершина, мы должны знать, как парабола смещается по горизонтали и вертикали, но нам также нужно знать еще одну часть информации, прежде чем построить график. парабола.
«а»:
Если «а» параболы является целым числом , это означает, что растягивает параболу по вертикали в *число* .
Если у параболы есть «а» , которое не является целым числом , это означает, что парабола по горизонтали
растягивается в *число* раз.
Если парабола переворачивает от базовой параболы или открывается в противоположную сторону, (имея противоположный символ для «а») отражает базовую параболу по оси x . )
«k»:
Если «k» отрицательное , оно смещается вниз, что также означает вертикальное смещение на ____ единиц вниз.
Если «k» положительное , парабола движется вверх, то есть имеет вертикальное смещение на ____единиц вверх.
Обзор терминологии преобразований
1. Мы знаем, что парабола перевернулась и теперь раскрывается вниз и пересекает ось x. Следовательно, отражает базовую параболу по оси X.
2. «а» или -1/2 сжимает параболу или делает ее шире.
Другими словами, растягивает параболу по горизонтали с коэффициентом -1/2.
3. «h» или 3 перемещает параболу влево на 3 единицы. Итак, парабола имеет сдвиг по горизонтали на 3 единицы влево.
4. Наконец, «k» или -4 перемещает параболу вниз на 4 единицы. Это означает, что имеет вертикальный сдвиг на 4 единицы вниз.
Вот пример: 92-4
Теперь, когда вы знаете, как каждая часть преобразует параболу, вот как сообщить, как изменилась парабола. Другими словами, это то, как говорить на математическом языке при описании парабол.
Используя правильную терминологию
Если «а» — это , а не целое число, парабола вытягивается горизонтально.

Пример 2. Когда «а» не является целым числом
Если «а» является целым числом, парабола вытягивается вертикально.

Теперь, когда вы знаете, как каждая часть формы вершины преобразует параболу (которая также включена в «Сводку частей формы вершины»), вот объяснение того, как они делают то, что делают.
No related posts.