Шаблоны квадратичной функции распечатать: График квадратичной функции

Содержание

График квадратичной функции

Тема. «Графики функций вида у = ах² +n, у = a (х — m)² , у = a (х — m)² + n»

Ход урока.

Самостоятельная работа.

Вариант1

Построить линии, симметричные данным относительно оси ОУ

2.Функция задана формулой

у= 3х².

а) Найдите у(5).

б) При каких значениях х значение функции равно 12?

в) Определите, принадлежат ли графику данной функции точки А(1;-3). В (-1;3)?

3. Постройте график функции

у= -3х².

Вариант2

1. Построить линии, симметричные данным относительно оси ОХ

2.Функция задана формулой

у= -2х².

а) Найдите у(3).

б) При каких значениях х значение функции равно -50?

в) Определите, принадлежат ли графику данной функции точки А(1;-2). В (-1;2)?

3. Постройте график функции

у= 2х².

Вариант 3.

1. Разложите квадратный трёхчлен 3х² +2х -5

на множители.

2. Постройте график функции у= 0,5х².

Укажите промежутки возрастания функции.

3. Найдите координаты точек пересечения графика функции у= х² + 4х -5 с осями координат.

Вариант5.

1)Приведите основные свойства и график функции у=ах² при а0.

2)Постройте график функции у= .

3) При каком значении а прямая у= х+а касается параболы у = 0,5 х²?

Вариант 4

1. Разложите квадратный трёхчлен 7х² -5х -2

на множители.

2. Постройте график функции у= -0,5х².

Укажите промежутки возрастания функции.

3. Найдите координаты точек пересечения графика функции у= -х² + 4х -3 с осями координат.

Вариант 6.

1) Приведите основные свойства и график функции у=ах² при а

2)Постройте график функции у= .

3) При каком значении а прямая у= х-а касается параболы у = -2 х²?

Объяснение нового материала.

1)Мы знаем , как выглядит график функции у = . Для того чтобы построить график мы на предыдущем уроке заполняли следующую таблицу.

х	-4	-3	-2	-1	0	1	2	3	4
у	8	4,5	2	0,5	0	0,5	2	4,5	8

Построим график функции у = + 3. Для этого заполним таблицу:

х	-4	-3	-2	-1	0	1	2	3	4
у	11	7,5	5	3,5	3	3,5	5	7,5	11

Сравнивая формулы, получаем, что для заполнения таблицы достаточно к соответствующим значениям функции у = прибавить 3.

Значит для того, чтобы построить график функции у = + 3, надо переместить каждую точку графика функции у = на 3 единицы вверх.

Вопрос. Как можно построить график функции у = — 4?

Построение графиков функций у = , у = + 3, у = — 4 в одной системе координат, используя шаблоны.

(Обсуждения и выводы)

Вывод. График функции у = ах² + n является параболой, которую можно получить из графика функции

у = ах² с помощью параллельного переноса вдоль оси у на n единиц вверх, если n0, или на единиц вниз, если n

2) Рассмотрим функцию у = . Построим её график. Для чего составим таблицу значений функции, выбрав такие значения аргумента, которые на 5 больше соответствующих значений аргумента в таблице для функции у =

х	1	2	3	4	5	6	7	8	9
у	8	4,5	2	0,5	0	0,5	2	4,5	8

Значения аргумента увеличились на 5, а значения функции остались прежними.

Значит для того, чтобы построить график функции у = , надо переместить каждую точку графика функции у = на 5 единицы вправо вдоль оси х.

Вопрос. Как можно построить график функции у = ?

Построение графиков функций у = , у = , у = в одной системе координат, используя шаблоны.

(Обсуждения и выводы)

Вывод. График функции у = a (х — m)²является параболой, которую можно получить из графика функции у = ах² с помощью параллельного переноса вдоль оси х на m единиц вправо, если m0, или на единиц влево, если m

3)Вопрос. а)Как можно построить график функции у = ?

б)Как можно построить график функции у = ?

Вывод. График функции у = a (х — m)²+ n является параболой, которую можно получить из графика функции у = ах² с помощью двух параллельных переносов: параллельного переноса вдоль оси х на m единиц вправо, если m0, или на единиц влево, если mn единиц вверх, если n0, или на единиц вниз, если n

( на практике достаточно перемещать вершину параболы соответствующего шаблона в точку с координатами (m;n))

4) Полученные нами выводы о преобразовании графиков применимы к любым функциям.

График функции у = f(x) + n можно получить из графика функции у = f(x) с помощью параллельного переноса вдоль оси у на n единиц вверх, если n0, или на единиц вниз, если n

График функции у = f(x + m) можно получить из графика функции у = f(x) с помощью параллельного переноса вдоль оси х на m единиц вправо, если m0, или на единиц влево, если m

График функции у = f(x + m) + n можно получить из графика функции у = f(x) с помощью двух параллельных переносов:

1)параллельного переноса вдоль оси х на m единиц вправо, если m0, или на единиц влево, если m

2) с помощью параллельного переноса вдоль оси у на n единиц вверх, если n0, или на единиц вниз, если n

4) Обучающая самостоятельная работа.

Постройте в одной системе координат графики следующих функций, выбрав соответствующий шаблон.

а) у = х² +1, в) у = , д) у = .

б) у = х² — 3, г) у = ,

Проверить работу по готовым чертежам с помощью мультимедийного проектора.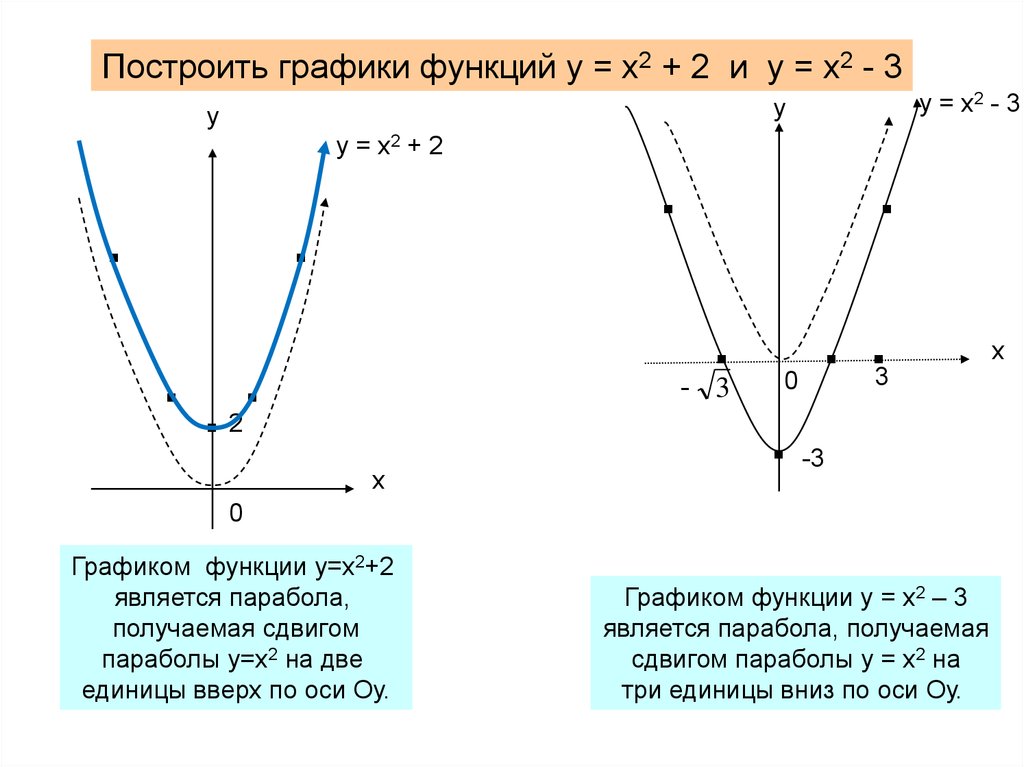

4. Выполнение упражнений №108, 110(письменно), 116 (устно)

6. Д/з п.6, №107, 111,113, 235^*.

НОУ ИНТУИТ | Лекция | Графика

< Лекция 2 || Лекция 3: 123456 || Лекция 4 >

Аннотация: В лекции представлены методы построения типичных графиков функций на плоскости и в пространстве, а также инструменты их редактирования, форматирования и настройки. Описаны разные технологические приемы построения графиков функций: автоматически, с помощью сетки и с применением специальных функций.

Ключевые слова: программа, координаты, панель инструментов, графика, меню, список, шаблон, прямоугольник, имя функции, курсор, область определения, функция, график, множества, значение, опция, радиус, массив

Цель лекции. Научить строить графики функций в разных системах координат с помощью различных технологических приемов. Показать способы форматирования и настройки разных типов графиков и диаграмм.

3.1. Инструменты графики

MathCAD предоставляет широкие возможности для построения графиков. Графические построения являются универсальными и легкими в использовании. Программа позволяет строить графики на плоскости и в трехмерном пространстве. Можно использовать декартовы и полярные координаты на плоскости, сферическую и цилиндрическую систему координат в пространстве.

Панель Математика содержит панель инструментов графики. Для построения графиков используются шаблоны. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения графика того или иного вида достаточно задать тип графика. На панели Graph (Графика) или в меню Insert/ Graph (Вставка/Графика) содержится список из семи основных типов графиков.

Рис.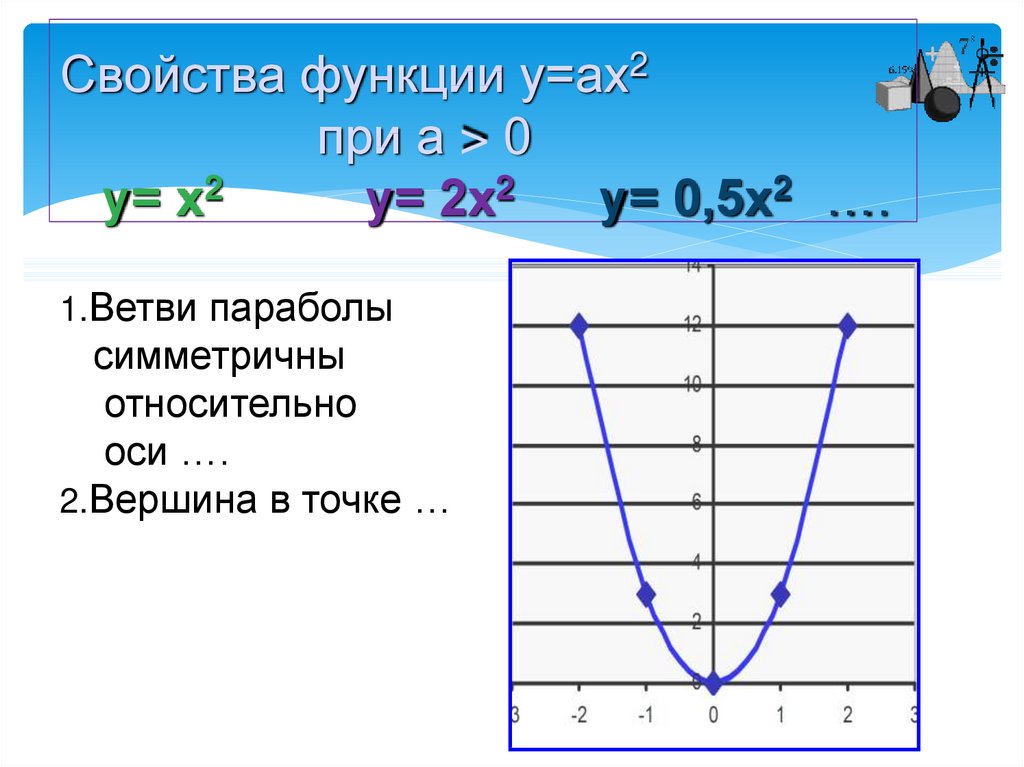 3.1. Панель Графика

Декартов график [@] —шаблон двухмерного графика;
Полярный график [Ctrl+ 7] —шаблон графика в полярной системе координат;

График поверхности [Ctrl+ 2] — шаблон для построения трехмерного графика;
Карта линий уровня [Ctrl+ 5] —шаблон для контурного графика трехмерной поверхности;
3D точечный график –шаблон для графика в виде точек в трехмерном пространстве;
3D столбиковая гистограмма –шаблон для изображения в виде совокупности столбиков в трехмерном пространстве;
Векторное поле— создать шаблон для графика векторного поля на плоскости.

intuit.ru/2010/edi»>Для вывода шаблона двухмерной графики в декартовой системе координат служит кнопка декартов график на панели

Graph [3, 8]. Она выводит в текущее положение курсора шаблон графиков в декартовых координатах (Рис.3.2). Незаполненный шаблон графика — пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика.
Рис. 3.2. Шаблон графика в декартовых координатах
В средние шаблоны данных надо поместить имя функции F(x) оси абсцисс x. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически.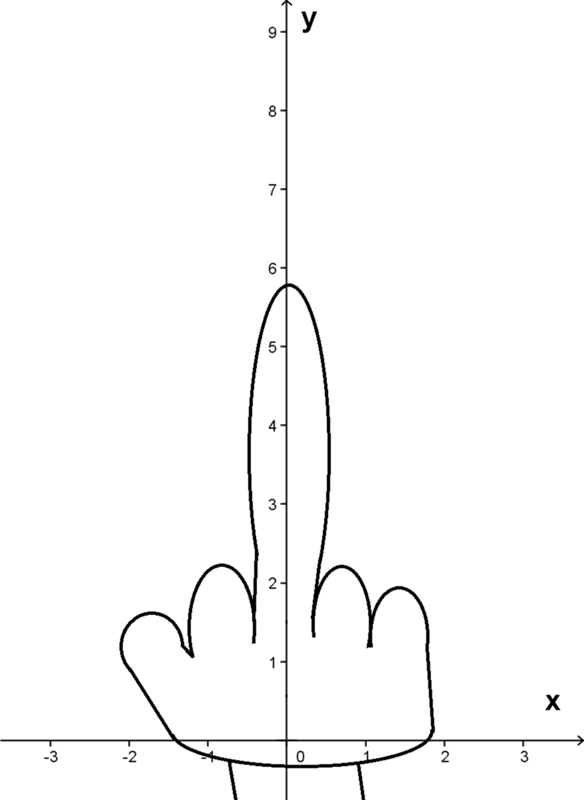
Масштабы, могут оказаться неудобными для представления целиком всего графика в максимальном размере. Рекомендуется всегда вначале использовать автоматическое масштабирование, а затем изменять масштабы на более подходящие. Для построения графика достаточно вывести курсор за пределы графического объекта.
3.2. Построение графиков функций на плоскости
Для построения графика функции надо написать функцию, выбрать интервалы построения графика по оси X и Y и обозначить параметры графика. При этом следует учитывать область допустимых значений существования функции или область определения. Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл. График функции может быть представлен в различных системах координат. Наиболее употребительна прямоугольная координатная система – декартова. На плоскости применяют полярные системы координат, а в пространстве, наряду с декартовыми, цилиндрические и сферические системы координат.
3.2.1.Декартов график
Пример 3.1. Построить графики функций : , , . Функция не существует в точке . Но график строится и никаких дополнительных действий предпринимать не нужно. В отличие от построения графиков поверхности. Но эту проблему рассмотрим ниже.
Построение графика
Форматирование графика
Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) можно изменить, вызвав команду меню Format/Graph/X-Y Plot (Формат/График/декартов график) или щелкнув дважды по полю графика. Появится окно Formatting Currently Selected X-Y Plot (Форматирование выбранного графика), в котором устанавливаются настройки в соответствующих вкладках (Рис.3.7).
Рис. 3.7. Окно форматирования декартова графика
intuit.ru/2010/edi»>Вкладка X-Y оси устанавливает для осей X и Y : тип шкалы: логарифмическая Log scale, цифровая Numbered), линии сетки (Grid Lines), Сетку автоматическую (Auto Grid) или режим задания количества меток (Number of Grid). Внизу устанавливается стиль вида осей (Axes Style)/
Вкладка Traces устанавливает условные обозначения различных кривых графика.
Вкладка Надпись (Labels) расположение надписей.
Установка границ на осях координат
MathCAD обеспечивает следующие возможности устанавливать границы на осях координат:
Автоматически, с включенным режимом Авто масштаб (Autoscale)(см. закладка » X-Y Оси » ).
Автоматически, с выключенным режимом Авто масштаб.
intuit.ru/2010/edi»>Вручную, вводя границы непосредственно на графике.
При включенном режиме Авто масштаб MathCAD устанавливает границу на каждой оси соответствующей первому главному делению, выходящему за пределы значений данных
При выключенном режиме Авто масштаб MathCAD устанавливает границы на осях точно равными пределам данных.
Добавление горизонтальных и вертикальных линий
Чтобы добавить горизонтальную или вертикальную линию к графику:
вызвать окно форматирования графика в декартовых координатах,
в диалоговом окне Форматирование— закладка

» X-Y Оси » ,
щёлкнуть » Нанести риски » (для X-оси, или Y-оси). MathCAD показывает два дополнительных пустых поля на каждой оси, для которой включена опция » Нанести риски «,
intuit.ru/2010/edi»>впечатать значение, для которого нужно провести линию,
чтобы удалить линию, удалить это число или щёлкните на поле » Нанести риски «
Дальше >>
< Лекция 2 || Лекция 3: 123456 || Лекция 4 >
Памятка по квадратичным функциям
— заполнить и подписать шаблон для печати онлайн
Мы используем файлы cookie для повышения безопасности, персонализации взаимодействия с пользователем, улучшения нашей маркетинговой деятельности (включая сотрудничество с нашими маркетинговыми партнерами) и для других целей бизнеса.
Нажмите «здесь», чтобы ознакомиться с нашей Политикой использования файлов cookie. Нажимая «Принять», вы соглашаетесь на использование файлов cookie. Читать меньше

Читать дальше
Принять
Загрузка
Три квадратные формы Используйте только электронный граф для проверки своих ответов! Факторная форма 1.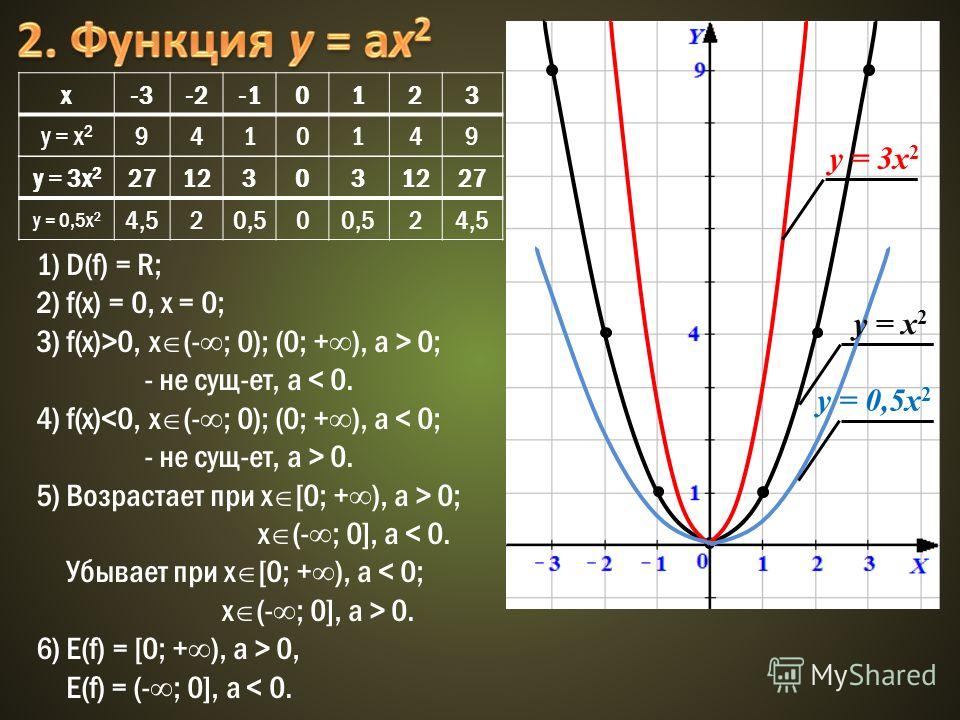 Для функции y 2 (x + 3) (x 4): а. Каковы корни (х-перехваты)? (Подсказка: какое значение.
Как это работает
Открыть форму следуйте инструкциям
Легко подпишите форму пальцем
Отправить заполненную и подписанную форму или сохранить
рейтинг шпаргалки по квадратике
★ ★ ★ ★ ★
★ ★ ★ ★

★ ★ ★
★ ★
★
4. 8Доволен
54 голоса
Как заполнить и подписать шпаргалку по квадратным уравнениям онлайн?
Получите онлайн-шаблон и заполните его, используя прогрессивные функции. Наслаждайтесь умными заполняемыми полями и интерактивностью. Следуйте простым инструкциям ниже:
Подготовка законных документов может быть дорогостоящей и занимать много времени. Однако с нашими предварительно разработанными веб-шаблонами все становится проще. Теперь для работы со шпаргалкой по квадратичным функциям требуется не более 5 минут. Наши государственные веб-заготовки и кристально чистые инструкции устраняют ошибки, связанные с человеческим фактором.

Следуйте нашим простым инструкциям, чтобы быстро подготовить шпаргалку по квадратичным функциям:
Найдите веб-образец в каталоге.
Введите всю необходимую информацию в необходимые поля. Простой в использовании пользовательский интерфейс с функцией перетаскивания упрощает добавление или перемещение полей.
Убедитесь, что все выполнено правильно, без опечаток и пропусков блоков.
Примените электронную подпись к странице.
Просто нажмите Готово для подтверждения настроек.
Сохраните документ или распечатайте копию.
Немедленно отправить получателю.
Воспользуйтесь быстрым поиском и мощным облачным редактором, чтобы создать правильную шпаргалку по квадратичным функциям. Избавьтесь от рутины и оформляйте документы онлайн!
Получить форму
Попробуйте более быстрый способ заполнения и подписания форм в Интернете. Получите доступ к самой обширной библиотеке доступных шаблонов.
Ax2 Сопутствующее содержимое
Памятка по решению квадратных уравнений — CA.gov
Скачать бесплатно. Решение квадратного уравнения. Уравнения Чит. Лист. В конце концов, вы…
Учить больше
«Шпаргалка» — Квадратика
«Справочный лист» — Квадратика. Общая форма: ax + bx + c = 0 См. также: f(x) = ax2 +…
Учить больше
Обозначение Big O — Википедия
Обозначение Big O — это математическое обозначение, описывающее предельное поведение…
Учить больше
Форма ссылок по теме
Получите эту форму сейчас!
Используйте профессиональные готовые шаблоны, чтобы быстрее заполнять и подписывать документы онлайн. Получите доступ к тысячам форм.
Ключевые слова, относящиеся к шпаргалкам по квадратичным функциям
Пиччиотто
MathEducationСтраница
х-перехватов
6e
принтер
ХР
4ас
акс2
БС
ВЕРТЕКС
неравенство
Квадратичный
пересекается с
хитрый
факторинг
Если вы считаете, что эту страницу следует удалить, следуйте нашей процедуре удаления DMCA здесь.
Обеспечьте безопасность ваших данных и транзакций
USLegal соответствует ведущим в отрасли стандартам безопасности и соответствия требованиям.
VeriSign защищен
#1 Знак безопасности, которому доверяют в Интернете. Гарантирует, что веб-сайт свободен от вредоносных атак.
Аккредитованный бизнес
Гарантирует, что бизнес соответствует стандартам аккредитации BBB в США и Канаде.
TopTen Отзывы
Самые высокие отзывы клиентов на одной из самых надежных платформ обзора продуктов.
Квадратичные функции Поиск слов — WordMint
Что такое поиск слов?
Поиск слов — это головоломка, в которой ряды букв расположены в форме квадрата, а слова написаны вперед, назад, по горизонтали, вертикали или диагонали. Будет список слов, которые игрок должен искать, и цель игрока — найти эти слова, скрытые в головоломке поиска слов, и выделить их.
Как выбрать слова для поиска слов?
Выбрав тему, выберите слова разной длины, уровня сложности и букв. Вам не нужно беспокоиться о том, чтобы сопоставить слова друг с другом, потому что WordMint сделает это за вас!
Как поиск по словам используется в классе?
Игры на поиск слов — отличный инструмент для учителей и отличный ресурс для учащихся. Они помогают расширять словарный запас, а также проверяют когнитивные способности и навыки поиска закономерностей.
Поскольку шаблоны поиска слов полностью индивидуальны, вы можете создавать подходящие поисковые запросы для детей в детском саду, вплоть до студентов колледжей.
Кому подходит поиск по словам?
Один из часто задаваемых вопросов по поиску слов касается того, существуют ли возрастные ограничения и дети какого возраста могут начинать поиск слов. Фантастическая вещь в упражнениях по поиску слов заключается в том, что они полностью гибкие для любого возраста или уровня чтения, которые вам нужны.
При поиске слова можно использовать любое слово, большое или маленькое, поэтому существует буквально бесчисленное множество комбинаций, которые вы можете создавать для шаблонов. Шаблон легко настроить в соответствии с возрастом или уровнем обучения ваших учеников.
Как создать шаблон поиска слов?
Для самых простых шаблонов поиска по словам подойдет WordMint!
Готовые шаблоны
Чтобы быстро получить готовый шаблон, просто выполните поиск среди более чем 500 000 существующих шаблонов WordMint. Из такого большого выбора вы обязательно найдете то, что подходит именно вам!
Создайте свою учетную запись с нуля
Войдите в свою учетную запись (присоединение бесплатно!)
Перейти к «Моим головоломкам»
Нажмите «Создать новую головоломку» и выберите «Поиск слов».
No related posts.