Схема горнера калькулятор: Метод Горнера. Деление многочлена онлайн

Метод Горнера. Деление многочлена онлайн

Коэффициенты многочлена разделенные пробелами

Коэффициент C в биноме вида x-C

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

Рассмотрим процедуру деления многочлена вида

 

на бином вида  

результат  деления  есть функция вида

Такой результат получается  только в  результате деления исходного  многочлена на бином без остатка.

В общем же случае говорится, что функцию   можно  представить в виде 

где r — это остаток от деления.

Коэффициенты функции   рассчитываются по рекуррентным формулам

 

Схема Горнера очень удобна своей простой и отсутствием функции деления.

 Это позволяет решать с повышенной точностью подобные уравнения, а также решать целочисленные уравнения, без каких либо машинных(компьютерных) погрешностей.

Кстати!

Есть новый калькулятор который осуществляет деление многочлена на многочлен с остатком . Работает в том числе и в комплексном поле, кроме того, делящий многочлен может быть на самом деле многочленом(!), а не биномом, как в этой статье.

Кроме  этого, эта же схема позволяет решать задачу  определения значения функции при каком либо значении. «Фи!» — скажете Вы. «Это же элементарно, любой калькулятор это может».

 

да конечно, поставивив вместо неизвестного x необходимое значение мы получим нам нужный результат, но какой ценой?

Нам придется  возводить значения в степень, что несомненно внесет свою погрешность в расчеты.

Это  явно проявляется при работе в поле комплексных чисел, при делении многочлена на комплексный бином.

Нам проще воспользоватся теоремой Безу, которая гласит: Остаток r от деления многочлена на   на линейный двучлен  равен значению многочлена  при 

Бот созданный на этом сайте, позволяет Вам решать  поставленную задачу методом Горнера, не только для действительных чисел, но и для комплексных.  Это расширяет возможности применения бота и позволяет более полно исследовать функцию.

Если делящий многочлен не является одночленом, то стоит воспользоватся калькулятором который делит произвольные многочлены друг на друга с вычислением остатка.Деление многочлена на многочлен.Division of complex polynomialsТеперь рассмотрим  примеры.

  разделить с остатком  

Пишем коэффициенты 2 0 -3 2 и через точку запятой -2. Надеюсь понятно почему пишем -2, а не+2 ?

Получаем ответ

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

 

Следующий пример  исходный полином тот же, но значение С будет комплексным например 1+i

Пишем коэффициенты 2 0 -3 2 и через точку запятой 1+i

Получаем

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

 

Таким образом мы можем писать любые значения, в том числе и комплексные,  в коэффицентах как делимого полинома так и делящего бинома

Удачных расчетов!

Схема Горнера

Обычно многочлен представлен в виде:

$f(x)=\sum\limits_{k=0}^{n} a_k x^k$

или

f(x) = a₀ + a₁x + a₂x² + . .. + a_kx^k

Где a_k это действительные числа, представляющие коэффициенты многочлена и
x^k это переменные многочлена.

Вышеупомянутый многочлен называют многочленом n^-ой степени, то есть deg(f(x)) = n, где n представляет наивысшую степень переменной.

Схема Горнера для деления многочлена — это алгоритм упрощения вычисления значения многочлена f(x) при определённой величине x = x₀ методом деления многочлена на одночлены (многочлены 1^ой степени). Каждый одночлен включает в себя максимум один процесс умножения и один процесс сложения. Результат, полученный из одного одночлена, прибавляют к результату полученному от следующего одночлена и так далее в аккумулятивной манере. Такой процесс деления также называют синтетическим делением.

Чтобы объяснить вышесказанное, давайте перепишем многочлен в развёрнутой форме;

f(x₀) = a₀ + a₁x₀ + a₂x₀² + . .. + a_nx₀ⁿ

Это также может быть записано как:

f(x₀) = a₀ + x₀(a₁ + x₀(a₂ + x₀(a₃ + … + (a_n-1 + a_nx₀)….)

Алгоритм, предложенный данной схемой, основан на нахождении значений одночленов образованных выше, начиная с тех которые заключены в больше скобок и двигаясь наружу, для нахождения значения одночленов во внешних скобках.

Алгоритм приводится в действие, следуя нижеизложенным шагам:

1. Дано k = n
2. Пусть b_k = a_k
3. Пусть b_{k — 1} = a_{k — 1} + b_kx₀
4. Пусть k = k — 1
5. Если k ≥ 0, то вернуться на шаг 3
иначе Конец

Этот алгоритм может быть также графически визуализирован, принимая во внимание данный многочлен 5^ой степени:

f(x) = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴ + a₅x⁵

значение которого находится как x = x₀, путём перестановки его следующим образом:

f(x₀) = a₀ + x₀(a₁ + x₀(a₂ + x₀(a₃ + x₀(a₄ + a₅x₀))))

Другим способом представить результаты используя этот алгоритм можно в виде данной ниже таблицы:

K	5	4	3	2	1	0
	b5 = a5	b4 = a4 + x0b5	b3 = a3 + x0b4	b2 = a2 + x0b3	b1 = a1 + x0b2	b0 = a0 + x0b1

Пример: Найти значение многочлена f(x) = x⁴ + 3x³ + 5x² + 7x + 9 at x = 2

Решение:

Так как многочлен 4^ой степени, то n = 4

K	4	3	2	1	0
Шаг	b4 = 1	b3 = 3 + 2 * 1	b2 = 5 + 2 * 5	b1 = 7 + 2 * 15	b0 = 9 + 2 * 37
Результат	1	5	15	37	83

Таким образом, f(2) = 83.

Почему нам это необходимо делать?

Обычно, находя значения многочлена при определённом значении переменной, мы привыкли подставлять это значение в многочлен и производить вычисления. Мы также можем разработать копьютерную программу для математического вычисления, которая является необходимостью, когда мы имеем дело со сложными многочленами высоких степеней.

Метод, с помощью которого компьютер обрабатывает проблему, зависит, в основном, от того как Вы, как программист, описываете это компьютеру. Вы можете разработать Вашу программу для нахождения значения многочлена методом прямой подстановки значения переменной или использовать синтетическое деление, данное в схеме Горнера. Единственное отличие между этими двумя подходами это скорость, с которой компьютер будет находить решение том или ином случае.

Преимущество схемы Горнера в том, что оно снижает количество операций умножения. Принимая во внимание то, что время обработки каждого процесса умножения от 5 до 20 раз больше, чем время обработки процесса сложения, Вы можете утверждать, что построение программы для нахождения значения многочлена по схеме Горнера существенно уменьшит затрачиваемое компьютером время вычисления.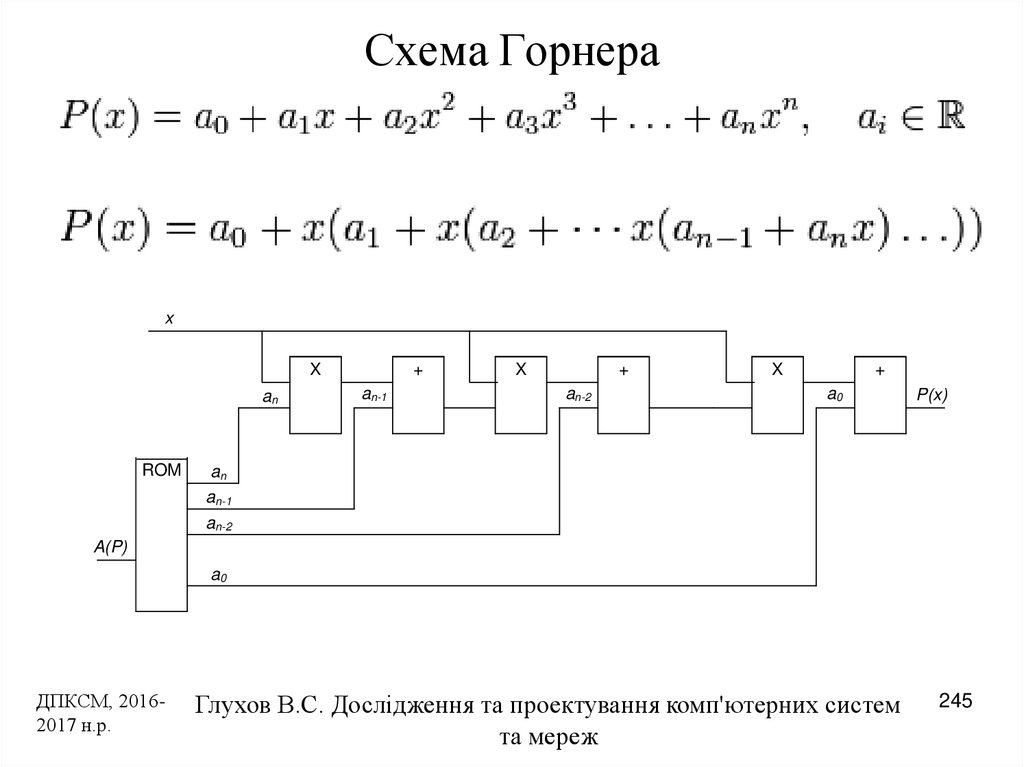

Калькулятор деления полиномов

Метод Хорнера онлайн калькулятор — AbakBot-онлайн калькуляторы

Коэффициенты полинома деленные на разрывы

Коэффициент C в виде бинома X-C

9 0003

Многочлен множества имеет вид

, если разделить его на

Получим многочлен 9{n-3}+…..+b_{n-2}x+b_{n-1}$$ Такой результат получается только путем деления исходного полинома на бин без остатка. В общем случае говорят  , что функция  $$f(x)$$  может быть представлена ​​в виде  $$f(x)=q(x)(x-c)+r$$ , где r  – остаток от деления. Функциональные коэффициенты, рассчитанные по рекуррентным формулам $$b_0=a_0\\b_1=cb_0+a_1\\…\\b_{n-1}=cb_{n-2}+a_{n-1}] $$  $$r=cb_{n-1}+a_n$$ Схема Горнера очень удобна своей простотой и отсутствием функции деления. Это позволяет решать подобные уравнения с повышенной точностью, а также решать целочисленные уравнения, без каких-либо машинных (компьютерных) ошибок. Кстати! Появился новый калькулятор, который делит многочлен на многочлен с остатком.   Работает и в сложном поле, кроме того, делящий многочлен может быть действительно многочленом (!), а не двучленом, как в этой статье. Кроме того, эта же схема позволяет решить задачу определения значения функции для любого значения. «Фай!» — ты говоришь. «Это элементарно, любой калькулятор может это сделать».   да конечно, поставив вместо неизвестного x нужное значение, мы получим желаемый результат, но какой ценой? Придется возводить значения в степень, что несомненно внесет свою погрешность в расчеты. Это ярко проявляется при работе в области комплексных чисел, при делении многочлена на комплексный бин. Нам проще использовать Безу теорему , которая гласит: Остаток r  от деления многочлена на 9006 8 на линейном биноме  $$x-c$$  равно значению полином at Бот, созданный на этом сайте, позволяет решить задачу методом Горнера не только для действительных чисел, но и для комплексных. Это расширяет область применения бота и позволяет более полно изучить функцию. 91+(-3+4i)$$

и остаток

$$r=-5+i$$

 

Таким образом, в коэффициенты делимого многочлена и делящего двучлена можно записать любые значения, в том числе и комплексные

Удачи!

 

python — Вычисление обратных тригонометрических функций с помощью формул

Вопрос широк, но вот несколько простых идей (и код!), которые могут послужить отправной точкой для вычислений арктан . Во-первых, старый добрый сериал о Тейлоре. Для простоты мы используем фиксированное количество терминов; на практике вы можете захотеть определить количество терминов для динамического использования на основе размера x или ввести какой-либо критерий сходимости. При фиксированном количестве терминов мы можем эффективно оценивать, используя что-то вроде схемы Хорнера.

 def arctan_taylor(x, terms=9):
    """
    Вычислите arctan для малых x с помощью полиномов Тейлора. 
    Использует фиксированное количество терминов. По умолчанию 9должны дать хорошие результаты для
    абс(х) < 0,1. Результаты будут ухудшаться по мере увеличения abs(x), становясь
    непригодным для использования, поскольку abs(x) приближается к 1,0 (радиус сходимости
    ряд).
    """
    # Использует метод Хорнера для оценки.
    т = 0,0
    для n в диапазоне (2 * термины-1, 0, -2):
        т = 1,0/n - х*х*т
    вернуть х * т
 

Приведенный выше код дает хорошие результаты для небольших x (скажем, меньше, чем 0,1 по абсолютной величине), но точность падает при x 92))) . Это дает следующий код, основанный на arctan_taylor , чтобы дать приемлемые результаты для широкого диапазона

x (но остерегайтесь возможного переполнения и потери значимости при вычислении x*x ).

 импорт математики
def arctan_taylor_with_reduction(x, terms=9, threshold=0.1):
    """
    Вычислите арктангенс с помощью сокращения аргумента и ряда Тейлора. 
    Применяет шаги сокращения до тех пор, пока x не станет ниже «порога»,
    затем использует ряд Тейлора.
    """
    сокращения = 0
    в то время как абс (х)> порог:
        х = х / (1 + math.sqrt (1 + х * х))
        сокращения += 1
    return arctan_taylor(x, terms=terms) * 2**сокращения
 

В качестве альтернативы, учитывая существующую реализацию для tan , вы можете просто найти решение y уравнения tan(y) = x , используя традиционные методы поиска корня. Поскольку arctan уже естественным образом ограничен интервалом (-pi/2, pi/2)

, поиск пополам работает хорошо:

 def arctan_from_tan(x, допуска=1e-15):
    """
    Вычислите arctan как инверсию tan с помощью поиска пополам. Это предполагает
    что у вас уже есть высококачественная функция загара.
    """
    низкий, высокий = -0,5 * math.pi, 0,5 * math.pi
    в то время как высокий - низкий > допуск:
        средний = 0,5 * (низкий + высокий)
        если math. tan(mid) < x:
            низкий = средний
        еще:
            высокий = средний
    возврат 0,5 * (низкий + высокий)
 

Наконец, просто для удовольствия, вот реализация, подобная CORDIC, которая действительно больше подходит для низкоуровневой реализации, чем для Python. Идея здесь состоит в том, что вы предварительно вычисляете раз и навсегда таблицу значений арктангенса для 1 , 1/2, 1/4, и т. д., а затем используете их для вычисления общих значений арктангенса, в основном путем вычисление последовательных приближений к истинному углу. Примечательно то, что после этапа предварительного вычисления вычисление арктангенса включает только сложения, вычитания и умножения на степени двойки. (Конечно, эти умножения не более эффективны, чем любое другое умножение на уровне Python, но ближе к оборудованию это может иметь большое значение.)

 Cordic_table_size = 60
cordic_table = [(2**-i, math.atan(2**-i))
 для i в диапазоне (cordic_table_size)]
def arctan_cordic (у, х = 1,0):
 """
 Вычислите arctan(y/x), считая x положительным, с помощью метода, подобного CORDIC.
No related posts.