Векторы формулы 11 класс: Координаты точки и вектора — урок. Геометрия, 11 класс.

Скалярное произведение векторов

Урок 6. Геометрия 11 класс ФГОС

Этот урок посвящён скалярному произведению двух векторов, в том числе правилу вычисления скалярного произведения двух векторов в координатах. Проводится анализ формулы вычисления скалярного произведения, в результате которого выделяют несколько частных случаев. Так же учащиеся вспомнят понятие скалярного квадрата вектора и правило его вычисления.

Конспект урока «Скалярное произведение векторов»

Вы уже знакомы с понятием угла между векторами в пространстве. Поэтому на этом уроке мы приступим к рассмотрению скалярного произведения векторов в пространстве.

Как и на плоскости, скалярное произведение двух векторов в пространстве равно произведению длин этих векторов на косинус угла между ними.

Задание: по рисунку определить величину угла между векторами.

Рассмотрим куб АBCDА₁B₁C₁D₁

, сторона которого равна a, а точка О₁ — центр грани А₁B₁C₁D₁.

Мы с вами выполнили задание, где нашли скалярное произведение данных пар векторов.

Можно заметить, что, если угол между векторами острый, то скалярное произведение больше нуля. А если угол между векторами тупой, то их скалярное произведение меньше нуля. И только лишь когда векторы перпендикулярны, их скалярное произведение равно нулю. В данном случае, конечно, имеется в виду, что рассматриваемые векторы ненулевые.

А сейчас попробуем разобраться, как находить скалярное произведение векторов по их координатам.

На плоскости скалярное произведение двух векторов равнялось сумме произведений соответствующих координат. В пространстве имеет место такая же формула.

Задание: по координатам векторов ,  и  найти значения выражений: , , , , .

Решение:

Задание: пользуясь координатами векторов , , , выяснить, каким является угол между парами векторов: острым, прямым или тупым.

а)                             б)                             в)

Решение:

Итак, мы узнали и использовали 2 формулы скалярного произведения.

Выразив из первой формулы косинус угла между векторами, скалярное произведение можно расписать по второй формуле. А вот длины векторов запишем как корни квадратные из сумм квадратов их соответствующих координат.

Так мы получили формулу вычисления косинуса угла между векторами по их координатам.

Задание: найти угол между векторами  и .

а) , , б) , , в) , , г) , , д) , .

Решение:

Стоит отметить, что для скалярного произведения векторов в пространстве справедливы те же свойства, что и для скалярного произведения на плоскости.

Скалярный квадрат вектора всегда больше либо равен нулю.

; , если

А также можно записать переместительный, распределительный и сочетательный законы скалярного произведения. Они позволят в будущем преобразовывать выражения с векторами.

 (переместительный закон)

 (распределительный закон)

 (сочетательный закон)

Итоги:

На этом уроке мы сформулировали определение скалярного произведения двух векторов в пространстве, записали формулу вычисления скалярного произведения векторов по их координатам и получили формулу вычисления косинуса угла между двумя векторами. Помимо этого, для скалярного произведения в пространстве имеют место те же свойства, что и на плоскости.

Предыдущий урок 5 Угол между векторами

Следующий урок 7 Вычисление углов между прямыми и плоскостями

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 11 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Простейшие задачи в координатах 11 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Мы уже ввели понятие системы координат в пространстве, а также задали основные связанные с ней термины. Рассмотрим простейшие, базовые задачи в координатах, на которых в дальнейшем будет строиться решение большинства задач.

 

 

Задача.

Нахождение координат середины отрезка

 

 

Дано: ; ,  – се­ре­ди­на . Найти: .

 

Ре­ше­ние: Обо­зна­чим в про­стран­стве точки  и  – се­ре­ди­ну от­рез­ка . (См. Рис. 1.)

Рис. 1. Ввели систему координат

Век­тор  яв­ля­ет­ся по­ло­ви­ной суммы век­то­ров и , по­то­му что  – это по­ло­ви­на диа­го­на­ли па­рал­ле­ло­грам­ма, по­стро­ен­но­го на век­то­рах  и . (См. Рис. 2.)

Рис. 2. Использование правила параллелограмма

Так как  и , и  (по правилу параллелограмма),

то значит:

Осталось заметить, что координаты точки  совпадают с координатами вектора , так как  – начало координат. То есть .

Таким образом, координаты середины отрезка есть полусуммы соответствующих координат его концов.

Можно было действовать и иначе: . Координаты вектора  мы знаем, значит, можем найти координаты вектора , а отсюда, зная координаты начала этого вектора  находим координаты конца – .

Ответ: .

 

Задача (координаты точки на отрезке)

 

 

Пусть даны две точки: ; , точка  делит отрезок  в отношении  от вершины . Найти: . (См. Рис. 3.)

 

Рис. 3. Иллюстрация к условию задачи

Решение

Если , то мы получаем тот самый случай, который мы уже разобрали, то есть деление в отношении  или середину отрезка.

Как мы будем находить координаты точки ? Заметим, что векторы  и  сонаправлены. Значит, они отличаются в константу раз, причем эту константу мы знаем. Ведь на весь отрезок  приходится  частей, а на отрезок  –  частей.

Значит, вектор .

Так как , то .

Но тогда координаты точки  находятся как сумма соответствующих координат вектора  и точки . Найдем абсциссу, остальное – аналогично.

.

Значит,  имеет координаты:

 

Разберем пример: , . Найти координаты точки , если . (См. Рис. 4.)

Рис. 4. Иллюстрация к примеру

Решение: по нашим формулам: С.

Ответ: .

 

Задача. Длина вектора

 

 

Пусть дан век­тор . Тогда: .

 

Доказательство

Чтобы вывести эту формулу, рассмотрим прямоугольный параллелепипед с измерениями ,  и . (См. Рис. 5.)

Рис. 5. Иллюстрация к доказательству

Тогда вектор , так как их координаты попарно равны. (См. Рис. 6.)

Рис. 6.

Значит, , где  – диагональ параллелепипеда. Но диагональ прямоугольного параллелепипеда равна корню из суммы квадратов его измерений (по свойству): , что и требовалось доказать.

Коротко напомним: достаточно рассмотреть теоремы Пифагора для треугольника в основании параллелепипеда (таким образом найдем диагональ основания ) и затем для треугольника . (См. Рис. 7.)

 

Рис. 7. Как найти диагональ параллелепипеда

Следствие. Как вы помните, координаты вектора – это разность координат его конца и начала. То есть если ; , то . Тогда получим, что .

 

Задачи на использования выведенных формул

 

 

Задача 1. Найти длину медианы  треугольника , где , , .

 

Решение. Найдем координаты точки  – середины отрезка . По формуле нахождения координат середины отрезка  получаем, что .

По формуле нахождения длины вектора  получаем, что .

Ответ: .

Задача 2. Определите вид треугольника  и найдите его периметр, если , , .

Решение. По формуле , найдем длины ,  и :

 

Значит, треугольник равнобедренный, т. к. .

.

Тогда периметр .

Ответ: треугольник равнобедренный; .

 

Заключение

 

 

На этом уроке были разобраны три классические задачи координатного метода в стереометрии: мы научились находить координаты середины отрезка по координатам его концов: , длину вектора и, как следствие, длину любого отрезка: .

 

 

Список литературы

1. Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
3. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия. 11 класс. Рабочая тетрадь. 8-е изд. – М.: Просвещение, 2013. – 78 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Yaklass.ru (Источник).
2. Cleverstudents.ru (Источник).
3. Cleverstudents.ru (Источник).

 

Домашнее задание

1. Найти координаты точки  если известны координаты точки , середины отрезка  и точки .
2. Вычислить длину вектора , если даны точки  и .
3. Вычислить длину вектора , если ; ; .

 

Формула результирующего вектора — GeeksforGeeks

В математике мы часто слышали о двух терминах скаляр и вектор. Скаляр — это величина, которая имеет только величину, т.е. скалярная величина описывает расстояние. С другой стороны, Вектор — это величина, которая имеет дело как с величиной, так и с направлением. Векторная величина имеет как величину, так и направление.

Формула результирующего вектора дает результирующее значение двух или более векторов. Результат получается путем вычисления векторов с учетом направления каждого вектора по отношению к другим. Эта формула имеет различные приложения в технике и физике. В зависимости от направления вектора относительно других векторов формула результирующего вектора подразделяется на три типа.

Результирующий вектор 1-я формула

Если векторы имеют одинаковое направление, то результирующая вектора может быть вычислена путем сложения векторов, направленных в одном направлении. Пусть « a» и « b» — векторы с одинаковым направлением, тогда результирующий вектор « r» определяется как-

r = а + б

Результирующий вектор 2-я формула

Если векторы разнонаправлены, то результирующий вектора можно вычислить путем вычитания векторов друг из друга. Пусть » b» вектор, противоположный вектору » a» , тогда результирующий вектор » р» дается по-

г = а – б

Результирующий вектор 3-я формула

Если какие-либо векторы наклонены друг к другу под некоторым углом, то по этой формуле можно вычислить равнодействующую этих векторов. Пусть «а» и «b» — два вектора, наклоненные друг к другу под углом θ , тогда результирующий вектор «r» равен: + b ² + 2abcosθ

Здесь a ² , b ² представляет модуль вектора a, b.

Представление результирующего вектора

Примеры задач

Вопрос 1. Найдите результирующий вектор для векторов i+2j+3k и 4i+8j+12k

Решение: 900 03

Даны два вектора a= i+2j+3k и b=4i+8j+12k

Отношения направлений двух векторов равны. Итак, два вектора направлены в одну сторону.

Формула результирующего вектора для заданных векторов:

r = a + b

= (i+2j+3k) + (4i+8j+12k)

= 5i+10j+15k

Результирующий вектор из данных векторов равен 5i+10j+15k

9 0007 Вопрос 2: Найдите результирующий вектор для векторов i-2j+5k и 2i-4j+10k

Решение:

Даны два вектора: a=i-2j+5k и b=2i-4j+10k

отношения направлений двух векторов находятся в равной пропорции. Итак, два вектора направлены в одну сторону.

Результирующая векторная формула для заданных векторов имеет вид-

r = a + b

= (i-2j+5k) + (2i-4j+10k)

= 3i-6j+15k

Результирующий вектор из данных векторов равен 3i-6j+15k

Вопрос 3: Найдите результирующий вектор для векторов 2i-2j+k и 2i+7j+3k

Решение:

Даны два вектора a=2i-2j+k и b= 2i +7j+3k

Отношения направлений двух векторов не равны. Итак, два вектора направлены в противоположные стороны.

Формула результирующего вектора для заданных векторов: Результирующий вектор из данных векторов равен 0i-9j-2k

Вопрос 4: Найдите результирующий вектор для векторов 9i+2j-3k и i-3j+2k

Решение:

9003 0

Дано два вектора: a=9i+2j-3k и b=i-3j+2k

Отношения направлений двух векторов не равны. Итак, два вектора направлены в противоположные стороны.

Формула результирующего вектора для заданных векторов:

r = a – b

= (9i+2j-3k) – (i-3j+2k)

= 8i+5j-5k

Результирующий вектор из данных векторов равен 8i+5j-5k

Вопрос 5: Найдите равнодействующую векторов 2i+2j+2k и i+2j+3k, наклоненных друг к другу под углом 30°.

Решение:

Даны два вектора: a=2i+2j+2k и b=i+2j+3k

92}

= \sqrt{1+4+9}

=√14

b ² =√14

r = a ² + b ^{2 900 84 + 2abcosθ}

= 2√3 + √14 + 2(2√3)(√14)cos30°

= 2√3 + √14 + 4(√3)(√14)(√3/2)

= 29,65

Результирующий вектор из заданных векторов равно 29,65

Вопрос 6: Найдите равнодействующую вектора с величиной 2, 4, наклоненного под углом 45°.

Ответ:

Дано,

Величина вектора a (a ² )=2

Величина вектора b (b ² )=4

θ = 45°

Итак результирующая векторная формула для заданных векторов имеет вид определяется как-

r = a ² + b ² + 2abcosθ

= 2+4+2(2)(4)cos45°

= 6+16×(1/√2)

9 0002 = 17.31

Результирующий вектор данных векторов равен 17.31

Величина и направление векторов

Горячая математика

Величина вектора

Величина вектора п Вопрос → это расстояние между начальной точкой п и конечная точка Вопрос . В символах величина п Вопрос → записывается как | п Вопрос → | .

Если заданы координаты начальной и конечной точек вектора, то Формула расстояния можно использовать для нахождения его величины.

| п Вопрос → | «=» ( Икс 2 − Икс 1 ) 2 + ( у 2 − у 1 ) 2

Пример 1:

Найдите величину вектора п Вопрос → чья начальная точка п Я сидел ( 1 , 1 ) и конечная точка находится в Вопрос Я сидел ( 5 , 3 ) .

Решение:

Используйте формулу расстояния.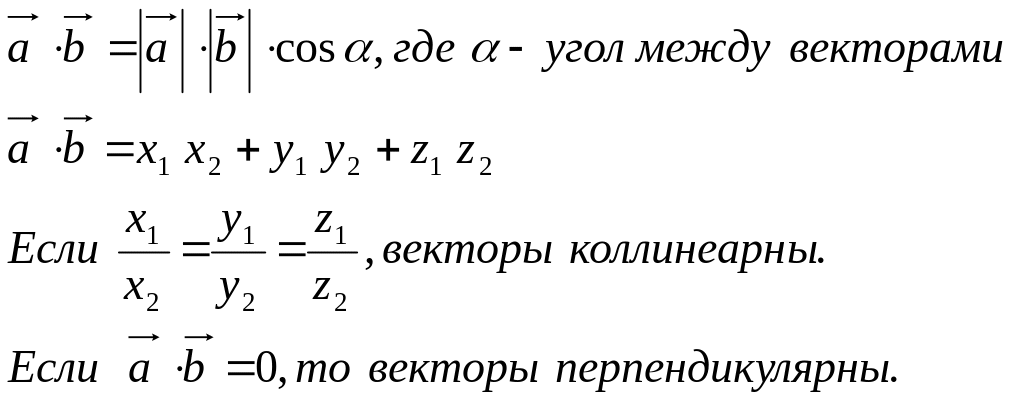

Подставьте значения Икс 1 , у 1 , Икс 2 , и у 2 .

| п Вопрос → | «=» ( 5 − 1 ) 2 + ( 3 − 1 ) 2 «=» 4 2 + 2 2 «=» 16 + 4 «=» 20 ≈ 4,5

Величина п Вопрос → около 4,5 .

Направление вектора

Направление вектора — это мера угла, который он образует с горизонтальная линия .

Для нахождения направления вектора можно использовать одну из следующих формул:

загар θ «=» у Икс , где Икс горизонтальное изменение и у вертикальное изменение

или

загар θ «=» у 2 − у 1 Икс 2 − Икс 1 , где ( Икс 1 , у 1 ) является начальной точкой и ( Икс 2 , у 2 ) является конечной точкой.

Пример 2:

Найдите направление вектора п Вопрос → чья начальная точка п Я сидел ( 2 , 3 ) и конечная точка находится в Вопрос Я сидел ( 5 , 8 ) .

Заданы координаты начальной и конечной точек. Подставляем их в формулу загар θ «=» у 2 − у 1 Икс 2 − Икс 1 .

загар θ «=» 8 − 3 5 − 2 «=» 5 3

Найдите обратный загар, затем воспользуйтесь калькулятором.