или
f(x) = a0 + a1x + a2x2 + … + akxk
Где ak это действительные числа, представляющие коэффициенты многочлена и
xk это переменные многочлена.
Вышеупомянутый многочлен называют многочленом n-ой степени, то есть deg(f(x)) = n, где n представляет наивысшую степень переменной.
Схема Горнера для деления многочлена — это алгоритм упрощения вычисления значения многочлена f(x) при определённой величине x = x0 методом деления многочлена на одночлены (многочлены 1ой степени). Каждый одночлен включает в себя максимум один процесс умножения и один процесс сложения. Результат, полученный из одного одночлена, прибавляют к результату полученному от следующего одночлена и так далее в аккумулятивной манере. Такой процесс деления также называют синтетическим делением.
Чтобы объяснить вышесказанное, давайте перепишем многочлен в развёрнутой форме;
f(x0) = a0 + a1x0 + a2x02 + . .. + anx0n
.. + anx0n
Это также может быть записано как:
f(x0) = a0 + x0(a1 + x0(a2 + x0(a3 + … + (an-1 + anx0)….)
Алгоритм, предложенный данной схемой, основан на нахождении значений одночленов образованных выше, начиная с тех которые заключены в больше скобок и двигаясь наружу, для нахождения значения одночленов во внешних скобках.
Алгоритм приводится в действие, следуя нижеизложенным шагам:
1. Дано k = n
2. Пусть bk = ak
3. Пусть bk — 1 = ak — 1 + bkx0
4. Пусть k = k — 1
5. Если k ≥ 0, то вернуться на шаг 3
иначе Конец
Этот алгоритм может быть также графически визуализирован, принимая во внимание данный многочлен 5ой степени:
f(x) = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5
значение которого находится как x = x0, путём перестановки его следующим образом:
f(x0) = a0 + x0(a1 + x0(a2 + x0(a3 + x0(a4 + a5x0))))
Другим способом представить результаты используя этот алгоритм можно в виде данной ниже таблицы:
| K | 5 | 4 | 3 | 2 | 1 | 0 |
| b5 = a5 | b4 = a4 + x0b | b3 = a3 + x0b4 | b2 = a2 + x0b3 | b1 = a1 + x0b2 | b0 = a0 + x0b1 |
Пример: Найти значение многочлена f(x) = x4 + 3x3 + 5x2 + 7x + 9 at x = 2
Решение:
Так как многочлен 4ой степени, то n = 4
| K | 4 | 3 | 2 | 1 | 0 |
| Шаг | b4 = 1 | b3 = 3 + 2 * 1 | b2 = 5 + 2 * 5 | b1 = 7 + 2 * 15 | b0 = 9 + 2 * 37 |
| Результат | 1 | 5 | 15 | 37 | 83 |
Таким образом, f(2) = 83.
Почему нам это необходимо делать?
Обычно, находя значения многочлена при определённом значении переменной, мы привыкли подставлять это значение в многочлен и производить вычисления. Мы также можем разработать копьютерную программу для математического вычисления, которая является необходимостью, когда мы имеем дело со сложными многочленами высоких степеней.
Метод, с помощью которого компьютер обрабатывает проблему, зависит, в основном, от того как Вы, как программист, описываете это компьютеру. Вы можете разработать Вашу программу для нахождения значения многочлена методом прямой подстановки значения переменной или использовать синтетическое деление, данное в схеме Горнера. Единственное отличие между этими двумя подходами это скорость, с которой компьютер будет находить решение том или ином случае.
Преимущество схемы Горнера в том, что оно снижает количество операций умножения. Принимая во внимание то, что время обработки каждого процесса умножения от 5 до 20 раз больше, чем время обработки процесса сложения, Вы можете утверждать, что построение программы для нахождения значения многочлена по схеме Горнера существенно уменьшит затрачиваемое компьютером время вычисления.
Калькулятор деления полиномов
Схема Горнера
В этой статье мы расскажем об удобной схеме решения примеров на деление многочленов. Если нам нужно вычислить коэффициент частного Pn(x)=anan+an-1xn-1+…+a1x+a0 и остаток от деления многочлена на линейный двучлен x-s, то удобно будет воспользоваться схемой (методом) Горнера.
Она заключается в создании особой таблицы и занесении в нее исходных данных:
| si | коэффициенты многочленов | ||||
| an | an-1 | an-2 | … | a0 | |
| s | an=bn | an-1+bn·s=bn-1 | an-2+bn-1·s=bn-2 | … | a0+b1·s=b0 |
Числа bn, bn-1, bn-2,…, b1 и будут нужными нам коэффициентами от деления Pn(x)=anan+an-1xn-1+…+a1x+a0 на x-s. Остаток обозначен здесь как b0. Иначе можно записать решение так:
Теперь покажем , как именно применять эту схему на практике.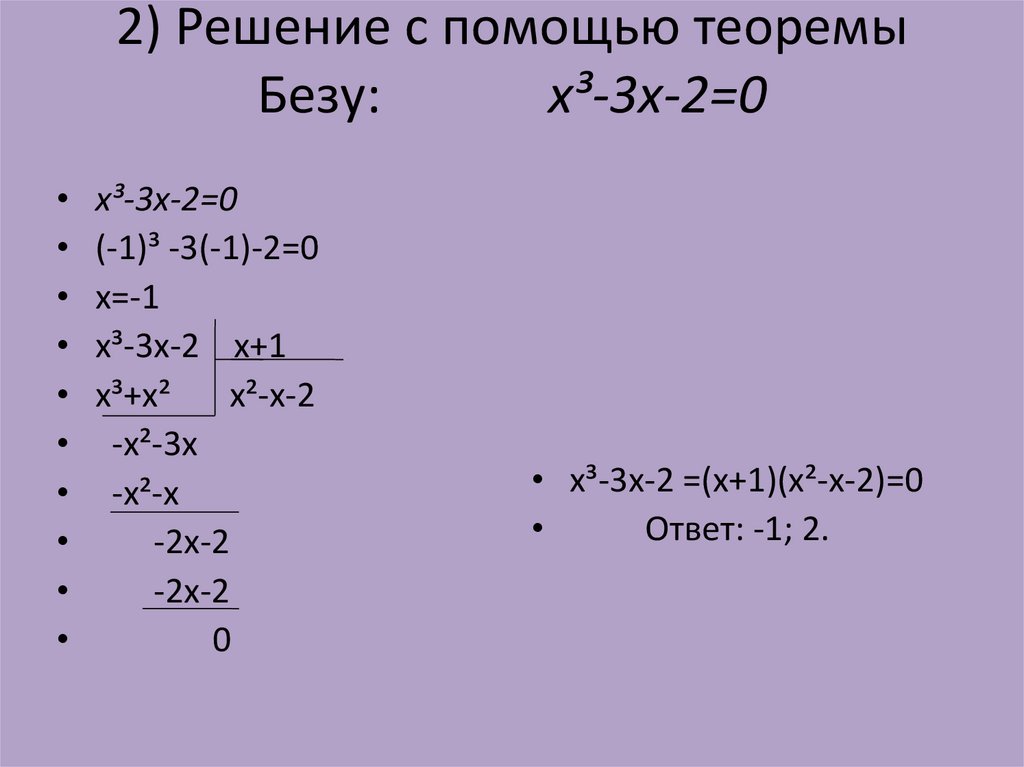
Условие: разделите многочлен 2×4-3×3-x2+4x+13 на линейный двучлен х-1, используя схему Горнера.
Решение
Заполним таблицу. У нас есть s, равный единице, и коэффициенты a4=2, a3=-3, a2=-1, a1=4, a0=13.
| si | коэффициенты многочленов | ||||
| a4=2 | a3=-3 | a2=1 | a1=4 | a0=13 | |
| s=1 | a4=2=b4 | a3+b4·s==-3+2·1==-1=b3 | a2+b3·s==-1+(-1)·1==-2=b2 | a1+b2·s=4+(-2)·1==2=b1 | a0+b1·s==13+2·1==15=b0 |
Ответ: получили частное, равное b4x3+b3x2+b2x+b1=2×3-x2-2x+2 , и остаток b0=15.
Во второй задаче мы обойдемся без подробных комментариев.
Пример 2Условие: определите, можно ли разделить многочлен 2×3-11×2+12x+9 на двучлен x+12 без остатка. Вычислите частное.
Решение
Заполним таблицу согласно схеме Горнера.
| si | коэффициенты многочленов | ||||
| 2 | -11 | 12 | 9 | ||
| -12 | 2 | -11+2·-12=-12 | 12+-12·-12=18 | 9+18·-12=0 | |
В последней ячейке мы видим нулевой остаток, следовательно, разделить исходный многочлен на двучлен можно.
Ответ: частное будет представлять из себя многочлен 2×2-12x+18.
Если b0=0, то можно говорить о делимости многочлена Pn(x)=anan+an-1xn-1+…+a1x+a0 на двучлен x-s, и мы имеем корень исходного многочлена, равный s. Используя следствие из теоремы Безу, можем представить этот многочлен в виде произведения:
Pn(x)=anan+an-1xn-1+…+a1x+a0==x-s(bnxn+1+bn-1xn-2+…+b1)
Благодаря этому схема Горнера хорошо подходит для тех случаев, когда нужно отыскать целые корни уравнений высших степеней, имеющих целые коэффициенты, или же разложить многочлен на простые множители.
Условие: решите уравнение x3-7x-6=0. Разложите многочлен слева на отдельные множители.
Решение
Мы знаем, что целые корни уравнения (если они есть) нужно искать среди делителей свободного члена. Запишем их отдельно 1, -1, 2, -2, 3, -3, 6, -6 и проверим, используя схему Горнера.
| xi | коэффициенты многочленов | ||||
| a3=1 | a2=0 | a1=-7 | a0=-6 | ||
| 1 | 1 | 0+1·1=1 | -7+1·1=-6 | -6+-6·1=-12 | |
Из данных таблицы видно, что единица не будет входить в число корней данного уравнения.
Дополним таблицу еще одним возможным корнем.
| xi | коэффициенты многочленов | ||||
| a3=1 | a2=0 | a1=-7 | a0=-6 | ||
| 1 | 1 | 0+1·1=1 | -7+1·1=-6 | -6+-6·1=-12 | |
| -1 | 1 | 0+1·(-1)=-1 | -7+-1·-1=-6 | -6+(-6)·(-1)=0 | |
А вот -1 подходит, значит, мы можем представить исходный многочлен как x3-7x-6=(x+1)(x2-x-6).
Проверяем делители дальше. Начнем с -1, поскольку возможно повторение корней, но в качестве коэффициентов будем брать значения последней строки:
| xi | коэффициенты многочленов | ||||
| a3=1 | a2=0 | a1=-7 | a0=-6 | ||
| 1 | 1 | 0+1·1=1 | -7+1·1=-6 | -6+-6·1=-12 | |
| -1 | 1 | 0+1·(-1)=-1 | -7+-1·-1=-6 | -6+(-6)·(-1)=0 | |
| -1 | 1 | -1+1·-1=-2 | -6+-2·-1=-4 | ||
Из этого следует, что -1 не будет кратным (повторяющимся) корнем. Берем следующий вариант и вычисляем:
| xi | коэффициенты многочленов | ||||
| a3=1 | a2=0 | a1=-7 | a0=-6 | ||
| 1 | 1 | 0+1·1=1 | -7+1·1=-6 | -6+-6·1=-12 | |
| -1 | 1 | 0+1·(-1)=-1 | -7+-1·-1=-6 | -6+(-6)·(-1)=0 | |
| -1 | 1 | -1+1·-1=-2 | -6+-2·-1=-4 | ||
| 2 | 1 | -1+1·2=1 | -6+1·2=-4 | ||
Число 2 не входит в число корней уравнения. Дополним таблицу Горнера для х=-2:
Дополним таблицу Горнера для х=-2:
| xi | коэффициенты многочленов | ||||
| a3=1 | a2=0 | a1=-7 | a0=-6 | ||
| 1 | 1 | 0+1·1=1 | -7+1·1=-6 | -6+-6·1=-12 | |
| -1 | 1 | 0+1·(-1)=-1 | -7+-1·-1=-6 | -6+(-6)·(-1)=0 | |
| -1 | 1 | -1+1·-1=-2 | -6+-2·-1=-4 | ||
| 2 | 1 | -1+1·2=1 | -6+1·2=-4 | ||
| -2 | 1 | -1+1·-2=-3 | -6+-3·-2=0 | ||
Минус два будет корнем исходного уравнения. Мы можем записать многочлен так:
x3-7x-6=(x+1)(x2-x-6)==(x+1)(x+2)(x-3)
Третий и последний корень уравнения будет равен трем. Закончим заполнение таблицы, взяв значения последней полученной строки в качестве коэффициентов:
| xi | коэффициенты многочленов | ||||
| a3=1 | a2=0 | a1=-7 | a0=-6 | ||
| 1 | 1 | 0+1·1=1 | -7+1·1=-6 | -6+-6·1=-12 | |
| -1 | 1 | 0+1·(-1)=-1 | -7+-1·-1=-6 | -6+(-6)·(-1)=0 | |
| -1 | 1 | -1+1·-1=-2 | -6+-2·-1=-4 | ||
| 2 | 1 | -1+1·2=1 | -6+1·2=-4 | ||
| -2 | 1 | -1+1·-2=-3 | -6+-3·-2=0 | ||
| 3 | 1 | -3+1·3=0 | |||
Из этого можно сделать вывод, что последняя полученная таблица, заполненная по методу Горнера, и будет решением нашего примера. Эту задачу можно было решить и делением многочлена на линейный двучлен столбиком, однако показанная здесь схема нагляднее и проще.
Эту задачу можно было решить и делением многочлена на линейный двучлен столбиком, однако показанная здесь схема нагляднее и проще.
Ответ: х=-1, х=-2, х=3, x3-7x-6=(x+1)(x+2)(x-3).
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Урок 10. многочлены от одной переменной. схема горнера — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №10. Многочлен от одной переменной. Схема Горнера.
Перечень вопросов, рассматриваемых в теме
1) что такое одночлен и многочлен;
2) основные действия над многочленами;
3) правило деления многочленов «углом»;
4) схему Горнера.
Глоссарий по теме
Одночлен- это произведение чисел, переменных и их степеней.
Многочлен стандартного вида — это многочлен, в котором каждый член — одночлен стандартного вида и многочлен не содержит подобных членов.
Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Рассмотрим многочлены
7х²-6х-2
-9х³+2х²-3х
х⁵+6
Эти многочлены записаны в стандартном виде.
Давайте вспомним, что такое многочлен стандартного вида.
Многочлен стандартного вида — это многочлен, в котором каждый член — одночлен стандартного вида и многочлен не содержит подобных членов.
Чтобы привести многочлен к стандартному виду, нужно:
- каждый член многочлена представить в стандартном виде
- привести подобные члены многочлена.
Пример 1
Привести многочлен к стандартному виду 3а·5в+3ав+2а·(-4в)+в·в
Воспользуемся алгоритмом, который мы рассмотрели:
- каждый член многочлена представляем в стандартном виде, т.е. выполним действия умножения, получим:
15ав+3ав-8ав+в²
- Приведем подобные, получим:
в²+10ав
Обычно многочлен записывают по убывающим степеням переменной, т.е. степени переменной постепенно уменьшаются.
Всякое целое выражение можно преобразовать в многочлен стандартного вида- в этом состоит цель преобразований (упрощений) целых выражений.
Многочлен от одной переменной обозначается следующим образом: Р(х).
Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.
Пример 2
Р(х)=х³+2х²-7х-2
Корнем данного многочлена будет число 2, т. к.
к.
Р(2)=2³+2·2²-7·2-2=0.
Многочлены можно складывать, вычитать, умножать и возводить в степень. Иногда выполнимо деление многочлена на многочлен. А именно, если существует такой многочлен S(x), что P(x)=Q(x)·S(x), то говорят, что много член Р(х) делится на многочлен Q(x) и называют Р(х)- делимым, Q(x)- делителем, S(x)- частным.
Пример 3
Р(х)=х³-3х²+5х-15 делится на Q(x)= х²+5, т.к. Р(х) можно разложить на множители
х³-3х²+5х-15= (х²+5)(х-3)
Частным является S(x)=х-3.
Если же многочлен Р(х) не делится на многочлен Q(x), то рассматривают деление с остатком.
Свойство: для любых двух многочленов Р(х) и Q(x) таких, что степень Р(х) не меньше степени Q(x), существует одна и только одна пара многочленов S(x) и R(x) таких, что справедливо тождество
Р(х)=Q(x)·S(x)+R(x),
Причем степень многочлена R(x) меньше степени многочлена Q(x). (многочлен R(x) называют остатком).
При делении многочленов стандартного вида используют правило деления «углом», аналогичное правилу деления многозначных чисел.
Пример 4
Разделим Р(х)= 3х⁴+2х³+70х²+3х-4 на Q(x)= x²+5x+1.
Выполним деление «углом»:
Итак, S(x)=3x²-13x+132- частное, R(x)= -644х-136- остаток.
При этом выполняется тождество
3х⁴+2х³+70х²+3х-4= (х²+5х+1)·(3х²-13х+132)+(-644х-136).
Рассмотрим еще один метод деления многочленов- схему Горнера.
Схема Горнера для деления многочлена — это алгоритм упрощения вычисления значения многочлена Р(x) при определённой величине x = x0 методом деления многочлена на одночлены (многочлены 1ой степени). Каждый одночлен включает в себя максимум один процесс умножения и один процесс сложения. Результат, полученный из одного одночлена, прибавляют к результату, полученному от следующего одночлена, и так далее. Такой процесс деления также называют синтетическим делением.
Чтобы объяснить вышесказанное, давайте перепишем многочлен в таком виде:
Р(x0) = a0 + a1x0 + a2x02 + . .. + anx0n
.. + anx0n
Это также может быть записано как:
Р(x0) = a0 + x0(a1 + x0(a2 + x0(a3 + … + (an-1 + anx0)….)
Алгоритм, предложенный данной схемой, основан на нахождении значений одночленов, образованных выше, начиная с тех, которые заключены в большее количество скобок и, двигаясь наружу, для нахождения значения одночленов во внешних скобках.
Алгоритм приводится в действие, следуя нижеизложенным шагам:
1. Дано k = n
2. Пусть bk = ak
3. Пусть bk — 1 = ak — 1 + bkx0
4. Пусть k = k — 1
5. Если k ≥ 0, то вернуться на шаг 3, иначе конец.
Этот алгоритм может быть также графически визуализирован, принимая во внимание данный многочлен 5ой степени:
Р(x) = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5
значение которого находится как x = x0, путём перестановки его следующим образом:
Р(x0) = a0 + x0(a1 + x0(a2 + x0(a3 + x0(a4 + a5x0))))
Другим способом представить результаты используя этот алгоритм можно в виде данной ниже таблицы:
k | 5 | 4 | 3 | 2 | 1 | 0 |
b5 = a5 | b4 = a4 + x0b5 | b3 = a3 + x0b4 | b2 = a2 + x0b3 | b1 = a1 + x0b2 | b0 = a0 + x0b1 |
Пример 5
Разделить многочлен x⁴+3x³+4x²−5x−47 на x+3 по схеме Горнера.
Сразу оговорим, что выражение x+3 нужно представить в форме x−(−3). В схеме Горнера будет участвовать именно −3, так как степень исходного многочлена x⁴+3x³+4x²−5x−47 равна четырём, то в результате деления получим многочлен третьей степени:
Полученный результат означает, что
x⁴+3x³+4x²−5x−47 =(x+3)(x³+0⋅x²+4x−17)+4=(x+3)(x³+4x−17)+4
В этой ситуации остаток от деления x⁴+3x³+4x²−5x−47 на x+3 равна 4. Или, что то самое, значение многочлена x⁴+3x³+4x²−5x−47 при x=−3 равно 4. Кстати, это несложно перепроверить непосредственной подстановкой x=−3 в заданный многочлен:
x⁴+3x³+4x²−5x−47 =(−3)4+3⋅(−3)3−5⋅(−3)−47=4.
Т.е. схему Горнера можно использовать, если необходимо найти значение многочлена при заданном значении переменной. Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд.
Схема Горнера в решении уравнений с параметрами из группы «С» при подготовке к ЕГЭ
СХЕМА ГОРНЕРА В РЕШЕНИИ УРАВНЕНИЙ С ПАРАМЕТРАМИ ИЗ ГРУППЫ «С» ПРИ ПОДГОТОВКЕ К ЕГЭ
Казанцева Людмила Викторовна
учитель математики МБОУ «Уярская СОШ № 3»
Содержание текстов Единого государственного экзамена показало, что материал учебника не достаточен для успешной сдачи экзамена. Знаний, полученных на школьных уроках, хватает только для решения примеров из группы «В».
Знаний, полученных на школьных уроках, хватает только для решения примеров из группы «В».
На факультативных занятиях необходимо расширить круг имеющихся знаний за счет решения заданий повышенной сложности группы «С».
Даная работа освещает часть вопросов, рассматриваемых на дополнительных занятиях.
Целесообразно ввести схему Горнера после изучения темы «Деление многочлена на многочлен». Этот материал позволяет решать уравнения высших порядков не способом группировки многочленов, а более рациональным путем, экономящим время.
План занятий
Решение уравнений высших степеней.
Занятие 1
. Объяснение теоретического материала.
. Решение примеров а), б), в), г).
Занятие 2
. Решение уравнений а), б), в), г).
. Нахождение рациональных корней многочлена
Применение схемы Горнера при решении уравнений с параметрами.
Занятие 3
1.Задания а), б), в).
Занятие 4
. Задания г), д), е), ж), з).
Решение уравнений высших степеней. Схема Горнера
Схема Горнера
Теорема: Пусть несократимая дробь является корнем уравнения
xn + a1 xn-1 + … + an-1×1 + an = 0
целыми коэффициентами. Тогда число р является делителем старшего коэффициента ао.
Следствие: Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.
Следствие: Если старший коэффициент уравнения с целыми коэффициентами равен 1, то все рациональные корни, если они существуют — целые.
Пример 1.2х3 — 7х2 + 5х — 1 = 0
Пусть несократимая дробь является корнем уравнения, тогда р является делителем числа 1 : ± 1
q является делителем старшего члена: ± 1; ± 2
Рациональные корни уравнения надо искать среди чисел: ± 1; ± .
f(1) = 2 — 7 + 5 — 1 = — 1 ? 0(-1) = -2 — 7 — 5 — 1 ? 0() = — + — 1 = — + — = 0
Корнем является число .
Деление многочлена Р(х) = аохп + a1 xn-1 + … + an на двучлен (х — £) удобно выполнять по схеме Горнера.
Обозначим неполное частное Р(х) на (х — £) через Q(x) = boxn-1 + b1xn-2 + …bn-1,
а остаток через bn
Р(х) = Q(x) (x — £) + bn , то имеет место тождество
аохп + a1 xn-1 + … + an = (boxn-1 + … + bn-1) (х — £) + bn
Q(x) — многочлен, степень которого на 1 ниже степени исходного многочлена. Коэффициенты многочлена Q(x) определяются по схеме Горнера.
Коэффициенты многочлена Q(x) определяются по схеме Горнера.
аоa1a2…an-1an£bo = aоb1 = a1 + £·bob2 = a2 + £·b1bn-1 = an-1 + £·bn-2bn = an + £·bn-1
В первой строке этой таблицы записывают коэффициенты многочлена Р(х).
Если какая-то степень переменной отсутствует, то в соответствующей клетке таблицы пишется 0.
Старший коэффициент частного равен старшему коэффициенту делимого (ао = bo). Если £ является корнем многочлена, то в последней клетке получается 0.
Пример 2. Разложить на множители с целыми коэффициентами
Р(х) = 2х4 — 7х3 — 3х2 + 5х — 1
Ищем целые корни среди делителей свободного члена: ± 1.
Подходит — 1.
Делим Р(х) на (х + 1)
2- 7- 35- 1- 12- 96- 10
х4 — 7х3 — 3х2 + 5х — 1 = (х + 1) (2х3 — 9х2 + 6х — 1)
Ищем целые корни среди свободного члена: ± 1
Так как старший член равен 1, то корнями могут быть дробные числа: — ; .
Подходит .
многочлен уравнение корень коэффициент
2- 96- 12- 820
2х3 — 9х2 + 6х — 1 =(х — ) (2х2 — 8х + 2) = (2х — 1) (х2 — 4х + 1)
Трехчлен х2 — 4х + 1 на множители с целыми коэффициентами не раскладывается.
Задание:
. Разложите на множители с целыми коэффициентами:
а) х3 — 2х2 — 5х + 6
q: ± 1;
р: ± 1; ± 2; ± 3; ± 6
:± 1; ± 2; ± 3; ± 6
Находим рациональные корни многочлена f(1) = 1 — 2 — 5 + 6 = 0
х = 1
1- 2- 5611- 1- 60
х3 — 2х2 — 5х + 6 = (х — 1) (х2 — х — 6) = (х — 1) (х — 3) (х + 2)
Определим корни квадратного уравнения
х2 — х — 6 = 0
х = 3; х = — 2
б) 2х3 + 5х2 + х — 2
р: ± 1; ± 2
q: ± 1; ± 2
:± 1; ± 2; ±
Найдем корни многочлена третьей степени
f(1) = 2 + 5 + 1 — 2 ? 0
f(-1) = — 2 + 5 — 1 — 2 = 0
Один из корней уравнения х = — 1
251- 2- 123- 20
х3 + 5х2 + х — 2 = (х + 1) (2х2 + 3х — 2) = (х + 1) (х + 2) (2х — 1)
Разложим квадратный трехчлен 2х2 + 3х — 2 на множители
2х2 + 3х — 2 = 2 (х + 2) (х — )
D = 9 + 16 = 25
х1 = — 2; х2 =
в)х3 — 3х2 + х + 1
р: ± 1
q: ± 1
:± 1
f(1) = 1 — 3 + 1 — 1 = 0
Одним из корней многочлена третьей степени является х = 1
1- 31111- 2- 10
х3 — 3х2 + х + 1 = (х — 1) (х2 — 2х — 1)
Найдем корни уравнения х2 — 2х — 1 = 0
D = 4 + 4 = 8
х1 = 1 —
х2 = 1 +
х3 — 3х2 + х + 1 = (х — 1) (х — 1 + ) (х — 1 — )
г)х3 — 2х — 1
р: ± 1
q: ± 1
:± 1
Определим корни многочлена
f(1) = 1 — 2 — 1 = — 2
f(-1) = — 1 + 2 — 1 = 0
Первый корень х = — 1
10- 2- 1- 11- 1- 10
х3 — 2х — 1 = (х + 1) (х2 — х — 1)
х2 — х — 1 = 0
D = 1 + 4 = 5
х1,2 =
х3 — 2х — 1 = (х + 1) (х — ) (х — )
. Решить уравнение:
Решить уравнение:
а)х3 — 5х + 4 = 0
Определим корни многочлена третьей степени
:± 1; ± 2; ± 4
f(1) = 1 — 5 + 4 = 0
Одним из корней является х = 1
10- 54111- 40
х3 — 5х + 4 = 0
(х — 1) (х2 + х — 4) = 0
Найдем корни квадратного уравнения х2 + х — 4 = 0
D = 1 + 16 = 17
х1 = ; х2 =
Ответ: 1; ;
б)х3 — 8х2 + 40 = 0
Определим корни многочлена третьей степени.
:± 1; ± 2; ± 4; ± 5; ± 8; ± 10; ± 20; ± 40
f(1) ? 0
f(-1) ? 0
f(-2) = — 8 — 32 + 40 = 0
Одним из корней является х = — 2
1- 8040- 21- 10200
Разложим многочлен третьей степени на множители.
х3 — 8х2 + 40 = (х + 2) (х2 — 10х + 20)
Найдем корни квадратного уравнения х2 — 10х + 20 = 0
D = 100 — 80 = 20
х1 = 5 — ; х2 = 5 +
Ответ: — 2; 5 — ; 5 +
в)х3 — 5х2 + 3х + 1 = 0
Ищем целые корни среди делителей свободного члена: ± 1
f(-1) = — 1 — 5 — 3 + 1 ? 0
f(1) = 1 — 5 + 3 + 1 = 0
Подходит х = 1
1- 53111- 4- 10
х3 — 5х2 + 3х + 1 = 0
(х — 1) (х2 — 4х — 1) = 0
Определяем корни квадратного уравнения х2 — 4х — 1 = 0
D = 20
х = 2 + ; х = 2 —
Ответ: 2 — ; 1; 2 +
г)2х4 — 5х3 + 5х2 — 2 = 0
Найдем рациональные корни многочлена
р: ± 1; ± 2
q: ± 1; ± 2
:± 1; ± 2; ±
f(1) = 2 — 5 + 5 — 2 = 0
Один из корней уравнения х = 1
2- 550- 212- 3220
х4 — 5х3 + 5х2 — 2 = 0
(х — 1) (2х3 — 3х2 + 2х + 2) = 0
Находим по такой же схеме корни уравнения третьей степени.
х3 — 3х2 + 2х + 2 = 0
р: ± 1; ± 2
q: ± 1; ± 2
:± 1; ± 2; ±
f(1) = 2 — 3 + 2 + 2 ? 0
f(-1) = — 2 — 3 — 2 + 2 ? 0
f(2) = 16 — 12 + 4 + 2 ? 0
f(-2) = — 16 — 12 — 4 + 2 ? 0
f() = — + 1 + 2 ? 0
f(-) = — — — 1 + 2 ? 0
Следующий корень уравнения х = —
2- 322-2- 440
х3 — 3х2 + 2х + 2 = 0
(х + ) (2х2 — 4х + 4) = 0
Определим корни квадратного уравнения 2х2 — 4х + 4 = 0
х2 — 2х + 2 = 0
= — 4 < 0
Следовательно, корнями исходного уравнения четвертой степени являются
1 и —
Ответ: -; 1
. Найдите рациональные корни многочлена
а)х4 — 2х3 — 8х2 + 13х — 24
р: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
:± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
Подберем один из корней многочлена четвертой степени:
f(1) = 1 — 2 — 8 + 13 — 24 ? 0
f(-1) = 1 + 2 — 8 — 13 — 24 ? 0
f(2) = 16 — 16 — 32 + 26 — 24 ? 0
f(-2) = 16 + 16 — 72 — 24 ? 0
f(-3) = 81 + 54 — 72 — 39 — 24 = 0
Один из корней многочлена х0= — 3.
х4 — 2х3 — 8х2 + 13х — 24 = (х + 3) (х3 — 5х2 + 7х + 8)
Найдем рациональные корни многочлена
х3 — 5х2 + 7х + 8
р: ± 1; ± 2; ± 4; ± 8
q: ± 1
f(1) = 1 — 5 + 7 + 8 ? 0
f(-1) = — 1 — 5 — 7 — 8 ? 0
f(2) = 8 — 20 + 14 + 8 ? 0
f(-2) = — 8 — 20 — 14 + 8 ? 0
f(-4) = 64 — 90 — 28 + 8 ? 0
f(4) ? 0
f(-8) ? 0
f(8) ? 0
Кроме числа x0 = — 3 других рациональных корней нет.
б)х4 — 2х3 — 13х2 — 38х — 24
р: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
f(1) = 1 + 2 — 13 — 38 — 24 ? 0
f(-1) = 1 — 2 — 13 + 38 — 24 = 39 — 39 = 0, то есть х = — 1 корень многочлена
12- 13- 38- 24- 111- 14- 240
х4 — 2х3 — 13х2 — 38х — 24 = (х + 1) (х3 — х2 — 14х — 24)
Определим корни многочлена третьей степени х3 — х2 — 14х — 24
р: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
f(1) = — 1 + 1 + 14 — 24 ? 0
f(-1) = 1 + 1 — 14 — 24 ? 0
f(2) = 8 + 4 — 28 — 24 ? 0
f(-2) = — 8 + 4 + 28 — 24 ? 0
Значит, второй корень многочлена х = — 2
11- 14- 24- 21- 1- 120
х4 — 2х3 — 13х2 — 38х — 24 = (х + 1) (х2 + 2) (х2 — х — 12) =
= (х + 1) (х + 2) (х + 3) (х — 4)
Ответ: — 3; — 2; — 1; 4
Применение схемы Горнера при решении уравнений с параметром
Найдите наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три различных корня, один из которых х0 .
а)f(х) = х3 + 8х2 + ах + b, х0 = — 3
Так один из корней х0 = — 3 , то по схеме Горнера имеем:
18аb- 315- 15 + а0
= — 3 (- 15 + а) + b
= 45 — 3а + b
b = 3а — 45
х3 + 8х2 + ах + b = (х + 3) (х2 + 5х + (а — 15))
Уравнение х2 + 5х + (а — 15) = 0 должно иметь два корня. Это выполняется только в том случае, когда D > 0
а = 1; b = 5; с = (а — 15),= b2 — 4ac = 25 — 4 (a — 15) = 25 + 60 — 4a > 0,
— 4a > 0;
a < 85;
a < 21
Наибольшее целое значение параметра а, при котором уравнение
f(х) = 0 имеет три корня, а = 21
Ответ: 21.
б)f(x) = x3 — 2×2 + ax + b, x0 = — 1
Так как один из корней х0= — 1, то по схеме Горнера имеем
1- 2ab- 11- 33 + а0- 2×2 + ax + b = (x + 1) (x2 — 3x + (3 + a))
Уравнение x2 — 3x + (3 + a) = 0 должно иметь два корня. Это выполняется только в том случае, когда D > 0
= 1; b = — 3; c = (3 + a),= b2 — 4ac = 9 — 4 (3 + a) = 9 — 12 — 4a = — 3 — 4a > 0,
3 — 4a > 0;
4a < 3;
a < —
Наибольшее значение а = — 1
Ответ: — 1
в)f(x) = x3 + 11×2 + ax + b, x0 = — 4
Так как один из корней х0 = — 4, то по схеме Горнера имеем
3 + 11×2 + ax + b = (х + 4) (х2 + 7х + (а — 28))
f(x) = 0, если х = — 4 или х2 + 7х + (а — 28) = 0
Уравнение имеет два корня, если D > 0
D = b2 — 4ac = 49 — 4 (a — 28) = 49 + 112 — 4a = 161 — 4a >0,
— 4a > 0;
4a < — 161;< 40
Уравнение имеет три корня при наибольшем целом значении а = 40
Ответ: а = 40
г)f(x) = x3 — 11×2 + ax + b, x0 = 4
Так как один из корней х0 = 4, то по схеме Горнера имеем
1- 11ab41- 7- 28 + а0- 11×2 + ax + b = (x — 4) ( x2 — 7x + (a — 28))(x) = 0, если х = 4 или x2 — 7x + (a — 28) = 0
Второе уравнение имеет два корня, если D > 0, то есть
= b2 — 4ac = 49 — 4 (a — 28) = 49 + 112 — 4a = 161 — 4a >0,
— 4a > 0;
4a < — 161;
a < 40
Уравнение имеет три корня при наибольшем целом значении а = 40
Ответ: а = 40
д) f(x) = x3 — 13×2 + ax + b, x0 = 4
Так как один из корней х0 = 4, то по схеме Горнера имеем
1- 13ab41- 9- 36 + а0
x3 — 13×2 + ax + b = (x — 4) ( x2 — 9x + (a — 36))
f(x) = 0, если х = 4 или x2 — 9x + (a — 36) = 0
Второе уравнение имеет два корня, если D > 0, то есть
= b2 — 4ac = 81 — 4 (a — 36) = 81 + 144 — 4a = 225 — 4a >0,
225 — 4a >0;
— 4a < — 225;
a < 56
Уравнение f(x) = 0 имеет три корня при наибольшем значении а = 56
Ответ: а = 56
е)f(x) = x3 + 13×2 + ax + b, x0 = — 5
Так как один из корней x0 = — 5, то по схеме Горнера имеем
113ab- 518- 40 + а0
x3 + 13×2 + ax + b = (x + 5) ( x2 + 8x + (a — 40))
f(x) = 0, если х = — 5 или x2 + 8x + (a — 40) = 0
Уравнение имеет два корня, если D > 0
D = b2 — 4ac = 64 — 4 (a — 40) = 64 + 160 — 4a = 224 — 4a >0,
224 — 4a >0;
a < 56
Уравнение f(x) имеет три корня при наибольшем значении а = 55
Ответ: а = 55
ж)f(x) = x3 + 19×2 + ax + b, x0 = — 6
Так как один из корней — 6, то по схеме Горнера имеем
119ab- 6113а — 780
x3 + 19×2 + ax + b = (x + 6) ( x2 + 13x + (a — 78)) = 0
f(x) = 0, если х = — 6 или x2 + 13x + (a — 78) = 0
Второе уравнение имеет два корня, если D > 0
= b2 — 4ac = 169 — 4 (a — 78) = 169 + 312 — 4a = 481 — 4a >0,
481 — 4a >0;
4a < — 481;
a < 120
Наибольшее целое значение а, при котором уравнение f(x) = 0 имеет три корня, 120.
Ответ: 120
з)f(x) = x3 + 22×2 + ax + b, x0 = — 7
Так как один из корней x0 = — 6, то по схеме Горнера имеем
122ab- 7115а — 1050
x3 + 22×2 + ax + b = (x + 7) ( x2 + 15x + (a — 105)) = 0
f(x) = 0, если х = — 7 или x2 + 15x + (a — 105) = 0
Второе уравнение имеет два корня, если D > 0
= b2 — 4ac = 225 — 4 (a — 105) = 225 + 420 — 4a = 645 — 4a >0,
— 4a >0;
4a < — 645;
a < 161
Уравнение имеет три корня при наибольшем целом значении а = 161.
Ответ: 161
Теги:
Схема Горнера в решении уравнений с параметрами из группы «С» при подготовке к ЕГЭ
Реферат
Математика
Просмотров: 25266
Найти в Wikkipedia статьи с фразой: Схема Горнера в решении уравнений с параметрами из группы «С» при подготовке к ЕГЭ
Простая физика — EASY-PHYSIC
Всем доброго времени суток! В этой статье мы научимся делить многочлены по схеме Горнера. Это простой и мощный механизм, которым совершенно необходимо владеть, чтобы решать некоторые рациональные уравнения задания 15 профильного ЕГЭ.
При решении таких уравнений корни заранее неизвестны, да и при разложении многочлена на множители мы также не знаем заранее, на какой бином поделится наш многочлен. Как же узнать, на какой бином разделить многочлен?
Если многочлен имеет целые корни, то они являются делителями свободного члена — правило вытекает из теоремы Безу
Пример 1.
Определим, какие числа являются, например, корнями многочлена . Если этот многочлен имеет целые корни, то они являются делителями числа (-2): это могут быть . Проверим подстановкой — если при подстановке этих чисел в исходный многочлен получим ноль, то данное число — корень:
Кроме 1, ни одно число не подошло, значит, бином поделит этот многочлен нацело (без остатка). Деление теперь можно выполнить как в столбик (уголком), так и по схеме Горнера — сейчас мы до нее дойдем, только еще раз потренируемся в определении корней.
Пример 2.
Определим корни многочлена . Целые делители свободного члена — только 1 и (-1):
Целые делители свободного члена — только 1 и (-1):
Корнем многочлена является 1, поэтому многочлен без остатка поделится на бином .
Пример 3.
Определим корни многочлена . Целые делители свободного члена — . Проверим их:
Корнями многочлена являются как 1, так и (-1), поэтому многочлен без остатка поделится на биномы и — а в итоге на .
Теперь, когда мы научились определять, есть ли у многочлена целые корни, можем перейти собственно к схеме Горнера. Чтобы ею воспользоваться, нужно составить таблицу, в верхней строке которой будут расположены коэффициенты нашего многочлена. Поучимся заполнять эту строку. Определим коэффициенты многочлена и запишем их в таблицу. Этот многочлен пятой степени, поэтому коэффициентов будет 6: при каждой из степеней , включая нулевую (свободный член). Если какой-то степени нет в записи многочлена, то это означает, что коэффициент при ней нулевой:
Получили эдакую зашифрованную запись многочлена.
Еще пример, многочлен , его коэффициенты:
Полдела сделано: верхнюю строку научились заполнять, а нижняя — это уже решение, то есть результат деления в таком же, «зашифрованном», виде. Каков же порядок заполнения нижней строки? Во-первых, у нее будет дополнительная ячейка слева, куда мы впишем корень многочлена, образующий бином, на который мы собираемся делить. Например, если делим на , то корнем многочлена является число 2, если делим на , то в эту ячейку впишем (-9). Пример: хотим разделить на , таблица изначально будет выглядеть так:
Как уже было сказано, ответ будет «зашифрован» в пустых пока ячейках. Наверное, вы догадались, что там окажутся коэффициенты нового, полученного при делении, многочлена. Только внимание! Степень полученного многочлена уменьшится на 1: ведь мы делим на бином, куда входит в первой степени. Например, если сейчас мы начнем заполнять эту табличку, то под двойкой, которая была в делимом коэффициентом при пятой степени, окажется коэффициент при четвертой степени искомого частного, под 4 — коэффициент при кубе частного и т. д.
д.
Так же просто заполнить вторую ячейку нижней строки: в нее просто вписывается число, стоящее в первой строчке:
Рассмотрим дальнейшее заполнение таблицы на конкретном примере: разделим на бином (так как (-1) — это корень данного многочлена). Заполняем таблицу, пока только ту часть, которую умеем:вписываем коэффициенты в верхнюю строку, в дополнительную ячейку слева — корень (-1), в следующую переносим 1 из верхней строки:
Чтобы заполнить следующую ячейку, берем корень, умножаем его на имеющийся коэффициент и прибавляем к полученному числу то, которое стоит над пустой ячейкой:
Чтобы заполнить следующую, все повторяем:
И опять:
И вот так закончится заполнение таблицы:
«Расшифровываем» ответ, при этом помним, что степень понизилась на 1::
Ответ:
Ноль в последней графе — это нулевой остаток от деления — то есть один многочлен поделился на другой «нацело».
Решим еще пример. Разделим на . Составим таблицу:
Начинаем рассчитывать коэффициенты и заполнять таблицу. Первое число из верхней строки переписываем вниз, умножаем на него корень, к результату добавляем число из верхней строки:
Также вычисляем следующий коэффициент:
И далее:
Получили ответ: . Здесь остаток от деления также равен нулю.
Этот способ хорош своей быстротой и простотой. Им можно пользоваться и при делении с остатком: тогда в последней графе таблицы будет стоять не ноль, а этот самый остаток. Недостаток способа — неудобство деления в случае, если корень не целый, а представляет собой дробь.
Попробуем выполнить деление по схеме Горнера, если корень не целый, да еще и остаток есть. Поделим многочлен на бином . Заполняем таблицу:
Расшифруем ответ:
Итак, получилось следующее. При делении получился многочлен и остаток . Запишем это иначе: . Если есть желание проверить — раскройте скобки в этой формуле.
Если есть желание проверить — раскройте скобки в этой формуле.
Наконец, об уравнениях высоких степеней. Иногда однократное деление не приводит к окончанию решения, потому что корней несколько и многочлен можно продолжать делить. В этом случае, выполнив деление и получив новый многочлен степенью ниже, снова пытаются найти целые корни среди делителей его свободного члена. При этом подстановка предполагаемых корней в многочлен может занимать даже больше времени, чем заполнение таблицы по Горнеру. Тогда таблицу продолжают вниз, дополняя ее просто новыми строками, а в случае появления остатка (деление не выполнено) эту строчку зачеркивают и пробуют новый корень в следующей строке. Пример:
Решить уравнение: . Делителями свободного члена являются: и так далее. Пробуем сначала подставить 1 и (-1) в сам многочлен — такая подстановка дает нам один корень, это 1. Выполняем деление по схеме Горнера:
Запишем, что получилось: — получили тот же свободный член, и можем снова использовать те же делители, чтобы проверить, не являются ли они корнями. Однако теперь подстановка 1 и (-1) показывает, что эти два числа не являются корнями. Проверяем тогда 2 и (-2) — только не будем подставлять их в многочлен, а сразу попытаемся делить по Горнеру. А таблица у нас уже готова, и в ней все коэффициенты! Поэтому продолжаем ее заполнять, добавляя строки:
Однако теперь подстановка 1 и (-1) показывает, что эти два числа не являются корнями. Проверяем тогда 2 и (-2) — только не будем подставлять их в многочлен, а сразу попытаемся делить по Горнеру. А таблица у нас уже готова, и в ней все коэффициенты! Поэтому продолжаем ее заполнять, добавляя строки:
Так как остаток ненулевой, то 2 — не корень. Строку вычеркнем и попробуем (-2):
Та же картина, опять получили ненулевой остаток. Далее пробуем 3 и (-3):
Получилось! Теперь имеем: . Делителями нового свободного члена являются . Пробовать не будем: очевидно, что они не могут быть корнями — это выяснилось на предыдущих этапах. Поэтому пробуем .
Получили: . Дальше деление по Горнеру можно и не выполнять: корни с очевидностью можно найти по теореме Виета — это 5 и 6. Тогда . Разложение выполнено, корни уравнения найдены.
Надеюсь, статья вам помогла, до следующих исследований!
Схема Горнера и теорема Безу на занятиях у репетитора по математике — Колпаков Александр Николаевич
Сайт «профессиональный репетитор по математике» продолжает цикл методических статей о преподавании. Я публикую описания методик своей работы с наиболее сложными и проблемным темами школьной программы. Данный материал будет полезен преподавателям и репетиторам по математике, работающим с учениками 8-11 классов как по обычной программе, так и по программе математических классов.
Я публикую описания методик своей работы с наиболее сложными и проблемным темами школьной программы. Данный материал будет полезен преподавателям и репетиторам по математике, работающим с учениками 8-11 классов как по обычной программе, так и по программе математических классов.
Репетитор по математике не всегда может объяснить материал, который неудачно изложен в учебнике. К сожалению, таких тем становится все больше и больше, и ошибки изложения вслед за авторами пособий совершаются в массовом порядке. Это относится не только к начинающим репетиторам по математики и репетиторам по совместительству (репетиторы — студенты и репетиторы ВУЗов), но и к опытным преподавателям, репетиторам — профессионалам, репетиторам со стажем и квалификацией. Талант грамотного корректора шероховатостей школьных учебников имеют далеко не все репетиторы математики. Не все также понимают, что эти коррекции (или дополнении) необходимы. Адаптацией материала для его качественного восприятия детьми занимаются единицы. К сожалению, ушло то время, когда преподаватели математики вместе методистами и авторами изданий в массовом порядке обсуждали каждую букву учебника. Раньше, прежде чем пустить учебник в школы, проводили серьезные анализы и исследования результатов обучения. Пришло время дилетантов, стремящихся сделать пособия универсальными, подгоняя их под стандарты сильных математических классов.
К сожалению, ушло то время, когда преподаватели математики вместе методистами и авторами изданий в массовом порядке обсуждали каждую букву учебника. Раньше, прежде чем пустить учебник в школы, проводили серьезные анализы и исследования результатов обучения. Пришло время дилетантов, стремящихся сделать пособия универсальными, подгоняя их под стандарты сильных математических классов.
Гонка за увеличение количества информации приводит только к снижению качества ее усвоения и, как следствие снижению уровня реальных знаний по математике. Но на это никто не обращает внимание. И наши дети вынуждены уже в 8 классе изучать то, что мы с вами проходили в институте: теорию вероятности, решение уравнений высоких степеней и кое-что еще. Адаптация материала в книжках для его полноценного восприятия ребенком оставляет желать лучшего и репетитор по математике вынужден как-то с этим бороться.
Поговорим о методике преподавания такой специфической темы, как «деление уголком многочлена на многочлен», более известной во взрослой математике как «теорема Безу и схема Горнера». Еще каких-нибудь пару лет назад вопрос не стоял перед репетитором по математике так остро, ибо он не входил в основную школьную программу. Теперь уважаемые авторы учебника под редакцией Теляковского внесли изменения в последнее издание лучшего, на мой взгляд, учебника, и, окончательно испортив его, только добавили репетитору лишних забот. Преподаватели школ и классов, не имеющих статус математических, ориентируясь на нововведения авторов, стали чаще включать дополнительные параграфы в свои уроки, а любознательные дети, рассматривая красивые странички их учебника математики, все чаще спрашивают репетитора: «Что это за деление уголком? Мы будем это проходить? Как делить уголком?» От таких прямых вопросов уже не спрятаться. Репетитору придется что-то рассказывать ребенку.
Еще каких-нибудь пару лет назад вопрос не стоял перед репетитором по математике так остро, ибо он не входил в основную школьную программу. Теперь уважаемые авторы учебника под редакцией Теляковского внесли изменения в последнее издание лучшего, на мой взгляд, учебника, и, окончательно испортив его, только добавили репетитору лишних забот. Преподаватели школ и классов, не имеющих статус математических, ориентируясь на нововведения авторов, стали чаще включать дополнительные параграфы в свои уроки, а любознательные дети, рассматривая красивые странички их учебника математики, все чаще спрашивают репетитора: «Что это за деление уголком? Мы будем это проходить? Как делить уголком?» От таких прямых вопросов уже не спрятаться. Репетитору придется что-то рассказывать ребенку.
А как? Наверное, я бы не стал описывать метод работы с темой, если бы в учебниках она грамотно преподносилась. У нас ведь как все происходит? Учебники нужно печатать и продавать. А для этого их надо регулярно обновлять. Преподаватели Вузов жалуются, что дети приходят к ним с пустыми головами, без знаний и навыков? Требования к математическим знаниям растут? Отлично! Давайте мы уберем некоторые упражнения, а вместо них вставим темы, которые изучаются по другим программам. Чем наш учебник хуже? Включим какие-нибудь дополнительные главы. Школьники не знают правило деления уголком? Это же элементарная математика. Надо сделать такой параграф необязательным, озаглавив его «для тех, кто хочет знать больше». Репетиторы против? А какое нам дело до репетиторов вообще? Методисты и преподаватели школ тоже против? Мы не будем усложнять материал и рассмотрим наиболее простую его часть.
Преподаватели Вузов жалуются, что дети приходят к ним с пустыми головами, без знаний и навыков? Требования к математическим знаниям растут? Отлично! Давайте мы уберем некоторые упражнения, а вместо них вставим темы, которые изучаются по другим программам. Чем наш учебник хуже? Включим какие-нибудь дополнительные главы. Школьники не знают правило деления уголком? Это же элементарная математика. Надо сделать такой параграф необязательным, озаглавив его «для тех, кто хочет знать больше». Репетиторы против? А какое нам дело до репетиторов вообще? Методисты и преподаватели школ тоже против? Мы не будем усложнять материал и рассмотрим наиболее простую его часть.
И вот тут начинается. Простота темы и качество ее усвоения заключатся, прежде всего, в понимании ее логики, а не в том, чтобы согласно предписанию авторов учебника выполнить некий набор не понятно как связанных друг с другом операций. Иначе туман в голове школьника будет обеспечен. Если расчет авторов идет на относительно сильных учеников (но обучающихся по обычной программе), то не стоит подавать тему в командной форме. А что мы видим в учебнике? Дети, надо делить по такому правилу. Получите многочлен под уголком. Таким образом, первоначальный многочлен разложится на множители. Однако, понять, почему именно так подбираются слагаемые под уголком, почему их надо умножать на многочлен над уголком, а затем вычитать из текущего остатка — непонятно. И самое главное не понятно, почему подобранные одночлены надо в итоге сложить и почему получившиеся скобки будут разложением первоначального многочлена. Любой грамотный математик поставит жирный знак вопроса над теми объяснениями, которые даются в учебнике.
А что мы видим в учебнике? Дети, надо делить по такому правилу. Получите многочлен под уголком. Таким образом, первоначальный многочлен разложится на множители. Однако, понять, почему именно так подбираются слагаемые под уголком, почему их надо умножать на многочлен над уголком, а затем вычитать из текущего остатка — непонятно. И самое главное не понятно, почему подобранные одночлены надо в итоге сложить и почему получившиеся скобки будут разложением первоначального многочлена. Любой грамотный математик поставит жирный знак вопроса над теми объяснениями, которые даются в учебнике.
Я предлагаю вниманию репетиторов и преподавателей математики свое решение проблемы, которое практически делает для ученика очевидным все то, что изложено в учебнике. Фактически мы докажем теорему Безу: если число а — корень многочлена, то этот многочлен можно разложить на множитлей, один из который x-a, а второй получается из первоначального одним из трех способов: выделением линейного множителя через преобразования, делением уголком или по схеме Горнера. Именно с такой форомулировкой репетитору по математике будет легче работать.
Именно с такой форомулировкой репетитору по математике будет легче работать.
Что такое методика преподавания? Прежде всего это четкий порядок в последовательности объяснений и примеров, на основе которых делаются математические выводы. Данная тема не исключение. Репетитору по математике очень важно познакомить ребенка с теоремой Безу до того, как будет выполняться деление уголком. Это очень важно! Добиться понимания лучше всего на конкретном примере. Возьмем какой-нибдуь многочлен с подобранным корнем и показажем технику его разложения на множители при помощи знакомого школьнику еще с 7 класса метода тождественных преобразований. При соответствующих сопроводительных пояснениях, акцентах и подсказках репетитора по математике вполне реально донести материал без каких-либо общих математических выкладок, произвольных коэффициентов и степеней.
Важный совет репетитору по математике — следовать инструкциям от начала и до конца и не менять эту последовательнотсь.
Итак, допустим, что перед нами многочлен . Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить на два слагаемых так, чтобы одно из них было произведением линейного выражения и некоторого одночлена, а второе имело бы степень на единицу меньше, чем . То есть представим его в виде
Одночлен для красного поля подберем так, чтобы при при умножении его на старший член полностью совпадал со старшим членом первоначального многочлена. Если ученик не самый слабый, то он вполне способен будет назвать репетитору по математике искомое выражение: . Репетитору следует тут же предложить вставить его в красное поле и показать что будет получаться при их раскрытии. Лучше всего этот виртуальный временный многочлен подписать под стрелочками (под фотанчиком), выделяя его каким-нибудь цветом, например, синим. Это поможет подоборать слагаемое для красного поля, называемое остатком от выделения. Я бы советовал репетиторам именно здесь указывать на то, что этот остаток можно находить вычитанием. Выполняя такую операцию получим:
Выполняя такую операцию получим:
Репетитор по математике должен обратить внимание ученика на то, что подставляя единицу в данное равенство, мы гарантировано получим нуль в его левой части (так как 1 — корень первоначального многочлена), а в правой, очевидно, тоже обнулим первое слагаемое. Значит без всякой проверки можно сказать, что единица — корень «зеленого остатка».
Поступим с ним так же, как мы это сделали с первоначальным многочленом, выделяя из него такой же линейный множитель . Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо.
Ученик подбирает репетитору одночлен для красного поля так, чтобы он при умножении на старшее слагаемое линейного выражения давал старшее слагаемое раскладывающегося многочлена. Вписываем в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем
И, наконец, проделывая тоже самое с последним остатком
получим окончательно
Теперь вынесем выражение за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень».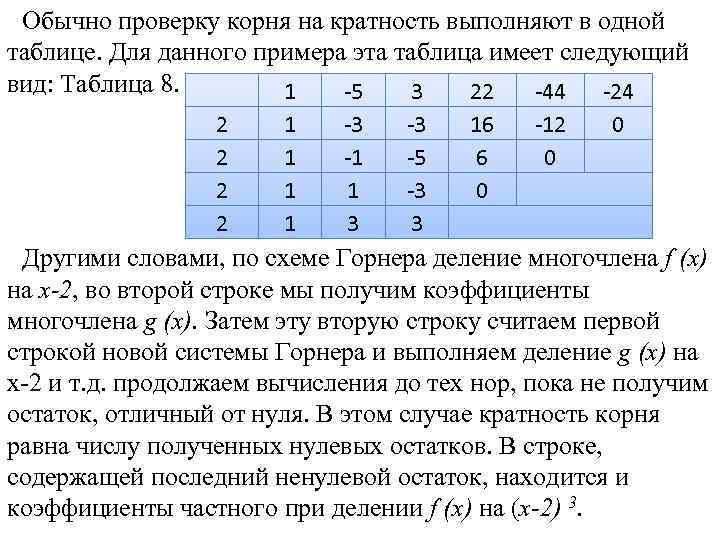
Для того, чтобы ученику не казалось, что последний «зеленый остаток» случайно разложился на нужные множители, репетитор по математкие должен указать на важное свойство всех зеленых остатков — каждый из них имеет корень 1. Поскольку степени этих остатков убывают, то какая бы степень начального многочлена ни была нам дана, рано или поздно, мы получим линейный «зеленый остаток» с корнем 1, а следовательно он обязательно разложиться на произведение некоторого числа и выражения .
После такой подготовительной работы репетитору по математкие не составит труда объяснить ученику, что происходит при делении уголком. Это тот же самый процесс, только в более краткой и компактной форме, без знаков равно и без переписываний одних и тех же выделенных слагаемых. Многочлен из которого выделяется линейный множитель записываем слева от уголка, подбираемые красные одночлены собираем под уголом (теперь становится понятно, почему они должны складываться), для получения «синих многочленов» надо «красные» умножать на x-1, а затем вычитать из текущего выделяемого как это делается при обычном делении чисел в столбик (вот она аналогия с раннее изученным). Получаемые «зеленые остатки» подвергаются новому выделению и подбору «красных одночленов» . И так до получения нулевого «зеленого остатка». Самое главное, что ученику становится понятна дальнейшая судьба записанных многочленов над и под уголком. Очевидно, это скобки, произведение которых равно первоначальному многочлену.
Получаемые «зеленые остатки» подвергаются новому выделению и подбору «красных одночленов» . И так до получения нулевого «зеленого остатка». Самое главное, что ученику становится понятна дальнейшая судьба записанных многочленов над и под уголком. Очевидно, это скобки, произведение которых равно первоначальному многочлену.
Следующий этап работы репетитора по математике — формулирование теоремы Безу. Cобственно ее формулировка при таком подходе репетитора становится очевидной: если число а — корень многочлена, то его можно разложить на множители, один из которых , а другой получается из первоначального одним из трех способов:
- непосредственным разложением (аналогом метода группировки)
- делением уголком (в столбик)
- через схему Горнера
Надо сказать, что схему горнера показывают ученикам далеко не все репетиторы математики и не все школьные преподаватели (к счастью для самих репетиторов) заходят на уроках так глубоко в тему. Однако, для учащегося математического класса я не вижу никаких оснований для остановки на делении в столбик.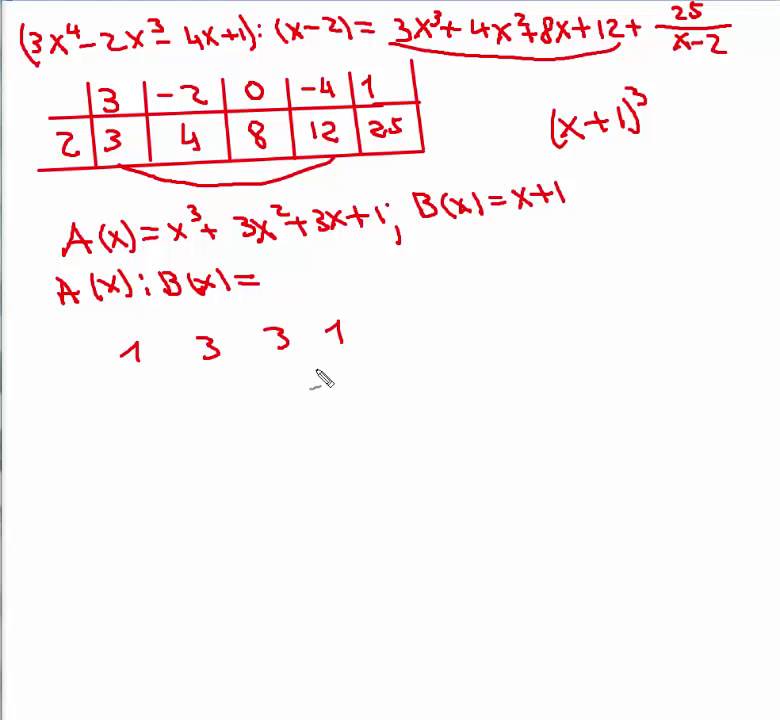 Более того, самый удобный и быстрый прием разложения основан именно на схеме Горнера. Для того, чтобы объяснить ребенку откуда она берется достаточно проследить на примере деления уголком появление старших коэффициентов у зеленых остатках. Становится ясно, что старший коэффициент начального многочлена сносится в коэффициент первого «красного одночлена», а дальше от второго коэффициента текущего верхнего многочлена вычитается результат умножения текущего коэффициента «красного одночлена» на . Поэтому можно прибавлять результат умножения на . После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:
Более того, самый удобный и быстрый прием разложения основан именно на схеме Горнера. Для того, чтобы объяснить ребенку откуда она берется достаточно проследить на примере деления уголком появление старших коэффициентов у зеленых остатках. Становится ясно, что старший коэффициент начального многочлена сносится в коэффициент первого «красного одночлена», а дальше от второго коэффициента текущего верхнего многочлена вычитается результат умножения текущего коэффициента «красного одночлена» на . Поэтому можно прибавлять результат умножения на . После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:
Если в многочлене пропущена какая-нибудь степень, то в таблицу принудительно вносится ее нулевой коэффициент. В нижнюю строчку поочередно вписываются коэффициенты «красных многочленов» по правилу «крючка»:
В нижнюю строчку поочередно вписываются коэффициенты «красных многочленов» по правилу «крючка»:
Корень умножается на последний снесенный «красный коэффициент», прибавляется к следующему коэффициенту верхней строки и результат сносится в нижнюю строчку . В последней колонке гарантированно получим старший коэффициент последнего «зеленого остатка», то есть нуль. После завершения процесса, числа, зажатые между подобранным корнем и нулевым остатком оказываются коээффициентами второго (нелинейного) множителя.
Поскольку корень а дает в конце нижней строки нуль, то схему Горнера можно использовать для проверки чисел на звание корень многочлена. Если специальная теорема о подборе рационального корня. Все кандидаты на это звание, полученные с ее помощью, просто вставляются по очереди слева в схему Горнера. Как только мы получим нуль, тестируемое число будет корнем, и одновременно его строчке получим коэффициенты разложения первоначального многочлена на множители. Очень удобно.
Очень удобно.
В завершение хотелось бы отметить, что для аккуратного ввдения схемы Горнера , а также для практического закрепления темы, репетитор по математике должен иметь в своем распоряжении достаточное количество часов. Репетитору, работающему с режимом «раз в неделю» не стоит заниматься делением уголком. На Егэ по математике и на ГИА по математике вряд ли в первой части когда-нибудь встретится уравнение третьей степени, решаемое такими средствами. Если репетитор готовит ребенка экзамену по математике в МГУ — изучение темы становится обязательным. Очень уж любят преподаватели ВУЗов, не в пример составителям ЕГЭ, проверить глубину знаний абитуриента.
Колпаков Александр Николаевич, репетитор по математике Москва, Строгино
Метки: Примеры объяснений, Репетиторам по математике
к$или же
f(x) = a 0 + a 1 x + a 2 x 2 + … + a n x n
Где a k — действительные числа, представляющие полиномиальные коэффициенты, а
x k — полиномиальные переменные.
Говорят, что приведенный выше полином имеет степень n -й , т. е. deg(f(x)) = n , где n представляет наивысший переменный показатель степени.
Правило Хорнера для полиномиального деления — это алгоритм, используемый для упрощения процесса вычисления многочлена f(x) при некотором значении x = x 0 делением полинома на мономы (многочлены 1-й -й степени). Каждый моном включает максимум один процесс умножения и один процесс сложения. Результат, полученный от одного монома, добавляется к результату, полученному от следующего монома, и так далее в режиме накопительного сложения. Этот процесс деления также известен как синтетическое деление.
Чтобы пояснить вышеизложенное, давайте перепишем полином в его расширенной форме;
F (x 0 ) = A 0 + A 1 x 0 + A 2 x 0 2 + … + N x 0 N .
Это также может быть записано как:
f(х 0 ) = а 0 + х 0 (а 1 + х 0 (а 2 + х 0 … n-1 + a n x 0 )….)
Алгоритм, предложенный этим правилом, основан на оценке мономов, образованных выше, начиная с монома в самой внутренней скобке и продвигаясь к оценке мономов во внешней скобке.
Алгоритм выполняется по следующим шагам:
1. Положим k = n
2. Пусть b k = a k
3. Пусть b k — 1 = a k — 1 + b k x 0
4. Пусть k = k — 1
5. Если k ≥ 0 , то перейти к шагу 3
Иначе Конец
Этот алгоритм также можно изобразить графически, рассмотрев полином степени 5 , определяемый следующим образом:
F (x) = A 0 + A 1 x + A 2 x 2 + A 3 x 3 + A 4 x 4 + A 5 x 5
который можно оценить в x = x 0 , переставив его как:
F (x 0 ) = A 0 + x 0 (A 1 + x 0 (A 2 + x 0 (A 3 + x 0 (A A 4 + а 5 х 0 ))))
Другой способ представить результаты с использованием этого алгоритма — использовать таблицу, приведенную ниже:
| К | 5 | 4 | 3 | 2 | 1 | 0 |
| б 5 = а 5 | б 4 = а 4 + х 0 б 5 | б 3 = а 3 + х 0 б 4 | б 2 = а 2 + х 0 б 3 | б 1 = а 1 + х 0 б 2 | б 0 = а 0 + х 0 б 1 |
Пример: Вычисление многочлена f(x) = x 4 + 3x 3 + 5x 2 + 7x + 9 при x = 2
Решение:
Так как полином 4-й -й степени, то n = 4
| К | 4 | 3 | 2 | 1 | 0 |
| Шаг | б 4 = 1 | б 3 = 3 + 2 * 1 | б 2 = 5 + 2 * 5 | б 1 = 7 + 2 * 15 | б 0 = 9 + 2 * 37 |
| Результат | 1 | 5 | 15 | 37 | 83 |
Следовательно, f(2) = 83.
Почему мы должны это делать?
Обычно при вычислении полинома с определенным значением мы привыкли подставлять это значение в полином и выполнять вычисления. Для этого мы также можем использовать или разработать приложение для математических вычислений, что необходимо, когда мы имеем дело со сложными полиномами высокой степени.
То, как компьютер обрабатывает проблему, зависит главным образом от того, как вы, как программист, описываете ее компьютеру. Вы можете разработать приложение для решения полинома прямой подстановкой или синтетическим делением по правилу Горнера. Единственная разница между этими двумя подходами заключается в скорости, с которой компьютер решит задачу в любом случае.
Преимущество правила Горнера состоит в том, что оно уменьшает количество операций умножения. Зная, что время обработки компьютером одного процесса умножения в 5-20 раз превышает время обработки процесса сложения, вы можете сказать, что разработка вашего приложения для вычисления полинома с использованием правила Хорнера значительно улучшит время выполнения, затрачиваемое компьютером. .
.
Калькулятор полиномов деления
Метод Горнера — видео
Ванна | Англия, Великобритания
Сводка
Прочтите краткий обзор этой темы
Бат , город, унитарная администрация Бата и Северо-Восточного Сомерсета, историческое графство Сомерсет, юго-западная Англия. Бат лежит на берегу реки Эйвон (Нижний, или Бристоль, Эйвон) на естественной арене крутых холмов. Он был построен из местного известняка и является одним из самых элегантных и архитектурно выдающихся британских городов. Его аббатская церковь Святых Петра и Павла 16-го века построена в стиле поздней перпендикулярной готики и известна своими окнами, но богатство классических георгианских зданий, возвышающихся на крутых склонах долины, придает Бату особую известность. В 19 году город был включен в список Всемирного наследия ЮНЕСКО.87.
В 19 году город был включен в список Всемирного наследия ЮНЕСКО.87.
Горячие (115 °F [46 °C]) минеральные источники на этом месте привлекли римлян, которые основали Бат как Aquae Sulis, посвященный богине Сулис Минерве, слияние кельтского (Sul) и римского (Minerva ) божества. Саксы построили аббатство на том месте, где в 973 году Эдгар был коронован как первый король всей Англии. Впоследствии норманны перестроили церковь между 1088 и 1122 годами, перенеся туда епархию, которую они основали в Уэллсе. Епископский трон вернулся в Уэллс в 1206 году, и между канониками Уэллса и монахами Бата, титулярным аббатом которых был епископ, возникло долгое соперничество. Епархия по-прежнему называется Бат и Уэллс.
Викторина «Британика»
Объекты всемирного наследия в Соединенном Королевстве Викторина
Какое природное оборонительное сооружение было выбрано Вильгельмом Завоевателем в качестве крепости и бастиона против шотландцев? Какой дворец в Оксфордшире, Англия, был построен английским парламентом в качестве национального подарка Джону Черчиллю, 1-му герцогу Мальборо? Проверьте свои знания. Пройди тест.
Пройди тест.
Средневековая баня, зарегистрированная хартией в 1189 году, участвовала в торговле шерстью на западе Англии, а затем и в торговле тканью, но бани, хотя все еще использовались королевской семьей, содержались в плохом состоянии. Когда в 1755 году части римских бань были заново открыты, Бат уже возродился как курорт. В период своего расцвета в качестве фешенебельного курорта — под руководством общественного деятеля Ричарда («Красавчика») Нэша, одного из величайших английских денди, — елизаветинский город был перестроен и расширен в палладианском стиле архитекторами Джоном Вудом Старшим и Младшим и их покровитель, Ральф Аллен, который предоставил камень из своих местных каменоломен и построил особняк Прайор-Парк (1735–1748 гг.) С видом на город. В 1769 г.–74 Роберт Адам построил мост Пултни, чтобы соединить Бат с новым пригородом Батвик через реку Эйвон.
Недалеко от аббатства, в укрепленной долине реки Эйвон, находится насосная 18-го века, откуда можно добраться до горячих источников и римских бань. Среди примерно 140 исторических террас и отдельных зданий, украшающих город, — площадь Королевы, построенная Джоном Вудом Старшим между 1728 и 1735 годами; Цирк, начатый Вудом в 1754 году и завершенный его сыном; Королевский полумесяц 1767–1775 годов, также разработанный отцом и завершенный сыном; Ратуша, 1775 г .; Lansdown Crescent, построенный Джоном Палмером, 179 г.6–97; и павильон 1795 года в Сиднейских садах, Батвик, в котором сейчас находится коллекция произведений искусства музея Холберна. В 1942 году Актовые залы 1771 года были разрушены во время авианалета, от которого сильно пострадал весь город, но с тех пор была проведена обширная реконструкция, а также ремонт. В актовых залах, вновь открытых в 1963 году, теперь находится Музей моды, коллекция модной одежды мирового класса с 17 по 21 век. Claverton Manor, в 2 милях (3 км) от города, раннее 19Особняк 19-го века, в котором находится Американский музей в Британии, большой музей Американы.
Среди примерно 140 исторических террас и отдельных зданий, украшающих город, — площадь Королевы, построенная Джоном Вудом Старшим между 1728 и 1735 годами; Цирк, начатый Вудом в 1754 году и завершенный его сыном; Королевский полумесяц 1767–1775 годов, также разработанный отцом и завершенный сыном; Ратуша, 1775 г .; Lansdown Crescent, построенный Джоном Палмером, 179 г.6–97; и павильон 1795 года в Сиднейских садах, Батвик, в котором сейчас находится коллекция произведений искусства музея Холберна. В 1942 году Актовые залы 1771 года были разрушены во время авианалета, от которого сильно пострадал весь город, но с тех пор была проведена обширная реконструкция, а также ремонт. В актовых залах, вновь открытых в 1963 году, теперь находится Музей моды, коллекция модной одежды мирового класса с 17 по 21 век. Claverton Manor, в 2 милях (3 км) от города, раннее 19Особняк 19-го века, в котором находится Американский музей в Британии, большой музей Американы.
Будучи ведущим центром английского высшего общества за пределами Лондона в 18-м и начале 19-го веков, город богат литературными ассоциациями. Жизнь того времени наглядно изображена в романах Тобайаса Смоллетта и в пьесах Ричарда Бринсли Шеридана. В романах Джейн Остин Нортенгерское аббатство и Убеждение (оба 1817 г.) с тонкой сатирой и проницательным восприятием изображена светская жизнь Бата около 1800 г. Королевская национальная больница ревматических заболеваний), булочки для ванн, кирпичи для ванн и стулья для ванн (для инвалидов) получили свои названия от города.
Жизнь того времени наглядно изображена в романах Тобайаса Смоллетта и в пьесах Ричарда Бринсли Шеридана. В романах Джейн Остин Нортенгерское аббатство и Убеждение (оба 1817 г.) с тонкой сатирой и проницательным восприятием изображена светская жизнь Бата около 1800 г. Королевская национальная больница ревматических заболеваний), булочки для ванн, кирпичи для ванн и стулья для ванн (для инвалидов) получили свои названия от города.
По мере того, как общественная поддержка ослабевала, к 1970-м годам все городские спа-центры были закрыты. Однако, на фоне возрождения интереса к курортной культуре, рядом с горячими источниками в 2006 г. был открыт новый объект Thermae Bath Spa в фирменном здании, строительство которого также включало реставрацию пяти исторических зданий в традиционном курортном квартале города.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Туризм играет важную роль в местной экономике. Хотя Бат не является в первую очередь производственным центром, он также имеет значительную издательскую и легкую промышленность. Поп. (2001) 90,144; (2011) 94 782.
Хотя Бат не является в первую очередь производственным центром, он также имеет значительную издательскую и легкую промышленность. Поп. (2001) 90,144; (2011) 94 782.
Эта статья была недавно пересмотрена и обновлена Джеффом Валленфельдтом.
Англия | История, карта, флаг, население, города и факты
флаг Англии
Смотреть все СМИ
- Население:
- (2011) 53 012 456
- Форма правления:
- Официальный язык:
- нет
- Национальная религия:
- Англиканская церковь
- Общая площадь (кв. км):
- 130 278
Посмотреть все факты и статистику →
Резюме
Прочтите краткий обзор этой темы
Англия , преобладающая составная часть Соединенного Королевства, занимающая более половины острова Великобритании.
За пределами Британских островов Англия часто ошибочно считается синонимом острова Великобритании (Англии, Шотландии и Уэльса) и даже всего Соединенного Королевства. Несмотря на политическое, экономическое и культурное наследие, обеспечившее увековечивание ее имени, Англия больше официально не существует как государственная или политическая единица — в отличие от Шотландии, Уэльса и Северной Ирландии, которые имеют разную степень самоуправления во внутренних делах. дела. Учреждения редко работают только в Англии. Заметными исключениями являются англиканская церковь (Уэльс, Шотландия и Ирландия, включая Северную Ирландию, имеют отдельные отделения англиканской общины) и спортивные ассоциации крикета, регби и футбола. Во многих отношениях Англия, по-видимому, была поглощена большей массой Великобритании после принятия Акта об унии 1707 года9.0003
Пронизанная великими реками и небольшими ручьями, Англия представляет собой плодородную землю, и щедрость ее почвы на протяжении тысячелетий поддерживала процветающую сельскохозяйственную экономику. В начале 19 века Англия стала эпицентром всемирной промышленной революции и вскоре стала самой промышленно развитой страной мира. Извлекая ресурсы со всех заселенных континентов, такие города, как Манчестер, Бирмингем и Ливерпуль, превращали сырье в промышленные товары для глобального рынка, а Лондон, столица страны, превратился в один из выдающихся городов мира и центр политической и экономической жизни. , и культурная сеть, простиравшаяся далеко за пределы Англии. Сегодня столичный район Лондона охватывает большую часть юго-восточной Англии и продолжает служить финансовым центром Европы и быть центром инноваций, особенно в популярной культуре.
В начале 19 века Англия стала эпицентром всемирной промышленной революции и вскоре стала самой промышленно развитой страной мира. Извлекая ресурсы со всех заселенных континентов, такие города, как Манчестер, Бирмингем и Ливерпуль, превращали сырье в промышленные товары для глобального рынка, а Лондон, столица страны, превратился в один из выдающихся городов мира и центр политической и экономической жизни. , и культурная сеть, простиравшаяся далеко за пределы Англии. Сегодня столичный район Лондона охватывает большую часть юго-восточной Англии и продолжает служить финансовым центром Европы и быть центром инноваций, особенно в популярной культуре.
Одной из основных характеристик английского языка является разнообразие в пределах небольшого компаса. Ни одно место в Англии не находится на расстоянии более 75 миль (120 км) от моря, и даже самые дальние точки страны находятся не более чем в дне пути по дороге или по железной дороге от Лондона. Сформированная союзом небольших кельтских и англо-саксонских королевств в период раннего средневековья, Англия долгое время состояла из нескольких отдельных регионов, каждый из которых отличался диалектом, экономикой, религией и характером; действительно, даже сегодня многие англичане идентифицируют себя по регионам или графствам, из которых они происходят, например, Йоркшир, Уэст-Кантри, Мидлендс, и сохраняют прочные связи с этими регионами, даже если они живут в другом месте. Однако общие черты важнее этих различий, многие из которых начали исчезать в эпоху после Второй мировой войны, особенно с превращением Англии из сельского общества в высокоурбанизированное. Островное расположение страны имело решающее значение для развития английского характера, который воспитывает, казалось бы, противоречивые качества откровенности и сдержанности наряду с конформизмом и эксцентричностью, ценит социальную гармонию и, как и многие островные страны, хорошие манеры. которые обеспечивают упорядоченные отношения в густонаселенном ландшафте.
Однако общие черты важнее этих различий, многие из которых начали исчезать в эпоху после Второй мировой войны, особенно с превращением Англии из сельского общества в высокоурбанизированное. Островное расположение страны имело решающее значение для развития английского характера, который воспитывает, казалось бы, противоречивые качества откровенности и сдержанности наряду с конформизмом и эксцентричностью, ценит социальную гармонию и, как и многие островные страны, хорошие манеры. которые обеспечивают упорядоченные отношения в густонаселенном ландшафте.
Викторина «Британника»
Викторина «Знай свою географию Великобритании»
Кто такие «бродяги» Норфолка, Англия? Какое самое большое озеро на Британских островах? Проверьте свои знания. Пройдите этот тест.
С потерей британской обширной заморской империи в середине 20-го века Англия пережила кризис идентичности, и много энергии было посвящено дискуссиям об «английскости» — то есть не только о том, что значит быть англичанином в стране. в котором сейчас проживает большое количество иммигрантов из многих бывших колоний, и он гораздо более космополитичен, чем замкнут, но также и о том, что значит быть англичанином, а не британцем. Хотя английская культура опирается на культуры мира, она совершенно не похожа ни на одну другую, хотя ее трудно идентифицировать и определить. Из них английский писатель Джордж Оруэлл, «революционный патриот», который вел хронику политики и общества в XIX веке.30-е и 40-е годы, отмечено в Лев и Единорог (1941):
в котором сейчас проживает большое количество иммигрантов из многих бывших колоний, и он гораздо более космополитичен, чем замкнут, но также и о том, что значит быть англичанином, а не британцем. Хотя английская культура опирается на культуры мира, она совершенно не похожа ни на одну другую, хотя ее трудно идентифицировать и определить. Из них английский писатель Джордж Оруэлл, «революционный патриот», который вел хронику политики и общества в XIX веке.30-е и 40-е годы, отмечено в Лев и Единорог (1941):
Есть что-то самобытное и узнаваемое в английской цивилизации… Она как-то связана с плотными завтраками и хмурыми воскресеньями, прокуренными городами и извилистыми дорогами, зеленые поля и красные ящики-колонны. Он имеет свой собственный вкус. При этом она непрерывна, она простирается в будущее и прошлое, в ней есть нечто сохраняющееся, как в живом существе.
Для многих Оруэлл не хуже других уловил суть того, что Шекспир называл «этот благословенный сюжет, эта земля, это царство, эта Англия».
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Земля
Англия граничит на севере с Шотландией; на западе Ирландским морем, Уэльсом и Атлантическим океаном; на юге у Ла-Манша; и на востоке Северным морем.
Рельеф
Рельеф Англии низкий, но, за исключением востока, редко равнинный. Большая часть его состоит из холмистых склонов с самыми высокими возвышенностями на севере, северо-западе и юго-западе. Этот ландшафт основан на сложных базовых структурах, образующих замысловатые узоры на геологической карте Англии. Самые старые осадочные породы и некоторые изверженные породы (в виде изолированных гранитных холмов) находятся в Корнуолле и Девоне на юго-западе полуострова, древние вулканические породы лежат под частями Камбрийских гор, а самые современные аллювиальные почвы покрывают болота Кембриджшира, Линкольншира и Норфолк. Между этими областями лежат полосы песчаников и известняков разных геологических периодов, многие из которых являются реликтами первобытных времен, когда большие части центральной и южной Англии были затоплены теплыми морями. Геологические силы подняли и сложили некоторые из этих горных пород, образовав хребет северной Англии — Пеннины, которые возвышаются на 2,9 м над уровнем моря.30 футов (893 метра) в Кросс-Фелл. Камбрийские горы, которые включают в себя знаменитый Озерный край, достигают 3210 футов (978 метров) в Скафелл-Пайк, самой высокой точке Англии. Сланец покрывает большую часть северной части гор, а толстые слои лавы находятся в южной части. Другие осадочные слои образовали цепи холмов высотой от 965 футов (294 метра) в Норт-Даунс до 1083 футов (330 метров) в Котсуолдсе.
Геологические силы подняли и сложили некоторые из этих горных пород, образовав хребет северной Англии — Пеннины, которые возвышаются на 2,9 м над уровнем моря.30 футов (893 метра) в Кросс-Фелл. Камбрийские горы, которые включают в себя знаменитый Озерный край, достигают 3210 футов (978 метров) в Скафелл-Пайк, самой высокой точке Англии. Сланец покрывает большую часть северной части гор, а толстые слои лавы находятся в южной части. Другие осадочные слои образовали цепи холмов высотой от 965 футов (294 метра) в Норт-Даунс до 1083 футов (330 метров) в Котсуолдсе.
Холмы, известные как Чилтернс, Северный Йорк-Мурс и Йоркшир- и Линкольншир-Уолдс, были округлены до характерных плато с обращенными на запад откосами в течение трех последовательных ледниковых периодов эпохи плейстоцена (примерно от 2 600 000 до 11 700 лет назад). Когда растаял последний ледяной щит, уровень моря поднялся, затопив сухопутный мост, соединявший Великобританию с материковой частью Европы. Глубокие отложения песка, гравия и ледниковой грязи, оставленные отступающими ледниками, еще больше изменили ландшафт. Эрозия дождем, рекой, приливами и оседанием в некоторых частях восточной Англии впоследствии сформировала холмы и береговую линию. Плато известняка, гравелита и каменноугольных отложений связаны с крупными угольными месторождениями, некоторые из которых существуют в виде выходов на поверхность.
Эрозия дождем, рекой, приливами и оседанием в некоторых частях восточной Англии впоследствии сформировала холмы и береговую линию. Плато известняка, гравелита и каменноугольных отложений связаны с крупными угольными месторождениями, некоторые из которых существуют в виде выходов на поверхность.
Геологическая сложность Англии ярко проявляется в каменистой структуре береговой линии. Вдоль южного побережья от древних гранитных утесов Лендс-Энда на крайнем юго-западе тянется череда песчаников разного цвета и известняков разного возраста, завершающаяся белым мелом от острова Уайт до Дувра. Разнообразная панорама скал, заливов и устьев рек отличает английскую береговую линию, длина которой с ее многочисленными углублениями составляет около 2000 миль (3200 км).
Анализ Хорнера для отрицательных испытаний притока скважинных барьеров | SPE Бурение и заканчивание
Пропустить пункт назначения
08 сентября 2021 г.
Джеймс Пейтон;
Джоанна Саламага;
Аарон МакФи;
Артур Йонгеджан
SPE Drill & Compl 36 (03): 529–541.
Номер бумаги: SPE-204479-PA
https://doi.org/10.2118/204479-PA
История статьи
Получены:
сентября 102020
Полученная пересмотр:
Октябрь 30 2020
Принято:
ноябрь 03 2020
Опубликовано в Интернете:
Январь 14 2021
- Цитировать
- Посмотреть эту цитату
- Добавить в менеджер цитирования
- Делиться
- MailTo
- Твиттер
Получить разрешения
- Поиск по сайту
Цитирование
Пейтон, Джеймс, Саламага, Джоанна, Макфи, Аарон и Артур Йонгеджан. «Анализ Хорнера для отрицательных испытаний притока скважинных барьеров». SPE Drill & Compl 36 (2021): 529–541. doi: https://doi.org/10.2118/204479-PA
«Анализ Хорнера для отрицательных испытаний притока скважинных барьеров». SPE Drill & Compl 36 (2021): 529–541. doi: https://doi.org/10.2118/204479-PA
Скачать файл цитаты:
- Ris (Zotero)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- Конечная примечание
- РефВоркс
- Бибтекс
Расширенный поиск
Отрицательные испытания или испытания на приток проводятся для проверки целостности барьеров скважины в направлении потенциального потока, подвергая барьер отрицательному перепаду давления при мониторинге признаков утечки. Обычной практикой является наблюдение за скоростью обратного оттока из скважины. Отработка может быть признаком негерметичности из-за притока пластовых флюидов в скважину. Однако даже при отсутствии утечек обычно наблюдается обратный приток из-за теплового расширения скважинных флюидов. Теплопередача будет происходить между скважинными флюидами в каждом кольцевом пространстве и с окружающим пластом до тех пор, пока температуры не достигнут равновесия. Такое поведение описывается процессом термодиффузии, в результате чего повышение температуры вызывает расширение скважинных флюидов и обратный отток из скважины.
Однако даже при отсутствии утечек обычно наблюдается обратный приток из-за теплового расширения скважинных флюидов. Теплопередача будет происходить между скважинными флюидами в каждом кольцевом пространстве и с окружающим пластом до тех пор, пока температуры не достигнут равновесия. Такое поведение описывается процессом термодиффузии, в результате чего повышение температуры вызывает расширение скважинных флюидов и обратный отток из скважины.
В отраслевых рекомендациях указано, что анализ по Хорнеру может использоваться при мониторинге обратного выноса или повышения давления во время испытания притока. При этом инженеры и руководители буровых площадок могут использовать «график Хорнера», чтобы определить, связаны ли обратный приток или повышение давления с тепловыми эффектами. Те, у кого нет опыта работы в области разработки месторождений, могут не знать, что этот метод был первоначально получен из уравнения радиального потока для целей контроля роста давления в скважине, когда она закрывается после периода добычи. Очевидное сходство уравнений радиального потока и термодиффузии привело к тому, что метод Хорнера впоследствии был применен для прогнозирования статической температуры пласта по каротажным диаграммам. Однако, несмотря на то, что тепловое расширение является функцией температуры пласта, анализ Хорнера обратного притока или повышения давления во время испытания притока остается черным ящиком, который плохо изучен.
Очевидное сходство уравнений радиального потока и термодиффузии привело к тому, что метод Хорнера впоследствии был применен для прогнозирования статической температуры пласта по каротажным диаграммам. Однако, несмотря на то, что тепловое расширение является функцией температуры пласта, анализ Хорнера обратного притока или повышения давления во время испытания притока остается черным ящиком, который плохо изучен.
Впервые, опираясь на эмпирические данные по морским скважинам, мы показываем, что анализ Хорнера теплового расширения является практикой без теоретического обоснования. Радиальное уравнение, от которого зависит анализ Хорнера, наряду с ограничениями, вытекающими из граничных условий, не может точно учесть условия теста притока. В результате этот метод не следует использовать для анализа обратного притока или повышения давления во время испытания притока. Вместо этого предлагается новый метод интерпретации тенденции обратного притока при мониторинге перегородок скважины. Результаты этого исследования могут помочь улучшить понимание анализа Хорнера и методов интерпретации тестов притока.
Результаты этого исследования могут помочь улучшить понимание анализа Хорнера и методов интерпретации тестов притока.
Ключевые слова:
испытание бурильной колонны, термодиффузия, статическая температура пласта, наблюдение за резервуаром, тест притока, обратный поток, производственный контроль, добыча нефти и газа, пластовая температура, Горнер анализ
Предметы:
Испытания бурильной колонны/скважины, Оценка пласта и управление, Наблюдение и мониторинг за скважинами и резервуарами
Вы можете получить доступ к этой статье, если купите или потратите загрузку.
У вас еще нет аккаунта? регистр
Просмотр ваших загрузок
40-й ежегодный математический симпозиум WKU
Вернуться на главную страницу
Сессия 1: Теория управления дифференциальными уравнениями в частных производных
Председатель: д-р Озкан Озер, сопредседатели: Уилсон Хорнер и Ахмет Каан Айдин
9:45 — 11:40
Время: 9:45-10:10
Докладчики: Дональд Дж. Прайс и д-р Ахмет Озкан Озер
Прайс и д-р Ахмет Озкан Озер
Аннотация : Мы рассматриваем конечно-разностные полудискретизации (аппроксимации) печально известных одномерные волновые и пучковые уравнения. Соответствующее уравнение в частных производных Известно, что все аналоги (PDE) управляются одним граничным контроллером, применяемым на конце струны или луча. Однако полудискретные модели не стабилизируются. без фильтрации, которая не имитирует поведение PDE. Поэтому динамическая граница вводятся контроллеры вместе с косвенной фильтрацией. Мы показываем
Стабилизация граничной обратной связи вибрирующей струны с использованием отфильтрованного конечного разностный метод.
Мы также показываем граничную стабилизацию вибрирующей балки с обратной связью для двух различных модели: типа Эйлера-Бернулли и типа Рэлея.

Эти решения были построены таким образом, чтобы соответствовать уравнениям таким образом, чтобы все элементы управления параметры и даже исходные уравнения с высокими и низкими частотами могут быть изменены через программу Mathematica. Демонстрации и коды, используемые в презентации были опубликованы на веб-сайте демонстрационного проекта Wolfram: Demo 1 и Demo 2.
Этот проект спонсируется через KY NSF.
Время: 10:15-11:40
Докладчики: Эмма Мур, д-р Ахмет Озкан Озер
Аннотация: В теории управления система точно наблюдаема, если при измерении некоторого
свойство системы за конечное время, вы способны различать любые два различных начальных
состояния в строке. С уравнениями в частных производных (УЧП), такими как одномерные
волновое уравнение имеет бесконечно много собственных значений, что делает УЧП бесконечномерным,
поэтому точная наблюдаемость колебаний струны является бесконечномерной задачей.
На практике, однако, свойства системы наблюдают датчики, и датчики могут
наблюдать только конечное число колебательных мод. Поэтому конструкция датчика для наблюдаемого
свойство должно быть сделано для численной аппроксимации PDE, что делает его
конечномерная система. Однако точная наблюдаемость не имеет места для известных
методы численной аппроксимации, такие как метод конечных разностей (FDM) и метод конечных
Элементный метод (МКЭ). Основная проблема, с которой мы сталкиваемся, пытаясь показать точную наблюдаемость
аппроксимируемой системы заключается в том, что свойство равномерной щели собственных значений теряется,
что не так для бесконечномерной системы.
С уравнениями в частных производных (УЧП), такими как одномерные
волновое уравнение имеет бесконечно много собственных значений, что делает УЧП бесконечномерным,
поэтому точная наблюдаемость колебаний струны является бесконечномерной задачей.
На практике, однако, свойства системы наблюдают датчики, и датчики могут
наблюдать только конечное число колебательных мод. Поэтому конструкция датчика для наблюдаемого
свойство должно быть сделано для численной аппроксимации PDE, что делает его
конечномерная система. Однако точная наблюдаемость не имеет места для известных
методы численной аппроксимации, такие как метод конечных разностей (FDM) и метод конечных
Элементный метод (МКЭ). Основная проблема, с которой мы сталкиваемся, пытаясь показать точную наблюдаемость
аппроксимируемой системы заключается в том, что свойство равномерной щели собственных значений теряется,
что не так для бесконечномерной системы. Этот равномерный зазор обеспечивает
точные наблюдения вибрации датчиками. Без него датчики не могут различить
одной формы колебаний от другой. Это происходит из-за недостатков числового
методы вызывают искусственные высокочастотные собственные значения, что приводит к равномерному
зазор приближается к нулю, когда параметр сетки становится равным нулю.
Этот равномерный зазор обеспечивает
точные наблюдения вибрации датчиками. Без него датчики не могут различить
одной формы колебаний от другой. Это происходит из-за недостатков числового
методы вызывают искусственные высокочастотные собственные значения, что приводит к равномерному
зазор приближается к нулю, когда параметр сетки становится равным нулю.
Этот доклад будет посвящен
отсутствие наблюдаемости для МКЭ пространственно-аппроксимации волнового уравнения
средство, так называемая «методика прямой фильтрации», которая позволяет нам доказать точную наблюдаемость.
Доказательства основаны на так называемом «методе дискретных множителей». Этот проект
спонсируется через KY NSF и WKU RCAP.
Этот проект
спонсируется через KY NSF и WKU RCAP.
Время: 10:45-11:10
Докладчики: Райан Сент-Клер и д-р Ахмет Озкан Озер
Аннотация: В этом проекте выполняется полный спектральный анализ для непрерывного и дискретного
версии одномерных моделей УЧП для волнового уравнения с Дирихле-Нейманом
и граничные условия Неймана-Неймана. Дискретизированный по пространству метод конечных разностей
используется для дискретной модели. Наше исследование показывает, что дискретизированная модель для
каждому типу граничных условий не хватает свойства зазора в собственных значениях, особенно
для высокочастотных мод колебаний, так как параметр дискретизации стремится к
нуль. Однако для непрерывной модели это не так.
Однако для непрерывной модели это не так.
Время: 11:15-11:40
Ведущий: Уилсон Хорнер, д-р Ахмет Озкан Озер
Аннотация: В теории управления время, необходимое для получения сигнала после его отправки, равно упомянутый
в качестве времени наблюдения. Для некоторых типов материалов время наблюдения до
прием волнового сигнала различается в зависимости от множества факторов, таких как материал
плотность, гибкость и т. д. Предположим, что у нас есть сильно связанные волновые уравнения, описывающие
колебания на пьезоэлектрической балке длиной L. Волновые уравнения имеют разные
скорости волны c_1 и c_2. Доказано, что минимальное время наблюдения удовлетворяет T>T_1=2L/(min{c_1,c_2}). Далее мы дискретизируем пространственную переменную для связанных волновых уравнений с помощью конечного
Отличия. Получаем, что для этой конкретной дискретизации наблюдаемость
время приближается к бесконечности, что не соответствует непрерывному случаю. Чтобы решить эту
проблема, применяется метод фильтрации, известный как прямая фильтрация, и (неоптимальный)
время наблюдения T>T_1>T_2 получается.
Получаем, что для этой конкретной дискретизации наблюдаемость
время приближается к бесконечности, что не соответствует непрерывному случаю. Чтобы решить эту
проблема, применяется метод фильтрации, известный как прямая фильтрация, и (неоптимальный)
время наблюдения T>T_1>T_2 получается.
Сессия 2: Математическая биология
Стулья: доктор Ричард Шугарт и доктор Нгок Нгуен
9:45 — 11:40
Время: 9: 45-10: 10000903 : 9: 45-10: 10000
. Докладчики: Мэгги Джонс и Глория Хуанг
Аннотация: Biosystem Balancer — игра-симулятор экосистемы, моделирующая взаимодействие хищника и жертвы.
в пищевой цепи из четырех видов в четырех различных биомах. Взаимодействие хищник-жертва
реализуются через модель дифференциального уравнения с четырьмя уравнениями. Наша программа учит
пользователю о модели и о том, как изменение взаимодействия между видами влияет на
популяции других видов в экосистеме. Цель пользователя в нашей программе —
найти правильные стартовые популяции для каждого вида, чтобы предотвратить перенаселение/вымирание
в виде. Поиск правильных стартовых популяций приведет к экосистеме
в равновесии, при котором все четыре популяции остаются постоянными во времени, или сбалансированным
биосистема.
Наша программа учит
пользователю о модели и о том, как изменение взаимодействия между видами влияет на
популяции других видов в экосистеме. Цель пользователя в нашей программе —
найти правильные стартовые популяции для каждого вида, чтобы предотвратить перенаселение/вымирание
в виде. Поиск правильных стартовых популяций приведет к экосистеме
в равновесии, при котором все четыре популяции остаются постоянными во времени, или сбалансированным
биосистема.
Время: 10:15-10:40
Ведущие: Глория Хуанг, Дикша Сатиш, д-р Ричард Шугарт
Резюме: Лечение хронических ран долгое время было проблемой для медицинских работников.
и представляет собой экономическое бремя для здравоохранения во всем мире. Чтобы помочь исцеляющему ответу
хронических ран ранее использовались четыре дифференциальных уравнения для моделирования зависимостей
между матриксными металлопротеиназами (ММП-1), их ингибиторами (ТИМП-1) и внеклеточным
матрица (ECM) с использованием усредненных данных пациента в процессе заживления диабетической язвы стопы.
В этой работе используется математическая модель и анализируются отдельные данные.
от шестнадцати пациентов в течение двенадцати недель. Подход к моделированию смешанных эффектов был
используется для подгонки кривой под математическую модель. Моделирование смешанных эффектов было реализовано в
MONOLIX, где был использован алгоритм стохастической аппроксимации ожидания-максимизации.
используется для расчета параметров населения на основе данных пациентов.
Чтобы помочь исцеляющему ответу
хронических ран ранее использовались четыре дифференциальных уравнения для моделирования зависимостей
между матриксными металлопротеиназами (ММП-1), их ингибиторами (ТИМП-1) и внеклеточным
матрица (ECM) с использованием усредненных данных пациента в процессе заживления диабетической язвы стопы.
В этой работе используется математическая модель и анализируются отдельные данные.
от шестнадцати пациентов в течение двенадцати недель. Подход к моделированию смешанных эффектов был
используется для подгонки кривой под математическую модель. Моделирование смешанных эффектов было реализовано в
MONOLIX, где был использован алгоритм стохастической аппроксимации ожидания-максимизации.
используется для расчета параметров населения на основе данных пациентов. Генерируемое население
затем значения параметров использовались в качестве отправной точки для расчета отдельных параметров.
индивидуальны для данных каждого пациента. С помощью MONOLIX все шестнадцать пациентов были успешно
кривая подходит для создания более индивидуальной реакции пациента. Чтобы изучить идентифицируемость параметров,
трехмерная геометрия пространства параметров визуализировалась для всех попарно
комбинации параметров всех пациентов, чтобы увидеть влияние на биологическую систему.
Этот подход отображает два параметра в зависимости от суммы квадратов ошибок для создания
трехмерный график. Алгоритм Delayed Rejection Adaptive Metropolis (DRAM)
в MATLAB затем использовали для подтверждения результатов геометрии. Эти результаты показывают, что
параметры в уравнении TIMP больше всего влияют на реакцию заживления раны.
Генерируемое население
затем значения параметров использовались в качестве отправной точки для расчета отдельных параметров.
индивидуальны для данных каждого пациента. С помощью MONOLIX все шестнадцать пациентов были успешно
кривая подходит для создания более индивидуальной реакции пациента. Чтобы изучить идентифицируемость параметров,
трехмерная геометрия пространства параметров визуализировалась для всех попарно
комбинации параметров всех пациентов, чтобы увидеть влияние на биологическую систему.
Этот подход отображает два параметра в зависимости от суммы квадратов ошибок для создания
трехмерный график. Алгоритм Delayed Rejection Adaptive Metropolis (DRAM)
в MATLAB затем использовали для подтверждения результатов геометрии. Эти результаты показывают, что
параметры в уравнении TIMP больше всего влияют на реакцию заживления раны.
Время: 10:45-11:10
Докладчики: Руби Мейсон и Оливия Шарп
Резюме: Различные общедоступные компьютерные программы были разработаны с использованием стандартного дифференциала SIR.
модель уравнения для отображения элементарного распространения эпидемии; тем не менее, расширенный
версия уравнений SIR, примененная к практическому образовательному опыту, не
были обнаружены в исследованиях. Этот проект включает расширенное уравнение SIR, используемое для моделирования
различные эпидемии, зависящие от нескольких определяемых пользователем переменных. Этот математический
система была реализована в Wolfram Mathematica для создания педагогической программы. Этот
тренажер распространения болезни предназначен для использования учащимися средних и старших классов
введение в эпидемиологию. Программа не производит научного
точные данные, чтобы их можно было использовать для прогнозирования ситуаций в реальной жизни или для расширенных
эпидемиологическая работа. Вместо этого он предоставляет оценки, достаточные для того, чтобы учащиеся
выявить причинно-следственные связи между параметрами, которые они вводят, и результатом
их эпидемии. Разработанная модель представлена через удобный интерфейс
с соответствующими визуальными и информационными подсказками. В качестве средства обучения он обеспечивает
тщательный опыт обучения, подходящий для целевой аудитории и помогающий в создании
фундаментальные понятия эпидемиологии более доступными.
Программа не производит научного
точные данные, чтобы их можно было использовать для прогнозирования ситуаций в реальной жизни или для расширенных
эпидемиологическая работа. Вместо этого он предоставляет оценки, достаточные для того, чтобы учащиеся
выявить причинно-следственные связи между параметрами, которые они вводят, и результатом
их эпидемии. Разработанная модель представлена через удобный интерфейс
с соответствующими визуальными и информационными подсказками. В качестве средства обучения он обеспечивает
тщательный опыт обучения, подходящий для целевой аудитории и помогающий в создании
фундаментальные понятия эпидемиологии более доступными.
Время: 11:15-11:40
Докладчики: Ферхан М. Атичи и Нгок Нгуен
Атичи и Нгок Нгуен
Резюме: дробное представление фармакокинетики-фармакодинамики (ПК-ПД)
модель, описывающая рост опухоли и противораковые эффекты в непрерывном времени с учетом
шкала времени hN_0 , где ч>0 . Поскольку измерения концентрации препарата в плазме проводились ежечасно, мы
рассмотрим ч = 1/24 и получим модель в дискретном времени (т.е. ежечасно). Затем мы продолжаем дробление
-дискретный оператор набла в h -дискретную модель для получения модели в виде системы набла h — дробных разностных уравнений. Для аналитического решения дробной h -дискретной системы мы сформулируем и докажем некоторые теоремы теории дискретных
дробное исчисление. После оценки и получения доверительных интервалов модели
параметров, мы сравниваем остаточные значения квадратов суммы моделей в одной таблице. Наш
исследование показывает, что новые представленные модели обеспечивают подгонку так же хорошо, как и существующие
модели в непрерывном времени.
Наш
исследование показывает, что новые представленные модели обеспечивают подгонку так же хорошо, как и существующие
модели в непрерывном времени.
Сессия 3: Теория узлов
Стулья: Доктор Клаус Эрнст
9:45 — 11:40
Время: 9: 45-10: 100003
768. Abstract: Используя простой класс узлов, называемых рациональными узлами, мы обсудим взаимосвязь эти узлы с концепцией непрерывных дробей в теории чисел.
Время: 10:15-10:40
Докладчики: Benjamin Handshoe and Calvin Higdon
Abstract: Некогерентное обнуление — это операция на диаграмме узла, которая упрощает узел.
Упрощенные диаграммы узлов называются «дочерними» диаграммами узлов. Презентация
объясним эту операцию и как ее выполнить на многих узлах с помощью компьютера
программа Математика. Некоторые примеры того, что будет показано, следующие: отношения между узлами и их потомками путем некогерентного обнуления, частоты узлов
в результате аннулирования и анализа количества уникальных детей узла
имеет бессвязной аннулированием.
Презентация
объясним эту операцию и как ее выполнить на многих узлах с помощью компьютера
программа Математика. Некоторые примеры того, что будет показано, следующие: отношения между узлами и их потомками путем некогерентного обнуления, частоты узлов
в результате аннулирования и анализа количества уникальных детей узла
имеет бессвязной аннулированием.
Время: 10:45-11:10
Ведущий: Харрисон Говер
Аннотация: Мы опишем несколько способов того, как узел может изгибаться, если его нарисовать на бумаге. Мы определим несколько терминов, таких как «спираль» и «кудрявый», для описания того, как рисунок узла может кривой и доказать некоторые результаты.
Время: 11:15-11:40
Ведущие: Дональд Дж. Прайс и Натан Гиллиспи
Прайс и Натан Гиллиспи
Abstract: Узел можно определить как замкнутую несамопересекающуюся кривую, вложенную в 3 измерения. Узлы традиционно рассматриваются как проекция на 2 измерения, такие как как рисунки. Одним заметным исключением является программное обеспечение KnotPlot, которое позволяет пользователь для просмотра узлов в 3-х измерениях. Мы показываем работу над решением с помощью Oculus гарнитура и игровой движок Unity, который позволит пользователям просматривать узлы в 3D на компьютере. и/или в виртуальной реальности.
Сессия 4: Вычислительная математика I
Стулья: Доктор Марк Робинсон и доктор Саманги Мунасингхе
9:45 — 11:40
Время: 9: 45-10: 100009
. : Михаил Хеннер
: Михаил Хеннер
Abstract: Электрические токи обычно используются в материаловедении и нанонауке для структурирования поверхности проводящих твердых пленок. Я представлю и обсужу модель, ее анализ и вычисления, где поверхность представляет собой бинарный кристалл. Таким образом, динамика поверхности эволюция формы и динамика эволюции композиции связаны. Модель основан на паре сильно нелинейных параболических УЧП 4-го и 2-го порядков.
Время: 10:15-10:40
Докладчик: Итан Келли
Аннотация: В этой статье получены реализация и графические результаты, из серии
расширение ранее обнаруженной функции напряжения бегущей волны, описываемой выражением
решение уравнения потенциала действия Ходжкина-Хаксли.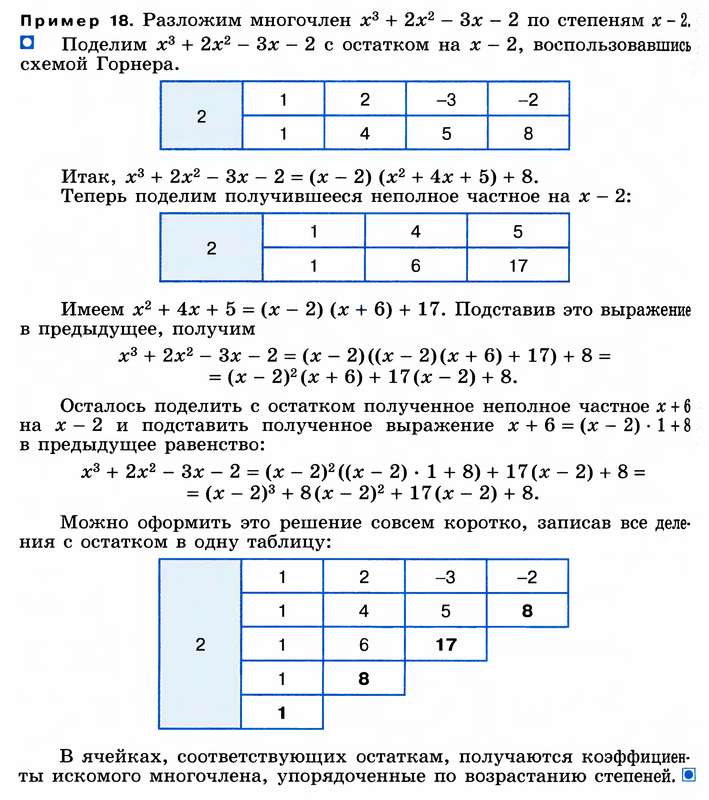 Использование системы на базе Mathematica
анализа ранее полученной функции напряжения получаются хорошо сформированные
графики, которые ведут себя как солитоны при взаимодействии с другими волнами. Расчеты,
используя вышеупомянутую функцию напряжения с числовыми значениями параметров системы,
указывают, что теоретически предсказанное решение потенциала бегущей волны соответствует
экспериментально наблюдаемый потенциал действия нейрона; эти результаты были
показано здесь
Использование системы на базе Mathematica
анализа ранее полученной функции напряжения получаются хорошо сформированные
графики, которые ведут себя как солитоны при взаимодействии с другими волнами. Расчеты,
используя вышеупомянутую функцию напряжения с числовыми значениями параметров системы,
указывают, что теоретически предсказанное решение потенциала бегущей волны соответствует
экспериментально наблюдаемый потенциал действия нейрона; эти результаты были
показано здесь
Время: 10:45-11:10
Ведущий: Шрия Арора и Брюс Кесслер
Резюме: Партизанское манипулирование границами районов с целью установления
несправедливое политическое преимущество для конкретной партии или группы. Цель этого исследования
проект заключается в разработке кода для оценки текущего районирования штата с использованием вычислительных
математика. Мы разработали модель случайного блуждания с помощью Wolfram Mathematica, которая генерирует
тысячи районных планов. Новые районы по-прежнему соответствуют критериям, касающимся
границы населения и прилегающие территории. Затем эти планы анализируются, чтобы найти
нормальные распределения. Чтобы проверить алгоритм, состояние модели «Пентукки»
в составе 6 районов и 100 участков. Два разрозненных начальных района
планы использовались в качестве входных данных для алгоритма; стабильное среднее число победителей в результате
из обоих районных планов. Эта концепция в дальнейшем применяется с 3,692 участка
в Кентукки.
Цель этого исследования
проект заключается в разработке кода для оценки текущего районирования штата с использованием вычислительных
математика. Мы разработали модель случайного блуждания с помощью Wolfram Mathematica, которая генерирует
тысячи районных планов. Новые районы по-прежнему соответствуют критериям, касающимся
границы населения и прилегающие территории. Затем эти планы анализируются, чтобы найти
нормальные распределения. Чтобы проверить алгоритм, состояние модели «Пентукки»
в составе 6 районов и 100 участков. Два разрозненных начальных района
планы использовались в качестве входных данных для алгоритма; стабильное среднее число победителей в результате
из обоих районных планов. Эта концепция в дальнейшем применяется с 3,692 участка
в Кентукки. Используя регистрационную статистику, алгоритм сгенерирует распределение
планов распределения округов в надежде гарантировать равное представительство избирателей.
Используя регистрационную статистику, алгоритм сгенерирует распределение
планов распределения округов в надежде гарантировать равное представительство избирателей.
Время: 11:15-11:40
Докладчик: Марк П. Робинсон, Университет Западного Кентукки
Аннотация: Метод Ньютона и его варианты оказались полезными при решении многих задач в нелинейная оптимизация. Введение в эти методы представлено в этой презентации.
Сессия 5: Теория чисел и информатика
Председатели: д-р Доминик Ланфьер и д-р Лан Нгуен
2:30 — 4:25
Время: 3 3:50-02:00 Докладчики: Мина Рюмаэ, д-р Ута Зиглер Аннотация: Стратегическая игра с нулевой суммой для двух человек «Точки и коробки» имеет большие вычислительные
бремя, что затрудняет использование грубой силы для рассмотрения возможных конфигураций платы
которые экспоненциально увеличиваются с размером платы. Эта работа посвящена транспозициям, то есть конфигурациям доски, которые могут быть достигнуты
через несколько последовательностей ходов, которые довольно распространены во многих играх. Конкретно,
цель состоит в том, чтобы улучшить соотношение выигрыша/проигрыша/ничьи и эффективность игрока MCTS за счет
влияет на количество и качество информации, полученной в результате моделирования. Основа
Процесс выбора MCTS использует преимущество перемещения для расчетов выбора.
предлагаемый процесс отбора модифицирует базовый процесс, используя преимущества результирующего
конфигурации доски после того, как ход был сделан для расчетов выбора. Рамки
была разработана, которая позволяет игрокам, использующим различные процессы выбора, играть напрямую
друг против друга. Время: 3:00-3:25 Докладчики: Брайан Маццони, К. Тейт Томсон и Шейн Мэтью Палмквист Резюме: Посвященная работе профессора доктора Георга Кантора имеет большое значение. важность для математики
поскольку это ясно демонстрирует, что существуют различные бесконечности, а бесконечность гораздо более
чем просто концепция. Однако его работа, как и все другие работы по математике и естественным наукам,
относительна и подлежит интерпретации. В то время как его работа предлагает уникальную и критическую
точки зрения на тему бесконечностей, особенно в отношении алефов и омег, других
перспективы возможны и в равной степени действительны и эффективны. Время: 3:30-3:55 Ведущий: Аллен Лин Аннотация. Мы обобщаем результаты знакопеременных рядов Дирихле, впервые рассмотренных Джунсунгом.
Чой. В частности, мы исследуем его аналитическое продолжение и его специальные значения.
Мы также связываем значения ряда Дирихле Чоя со значениями другого ряда Дирихле.
серии. Наконец, мы связываем этот последний класс рядов Дирихле с L-функциями Дирихле,
в конечном итоге получая значения знакопеременного ряда Дирихле. Время: 4:00-4:25 Докладчики: К. Тейт Томпсон, Кэмерон Джексон и Шейн Мэтью Палмквист Аннотация: Числа являются основополагающими понятиями и принципами в математике. Они позволяют нам
измерять, сравнивать, количественно определять и анализировать явления в технике, прикладных науках,
бизнес и многое другое. Сессия 6: Вероятность, статистика и математика Эд Председатели: д-р Лукун Чжэн и д-р Ричард Шугарт 2:30 — 4:25 Время: 2:59-2:30 Докладчик: Лукун Чжэн Аннотация: В этой статье мы изучаем моделирование и оценку структуры зависимости между
рынки валютных курсов, использующие доходность обменных курсов, основанных на долларах США
(Японская иена, евро, австралийские доллары и британские фунты стерлингов по отношению к долларам США).
Предлагается новый подход, основанный на модели смешанной связки, которая может фиксировать различные
модели взаимозависимости между обменными курсами. Доходность каждого обменного курса
отфильтровано с использованием фильтрации ARMA-GARCH для удаления последовательной зависимости. Время: 3:00-3:25 Ведущие: Эндрю Дэвисон, Морган Пробы Резюме: В карточной игре Love Letter игроки делают несколько предположений о содержании своего противника. Время: 3:30-3:55 Ведущие: Ахмет Озкан Озер, Наташа Герстеншлагер, Лукун Чжэн Резюме: Исчисление I является наиболее фундаментальным курсом для науки, технологии,
специальность, предназначенная для инженеров и математиков (STEM). За последние два года было разработано более 700 защищенных авторским правом обучающих и обучающих видеороликов, некоторые из которых были опубликованы на канале доктора Озера в YouTube: MathbyDrOzz. Производство этих видеороликов было первым этапом перехода к традиционным
чтение лекций на видео-площадку по проработанному контенту и новейшей видеозаписи
и технологии редактирования. Эти видеоролики демонстрируются экспериментальной и контрольной группам.
На основании анализа собранных данных видно, что существует значительное
долгосрочный эффект (около четырех месяцев) в успехе учащихся. Разговор будет посвящен
аспекты производства, дизайна, разработки и реализации этих видеороликов. Время: 4:00-4:25 Ведущий: Ричард Шугарт Аннотация: Я написал и использовал либо в своем классе, либо в тесте. Сессия 7: Компьютерная математика II ПРЕДЛОЖЕНИЕ: Доктор Джон Спрейкер 2:30 — 4:25 Время: 2: 30-2: 55 . Принчики: 2: 30-2: 55 767. Raychel Kool Abstract: Головоломка танграм представляет собой тип головоломки с рассечением, состоящей из семи частей многоугольника.
Чтобы «решить» танграм-головоломку, вы следуете данному вам плану и пытаетесь воссоздать
это с кусочками, которые вам даны. Наша программа Mathematica позволяет пользователю решать такие
головоломки двумя различными способами: один, используя стандартный набор кусочков танграма (два
маленькие треугольники, один средний треугольник, два больших треугольника, один квадрат и один параллелограмм)
решать предустановленные конструкции головоломок; два, используя наш интерфейс Create-Your-Own, чтобы сначала
нарисуйте контур, а затем разрешите нашей программе разделить созданную пользователем головоломку на
7 случайных форм. Время: 3:00-3:25 Ведущие: Старр Мэй и Амариа Стрит Аннотация: Сэмплирование — один из самых полезных инструментов в производстве электронной музыки, но он
ограничен как цифровой инструмент из-за небольшой длины, связанной с семплами
которые повторно переданы выше. Используя Mathematica и быстрое преобразование Фурье, мы создали
программный синтезатор, который решает эту проблему. Синтезатор работает в двух
основные режимы, как синтезатор сэмплера и как аппроксиматор сэмпла с восемью осцилляторами. Время: 3:30-3:55 Докладчики: Ферхан М. Атичи и С. Chang Abstract: В этом докладе мы представляем введение в дробное h-дискретное исчисление. Дробный
операторы h-разности и дробной h-суммы заданы в смысле установленных
Определение Римана-Лиувилля. Продолжаем вводить дробно-линейный порядок
h-разностные уравнения, где порядок уравнения — любое нецелое положительное
настоящий номер. Время: 4:00-4:25 Ведущие: Сачи Барнаби и Лола Обиелодан Резюме: В этом проекте мы создали генератор случайной музыки, который записывает ноты в соответствии с
правила музыкальной композиции. Этот музыкальный генератор помогает музыкантам практиковаться в чтении с листа.
Чтение с листа — это навык, при котором музыканты играют незнакомую музыку настолько точно, насколько они
можно с первой попытки. Будучи лучшим читателем с листа, музыканты могут научиться
их музыка более эффективно. Первым шагом было представление мелодии в виде последовательности
нот в Mathematica, где каждая нота имеет высоту тона и длину. Для просмотра некоторых ссылок на этой странице может потребоваться дополнительное программное обеспечение. Загрузить Acrobat Reader Скачать QuickTime Вводится задача игры
когда игрок вынужден сделать еще один ход после подсчета очков, что создает огромное количество
последовательности движений игрока. Алгоритм поиска по дереву Монте-Карло (MCTS) представляет собой машину
подход к обучению, который строит частичное игровое дерево из позиций на доске и их ходов
считаются важными для игры, а не с использованием методов обрезки или поиска
все дерево игры. Для каждой конфигурации платы выполняется большое количество симуляций.
добавлены в дерево для сбора статистических данных (например, количество раз, когда каждый ход
возможный в этой конфигурации был протестирован и общая польза от переезда). Каждое моделирование
использует предварительно собранные данные для выбора ходов и обновляет данные после нахождения симуляции
полученные результаты.
Вводится задача игры
когда игрок вынужден сделать еще один ход после подсчета очков, что создает огромное количество
последовательности движений игрока. Алгоритм поиска по дереву Монте-Карло (MCTS) представляет собой машину
подход к обучению, который строит частичное игровое дерево из позиций на доске и их ходов
считаются важными для игры, а не с использованием методов обрезки или поиска
все дерево игры. Для каждой конфигурации платы выполняется большое количество симуляций.
добавлены в дерево для сбора статистических данных (например, количество раз, когда каждый ход
возможный в этой конфигурации был протестирован и общая польза от переезда). Каждое моделирование
использует предварительно собранные данные для выбора ходов и обновляет данные после нахождения симуляции
полученные результаты.
 Соотношение побед/проигрышей/ничьи и сравнение эффективности между игроками
будут представлены основные и предлагаемые процессы отбора.
Соотношение побед/проигрышей/ничьи и сравнение эффективности между игроками
будут представлены основные и предлагаемые процессы отбора. Эта работа строится на
Фонд Кантора предлагает новый и несколько иной взгляд на предмет
бесконечности. Новый и отличающийся набор чисел, называемый лемнискатными числами.
предлагается. Однако этот новый набор предлагаемых чисел напрямую связан обратно
в рай Кантора, чтобы помочь объединить математику для будущих достижений. Результаты, достижения
удивительны, но просты и окажут значительное влияние на числовую математику
сейчас и в ближайшем будущем. Эта работа помогает преодолеть разрыв между нашим нынешним
понимание бесконечности и действительной бесконечности, предлагая подход, который ближе
к математической истине, чем существует в настоящее время. Надеемся, что эта работа послужит
как катализатор будущих математических разработок, влияющих на многие области знаний
требующие большего понимания чисел, таких как прикладная математика, естественные науки, инженерия,
и технологии.
Эта работа строится на
Фонд Кантора предлагает новый и несколько иной взгляд на предмет
бесконечности. Новый и отличающийся набор чисел, называемый лемнискатными числами.
предлагается. Однако этот новый набор предлагаемых чисел напрямую связан обратно
в рай Кантора, чтобы помочь объединить математику для будущих достижений. Результаты, достижения
удивительны, но просты и окажут значительное влияние на числовую математику
сейчас и в ближайшем будущем. Эта работа помогает преодолеть разрыв между нашим нынешним
понимание бесконечности и действительной бесконечности, предлагая подход, который ближе
к математической истине, чем существует в настоящее время. Надеемся, что эта работа послужит
как катализатор будущих математических разработок, влияющих на многие области знаний
требующие большего понимания чисел, таких как прикладная математика, естественные науки, инженерия,
и технологии.
 В этой статье рассматривается работа двух студентов-строителей.
студенты, которые изучают, что такое число в математике, изучая значение и применение.
Исследуются числовые типы и группы известных конечных чисел. На основании этого расследования,
потенциально новые цифры разработаны и представлены, чтобы заполнить пробел в понимании
которая существует в нашей системе числовых линий. Результаты удивительны и служат
средство, помогающее унифицировать и прояснить числовую математику по итогам работы
Куртом Гёделем и его теоремами о неполноте. Кроме того, эта работа служит
маяк, чтобы помочь осветить новые возможности для будущих разработок в области прикладной математики.
Представлена студенческая оценка этого исследовательского проекта.
В этой статье рассматривается работа двух студентов-строителей.
студенты, которые изучают, что такое число в математике, изучая значение и применение.
Исследуются числовые типы и группы известных конечных чисел. На основании этого расследования,
потенциально новые цифры разработаны и представлены, чтобы заполнить пробел в понимании
которая существует в нашей системе числовых линий. Результаты удивительны и служат
средство, помогающее унифицировать и прояснить числовую математику по итогам работы
Куртом Гёделем и его теоремами о неполноте. Кроме того, эта работа служит
маяк, чтобы помочь осветить новые возможности для будущих разработок в области прикладной математики.
Представлена студенческая оценка этого исследовательского проекта.
 Двухэтапный алгоритм
затем используется для оценки модели: во-первых, предельное распределение каждого отдельного
отфильтрованная доходность оценивается непараметрически; во-вторых, параметры в смешанном
модели копулы оцениваются с использованием метода оценки максимального правдоподобия (MLE). Соответствие
Тест проводится для оценки производительности оцениваемой модели. Эмпирический
результаты показывают сильную взаимозависимость между этими основными рынками обменных курсов, которые
обеспечивает важные последствия для различных заинтересованных сторон на рынке.
Двухэтапный алгоритм
затем используется для оценки модели: во-первых, предельное распределение каждого отдельного
отфильтрованная доходность оценивается непараметрически; во-вторых, параметры в смешанном
модели копулы оцениваются с использованием метода оценки максимального правдоподобия (MLE). Соответствие
Тест проводится для оценки производительности оцениваемой модели. Эмпирический
результаты показывают сильную взаимозависимость между этими основными рынками обменных курсов, которые
обеспечивает важные последствия для различных заинтересованных сторон на рынке. передать через
сочетание человеческого мышления и ясной вероятности. Информация, собранная в
этот процесс не является определенным, но часто имеет жизненно важное значение для хорошей игры. Мы разработали
версия Любовное письмо в Mathematica , чьи игроки с искусственным интеллектом справляются с использованием неопределенных данных о противоборствующих игроках путем
взвешивание определенных возможностей с выводами, сделанными компьютерным игроком. Мы представляем
наш конечный продукт, который наряду с потрясающей графикой часто может обыграть конкурента-человека.
передать через
сочетание человеческого мышления и ясной вероятности. Информация, собранная в
этот процесс не является определенным, но часто имеет жизненно важное значение для хорошей игры. Мы разработали
версия Любовное письмо в Mathematica , чьи игроки с искусственным интеллектом справляются с использованием неопределенных данных о противоборствующих игроках путем
взвешивание определенных возможностей с выводами, сделанными компьютерным игроком. Мы представляем
наш конечный продукт, который наряду с потрясающей графикой часто может обыграть конкурента-человека. Осенью 2010 года были
более 300 000 студентов, изучающих исчисление I в США, а также в колледжах и университетах США
борются с высоким процентом отсева и неудач в исчислении. В самом деле, недавний
Национальное исследование университетского исчисления, проведенное Математической ассоциацией Америки.
при поддержке Национального научного фонда отмечается, что показатели успеха
по исчислению я очень низок для традиционных студентов, и еще ниже для нетрадиционных
студенты: женщины, студенты из недостаточно представленных меньшинств, экономически неблагополучные
школьники и учащиеся колледжей в первом поколении. В том же отчете подчеркивается
что уровень удержания довольно низок на курсах математического анализа. Студенты также выражают озабоченность
о недостаточности освещенной в курсе информации и отсутствии возможностей
практиковать изученную педагогику.
Осенью 2010 года были
более 300 000 студентов, изучающих исчисление I в США, а также в колледжах и университетах США
борются с высоким процентом отсева и неудач в исчислении. В самом деле, недавний
Национальное исследование университетского исчисления, проведенное Математической ассоциацией Америки.
при поддержке Национального научного фонда отмечается, что показатели успеха
по исчислению я очень низок для традиционных студентов, и еще ниже для нетрадиционных
студенты: женщины, студенты из недостаточно представленных меньшинств, экономически неблагополучные
школьники и учащиеся колледжей в первом поколении. В том же отчете подчеркивается
что уровень удержания довольно низок на курсах математического анализа. Студенты также выражают озабоченность
о недостаточности освещенной в курсе информации и отсутствии возможностей
практиковать изученную педагогику. Поэтому ученики с трудом отрабатывают сложные шаги.
исчисления.
Поэтому ученики с трудом отрабатывают сложные шаги.
исчисления. Проблемы демонстрируют нашу
таланты уходящего начальника отдела в решении проблем и музыке. *ода не выдерживает
для обыкновенного дифференциального уравнения.
Проблемы демонстрируют нашу
таланты уходящего начальника отдела в решении проблем и музыке. *ода не выдерживает
для обыкновенного дифференциального уравнения.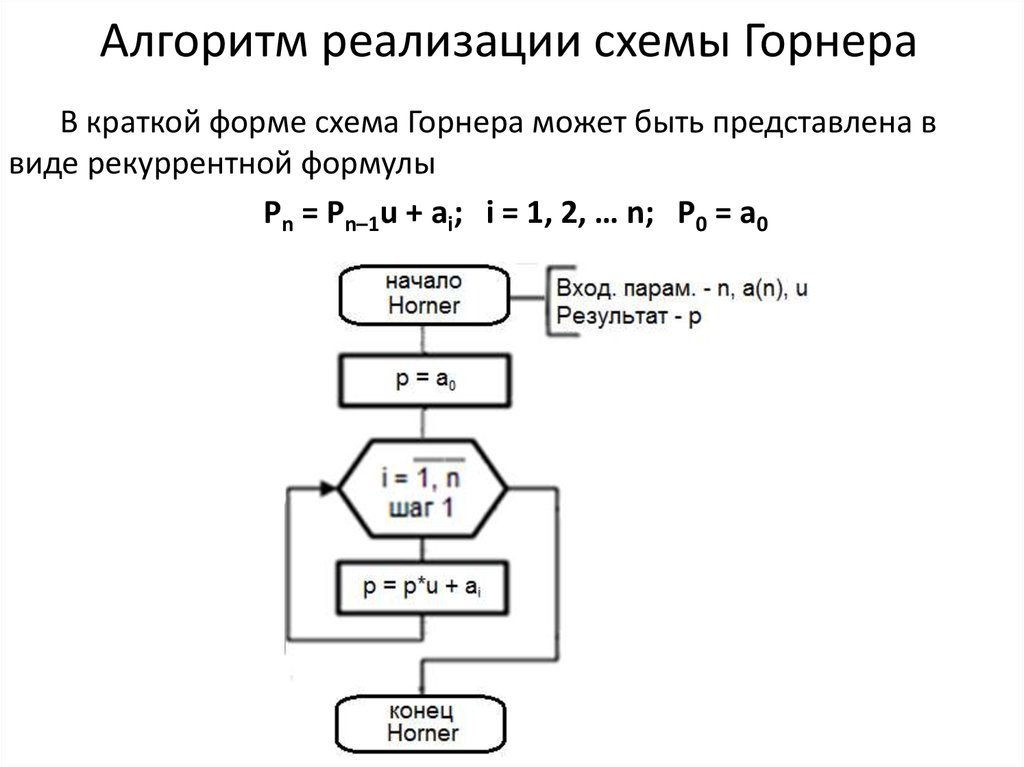 Чтобы гарантировать, что головоломка пользователя «Создай свою собственную» будет разделена
жизнеспособным образом, мы использовали комбинацию плоских и линейных пересечений, чтобы определить
в какой точке и на каком склоне линия «разрежет» их первоначальный кусок на семь
более мелкие кусочки.
Чтобы гарантировать, что головоломка пользователя «Создай свою собственную» будет разделена
жизнеспособным образом, мы использовали комбинацию плоских и линейных пересечений, чтобы определить
в какой точке и на каком склоне линия «разрежет» их первоначальный кусок на семь
более мелкие кусочки. Программа использует быстрое преобразование Фурье, чтобы найти восемь наиболее влиятельных синусоид.
в заданном образце и воссоздает волну таким образом, чтобы ее можно было интерпретировать
синтезатор и манипулировать более полезными способами, чем позволяет обычный сэмпл.
Программа использует быстрое преобразование Фурье, чтобы найти восемь наиболее влиятельных синусоид.
в заданном образце и воссоздает волну таким образом, чтобы ее можно было интерпретировать
синтезатор и манипулировать более полезными способами, чем позволяет обычный сэмпл. Общее решение уравнения дробного порядка получим с помощью
функций типа Миттаг-Леффлера. Этот доклад включает в себя несколько иллюстраций, созданных
с помощью Mathematica-12.
Общее решение уравнения дробного порядка получим с помощью
функций типа Миттаг-Леффлера. Этот доклад включает в себя несколько иллюстраций, созданных
с помощью Mathematica-12. Алгоритмы были
разработан для генерации случайной последовательности значений шага и длины, которые затем
изменены, чтобы соответствовать правилам контрапункта музыки. Выбранные пользователем значения сложности
сгенерированные случайные последовательности, а для записи листа использовалось стороннее программное обеспечение
музыку к этим мелодиям. Программа работает как увлекательный инструмент для музыкантов, чтобы
улучшить свои навыки чтения с листа.
Алгоритмы были
разработан для генерации случайной последовательности значений шага и длины, которые затем
изменены, чтобы соответствовать правилам контрапункта музыки. Выбранные пользователем значения сложности
сгенерированные случайные последовательности, а для записи листа использовалось стороннее программное обеспечение
музыку к этим мелодиям. Программа работает как увлекательный инструмент для музыкантов, чтобы
улучшить свои навыки чтения с листа. MathSciDoc: архив для математиков
[1] Гибридная схема WENO для стационарного моделирования уравнений Эйлера Ифэй Ван Университет науки и технологий Китая Иньхуа Ся Университет науки и технологий Китая
Численный анализ и научные вычисления математикаdoc:2208.
 25004
25004Журнал вычислительной физики, 463, 111292, 2022.8
[Скачать ] [ 2022-08-24 11:14:01 загружено пользователем ] [ 34 загрузки ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[2] Упрощенный многослойный детектор персептрона для гибридной схемы WENO Чжэнъян Сюэ Университет науки и технологий Китая Иньхуа Ся Университет науки и технологий Китая Чен Ли Государственная ключевая лаборатория аэродинамики Сяньсюй Юань Государственная ключевая лаборатория аэродинамики
Численный анализ и научные вычисления математикаdoc:2208.
 25003
25003Компьютеры и жидкости, 244, 105584, 2022.8
[Скачать ] [ 2022-08-24 11:12:20 загружено пользователем ] [ 13 загрузок ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[3] Новая гибридная схема WENO с высокочастотной областью для гиперболических законов сохранения Ифэй Ван Университет науки и технологий Китая Иньхуа Ся Университет науки и технологий Китая
Численный анализ и научные вычисления математикаdoc:2208.25002
Связь по прикладной математике и вычислениям, 2021.7
[Скачать ] [ 2022-08-24 11:07:10 загружено пользователем ] [ 62 загрузки ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[4] Произвольные лагранжево-эйлеровы разрывные методы Галеркина для уравнений типа КдФ Сюэ Хун Университет науки и технологий Китая Иньхуа Ся Университет науки и технологий Китая
Численный анализ и научные вычисления математикаdoc:2208.
 25001
25001Сообщения по прикладной математике и вычислениям, 4, 530-562, 2022.6
[Скачать ] [ 2022-08-24 11:02:30 загружено пользователем ] [ 24 загрузки ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[5] Дихотомия самоподобия аттракторов, ориентированных на граф Кеннет Дж. Фальконер Университет Сент-Эндрюс, Шотландия, Великобритания Цзясинь Ху Кафедра математических наук, Университет Цинхуа, Пекин, Китай Джунда Чжан Кафедра математических наук, Университет Цинхуа, Пекин, Китай
Динамические системы mathscidoc:2208.11001
2022,8
[Скачать ] [ 2022-08-10 09:09:35 загружено пользователем ] [ 67 загрузок ]
Тезисы не загружены!
[ Реферат ][ Полный ]
Самые скачиваемые статьи
Подробнее .
 .. [1] Городской шаблон: проектирование макета с помощью иерархического разделения доменов Юн-Лян Ян КАУСТ Джун Ван КАУСТ Этьен Вуга Колумбийский университет Питер Вонка КАУСТ
.. [1] Городской шаблон: проектирование макета с помощью иерархического разделения доменов Юн-Лян Ян КАУСТ Джун Ван КАУСТ Этьен Вуга Колумбийский университет Питер Вонка КАУСТГеометрическое моделирование и обработка математика: 1608.16073
ACM Transactions on Graphics, 32, (6), 181:1–181:12, 2013.12
[ Скачать ] [ 2016-08-26 00:14:57 загружено пользователем ] [ 13450 скачиваний ]
1
Чихан Пэн · Юнлян Ян · Питер Вонка. Вычисление макетов с деформируемыми шаблонами. В транзакциях ACM на графике. Том 33. Выпуск 4.2014.
2
Педринис Ф. , Морель М., Гескьер Г. и др. Обнаружение изменений городов[C]., 2015: 123-139.
, Морель М., Гескьер Г. и др. Обнаружение изменений городов[C]., 2015: 123-139.
3
Тесо С., Себастиани Р., Пассерини А. и др. Теории структурированного обучения по модулю[J]. Искусственный интеллект, 2014.
4
Альхалавани С., Ян Ю., Вонка П. и др. Что заставляет Лондон работать как Лондон[J]. симпозиум по обработке геометрии, 2014, 33(5): 157-165.
5
Ваксман А., Кампен М., Диаманти О. и др. Синтез направленного поля, проектирование и обработка[C]. международная конференция по компьютерной графике и интерактивным технологиям, 2016.
6
Feng T, Yu L, Yeung S, et al. Ориентированный на толпу макет среднего масштаба[J]. Транзакции ACM по графике, 2016, 35 (4).
7
Нисида Г., Гарсиадорадо И., Алиага Д. Г. и др. Процедурные городские дороги на основе примеров[J]. Форум компьютерной графики, 2015.
8
Zhou J, Sun Z, Yang K, et al. Стратегия управляемого расположения стежков для вышивания произвольной иглой[J].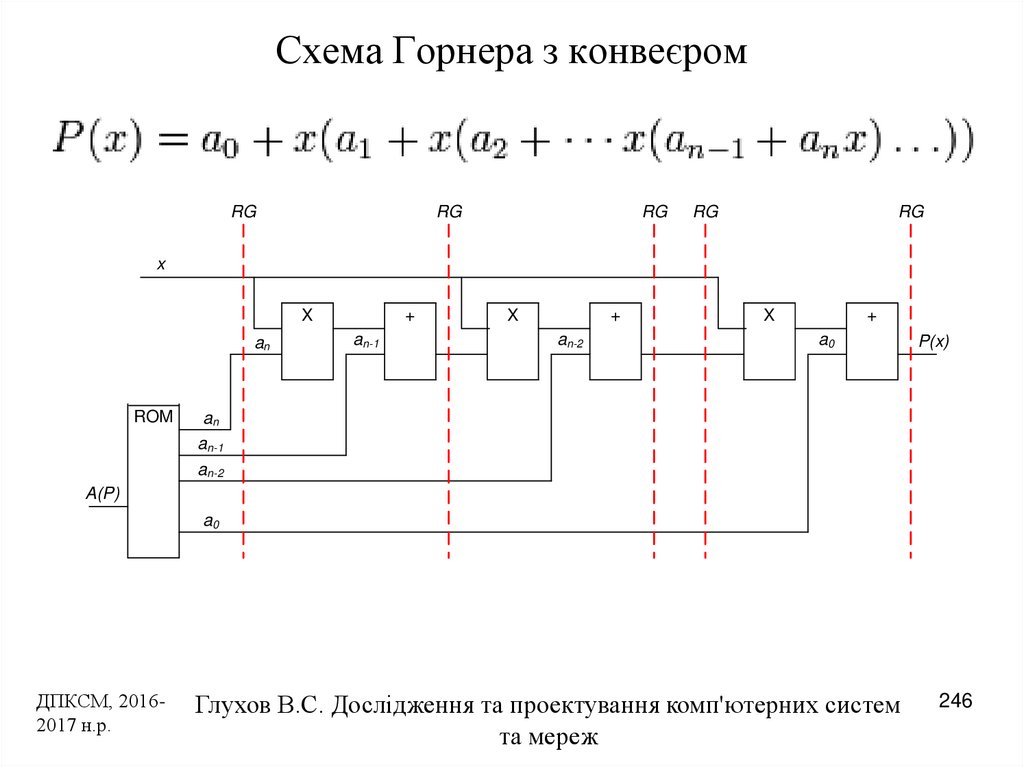 Журнал науки Чжэцзянского университета C, 2014, 15 (9): 729-743.
Журнал науки Чжэцзянского университета C, 2014, 15 (9): 729-743.
9
Ваксман А., Кампен М., Диаманти О. и др. Синтез направленного поля, проектирование и обработка[C]. международная конференция по компьютерной графике и интерактивным технологиям, 2016.
10
Чихан Пэн · Юнлян Ян · Фан Бао · Даниэль Финк · Дунмин Ян · Питер Вонка · Нилой Джей Митра. Проектирование вычислительной сети на основе функциональных спецификаций. В транзакциях ACM на графике. Том 35. Выпуск 4. Страница 131.2016.
[Цитируется 14]
Мы представляем основу для создания сетей улиц и планировок участков. Наша цель — создание высококачественных макетов, которые можно использовать для городского планирования и виртуальной среды. Мы предлагаем решение, основанное на иерархическом разделении домена с использованием двух типов разделения: разделение на основе линий тока, которое разбивает регион вдоль одной или нескольких линий тока поперечного поля, и разделение на основе шаблона, которое деформирует предварительно разработанные шаблоны в область и использует внутренняя геометрия шаблона в виде линий разделения. Мы объединяем эти два подхода к разделению в иерархическую структуру, предоставляя автоматические и интерактивные инструменты для исследования пространства дизайна.
Мы объединяем эти два подхода к разделению в иерархическую структуру, предоставляя автоматические и интерактивные инструменты для исследования пространства дизайна.
[ Реферат ][ Полный ]
[2] Обзор дискретизации синего шума и ее приложений Дун-Мин Ян NLPR-CASIA Цзянь-Вэй Го NLPR-CASIA Бин Ван Университет Цинхуа Сяопэн Чжан NLPR-CASIA Питер Вонка КАУСТ
Геометрическое моделирование и обработка математикаdoc:1608.16011
[ Скачать ] [ 2016-08-19 16:21:46 загружено пользователем ] [ 7171 загрузок ]
1
Zhang S F, Guo J, Zhang H, et al.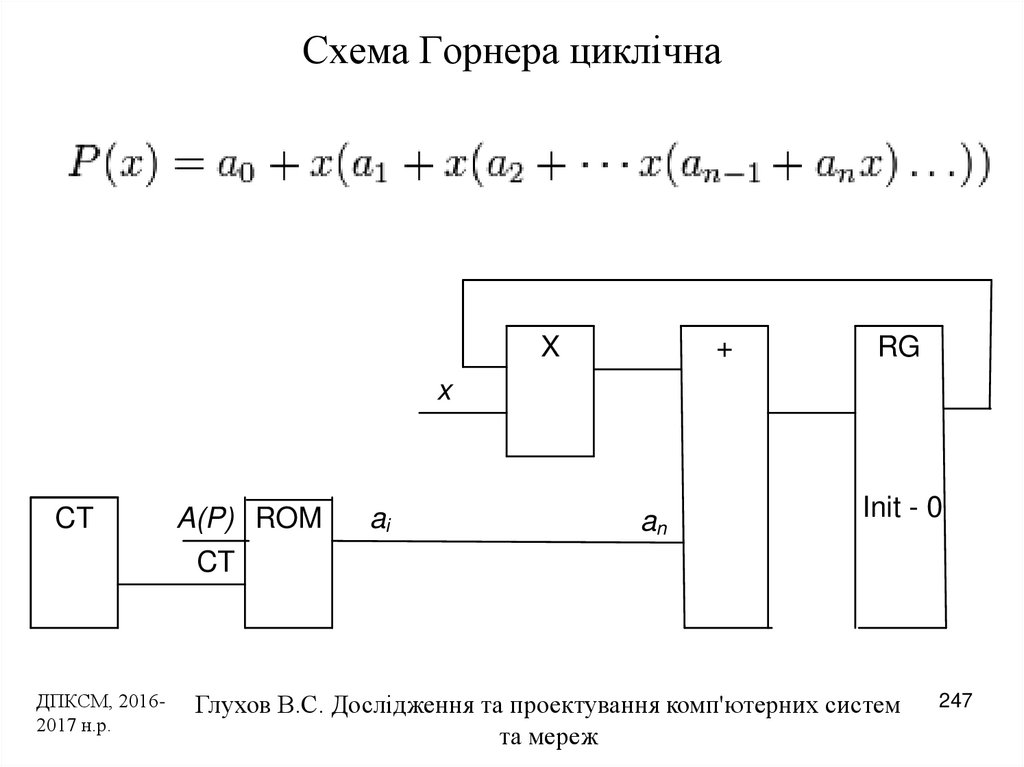 Ограниченная емкость выборки синего шума на поверхностях[J]. Компьютеры и графика, 2016, 55(55): 44-54.
Ограниченная емкость выборки синего шума на поверхностях[J]. Компьютеры и графика, 2016, 55(55): 44-54.
2
Кита Н., Мията К. Мультиклассовая анизотропная выборка синего шума для генерации шаблонов дискретных элементов [J]. Визуальный компьютер, 2016: 1035-1044.
3
Boivin C, Olliviergooch C. Генерация треугольной сетки гарантированного качества для областей с искривленными границами[J]. Международный журнал численных методов в технике, 2002 г., 55 (10): 1185-1213.
4
Рушил Анируд · Анаф Масрур · Паван Турага. Разнообразие, способствующее онлайн-семплингу для суммирования потокового видео. 2016.
5
Вейцзе Цюань · Цзяньвэй Го · Дунмин Янь · Вейлян Мэн · Сяопэн Чжан. Анализ шаблонов выборки поверхности с использованием локализованной парной корреляционной функции. 2016.
6
Guo J, Yan D, Chen L, et al. Тетраэдрическая сетка с помощью максимальной выборки диска Пуассона [J]. Компьютерное геометрическое проектирование, 2016, 43(43): 186-199.
7
Шицин Синь · Бруно Леви · Чжунгуй Чен · Лей Чу · Яохуэй Юй · Чанхэ Ту · Вэньпин Ван. Диаграммы центроидальной мощности с ограничениями мощности: вычисления, приложения и расширение. 2016.
[ Процитировано 7 ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[3] Асимптотическое распределение резонансов для выпуклых препятствий Йоханнес Шёстранд Центр математики, Политехническая школа UMR 7640, CNRS Мачей Зворски Департамент математики, Университет Торонто
подлежит уточнению математикаdoc:1701.331878
Acta Mathematica, 183, (2), 191-253, 1998.5
[Скачать ] [ 2017-01-08 20:33:34 загружено пользователем ] [ 5687 скачиваний ]
[ Процитировано 35 ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[4] Исследование магического шестиугольника порядка 3, его свойств, конструкции и расширений Фаньсин Мэн Тяньцзиньская средняя школа №1
С.
 -Т. Награды за научные достижения средней школы Яу
математикаdoc:1608.35005
-Т. Награды за научные достижения средней школы Яу
математикаdoc:1608.35005[ Скачать ] [ 2016-08-13 21:51:54 загружено пользователем ] [ 4796 загрузок ]
Магический шестиугольник 3-го порядка напоминает по форме соты с 19 ячейками, расположенными по схеме 3 4 5 4 3. Требуется заполнить цифры 1-19в сетках так, чтобы каждая строка (всего 15) давала в сумме 38.
Придуманные ранее методы, направленные на решение этой задачи и доказательство ее единственности, были либо недостаточно строгими, либо слишком замысловатыми. Поэтому, анализируя его свойства, я хотел найти комбинаторное решение его конструкции, доказать его уникальность и выяснить, можно ли использовать его математические принципы в реальных приложениях. Сложность зависит от точки зрения, поэтому первым шагом было обозначить каждую сетку удобным способом. Я решил рассматривать магический шестиугольник как сеть, состоящую из центра и колец. Тогда связи и ограничения каждого набора чисел можно было бы найти по формуле
вывод. Аналогичным образом были обнаружены и симметричные свойства. Следующим шагом был анализ возможных распределений нечетных и четных чисел. Из 9конфигурации, только 1 оказался пригодным для использования. Завершающим этапом было строительство. При всех известных свойствах немногие невозможности были легко устранены, и осталось только одно решение, что доказывает его единственность.
Процедуры, используемые для магического шестиугольника порядка 3, могут быть расширены до процедур более высоких порядков, что упрощает их построение. Уникальные свойства магических шестиугольников могут быть использованы в некоторых областях применения, например, в системах паролей, крупномасштабных конструкциях крыш, композитных материалах, системах национальной безопасности и многих других областях.
Тогда связи и ограничения каждого набора чисел можно было бы найти по формуле
вывод. Аналогичным образом были обнаружены и симметричные свойства. Следующим шагом был анализ возможных распределений нечетных и четных чисел. Из 9конфигурации, только 1 оказался пригодным для использования. Завершающим этапом было строительство. При всех известных свойствах немногие невозможности были легко устранены, и осталось только одно решение, что доказывает его единственность.
Процедуры, используемые для магического шестиугольника порядка 3, могут быть расширены до процедур более высоких порядков, что упрощает их построение. Уникальные свойства магических шестиугольников могут быть использованы в некоторых областях применения, например, в системах паролей, крупномасштабных конструкциях крыш, композитных материалах, системах национальной безопасности и многих других областях.
[ Реферат ][ Полный ]
[5] Ценообразование европейских опционов на акции на основе модели процентной ставки Васичека Юэран Ма Средняя школа при Китайском университете Жэньминь Хао Вэнь Средняя школа при Китайском университете Жэньминь
С.
 -Т. Награды за научные достижения средней школы Яу
математикаdoc:1608.35030
-Т. Награды за научные достижения средней школы Яу
математикаdoc:1608.35030[ Скачать ] [ 2016-08-13 21:51:55 загружено пользователем ] [ 4475 скачиваний ]
Опционы — важная часть мирового финансового рынка, оказывающая большое влияние на национальную экономику. В то время как большинство классических моделей ценообразования опционов основаны на предположении о постоянной процентной ставке, экономические данные показывают, что в действительности процентные ставки часто колебались под влиянием различных экономических показателей и денежно-кредитной политики. Поскольку колебания процентной ставки тесно связаны со стоимостью и ожидаемой доходностью опционов, стоит обсудить ценообразование опционов при стохастической процентной ставке.
оценочные модели. С 19В 90-х годах отечественные и зарубежные ученые проводили исследования по этой теме и сформулировали ценовые формулы для некоторых видов опционов. Однако, поскольку процесс ценообразования включает две стохастические переменные, в большинстве предыдущих исследований использовались сложные методы. В результате их ценовые формулы были слишком сложны, чтобы дать прямое объяснение влияния параметров на цены опционов, и не могли предложить инвесторам прямую помощь.
В этой статье для описания стохастического движения процентной ставки выбрана модель процентной ставки Васичека, и обсуждается ценообразование европейских опционов на акции, цена базового актива которых соответствует геометрическому броуновскому движению на полном рынке. Ценность и новаторство статьи заключаются в следующих аспектах: ① В ней улучшены и упрощены методы оценки опционов в рамках стохастических моделей процентных ставок, применены сравнительно простые математические методы и получены краткие ценовые формулы; ② это
52 проводит углубленный анализ финансовой значимости основных параметров, который помогает инвесторам принимать более обоснованные инвестиционные решения, оценивая колебания цен опционов, соответствующие различным параметрам.
Однако, поскольку процесс ценообразования включает две стохастические переменные, в большинстве предыдущих исследований использовались сложные методы. В результате их ценовые формулы были слишком сложны, чтобы дать прямое объяснение влияния параметров на цены опционов, и не могли предложить инвесторам прямую помощь.
В этой статье для описания стохастического движения процентной ставки выбрана модель процентной ставки Васичека, и обсуждается ценообразование европейских опционов на акции, цена базового актива которых соответствует геометрическому броуновскому движению на полном рынке. Ценность и новаторство статьи заключаются в следующих аспектах: ① В ней улучшены и упрощены методы оценки опционов в рамках стохастических моделей процентных ставок, применены сравнительно простые математические методы и получены краткие ценовые формулы; ② это
52 проводит углубленный анализ финансовой значимости основных параметров, который помогает инвесторам принимать более обоснованные инвестиционные решения, оценивая колебания цен опционов, соответствующие различным параметрам.

