Сочетания размещения и перестановки: Различия размещений и сочетаний — урок. Алгебра, 11 класс.

Содержание

Перестановки. Размещения. Сочетания. комбинаторика — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Перестановки.
Размещения.
Сочетания.
комбинаторика

2. Определение

Область математики,
в которой изучают
комбинаторные задачи,
называется
комбинаторикой
Слово «комбинаторика» происходит от латинского
«combinare», которое означает «соединять, сочетать».
Комбинаторика — раздел математики, в котором
изучаются вопросы о том, сколько различных
комбинаций, подчиненных тем или иным условиям,
можно составить из заданных объектов.

Комбинаторными задачами интересовались и
математики, занимавшиеся составлением и
разгадыванием шифров, изучением древних
рукописей.
Сейчас комбинаторика находит приложения во многих
областях науки: в биологии, в химии, механике и т.д.

4. Факториал

Факториа́л числа n (обозначается n!,
произносится эн факториа́л) — это
произведение всех натуральных чисел
до n включительно:
1 • 2 • 3 • … • n = n!

5. Факториал

4! = 1•2•3•4 = 24
3! = 1•2•3 = 6
6! = 1•2•3•4•5•6 = 720

6. Главное свойство факториала

(n+1)! = (n+1) • n!
Следствие
1! = 1
0! = 1
Пусть имеются три кубика с буквами А, В и С.
Составьте всевозможные комбинации из этих
букв.
В
А
ABC
ВСА
CAB
С
АСВ
ВАС
CBA
Эти комбинации отличаются друг от друга только
расположением букв (перестановка букв).
Перестановки
Перестановки — это комбинации, составленные из одних и тех же
элементов и отличающиеся порядком их следования.

Число всех возможных перестановок элементов обозначается Pn, и
может быть вычислено по формуле:
Формула перестановки:
Рn=n!
При перестановке число объектов остается неизменными,
меняется только их порядок
С ростом числа объектов количество перестановок очень
быстро растет и изображать их наглядно становится
затруднительно.
3 объекта
Рn=n!
Р3=3!=1∙2∙3=6
количество перестановок 6
Задача 1. В турнире участвуют семь команд. Сколько
вариантов распределения мест между ними возможно?
Р7=7!=1*2*3*4*5*6*7=5040
Ответ: 5040
Задача 2. Сколькими способами могут разместиться за круглым

столом 10 человек?
Р10 =10! = = 1*2*3*4*5*6*7*8*9*10 = 3628800
Ответ: 3628800
1. Вычислить:
а) 5!
7!
б)
3!
11!
в)
8!
2. В среду в 9 классе 6 уроков: алгебра, русский язык, черчение, биология,
химия, обществознание. Сколько вариантов расписания можно составить на
среду?
Размещения
Пусть имеется n различных объектов.

Будем выбирать из них m объектов и переставлять всеми
возможными способами между собой .
Получившиеся комбинации называются размещениями из
n объектов по m, а их число равно:
Формула размещения:
n!
А
n m !
m
n
При размещениях меняется и состав выбранных объектов, и их порядок.
n!
А
n m !
m
n
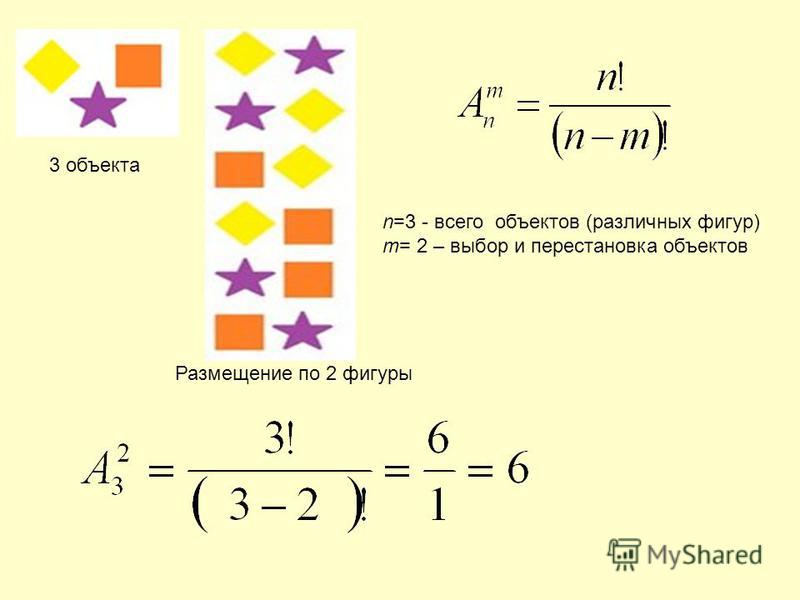
3 объекта
n=3 — всего объектов (различных фигур)
m= 2 – выбор и перестановка объектов
Размещение по 2 фигуры
А
2
3
3!
6
6
3 2 ! 1
Сколькими способами можно расставить 5 томов на книжной полке, если
выбирать их из имеющихся в наличии семи книг?
n!
А
n m !
m
n
А
5
7
7!
7! 2! 3 4 5 6 7
2520
7 5 ! 2!
2!
Ответ: 2520 способов
1. Вычислить:
а) А
2
6
А А
б)
3
А10
4
12
4
11
2. Найти количество трехзначных чисел с неповторяющимися
цифрами, которые можно составить из цифр: 1, 2, 3, 4, 5.

Ответ: 60 чисел
Сочетания
3 объекта
Пусть имеется n различных объектов.
Будем выбирать из них m объектов все возможными способами
Получившиеся комбинации называются сочетаниями из n объектов по m,
n!
С
(n m)! m!
m
n
В сочетаниях меняется состав выбранных объектов, но порядок не важен
Задача: Сколькими способами можно распределить три путевки в
один санаторий между пятью желающими?

Так как путевки предоставлены в один санаторий, то
варианты распределения отличаются друг от друга хотя бы
одним желающим. Поэтому число способов распределения
n!
С
(n m)! m!
m
n
Ответ: 10 способов.
Задача: В цехе работают 12 человек: 5 женщин и 7 мужчин. Сколькими
способами можно сформировать бригаду из 7 человек, чтобы в ней было
3 женщины?
Из пяти женщин необходимо выбирать по три, поэтому число способов отбора
Так как требуется отобрать четырех мужчин из семи,
то число способов отбора мужчин
Ответ: 350
.

Задача:
Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой
партой. Порядок их размещения не имеет значения. Определить количество
возможных вариантов сочетаний.
Ответ: 190

English Русский Правила

Перестановки сочетания и размещения (с и без…

Привет, сегодня поговорим про перестановки, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое перестановки, сочетания, размещения, перестановки с повторениями , перестановки без повторений, соединения в комбинаторике , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Таблица Отличие и признаки сочетаний, размещений и перестановок

Признаки
	перестановки	сочетания	размещения
Порядок следования элементов	+	–	+
Состав элементов	–	+	+

Сводка формул для всех видов соединений в комбинаторике

6 перестановок 3-х шаров

В комбинаторике перестановка — это упорядоченный набор чисел обычно трактуемый как биекция на множестве , которая числу i ставит в соответствие i-й элемент из набора.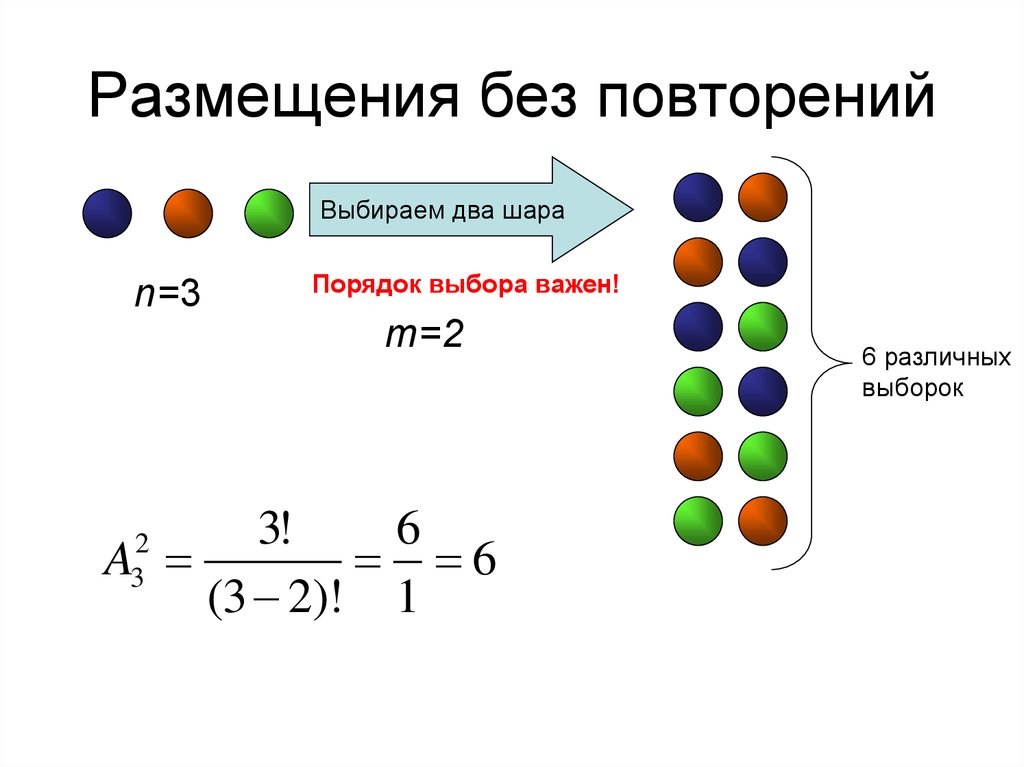 Число n при этом называется порядком перестановки. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово расстановка.

В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)

Свойства перестановок

Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:[

Композиция определяет операцию произведения на перестановках одного порядка: Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают .
Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент сопоставляется с перестановкой , задаваемой тождеством где g — произвольный элемент группы G, а — групповая операция.

Связанные определения

Носитель перестановки — это подмножество множества , определяемое как
Неподвижной точкой перестановки является всякая неподвижная точка отображения , то есть элемент множества Множество всех неподвижных точек перестановки является дополнением ее носителя в .

Инверсией в перестановке порядка n называется всякая пара индексов такая, что и . Четность числа инверсий в перестановке определяет четность перестановки.

Специальные типы перестановок

Тождественная перестановка — перестановка которая каждый элемент отображает в себя:
Инволюция — перестановка которая является обратной самой себе, то есть
Беспорядок — перестановка без неподвижных точек.
Циклом длины называется такая подстановка которая тождественна на всем множестве кроме подмножества и Обозначается . Число перестановок, содержащих k циклов, — есть числа Стирлинга первого рода
Транспозиция — перестановка элементов множества , которая меняет местами два элемента. Транспозиция является циклом длины 2.

Подстановка

Перестановка множества может быть записана в виде подстановки, например:

где и

Произведения циклов и знак перестановки[править ]

Любая перестановка может быть разложена в произведение (композицию) непересекающихся циклов длины причем единственным образом с точностью до порядка следования циклов в произведении . Об этом говорит сайт https://intellect.icu . Например:

Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций. Для произвольного цикла длины разложение можно написать так: Циклы длины 1 действуют как тождественная перестановка и тоже могут быть легко разложены, так как квадрат любой транспозиции есть тождественная перестановка: Такое разложение циклов на произведение транспозиций не будет единственным:

Таким образом любая перестановка может быть разложена в произведение транспозиций. Хотя это разложение и не будет единственным, но четность числа транспозиций, входящих в разложение, сохраняется. Пусть перестановка разложена в произведение транспозиций, тогда

знаком перестановки (иначе:четностью перестановки или сигнатурой перестановки) называют число при этом называют четной перестановкой, если инечетной перестановкой, если

Знак перестановки также может быть определен через число инверсий в этой перестановке:

Замечание. Имеется два соглашения по умножению перестановок и циклов:

1) .

Например: .

2) .

Например: .

Перестановки с повторением в комбинаторике

Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту

Случайная перестановка

Обобщенная схема размещения

Случайной перестановкой называется случайный вектор все элементы которого принимают натуральные значения от 1 до и при этом вероятность совпадения любых двух элементов равна 0.

Независимой случайной перестановкой называется такая случайная перестановка , для которой

для некоторых таких что

Если при этом не зависят от , то перестановку называют одинаково распределенной. Если же нет зависимости от , то есть то называют однородной.

В комбинаторике размещением (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.

Пример 1: — это 4-элементное размещение из 6-элементного множества .

Пример 2: некоторые размещения элементов множества по 2: … … …

В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов (то есть совпадают как сочетания).

Пример

• В фирме работают 8 человек одинаковой квалификации, среди них Иванов, Петров, Сидоров. Сколькими способами можно случайно выбрать
трех из восьми?

Решение

• Всего вариантов — выбрать три из восьми без повторения, т. к. один и тот же не может выполнять две работы

Количество размещений

Количество размещений из n по k, обозначаемое , равно убывающему факториалу:

Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из nпо k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту , в то время как перестановок наk элементах ровно k! штук.

При k=n количество размещений равно количеству перестановок порядка n:

Размещение с повторениями

Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.

Пример задач

Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; насекторах каждого из дисков написаны цифры 0, 1, …, 9.

• Какова вероятность открыть закрытую камеру для человека:
1. забывшего все, что он набрал на дисках, закрывая камеру;
2. помнящего только цифру, набранную на первом диске;
3. помнящего только, что ни на втором, ни на третьем, ни на четвертом, диске не набирал цифру 6?

. Решение

3) Всего вариантов N=10*9*9*9

Количество размещений с повторениями

По правилу умножения количество размещений с повторениями из n по k, обозначаемое , равно:

Например, количество вариантов 3-значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

Еще один пример: размещений с повторениями из 4 элементов a, b, c, d по 2 равно эти размещения следующие:

В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, ) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} () являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать элементов из множества, содержащего различных элементов, стоит на пересечении -й диагонали и -й строки треугольника Паскаля.

Пример

В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии. Сколько всего партий было сыграно?

Число сочетаний

Биномиальный коэффициент

Число сочетаний из по равно биномиальному коэффициенту

При фиксированном производящей функцией последовательности чисел сочетаний , , , … является:

Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из по равно биномиальному коэффициенту

Доказательство

Пусть имеется типов объектов, причем объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше ) количество объектов каждого типа. Из этого ассортимента выберем объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через количество выбранных объектов -го типа, , . Тогда . Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд шаров и перегородок так, чтобы между -й и -й перегородками находилось ровно шаров. Но таких расстановок в точности , что и требовалось доказать.

При фиксированном производящей функцией чисел сочетаний с повторениями из по является:

Двумерной производящей функцией чисел сочетаний с повторениями является:

Пример Имеется 2 типа цветов, количество цветов не ограничено.

Сколько различных букетов можно составить из 3-х цветов?
• 111
• 222
• 122
• 211
• Всего 4 различных букета

Пример Имеется 5 типов цветов, количество цветов не ограничено. Сколько различных букетов можно составить из 3-х цветов?

Решение

• Сочетание с повторением:
(5+3-1)!/(3!*(5-1) !)=35

См. также

перестановки , сочетания , размещения , бином ньютона ,
сводка формул для всех видов соединений , комбинаторика , перестановки , размещения с повторениями ,

Напиши свое отношение про перестановки. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое перестановки, сочетания, размещения, перестановки с повторениями , перестановки без повторений, соединения в комбинаторике и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Размещения, перестановки, сочетания — Математика для юристов (Математика)

§3. Размещения, перестановки, сочетания

При решении комбинаторных задач мы имеем дело с комбинациями из некоторых предметов. Эти комбинации могут отличаться одна от другой числом предметов, их составом или порядком.

Пример 1. Пять бойцов сержанта Сбруева.

В отделении сержанта Сбруева проходят службу 5 новобранцев: Белкин, Пенкин, Фенькин, Свечкин и Овечкин. В свободное от нарядов время сержант обучает их, как рассчитаться по порядку. По команде «В одну шеренгу становись! » солдаты выстраиваются справа от Сбруева и по команде «По порядку номеров рассчитайсь! » производят расчет: «первый-второй-третий-четвертый-пятый » . После этого сержант перестраивает новобранцев по-новому и расчет повторяется. Сколько раз может Сбруев повторить это упражнение, используя только разные способы построения солдат?

Решение. Договоримся указывать порядок расположения солдат первыми буквами их фамилий. Например, комбинация ПСОФБ означает, что первым является Пенкин, вторым — Свечкин и т.д. Все комбинации отличаются одна от другой порядком букв и называются перестановками из пяти букв. Нам нужно найти число всех таких перестановок. Сначала мы выведем общую формулу, а потом закончим обсуждение примера.

Пусть дано множество из п элементов. Занумеруем все элементы каким-нибудь способом от 1 до п (в случае с новобранцами п = 5). Ясно, что занумеровать можно многими способами.

Определение. Перестановкой из п элементов называется всякий способ нумерации этих элементов.

Теорема 2. Число всех различных перестановок из п элементов равно п!

Доказательство. Всякую перестановку из п элементов можно получить с помощью п действий: первое действие — выбор первого элемента, второе действие — выбор второго элемента, и т. д., наконец, n-е действие — выбор элемента с номером п.

Первый элемент можно выбрать п различными способами; второй выбирается из оставшихся п — 1 элементов, поэтому число всех способов выполнения второго действия будет п — 1. После выбора второго элемента их останется п — 2, следовательно, число способов, которыми можно выполнить третье действие, будет п — 2. Таким образом, число способов, которыми выполняется очередное действие, будет на единицу меньше предыдущего. Следовательно, четвертое действие можно выполнить (п — 2) способами, пятое — (п — 4) способами и т.д., наконец, последнее действие — одним способом.

По правилу умножения (теорема 1) число всех способов выполнения действий, т.е. число всех перестановок, равно п(п — 1)(п — 2) • … • 1 = п!. Теорема доказана.

Число всех перестановок из п элементов обозначают Р_п. Согласно теореме 1 его можно найти по формуле

Р_п = п!. (4)

Например, в случае с новобранцами (п = 5) мы получим Р₅ = 5! = 120.

УПРАЖНЕНИЯ

7. Выпишите все перестановки из букв а, b, с.

8. Сколько различных четырехзначных чисел можно составить из цифр 7, 2, 4, 9, если каждая цифра используется в записи числа только один раз?

9. Проверьте равенство Р₆ = 6Р₅.

10. Что больше: Р₇ или 2⁷?

11. С помощью цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 закодируйте буквы А, В, Д, Е, Л, О, С, Т, Ь, заменив каждую букву какой-нибудь цифрой, и зашифруйте слово СЛЕДОВАТЕЛЬ. Каково число возможных вариантов кода?

Пример 2. Однажды утром

Однажды утром по улицам города Дрюкова на высокой скорости пронеслась машина. Она сбила зазевавшегося поросенка и скрылась в неизвестном направлении. Возвращавшийся из ресторана житель N, заметил номер автомобиля. Но когда появилась милиция, он с перепугу вспомнил только, что номер четырехзначный, все цифры разные, причем первая цифра 1, а последняя 4. Сколько автомобилей должна проверить автоинспекция?

Решение. Второй и третьей цифрами номера могут быть любые две из следующих: 2, 3, 5, 6, 7, 8, 9, 0. Выбрав любую пару цифр, автоинспектор получит номер какого-либо автомобиля. Например, пара 5, 7 дает номер 1574. Эти же цифры, но в другом порядке дают номер 1754. Следовательно, нужно перебрать столько номеров, сколько будет всевозможных комбинаций из восьми перечисленных цифр по две с учетом их порядка. Такие комбинации называют размещениями. В данном случае мы ищем число размещений из восьми цифр по две.

Определение. Размещением из п элементов по k называется всякая перестановка из k элементов, выбранных каким-либо способом из данных п.

Число всех размещений из п элементов по k обозначается А_п.

Теорема 3. Число всех размещений из п элементов по k вычисляется по формуле

(5)

Эта теорема доказывается так же, как и теорема 2. Каждое размещение можно получить с помощью k действий. Первое действие — выбор первого элемента — осуществляется п способами, второе действие — выбор второго элемента — (п — 1) способами, и т.д., наконец, последнее действие — выбор k-того элемента — (п — k + 1) способами. По правилу умножения число всех размещений будет п(п — 1) • • • (п — k + 1), что и требовалось доказать.

Вернемся к примеру 2. Согласно формуле (5) автоинспекция должна проверить = 8 • 7 = 56 автомобилей.

УПРАЖНЕНИЯ

12. На трех карточках написаны буквы Р, А, К. Сколько различных слов можно составить, если словом считается любой набор из двух букв? Запишите эти слова.

13. В домоуправлении трудится 6 человек. Поступило распоряжение о премировании трех сотрудников (различными суммами). Сколькими способами можно это сделать?

14. На железнодорожной ветке Дрюково—Стуково имеется 10 станций. В течение дня с каждой станции на каждую другую выехало в точности по одному пассажиру. Сколько билетов было куплено в этот день?

15. Сколькими способами можно выбрать из семи разных книг какие-либо четыре и подарить их четырем милиционерам, занявшим первые четыре призовых места на конкурсе «Настоящий мужчина города Брюкова » ?

16. Студенты одной группы должны сдать 5 экзаменов в течение восемнадцати дней. Сколькими способами можно составить расписание экзаменов, если в один день разрешается сдавать не более одного экзамена?

17. В течение дня из Брюкова в Стуково отправляется 8 автобусов. Разведенные супруги гражданин N и гражданка М не хотят ехать в одном автобусе. Сколькими способами они могут отправиться в разных автобусах?

Пример 3. День Брюквы

Согласно древнему обычаю, самый главный праздник в Брюкове — День Брюквы, проводится за счет средств городского бюджета и празднуется столько дней, сколько депутатов проголосует за то, чтобы праздник состоялся. Из десяти депутатов «за » проголосовали семь.

Каково число всех возможных вариантов голосования?

Решение. Мы должны найти число всех возможных групп из семи депутатов. Здесь порядок выбора не играет никакой роли, поэтому рассматриваемые комбинации отличаются одна от другой только составом лиц. Комбинации такого типа называются сочетаниями.

Определение. Сочетанием из п элементов по k называется всякая совокупность k элементов, выбранных каким-либо способом из данных п элементов.

Число всех сочетаний из п элементов по k обозначается . В примере 3 нужно найти .

Теорема 4. Число всех сочетаний из п элементов по k вычисляется по формуле

(6)

Доказательство. Возьмем какое-нибудь сочетание из п элементов по k

Переставляя эти элементы всевозможными способами, получим k! всех размещений из п по k одного и того же состава. Таким образом, из одного сочетания получается k! размещений. Следовательно, из С_п сочетаний получится С_п • k! размещений, т.е.

Отсюда, с учетом формулы (5) получаем:

что и требовалось доказать.

В примере 3 было п = 10, k = 7, поэтому число всех вариантов голосования присяжных равно

УПРАЖНЕНИЯ

18. В группе 30 студентов. Сколькими способами можно выбрать 6 делегатов для переговоров с администрацией института по вопросу о свободной продаже пива в студенческом буфете?

19. Сколькими способами можно поставить три пешки на белые клетки шахматной доски?

20. Для участия в соревнованиях тренер отбирает 5 спортсменов из двенадцати. Сколькими способами он может составить команду?

21. На окружности выбрано 7 точек. Сколько можно построить треугольников с вершинами в этих точках?

22. На карточке спортлото 36 клеток. Играющий должен отметить 4.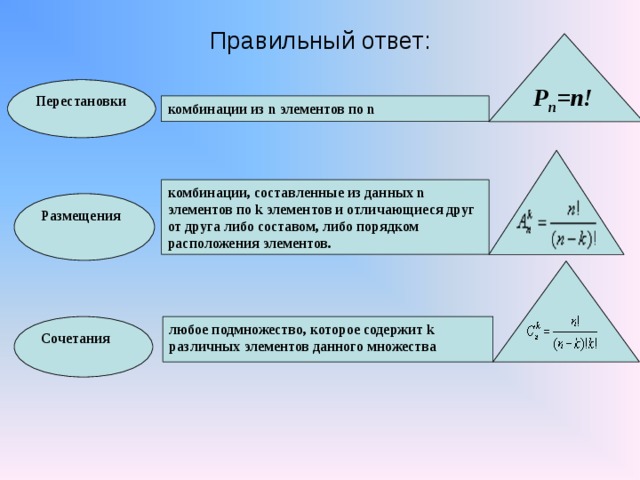 Каково число всех возможных вариантов?

Числа сочетаний обладают многими важными свойствами. Некоторые из них понадобятся нам в дальнейшем. Например,

= (7)

Доказательство. Если из п элементов выбрать k элементов, то останется n — k элементов. Следовательно, каждому сочетанию из п элементов по k соответствует определенное сочетание из п элементов по п — k. Поэтому число тех и других сочетаний одинаково. Доказательство закончено.

Формула (7) сокращает вычисления, например:

Заметим, что формулы (4)-(6) допускают более широкое толкование. По определению полагают 0! = 1, А_п =1, =1.

Числа также называют биномиальными коэффициентами, с их помощью записывается так называемая формула бинома Ньютона:

(а + b)^п = аⁿ + a^n-1b + a^n-1b² + . .. + аbⁿ^-1 +bⁿ

В лекции «9 Художественная культура Древнего Египта» также много полезной информации.

Эту формулу можно доказать, например, методом математической индукции. Попробуйте сделать это самостоятельно .

ТИПОВЫЕ ЗАДАНИЯ

1. Анкета по изучению общественного мнения содержит 10 вопросов, на каждый из которых отвечающий дает один из трех ответов: «да » , «нет » , «не знаю » . Найти число всех различных способов заполнения анкеты.

2. Одна из воюющих сторон захватила в плен 12 солдат, а вторая 14. Сколькими способами можно обменять 5 военнопленных?

3. В партии из ста деталей имеется 10 бракованных. Наудачу выбирают 4 детали. Сколькими способами можно это сделать? Сколько будет четверок, не содержащих бракованных деталей? Найдите отношение числа последних к числу первых.

План конспект урока «Комбинаторика (перестановки, сочетания, размещения)»

План – конспект занятия

Тема занятия: Элементы комбинаторики (размещения, перестановки, сочетания)

Цели занятия:

Дидактическая: Ввести понятие предмета комбинаторики, познакомить с историей развития и применения в жизни; рассмотреть различные виды комбинаторных соединений: размещения, перестановки и сочетания; сформировать у обучающихся первичные умения и навыки решения задач.

Развивающая: Развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать умения сравнивать, систематизировать, обобщать; навыки контроля и самоконтроля.

Воспитательная: Формировать научное мировоззрение у обучающихся, культуру математической речи, информационную и коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.

Методы: индивидуальный, частично-поисковой, практический, проблемный, логический (индукция, аналогия), фронтальный опрос, лекция с элементами эвристической беседы, практическая тренировка, самостоятельная работа, взаимоконтроль, информационно-рецептивный.

Квалификационные требования:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Сроки реализации 1 занятие (2 часа)

Материально – техническое оснащение:

1) проектор, экран, ПК

2) презентация;

3) раздаточный материал

Подготовительная работа.

За две недели до проведения данного урока студентам дается задание:

Исследовать различные источники, и найти информацию, так или иначе связанную с темой данного урока. (Студентам выдаются темы сообщений, список литературы, возможно, ссылки на Интернет ресурсы.)

Собранная студентами информация изучается учителем, систематизируется. Учитель выясняет, какая тема больше всего интересна каждому студенту, окончательно утверждает темы сообщений и вбираются докладчики.

Темы сообщений:

· «Что такое комбинаторика? Истоки комбинаторики»

· «Комбинаторика в реальной жизни»

Примерный перечень вопросов при работе над темой:

· Основные понятия по данной теме;

· Исторические комментарии;

· Связь рассматриваемых объектов с природой и жизнью человека;

· Интегрирование полученных знаний в различные области науки, техники, технологии, в творческие области;

· Упражнения и задачи решения.

ХОД ЗАНЯТИЯ:

1 Организационный момент. Постановка цели и задач урока. (2 мин)

Преподаватель проверяет готовность к уроку.

Я рада приветствовать всех Вас на сегодняшнем уроке. Все мы с вами пришли на урок с разным настроением, но я надеюсь, что в конце нашего занятия у нас у всех будут только положительные эмоции.

Девизом нашего занятия я предлагаю взять слова английского математика Д. Сильвестра

«Число, положение и комбинация —

три взаимно пересекающиеся,

но различные сферы мысли,

к которым можно отнести

все математические идеи»

Английский математик

Джеймс Джозеф Сильвестр
(1814-1897)

2 Мотивация к усвоению нового материала. Фронтальная работа с группой. (5 мин)

Давайте здороваться, т.е. все пожмем друг другу руки. Рядом сидящим пожмем руку, а с остальными будем здороваться мысленным рукопожатием.

– В классе нас сколько?

Вопрос: Сколько было всего рукопожатий?

– Итак, какие будут ответы?

Допустим нас 25.

Каждый из 25-и человек пожал руки 24-м. Однако произведение 25 * 24 = 600 дает удвоенное число рукопожатий (так как в этом расчете учтено, что первый пожал руку второму, а затем второй первому, на самом же деле было одно рукопожатие). Итак, число рукопожатий равно: (25 * 24) : 2 = 300.

– Мы с вами столкнулись с комбинаторной задачей.
Поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае, занят целый раздел математики, и мы познакомимся с ним. Особая примета подобных задач – это вопрос, который можно сформулировать таким образом, что он начинался бы словами:

· Сколькими способами…?

· Сколько вариантов…?

Итак тема нашего урока: «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов»

3 Изучение и первичное усвоение новых знаний.

I. Выступление учащихся с итогами своей работы:

· «Что такое комбинаторика? Истоки комбинаторики» (5 мин)

Представителям самых различных специальностей приходиться решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.

При рассмотрении простейших вероятностных задач нам приходилось подсчитывать число различных исходов (комбинаций). Для небольшого числа элементов такие вычисления сделать несложно. В противном случае такая задача представляет значительную сложность.

Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.

Комбинаторика — раздел математики, в котором изучаются простейшие «соединения». Перестановки — соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их Размещения — соединения, содержащие по m предметов из числа n данных, различающиеся либо порядком предметов, либо самими предметами; число их Сочетания — соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом (в современном толковом словаре изд. «Большая Советская Энциклопедия»).

С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов – во время работы.

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Первоначально комбинаторика возникла в XVI в в связи с распространением различных азартных игр.

Основы комбинаторики и теории вероятностей создали и разработали французские математики XVII века Пьер Ферма и Блез Паскаль.

Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.

В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.

В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.

Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей.

Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» впервые встречается у Паскаля. Термин «перестановка» употребил в указанной книге Якоб Бернулли. Бернулли использовал и термин «размещение».

Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.

· «Комбинаторика в реальной жизни» (3 мин)

Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания. Ведь большей частью жизненные вопросы являются на самом деле задачами из теории вероятностей.

П. Лаплас

Проведём небольшой эксперимент, вы можете представить себя отцом дочерей-двойняшек, которым вы накупили дюжину платьев. А теперь ответьте на вопрос: сколько же существует разных вариантов одеть ваших девочек? Чтобы получить ответ, достаточно провести подсчеты на обычном листке бумаги. Но представьте на минуту, что вы — этот самый человек, который выдает штрих коды на товары. Но производителю товара уже точно не обойтись одной бумагой и карандашом; для этого необходимо владеть специальной техникой, которая обеспечит гарантированное использование всех возможных вариантов, другими словами, нужна лучшая «техника счета».

В царице наук – математике, все эти техники объединяются в одну отрасль науки, которую называют комбинаторикой. Кроме всего прочего, комбинаторика — это прелюдия к расчету вероятностей.

Области применения комбинаторики:

• учебные заведения (составление расписаний)

• сфера общественного питания (составление меню)

• лингвистика (рассмотрение вариантов комбинаций букв)

• география (раскраска карт)

• спортивные соревнования (расчёт количества игр между участниками)

• производство (распределение нескольких видов работ между рабочими)

• агротехника (размещение посевов на нескольких полях)

• азартные игры (подсчёт частоты выигрышей)

• химия (анализ возможных связей между химическими элементами)

• экономика (анализ вариантов купли-продажи акций)

• криптография (разработка методов шифрования)

• доставка почты (рассмотрение вариантов пересылки)

· «Решение комбинаторных задач» (7 мин)

Решить комбинаторную задачу — это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др. , отвечающих условию задачи.

Рассмотрим несколько типичных для комбинаторики задач.

Задача 1. Мастер Зимин ежедневно формирует наряд для работы на определенном участке дороги. Наряд состоит из двух человек: бригадира и дежурного. В расположении мастера находится 20 дорожных рабочих. На сколько дней подряд мастер Зимин составит график?

Решение. Пусть сначала избирается бригадир. Поскольку каждый рабочий может быть выбран бригадиром, то, очевидно, есть 20 способов его выбора. Тогда дежурным может стать каждый из оставшихся 19 рабочих. Любой из 20 способов выбора бригадира может осуществиться вместе с любыми из 19 способов выбора дежурного. Поэтому всего существует 20 ∙ 19 = 380 способов формирования наряда. Т.о. на 380 дней мастер Зимин может составить график.

Задача 2. В бригду Сбруева проходят на работу 4 молодых специалиста: Белкин, Пенкин, Свечкин и Овечкин. Бригадир для распределения их просит рассчитаться по порядку. Он просит их выстроиться справа от Сбруева и по команде «По порядку номеров рассчитайсь!» производят расчет: «первый-второй-третий-четвертый-пятый». После этого бригадир перестраивает новеньких по-новому и расчет повторяется. Сколько раз может Сбруев повторить это упражнение, используя только разные способы перестроения новеньких по участкам?

Решение. Первого новичка стоящего в шеренге можно выделить четырьмя способами; второго, очевидно, тремя способами. На третье место будут претендовать только два человека, и, следовательно, есть два способа заполнить третье место. Для четвертого новичка места уже не остается, и он выступает последним.

Занумеруем новобранцев: 1 – Белкина, 2 – Пенкин, 3 – Свечкин, 4 – Овечкин.

Составим схему.

Каждый способ выбора первого новичка может быть скомбинирован с шестью случаями выбора остальных, то число способов составляет

4 ∙ 6 = 24.

Задача 3. Сколькими способами можно выбрать из пяти разных книг какие-либо две и подарить их двум строителям дорог, в день дорожного рабочего в городе Брюково?

Решение. Обозначим книги буквами A, B, C, D, E, можно выписать все возможные пары книг, а именно: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE. Мы видим, что их число равно десяти.

II. Введение новых понятий (30 мин)

В практической человеческой деятельности часто приходится иметь дело с различными ситуациями. Умение анализировать сложившуюся обстановку, адекватно ее оценивать и делать правильные выводы является важным качеством каждого профессионала. Во многих случаях практика приводит к комбинаторным задачам.

1) Факториал

Определение. Произведение всех последовательных натуральных чисел от 1 до n обозначается n!

n! = 1 · 2 · 3 · … · n.

Используя знак факториала, можно, например, записать

Факториалы растут удивительно быстро.

Точные значения факториалов

2) Размещения

Определение.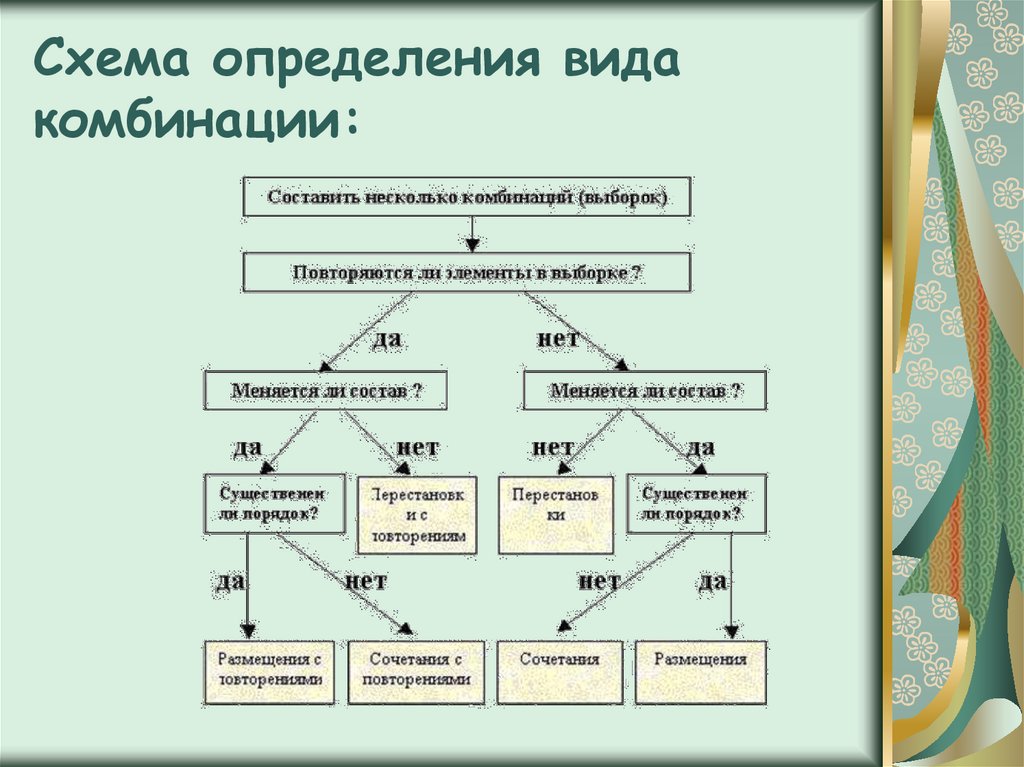 Размещениями из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.

Пример. При приеме на работу очень нужного специалиста у будущего сотрудника семизначный телефонный номер, в котором ни одна цифра не повторяется и нет нуля. Сотрудник отдела кадров, предположил, что перебор этих номеров потребует одного-двухчасов. Прав ли он?

Решение. Число номеров равно числу размещений из 9 элементов по 7, т.е. равно По формуле получаем номеров.

Даже если на проверку одного номера тратить 1 минуту, то на все уйдет 3024 часа или 126 суток. Таким образом, кадровик – не прав.

3) Сочетания

Определение. Сочетаниями из n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. (Подмножества, отличающиеся друг от друга только порядком следования элементов, не считаются различными. )

Число сочетаний из n элементов по m обозначается символом и вычисляется по формуле:

Пример. В штате ДРСУ города имеется 16 начальников отделов. Сколькими способами можно выбрать 2 из них для перевода в областное управление?

Решение. Способов столько, сколько существует двухэлементных подмножеств у множества, состоящего из 16 элементов, т.е. их число равно , т.е. всего 120 способов выбора начальников.

4) Перестановки

Определение. Перестановками из n элементов называются такие соединения из n элементов, которые отличаются друг от друга лишь порядком следования элементов.

Пример. Замок сейфа, в котором лежит документация по строительству участка дороги открывается, если введена правильная комбинация. Сотрудник забыл код и пытается открыть сейф, набирая код наудачу. Он знает, что код состоит из цифр 1, 2, 3, 4, 5, 6 при условии, что все числа не повторяются и последней является 5. Сколько попыток ему придется сделать.

Решение. Так как число пять должно стоять на последнем месте, то остальные пять цифр могут стоять на оставшихся местах в любом порядке. Следовательно, количество кодов из шестизначных чисел, с пятеркой на конце, равно числу перестановок из пяти элементов, т.е. .

4 Закрепление нового материала. (20 мин)

А теперь перейдем к работе в парах. Ваша задача: решить задачи, оформить их в своем конспекте, проверить и оценить свою работу. Задания на столах в ваших конспектах. Помогайте друг другу при решении. (Учитель, в процессе работы учащихся, оказывает помощь каждой паре).

Вариант 1.

1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

1) 30 2) 100 3) 120 4) 5

2. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

1) 128 2) 495 3) 36 4) 48

3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

1) 10 2) 60 3) 20 4) 30

№ задания 1 2 3

№ ответа 3 2 4

Вариант 2.

1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

1) 100 2) 30 3) 5 4) 120

2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

1) 3 2) 6 3) 2 4) 1

3. Сколькими способами из 8 учебных предметов можно составить расписание учебного дня из 4 различных уроков.

1) 10000 2) 1680 3) 32 4) 1600

№ задания 1 2 3

№ ответа 4 1 2

Вариант 3.

1. Сколькими способами можно расставить 4 различные книги на книжной полке?

1) 24 2) 4 3) 16 4) 20

2. Сколько диагоналей имеет выпуклый семиугольник?

1) 30 2) 21 3) 14 4) 7

3. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

1) 22 2) 11 3) 150 4) 110

№ задания 1 2 3

№ ответа 1 2 4

Вариант 4

1. Сколькими способами могут встать в очередь в билетную кассу 5 человек?

1) 5 2) 120 3) 25 4) 100

2. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?

1) 455 2) 45 3) 475 4) 18

3. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?

1) 600 2) 100 3) 300 4)720

№ задания 1 2 3

№ ответа 2 1 4

Вариант 5

1. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?

1) 10 2) 20 3) 120 4) 50

2. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?

1) 35 2) 30 3) 70 4) 45

3. На соревнованиях по лёгкой атлетике наш техникум представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?

1) 120 2) 1560 3) 4800 4) 5040

№ задания 1 2 3

№ ответа 3 1 4

Сейчас каждый из вас выступит в роли учителя. Студент решил задачу. Проверьте, верно, ли решена задача:

Задача. Сколько четырехбуквенных слов можно образовать из букв слова сапфир?

Решение. P₄=4! = 1*2*3*4 =24 (неверно)

5 Подведение итогов занятия (3мин)

Подведем итоги нашего занятия. Обсуждение и выставление оценок за урок.

6 Домашнее задание (1 мин)

Решить задачу (дифференцированные задачи)

Задача на «3»

1. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.

Задачи на «4»

2. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

3. Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?

Задачи на «5»

4. Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

7 Рефлексия. (3 мин)

Достиг ли ты своих целей? _____________________

Оцени степень усвоения: ________________________

Продолжи одно из предложений:

“Мне понятно…

“Я запомнил…

“Мне на уроке…

“Я думаю…

Презентация по математике Перестановки, размещения, сочетания доклад, проект

Главная
Разное
Образование
Спорт
Естествознание
Природоведение
Религиоведение
Французский язык
Черчение
Английский язык
Астрономия
Алгебра
Биология
География
Геометрия
Детские презентации
Информатика
История
Литература
Математика
Музыка
МХК
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
Педагогика
Русский язык
Технология
Физика
Философия
Химия
Шаблоны, фоны, картинки для презентаций
Экология
Экономика

Презентация на тему Презентация по математике Перестановки, размещения, сочетания, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 18 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.

Слайд 1Текст слайда:

Элементы комбинаторики Перестановки, сочетания и размещения

Слайд 2Текст слайда:

Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.
Слово «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает «соединяю».

Слайд 3Текст слайда:

Термин комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем (1646-1716 г. г.), — всемирно известным немецким учёным.

Слайд 4Текст слайда:

Комбинаторные задачи делятся на несколько групп:

Задачи на перестановки

Задачи на размещение

Задачи на сочетание

Слайд 5Текст слайда:

Сколькими способами можно расставить 3 различные книги на книжной полке?

Слайд 6Текст слайда:

Перестановки – соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок. Число n называется порядком перестановки.

Слайд 7Текст слайда:

Факториал — это произведение всех натуральных чисел от 1 до n.

n! = 1 · 2 · 3 · … · n

Например, 4! = 1·2·3·4 = 24

Слайд 8

Слайд 9Текст слайда:

Задача

Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…

P4 = 4! = 1 · 2 · 3 · 4 = 24

И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…

Слайд 10Текст слайда:

В группе ПСО-23 обучается 28 студентов.

Сколькими способами можно составить график дежурства по колледжу, если группа дежурных состоит из пяти студентов?

Слайд 11Текст слайда:

Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком элементов, либо самими элементами.

Слайд 12Текст слайда:

Задача.
Студенты группы изучают 9 дисциплин. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных дисциплины?

A49 = = 6∙ 7∙ 8∙ 9 = 3024 способа

Слайд 13Текст слайда:

Решите самостоятельно:

В группе 29 студентов. Нужно отправить одного студента за мелом, второго дежурить в столовую, а третьего вызвать к доске. Сколькими способами можно это сделать?

Слайд 14Текст слайда:

Студентам дали список из 10 учебников, которые рекомендуется использовать для подготовки к экзамену . Сколькими способами студент может выбрать из них 3 книги?

Слайд 15Текст слайда:

Сочетания– соединения, содержащие по m элементов из n, различающихся друг от друга, по крайней мере, одним элементом.

Слайд 16Текст слайда:

Решение задачи:

Слайд 17Текст слайда:

Задача.
В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

C72 = = 21

Слайд 18Текст слайда:

Домашнее задание: 1. В соревнованиях участвуют 12 команд. Сколько существует вариантов распределения призовых (I, II, III) мест? 2. Студенты Женя, Сергей, Коля, Наташа и Ольга побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие студенты могут занять очередь для игры в настольный теннис?

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Основы комбинаторики. Размещения, перестановки, сочетания презентация, доклад, проект

Слайд 1Текст слайда:

Основы комбинаторики.
Размещения, перестановки,
сочетания.

Слайд 2Текст слайда:

Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…

Слайд 3Текст слайда:

знать:
определения трех важнейших понятий комбинаторики:
размещения из n элементов по m;
сочетания из n элементов по m;
перестановки из n элементов;
основные комбинаторные формулы
уметь:
отличать задачи на «перестановки», «сочетания», «размещения» друг от друга;
применять основные комбинаторные формулы при решении простейших комбинаторных задач.

Слайд 4Текст слайда:

множество

Множество характеризуется объединением некоторых однородных объектов в одно целое.
Объекты, образующие множество, называются элементами множества.
Множество будем записывать, располагая его элементы в фигурных скобка {a, b, c, … , e, f}.
Во множестве порядок элементов роли не играет, так {a, b} = {b, a}.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается символом ø.

Слайд 5Текст слайда:

множество

Если каждый элемент множества А является элементом множества В, то говорят, что множество А является подмножеством множества В.

Множество {a, b} является подмножеством множества {a, b, c, … , e, f}.

Обозначается

Пример:

Задача

Перечислите возможные варианты подмножества множества {3, 4, 5, 7, 9}.

Слайд 6Текст слайда:

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству.

Комбинаторика является важным разделом математики, который исследует закономерности расположения, упорядочения, выбора и распределения элементов с фиксированного множества.

Слайд 7Текст слайда:

ПРАВИЛО СУММИРОВАНИЯ

Если два взаимоисключающие действия могут быть выполнены в соответствии k и m способами, тогда какое-то одно из этих действий можно выполнить k + m способами.

Пример №1
Из города А в город В можно добраться 12 поездами, 3 самолетами, 23 автобусами. Сколькими способами можно добраться из города А в город В?
Решение

N=12+13+23=38

Слайд 8Текст слайда:

Пример № 2
В ящике имеется n разноцветных шариков. Произвольным образом вынимаем один шарик. Сколькими способами это можно сделать?

Решение. Конечно, n способами.

Теперь эти n шариков распределены по двум ящикам: В первом m шариков, во втором k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами это можно сделать?

Решение.
Из первого ящика шарик можно вытянуть m различными способами, из второго k различными способами, всего N = m + k способами.

Слайд 9Текст слайда:

ПРАВИЛО ПРОИЗВЕДЕНИЯ

Пусть две выполняемые одно за другим действия могут быть осуществлены в соответствии k и m способами Тогда обе они могут быть выполнены k ∙ m способами.

Пример № 3
В турнире принимают участие 8 хоккейных команд. Сколько существует способов распределить первое, второе и третье места?
Решение

N=8∙7∙6=336

Слайд 10Текст слайда:

Пример № 4
Сколько можно записать двузначных чисел в десятичной системе счисления?

Решение. Поскольку число двузначное, то число десятков (m) может принимать одно из девяти значений: 1,2,3,4,5,6,7,8,9. Число единиц (k) может принимать те же значения и может, кроме того быть равным нулю. Отсюда следует, что m = 9, а k= 10. Всего получим двузначных чисел
N = m ·k = 9·10 =90.

Слайд 11Текст слайда:

Пример № 5
В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

Решение. По правилу умножения двух девушек можно выбрать 14 ·13 = 182 способами, а двух юношей 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студентов или студенток. Согласно правилу сложения таких способов выбора будет
N =182 + 30 = 212.

Слайд 12Текст слайда:

Типы соединений

Множества элементов называются соединениями.

Различают три типа соединений:
перестановки из n элементов;
размещения из n элементов по m;
сочетания из n элементов по m (m

Слайд 13Текст слайда:

Определение: Перестановкой из n элементов называется любое упорядоченное множество из n элементов.
Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой – на втором, какой- на третьем, …, какой – на n-м месте.

ПЕРЕСТАНОВКИ

Перестановки – это такие соединения по n элементам из данных элементов, которые отличаются одно от другого порядком элементов.

Число перестановок из n элементов обозначают Рn.

Рn = n · (n — 1) · (n – 2) · … · 2 · 1 = n!

Слайд 14Текст слайда:

Определение:
Пусть n — натуральное число. Через n! (читается «эн факториал») обозначается число, равное произведению всех натуральных чисел 1 от до n:
n! = 1 · 2 · 3 · … · n.

В случае, если n = 0, по определению полагается: 0! = 1.

ФАКТОРИАЛ

Слайд 15Текст слайда:

Пример № 6
Найдем значения следующих выражений: 1! 2! 3!
7!
Пример № 7
Чему равно
а)Р5 ;
б) Р3.

Пример № 8
Упростите
а) 7! · 8
б) 12! · 13 ·14
в) κ! · (κ + 1)

Слайд 16Текст слайда:

Пример № 9
Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?

Решение.

n =8

Р8=8! = 8·7·6·5 · 4 · 3 · 2 ·1 =40320

Слайд 17Текст слайда:

РАЗМЕЩЕНИЯ

Определение. Размещением из n элементов по m называется любое упорядоченное множество из m элементов, состоящее из элементов n элементного множества.

Число размещений из m элементов по n обозначают:

вычисляют по формуле:

Слайд 18Текст слайда:

Пример № 9
Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день?
Решение.

Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество (уроков) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре (m=9, n=4) то есть A94:

Слайд 19Текст слайда:

Пример № 10
Сколькими способами из класса, где учатся 24 ученика, можно выбрать старосту и помощника старосты?
Решение.

Имеем 24-элементное множество, элементы которого ученики класса. При выборах старосты и помощника старосты мы будем выбирать 2-элементное подмножество (ученика) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре(m=24, n=2), то есть A242:

Слайд 20Текст слайда:

СОЧЕТАНИЯ

Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества

Число сочетаний из n элементов по m обозначают

и вычисляют по формуле:

Слайд 21Текст слайда:

Пример № 11
Сколькими способами из класса, где учатся 24 ученика, можно выбрать два дежурных ?
Решение.

n =24, m=2

Слайд 22Текст слайда:

Учитывается ли порядок следования элементов в соединении?

Д А

НЕТ

Все ли элементы входят в соединение?

СОЧЕТАНИЯ

РАЗМЕЩЕНИЯ

ПЕРЕСТАНОВКИ

Рn = n!

Д А

НЕТ

Слайд 23Текст слайда:

Определить к какому типу относится соединений относится задача.

1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

2. В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

Учитывается ли порядок следования элементов в соединении?

( да)

Все ли элементы входят в соединение?

( да)

Вывод: перестановка

Учитывается ли порядок следования элементов в соединении?

Все ли элементы входят в соединение?

(нет)

(на этот вопрос ответ не нужен)

Вывод: сочетания

Слайд 24Текст слайда:

Учитывается ли порядок следования элементов в соединении?

Все ли элементы входят в соединение?

(нет)

( да)

Вывод: размещение

Слайд 25Текст слайда:

Сколько различных вариантов расположения музыкантов возможно?

Слайд 26Текст слайда:

Решение.

Учитывается ли порядок следования элементов в соединении?

( да)

Все ли элементы входят в соединение?

(да)

Вывод: перестановка

Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1

n =4

Р4 = 4! = 4 · 3 · 2 ·1=24

Слайд 27Текст слайда:

«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»?

Кто автор высказывания?

Слайд 28Текст слайда:

перестановки

размещение

сочетание

120

132

720

6720

5040

Слайд 29Текст слайда:

Результаты решения задач

Слайд 30Текст слайда:

Скачать презентацию

Перестановка и комбинация — GeeksforGeeks

Перестановка:

Перестановка представляет собой набор или комбинацию объектов из набора, где порядок или расположение выбранных объектов имеет значение. Другими словами, перестановка — это расположение объектов в определенном порядке, . Например, если у нас есть два элемента A и B, то возможны два расположения: (AB) и (BA).

Ключевой момент

ⁿ P _n = n(n – 1) (n -2)… 3x2x1=n!
^N P ₀ = 1
^N P ₁ = N
^N P _N-1 = N! N!!
ⁿ P _r = n. ^n-1 P _r-1 = n(n-1) ^n-2 P _r-2

Количество перестановок, когда ‘ r ‘ элементов расположены из общего числа из n элементов равно ⁿ P _r = n! / (н – р)! Например, пусть n = 4 (A, B, C и D) и r = 2 (все перестановки размера 2). Ответ 4!/(4-2)! = 12. Двенадцать перестановок: AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB и DC.

Комбинация:

Комбинация представляет собой различные выборки заданного количества элементов, взятые по одному, по частям или все одновременно. Например, если у нас есть два элемента A и B , то есть только один способ выбрать два элемента, мы выбираем оба из них.

Ключевой пункт

^N C _R — натуральное число
^N C ₀ = (^N C _N) = = (^N C _N) = = C _N) =
=
=
=
=
=
=
=
=
=

₁

ⁿ C _r =( ⁿ C _n−r )
90 024 n 50024 n C _y ⇒x=y или x+y=n
n. ⁿ⁻¹ C _r−1 =(n−r+1)× ⁿ C _r−1

Количество комбинаций при выборе ‘r’ элементов из Всего n элементов равно ⁿ C _r = n! / ((г!) х (п – г)!). Например, пусть n = 4 (A, B, C и D) и r = 2 (все комбинации размера 2). Ответ: 4!/((4-2)!*2!) = 6. Шесть комбинаций: AB, AC, AD, BC, BD и CD.

Примечание: В том же примере у нас есть разные случаи перестановки и комбинации. Для перестановки AB и BA — разные вещи, но для выбора AB и BA — одно и то же.

Примеры задач

Вопрос 1: Сколько слов можно составить, используя 3 буквы из слова «ДЕЛИ» ?

Решение: Слово «ДЕЛИ» состоит из 5 разных слов. Следовательно, необходимое количество слов = ⁵ P ₃ = 5! / (5 – 3)!
Необходимое количество слов = 5! / 2! = 120 / 2 = 60

Вопрос 2: Сколько слов можно составить из букв слова «ВОДИТЕЛЬ» так, чтобы все гласные всегда были вместе?

Решение: В вопросах такого типа мы предполагаем, что все гласные — это один символ, т. е. «IE» — это один символ. Итак, теперь у нас в слове 5 символов, а именно D, R, V, R и IE. Но, R встречается 2 раза . => Количество возможных аранжировок = 5! / 2! = 60 Теперь две гласные можно расположить в 2! = 2 способа. => Общее количество возможных слов, в которых гласные всегда вместе = 60 x 2 = 120

Вопрос 3: Сколькими способами мы можем выбрать команду из 4 студентов из заданного выбора из 15 ?

Решение: Количество возможных способов выбора = ¹⁵ C ₄ = 15 ! / ((4 !) x (11 !))
Количество возможных способов выбора = (15 x 14 x 13 x 12) / (4 x 3 x 2 x 1) = 1365

Вопрос 4: Сколькими способами можно составить группу из 5 человек, выбрав 3 мальчиков из 6 мальчиков и 2 девочек из 5 девочек ?

Решение: Количество способов выбрать 3 мальчиков из 6 = ⁶ С ₃ = 6 ! / [(3 !) x (3 !)] = (6 x 5 x 4) / (3 x 2 x 1) = 20 Количество способов выбрать 2 девушек из 5 = ⁵ C ₂ = 5 ! / [(2 !) x (3 !)] = (5 x 4) / (2 x 1) = 10 Следовательно, общее количество способов формирования группы = 20 x 10 = 200

Вопрос 5: Как сколько слов можно составить из букв слова «ВОДИТЕЛЬ» так, что все гласные никогда не будут вместе?

Решение: мы предполагаем, что все гласные являются одним символом, т. е. «IE» — это одиночный символ. Итак, теперь у нас в слове 5 символов, а именно D, R, V, R, и IE . Но R встречается 2 раза. => Количество возможных аранжировок = 5! / 2! = 60 Теперь две гласные можно расположить в 2! = 2 способа. => Общее количество возможных слов, в которых гласные всегда вместе = 60 x 2 = 120 ,
общее количество возможных слов = 6! / 2! = 720 / 2 = 360 Таким образом, общее количество возможных слов, в которых гласные никогда не встречаются вместе 240

Перестановки и комбинации — тест на способности, вопросы, сокращения, видео-примеры решения

Видео о перестановках и сочетаниях — сокращения, советы и рекомендации

Мы всегда сталкивались с проблемой понимания разницы между перестановкой и комбинацией.

Эта глава определенно прояснит понятия перестановки и комбинации, единственное, что вам нужно сделать, это полностью понять разницу между двумя терминами, а также изучить быстрые советы по решению проблем на основе этой главы

Разница между перестановкой и комбинацией

Что такое перестановка?

Перестановка: Различные способы упорядочивания заданного количества вещей путем одновременного взятия некоторых или всех вещей называются перестановками.
Перестановка включает словообразование, числообразование, круговую перестановку и т. д. При перестановке объекты должны располагаться в определенном порядке. Обозначается ⁿ P _r или P(n, r).

Пример: Расставьте данные 3 числа 1, 2, 3, взяв по два за раз.
Теперь эти числа можно расположить 6 различными способами: (12, 21, 13, 31, 23, 32).

Здесь

12 и 21, 13 и 31 или 23 и 32 не означают одно и то же, потому что здесь важен порядок чисел.

Что такое комбинация?

Комбинация: Каждая из различных групп или выборок, образованных путем взятия некоторого или всего количества объектов, называется комбинацией.

Комбинация используется в различных случаях, включая команду/группу/комитет.

В комбинации объекты выбираются случайным образом и здесь порядок объектов не имеет значения. Обозначается ⁿ C _r или C(n, r)

Пример: Если из 3 девочек X, Y, Z нужно выбрать двух, то найти количество возможных комбинаций. .

Теперь нужно выбрать и устроить только двух девушек. Следовательно, это возможно тремя различными способами: (XY, YZ, XZ,).

Здесь
Вы не можете составить комбинацию XY и YX, потому что эти комбинации означают одно и то же.

Краткие советы и рекомендации

Факториал n!: Произведение всех положительных целых чисел, меньших или равных n.
Пример: 4! = 4 × 3 × 2 × 1 = 24

Теорема счета:

1) Правило сложения: Если первое задание выполняется x способами, а второе задание выполняется y способами, то любой из две операции можно выполнить (x + y) способами

2) Правило умножения: Если первая задача выполняется x способами, а вторая задача выполняется y способами, то обе операции можно выполнить (x × y) способами

Предположим, что n различных торты делаются ₁ , ₂ , ₃ , … _n различными способами соответственно, независимо друг от друга, тогда:

1) Любой из них можно сделать в ₁ + ₂ + ₃ + … + a _n способов. (a ₁ способ или ₂ способ или ₃ + … + a _n способ)
2) Все они могут быть выполнены в виде ₁ × a ₂ × a _{3 × … × a _n способов (a ₁ способов и a ₂ способов и a ₃ + … + a _n способов)}

Все о перестановке: 1:0 3 1 0

5 Число перестановок n вещей, взятых по r за раз, определяется следующим образом:

ⁿ P _r = n (n – 1) (n – 2) (n – 3)……. (n – r + 1) =	n!
	(н-р)!

2) Условие 2: Если есть N шаров и из них B ₁ одинаковых шаров, B ₂ одинаковых шаров, B ₃ одинаковых шаров и т.д. 902 и т.д. r подобны r ^{-му виду}, так что (B ₁ шаров + B ₂ шаров + B ₃ шаров —— B _r шаров) = N шаров.

В таком состоянии

Количество перестановок этих N шаров =	N!
	(Б ₁)! × (В ₂ )! × (В ₃ )! × — — — — — (B _r )!

3) Условие 3: Если количество перестановок n объектов одновременно,

, тогда ⁿ P _r0449	н!	= н!
	0!

Важно помнить:

1) Если нужно расположить N различных объектов, то их можно расположить N! способы.

2) N объектов можно расположить по кругу за (N – 1)! способы.

3) Иногда приходится решать задачи на перестановку с учетом условия Повторение

Повторение: Это условие не используется, если не указано иное. (Помните)
Количество перестановок N объектов, взятых r за раз , когда каждый выбранный объект может быть повторен любое количество раз, определяется как:

Количество перестановок = n ^r

4) Ограничено Перестановка: Количество перестановок n объектов, взятых r за раз, в котором если k конкретных объектов:

а) Никогда не включались: ^{(n – k)} P _r —- (k – количество неучтенных объектов)
b) Всегда включено: ^{(n – k)} C _{r–k x r!} —- (k — количество всегда включенных предметов)

Все о комбинациях:

1) Количество комбинаций из n предметов, взятых по r за раз, определяется следующим образом:

ⁿ C _r =	n!	=	n(n – 1) (n – 2)…….to r коэффициенты
	(р!)(н – р)!		р!

Этот пример, безусловно, прояснит концепцию!

Подсказка: В приведенном ниже примере будет устранена путаница, связанная со сложением и умножением терминов.

Пример: Предположим, есть 12 мальчиков и 8 девочек, и мы должны выбрать 5 добровольцев для выполнения определенной задачи. Поэтому нам нужно найти количество возможных вариантов выбора, которые мы можем сделать.

Всего студентов (12 + 8) = 20, и мы должны выбрать 5 добровольцев.

Всего можно выбрать _n C ^r способов = ₂₀ C ⁵	n!
	(р!)(н-р)!

Вопрос можно задать по-разному. Ниже указаны 2 различных условия:

1) Из 5 добровольцев должны присутствовать 3 мальчика и 2 девочки.
2) Мальчиков должно быть большинство.

Условие 1: 3 мальчика 2 девочки нужны	Условие 2: Если мальчики составляют большинство
Из 12 мальчиков выбираются 3, а из 8 девочек выбираются 2. (Мальчики) ¹² C ₃ и (Девочки) ⁸ C ₂ Нужны и девочки, и мальчики, поэтому их размножают. ¹² C ₃ × ⁸ C ₂	1) Если только мальчики выбираются в качестве добровольцев: ¹² C ₅ 2) 4 мальчики: C ₅ 2)0024 12 C ₄ × ⁸ C ₁ 3) 3 мальчика и 2 девочки: ¹² C ₃ × ⁸ C ₂ Это будут 3 C ₂ в большинстве. (¹² C ₅) или (¹² C ₄ × ⁸ C ₁) или (¹² C ₃ × C ₂ 2 × C _{6 2} ( C ₇ 2 × ⁸ C _{7 2} ( 2 (). ¹² С ₅ ) + ( ¹² С ₄ × ⁸ C ₁ ) + ( ¹² C ₃ × ⁸ C ₂ )

Условие 1: 3 мальчика 2 девочки нужны

Условие 2: Если мальчики составляют большинство

Из 12 мальчиков выбираются 3, а из 8 девочек выбираются 2.

(Мальчики) ¹² C ₃ и (Девочки) ⁸ C ₂

Нужны и девочки, и мальчики, поэтому их размножают.

¹² C ₃ × ⁸ C ₂

1) Если только мальчики выбираются в качестве добровольцев: ¹² C ₅
2) 4 мальчики: C ₅
2)0024 12 C ₄ × ⁸ C ₁
3) 3 мальчика и 2 девочки: ¹² C ₃ × ⁸ C ₂

Это будут 3 C ₂

в большинстве.

(¹² C ₅) или (¹² C ₄ × ⁸ C ₁) или (¹² C ₃ × C ₂ 2 × C _{6 2} ( C ₇ 2 × ⁸ C _{7 2} ( 2 (). ¹² С ₅ ) + ( ¹² С ₄ × ⁸ C ₁ ) + ( ¹² C ₃ × ⁸ C ₂ )

Important Formulae:

1) ⁿ C _n = ⁿ C ₀ = 1

2) ⁿ C _{n – 1} = ⁿ C ₁ = n

3) ⁿ C _r = ^н С _{н – г}

4) 0! = 1

5) н! = n (n – 1)!

6) ⁿ P _r =	n!
	(н-р)!

7) ⁿ C _r =	нПр!
	р!

Типы вопросов

Тип 1: Перестановка

Q 1. Найдите значение ⁵⁰ P ₂

a. 4500
б. 3260
г. 2450
д. 1470
Посмотреть решение

Правильный вариант: (c)

Подсказка:

ⁿ P _r =	9 n!
	(н-р)!

Здесь n = 50 и r = 2

50!	=	50 × 49 × 48	= 50 × 49= 2450
(50 – 2)!		48!

Значение ⁵⁰ P ₂ = 2450

Q 2. Сколько слов можно составить из букв слова «ДЕЛИ»?

а. 50
б. 72
г. 85
д. 120
Посмотреть решение

Правильный вариант: (d)

Подсказка:
Слово «DELHI» состоит из 5 букв
Следовательно, необходимое количество слов = ⁵ P ₅ = 5! = (5 × 4 × 3 × 2 × 1) = 120
120 слов можно составить, используя буквы слова «ДЕЛИ»

Q 3. Найдите количество способов, которыми можно составить буквы слова «РЕЗИНА». согласованный?

а. 450
б. 362
г. 250
д. 180
Посмотреть решение

Правильный вариант: (d)

Подсказка:
Слово «РЕЗИНА» состоит из 6 букв: 2R, 2B, 1 U, 1 E
Следовательно,

3 90 требуемых путей :	Н!
	(2R!) × (2B!) × (1U!) × (1E!)

=	6!
	(2 × 1) × (2 × 1) × (1) × × (1)

=	6 × 5 × 4 × 3 × 904 1 9044 4

= 6 × 5 × 3 × 2
= 180

Q 4. Найдите, сколькими различными способами можно расставить буквы слова «НАЧАЛО» так, чтобы гласные всегда стояли вместе?

а. 548
б. 426
г. 720
д. 790
Посмотреть решение

Правильный вариант: (c)

Букв в слове «НАЧАЛО» 7.
Количество гласных = EAI
Количество согласных: LDNG
Условие: Гласные всегда идут вместе. Поэтому будем считать гласные одной группой «EAI»
Следовательно, гласные «EAI» и согласные LDNG вместе образуют 5 букв.
Следовательно, эти 5 букв можно сложить в 5! Способов = 5! = 5 × 4 × 3 × 2 = 120 способов
Буквы в группе гласных «EAI» также могут быть заменены местами. Итак, эти гласные можно расположить в 3! Пути = 6 способов.
Все вместе, необходимое количество путей = 120 x 6 = 720 способов

Перестановки и комбинации: примеры и различия

Когда дело доходит до компоновки, это может быть довольно сложно. Представьте себе, что тренер пытается отобрать игроков на футбольный матч из своей команды. Сколькими возможными способами он может этого добиться? Или, может быть, учитель ищет лучшее сочетание девочек и мальчиков в своем классе, чтобы отправиться в путешествие, для которого требуется всего 7 учеников. Сколькими способами он может составить свою команду из 7 человек?

В этой статье мы узнаем о способах решения вопросов, подобных двум упомянутым выше, при определении перестановок и комбинаций .

Что такое перестановка?

Перестановка — это расположение объектов посредством в соответствии с определенным порядком или образцом . Произведенный упорядоченный выбор называется переставленным. У нас есть два вида перестановок: линейная перестановка и круговая перестановка.

Линейная перестановка

Когда расположение с порядком выполняется на прямой линии, это известно как линейная перестановка . Например, когда вам нужно найти количество способов, которыми можно расположить следующие 6 шаров по порядку. Такое расположение объектов по прямой можно увидеть на изображении ниже.

Изображение линейно расположенных шаров для линейной перестановки, StudySmarter Originals

Круговая перестановка

Однако, когда расположение с порядком выполнено круговым или изогнутым образом, оно известно как круговая перестановка . Пример можно увидеть, когда нужно расположить разноцветные камни на бусине. Рисунок ниже дает представление о круговых схемах.

Иллюстрация шаров, расположенных по кругу, StudySmarter Originals

В отличие от линейных перестановок, где элементы расположены по прямой линии, круговые перестановки располагаются по кругу, как показано выше. В дальнейшем у вас будут дополнительные подробности и примеры циклических перестановок.

Что такое знак перестановки?

Несколько знаков используются для представления перестановок; это:

Типы линейной перестановки и соответствующие формулы

Существует два типа перестановки: перестановка с повторением и перестановка без повторения.

Перестановка с повторением

В таком случае расположения или выделения объект можно повторно использовать на всех этапах выделения. Это означает, что каждый компонент группы может использоваться всякий раз, когда делается выбор.

Например, если необходимо выбрать три буквы из алфавитов от A до Z, то буква A может быть выбрана в эти 3 раза, как AAA. То же самое относится к B и C и т. д. И т. д. Поскольку у нас есть 26 алфавитов, каждый раз у нас есть 26 вариантов! Таким образом, количество раз, которое будут выбраны три буквы, равно

, где основание 26 означает, что существует 26 алфавитов, а показатель степени 3 представляет количество алфавитов, которые необходимо выбрать. Это означает, что для отбора с повторением по формуле

где n — количество объектов в наборе, а r — количество раз, когда делается выбор.

Перестановка без повторения

В этом случае нет повторения элемента набора, используемого при выборе. После того, как элемент используется, его нельзя использовать повторно, что снижает имеющиеся шансы.

Например, если нужно выбрать один алфавит и выбрать Z, после использования Z его нельзя будет использовать повторно, что снижает наши шансы с 26 до 25. Аналогичным образом, если нужно выбрать два алфавита и выбрать Z и Y, как только используются Z и Y, это еще больше уменьшает нашу вероятность с 26 до 24 и так далее. Таким образом, у нас остается:

Таким образом, в отличие от перестановки с повторением, которая позволяет заменять и повторно использовать элемент в наборах, перестановки без повторения не допускают замены и последующего использования какого-либо элемента после его использования.

В каком порядке можно расположить буквы от A до F без повторения букв?

Решение:

В этом случае буква не может появляться более одного раза. Таким образом, если А начинает набор или занимает первую позицию среди шести вакантных буквенных позиций, то А должна оставаться только в первой позиции, не появляясь снова в другой позиции, если только она не будет удалена из первой позиции и помещена в другую позицию. Это правило распространяется и на другие буквы в наборе. Кроме того, как только A начинает последовательность, она уменьшает следующую букву на одну цепочку. Таким образом, A представляет собой 6 цепочек возможностей, B имеет 5 и C имеет 4, пока F не имеет только цепочку, потому что она должна была повторяться во всех других цепочках.

Таким образом, количество способов упорядочения от A до F равно:

В предыдущем примере выбираются и упорядочиваются все элементы чисел. А что произойдет, если некоторые из них будут выбраны из всех? Например, вам даны числа от 1 до 10, и вы должны выбрать 6.

Вспомните, мы можем расположить числа от 1 до 10 в

Однако, поскольку сейчас мы выбираем только 6 чисел, это означает, что у нас есть

Но. Таким образом, мы можем вывести формулу перестановки:

, где n — количество объектов, r — количество объектов, из которых нужно выбрать.

Таким образом, чтобы решить вопрос заново, мы имеем

Что касается этой формулы, то она предполагает, что если выбрать и расположить все элементы множества, то r станет равным n. Таким образом, это выражается как

Использование перестановок в расположении букв

Вспомним, что для того, чтобы сделать упорядоченное расположение без повторения, включающее все элементы набора из n элементов, мы имеем P(n,n) = n! способы.

Между тем, если некоторые члены, r , из множества, n , должны были быть выбраны и расположены, мы имеем,

способов

Однако бывают случаи, когда член множества повторяется внутри множество. Например, в слове ПОБЕДИТЕЛЬ N повторяется дважды. Следовательно, для учета двойного N получается:

Обратите внимание, что перестановка всех элементов делится на количество повторений перестановки (в данном случае 2). Итак, если бы N повторилось трижды, перестановка была бы разделена на P(3,3), что равно 3!.

Аналогичным образом, если у вас есть более одного повторяющегося элемента набора, перестановка всех элементов делится на произведение перестановки каждого повторяющегося элемента. Например, в слове LESSES у нас есть две E и три S, всего шесть алфавитов. Для этого используем:

Основываясь на этом знании, чтобы расположить буквы в одном алфавите, получается

, где n — общее количество букв, p и q — количество повторений алфавита.

Сколькими способами можно составить слово МИССИСИППИ?

Решение:

Слово MISSISSIPPI состоит из 11 букв, в которых I повторяется 4 раза, S повторяется 4 раза и P повторяется 2 раза.

Поэтому применим формулу.

Однако в этом случае у нас есть 3 повторения, поэтому мы не останавливаемся на q, а добавляем s, чтобы нашу формулу можно было скорректировать до:

После применения мы имеем:

Круговой формула перестановки

Мы рассмотрели перестановку объектов линейным образом, но иногда расположение выполняется по кругу или по кругу, как упоминалось ранее в этом исследовании. Это требует другого подхода, потому что в отличие от прямой линии, которая начинается из точки и заканчивается в другой точке, окружность начинается в точке и заканчивается в той же точке. Это означает, что для n набор чисел, n повторяется, так что мы имеем:

Таким образом, перестановка в этом случае следует за использованием .

Джона попросили усадить 5 учеников за круглый обеденный стол. Сколькими способами он может этого добиться?

Решение:

Что такое комбинация?

Комбинация — это метод выбора, который не следует порядку. В отличие от перестановки, если бы нужно было выбрать три буквы из букв от A до E, ABC, ACB, BAC, BCA, CAB и CBA все были бы результатами, поскольку задействован порядок. Но в комбинации, где порядок не нужен, только одна азбука обозначает остальные, потому что все они являются повторениями, если порядок не задействован.

Результаты комбинации ниже, чем результаты перестановки, потому что при удалении порядка только один результат заменяет похожие порядки. Например, вместо того, чтобы писать эти шесть результатов; ABC, ACB, BAC, BCA, CAB и CBA, вы пишете только одну ABC. уменьшая количество вариантов этой комбинации с 6 до 1.

Для расчета комбинаций мы используем:

Где

n означает общее количество элементов, которые необходимо выбрать из

r означает количество выбранных элементов.

Что такое комбинированный знак?

Несколько знаков используются для представления перестановок; это:

Для посещения музея нужно выбрать трех учеников из 8 класса, сколькими способами можно принять решение?

Решение:

Обратите внимание, что:

Таким образом, можно выбрать трех учеников из 8 классов для посещения музея 56 способами.

Комбинация нескольких событий

В комбинации с несколькими событиями из набора, содержащего более одной группы, делается более одного вида выбора.

Например, если в классе из 14 учеников 8 девочек и 6 мальчиков, и вы должны выбрать 4 мальчиков и 5 девочек, вам придется учитывать свой выбор в зависимости от пола. Таким образом, становится выбор 4 мальчиков из 6 и 5 девочек из 8. Это означает, что:

следовательно,

Комбинации без повторения 3,9 выбора

Иногда порядок , но с повторением .

Такая операция является комбинацией с повторением, и вы применяете формулу

где n — общее количество вещей, из которых можно выбрать, r — количество вещей, которые мы должны выбрать из n, и повторение разрешено без участия порядка.

У Дороти есть коллекция из шести бильярдных шаров разного цвета. Если Кохе, ее подруга, должна выбрать из них 4 шара, цвета которых повторяются несколько раз без порядка, сколькими способами это можно сделать?

Решение:

Здесь нет порядка и выбор конкретного цвета можно повторить. Таким образом, это комбинация с проблемой повторения.

n (общее количество шаров) равно 6

r (количество выбираемых шаров) равно 4

Таким образом, используя:

Количество способов, которыми Коэ мог бы добиться этого:

Что разница между перестановкой и комбинацией?

Возникают вопросы о перестановке и комбинации. Они действительно очень похожи в том, что оба имеют дело с возможными событиями. Однако они различаются по следующим основным параметрам:

Порядок

При перестановке расположение включает элементы, расположенные по порядку. Это означает, что положение предметов очень важно. А вот по совместительству подбор предметов без порядка. Поэтому порядок не имеет значения в комбинации.

Например, если буквы A, B, C нужно переставить местами без повторения, то мы имеем; АВ, ВА, АС, СА, ВС и СВ. Между тем, если A, B и C должны быть объединены без повторения, мы имеем; АВ, АС и ВС. Обратите внимание, что в перестановке AB и BA не совпадают, потому что в AB A предшествует B то же самое относится к BA и остальным результатам. Это на самом деле делает результаты перестановки больше, чем результаты комбинации.

Терминология

Некоторые люди допускают ошибки при использовании правильных терминов в отношении перестановок и комбинаций. В перестановке вы организуете или организуете , но в комбинации вы выбираете или выбираете . Никогда не делайте ошибку, меняя эти термины местами, когда речь идет о перестановке или комбинации.

Формула

Очень важно и ясно заметить, что формула перестановки отличается от формулы комбинации. формула перестановки:

однако комбинация рассчитывается с помощью:

Разница в формуле равна r!, таким образом, мы можем создать математическое соотношение между перестановкой и комбинацией как:

Это еще раз подтверждает, почему результаты перестановки больше, чем комбинации, на мультипликативный коэффициент r !.

Дополнительные примеры перестановок и комбинаций

Вам следует попробовать еще много задач, чтобы иметь представление о том, как вам могут быть поставлены задачи на экзамене. Несколько примеров здесь помогут вам.

Сколькими способами можно написать буквы слова ЗЛОБА так, чтобы все согласные буквы всегда стояли рядом?

Решение:

В слове MALICE 6 букв, среди которых 3 согласные M, L и C. Расположить эти согласные в буквах так, чтобы все согласные буквы оставались вместе, значит, примером такого расположения может быть MLCAIE. Для этого возьмем все согласные буквы за одну букву, поскольку они появляются как группа в нескольких позициях. Это оставляет нам 4 позиции, которые включают A, I, E и группу согласных.

Затем найдите количество способов расстановки во всех четырех позициях.

Итак, теперь мы можем найти количество способов расположения этих согласных, даже если они остаются близко друг к другу.

Это означает, что общее количество способов, которыми буквы в слове MALICE можно расположить так, чтобы все согласные оставались близко друг к другу, равно

Набор столовых приборов состоит из 5 вилок, 3 ложек и 4 ножей. Мальчик выбирает 3 столовых прибора и должен выбрать хотя бы один нож, сколькими способами он может этого добиться?

Решение:

Если мальчик должен выбрать нож, у него есть три возможных варианта:

1. Выбрать все 3 ножа

В этом случае он может добиться этого

2. Выберите 2 ножа и любой другой 1 столовый прибор

В этом случае он может добиться этого

3. Выберите 1 нож и любые другие 2 столовых прибора.

В этом случае он может добиться этого

Таким образом, количество способов, которыми он может выбрать хотя бы нож среди 3 столовых приборов, равно сумме всех возможных событий, равной

Перестановки и комбинации. Ключевые выводы

Перестановка — это расположение объектов или людей в соответствии с порядком или образцом.
Перестановки могут быть с повторением или без него.
Линейные перестановки рассчитываются с помощью, а круговые перестановки рассчитываются с помощью.
Комбинация — это метод выбора, который не следует порядку.
Комбинация рассчитывается с использованием
Перестановка и комбинация различаются по важности и размещению в порядке, используемой терминологии и применяемой формуле.

Перестановки и комбинации и вероятность ~ от кампуса до размещения

A] ПЕРЕСТАНОВКИ И КОМБИНАЦИИ

Факториальная запись: Пусть n положительное число целое число. Тогда факториал n, обозначаемый н! определяется как:

n! = n(n-1)(n-2)……..3.2.1.

Примеры: (i) 5! = (5 х 4 х 3 х 2 х 1) = 120; (ii) 4! знак равно (4x3x2x1) = 24 и т. д.

Определяем, 0! = 1.

Перестановки: различное расположение данного количества вещей, беря некоторые или все сразу время, называются перестановками.

Пример. 1. Все перестановки (или договоренности), сделанные с буквы а, б, в, беря по две за раз являются: (ab, ba, ac, bc, cb).

Пример. 2. Все перестановки букв a,b,c, принимая все одновременно:

(abc, acb, bca, cab, cba).

Количество перестановок: Количество всех перестановок из n вещей, взятых по r за раз, учитывая by:

ⁿ P _r = n(n-1)(n-2). ….(n-r+1) = n!/(n-r)!

Примеры: (i) ⁶ p ₂ = (6×5) = 30. (ii) ⁷ p ₃ = (7x6x5) = 210.

Кор. Количество всех перестановок n вещей, взятых все сразу = n!

Важный результат: Если есть n объектов из которых p ₁ одинаковы одного вида; p ₂ похожи друг на друга Добрый; p ₃ одинаковы третьего рода и так далее и p _r одинаковы r-го вида, так что (p ₁ +p ₂ +…….p _r ) = н.

Тогда число перестановок этих n объектов равно:

n! / (p ₁ !).p ₂ !)……(p _r !)

Комбинации: Каждая из различных групп или выборок, которые может быть образован путем взятия некоторых или всех объектов, называется комбинация.

Пример. 1. Предположим, мы хотим выбрать двух из трех мальчиков А, B, C. Тогда возможные варианты: AB, до н. э. и ЦА.

Обратите внимание, что AB и BA представляют один и тот же выбор.

Пример. 2. Все комбинации, образованные элементами a, b, c из двух в то время ab, bc, ок.

Пример. 3. Единственная комбинация, которую можно составить из трех буквы a, b, c, взятые все за один раз, составляют abc.

Пример. 4 . Различные группы по 2 из 4 детей A, B, C, D являются:

AB, AC, AD, BC, BD, CD.

Пример. 5. Обратите внимание, что ab и ba — две разные перестановки. но они представляют одну и ту же комбинацию.

Количество комбинаций: Количество всех комбинация n вещей,

взято r за раз:

ⁿ C _r = н! / (р!) (н-р)! = n(n-1)(n-2)….. до r факторов / r!

Обратите внимание, что: ⁿ c _r = 1 и ⁿ c ₀ = 1.

Важный результат: ⁿ c _r = ⁿ c _(n-r) .

Пример: (i) ¹¹ c ₄ = (11x10x9x8)/(4x3x2x1) = 330,

(ii) ¹⁶ в ₁₃ = ¹⁶ в _(16-13) = 16х15х14/3! = 16x15x14/3x2x1 = 560.

РЕШЕННЫЕ ПРИМЕРЫ

Пр. 1. Оценка: 30!/28!

Соль. У нас есть, 30!/28! = 30x29x(28!)/28! = (30×29) = 870.

Пр. 2 . Найдите значение (i) ⁶⁰ p ₃ (ii) ⁴ p ₄

Sol. (и) ⁶⁰ р ₃ = 60!/(60-3)! = 60!/57! = 60×59х58х(57!)/57! = (60x59x58) = 205320.

(ii) ⁴ p ₄ = 4! = (4x3x2x1) = 24.

Пр. 3. Найти стоимость (i) ¹⁰ c ₃ (ii) ¹⁰⁰ c ₉₈ (iii) ⁵⁰ c ₅₀

Sol. (i) ¹⁰ с ₃ = 10x9x8/3! = 120.

(ii) ¹⁰⁰ c ₉₈ = ¹⁰⁰ с _(100-98) = 100×99/2! = 4950.

(iii) ⁵⁰ c ₅₀ = 1. [ ⁿ c _n = 1]

Пр. 4. Сколько слов можно составить, используя все буквы слова «БИХАР»

Сол. Слово БИХАР содержит 5 разных букв.

Необходимое количество слов = ⁵ p ₅ = 5! = (5x4x3x2x1) = 120.

Пр. 5. Сколько слов можно составить, используя все буквы слова «ДОЧЬ» так, чтобы гласные всегда совпадали?

Соль. Данное слово содержит 8 разных букв. Когда гласные АУЕ всегда вместе, мы можем предположить, что они образуют единое целое, рассматриваемое как одна буква.

Затем следует расположить буквы ДГНТР (АУЕ).

Затем 6 букв в ⁶ p ₆ = 6! = 720 способов.

Гласные в группе (АУЕ) могут располагаться по 3! = 6 способов.

Требуемое количество слов = (720×6) = 4320.

Пример. 6. Сколько слов можно составить из букв слово «ДОПОЛНИТЕЛЬНО», чтобы гласные никогда не были вместе?

Соль. Данный слово содержит 5 разных букв.

Взятие гласные EA вместе, мы рассматриваем их как одну букву.

Тогда буквы, которые нужно расположить, — XTR (EA).

Эти буквы можно расположить в 4! = 24 способа.

гласные EA могут располагаться между собой по 2! = 2 пути.

Номер слов, в каждом из которых есть гласные вместе = (24×2) = 48 способов.

Всего количество слов, образованных из всех букв данных слов

= 5! = (5x4x3x2x1) = 120.

Количество слов, в каждом из которых гласные никогда не встречаются вместе = (120-48) = 72.

Пр. 7. Сколько слова можно составить из букв слова «ДИРЕКТОР»

Чтобы гласные всегда были вместе?

Соль. В данном слове мы рассматриваем гласные IEO как один письмо.

Таким образом, у нас есть DRCTR (IEO).

Это группа состоит из 6 букв, из которых R встречается 2 раза, а остальные разные.

Номер способов расположения этих букв = 6!/2! = 360.

Теперь 3 гласные можно расположить между собой в 3! = 6 способов.

Необходимое количество путей = (360×6) = 2160.

Пр. 8. Через сколько Как можно выбрать крикет одиннадцать из

15 игроков?

Соль. Обязательно количество путей = ¹⁵ c ₁₁ = ¹⁵ c _(15-11) = ¹¹ с ₄

= 15x14x13x12/4x3x2x1 = 1365.

Пример. 9 . Через сколько способами можно выбрать комитет из 5 членов из

6 мужчин и 5 женщин, состоящий из 3 мужчин и 2 дамы?

Соль. (3 человека вышли 6) и (2 дамы из 5).

Требуемое количество путей = ( ⁶ c ₃ x ⁵ c ₂ ) = [6x5x4/3x2x1] x [5×4/2×1] = 200.

Б]. вероятность

Важные факты и формулы

1. Эксперимент : операция, которая может произвести некоторые четко определенный результат называется экспериментом

2. Случайный эксперимент: Эксперимент, в котором все возможный результат известен, и точный результат не может быть предсказан заранее называется случайным экспериментом

Например, выполнение случайного эксперимента:

(i) бросание беспристрастной кости

(ii) бросание правильной монеты

(iii) взятие карты из хорошо перетасованной колоды карточка

(iv) взятие шара определенного цвета из мешок с шариками разных цветов

Детали:

(i)когда бросаем монетку. Потом либо головка (h) или появляется хвост (t).

(ii) игральная кость цельный куб, имеющий 6 граней, отмеченный соответственно 1,2,3,4,5,6, когда мы бросаем умирают, результатом является число, которое появляется на его верхней стороне.

(iii) в колоде карт 52 карты, в ней 13 карты каждой масти, а именно пики, трефы ,сердечки и бриллианты

Карты пик и треф черные карты

Карты червей и бубнов красные карточки

Каждой масти по 4 награды

Это туза, короля, дамы и валета

. Это так называемые лицевые карты

3.S достаточно места :W когда мы выполняем эксперимент, то множество S всех возможный результат называется пространством выборки

например, пространства для выборки:

(i) при подбрасывании монеты, s={h,t}

(ii) если подбрасываются две монеты, то с={чч,тт,хт,й}.

(iii) при бросании игральной кости имеем s={1,2,3,4,5,6}.

4.event:A ny подмножество демонстрационного пространства.

5. Вероятность возникновения события.

пусть S будет образцом пространства, а E будет событием.

затем,EÍS.

P(E)=n(E)/n(S).

6.Результаты вероятности:

(i)P(S) = 1 (ii)0

(E) < 1 (iii)P(f)=0

(iv)Для любого события a и b имеем:

P(aÈb)=P(a)+P(b)-P(aÈb)

(v) Если А обозначает (не-а), то Р(А)=1-Р(А).

ПРИМЕРЫ РЕШЕНИЙ

Пример 1 . Найдите вероятность того, что при бросании монеты получение головы.

соль. Здесь s={h,t} и е={ч}.

P(E)=n(E)/n(S)=1/2

Ex2 .Два несмещенных подбрасываются монеты. Какова вероятность того, что выпадет не более одного орла?

sol.H ere s={hh,ht,th,tt}

Пусть Ee=событие получения одной головы

e={tt,ht,th}

p(e)=n(e )/n(s)=3/4

Пр.3. Подбрасывается беспристрастная игральная кость. Найдите вероятность получения кратна 3

соль . Здесь s={1,2,3,4,5,6}

Пусть е быть событием, кратным 3

, тогда e={3,6}

p(e)=n(e)/n(s)=2/6=1/3

e x4. i n одновременный бросок пары игральных костей .найдите вероятность получения на общую сумму более 7

сол. Здесь n(s)=(6*6)=36

пусть e=событие получения в сумме более 7

={(2,6),(3,5),(3,6),(4,4),(4,5),(4,6),(5,3),(5,4), (5,5),(5,6),(6,2),(6,3),(6,4),(6,5),(6,6)}

p(e)=n (д)/n(s)=15/36=5/12.

Упр.5. В пакете 6 белых и 4 черных шары .2 шара взяты наугад. найти вероятность того, что они одинаковые цвет.

Sol .пусть s будет выборочным пространством

Тогда n(s)=no способов вытащить 2 шара из (6+4)=10c2=(10*9)/(2*1)=45

Пусть e=событие получить оба шара одного цвета

Тогда n(e)=нет способов(2 шара из шести) или(2 шарики из 4)

=( ⁶ c2+ ⁴ c2)=(6*5)/(2*1)+(4*3)/(2*1)=15+6=21

p(e)=n(e)/n(s)=21/45=7/15

Ex6 .Два игральных кубика брошены вместе .Что такое вероятность того, что сумма чисел на двух гранях делится на 4 или 6

сол. Ясно, что n(s)=6*6=36

Пусть E будет если сумма чисел на двух гранях делится на 4 или 6. Тогда

e={(1,3),(1,5),(2,2),(2,4),(2 ,6),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(6,2 ),

(6,6)}

n(e)=14.

Следовательно, p(e)=n(e)/n(s)=14/36=7/18

Ex7 .Из колоды 52 карты наугад берутся две карты. карты. Какова вероятность того, что обе черные или обе королевы?

соль. W e имеют n(s)=52c2=(52*51)/(2*1)=1326.

Пусть A=событие получения обеих черных карт

B=событие получения обеих ферзей

aÇb=событие получения ферзя черного цвета карты

n(A)= ²⁶ c2=(26*25)/(2*1)=325,

n(b)= ⁴ c2=(4*3)/(2*1) =6 и

n(aÇb)=2c2=1

p(A)=n(A)/n(S)=325/1326;

p(B)=n(B)/n(S)=6/1326 и

p(aÇb)=n(aÇb)/n(s)=1/1326

p(aÈb)=p( а)+p(b)-p(aÇb)=(325+6-1/1326)=330/1326=55/221

Вероятности перестановок и комбинаций (видео и практика)

Привет, ребята. Добро пожаловать в это видео на Вероятность .

В этом видео мы рассмотрим два разных типа вероятности с использованием перестановки и комбинации.

Итак, первое, что вам нужно знать о перестановках и комбинациях, это когда их использовать.

При работе с задачей, где требуется перестановка или комбинация, чтобы определить, какая из них, все, что вам нужно сделать, это задать себе вопрос «имеет ли значение порядок?»

Например, если я скажу вам, что приготовил пирог с заварным кремом из сладкого картофеля, брокколи и болгарского перца, не имеет значения, в каком порядке я это скажу. Я мог бы сказать, что приготовил пирог с заварным кремом из брокколи, болгарского перца и сладкого картошки, и это не имело бы значения. Так что в данном случае порядок не важен. Однако, если я скажу вам, что пароль к моему компьютеру — 876, то порядок этих цифр важен. Если бы я попробовал 786, мне бы отказали в доступе.

Теперь, когда порядок не важен, как в первом примере, это комбинация ; но когда важен порядок, это перестановка .

Люди часто отпускают небольшую шутку. Они говорят, что «кодовый замок действительно должен быть замком перестановки».

Хорошо, давайте рассмотрим пару разных задач. {}\textrm{P}_{4}=\frac{12!}{(12-4 )!}=\frac{12\cdot 11\cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}\ )

Теперь, когда мы запишем все это, мы увидим, что наши числа от 8 до 1 внизу и вверху могут сокращаться друг с другом. И у нас осталось \(12\cdot 11\cdot 10\cdot 9=11 880\).

Другой способ продумать происходящее таков:

У вас есть четыре разных места на стене, так что это 1, 2, 3, 4. Теперь, во-первых, на нашей стене есть 12 различных вариантов покраски. выбирать из. Теперь, когда мы выбрали один из наших 12, у нас осталось 11 для второго варианта, 11 различных вариантов окраски. Затем, как только мы выбираем один из наших 11 вариантов, у нас остается 10, чтобы перейти на пятно 3. И как только мы выбираем один из них, у нас остается 94.

Таким образом, общее количество перестановок, различных способов, которыми мы могли бы расположить эти 4 картины, поскольку нам небезразличен порядок, в котором мы размещаем их на стене, составляет \(12\times 11\times 10\умножить на 9\).

Если мы посмотрим внимательно, то увидим, что это \(12\умножить на 11\умножить на 10\умножить на 9\), как только мы запишем это таким образом, когда мы думаем об этом с точки зрения наличия 4 точек на стене и 12 в первом, и когда мы убираем один, у нас есть 11, и так далее, мы можем видеть, что это то же самое, что мы имеем, когда мы фактически используем нашу формулу перестановки. Как только мы вычеркнем наши числа от 8 до 1 здесь сверху и снизу, у нас останется \(12\умножить на 11\умножить на 10\умножить на 9\).

Теперь все эти способы равны, и моя цель показать вам каждый из них — просто помочь вам добраться до основы того, откуда мы получили эту формулу перестановки.

Давайте рассмотрим пример задачи с комбинацией .

Игроку, играющему в покер, раздается пять карт. Сколько различных комбинаций может быть сдано игроку в покер.

Итак, в этой задаче нас не волнует порядок, в котором карты лежат в руке этого человека. Порядок не имеет значения для этой задачи, поэтому мы знаем, что нам нужно будет использовать комбинацию. 9{}\textrm{C}_{r}=\frac{n!}{r!(n-r)!}\)

n = общее количество игральных карт

r = карты в руке

Итак, поскольку n равно нашему общему количеству игральных карт, мы знаем \(n=52\). В нашей задаче этого не сказано, но мы должны знать, что в стандартной игровой колоде 52 карты. Теперь r — это количество карт в руке человека за раз, поэтому \(r=5\), и это говорит нам, что прямо здесь «раздал пять карт».

Теперь мы должны быть осторожны, потому что формулы перестановки и комбинации очень похожи. Итак, давайте поговорим о единственной разнице между ними и о том, что эта разница представляет.

Разница в том, что в нашей формуле объединения мы имеем \(r!\), умноженное на наше \((n-r)!\), но в нашей формуле перестановки этого нет. Итак, что это значит? О чем говорит нам это \(r!\), умноженное на все в знаменателе? Это говорит нам, что мы корректируем нашу формулу перестановки, уменьшая ее на то, сколькими способами карты могут быть в порядке, чтобы получить нашу формулу комбинации. И причина, по которой мы уменьшаем количество возможных порядков карт, заключается в том, что нам не важен порядок, когда речь идет о комбинациях. Именно по этой причине мы используем формулу комбинации, потому что порядок не имеет значения. 9{}\textrm{C}_{r}=\frac{52!}{5!(52-5)!}=\frac{52!}{5!\cdot 47!}=2 598 960\)

Теперь, в этом примере, я не выписал \(52!\) полностью, но это потому, что моя основная цель показать вам, ребята, как решить эту задачу, состоит в том, чтобы научить вас, ребята, разницу между перестановкой и комбинации, и показать вам, как применять ваши числа в формуле.

Надеюсь, это видео было для вас полезным. Для получения дополнительной помощи обязательно ознакомьтесь с другими нашими видео, подписавшись на наш канал ниже.

Увидимся в следующий раз!

Вопрос № 1:

Ким работает в смузи-баре, который предлагает 42 различных варианта фруктов, соков и добавок, которые покупатели могут заказать в своих смузи. В каждом смузи может быть пять уникальных предметов. Сколько возможных смузи можно приготовить?

620 495

747 116

812 944

850 668

Показать ответ

Ответ:

5 порядок не имеет значения. Используя \(n=42\) и \(r=5\), мы используем следующую формулу комбинации:
\(_nC_r=\text{ }_{42}C_5=\frac{42!}{5!(42-5)!}=\frac{42!}{5!37!}=\frac{42× 41×40×39×38×37!}{5×4×3×2×1×37!}=\frac{102{,}080{,}160}{120}=850{,}668\)

Скрыть ответ

Вопрос № 2:

Двадцать человек зарегистрировались для участия в предстоящем триатлоне, где первые пять мест получат денежные призы. Сколькими возможными способами можно составить пятерку лучших из этого пула из двадцати человек?

1 860 480

2 096 456

2 481,797

2 612 054

Показать Ответ

Ответ:

Нас интересует, кто из двадцати участников попадет в первую пятерку. Нас также интересует порядок первой пятерки, то есть нам нужно будет использовать следующую формулу перестановок:
\(_nP_r=\text{ }_{20}P_5=\frac{20!}{(20- 5)!}=\frac{20!}{15!}=\frac{20×19×18×17×16×15!}{15!}=1{,}860{,}480\)

Скрыть ответ

Вопрос №3:

Сколькими способами можно расположить четыре числа 1, 3, 5 и 7? (Например, 5731, 1537 и т. д.)

120

Показать ответ

Ответ:

\) и \(r=4\). Помните, что 0! в знаменателе равно 1.
\(_4P_4=\frac{4!}{(4-4)!}=\frac{4!}{0!}=4×3×2×1=24\)

Скрыть Ответ

Вопрос №4:

Чарльз в кафе-мороженом решает, какие вкусы мороженого он хочет. Одна тарелка мороженого состоит из трех шариков, и Чарльз хочет попробовать три разных вкуса. Если есть 21 вкус на выбор, сколько существует возможных комбинаций чаш?

880

1,330

1 520

2190

Показать ответ

Ответ:

Из 21 вкуса, Чарльз выберет 3. Таким образом, мы используем формулу для комбинаций (потому что заказ не имеет значения), где порядок). (n=21\) и \(r=3\).
\(_{21}C_3=\frac{21!}{3!(21-3)!}=\frac{21×20×19×18!}{3!×18!}=\frac{21 ×20×19}{3×2×1}=1{,}330\)

Скрыть ответ

Вопрос № 5:

Предположим, что Чарльз хочет получить рожок мороженого вместо тарелки, где три совки укладываются одна на другую. Сколькими возможными способами он мог бы расположить три вкуса стопкой? Помните, что на выбор предлагается 21 вкус.

5 140

5 960

6 220

7 980

Показать ответ

Ответ:

В этой задаче важен порядок. Поэтому мы снова используем формулу перестановки, где \(n=21\) и \(r=3\).
\(_{21}P_3=\frac{21!}{(21-3)!}=\frac{21!}{18!}=\frac{21×20×19×18!}{18! }=21×20×19=7{,}980\)

Скрыть ответ

10 Увлекательные игры и занятия для изучения перестановок и комбинаций

Переход от изучения элементарной математики к высшей математике требует больших усилий. Это время, когда учащийся сталкивается с понятиями, о которых он, вероятно, никогда раньше не слышал. Одной из таких тем является «Перестановка и комбинация» 9.0015

Перестановки и комбинации основаны на фундаментальном принципе счета. Оба эти метода используются для определения количества возможных исходов в различных ситуациях. Перестановки относятся к идее размещения различных элементов набора в предопределенной последовательности, в то время как комбинация — это скорее выбор некоторых элементов набора независимо от порядка.

Ученикам может быть трудно понять разницу между перестановками и комбинациями, если они не понимают логики, стоящей за ними. Чтобы усвоить предмет, важно получать удовольствие от процесса обучения. Поэтому в этом посте мы составили список онлайн-игр и занятий в классе, чтобы дети учились в веселой обстановке и были готовы овладеть искусством перестановок и комбинаций!

Игры и упражнения для ознакомления с перестановками и сочетаниями
1. Мороженое от transum.org
В игре используется идея мороженого, чтобы понять концепцию перестановок и комбинаций, что является отличным способом обучения математика. Игра проста и понятна. Основываясь на одном вопросе, сколько различных видов мороженого из двух шариков можно приготовить? Детям дается 6 разных вкусов мороженого, из которых они должны приготовить как можно больше разноцветных мороженых из двух шариков.
Шесть вкусов мороженого в игре: лимон, клубника, ваниль, персик, шоколад и мята. Малышу придется нажимать на кнопки вкуса, чтобы высыпать шарик мороженого в рожок внизу. После того, как вы насыпаете два шарика мороженого на один рожок, рожок размещается на стойке выше. Таким образом, пользователь должен заполнить разные конусы мороженым с разными вкусами, чтобы выиграть игру.
Ссылка на игру
2. Судоку
Игра Судоку представляет собой логическую игру с расстановкой чисел, которая представляет собой задачу на перестановку, которую должны решить учащиеся. Он поставляется с доской, которая имеет 9квадратная грань на 9 дюймов – и частично завершена. Основная цель самой игры состоит в том, чтобы разместить числа от 1 до 9 в каждой строке, каждом столбце и в каждом из подблоков размером 3 на 3. Играя в эту игру, вы можете задавать ученикам такие вопросы, как: Сколько существует различных способов игры во втором столбце чисел?; сколько существует различных способов игры во втором и третьем ряду чисел?; Сколько существует различных способов сыграть в судоку целиком, включая все девять рядов? Эти вопросы не только поддерживают любопытство, но и способствуют обучению.
Ссылка на игру
3. Обозначение комбинаций и перестановок
Подобно викторинам в классе, это онлайн-викторина, которая дает учащимся множество задач на перестановки и комбинации для решения. Их можно сделать простыми или сложными в зависимости от уровня ученика. Онлайн-викторина может стать отличным инструментом оценки для учащихся и может использоваться учителями и родителями. Эта игра P&C предназначена для учащихся, которые только начинают изучать концепцию, и даже для учащихся, которые уже изучили ее и находятся на пороге оценки. Эта викторина будет интересна даже в качестве занятия в классе, домашнего задания и даже для школьников.
Ссылка на игру
4. Полосатые конфеты
В этой игре, состоящей из 8 уровней, нужно раскрашивать обертки от ириски таким образом, чтобы все обертки отличались друг от друга. По сути, в игре даются два мелка, красный и синий, которые представляют собой несколько ирисок с обертками. На первом уровне 4 ириски, на втором 8 и так далее. Детям необходимо составить такие комбинации, используя понятие перестановки и сочетания, чтобы каждая обертка от ириски выглядела не так, как другая.
На каждой внешней обертке есть три коробки, которые дети должны раскрасить одним из двух цветов. Ящики должны быть заполнены таким образом, чтобы каждый узор был разнообразным и уникальным, и ни один из них не был похож. Только когда игрок сможет создавать разные узоры, он сможет пересечь уровень. Эта игра помогает детям понять концепцию комбинации и помогает им стимулировать свой мозг, чтобы формирование комбинаций не казалось им сложной задачей.
Ссылка на игру
5. Исследование ящика для яиц
В этой игре игрокам было дано два яйца, чтобы собрать их в ящик по 6 штук. Но загвоздка здесь в том, что комбинация укладки яиц каждый раз должна быть разной. На каждом ходу игрок может щелкнуть снимок комбинации, которую он составил из яиц. Сравнивая комбинации, им нужно составить как можно больше узоров, чтобы каждый выглядел по-своему.
Игра задает игрокам один вопрос: «Сколькими способами можно расположить 2 яйца в коробке из 6 яиц?». Ответом на это будет множество комбинаций, которые игрок должен составить. Уровень не закончится, пока не будет исчерпано количество шаблонов, которые можно сделать.
Ссылка на игру
6. Анализ кусочков фруктов:
Простой метод, который поможет детям понять основы перестановок и комбинаций, заключается в том, чтобы познакомить их с заданием, которое мы хотели бы назвать «Кусочки фруктов». Анализ.» Все, что вам нужно, это чашка кусочков фруктов или цветных зерен для каждой группы студентов. Каждая группа должна подсчитать количество кусочков фруктов каждого цвета и записать данные на листе. Они также должны подсчитать общее количество штук. После этого их можно попросить организовать различные возможные аранжировки или подсчитать количество определенного выбора. Например, вы можете попросить их выбрать три разных цвета из общего числа и спросить, сколькими способами они могут сделать свой выбор.
7. Выберите шляпу:
Для этого задания родитель или воспитатель должен выкопать игровую комнату и достать шляпы. По сути, цель задания — составить комбинацию из 3 головных уборов, которую Джон (вымышленный персонаж) может носить в течение недели. По сути, в этом упражнении дети могут предположить, что у Джона есть привычка носить шляпы, но у него есть только 3 шляпы, которые он должен носить, применяя стратегию перестановки и комбинирования.
Стратегия должна быть такой, чтобы каждый день он мог носить шапку, а так как есть 3 дня и 5 рабочих дней, то ему пришлось бы повторять шапки в два дня. Таким образом, учащиеся могут формировать несколько перестановок и комбинаций со шляпами, чтобы решить, сколько существует различных способов, которыми Джон может носить свои шляпы за одну неделю.
8. От одежды до нарядов:
Это задание требует от учащихся создания полноценной одежды на всю неделю. Для этого занятия учителю или родителю необходимо иметь выкройки изображений рубашек, брюк, обуви и аксессуаров, которые учащиеся могут комбинировать и превращать в разные наряды на все 6 дней недели. Цель состоит в том, чтобы сделать 6 разных нарядов из 3 рубашек, 3 пар брюк, 2 пар обуви и 2 видов аксессуаров. Например, если есть рубашки розового, фиолетового и черного цветов и брюки черного, белого и бежевого цветов, а также черные и коричневые туфли. Ученик может сделать наряды как –
Понедельник- Розовая рубашка с черными брюками и черными туфлями и один аксессуар.
Вторник- Фиолетовая рубашка с коричневыми брюками, коричневыми туфлями и другим аксессуаром.
Среда- Черная рубашка с бежевыми брюками и черными туфлями с первым аксессуаром.
Четверг- Розовая рубашка (снова), но на этот раз с коричневыми брюками и коричневыми туфлями и вторым аксессуаром.
Friday- Фиолетовая рубашка (снова), но на этот раз с бежевыми брюками и коричневыми туфлями и первым аксессуаром.
Суббота- Черная рубашка (снова), но на этот раз с коричневыми брюками и без аксессуаров.
Чтобы немного разнообразить задание, учителя могут рассчитать время выполнения задания, что заставит учащихся спешить и лучше понять концепцию перестановок и комбинаций.
Это задание основано на теме ресторана, где учащиеся должны составить меню ресторана. Но загвоздка здесь в том, что ресторан обслуживает клиентов только 4 видами овощей с рисом и лапшой, а в меню должно быть не менее 8 вариантов блюд. Задача здесь состоит в том, чтобы объединить два овоща вместе и подать их с рисом или лапшой. Учащиеся также могут соединить три и более овощей и приготовить другое блюдо, но в меню должно быть не менее 8 позиций. Это может быть отличным способом научить студентов комбинациям и живучести перестановок.
F или, например, , если доступными овощами являются лук, морковь, грибы и кукуруза, учащиеся могут выбрать следующие блюда –
Комбинация 1- Лапша с жареным луком.
Комбинация 2- Лапша с морковно-грибным карри.
Комбинация 3- Лапша с кукурузой и луком карри.
Комбинация 4- Лапша с жареной морковью и молодой кукурузой.
Комбинация 5- Рис с луком, морковью и грибным карри
Комбинация 6- Рис с жареными грибами
Комбинация 7- Рис с жареными грибами и кукурузой.
Комбинация 8- Рисовый суп с луком и морковью.
Более того, может быть и другое количество комбинаций, которые может составить ученик. Чтобы повысить уровень этого задания, преподаватели могут ограничить его по времени, попросив учащихся составить как можно больше комбинаций за 10 минут. Ученик, который сделает большинство из них, выиграет игру!
10. Блокировка-разблокировка
Чтобы заняться этим занятием, учителю или родителям понадобится замок, в котором есть кодовый замок. Идея игры состоит в том, чтобы дать учащимся три случайных числа и попросить их составить из них как можно больше комбинаций. Один из номеров будет правильным номером, который открывает замок. Например, замок открывается на число 982, поэтому учитель может дать ученикам 2, 8 и 9. Учащиеся могут составить такие комбинации, как 289., 829, 928, 982, 298 и многое другое.
Ученик, который первым откроет замок, перепробовав все возможные комбинации, побеждает в игре. Это занятие можно сделать еще более авантюрным и интересным, поставив не один, а много замков. Например, учитель может принести пять замков, каждый со своим числовым кодом. Теперь учащиеся должны составить комбинации из 5 наборов чисел. Сохранение этого действия на основе времени может быть отличным для студентов, которые хотят преуспеть в этом упражнении и концепции.
Потребность в перестановках и комбинациях в нашей повседневной жизни
Изучая множество тем по математике, учащиеся могут задаться вопросом: «Как я собираюсь использовать это на практике?» Это может быть алгебра, LCM или даже концепция перестановок и комбинаций. Тем не менее, это одна из тем, которую, освоив теоретически, можно использовать и на практике.
Вот различные события и случаи, когда концепция перестановок и комбинаций может активно использоваться:
Выбор меню- Для рестораторов и даже для тех, кто любит готовить себе еду — перестановки и комбинации используются всякий раз, когда они выбирают меню на день или хотят попробовать что-то новое в приготовлении. Например, вы можете подумать, что сочетание курицы с брокколи может стать хорошей едой. Или у вас может быть просто несколько ингредиентов, завалявшихся в вашем холодильнике, и вам нужно приготовить себе еду только из них. Что бы вы сделали в таком случае? Вам остается провести мозговой штурм и объединить оставшиеся предметы.
Выбор нарядов- Ни один из нарядов не подходит заранее. Вам нужно купить верхнюю одежду и нижнюю одежду отдельно, а затем объединить их и сделать из них наряд. Это касается не только одежды, но и обуви, ремней и многого другого. Формирование определенной комбинации с помощью P&C необходимо для повседневного подбора одежды.
Предметы- Студентам, возможно, придется снова и снова выбирать различные предметы, которые они хотят изучать. Здесь у студентов нет данных. количество часов, которое у них есть, объем учебной программы, которую нужно охватить, и тяжелая работа, которую им нужно выполнить по конкретному предмету.
Телефонные номера- Включая ноль, всего 10 цифр в системе счисления. Однако есть миллионы и миллиарды телефонных номеров, которые используются по всему миру одними и теми же 10 цифрами. Искусство комбинирования и перестановки различных чисел таким образом, чтобы каждый раз получать уникальное число, также требует P&C.
Номерные знаки- Номерной знак автомобиля представляет собой сочетание и сочетание нескольких цифр с буквами. Однако у каждой машины есть уникальный номерной знак. Чтобы каждый раз получать разные, во всем мире нужна концепция P&C.
Помимо этих повседневных действий, концепция перестановок и комбинаций используется в определенных областях, таких как –
Архитектура компьютера: В расположении логических вентилей, что является насущной необходимостью, когда речь идет об архитектуре компьютера.
Вычислительная молекулярная биология: P&C активно используется в атомах, молекулах, ДНК, генах и многом другом, когда речь идет о молекулярной биологии.
Анализ закономерностей: От визуальных образов до давления и температуры — концепция перестановок и комбинаций активно используется в этой отрасли для создания паттернов, которые представлены во всей области.
База данных: Формирование последовательности цифр, символов, битов и многого другого является частью базы данных и интеллектуального анализа данных. Для этой цели используется P&C.
Лучший способ использования этих действий
Перестановка и комбинация — это математическая концепция, которая используется на каждом этапе жизни. Поэтому мероприятия, упомянутые выше, будут очень полезными. Но как бы вы проводили эти мероприятия, будучи родителем или педагогом? Вот несколько способов сделать это!
В качестве занятий в классе: Хотя нельзя отрицать, что традиционные методы обучения хороши для детей всех возрастов, но занятия также имеют свой собственный набор жизненных сил. Таким образом, вовлечение детей в некоторые виды деятельности во время занятий в классе может принести педагогам действительно хорошие результаты! Это сделало бы процесс обучения более увлекательным и увлекательным, а также помогло бы учащимся лучше усваивать информацию.
Во время занятий: Можете ли вы представить, чтобы ваш ребенок учился во время занятий? Активный период в школе – это время, которого с нетерпением ждет каждый ученик. Но эти действия, когда они используются в идеальной обстановке, могут привести к отличному сочетанию веселья с обучением. Таким образом, выполнение этих действий во время игр или во время занятий может быть отличным вариантом, когда вы теоретически изучаете концепцию на уроке математики.
Для оценки: Всякий раз, когда мы говорим о том, «как проверить понимание определенного понятия», мы думаем только об одном – об Экзаменах! Но, напротив, эти действия могут быть весьма эффективным способом проверки того, усвоил ли учащийся концепцию перестановки и комбинации. Более того, учащийся будет с большим энтузиазмом относиться к этой деятельности, и, таким образом, педагогу и родителям будет легко увидеть, понял ли учащийся концепцию.
Домашнее задание на каникулы: Всякий раз, когда школа не работает в течение длительного времени, учителя, как правило, раздают домашнее задание на каникулы, чтобы учащиеся не теряли связь с понятиями, которым их учили перед каникулами. Тем не менее, есть еще одна проблема, с которой они сталкиваются: «Какую домашнюю работу учащийся готов выполнять во время каникул?» И чтобы ответить на этот вопрос, занятия, включающие концепцию P&C, идеально подходят, поскольку их можно легко выполнять дома, с друзей, а также в свободное время дома во время каникул.
Для обучения на дому: Родителям и преподавателям часто бывает трудно удерживать детей, обучающихся на дому, и находить новые и интересные способы помочь им учиться лучше и веселее. И эти действия сделают именно это.
No related posts.

Перестановки. Размещения. Сочетания. комбинаторика — презентация онлайн

2. Определение

4. Факториал

5. Факториал

6. Главное свойство факториала

Перестановки сочетания и размещения (с и без…

Свойства перестановок

Связанные определения

Специальные типы перестановок

Подстановка

Произведения циклов и знак перестановки[править ]

Перестановки с повторением в комбинаторике

Случайная перестановка

Пример

Решение

Количество размещений

Размещение с повторениями

Пример задач

Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; насекторах каждого из дисков написаны цифры 0, 1, …, 9.

. Решение

Количество размещений с повторениями

Пример

Число сочетаний

Сочетания с повторениями

Пример Имеется 2 типа цветов, количество цветов не ограничено.

Решение

См. также

Размещения, перестановки, сочетания — Математика для юристов (Математика)

План конспект урока «Комбинаторика (перестановки, сочетания, размещения)»

Презентация по математике Перестановки, размещения, сочетания доклад, проект

Что такое shareslide.ru?

Обратная связь

Основы комбинаторики. Размещения, перестановки, сочетания презентация, доклад, проект

Перестановка и комбинация — GeeksforGeeks

Перестановки и комбинации — тест на способности, вопросы, сокращения, видео-примеры решения

Перестановки и комбинации: примеры и различия

Что такое перестановка?

Линейная перестановка

Круговая перестановка

Что такое знак перестановки?

Типы линейной перестановки и соответствующие формулы

Перестановка с повторением

Перестановка без повторения

Использование перестановок в расположении букв

Круговой формула перестановки

Что такое комбинация?

Что такое комбинированный знак?

Комбинация нескольких событий

Комбинации без повторения 3,9 выбора

Что разница между перестановкой и комбинацией?

Порядок

Терминология

Формула

Дополнительные примеры перестановок и комбинаций

Перестановки и комбинации. Ключевые выводы

Перестановки и комбинации и вероятность ~ от кампуса до размещения

РЕШЕННЫЕ ПРИМЕРЫ

Вероятности перестановок и комбинаций (видео и практика)

10 Увлекательные игры и занятия для изучения перестановок и комбинаций

Добавить комментарий Отменить ответ