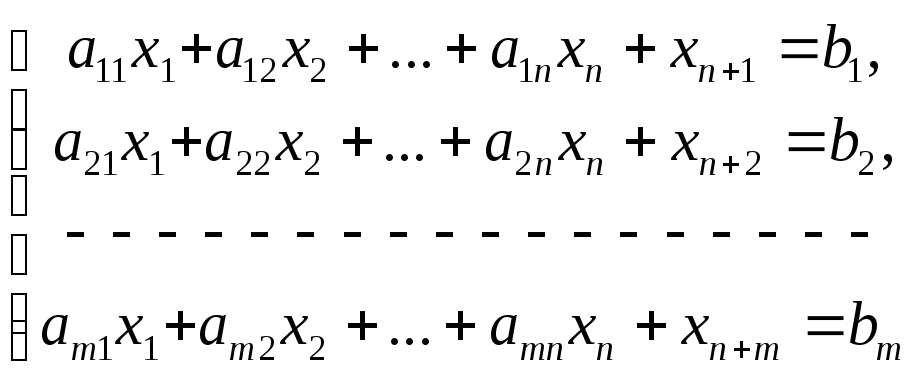Решение задач линейного программирования в MS Excel
1. Решение задач линейного программирования в MS Excel
LOGOОбщая задача линейного программирования
решается симплексным методом
Симплекс (лат. simplex — простой) –
простейший выпуклый многогранник
в n-мерном пространстве с n+1 вершиной
(например, тетраэдр в 3-мерном
пространстве)
На рисунке: оптимальное
решение находится в одной
из вершин многоугольника
решений А, В, С, D
Если задача линейного программирования
имеет оптимальное решение, то оно
соответствует хотя бы одной угловой точке
многогранника решений (и совпадает с
одним из допустимых базисных решений
системы ограничений)
Геометрический смысл симплексного метода
состоит в последовательном переходе от
одной вершины многогранника ограничений к
соседней, в которой целевая функция
принимает лучшее (по крайней мере, не
худшее) значение
Впервые симплексный метод был предложен
американским ученым Дж.

Джордж Бернард Данциг (1914-2005) –
американский математик, разработал симплексный
алгоритм, считается основоположником методов
линейного программирования
Идеи симплексного метода были
разработаны в 1939 г. российским
ученым Л.В.Канторовичем
Леонид Витальевич Канторович (1912-1986) –
советский математик и экономист, лауреат
Нобелевской премии по экономике 1975 года «за
вклад в теорию оптимального распределения
ресурсов». Один из создателей линейного
программирования
Симплексный метод позволяет решить
любую задачу линейного программирования
В настоящее время он используется для
компьютерных расчетов
Рассмотрим решение задачи линейного
программирования в MS Excel
В MS Excel для решения задачи линейного
программирования используется надстройка
ПОИСК РЕШЕНИЯ
Сначала надстройку Поиск решения
необходимо подключить (до первого
использования)
В MS Excel 2003:
Сервис /
Надстройки /
Поиск решения /
OK
После этого команда
Поиск решения включена
в меню Сервис
В MS Excel 2007:
1) Кнопка Office (левый верхний угол окна программы)
2) Кнопка Параметры Excel (внизу окна меню)
3) Надстройки
1
2
3
В MS Excel 2007:
4) Кнопка Перейти (внизу окна Параметры Excel)
3
4
В окне Надстройки установить флажок и
нажать ОК
В MS Excel 2007 кнопка
Поиск решения появится
во вкладке Данные
В MS Excel 2007 кнопка Поиск решения
появится во вкладке Данные
Решим в MS Excel задачу линейного программирования
1
2
Решим в MS Excel задачу линейного программирования
3
4
СРС
СРС
Ответы:
1
2
3
4
Решим в MS Excel задачу линейного программирования
1.
 Создадим область переменных
Создадим область переменныхроль переменных
(пока они пусты)
Решим в MS Excel задачу линейного программирования
2. Введем формулу вычисления значений
целевой функции
Например, в ячейку А8
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
В ячейках В11:В13 введем правые
части ограничений системы
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
Первое ограничение
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
Второе ограничение
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
Третье ограничение
Решим в MS Excel задачу линейного программирования
4.
 Вызовем окно диалога Поиск решения
Вызовем окно диалога Поиск решенияПри этом удобно,
если активной
ячейкой является
ячейка со
значением
целевой функции
Решим в MS Excel задачу линейного программирования
1) Устанавливаем целевую ячейку А8 (там где
вычисляется значение целевой функции)
2) Указываем направление оптимизации – минимизация
(по условию)
3) В поле Изменяя ячейки указываем ячейки
переменных В2:В6
Решим в MS Excel задачу линейного программирования
Укажем ограничения
4) Нажимаем кнопку Добавить
Появится окно Добавление ограничения
Решим в MS Excel задачу линейного программирования
Укажем ограничения
5) Неотрицательность переменных:
Нажать кнопку Добавить
6) Остальные ограничения:
Решим в MS Excel задачу линейного программирования
Осталось нажать кнопку Выполнить
Решим в MS Excel задачу линейного программирования
Результаты
Ответ:
Литература
1. Кремер Н.Ш., Путко Б.
 А. Исследование
А. Исследованиеопераций в экономике. — М.: ЮНИТИ, 2003. 407 с.
2. Красс М.С., Чупрынов Б.П. Математика для
экономистов. — СПб.: Питер, 2005. — 464 с.
«Решение задач оптимизации симплекс методом» | Методическая разработка на тему:
Пояснительная записка
Методическая разработка практической работы по теме «Решение задач оптимизации симплекс методом» по профессиональному модулю МДК 06-03 «Методы оптимизации систем автоматизации» предназначена для студентов 5-го курса специальности 15.02.07 «Автоматизация технологических процессов и производств по отраслям».
Студентам предлагаются типовые задачи оптимизации (оптимальное использование ограниченных ресурсов, раскрой промышленных материалов, смеси и т.п.). В примерах приводится подробное описание технологии получения оптимального решения симплекс методом и средствами Ms Excel.
Цель практической работы:
- закрепить теоретические знания по теме;
- приобретение навыков компьютерной реализации оптимизационных моделей симплекс методом;
- сформировать у обучающихся умение работать самостоятельно и в сотрудничестве в группе.

Порядок выполнения работы:
- Изучить теоретический материал.
- Ответить на вопросы по теме.
- Выполнить задания.
- Оформить отчет по практическим занятиям.
- Задача линейного программирования. Симплекс метод.
Составьте оптимальный план производства продукции, дающий максимальную прибыль. Предприятие выпускает продукцию четырех видов П1, П2, П3, П4 с использованием для этого ресурсов, виды и нормы расхода по которым, а также уровень получаемой от их реализации прибыли, приведены в таблице.
Вид ресурса | Запас ресурса | ||||
П1 | П2 | П3 | П4 | ||
Трудовые | 1 | 1 | 1 | 1 | 16 |
Сырье | 6 | 5 | 4 | 3 | 110 |
Оборудование | 4 | 6 | 10 | 13 | 100 |
Прибыль | 60 | 70 | 120 | 130 | |
Экономико-математическая модель задачи запишется следующим образом:
x1+x2+x3+x4≤16
6×1+5×2+4×3+3×4≤110
4×1+6×2+10×3+13×4≤100
xj≥0 (j=1, 2, 3, 4)
Решение
- Запустить табличный процессор Ms Excel.

- Укажем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Значения компонент Х(x1,x2,x3,x4) поместим в ячейках В3:Е3, оптимальное значение целевой функции – в ячейку F4.
- Введем исходные данные задачи в созданную форму-таблицу
- Введем зависимость для целевой функции:
Установить курсор в ячейку F4, кликнуть по кнопке Мастер Функций (fx). Выберите категорию Математические и функцию СУММПРОИЗВ. На экране появится диалоговое окно СУММПРОИЗВ. В строку Массив 1 введем В$3:Е$3, в строку Массив 2 введем В4:Е4 и ОК.
- Ввести зависимости для ограничений:
— курсор в ячейку F4: кнопка Копировать;
— вставить в ячейки F7, F8, F9.
В строке Меню установить указатель мыши на имя Сервис. В развернутом меню выбрать команду Поиск решения.
- Назначим целевую функцию (установим целевую ячейку):
— курсор в строку Установить целевую ячейку;
— введем адрес ячейки $F$4;
— введем направление целевой функции в зависимости от условия задачи – Максимальному значению;
— курсор в строку Изменяя ячейки, введем адреса искомых переменных B$3:E$3.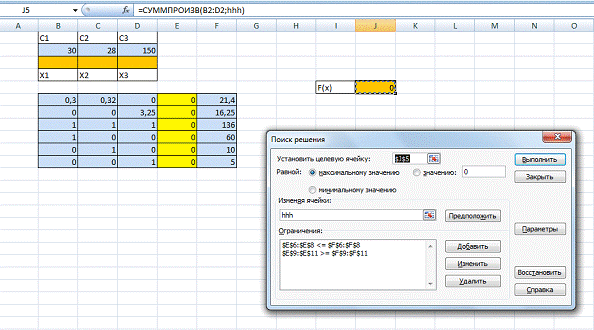
7. Введем ограничения:
— кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
— в строке Ссылка на ячейку введем адрес $F$7:$F$9, (или укажем на листе, т.е. щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу и выделить ячейки F7: F9, нажать клавишу F4, при этом ссылка станет абсолютной $F$7:$F$9, щелкнуть на красной стрелке и вернуться в блок Поиска решения, при этом нужный адрес будет введен).
— выберем знак ограничения ≤;
— в строке Ограничения введем адрес $Н$7:$Н$9, ОК.
8. Введем параметры для решения задачи линейного программирования:
— в диалоговом окне Поиск решения →Параметры;
— в окне Параметры решения установить флажки — Линейная модель (симплекс метод), Неотрицательные значения →ОК→в окне Поиск Решения нажать кнопку Выполнить.
— в окне Результаты поиска решения выбрать Сохранить найденное решение →ОК.
На экране отразится таблица с заполненными ячейками В3:Е3 для значений х и ячейка F4 с максимальным значением целевой функции.
Максимальный доход 1320 денежных единиц предприятие может получить при объемах выпуска продукции первого вида -10 единиц, третьего вида 6 единиц. Продукцию второго и четвертого вида выпускать невыгодно.
- Задача целочисленного линейного программирования. Симплекс метод.
Организация арендует баржу грузоподъёмностью 200 тонн. На барже предполагается перевозить груз 4-ех типов. Вес и стоимость единицы груза соответственно равны 20, 15, 20, 14 и 100, 80, 40, 30. Необходимо погрузить груз максимальной стоимости.
Экономико-математическая модель.
Пусть xj≥0 (j=1, 2, 3, 4) – число предметов , которое следует погрузить на баржу. Тогда задача о подборе для баржи допустимого груза максимальной стоимости запишется следующим образом:
max f(x1, x2, x3, x4)=100 x1+80 x2+40 x3+30 x4
20 x1+15 x2+20 x3+14 x4≤200 xj ≥ (j=1, 2, 3, 4)
Решение
- Создать таблицу и ввести исходные данные
- Ввести зависимость для целевой функции:
Установить курсор в ячейку F4, кликнуть по кнопке Мастер Функций (fx). Выберите категорию Математические и функцию СУММПРОИЗВ. На экране появится диалоговое окно СУММПРОИЗВ. В строку Массив 1 введем В$3:Е$3, в строку Массив 2 введем В4:Е4 и ОК.
Выберите категорию Математические и функцию СУММПРОИЗВ. На экране появится диалоговое окно СУММПРОИЗВ. В строку Массив 1 введем В$3:Е$3, в строку Массив 2 введем В4:Е4 и ОК.
- Ввести зависимость для ограничений:
— скопировать полученную формулу в ячейку F8.
В строке Меню установить указатель мыши на имя Сервис. В развернутом меню выбрать команду Поиск решения.
- Назначим целевую функцию (установим целевую ячейку)
— курсор в строку Установить целевую ячейку;
— введем адрес ячейки $F$4;
— введем направление целевой функции в зависимости от условия задачи – Максимальному значению;
— курсор в строку Изменяя ячейки, введем адреса искомых переменных B$3:E$3.
- Введем ограничения:
— кнопка Добавить. Появится окно Добавление ограничения; в строке Ссылка на ячейку введем адрес $F$8;
— выберем знак ≤; в строке Ограничение введем адрес $H$8 → кнопка Добавить;
— в строке Ссылка на ячейку введем адрес $В$3: $Е$3;
— выберем значение цел→ ОК. На экране появится окно Поиск решения с введенными условиями.
На экране появится окно Поиск решения с введенными условиями.
- Введем параметры для решения задачи:
— кнопка Параметры; в окне Параметры поиска решения установить флажки Линейная модель (симплекс метод), Неотрицательные значения →ОК→в окне Поиск Решения нажать кнопку Выполнить.
- — в окне Результаты поиска решения выбрать Сохранить найденное решение →ОК.
Получим решение.
Таким образом, рекомендуемое управленческое решение с позиций принятого критерия оптимизации – следует погрузить 1 предмет первого типа и 12 предметов второго типа. В этом случае стоимость груза составит 1060 денежных единиц, и грузоподъемность будет использована полностью.
Список используемой литературы
- Курицкий Б.Я. Поиск оптимальных решений средствами Excel 2007. С-П. BHV. 2014. -344с.
- Михеева Е.В. Информационные технологии в профессиональной деятельности – М.: Издательский центр «Академия», 2014.
 -384с.
-384с.
К вопросу использования надстройки Excel «Поиск решения» в задачах линейного программирования Текст научной статьи по специальности «Компьютерные и информационные науки»
Интернет-журнал «Науковедение» ISSN 2223-5167 http ://naukovedenie.ru/ Том 7, №3 (2015) http ://naukovedenie. ru/index.php?p=vol7-3 URL статьи: http://naukovedenie.ru/PDF/54TVN315.pdf DOI: 10.15862/54TVN315 (http://dx.doi.org/10.15862/54TVN315)
УДК [330.45]
Барышев Александр Владимирович
НОУ ВПО «Российский новый университет»
Россия, Москва1 Кандидат технических наук Доцент
E-mail: [email protected] Федотова Елена Леонидовна
ФГБОУ ВПО «Национальный исследовательский университет (МИЭТ)» 2
Москва, Россия Кандидат педагогических наук
Доцент
E-mail: fedotova-e2007@yandex. ru
ru
К вопросу использования надстройки Excel «поиск решения» в задачах линейного программирования
1 105005, г. Москва, ул. Радио, 22
2 124460, г. Москва, Филаретовская ул., корп. 1134, кв. 165 1
Аннотация. Существует насущная необходимость принятия эффективных управленческих решений.
В условиях полной определенности широко используются задачи линейного программирования, где требуется найти оптимальное решение. При этом оптимальность принимаемого решения во многом зависит от количества существующих альтернатив и их научно-технической обоснованности. В некоторых случаях существует несколько альтернативных оптимальных решений одной задачи. Их поиск в задачах линейного программирования процесс весьма трудоёмкий.
Обычно для решения задач линейного программирования используется надстройка Excel «поиск решения». Однако не все предлагаемые ей методы равнозначны при поиске альтернативных оптимальных решений. Кроме того, эффективность поиска зависит от начального приближения целевой функции. Поэтому целью настоящей работы являются выбор наиболее эффективного метода поиска альтернативных оптимальных решений задач линейного программирования с помощью надстройки Excel «поиск решения» и задание наилучших начальных приближений целевой функции.
Однако не все предлагаемые ей методы равнозначны при поиске альтернативных оптимальных решений. Кроме того, эффективность поиска зависит от начального приближения целевой функции. Поэтому целью настоящей работы являются выбор наиболее эффективного метода поиска альтернативных оптимальных решений задач линейного программирования с помощью надстройки Excel «поиск решения» и задание наилучших начальных приближений целевой функции.
В работе проведено сравнение эффективности симплексного метода и метода обобщенного приведенного градиента надстройки Excel «поиск решения» при нахождении альтернативных оптимальных решений задач линейного программирования и предложен эвристический способ задания начальных приближений целевой функции, позволяющий сократить время поиска.
Ключевые слова: надстройка Excel «поиск решения»; задачи линейного программирования; альтернативные оптимальные решения; симплексный метод; метод обобщенного приведенного градиента; целевая функция; ограничения; начальное приближение целевой функции.
Ссылка для цитирования этой статьи:
Барышев А.В., Федотова Е.Л. К вопросу использования надстройки Excel «поиск решения» в задачах линейного программирования // Интернет-журнал «НАУКОВЕДЕНИЕ» Том 7, №3 (2015) http://naukovedenie.ru/PDF/54TVN315.pdf (доступ свободный). Загл. с экрана. Яз. рус., англ. DOI: 10.15862/54TVN315
Менеджеру любого ранга повседневно приходится принимать целый ряд решений связанных с экономикой и управлением. При этом, с точки зрения эффективности, принятое решение должно быть оптимальным. Выполнить это требование бывает очень трудно, особенно если математическая модель задачи является негладкой и нелинейной или сама задача плохо структурирована.
Существует много методов принятия управленческих решений [1]. Здесь же мы остановимся на принятии управленческих решений в задачах линейного программирования [2, 3], а именно на использовании надстройки поиск решения Excel в задачах линейного программирования [4].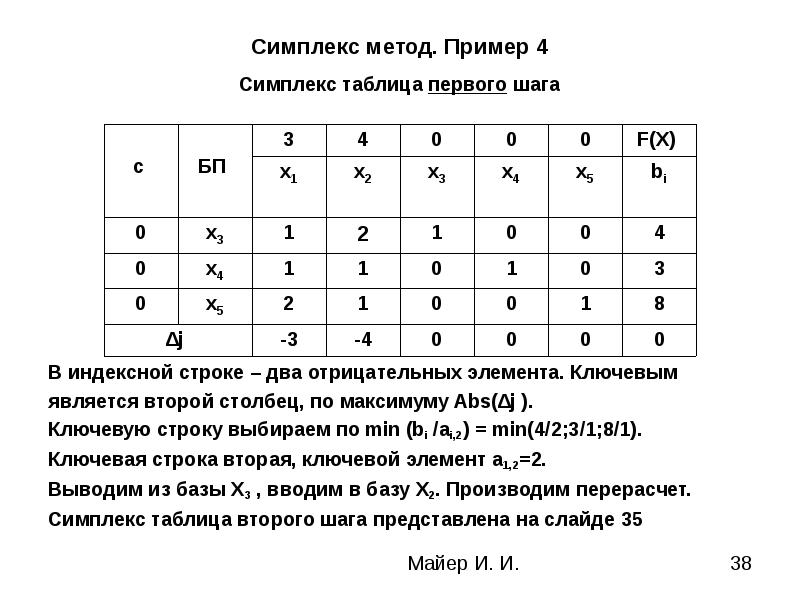
Как известно, эффективность принимаемого решения во многом зависит от количества существующих альтернатив и их научно-технической обоснованности [5, 6]. При решении задач линейного программирования, в некоторых случаях, найденное оптимальное решение оказывается не единственным [7]. Поэтому, с целью обеспечения большей свободы выбора управленческого воздействия, необходимо выявить все оптимальные альтернативные решения.
В работе предлагается эвристический способ задания начальных приближений целевой функции, позволяющий сократить время поиска.
Этим обусловлена актуальность и практическая ценность настоящей работы.
Существуют различные признаки, указывающие на наличие оптимальных альтернативных решений. При использовании надстройки поиск решения Excel в задачах линейного программирования в качестве таких признаков является наличие в отчете по устойчивости нулей «в таблице «Изменяемые ячейки» в столбцах «Допустимое увеличение» и «Допустимое уменьшение». ..» (отчет получают при использовании симплексного метода решения) [8]. Однако, найти эти оптимальные альтернативные решения не так просто, поскольку результат поиска решения зависит от начального приближения и не только. Рассмотрим этот вопрос подробнее. Для этого возьмем несколько конкретных примеров.
..» (отчет получают при использовании симплексного метода решения) [8]. Однако, найти эти оптимальные альтернативные решения не так просто, поскольку результат поиска решения зависит от начального приближения и не только. Рассмотрим этот вопрос подробнее. Для этого возьмем несколько конкретных примеров.
Пример 1 [7]. Найти максимум целевой функции
Внесем данные на лист Excel (см. рисунок 1).
В ячейки B2:D2 названия переменных, а в ячейки B3:D3 — коэффициенты при целевой функции F(x).
В ячейки B2:D2 диапазона (B5:D5; B7:D7) запишем коэффициенты при неизвестных в ограничениях.
В ячейки B10:D10, первоначально подставляются начальные условия, например, все единицы или нули.
В ячейках E5,E6,E7 записываются формулы вычисления левой части ограничений, а в ячейки G5,G6,G7 — значения правой части.
В ячейку E10 записывается формула вычисления целевой функции.
Р(х) =Х1+Х2+Хз
(1)
при ограничениях
(2).
AI
A В С D Е F G
1 перем лев часть знак прав часть
2 наименование Xl х2 ¡(3
3 коэф в цел.функции 1 1 1
4
5 коэф в 1 огранич -1 3 2 =СУ М М П РОИ ЗВ[ В5: D5; В10: D1 s &
S коэф в 2 ограним 2 4 2 =СУ М М П РО ШВ( В 6: D6; В10: D1 s а
7 коэф в 3 огранич 3 2 -1 =СУ М М П Р О И ЗВ( В 7: D7; В10: D1 £ 4
S
9 XI1 х2′ хЗг т
10 оптим значение 0 0 0 =СУММПРОИЗВ(ВЗ:ОЗ;В10: max
Рисунок 1. Фрагмент листа Excel, заполненный данными из формул (1) и (2)
Фрагмент листа Excel, заполненный данными из формул (1) и (2)
(произведен авторами)
Теперь можно непосредственно перейти к использованию «надстройки поиск решения».
Через меню «данные» и «поиск решения» входим в таблицу «параметры поиска решения» (см. рис. 2).
Параметры поиска решения I
Оптимизировать целевою функцию:
До: Максимум Минимум
Изменяя ячейки переменных:
шш
Значения:
Ш
Б соответствии с ограничениями:
ÎEÎUO >= 0
$C$U0 >= 0
IDE 10 >= □
ÎE$5 <= ÎG$5
$E$6 <= SGSo
SES7 <= $G$7
«W
Добавить
Изменить
Удалить
Сбросить
Загрузит ь/оохранить
Сделать переменные без ограничений неотрицательными Выберите
Поиск решения линейных задач симплекс-методом
Параметры
метод решения: Метод решения
Для гладких нелинейных задач используйте поиск решения нелинейных задач методом ОПГ, для линейных задач — поиск решения линейных задач симплекс-методом, а для негладких задач — эволюционный поиск решения.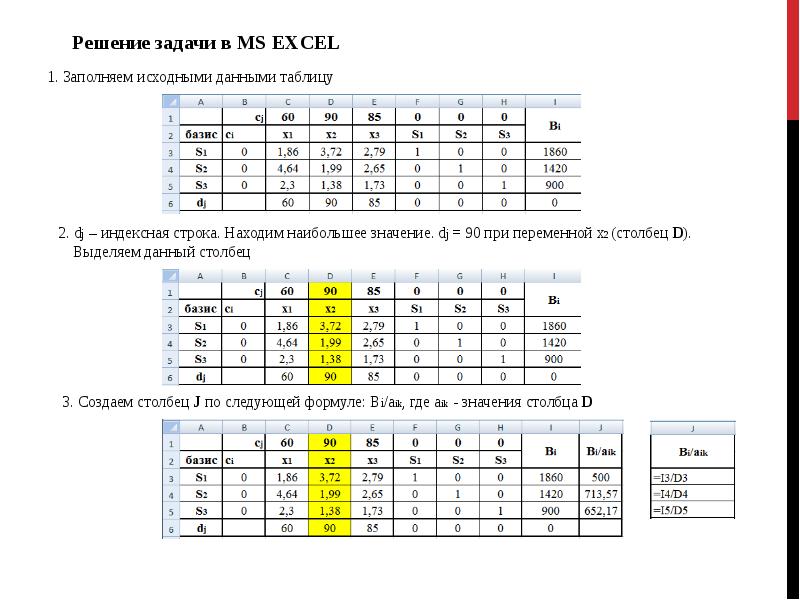
Справка
Найти решение
Закрыть
Рисунок 2. Окно параметры поиска решения MS Excel
В неё вводим указание на ячейку со значением целевой функции ($E$10). Указываем, что ищем максимум целевой функции, и указываем диапазон изменяемых ячеек ($B$10:$D$10). Затем через пункт таблицы «добавить» вводим указания на ограничения, предварительно установив параметры поиска:
1. Точность ограничения — 0.001.
2. Максимальное время (в секундах) — 100.
3. Число итераций — 100.
4. Максимальное число допустимых решений (установим, например) — 4.
При необходимости устанавливаем метки на такие пункты как «Использовать автоматическое масштабирование» и «Показывать результаты итераций» и др.
Минько А.А. рекомендует использовать автоматическое масштабирование во всех случаях [8]. Кроме того, многие авторы, например [4, 8] рекомендуют для решения задач линейного программирования использовать симплексный метод решения. Это же рекомендуется в самом окне «параметры поиска решения» MS Excel. Однако это, также как и использование автоматического масштабирования, как это будет показано ниже, не всегда оказывается целесообразным.
Теперь, нажав кнопку «найти решение» находим искомое решение. Максимум целевой функции будет помещен в ячейку E10. В ячейки В10, С10, D10 будут записаны соответственно Х1, Х2, хз.
В качестве начального приближения используем значения переменных Х1, х2, хз= 0.
После найденного оптимального решения убедимся, что существуют альтернативные оптимальные решения. Для этого создадим «отчет об устойчивости».
На рис. 3. поместим фрагмент отчета об устойчивости.
Ячейки переменных
Окончательное Приведенн. Целевая функция Допустимое Допустимое
Ячейка Имя Значение Стоимость Коэффициент Увеличение Уменьшение
$В$10 оптим значение xl1 2 0 1 1Е+30 0
$С$10 оптим значение х2′ 0 -1 1 1 1Е4-30
$D$10 оптим значение хЗ’ 2 0 1 0 1
Рисунок 3. Фрагмент отчета об устойчивости (получен авторами)
Как следует из рисунка, в двух крайних столбцах имеются нули.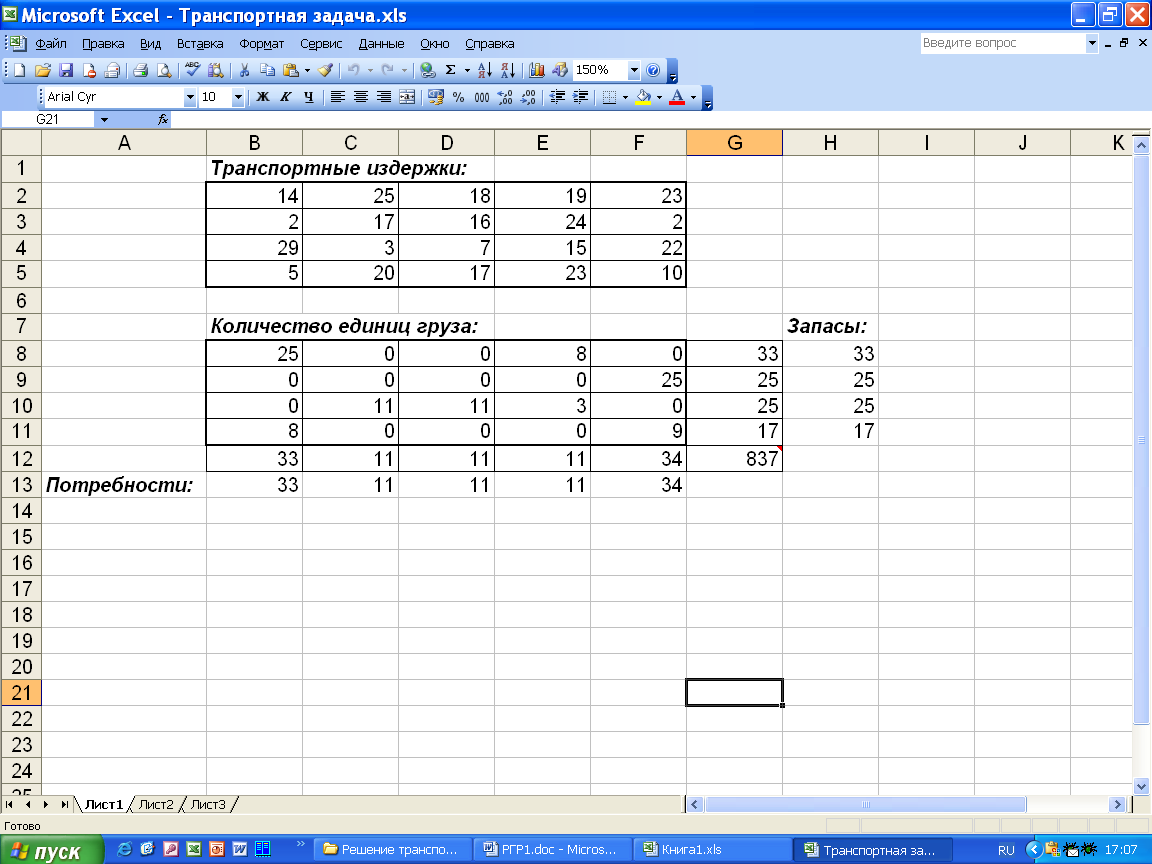 Это указывает на наличие альтернативных оптимальных решений.
Это указывает на наличие альтернативных оптимальных решений.
Исследуем возможности надстройки «поиск решения» для получения оптимальных альтернативных решений. С этой целью будем различным образом задавать начальное приближение целевой функции (методом случайного поиска и предлагаемым способом), а также будем изменять сам метод поиска (с симплексного на метод обобщенного приведенного градиента (ОПТ) [9]). Результаты поместим в таблицы 1 и 2.
Таблица 1
Поиск альтернативных решений целевой функции (1) симплексным методом
(составлено авторами)
Метод решения Способ задание начального приближения Начальное приближение Значение целевой функции Значение переменных
Симплекс ный метод решения Случайный поиск Х1,Х2,Х3= 0 4.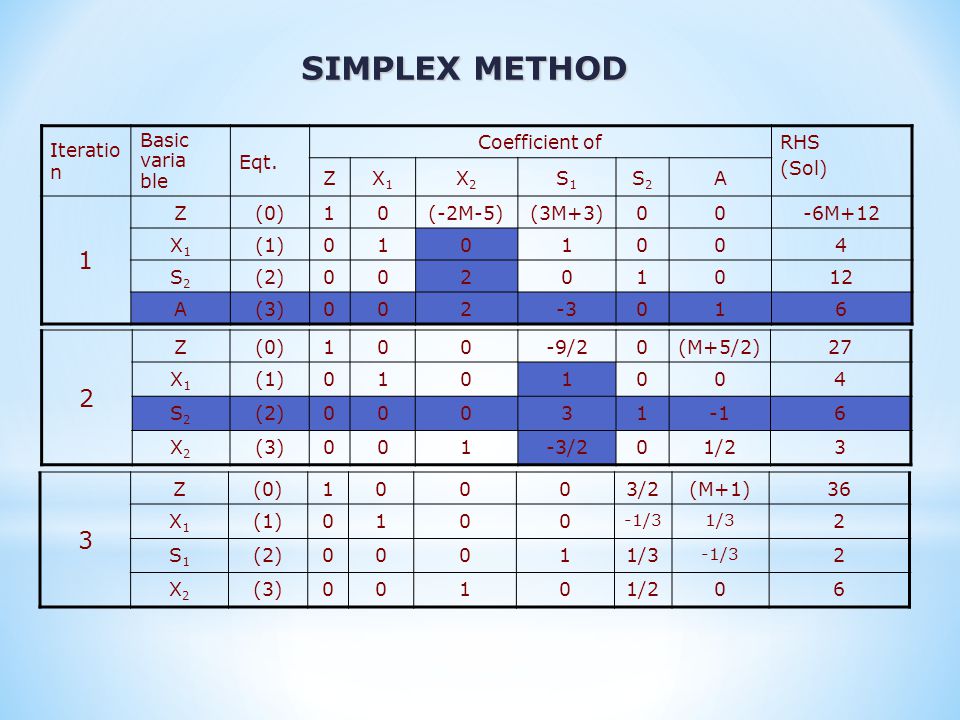 00 Х1= 2.00; Х2=0.00; хз= 2.00
00 Х1= 2.00; Х2=0.00; хз= 2.00
Х1,Х2,Х3= 1 4.00 Х1= 2.00; Х2=0.00; хз= 2.00
Х1,Х2,Х3 = 2 4.00 Х1= 2.00; Х2=0.00; хз= 2.00
Способ перестановки ограничений Х1,Х2,Х3= 0 4.00 Х1= 2.00; Х2=0.00; хз= 2.00
Х1 = 6; Х2 = 8; хз= 4 4.00 Х1= 2.00; Х2=0.00; хз= 2.00
Х1 = 4; Х2 = 6; хз= 8 4.00 Х1= 2.00; Х2=0.00; хз= 2.00
Х1 = 8; Х2 = 4; хз= 6 4.00 Х1= 2.00; Х2=0.00; хз= 2.00
Как следует из данных таблицы 1, при использовании различных способов задания начальных приближений симплексный метод не обеспечивает поиск альтернативных оптимальных решений. Изменим симплексный метод решения на метод обобщенного приведенного градиента (ОПТ).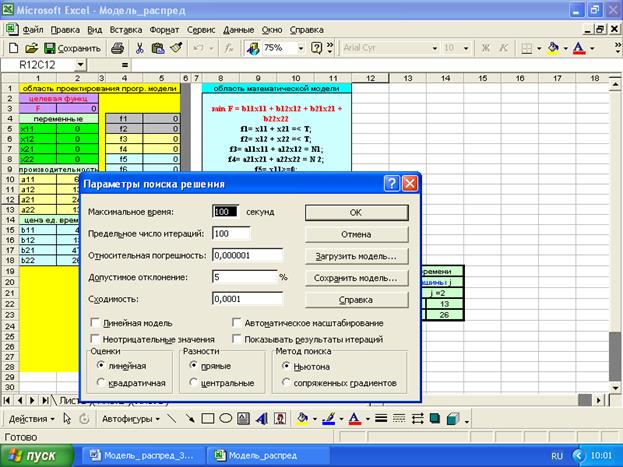 Результаты поместим в таблицу 2.
Результаты поместим в таблицу 2.
Как следует из данных таблицы 2, предлагаемый способ задания начальных приближений обеспечил поиск 4 альтернативных решений, если же использовать автоматическое масштабирование, то можно найти только два альтернативных решения.
Таблица 2
Поиск альтернативных решений целевой функции (1) методом ОПГ
(составлено автором)
Метод решения Способ задания начального приближения Начальное приближение Значение целевой функции Значение переменных
Метод решения нелинейных задач методом ОПГ Способ перестановки ограничений (без масштабирова ния) Х1,Х2,Х3= 0 4.00 Х1= 1.90; Х2= 0.00; хз= 2.10
Х1 = 6; Х2 = 8; хз= 4 4. 00 Х1= 1,27; Х2= 0.00; хз= 2,73
00 Х1= 1,27; Х2= 0.00; хз= 2,73
Х1 = 4; Х2 = 6; хз= 8 4.00 Х1= 0.67; Х2= 0.00; хз= 3.33
Х1 = 8; Х2 = 4; хз= 6 4.00 Х1= 2.00; Х2= 0.00; Х3= 2.00
Пример 2. Найти максимум целевой функции [10]:
Fx = х1 + 2х2 + 3х3 (3)
Ограничения:
!х1 + 2х2 + 3х3 < Ш
х1 + х2 < 5 }, х1, х2, х3 < 0 (4)
х1 < 1 )
Подобно примеру 1 вводим данные выражений (3) и (4) в таблицу Excel (см. рис. 4).
А1 £
А В С D Е F G
1 перем лев масть знак прав часть
2 наименование XI х2 хЗ
3 коэф в цел. функции 1 2 3
функции 1 2 3
4
5 коэф в 1 ограним 1 2 3 =СУММПР0ИЗВ(В5:05;ВЮ:Ш 10
6 коэф в 2 ограним 1 2 0 =СУ М М П РО И ЗВ( В 6: D6; Б10: D1 < 5
7 коэф в 3 ограним 1 0 0 =СУ М М П Р а И ЗВ( В 7: D7; В10: D1 1
а
э х1гх2,хЗ хГ х2′ хЗ’ F(x) > 0
10 оптим значение 0 0 0 =СУММПРОИЗВ(ВЗ:ОЗ;В10: max t
Рисунок 4. Фрагмент листа Excel, заполненный данными (3) и (4) (произведен авторами)
Произведем поиск альтернативных решений, используя метод решения нелинейных задач ОПГ и предлагаемый способ задания начальных приближений. Результаты поиска поместим в таблицу 3.
Результаты поиска поместим в таблицу 3.
Как видим из данных таблицы 3, найдено 3 альтернативных оптимальные решения, при этом мы избежали случайного поиска начальных значений.
Таблица 3
Поиск альтернативных решений целевой функции (3) методом ОПГ
(составлено авторами)
Метод решения Метод задания начального приближения Начальное приближение Значение целевой функции Значение переменных
Метод решения нелинейных задач методом ОПГ Способ перестановки ограничений (без масштабирова ния) Х1,Х2,Х3= 0 10.00 Х1= 0,71; х2= 1,43; хз= 2,14
Х1 = 10; Х2 = 5; хз = 1 4.00 Х1= 1,00; х2= 2,00; хз= 1,67
xi = 5; х2 = 1; хз = 10 4. 00 Х1= 0.00; х2= 0.00; хз= 3.33
00 Х1= 0.00; х2= 0.00; хз= 3.33
Х1 = 1; х2 = 10; хз= 5 4.00 Х1= 1,00; х2= 2,00; х3= 1,67
На основании изложенного материала можно сделать следующие выводы:
1. Начинать решение задачи линейного программирования с помощью надстройки Excel «поиск решения» следует с помощью симплексного метода, получив при этом отчет об устойчивости. Если в отчете по устойчивости «в таблице «Изменяемые ячейки» в столбцах «Допустимое увеличение» и «Допустимое уменьшение»…» есть нули, то необходимо искать альтернативные оптимальные решения.
2. Симплексный метод решения не обеспечивает поиск альтернативных оптимальных решений.
3. Поиск альтернативных оптимальных решений следует производить методом обобщенного приведенного градиента (ОПГ) без автоматического масштабирования, используя задание начальных приближений с помощью
предлагаемого способа перестановки ограничений. Это позволит сократить затраченное время.
Это позволит сократить затраченное время.
ЛИТЕРАТУРА
1. Орлов А.И. Организационно-экономическое моделирование: теория принятия решений: учебник. — М.: КНОРУС, 2011. — 568 с.
2. Титов В.В. Оценка эффективности оптимизационного планирования деятельности промышленного предприятия / Регион: экономика и социология. 2007. №1. С. 241-250.
3. Созонов С.В. Разработка моделей оптимизации производственной программы промышленного предприятия на основе формулирования целевых функций / Экономические науки. 2010. Т. 67. №6. С. 231-235.
4. Урубков А.Р., Федотов И.В. Методы и модели оптимизации управленческих решений: учебное пособие. — М.: Издательство «Дело» АНХ, 2009. — 240 с.
5. Баллод Б. А., Елизарова Н.Н. Методы и алгоритмы принятия решений в экономике: учебное пособие. — М.: Финансы и статистика; ИНФРА-М, 2009. -224 с.
А., Елизарова Н.Н. Методы и алгоритмы принятия решений в экономике: учебное пособие. — М.: Финансы и статистика; ИНФРА-М, 2009. -224 с.
6. Барышев А.В., Федотова Е.Л. К вопросу формирования творческих способностей выпускников вузов // Интернет-журнал «НАУКОВЕДЕНИЕ» 2014. №4 http:// http://naukovedenie.ru/PDF/80PVN414.pdf (доступ свободный). Загл. с экрана. Яз. рус.
7. Агальцов В.П. Математические методы в программировании: учебник. — М.: ИД «ФОРУМ», 2010. — 240 с.
8. Минько А.А. Принятие решений с помощью Excel. Просто как дважды два. -М.: Эксмо, 2007. — 240 с.
9. Метод обобщенного приведенного градиента. http://iasa.org.Ua/lections/iso/6/6.7.h tm.
10. Палий И.А. Линейное программирование. Учебное пособие. — М.: Эксмо, 2008. 256 с.
— М.: Эксмо, 2008. 256 с.
Рецензент: Ключников Анатолий Васильевич, доцент, кандидат технических наук, Национальный исследовательский университет «МИЭТ».
Barushev Alexsandr Vladimirowich
NOU VPO «Russian new University» Russia, Moscow E-mail: [email protected]
Vedotova Elena Leonidovha
National Research University of Electronic Technology
Russia, Moscow E-mail: [email protected]
Finding optimal solutions for linear programming decision problems using Microsoft Excel Solver Add-in.
Abstract. The vital necessity does exist for making effective management decisions.
Linear programming approach is widely used in case of the full certainty where an optimal decision must be found.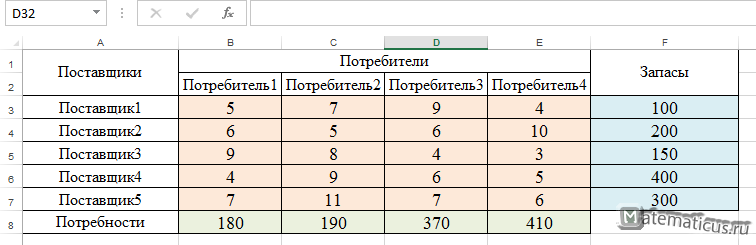 The optimality of a found decision mostly depends on the number of existing alternatives and their scientific feasibility. In some cases there can be several alternative optimal solutions for a single decision problem. Finding the best one of these alternatives is a quite difficult and hard-working process.
The optimality of a found decision mostly depends on the number of existing alternatives and their scientific feasibility. In some cases there can be several alternative optimal solutions for a single decision problem. Finding the best one of these alternatives is a quite difficult and hard-working process.
Often Microsoft Excel Solver Add-in is used to solve linear programming decision problems. However not all of its techniques are equal when finding an optimal solution for a decision problem. Further, the efficiency of finding a solution depends on initial approximation of the objective function. Therefore, the aim of this paper is to choose the most efficient method for finding optimal solutions of linear programming problems using Microsoft Excel Solver Add-in by providing the best input approximation for objective function.
This paper compares the efficiency of simplex and generalized reduced gradient methods in Microsoft Excel for finding alternative optimal solutions of linear programming problems. ита! «NAUKOVEDENIE» 2014. №4 http:// http://naukovedenie.ru/PDF/80PVN414.pdf (dostup svobodnyy). Zagl. s екгапа. Yaz. rus.
ита! «NAUKOVEDENIE» 2014. №4 http:// http://naukovedenie.ru/PDF/80PVN414.pdf (dostup svobodnyy). Zagl. s екгапа. Yaz. rus.
7. Agal’tsov У.Р. Matematicheskie metody V programmirovanii: иЛеЬшк. — М.: ID «FORUM», 2010. — 240 s.
8. Мт’ко А.А. Prinyatie resheniy s pomoshch’yu Ехсе1. Prosto как dvazhdy dva. — М.: Eksmo, 2007. — 240 s.
9. Metod obobshchennogo privedennogo gradienta. http://iasa.org.Ua/lections/iso/6/6.7.htm.
10. Paliy 1.А. Lineynoe programmirovanie. Uchebnoe posobie. — М.: Eksmo, 2008. 256 s.
Учебные задачи для Excel
Учебные задачи для ExcelЭлектронные таблицы MS Excel — очень удобный инструмент для вычислений.
- При вычислениях длинных выражений Excel удобнее любого калькулятора, особенно тем, что легко править ошибки во введённой формуле или изменять часть формулы
- в Excel удобно решать уравнения с одним неизвестным при помощи «подбора параметра»
- несложно решать системы линейных алгебраических уравнений (СЛАУ)
- можно решать задачи оптимизации (линейного, целочисленного программирования)
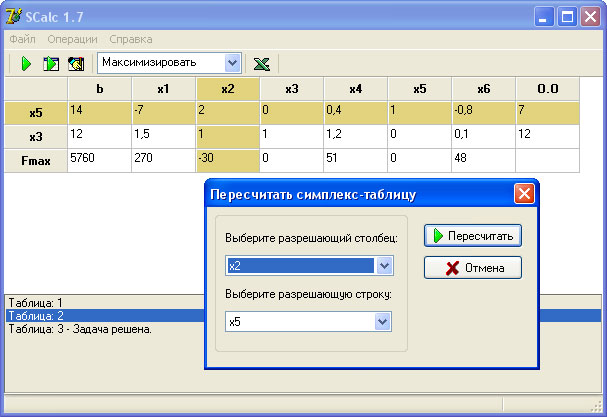 .. и многие другие задачи.
.. и многие другие задачи. Некоторые задачи сопротивления материалов, решённые с помощью Excel можно найти здесь
- Построение графика функции и решение уравнений с одним неизвестным
- Численное интегрирование
- Решение систем линейных алгебраических уравнений
- Решение задач линейного программирования (Л.П.)
- Тема 1. Практикуемся в построении математической модели. Методичка, описание решений (скачать 3 документа Word в RAR-архиве — 100кб)
- Тема 2. Формы записи задачи линейного программирования (общая задача Л.П., основная форма, каноническая форма, допустимый план, оптимальный план). Методичка, описание решений (скачать 3 документа Word в RAR-архиве — 100кб)
- Тема 3. Графический метод решения задачи Л.П. Методичка, описание решений, документ Excel с решениями (скачать 2 документа Word и 1 док. Excel в RAR-архиве — 100кб)
Графический метод (с использованием Excel) - Тема 4.
 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СИМПЛЕКСНОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ Л.П.
Методичка, описание решения (скачать 2 документа Word в RAR-архиве — 50кб)
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СИМПЛЕКСНОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ Л.П.
Методичка, описание решения (скачать 2 документа Word в RAR-архиве — 50кб) - Тема 5. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ Л.П. (скачать методичку, описание решений, решения в Excel RAR-архив — 200кб)
- Тема 6. МЕТОД ИСКУССТВЕННОГО БАЗИСА. ДВУХЭТАПНЫЙ СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ Л.П. (скачать методичку, описание решений, решения в Excel RAR-архив — 200кб)
- Тема 7. ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД (Р-МЕТОД) (скачать методичку, описание решений, решения в Excel RAR-архив — 100кб)
- Тема 8. Задача целочисленного Л.П. (скачать методичку, описание решений, решения в Excel RAR-архив — 450кб)
- Тема 9. РЕШЕНИЕ ЗАДАЧ Л.П. С ПОМОЩЬЮ MS EXCEL (скачать методичку, описание решений, решения в Excel RAR-архив — 350кб)
1. Численное интегрирование
Для численного интегрирования функции одной переменной применяют методы:
прямоугольников, трапеций, Симпсона. Подробнее об этих методах можно прочесть в «Справочнике по высшей математике М.Я. Выгодского»
( см библиотеку)
Подробнее об этих методах можно прочесть в «Справочнике по высшей математике М.Я. Выгодского»
( см библиотеку)
Метод прямоугольников
Метод трапеций
Метод Симпсона
Все эти методы заключаются в:
- Разбиении интервала (отрезка) интегрирования на n равных более мелких отрезков
- Замене на каждом таком мелком отрезке исходной функции (её графика) соответственно:
— горизонтальной прямой
— наклонной прямой
— параболой - Вычислении площади полученной фигуры, которая приблизительно равна площади под графиком функции, т е искомому интегралу.
Лист MS Excel с решением задачи
(Точное значение вычисляемого интеграла равно 30)
Скачать документ Excel с этим примером (в виде RAR-архива LAB1_win.rar — 22kB)
Решение игровых задач с нулевой суммой с помощью Microsoft Excel
Библиографическое описание:Захарова, Т. Н. Решение игровых задач с нулевой суммой с помощью Microsoft Excel / Т. Н. Захарова. — Текст : непосредственный // Актуальные задачи педагогики : материалы I Междунар. науч. конф. (г. Чита, декабрь 2011 г.). — Чита : Издательство Молодой ученый, 2011. — С. 176-181. — URL: https://moluch.ru/conf/ped/archive/20/1343/ (дата обращения: 12.06.2021).
Н. Решение игровых задач с нулевой суммой с помощью Microsoft Excel / Т. Н. Захарова. — Текст : непосредственный // Актуальные задачи педагогики : материалы I Междунар. науч. конф. (г. Чита, декабрь 2011 г.). — Чита : Издательство Молодой ученый, 2011. — С. 176-181. — URL: https://moluch.ru/conf/ped/archive/20/1343/ (дата обращения: 12.06.2021).
Рассмотрим общий случай игровой задачи m x n с нулевой суммой, когда модель задачи не имеет седловой точки. Такую модель можно представить в виде матрицы (табл.1):
Таблица 1. Общая таблица стратегий
|
Стратегии |
В1 |
В2 |
… |
Вn |
|
A1 |
a11 |
a12 |
a1n |
|
|
A2 |
a21 |
a22 |
a2n |
|
|
…. |
||||
|
Am |
am1 |
am2 |
amn |
Оптимальное решение необходимо искать в области смешанных стратегий. Обозначим вероятности применения стратегий первого игрока (игрока А) через , а цену игры — через v. Оптимальная смешанная стратегия игрока А определяется из условия
Пусть
Поскольку при оптимальной стратегии средний выигрыш не меньше v при любой стратегии противника, то справедлива система n неравенств:
Или
(1)
Тогда задача отыскания
оптимальной смешанной стратегии игрока А может быть сформулирована в
виде задачи линейного программирования.
Для этого необходимо максимизировать целевую функцию F =v при ограничениях
(2)
Введем новые неизвестные:
Поскольку
Разделим левую и правую части неравенств (1) и (2) на v, получим:
(3)
В силу того что
max v = min 1/v = min{x1+x2+…+xm}.
задача принимает вид
F= x1+x2+…+xm → min (4)
при ограничениях
(5)
Для второго игрока (игрока В) оптимальная стратегия определяется из условия:
при условии
q1+q2+…+qn = 1
Эта задача записывается как симметричная двойственная задача линейного программирования к задаче игрока A (4), (5):
L= y1 +y2+… +yn → max (6)
при ограничениях
(7)
Задачи игроков A
и В решают симплекс-методом.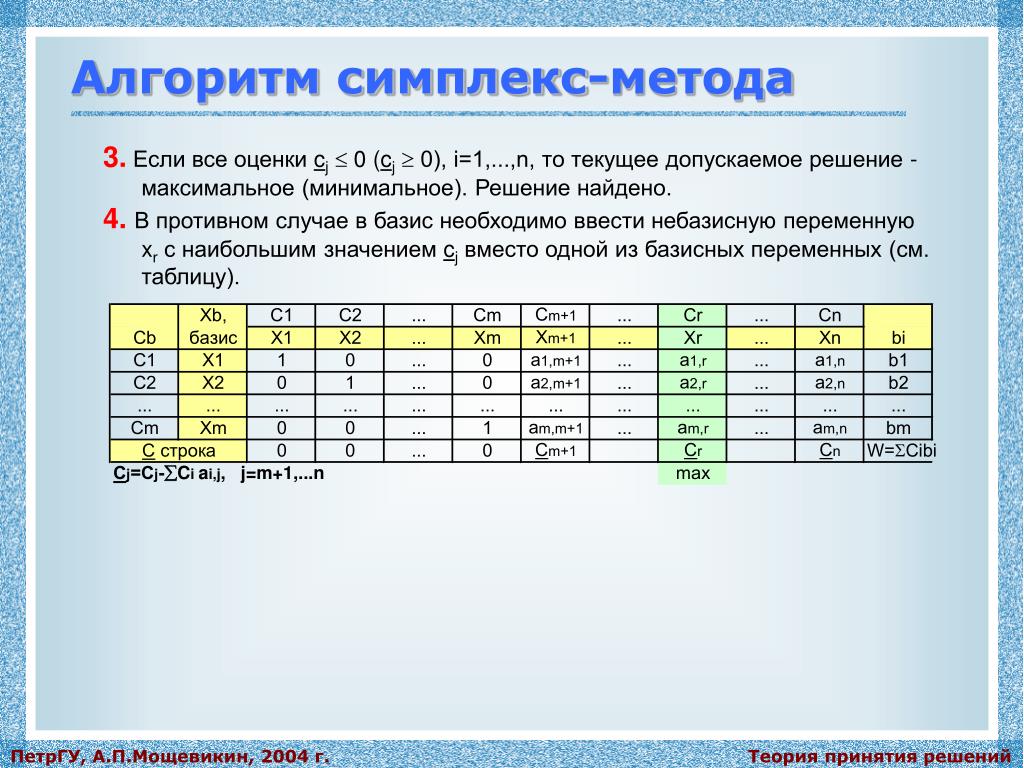
Использование возможностей Microsoft Excel позволяет существенно облегчить и ускорить решение этой задачи.
Сначала нужно создать исходную таблицу:
Затем, на основе этой таблицы записать формулы для нахождения решения:
Для нахождения решения используется надстройка Поиск решения. Нужно выделить ячейку, в которой вычисляется значение функции F и вызвать надстройку Поиск решения. Заполнить окно поиска решения:
В поле Ограничения нужно задать формулы для всех ограничений. Затем нажать кнопку Параметры и отметить поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК, затем Выполнить.
Чтобы найти значения вероятностей и цену игры нужно записать формулы:
Решение задачи для игрока В выполняется по аналогичной схеме согласно формулам (6), (7).
Рассмотрим пример решения задачи. Найдем решение игры, заданной матрицей .
Проверим наличие седловой точки.
В режиме отображения формул эта запись имеет вид:
Поскольку нижняя цена игры (минимальный выигрыш игрока А) и верхняя цена игры (максимальный проигрыш игрока В) не равны, то модель данной задачи не имеет седловой точки. Поэтому решение следует искать в смешанных стратегиях. Составим задачи линейного программирования для нахождения решений игроков А (согласно формулам (4), (5)) и В(согласно формулам (6), (7)):
для игрока А и для игрока В.
Для решения этих систем используем надстройку «Поиск решения». Сначала оформим задачу для поиска решения игрока А:
В режиме отображения формул:
Затем нужно активировать ячейку В7 и запустить надстройку Поиск решения. Далее заполнить окно Поиска решения:
Затем нажать кнопку Параметры и отметить поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК, затем Выполнить.
Получим результат:
Вероятности применения смешанных стратегий и цену игры найдем по формулам: pi=xi/F, v=1/F.
В режиме отображения формул:
Аналогично найдем решение для игрока В:
В режиме отображения формул:
Литература:
1. Акулич И.Л. Математическое программирование в примерах и задачах. М. «Высшая школа», 1993г.
2. Агальцов В.П., Волдайская И.В. Математические методы в программировании М. ИД «Форум» - ИНФРА-М, 2006г.
3. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем М. «Финансы и статистика», 2003г.
4. Партыка Т.Л., Попов И.И. Математические методы М. ИД «Форум» — ИНФРА-М, 2007г.
Основные термины (генерируются автоматически): игрок А, Поиск решения, режим отображения формул, игрок В, линейное программирование, цена игры, кнопка ОК, Линейная модель, оптимальная смешанная стратегия, оптимальная стратегия.
Похожие статьи
Создание и использование программы для статистического…
стратегия, игра, игрок, матричная игра, цена игры, решение игры, нулевая сумма, участник, верхняя цена игры, платежная матрица. Поиск решения как средство решения задач оптимизации…
Теория
игр: основные понятия, типы игр, примерыДля второго игрока самой оптимальной смешанной стратегией является стратегия . Запишем цену игры
Алгоритм. Иначе цена игры находится в промежутке и решение игры находится в смешанных стратегиях.
Поиск решения как средство решения задач оптимизации…Получится запись как на рис.1. В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок Линейная модель и задать условия неотрицательности переменных, установив флажок
Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.
Математическое моделирование
оптимальных стратегий…‒ аспект оптимальных решений — теория математических моделей принятия оптимальных решений вусловиях конфликтов.
игрок, функция распределения, стратегия, конфликтная ситуация, функция, математическая модель, непрерывная игра, обычный риманов интеграл…
Интеграл Стильтьеса в теории
игр | Статья в журнале…Аналогичным образом с помощью интеграла Стильтьеса находится цена непрерывной игры и оптимальная смешанная стратегия для обоих игроков-стратегов. Предположим, что есть платежная функция (или функция выигрыша)…
Целочисленное
решение задач линейного программирования…Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Решение многокритериальных задач линейного…Рис. 1. Оптимальное решение задачи.
Основные термины (генерируются автоматически): критерий, задача, учет уступок, полученное решение, поиск решения, матрица коэффициентов, важность критерия, допустимая уступка, линейное программирование.
Применение метода
линейного программирования для решения…Метод линейного программирования при решении текстовых задач графически имеет следующий алгоритм
Литература: 1. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели.
Линейное программирование | Статья в журнале «Молодой…»Модель линейного программирования имела бы множество переменных решений
Решение задач оптимального раскроя средствами MS Excel. Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века.
Решение задач линейного программирования » Привет Студент!
Факультет экономики и управления
Кафедра математических методов и моделей в экономике
ОТЧЕТ
по лабораторной работе
по курсу «Исследование операций»
на тему: «Решение задач линейного программирования»
Постановка задачи
На предприятии имеются три группы станков. Нужно изготовить два вида изделий – А и В. Фонд рабочего времени по первой группе станков составляет 400 часов, по второй- 360 часов, по третьей- 1320 часов. Время на обработку одного изделия вида А составляет для первой группы станков- 0,4 час., для второй – 0,84 час., для третьей- 8,0 часов. Соответственно для одного изделия группы В- 2,0; 1,2; 4,0 час. Каждое изделие вида А при его реализации дает прибыль предприятию в 1,2 ед., а изделие В- 4,8 ед. Найти план при котором прибыль будет максимальна.
Решить задачу:
- Симплекс- методом с помощью программного обеспечения DV SIMP;
- В МПП Excel с помощью надстройки «Поиск решения».
1 Обоснование симплекс- метода
Симплекс метод — это характерный пример итерационных вычислений, используемых при решении большинства оптимизационных задач. В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Пусть имеется задача линейного программирования в канонической форме:
F=c1x1+c2x2+…+cnxn→max(min), (1)
a11x1+a12x2+…+a1nxn=b1,
…………………………, (2)
am1x1+am2x2+…+amnxn≤bm;
xi ≥0, i=1,…,n;
Введем в рассмотрение вектора , j=1,…,n.
Тогда задачу можно переписать в следующем виде:
F=<c,x>→max(min), (3)
A1x1+A2x2+…+Anxn=b,
,
и трактовать следующим образом: из всех разложений вектора b по векторам с неотрицательными коэффициентами, требуется выбрать хотя бы одно такое, коэффициенты xi которого доставляют целевой функции F оптимальной значение. Не ограничивая общности, считаем ранг матрицы А: r=m и n>m.
Ненулевое допустимое решение называется опорным, если вектора , соответствующие отличным от нуля координатам , линейно независимы.
Ненулевое опорное решение называется невырожденным, если оно имеет m- положительных координат.
Если число положительных координат опорного решения меньше m, то оно называется вырожденным.
Упорядоченный набор из m- линейно независимых векторов , соответствующих положительным координатам опорного решения, назовем базисом.
Теорема: вектор тогда и только тогда является опорным решением задачи, когда точка является вершиной допустимого множества. Таким образом, задача нахождения вершины допустимого множества свелась к задаче нахождения опорного решения, а, следовательно, к нахождению базиса.
Будем считать, что исходный базис Ai1,…,Aim, тогда вектор b разложим по этому базису:
b==
.
Аналогично можно представить любой вектор :
В частности, в качестве исходного базиса могут быть взяты вектора, образующие единичную матрицу:
если они присутствуют в канонической форме задачи; в противном случае, исходный базис нужно строить, то есть имеет место задача с искусственным базисом.
Используя разложение вектора по базису векторами можно сформулировать утверждения:
- Если для данного базиса все оценки
неотрицательны, то опорное решение является оптимальной точкой задачи;
- Если для данного базиса существует хотя бы одна оценка для нее все то это означает, что целевая функция данной задачи линейного программирования не ограничена сверху на допустимом множестве;
- Если для данного базиса есть такая отрицательная оценка что среди координат вектора в данном базисе
координаты все векторов в новом базисе могут быть найдены через координаты векторов в старом базисе по формулам:
Алгоритм решения задачи симплекс методом.
Исходные данные:
- Вычисляем координаты разложения векторов по базису ;
- Рассчитываем оценки по формулам (1) и проверяем, являются ли они положительными. Если да, то алгоритм заканчивает свою работу, опорное решения является оптимальным, если нет, то проверяем, существуют ли такие , что все . Если существуют, то алгоритм заканчивает свою работу, задача неразрешима. Если нет, находим и находим
Далее производим замену в базисе вектора на вектор и снова выполняем разложение по новому базису.
В случае небольшого числа ограничений переменных указанный алгоритм легко реализовать без помощи ЭВМ, оформляя решение в виде симплекс-таблиц.
Пусть дана задача в канонической форме и найден исходный базис . Находим разложение всех векторов по базису. Результат оформляем в виде таблицы.
|
№ |
Базис |
В |
… |
||||
|
… |
|||||||
|
1 |
… |
||||||
|
2 |
… |
||||||
|
… |
… |
… |
… |
… |
… |
… |
… |
|
M |
… |
||||||
|
|
… |
|
|||||
2 Практическая часть
Представим данную задачу в виде таблицы 1.
Таблица 1- Исходные данные
|
Группа станков |
Фонд рабочего времени, час. |
Время на реализацию ед. продукции |
|
|
А |
В |
||
|
1 |
400 |
0,4 |
2 |
|
2 |
360 |
0,84 |
1,2 |
|
3 |
1320 |
8 |
4 |
Обозначим:
х1— количество произведенных изделий вида А;
х2 – количество произведенных изделий вида В.
Таким образом, целевая функция имеет следующий вид:
F=1,2*x1+4,8*x2→max;
Система ограничений запишется в виде:
0,4*х1+2*х2 ≤ 400;
0,84*х1+1,2*х2 ≤ 360;
8*х1+4*х2 ≤ 1320;
х1 ≥ 0, х2 ≥ 0.
Решим задачу с помощью программы DV SIMP. Введем исходные данные (рисунок 1).
Рисунок 1- Исходные данные
На следующем шаге необходимо привести систему к каноническому виду (рисунок 2).
Рисунок 2- Приведение к каноническому виду
После чего в целевой функции появятся переменные х3, х4, х5, и коэффициенты системы ограничений имеют следующий вид (рисунок 3):
Рисунок 3- Коэффициенты
Видим, что начальный базис можно указать. Он будет состоять из векторов А3, А4, А5 , которые образуют единичную матрицу.
Таким образом, на начальном этапе симплекс-таблица имеет следующий вид (рисунок 4):
Рисунок 4- Симплекс таблица
Для данной таблицы рассчитали оценки, среди которых оказались отрицательные, следовательно, решение не оптимально.
Так как решение не найдено, продолжаем решение, определяем новый базис (рисунок 5).
Рисунок 5- Определение базиса
По рисунку 5 видно, что ввести в базис нужно вектор А2, так как ему минимальная оценка.
Для определения вектора, который нужно вывести из базиса, рассчитаем ϴ для каждого вектора текущего базиса.
ϴ1=400/2=200;
ϴ2=360/1,2=300;
ϴ3=1320/4=330.
Минимальное значение ϴ соответствует вектору А3, следовательно, его выводим из базиса.
Для нового базиса симплекс- таблица представлена на рисунке 6.
Рисунок 6- Симплекс-таблица
Среди оценок текущей симплекс- таблицы есть отрицательная, следовательно, оптимальное решение не найдено, и нужно продолжать решение.
Минимальное значение оценки соответствует вектору А1, который введем в базис. Рассчитаем ϴ:
ϴ1=200/0,2=1000;
ϴ2=120/0,6=200;
ϴ3=520/7,2=72.222.
Минимальное значение ϴ соответствует вектору А5, следовательно, его выводим из базиса.
Для нового базиса симплекс- таблица представлена на рисунке 7.
Рисунок 7- Симплекс-таблица
Видим, что среди оценок нет отрицательных, а значит, оптимальное решение найдено (рисунок 8).
Рисунок 8- Решение задачи
В базис вошли вектора А2, А4, А1. Оптимальное значение целевой функции F=977,333. Соответственно оптимальные значения х1= 72,222; х2= 185,556.
Найдем решение данной задачи с помощью функции «Поиск решения» в МПП Excel.
Результат представлен на рисунке 9.
Рисунок 9- Решение задачи в МПП Excel
Получили аналогичный результат, то есть оптимально производить 72 изделия вида А и 185 изделий вида В. При этом максимальная прибыть будет равна 977,333 ед.
Скачать: У вас нет доступа к скачиванию файлов с нашего сервера. КАК ТУТ СКАЧИВАТЬ
Лабораторная работа №4. Реализация пошагового алгоритма решения задачи линейного программирования табличным симплекс-методом средствами Excel при выполнении всех условий
Задание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП.
Поясним последовательность действий при решения задачи ЛП табличным симплекс-методом на примере.
Задача. Решить задачу табличным симплекс-методом [8].
при ограничениях
Порядок выполнения работы:
I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом в чистом виде.
.
Задача каноническая.
В каждом ограничении есть базисная переменная: — в первом,- во втором,- в третьем.
В целевой функции нет базисных переменных.
II. Оформление исходных данных.
Откройте табличный процессор Excel и введите заголовок Табличный способ решения задач линейного программирования.
Заполните начальную симплекс-таблицу.
Шапка таблицы: столбец базисных переменных (B), столбец свободных членов, имеющиеся переменные.
Следующая строка таблицы соответствует первому ограничению. Базисная переменная, найденная в первом ограничении, свободный член, коэффициенты при переменных соответствующего ограничения. Аналогичным образом заполняются 2 и 3 строки.
Последняя строка – это строка целевой функции, которая заполняется следующим образом, свободный член без изменения знака, а коэффициенты при переменных с противоположным (рис. 26).
Рис. 26. Исходная симплекс таблица.
Проконтролируйте правильность заполнения таблицы. Так как ,,- базисные переменные, то на пересечении(5 строка) с (столбецD) должна стоять 1 (ячейка D5), а в соответствующем столбце ниже – нули, на пересечении (6 строка) с (столбецE) должна стоять 1 (ячейка E6), а в соответствующем столбце ниже – нули, (7 строка) с (столбецH) должна стоять 1 (ячейка H7), а в соответствующем столбце ниже – нули.
Запишите значение целевой функции, начальный опорный план, опираясь на столбец свободных членов (рис. 27).
Рис. 27. Значение целевой функции и начальный опорный план.
III. Нахождение оптимального плана и оптимального значения целевой функции.
Так в индексной строке есть отрицательные коэффициенты при переменных, то опорный план не является оптимальным. Организуйте процесс улучшения плана, выполнив предложенные шаги.
Среди отрицательных элементов индексной строки выберите наибольший по модулю элемент. Соответствующий столбец назовите ведущим. Данный столбец показывает, какую переменную необходимо включить в базис (рис. 28).
Рис. 28. Выбор ведущего столбца.
Теперь необходимо определить какую переменную исключить из базиса. Для этого составьте отношения для всех элементов столбца свободных членов () к соответствующим элементам ведущего столбца (). Например, в ячейку I5 введите формулу =B5/C5. Растяните формулы для ячеек I6, I7, исключая ячейку индексной строки (рис. 29).
Рис. 29. Составление отношений.
Определите результат отношений (таблица 5), учитывая, что в результате может получиться число, отличное от нуля, 0 или бесконечность (рис. 30).
Рис. 30. Результат отношений.
Выберите наименьшее из отношений. Строку, в которой получился наименьший результат, назовите ведущей (рис. 31). Данная строка показывает, какую переменную необходимо исключить из базиса.
Рис. 31. Выбор ведущей строки.
На пересечении ведущей строки и ведущего столбца получается ведущий элемент (рис. 32).
Рис. 32. Ведущий элемент.
Постройте новую симплексную таблицу. Выведите переменную из базиса, на ее место запишите ту переменную, которой соответствует ведущий столбец (рис. 33). В нашем случае – это переменная.
Рис. 33. Новый базис.
Так как теперь — базисная переменная, то на пересечении(13 строка) с (столбецC) должна стоять 1 (ячейка С13), а в соответствующем столбце ниже – нули. С помощью элементарных преобразований сделайте ведущий столбец базисным.
Для получения 1 в ячейке С13 необходимо каждый элемент ведущей строки поделить на ведущий элемент.
В ячейку С13 запишите формулу = С5/2 (рис 34), нажмите Enter.
Рис. 34. Получение 1 в ячейке С13.
Растяните формулу (рис. 35).
Рис. 35. Первая строка второй симплексной таблицы.
Затем получите нуль в ячейке С14.
Для этого во второй симплексной таблице 1 (ячейка С13) умножьте на элемент предыдущей таблицы, соответствующий элементу ячейки С14, взятый с противоположным знаком и сложите с этим же элементом.
Так как элемент, соответствующий элементу ячейки С14 равен 1 (ячейка С6), то это означает, что все элементы первой строки второй симплексной таблицы умножаются на (-1) и складывается с соответствующими элементами первой симплексной ьаблицы. Запишите в ячейку С14 формулу =C13*(-1)+C6 (рис. 36).
Рис. 36. Элемент С14 второй симплексной таблицы.
Аналогичным образом получите остальные элементы базисного столбца (рис. 37 и рис. 38).
Рис. 37. Элемент С15 второй симплексной таблицы.
Рис. 38. Элемент С16 второй симплексной таблицы.
Растяните формулы базисного столбца по строкам, получите вторую симплексную таблицу (рис. 39).
Рис. 39. Первая и вторая симплексные таблицы.
Так в индексной строке есть отрицательные коэффициенты при переменных, то опорный план не является оптимальным.
Запишите значение целевой функции, найденный новый опорный план, опираясь на столбец свободных членов (рис. 40). Проконтролируйте, что значение целевой функции максимизируется.
Рис. 40. Значение целевой функции и опорного плана второй симплексной таблицы.
Организуйте процесс улучшения плана, выполнив предложенные шаги, начиная с пункта 5, до тех пор пока не будет выполняться какой-нибудь из критериев остановки. Получите третью симплексную таблицу (рис. 41).
Рис. 41. Первая, вторая и третья симплексные таблицы.
В индексной строке нет отрицательных элементов, поэтому план оптимален,.
Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad.
Симплексный метод регрессии LAD | Реальная статистика с использованием Excel
Используя симплексный метод, мы решаем задачу нахождения минимума абсолютных отклонений между наблюдаемыми значениями y и предсказанными значениями y.
в задачу минимизации линейного программирования с учетом ограничений
для всех i = 1,…, n .
Мы можем использовать Excel Solver для решения этой задачи линейного программирования, применяя метод Simplex Linear Programming , где каждый элемент данных приводит к двум ограничениям.
Пример 1 : Повторите пример 1 наименьших квадратов для множественной регрессии с использованием регрессии LAD.
Мы повторяем данные из Примера 1 в диапазоне A3: E14 на Рисунке 1 вместе с настройкой, необходимой для использования симплексного метода Excel Solver.
Рисунок 1. Данные и настройка для симплекс-метода
Здесь ячейка D4 содержит формулу = $ F $ 15 + MMULT (A4: B4, $ F $ 16: $ F $ 17), E4 содержит = C4- D4, G4 содержит = -F4, а F19 содержит = СУММ (F4: F14). Ячейки в диапазоне F4: F14, которые представляют собой, установлены на начальное предположение 1, как и коэффициенты регрессии в диапазоне F15: F17.Мы могли бы заменить эти догадки какими-то другими значениями. Обратите внимание, что мы размещаем ячейки коэффициентов прямо под ячейками, чтобы у нас был непрерывный диапазон ячеек, который будет изменен во время работы алгоритма решателя.
Теперь мы выбираем Data> Analysis | Solver и заполняем диалоговое окно, которое появляется, как показано на рисунке 2.
Рисунок 2 — диалоговое окно Solver
Обратите внимание, что мы хотим минимизировать значение в ячейке F19, который будет содержать сумму абсолютного значения отклонения между наблюдаемыми значениями y (столбец C) и значениями, предсказанными регрессионной моделью (столбец D).Минимизация осуществляется путем изменения значений в диапазоне F4: F14, который содержит абсолютные отклонения, а также в диапазоне F15: F17, который содержит коэффициенты регрессии.
Мы указываем ограничения для процесса оптимизации обычным способом, за исключением того, что на этот раз мы объединяем такие ограничения, как E4 <= F4, E5 <= F5, E6 <= F6,…, E14 <= F14, используя неравенство диапазона E4: E14 <= F4: F14. Наконец, мы просим использовать метод Simplex LP . Когда мы нажимаем кнопку OK , мы получаем результаты, показанные на рисунке 3.
Рисунок 3 — Результаты регрессии LAD
Модель регрессии LAD —
Цена = 7,667 + 4,333 * Цвет + 2,778 * Качество
Поскольку у нас есть две независимые переменные, как отмечалось ранее, по крайней мере, три элемента данных будет иметь нулевой остаток, а именно строки 8, 10 и 11.
Одна проблема с использованием симплексного метода в Excel заключается в том, что он ограничен 100 ограничениями, что означает, что он будет поддерживать только модели LAD с не более чем 50 элементами данных .
3.3a. Решение стандартных задач максимизации с помощью симплекс-метода
В предыдущем разделе мы обнаружили, что графический метод решения задач линейного программирования, хотя и требует много времени, позволяет нам видеть области решения и определять угловые точки. Однако это невозможно при наличии нескольких переменных. Мы можем визуализировать до трех измерений, но даже это может быть сложно, когда есть множество ограничений.
Для решения задач линейного программирования, содержащих более двух переменных, математики разработали то, что теперь известно как симплекс-метод
.Это эффективный алгоритм (набор механических шагов), который «переключает» угловые точки, пока не найдет ту, которая максимизирует целевую функцию. Хотя это заманчиво, есть несколько вещей, на которые нам нужно обратить внимание, прежде чем использовать его.
Прежде чем приступить к математическим деталям, давайте рассмотрим пример задачи линейного программирования, для которой
соответствует симплекс-методу:
Пример 1
С помощью симплекс-метода можно решить следующую систему:
Цель Функция: P = 2 x + 3 y + z
При соблюдении ограничений:
3 x + 2 y ≤ 5
2 x + y — z ≤ 13
z ≤ 4
х, у, z≥0
Стандартная задача максимизации
С математической точки зрения, чтобы использовать симплексный метод для решения задачи линейного программирования, нам нужна стандартная задача максимизации:
- ,
- — целевая функция, а —
- одно или несколько ограничений вида a 1 x 1 + a 2 x 2 +… a n x n le В
- Все числа a представляют собой коэффициенты с действительными числами, а
- x номер представляет соответствующие переменные.
- V — неотрицательное (0 или большее) действительное число
Наличие ограничений с верхними пределами должно иметь смысл, поскольку при максимизации количества у нас, вероятно, есть ограничения на то, что мы можем сделать. Если бы у нас не было ограничений, мы могли бы продолжать увеличивать, скажем, прибыль, бесконечно! Это противоречит тому, что мы знаем о реальном мире.
Чтобы использовать симплексный метод, технологически или вручную, мы должны настроить исходную симплексную таблицу
, которая представляет собой матрицу, содержащую информацию о задаче линейного программирования, которую мы хотим решить.
Во-первых, матрицы плохо справляются с неравенством. Во-первых, у матрицы нет простого способа отслеживать направление неравенства. Уже одно это препятствует использованию неравенств в матрицах. Как же нам этого избежать?
Рассмотрим следующую задачу линейного программирования
Развернуть:
P = 7 x + 12 y
Субъект:
2 x + 3 y ≤ 6
3 x + 7 y ≤12
Поскольку мы знаем, что левые части обоих неравенств будут величинами, меньшими, чем соответствующие значения справа, мы можем быть уверены, что добавление «чего-то» к левой части сделает их в точности равными.То есть:
2 x + 3 y + с 1 = 6
3 x + 7 y + s 2 = 12
Например, предположим, что
x = 1, y = 1, тогда
2 + 3 + s 1 = 6 или s 1 = 1
3 + 7 + s 2 = 12 или s 2 = 2
Важно отметить, что эти две переменные, s 1 и s 2 , не обязательно одинаковы.Они просто действуют на неравенство, подбирая «слабину», которая не дает левой стороне выглядеть как правая. Следовательно, мы называем их резервными переменными . Это устраняет неравенство за нас. Поскольку расширенные матрицы содержат все переменные слева и константы справа, мы перепишем целевую функцию в соответствии с этим форматом:
–7 x — 12 y + P = 0
Теперь мы можем написать исходную систему уравнений :
| 2 x + 3 y + s 1 = 6 |
| 3 x + 7 y + s 2 = 12 |
| –7 x — 12 y + P = 0 |
Для этого нам потребуется матрица, которая может обрабатывать x , y , s 1 , s 2 и P .Мы разместим это в таком порядке. Наконец, симплексный метод требует, чтобы целевая функция была указана в нижней строке матрицы, чтобы мы имели:
Мы создали исходную симплексную таблицу . Обратите внимание, что горизонтальные и вертикальные линии используются просто для отделения коэффициентов ограничения от констант и коэффициентов целевой функции. Также обратите внимание, что столбцы переменных резервов вместе с выходными данными целевой функции образуют единичную матрицу.
Мы представим алгоритм решения, однако отметим, что он не совсем интуитивно понятен. Мы сосредоточимся на этом методе для одного примера, а затем перейдем к использованию технологий для выполнения процесса за нас.
1. Выберите столбец поворота
Сначала мы выбираем сводный столбец, который будет столбцом, содержащим наибольший отрицательный коэффициент в строке, содержащей целевую функцию. Обратите внимание, что наибольшее отрицательное число принадлежит члену, который больше всего влияет на целевую функцию.Это сделано намеренно, поскольку мы хотим сосредоточиться на значениях, которые делают вывод как можно большим.
Таким образом, наша точка поворота — это столбец и .
2. Выберите сводную строку
Сделайте это, вычислив отношение каждой константы ограничения к соответствующему коэффициенту в сводном столбце — это называется тестовым отношением . Выберите строку с наименьшим тестовым соотношением.
Сначала рассчитаем тестовые соотношения:
[латекс] \ displaystyle {\ left [\ matrix {{6 ÷ 3 = 2} \\ {12 ÷ 7≈1.7}} \ right]} [/ latex]
Поскольку тестовое соотношение для строки 2 меньше, мы выбираем ее в качестве сводной строки. Штучное значение теперь называется нашей опорной точкой . Чтобы объяснить, почему мы это делаем, заметим, что 2 и 1.7 — это просто вертикальные пересечения двух неравенств. Мы выбираем меньшее, чтобы убедиться, что угловая точка находится в допустимой области:
3. Используя метод исключения Гаусса, удалите строки 1 и 3
Умножьте R2 на (1/7), чтобы преобразовать 7 в 1.
Затем используйте 1, чтобы удалить 3 в R1: -3R 2 + R 1 → R 1
И используйте 1, чтобы удалить -12 в R3: 12R 2 + R 3 → R 3
Получаем следующую матрицу (возможно, дроби)
Что мы сделали? Во-первых, мы максимально увеличили вклад 2-2 входного коэффициента
y -значение в целевую функцию. Оптимизировали ли мы функцию? Не совсем так, поскольку мы все еще видим, что в первом столбце есть отрицательное значение.Это говорит нам о том, что все еще может вносить вклад в целевую функцию. Чтобы устранить это, мы сначала находим сводную строку, получая тестовые отношения:
[латекс] \ displaystyle {\ left [\ matrix {{5/7} & {0} & {1} & {- 3/7} & {0} & {|} {6/7} \\ {3 / 7} & {1} & {0} & {1/7} & {0} & {|} {12/7} \\ {- 13/7} & {0} & {0} & {12 / 7} & {1} & {|} {144/7}} \ right]} [/ latex]
[латекс] \ displaystyle {\ left [\ matrix {{(6/7) ÷ (5/7) ≈1.2} \\ {12 ÷ 3≈4}} \ right]} [/ latex]
Начиная с 1.2 <4, R1 - наша новая сводная строка.
Интересно, что это тестовое соотношение соответствует входному значению пересечения двух линий!
Аналогичным образом мы переходим к удалению всех неповоротных значений.
Умножьте R1 на (1 / 0,71), чтобы преобразовать 0,71 в 1.
Затем используйте 1, чтобы удалить 3 в R3: -3R 1 + R 2 → R 2
И используйте 1, чтобы устранить -12 в R3: 1.86R 1 + R 3 → R 3
Получаем следующую матрицу
[латекс] \ displaystyle {\ left [\ matrix {{1} & {0} & {7/5} & {- 3/5} & {0} & {|} {6/5} \\ {0 } & {1} & {- 3/5} & {2/5} & {0} & {|} {6/5} \\ {0} & {0} & {13/5} & {3 / 5} & {1} & {|} {114/5}} \ right]} [/ latex]
В строке целевой функции не осталось дополнительных отрицательных записей.Таким образом, мы имеем следующую матрицу:
[латекс] \ displaystyle {\ left [\ matrix {{1} & {0} & {7/5} & {- 3/5} & {0} & {|} {6/5} \\ {0 } & {1} & {- 3/5} & {2/5} & {0} & {|} {6/5} \\ {0} & {0} & {13/5} & {3 / 5} & {1} & {|} {114/5}} \ right]} [/ latex]
Таким образом, мы готовы читать решения.
4. Определите набор решений
Чтобы идентифицировать набор решений, мы сосредотачиваемся только на столбцах с ровно одной ненулевой записью — они называются базовыми переменными (столбцы с более чем одной ненулевой записью, таким образом, называются небазовыми переменными ) .
Мы замечаем, что оба столбца x any являются базовыми переменными. Нас действительно не волнуют переменные резервов, так же как мы игнорируем неравенство, когда находим пересечения. Теперь мы видим, что
[латекс] \ displaystyle {\ left [\ matrix {{1} & {0} & {7/5} & {- 3/5} & {0} & {|} {6/5} \\ {0 } & {1} & {- 3/5} & {2/5} & {0} & {|} {6/5} \\ {0} & {0} & {13/5} & {3 / 5} & {1} & {|} {114/5}} \ right]} [/ latex]
Установка переменных резервирования на 0 дает:
x ≈ 1.2
y ≈ 1,2
P = 22,8
Таким образом, x = 1,2, y = 1,2, P = 22,8 — это решение задачи линейного программирования. То есть входные данные x = 1,2 и y = 1,2 дадут максимальное значение целевой функции 22,8
.Хотя этот процесс несколько интуитивно понятен, за ним стоит больше, чем мы предполагаем. И вместо того, чтобы проходить эти изнурительные шаги до тошноты, мы позволим нашей технологии следовать этим шагам. Для этого нам понадобится специальная программа, которая будет распространяться в классе
.Для выполнения симплекс-метода с помощью графического калькулятора необходимы следующие программы:
- Поворот,
- Pivot1 и
- Симплекс
Pivot и Pivot1 напрямую не используются.Вместо этого программа Simplex обращается к этим двум приложениям, чтобы помочь ей с помощью довольно длинного и утомительного кода. Как работает код? Используя инструкции, он находит сводные столбцы, сводные строки, выполняет гауссовское исключение, проверяет наличие негативов в строке целевой функции и повторяет этот процесс по мере необходимости, пока все негативы не будут удалены.
Теперь, когда мы проиллюстрировали, что на самом деле симплекс-метод работает даже с двумя входными переменными, давайте покажем ситуацию, в которой этот метод особенно полезен.
Пример 2
Новая авиакомпания решила выйти на рынок. Он рассматривает возможность предложения рейсов из Феникса, штат Аризона, и первоначально хотел бы отправиться в три разных места: Сан-Диего, Сан-Франциско и Лас-Вегас. Расстояния каждого рейса туда и обратно, вылетающего из Феникса, составляют (приблизительно): 720 миль, 1500 миль и 1140 миль соответственно. Компания хотела бы использовать слоган: «Средняя цена за рейс никогда не превышает 200 долларов». Что касается затрат, ожидается, что полеты в Сан-Диего будут составлять около 10% от стоимости авиабилетов.Точно так же на Сан-Франциско будет приходиться 12%, а на Лас-Вегас — 14% авиаперевозок. Компания хочет, чтобы общая средняя стоимость не превышала 10% от заработанных авиабилетов. Недавнее исследование рынка позволяет компании сделать вывод, что она могла бы продать около 1900 билетов в Сан-Диего, 700 билетов в Сан-Франциско и 1000 билетов в Лас-Вегас. В этих условиях и при условии, что все проданные билеты являются рейсами в оба конца, какую сумму компания должна взимать за билет, чтобы максимизировать свой общий доход?
Решение
Мы хотим знать стоимость авиабилетов в каждый пункт назначения.Пусть,
x = цена билета в оба конца до Сан-Диего
y = цена билета в оба конца до Сан-Франциско
z = цена за билет в оба конца до Лас-Вегаса
Компания хочет максимизировать общий доход. Это основано на сумме количества проданных билетов, умноженной на цену за билет, которая составляет:
.R = 1900 x + 700 y + 1000 z
При соблюдении ограничений:
- Средняя цена за рейс не превышает 200 долларов США
- Средняя стоимость авиабилетов не более 10% от общей суммы
Математически,
- Добавьте цены и разделите на 3
[латекс] \ displaystyle \ frac {{{x} + {y} + {z}}} {{3}} \ le {200} [/ latex] - Или x + y + z ≤ 600
- Общий доход от билетов в Сан-Диего составит 10% от этой суммы.То есть Стоимость = 0,10 (1900 x ) = 190 x . Точно так же имеем 0,12 (700 y ) = 84 y и 0,14 (1000 z ) = 140 z . Мы хотим, чтобы сумма этих затрат была меньше или равной 10% от общего дохода, что составляет 0,10 (1900 x + 700 y + 1000 z ) = 190 x + 70 y . + 100 z .
- 190 x + 84 y + 140 z ≤ 190 x + 70 y + 100 z
- или 14 y + 40 z ≤ 0
Поскольку оба ограничения имеют правильную форму, мы можем приступить к настройке исходной симплексной таблицы.В качестве примечания будьте очень осторожны при использовании симплексного метода, поскольку невыполненные требования делают полученные результаты недействительными.
Переписанная целевая функция:
–1900 x — 700 y — 1000 z + R = 0
И упрощенные ограничения:
x + y + z ≤ 600 (умножить обе стороны на 3)
14 y + 40 z ≤ 0
х, y≥0
Для каждого из двух ограничений потребуется переменная Slack, поэтому мы перепишем их следующим образом:
x + y + z + s 1 = 600
14 y + 40 z + s 2 = 0
У нас будут следующие столбцы переменных:
x , y , z, s 1 , s 2 , R и постоянный столбец, всего 7 столбцы.Всего у нас есть два ограничения и одна целевая функция для трех строк. Теперь напишем исходную симплексную таблицу:
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1} & {1} & {1} & {0} & {0} & {|} {600} \\ {0} & { 14} & {40} & {0} & {1} & {0} & {|} {0} \\ {- 1900} & {- 700} & {- 1000} & {0} & {0} & {1} & {|} {0}} \ right]} [/ латекс]
Теперь таблица готова к решению с использованием Simplex.
Поворот по 1-му столбцу и 1-й строке. (Вы не можете делить на 0, чтобы получить сводную строку)
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1} & {1} & {1} & {0} & {0} & {|} {600} \\ {0} & { 14} & {40} & {0} & {1} & {0} & {|} {0} \\ {0} & {1200} & {900} & {1900} & {0} & {1} & {|} {1140000}} \ right]} [/ латекс]
Поскольку базовым будет только столбец x , мы можем видеть, что x = 600 является решением.Поскольку y и z не являются базовыми переменными, мы устанавливаем y = z = 0. То есть они не способствуют максимизации дохода. Кроме того, R является активной переменной, поэтому мы видим, что R = 1 140 000 долларов США — это максимальный доход, который компания может получить с учетом ограничений. Им следует продавать билеты в Сан-Диего за 600 долларов и не продавать рейсы в другие города. Как нетрудно догадаться, компания, вероятно, немного ошеломлена. Мы рассмотрим это в следующем примере.
Интересно, что поездки в Сан-Диего сами по себе приносят наибольший доход, исходя из данных ограничений. Почему это? Если мы посмотрим на ограничения, то увидим, что компания вполне уверена, что сможет продать 1900 рейсов в Сан-Диего. Компания также несколько озадачена тем, что предполагается продавать билеты по 600 долларов за штуку. На этом этапе он может решить добавить к модели некоторые дополнительные ограничения.
Пример 3
Предположим, что авиалайнер в Примере 2 решает, что он может взимать не более 150 долларов за билет до Сан-Диего, чтобы быть конкурентоспособным по сравнению с другими авиалайнерами, которые летают в тот же пункт назначения.Если предположить, что все остальные ограничения все еще будут использоваться, как это повлияет на цены на билеты и максимальный доход?
Решение
Мы используем ту же исходную таблицу, но мы должны иметь дело со следующим новым ограничением:
x ≤ 150
Добавляя третью переменную slack, получаем
x + с 3 = 150
Это добавляет один столбец и одну строку в нашу таблицу:
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1} & {1} & {1} & {0} & {0} & {0} & {|} {600} \\ { 0} & {14} & {40} & {0} & {1} & {0} & {0} & {|} {0} \\ {1} & {0} & {0} & {0} & {0} & {1} & {0} & {|} {150} \\ {- 1900} & {- 700} & {- 1000} & {0} & {0} & {0} & {1 } & {|} {0}} \ right]} [/ латекс]
Решение этого симплексом дает
[латекс] \ displaystyle {\ left [\ matrix {{0} & {0} & {- 13/7} & {1} & {- 1/14} & {- 1} & {0} & {| } {450} \\ {0} & {1} & {20/7} & {0} & {1/14} & {0} & {0} & {|} {0} \\ {1} & {0} & {0} & {0} & {0} & {1} & {0} & {|} {150} \\ {0} & {0} & {1000} & {0} & {50 } & {1900} & {1} & {|} {285000}} \ right]} [/ latex]
Решение: x = 150, y = 0, z = 450 и R = 285000
Пример 4
Кейтеринговая компания приготовит обед к деловой встрече.Здесь подают бутерброды с ветчиной, легкие бутерброды с ветчиной и вегетарианские бутерброды. Сэндвич с ветчиной состоит из 1 порции овощей, 4 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. Легкий бутерброд с ветчиной состоит из 2 порций овощей, 2 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. Вегетарианский бутерброд состоит из 3 порций овощей, 2 ломтиков сыра и 2 ломтиков хлеба. Всего доступно 10 пакетов ветчины, в каждой по 40 ломтиков; Доступно 18 буханок хлеба, каждая по 14 ломтиков; Доступно 200 порций овощей и 15 пакетов сыра, по 60 ломтиков в каждом.Учитывая ресурсы, сколько бутербродов можно произвести, если цель состоит в том, чтобы максимально увеличить количество бутербродов?
Решение
Мы хотим увеличить количество бутербродов, поэтому давайте:
x = количество бутербродов с ветчиной
y = Количество легких бутербродов с ветчиной
z = количество вегетарианских бутербродов
Общее количество бутербродов равно
.S = x + y + z
Ограничения будут даны с учетом общего количества доступных ингредиентов.То есть у компании ограниченное количество ветчины, овощей, сыра и хлеба.
Всего у компании есть
10 (40) = 400 ломтиков ветчины, 18 (14) = 252 ломтика хлеба, 200 порций овощей и 15 (60) = 900 ломтиков сыра. Максимум, компания может использовать вышеуказанные суммы.
Есть два бутерброда с ветчиной: для первого требуется 4 ломтика ветчины, а для второго — только 2 на бутерброд. То есть 4 x + 2 y ≤ 400
То есть общее количество ломтиков ветчины не может превышать 400.
Для каждого бутерброда требуется 2 ломтика хлеба, поэтому 2 x + 2 y + 2 z ≤ 252
В бутербродах с ветчиной 1 и 2 порции овощей соответственно, а в вегетарианском бутерброде 3 порции овощей. Итак, 1 x + 2 y + 3 z ≤ 200
Для обоих бутербродов с ветчиной требуется один ломтик сыра, а для вегетарианского бутерброда — два ломтика сыра, поэтому 1 x + 1 y + 2 z ≤ 900 Ниже представлена законченная модель линейного программирования для этого примера.
| Развернуть: S = x + y + z |
| Субъект Кому: 4 x + 2 y ≤ 400 |
| 2 x + 2 y + 2 z ≤ 252 |
| x + 2 y + 3 z ≤ 200 |
| 1 x + 1 y + 2 z ≤ 900 |
| х, у, z≥0 |
Эти ограничения удовлетворяют требованиям симплекс-метода, поэтому продолжаем.
Включая резервные переменные, получаем:
4 x + 2 y + 0 z + s 1 = 400
2 x + 2 y + 2 z + s 2 = 252
x + 2 y + 3 z + s 3 = 200
x + y + 2 z + s 4 = 900
— x — y — z + S = 0
Исходная симплексная таблица:
[латекс] \ displaystyle {\ left [\ matrix {{4} & {2} & {0} & {1} & {0} & {0} & {0} & {0} {|} & {400 } \\ {2} & {2} & {2} & {0} & {1} & {0} & {0} & {0} {|} & {252} \\ {1} & {2} & {3} & {0} & {0} & {1} & {0} & {0} {|} & {200} \\ {1} & {1} & {2} & {0} & { 0} & {0} & {1} & {0} {|} & {900} \\ {- 1} & {- 1} & {- 1} & {0} & {0} & {0} & {0} & {1} {|} & {0}} \ right]} [/ latex]
Поскольку наибольшее отрицательное число в нижней строке одинаково для трех столбцов, мы можем использовать любой столбец.Можно также использовать первый столбец. Наименьшее частное получается путем деления 4 на 400, так что строка 1 является сводным столбцом. Разворот на «4» в R1C1 дает доход.
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1/2} & {0} & {1/4} & {0} & {0} & {0} & {0} {| } & {100} \\ {0} & {1} & {2} & {- 1/2} & {1} & {0} & {0} & {0} {|} & {52} \\ {0} & {3/2} & {3} & {- 1/4} & {0} & {1} & {0} & {0} {|} & {100} \\ {0} & { 1/2} & {2} & {- 1/4} & {0} & {0} & {1} & {0} {|} & {800} \\ {0} & {- 1/2} & {- 1} & {1/4} & {0} & {0} & {0} & {1} {|} & {100}} \ right]} [/ latex]
Примечание: мы увеличили S с 0 до 200, но у нас все еще есть отрицательный знак в нижней строке.Поскольку «-1» более отрицательное значение, чем «-1/2», мы будем вращаться по столбцу 3. После деления положительных чисел выше «-1» на константы, мы получим наименьшее частное в строке 2. Вращаемся по «2». ”В выходах R2C3.
[латекс] \ displaystyle {\ left [\ matrix {{x} & {y} & {z} & {s1} & {s2} & {s3} & {s4} & {S} \\ {1} & {1/2} & {0} & {1/4} & {0} & {0} & {0} & {0} {|} & {100} \\ {0} & {1/2} & {1} & {- 1/4} & {1/2} & {0} & {0} & {0} {|} & {26} \\ {0} & {0} & {0} & { 1/2} & {- 3/2} & {1} & {0} & {0} {|} & {22} \\ {0} & {- 1/2} & {0} & {1 / 4} & {- 1} & {0} & {1} & {0} {|} & {748} \\ {0} & {0} & {0} & {1/2} & {0} & {0} & {0} & {1} {|} & {126}} \ right]} [/ latex]
Теперь у нас есть оптимальное решение
- x = 100 (базовая переменная в строке 1)
- y = 0 (небазовая переменная)
- z = 26 (основная переменная строка 2)
- s1 = 0 (небазовая переменная)
- s2 = 0 (небазовая переменная)
- s3 = 22 (строка основной переменной 3)
- s4 = 748 (строка базовой переменной 4)
- S = 126 (базовая переменная строка 5)
Конечно, нас действительно интересуют: x = 100, y = 0, z = 26, S = 126
Мы обнаружили, что необходимо приготовить 100 бутербродов с ветчиной, 26 вегетарианских бутербродов и 0 легких бутербродов с ветчиной, чтобы увеличить общее количество приготовленных бутербродов.
Переменные резерва не важны в решении. Просто в достижении решения.
Дополнительные примеры см. В следующем разделе. Во многих задачах используются переменные с индексами, такие как x 1 , x 2 , x 3 и т. Д. Это особенно полезно, если у вас есть несколько переменных. Вы увидите это в следующих примерах.
Дополнительные ресурсы перечислены ниже:
Milos Podmanik, By the Numbers, «Решение стандартных задач максимизации с помощью симплекс-метода», лицензия CC BY-NC-SA 3.0 лицензия.
MathIsGreatFun, «MAT217 HW 2.2 # 1», под лицензией Standard YouTube.
MathIsGreatFun, «MAT217 2.2 # 2» под стандартной лицензией YouTube.
MathIsGreatFun, «MAT217 2.2 # 3» под стандартной лицензией YouTube.
MathIsGreatFun, «MATh317 2.2 # 4» под стандартной лицензией YouTube.
Excel Solver — что может и чего не может Solver
Основная цель решателя— найти решение , то есть значения для переменных решения в вашей модели, которое удовлетворяет всем ограничениям и максимизирует или минимизирует цель значение ячейки (если есть).Тип , тип решения, которого вы можете ожидать, и сколько вычислительного времени может потребоваться для поиска решения, в первую очередь зависит от трех характеристик вашей модели:
- Размер вашей модели (количество переменных решения и ограничений, общее количество формул )
- Математические отношения (например, линейные или нелинейные) между целью и ограничениями и переменными решения
- Использование целочисленных ограничений для переменных в вашей модели
Другие проблемы, такие как плохое масштабирование , также могут повлиять на решение время и качество, но указанные выше характеристики влияют на внутреннюю разрешимость вашей модели.Хотя более быстрые алгоритмы и более быстрые процессоры могут помочь, для решения некоторых невыпуклых или негладких моделей могут потребоваться годы или десятилетия, чтобы добиться оптимальности на самых быстрых компьютерах, которые только можно себе представить.
Общий размер вашей модели и использование целочисленных ограничений относительно легко оценить, когда вы исследуете свою модель. Математические отношения, которые определяются формулами в вашей модели, может быть труднее оценить, но они часто имеют решающее влияние на время и качество решения — как далее объясняется, начиная с этой темы.
Подводя итог:
- Если ваша цель и ограничения — это линейные функции переменных решения, вы можете быть уверены, что достаточно быстро найдете глобально оптимальное решение , учитывая размер вашей модели. Это задача линейного программирования ; это также задача оптимизации выпуклых (поскольку все линейные функции выпуклые). Для этих задач разработан метод Simplex LP Solving.
- Если ваша цель и ограничения — это гладких нелинейных функций переменных решения, время решения будет больше.Если проблема выпуклый , вы можете быть уверены, что найдете глобально оптимальное решение , но если это невыпуклый , вы можете ожидать только локально оптимальное решение — и даже это может быть трудно найти . Метод нелинейного решения GRG разработан для этих задач.
- Если ваша цель и ограничения — это негладкие и невыпуклые функции переменных решения (например, если вы используете функции ЕСЛИ, ВЫБРАТЬ и ПРОСМОТР, аргументы которых зависят от переменных решения), лучшее, на что вы можете надеяться является «хорошим» решением (лучше, чем начальные значения переменных), а не локально или глобально оптимальным решением.Метод эволюционного решения предназначен для этих задач.
- Вы можете использовать целочисленные, двоичные и любые другие ограничения для переменных со всеми тремя методами решения. Однако эти ограничения значительно усложняют решение задачи невыпуклых и .
С помощью метода Simplex LP Solving вы можете найти глобально оптимальное решение за достаточно времени, но, возможно, вам придется довольствоваться решением, которое «близко к оптимальному», найденным за более разумный промежуток времени.От методов нелинейного и эволюционного решения GRG следует ожидать «хорошего», но не доказуемо оптимального решения.
Excel Solver: какой метод решения мне выбрать?
Если вы когда-либо заходили в надстройку Excel Solver, вы, вероятно, замечали, что есть много вариантов, и это может быть немного подавляющим. В этом посте я хотел бы предоставить некоторую практическую информацию, которая поможет вам выбрать правильный метод решения в Excel, чтобы эффективно найти оптимальное решение вашей проблемы.
Одна из вещей, которую вы должны выбрать при настройке Solver в Excel, — это метод решения. На выбор есть три метода или алгоритма:
- GRG Нелинейный
- эволюционный
- Симплекс LP
GRG Нелинейный и эволюционный лучше всего подходят для нелинейных задач, в то время как симплексный LP ограничивается только линейными задачами.
GRG означает «Обобщенный уменьшенный градиент». В своей основной форме этот метод решателя смотрит на градиент или наклон целевой функции при изменении входных значений (или переменных решения) и определяет, что он достиг оптимального решения, когда частные производные равны нулю.
Из двух методов нелинейного решения GRG Nonlinear является самым быстрым. Однако такая скорость идет с компромиссом.
Обратной стороной является то, что решение, которое вы получаете с помощью этого алгоритма, сильно зависит от начальных условий и может не быть глобальным оптимальным решением. Решающая программа, скорее всего, остановится на локальном оптимальном значении, ближайшем к начальным условиям, предоставив вам решение, которое может или не может быть оптимизировано глобально.
Еще одно требование к нелинейному решателю GRG для получения хорошего решения состоит в том, чтобы функция была гладкой.Любые нарушения непрерывности, вызванные, например, функциями IF, VLOOKUP или ABS, вызовут проблемы для этого алгоритма.
Эволюционный алгоритм более надежен, чем GRG Nonlinear, потому что он с большей вероятностью найдет глобально оптимальное решение. Однако этот метод решения также ОЧЕНЬ медленный.
Позвольте мне объяснить, почему:
Эволюционный метод основан на теории естественного отбора, который хорошо работает в данном случае, потому что оптимальный результат был определен заранее.
Проще говоря, решатель начинает со случайной «совокупности» наборов входных значений. Эти наборы входных значений вставляются в модель, и результаты оцениваются относительно целевого значения.
Наборы входных значений, которые приводят к решению, наиболее близкому к целевому значению, выбираются для создания второй популяции «потомков». Потомство — это «мутация» наилучшего набора входных значений из первой популяции.
Затем оценивается вторая популяция и выбирается победитель для создания третьей популяции.
Надеюсь, что приведенная ниже диаграмма проясняет ситуацию.
Так продолжается до тех пор, пока целевая функция не меняется очень мало от одной популяции к другой.
Что делает этот процесс настолько трудоемким, так это то, что каждый член населения должен оцениваться индивидуально. Кроме того, последующие «поколения» заполняются случайным образом вместо использования производных и наклона целевой функции для поиска следующего наилучшего набора значений.
Теперь Excel дает вам некоторый контроль над алгоритмом через окно параметров решателя.Например, вы можете выбрать частоту мутаций и размер популяции, чтобы потенциально сократить время решения.
Однако это имеет убывающую отдачу, потому что уменьшение размера популяции и / или увеличение скорости мутаций может потребовать еще большего количества популяций для достижения конвергенции.
Хороший компромисс между скоростью нелинейного алгоритма GRG и надежностью эволюционного алгоритма — это GRG Nonlinear Multistart. Вы можете включить эту опцию в окне Solver Options на вкладке GRG Nonlinear.
Алгоритм создает случайно распределенную совокупность начальных значений, каждое из которых оценивается с использованием традиционного нелинейного алгоритма GRG.
При многократном запуске с разных начальных условий существует гораздо большая вероятность, , что найденное решение является глобальным оптимумом.
Из трех методов решения я меньше всего использую Simplex LP. Его применение ограничено, поскольку его можно применять только к задачам, содержащим только линейные функции.
Часто задачи, которые я решаю, нелинейны. А когда они линейны, я предпочитаю решать их как матричное уравнение.
Однако он очень надежен, потому что, если проблема, которую вы решаете, является линейной, вы можете быть уверены, что решение, полученное методом Simplex LP, всегда является глобально оптимальным решением.
Линейное программирование с помощью электронных таблиц
Линейное программирование с помощью электронных таблицЛинейное программирование с помощью электронных таблиц
Представлено в Интернете
В стадии строительства
Обзор
Модуль 1.Что такое линейное программирование?
- Введение.
- Аспекты линейного программирования.
- История линейного программирования.
- Линейное программирование и электронные таблицы.
- Проблема узких мест в производстве.
- Решение уравнения.
- Упражнения.
- Литература.
Модуль 2. Простая модель и ее составление в виде электронной таблицы.
- Введение.
- Производство чизкейков для гурманов.
- Алгебраическая формулировка.
- Формулировка действия в среде электронной таблицы.
- Представление модели чизкейка с помощью числового графика.
- Построение графика модели чизкейка.
- Особые случаи.
- Безграничное решение.
- Нет подходящего решения.
- Множественные оптимальные решения.
- Вырожденное решение.
- Упражнения.
- Литература
Модуль 3. Оптимизация на основе электронных таблиц.
- Введение.
- Оптимизация электронных таблиц с помощью What’sBest.
- Самая лучшая установка и команды.
- Постановка задачи.
- Расчет и результаты.
- Неограниченное решение.
- Нет подходящего решения.
- Составы с верхними границами.
- Оптимизация электронных таблиц с помощью функции «Что, если».
- Присоединение надстройки.
- Формулировка задачи «Что, если».
- Решение проблемы.
- Сохранение настроек Whatif.
- Оригинальный состав WhatIf.
- Выбор симплекс-метода.
- Оптимизация электронных таблиц с Quattro Pro.
- Оптимизация электронных таблиц с помощью Excel.
- Упражнения.
- Литература.
Модуль 4. Симплексный метод.
- Введение.
- Простое возможное решение.
- Итерация симплекс-метода.
- Выбор новой базовой переменной.
- Выбор выходной базовой переменной.
- Преобразование системы уравнений.
- Пример симплекс-метода.
- Геометрия симплекс-метода.
- Выполнение симплекс-метода.
- Упражнения.
- Литература.
Модуль 5. Что поесть в McDonald’s?
- Введение.
- Лучшая покупка в гамбургер-меню.
- Большая проблема.
- Полное ежедневное питание.
- Упражнения.
- Литература.
Модуль 6. Смешивание и смешивание моделей.
- Введение.
- Купля-продажа.
- Структура купли-продажи.
- Совокупность видов деятельности.
- Модель с раздельной продажей и покупкой.
- Проблема минимизации затрат.
- Проблема кормов.
- Проблема смешивания кормов для крупного рогатого скота.
- Смешение бензина.
- Переменное производство и продажа бензина.
- Смешивание ряда бензиновых продуктов.
- Прочие проблемы при смешивании и смешивании.
- Упражнения.
- Литература.
Модуль 7. Анализ чувствительности.
- Введение.
- Изменение количества труда.
- Изменения констант ограничений.
- Изменение коэффициентов целевой функции.
- Анализ чувствительности для ограничений с WB.
- Анализ чувствительности для переменных решения с WB.
- Анализ чувствительности с помощью Excel Solver.
- Вырожденные решения.
- Множественные оптимальные решения.
- Одновременные изменения.
- Упражнения.
- Литература.
Модуль 8. Двойная проблема.
- Введение.
- Двойная оценка.
- Двойная проблема для простого случая.
- Двойная задача для примера с чизкейком.
- Общая постановка первичных и двойственных задач.
- Отношения между первичным и двойственным решениями.
- Первичная и двойная задачи для примера с чизкейком.
- Проблема минимизации.
- Двойственность транспонированием.
- Упражнения.
- Литература.
Модуль 9. Параметрическое программирование.
- Введение.
- Параметрическое программирование ограничений с WB.
- Чистый доход и двойная переменная труда.
- Первичные переменные и доход от продукта для различного количества рабочей силы.
- Стоимость ресурсов для различного количества рабочей силы.
- Доходы трудовых коллективов.
- Параметрическое программирование коэффициентов целевой функции с помощью Excel Solver.
- Переменные решения и их доходы для различных доходов от природных ресурсов.
- Стоимость ресурсов для различных доходов от природных ресурсов.
- Упражнения.
- Литература.
Модуль 10. Транспортные модели.
- Введение.
- Транспортные модели
- Проблемы с назначением.
- Упражнения.
Модуль 11. Целочисленное программирование и задачи присваивания.
- Введение.
- Целочисленное программирование.
- Пример инвестиций в недвижимость.
- Фиксированные затраты на деятельность.
- Проблемы с расположением.
- Упражнение.
- Задания.
- Проблема местоположения.
- Проблема с выбором программного обеспечения.
Модуль 12. Анализ охвата данных.
- Введение.
- Проблема Исполнительного совета факультета.
- Графическое определение эффективности.
- Формулировка линейного программирования для случая с одним входом.
- Несколько входов и выходов.
- Ценностный подход.
- Упражнения.
Модуль 13. Линейное программирование и экономический анализ.
Модуль 14. Энергетические модели.
Модуль 15. Финансовые инвестиционные модели.
Модуль 16. Нелинейные модели.
ാ 㰊 敭 浡 㵥 䜢 久 剅 呁 剏 • 潣 瑮 湥 㵴 䴢 䡓 䵔 ⁌⸸〰 㜮 〶⸰ ㈷∲ 㰾 栯 慥 㹤 戼 格 㸲 潓 癬 楌敮 牡 倠 潲 牧 浡 業 杮 倠 潲 汢 獕 湩 塅 䕃 㱌 栯 㸲 瑳 猠 牰 慥 敨 瑥 瀠 浡 慨 敶 琠 挠 瑩 ⁹ 潴 汯 敶慭 汬 氠 湩 慥 牰 杯 慲 浭 湩 獭 ☮ 扮 灳 ※ 硅 慨 潴 汯 挠 污 敬 䱏 䕖 ⁒ ⼼ 㹢 瑡 猠 慶 楲 慭桴 浥 瑡 捩 污 瀠 潲 浡 業 杮 汢 浥 吠 楨 獥 牣 扩 獥 琠 敨 甠 敳 体 体 噌 剅 琠 潳 瀠 潲 牧 業 杮瀠 潲 汢 浥 潔 搠 桴 獩 礠 畯 敲 瑡 潷 歲 桳 敥 敲 牰 獥 湥 慴 楴 湯 漠 桴 敤 㭬 ⠠⤲ 搠 晥 桴 牰 扯 敬 潴琠 敨 猠 汯 敶 ♲ 扮 灳 愻 摤 椭 灳 ⠻⤳ 猠 汯 敶 琠 敨 汢 浥 ※ 㐨 睥 愠 摮 牰 湩 ⁴ 桴 畳 㔨 慳 琠 敨潲 汢 浥 愠 摮 漯 桴 敲 畳 㰠 牢 㸠 戼 ㄾ 潗 敥 ⁴ 敲 牰 湥 慴 楴 桴 潭 敤 㩬 㹢 桔 扯 敬慣 敢 爠 灥 敲 敳 瑮 摥 椠 瘠 牡 敩 祴 漠 慷 獹 牥 獩 渠 楲 楧 潦 煥 極 敲 敭 瑮 湯 爠 煥 極 敲 敭瑮 牡 桴 瑡 礠 畯 栠 癡 潦 桴 牰 扯 慶 楲 扡 敬 愠 映 牯 爠 灥 敲 敳 瑮 湩 桴 瑣 癩 楴湡 潦 浲 汵 獡 爠 灥 敲 敳 瑮 敬 瑦 栠 湡 楳 景 琠 敨 挠 瑳 慲 湩 汁 桴 桧 洠 湡 ⁹ 潦 潰 扩 敬湯 楷 敤 祬 甠 敳 潦 浲 瑡 敧 桴 灳 敲 敥 ⁴ 敲 牰 湥 慴 楴 桴 牰 扯 敬 獡 牡 慲 汬牷 瑩 整 椠 攮 Ⱞ 爠 睯 敲 湥 楴 杮 挠 湯 瑳 慲 愠 摮 挠 汯 獮 爠 灥 瑮 湩 慶 楲 扡 獮 慴 据 琠 癬 㰊 牰 㹥 格 ാ☊ 扮 灳 ☻ 扮 扮 灳 ☻ 扮 灳 ☻ 扮 ☻ 扮 灳 ☻ 扮 灳 ☻ 扮 灳 灳 ☻ 扮 灳 ※ ♸ 扮 ☻ 扮 灳 ※ 〵〰⁅ 〴〰െ☊ 扮 灳 ☻ 扮 灳 ☻ 扮 灳 ☻ 扮 扮 灳 ☻ 扮 灳 ☻ 扮 ☻ 扮 灳 ☻ 扮 灳 ※ 呓 ☮ ☻ 扮 灳 ☻ 扮 ☻ 扮 ☻ 扮 灳 ※ 〱 ⁅ 㔱 ⁆ 氦 㭴 ㄽ 〵 渦 獢 㭰 㭰 渦 獢 㭰 渦 獢 㭰 㭰 渦 獢 㭰 獢 㭰 渦 渦 獢 㭰 渦 獢 渦 獢 㭰 渦 㭰 渦㭰 渦 獢 㭰 渦 獢 㭰 渦 獢 㭰 渦 ㈠ 䔰 ⬠ ㄠ 䘰 ☠ 瑬 ര☊ 扮 灳 ☻ 灳 ☻ 扮 扮 灳 ☻ 扮 灳 扮 灳 ☻ 扮 ☻ 扮☻ 扮 灳 ☻ 扮 灳 ☻ 扮 灳 ☻ 扮 扮 灳 ☻ 扮 灳 ☻ 扮 ☻ 扮 灳 ☻ 扮 灳 ※ 〳⁅〱⁆ 朦 㔳 渦 獢 㭰 獢 㭰 獢 㭰 渦 獢 㭰渦 獢 㭰 渦 獢 㭰 渦 獢 㭰 渦 獢 獢 㭰 渦 獢 㭰 渦 獢 獢 㭰 渦 獢 㭰 渦 獢 㭰 㭰 渦 獢 㭰 渦 獢 㭰 㭰 渦 獢 㭰 㭰渦 獢 㭰 ㌠⁆ 氦 㭴 〽 渦 獢 㭰 渦 獢 㭰 渦 獢 㭰 渦 渦 獢 㭰 渦 獢 㭰 渦 獢 獢 㭰 渦 獢 㭰 獢 㭰 㭰 渦 獢 渦 獢㭰 渦 獢 㭰 渦 獢 㭰 渦 獢㭰 渦 獢 㭰 渦 獢 㭰 渦 獢 㭰 䔠 㭰 渦 獢 㭰 䘠 ☠ വ☊ 扮 灳 ☻ 灳 ☻ 扮 扮 灳 ☻ 扮 灳 ☻ 扮 灳 ☻ ☻ 扮☻ 扮 灳 ☻ 扮 灳 ☻ 扮 灳 ☻ 扮 灳 ☻ 扮 灳 ☻ 扮 扮 灳 ☻ 扮 ☻ 扮 灳 灳 ※ ⱅ 䘠 朦 㭴 〽 格 湯 楳 桴 潦 汬 睯 湩 潷 歲 桳 敥 桴 慳 敭 瀠 潲 椼 杭 栠 灳 捡 㵥 ㄢ ∵ ∽ 瑨 灴 ⼺ 眯 眮 畦 縯 歡 湩 畢 ㉳㈰瀯 潲 楧 ≦ 愠 楬 湧 ∽ 瑦 • 獶 慰 散 ∽∸ 戠 牯 敤 㵲 〢 • 污 㵴 ∢ 㸠 瀼 䠾 牥 湭 䄠 椠 獵 摥 映 獥 牣 灩 楴 敶 氠 扡汥 潦 慶 楲 畯 潲 獷 牡 獵 摥 映 牯 琠 潷 瘠 牡 汢 獥 潒 ′ 潣 瑮 楡 獮 琠 漠 楴 敶 ഠ 昊 湵 瑣潩 潣 晥 楦 楣 湥 獴 潲 ⁷ ″ 畱 湡 楴 楴 獥 ⠠ 潳 畬 楴 愠 摮 映 湩 污 祬 爠 睯 ഠ 爊 灥 敲 敳 琠 敨 瑳 慲 湩 桔 扯 敪 瑣 癩 畦 据 楴 湯 整 愠 映 牯 ††††† ††††††† ഠ †††† ഠ ††††† †† †††††††††††††††††Тп ㉂ ″ ㉃ 䌪 ″ 湩 䐠 祡 呃 䈨䌤 ㌤ 桷 捩 獩 渦 獢 㭰 湥 整 敲 挠 汥 㕄 ☮ 扮 灳 灳 ☻ 扮 灳 汯 浵 敬 䡌 ⁓ 潣 楡 畭 慬 挠 污慬 整 琠 敨 氠 晥 慨 摮 猠 摩 桴 敲 灳 捥 楴 敶 瑳 慲 湩 獴 㝄 栠 獡 敨 映 牯 畭 慬 㴠 ㍂ 䈪 ⬷ ⨳ 㝃 ⠠ 牯 琠敨 匠 䵕 剐 䑏 䍕 ⁔ 潦 浲 瑥 瑣 晩 礠 畯 眠 楲 敨 映 牯 畭 慬 椠 㝄 扮 灳 ※ 啓 偍 啄 呃 䌮 ⰲ 䈤 䌤 ㌤潹 ⁵ 慣 楳 灭 祬 挠 灯 ⁹ 瑩 汬 㡄 琠 牨 畯 ㄱ 楆 慮 汬 潣 畬 湭 汥 摥 删 午 挠 湯 慴 楒 慨 摮摩 獥 漠 桴 潣 獮 慴 瑮 挠 湯 瑳 慲 湩 獴 ാ 㰊 牨 㸠 瀼 㰾 㹢 晥 湩 湩 桴 牰 扯 桴 癬 牥戯 ‾ 戼 㹲 潙 ⁵ 畭 瑳 搠 桴 牰 扯 敬 潦 潳 癬 牥 戠 ⁹ 摩 湥 湩 敳 敶 慲 ാ 㰊 汵 † 㰠伾 橢 捥 楴 敶 映 湵 瑣 潩 散 㭰 ⠠ 湉 琠 敨 攠 敬 琠 楨 獩 ഠ 挠 汥 † 㰠 楬 圾 敨 桴 畯 愠 敲 洠 浩 穩牯 洠 湩 浩 穩 湩 栨 牥 ⥸ഠ † 㰠 楬 吾 敨 爠 湡 敧 漠 散 潣 瑮 楡 楮 琠 敨 瀠 浥 瘠 牡 慩 ⠠ 散 ❬ 整 浲椠 戼 挾 慨 杮 慶 慶 敬 挾 汥 獬 ⸩ 䤠 桴 † 硥 浡 汰 桴 獩 椠 桴 慲 杮 ㍂⸮㍃ † †† 氼 㹩 潃 牴 楡瑮 䘠 牯 畭 慬 ⴭ 硅 散 潦 浲 灥 敲 敳 瑮 湩 桴 瑦 栠 湡 敤 䰨 景 琠 挠 湯 慲 湩 桴 硥 浡 汰 桴 獩 琠 敨 爠 湡 敧 䐠 ⸷ 䐮 楬 ാ 㰊 甯 㹬 潔 湩 桴 牰 扯 敬 Ɑ 瑳 ഠ 猊 汥 捥 ♴ 扮 㹢 慄 慴 ⼼爠 扩 潢 㱮 㹢 渦 獢 㭰 桴 湥 㰠 㹢 潓 癬 牥 㰠 戯 桴 敭 畮 汩 牢 湩桴 戼 匾 汯 敶 慐 慲 敭 整 戯 搾 慩 潬 潢 䴠 桴 湩 敳 潩 畣 ഠ 㰢 瑳 杮 传 橢 捥 楴 ⼼ 瑳杮 ‾ ††† ∢ 戠 硯 潰 湩 ⁴ 潴 摤 敲 獳 漠 桴 癩 畦 据 楴 湯 ⠠ 桴 獡 琠 敢 愠 映 敲 䐠 ⤵敓 敬 瑣 琠 敨 㰠 㹢 楍 牯 䴠 戯 爾 摡 潩 戠 瑵 潴 硡 栠 牥 ⥥ 敶 琠 敨 牥 湯 挠 牵 㹢 祂 䌠 慨 湩 慖扡 敬 渦 獢 㭰 敃 汬 ⼼ 㹢 潢 湥 整 牯 瀠 楯 桴 慲 景 瘠 汢 獥 ⠠ 敨 敲 䈠 ⸳ 桳 琠 㹢 摁⼼ 㹢 畢 瑴 湯 琠 敧 ⁴ 桴 挠 湯 瑳 慲 湩 ⁴ 楤 污 杯 戠 硯 湅 整 潰 湩 ⁴ 潴 桴 散 汬 慴 湩 湩 䡌⁓ 景 琠 敨 映 物 瑳 挠 湯 瑳 慲 栨 獡 琠 敢 愠 映 慬 ☬ 扮 灳 ※ 敨 敲 䐠 桴 潢 ⁸ 湯 琠 晥 ♴ 扮 灳 潨桴 灡 牰 灯 楲 瑡 潬 楧 慣 瑡 牯 戼 ‾☨ 瑬 㴻 ⰽ 㰠 戯 漾 ⤽ഠ ⠊ 敨 敲 㴻 潭 敶 琠 敨 敨 椠 獮 湯 瀠 楯 瑮 琠 桴 楲 桧 ⁴ 潢 ⁸ 湡 湥 整 摡 敲 獳 漠 桴 ⁓ 景 琠 楨 潣 獮 牴 眠 楨 档 椠 潄 琠 潦 污 潣 獮牴 楡 瑮 祢 渦 獢 㭰 汣 捩 楫 愠 摤 ⼼ 㹢 渦 獢 扡 爠 灥 慥 整 汤 圠 污 潣 獮 牴 瑮 湥 整 敲 汣 捩 戼 伾 ⁋ † ⼼ 㹢 ††††††††††† 㰾 㹢 灓 楴 湡 漠 挠 湯 慲 湩 ⁴瑡 愠 琠 浩 獡 氠 湯 獡 琠 敨 慨 敶 琠 敨 猠 浡 敲 瑣 潩 牯 椠 獮 潹 ⁵ 潣 汵 慨 牥 摥 琠 映 物琠 潷 挠 湯 瑳 慲 湩 ⁴ 潴 敧 桴 湯 灯 牥 瑡 潩 桴 摡 潣 獮 牴 搠 慩 潬 潢 ⁸ 琠 汬 爠 晥 湥 散硯 • 湥 整 㝄 ⸮ 㡄 档 潯 敳 ☠ 㴻 湡 湥 整 潦 獮 牴 楡 瑮 䔠 ⸷ 䔮 ⸸ 潷 汵 慨 敶 歡 楦 獲 ⁴ 睴 潣 獮 牴 楡 瑮 丠 瑯 捩 椠 污 桴 潣 獮 瑮 敷 敲 敨 猠 浡 数 眠 潣 汵 慨 扡 敬 湥 污 桴 潣 獮 牴 楡 瑮 据 䄠 ⁴ 桴 獩 瀠 礠 畯 栠 癡 敤 楦 敮 潭 敤 潦 桴 牥 戼 敨 氠⁴ 桴 湩 潴 搠 獩 琠 档 潯 桴 敓 敬 瑣 匠 杮 䴠 瑥 潨 匢 浩 汰 䰠 ≐ 摮 挠 敨 正 ∠ 湯 瑳 湩 摥ഠ 瘊 牡 慩 汢 獥 丠 湯 中 来 瑡 癩 ≥ 戠 硯 ☮ 扮 灳 ※ 潔 瀠 潲 汢 浥 挠 楬 正 獢 㭰 桴 猼 牴 潓 癬 㱥 猯 湯 㹧††††††††††††† 瑴 湯 潙 ⁵ ⁹ 敧 ⁴ 湯 景 琠 潬 楷 杮 琠 牨 敥 洠 瀯 ാ 㰊 楬 㸠†††††††††††† 楤 ††††††††† 匢 汯 敶 畬 楴 湯汁 潃 獮 楡 瑮 湡 灯 楴 慭 楬 祴 挠 湯 楤 楴 湯 楴 晳 敩 ≤ 渦 獢 牯 慭 整 浲 湩 瑡 瀭 椠 癬 摥 搯 癩ാ 㰠 楬 㸠 †††††††††††† ഠ 楤 㹶 †††††† 挠 畯 摬 渠 湩 猠 汯 瑵 潩 㩮☢ 扮 灳 ※ 敭 湡 桴 牥 獩 攠 敶 湯 敳 ⁴ 污 敵 桷 瑳 楡 晳 桴 潣 獮 楡 普 慥 楳 牰敬 㱭 搯 癩 ാ 㰠 楬 㸠 †††††††††††† 楤 †††††††† 楴 畬 獥 搠 潮 ⁴ 潣 癮 牥 敧 • 敭 湡 桴 楬 業 ⁴ 潴 漠 橢 捥 楴 敶 映 湵 瑣 潩 慶 畬 ⼼ 楤 㹶 ⼼ 楬 甯 㹬 瀼 潲删 灥 牯 獴 㰠 牢 㸠 ⼼ 瑳 潲 杮 桴 癥 湥 ⁴ 景 渠 整 浲 湩 潩 Ɱ 椠 楤 楴 湯 琠 桴 湡 睳 潷 歲 桳 敥 ⁴ 瑩 敳 晬 潓 癬 潲 楶 敤 摡 楤 楴 漠 瑵 異 ⁴ 琠 敨 挠 瑮 瀠 潲 汢 浥 琠 敨 敲 瀠 潲 捸 汥 眠 牯 獫 敨 瑥 潦 楶 猠 癡 湩 牯 瀠 楲 䘠 潲 潓 癬 爠 獥 獴 搠 潬 潢 潯 敳 愠 祮 漠 污 景 琠 敨 琠 牨 敥 爠 灥 牯 愼 栠 敲 㵦 栢 瑴 㩰 晷 摥 慾 楫 据 〲 ⼲ 湡 灪 䄾 ⼼ 㹡 愼 敲 㵦瑴 㩰 ⼯ 睷 晷 摥 ⽵ 慾 楫 〲 ⼲ 敳 獮 樮 杰 獮 瑩 癩 瑩 ⼼ 㹡 愼 㵦 栢 瑴 㩰 ⼯ 睷 ⽵ 慾 戯 獵⼲ 楬 獭 樮 杰 㸢 楌 業 獴 ⼼ 㹡 汣 捩 猼 牴 湯 㹧 潲 ††††††††† ⼼ 瑳 潲 杮 㰾 戯 㹹 ⼼ 瑨汭 ാ
Руководство по решению Excel с пошаговыми примерами
В руководстве объясняется, как добавить и где найти Solver в разных версиях Excel, с 2016 по 2003 год.Пошаговые примеры показывают, как использовать Excel Solver для поиска оптимальных решений для линейного программирования и других проблем.
Всем известно, что Microsoft Excel содержит множество полезных функций и мощных инструментов, которые могут сэкономить вам часы расчетов. Но знаете ли вы, что в нем также есть инструмент, который может помочь вам найти оптимальные решения проблем, связанных с принятием решений?
В этом руководстве мы рассмотрим все основные аспекты надстройки Excel Solver и предоставим пошаговое руководство по ее наиболее эффективному использованию.
Что такое Excel Solver?
Excel Solver принадлежит к специальному набору команд, часто называемому инструментами анализа «что, если». В первую очередь он предназначен для моделирования и оптимизации различных бизнес-моделей и инженерных моделей.
Надстройка Excel Solver особенно полезна для решения задач линейного программирования, так называемых задач линейной оптимизации, и поэтому иногда называется решателем линейного программирования . Кроме того, он может решать гладкие нелинейные и негладкие задачи.Дополнительные сведения см. В разделе «Алгоритмы решения Excel».
Хотя Solver не может решить все возможные проблемы, он действительно полезен при решении всех видов задач оптимизации, когда вам необходимо принять наилучшее решение. Например, он может помочь вам максимизировать возврат инвестиций, выбрать оптимальный бюджет для вашей рекламной кампании, составить оптимальный график работы для ваших сотрудников, минимизировать затраты на доставку и так далее.
Как добавить решатель в Excel
Надстройка Solver включена во все версии Microsoft Excel, начиная с 2003 года, но по умолчанию она не включена.
Чтобы добавить Solver в Excel, выполните следующие действия:
- В Excel 2010 , Excel 2013 , Excel 2016 и Excel 2019 щелкните Файл > Параметры .
В Excel 2007 нажмите кнопку Microsoft Office , а затем щелкните Параметры Excel . - В диалоговом окне Excel Options нажмите Add-Ins на левой боковой панели, убедитесь, что Excel Add-ins выбран в поле Manage внизу окна, и нажмите Go .
- В диалоговом окне Надстройки установите флажок Надстройка Solver и нажмите ОК :
Чтобы получить Решатель на Excel 2003 , перейдите в меню Инструменты и щелкните Надстройки . В списке надстроек доступных установите флажок Solver Add-in и нажмите ОК .
Примечание. Если Excel отображает сообщение о том, что надстройка Solver в настоящее время не установлена на вашем компьютере, щелкните Да , чтобы установить ее.
Где находится решатель в Excel 2019, 2016, 2013, 2010 или 2007?
В современных версиях Excel кнопка Solver отображается на вкладке Data в группе Analysis :
Где находится решатель в Excel 2003?
После загрузки надстройки Solver в Excel 2003 ее команда добавляется в меню инструментов :
Теперь, когда вы знаете, где найти Solver в Excel, откройте новый рабочий лист и приступим!
Примечание. В примерах, обсуждаемых в этом руководстве, используется Решатель в Excel 2013. Если у вас другая версия Excel, снимки экрана могут не совпадать с вашей версией, хотя функциональность Решателя в основном такая же.
Как использовать Solver в Excel
Перед запуском надстройки Excel Solver сформулируйте модель, которую вы хотите решить, на листе. В этом примере давайте найдем решение следующей простой задачи оптимизации.
Проблема . Предположим, вы владелец салона красоты и планируете предоставить своим клиентам новую услугу.Для этого нужно купить новое оборудование стоимостью 40 000 долларов, которое необходимо оплатить в рассрочку в течение 12 месяцев.
Цель : Рассчитать минимальную стоимость услуги, которая позволит вам оплатить новое оборудование в указанные сроки.
Для этой задачи я создал следующую модель:
А теперь давайте посмотрим, как Excel Solver может найти решение этой проблемы.
1. Запустите Excel Solver
На вкладке Data в группе Analysis нажмите кнопку Solver .
2. Определите проблему
Откроется окно параметров решателя , в котором необходимо настроить 3 основных компонента:
- Ячейка объектива
- Переменные ячейки
- Ограничения
Что именно делает Excel Solver с указанными выше параметрами? Он находит оптимальное значение (максимальное, минимальное или заданное) для формулы в ячейке Цель , изменяя значения в ячейках Переменная и с учетом ограничений в ячейках Ограничения .
Цель
Ячейка Цель (ячейка Цель в более ранних версиях Excel) — это ячейка , содержащая формулу , которая представляет цель или цель проблемы. Целью может быть максимальное, минимальное или достижение некоторого целевого значения.
В этом примере целевой ячейкой является B7, в которой срок платежа рассчитывается по формуле = B3 / (B4 * B5) , а результат формулы должен быть равен 12:
Переменные ячейки
Ячейки переменных ( Изменение ячеек или Регулируемые ячейки в более ранних версиях) — это ячейки, которые содержат переменные данные, которые можно изменять для достижения цели.Excel Solver позволяет указать до 200 ячеек переменных.
В этом примере у нас есть пара ячеек, значения которых можно изменять:
- Предполагаемое количество клиентов в месяц (B4), которое должно быть меньше или равно 50; и
- Стоимость услуги (B5), которую мы хотим, чтобы вычислить Excel Solver.
Наконечник. Если переменные ячейки или диапазоны в вашей модели несмежные , выберите первую ячейку или диапазон, а затем нажмите и удерживайте клавишу Ctrl при выборе других ячеек и / или диапазонов.Или введите диапазоны вручную через запятую.
Ограничения
Excel Solver Ограничения — это ограничения или пределы возможных решений проблемы. Другими словами, ограничения — это условия, которые должны выполняться.
Чтобы добавить ограничение (я), выполните следующие действия:
- Нажмите кнопку Добавить справа от поля « с учетом ограничений ».
- В окне Ограничение введите ограничение.
- Нажмите кнопку Добавить , чтобы добавить ограничение в список.
- Продолжайте вводить другие ограничения.
- После того, как вы ввели окончательное ограничение, нажмите OK , чтобы вернуться в главное окно Solver Parameters .
Excel Solver позволяет указать следующие отношения между ячейкой, на которую указывает ссылка, и ограничением.
- Меньше или равно , равно и больше или равно .Вы устанавливаете эти отношения, выбирая ячейку в поле Ссылка на ячейку , выбирая один из следующих знаков: <= , =, или > = , а затем вводя число, ссылку на ячейку / имя ячейки, или формулу в поле Ограничение (см. снимок экрана выше).
- Целое число . Если указанная ячейка должна быть целым числом, выберите int , и слово целое число появится в поле Ограничение .
- Разные значения . Если каждая ячейка в указанном диапазоне должна содержать разные значения, выберите dif , и в поле Constraint появится слово AllDifferent .
- Двоичный . Если вы хотите ограничить указанную ячейку 0 или 1, выберите bin , и двоичное слово появится в поле Constraint .
Примечание. Отношения int , bin и diff могут использоваться только для ограничений ячеек переменных.
Чтобы изменить или удалить существующее ограничение, выполните следующие действия:
- В диалоговом окне Solver Parameters щелкните ограничение.
- Чтобы изменить выбранное ограничение, щелкните Изменить и внесите нужные изменения.
- Чтобы удалить ограничение, нажмите кнопку Удалить .
В этом примере ограничения:
- B3 = 40000 — стоимость нового оборудования 40 000 долларов США.
- B4 <= 50 - количество планируемых пациентов в месяц в возрасте до 50 лет.
3. Решаем проблему
После того, как вы настроили все параметры, нажмите кнопку Solve в нижней части окна Solver Parameters (см. Снимок экрана выше) и позвольте надстройке Excel Solver найти оптимальное решение для вашей проблемы.
В зависимости от сложности модели, памяти компьютера и скорости процессора это может занять несколько секунд, несколько минут или даже несколько часов.
Когда Solver завершит обработку, отобразится диалоговое окно Solver Results , в котором вы выбираете Keep the Solver Solution и нажимаете OK :
Окно Solver Result закроется, и решение сразу же появится на рабочем листе.
В этом примере в ячейке B5 отображается 66,67 доллара, что является минимальной стоимостью услуги, которая позволит вам оплатить новое оборудование в течение 12 месяцев при условии, что в месяц есть не менее 50 клиентов:
- Если программа Excel Solver слишком долго обрабатывала определенную проблему, вы можете прервать процесс, нажав клавишу Esc.Excel пересчитает лист с последними значениями, найденными для ячеек переменной .
- Чтобы получить более подробную информацию о решенной проблеме, щелкните тип отчета в поле Отчеты , а затем щелкните ОК . Отчет будет создан на новом листе:
Теперь, когда у вас есть основное представление о том, как использовать Solver в Excel, давайте подробнее рассмотрим еще пару примеров, которые могут помочь вам лучше понять.
Примеры решения Excel
Ниже вы найдете еще два примера использования надстройки Excel Solver.Сначала мы найдем решение известной головоломки, а затем решим реальную задачу линейного программирования.
Excel Solver, пример 1 (магический квадрат)
Я считаю, что все знакомы с головоломками «магический квадрат», в которых вы должны поместить набор чисел в квадрат так, чтобы все строки, столбцы и диагонали в сумме давали определенное число.
Например, знаете ли вы решение для квадрата 3×3, содержащего числа от 1 до 9, где каждая строка, столбец и диагональ в сумме дают 15?
Вероятно, нет ничего страшного в том, чтобы решить эту головоломку методом проб и ошибок, но я уверен, что Решатель найдет решение быстрее.Наша часть работы — правильно определить проблему.
Для начала введите числа от 1 до 9 в таблицу, состоящую из 3 строк и 3 столбцов. Решателю Excel эти числа на самом деле не нужны, но они помогут нам визуализировать проблему. Что действительно нужно надстройке Excel Solver, так это формулы СУММ, суммирующие каждую строку, столбец и 2 диагонали:
После ввода всех формул запустите Solver и настройте следующие параметры:
- Комплект Объектив .В этом примере нам не нужно устанавливать какую-либо цель, поэтому оставьте это поле пустым.
- Ячейки переменных . Мы хотим заполнить числа в ячейках от B2 до D4, поэтому выберите диапазон B2: D4.
- Ограничения . Должны быть соблюдены следующие условия:
- $ B $ 2: $ D $ 4 = AllDifferent — все ячейки переменных должны содержать разные значения.
- $ B $ 2: $ D $ 4 = целое число — все ячейки переменных должны быть целыми числами.
- $ B $ 5: $ D $ 5 = 15 — сумма значений в каждом столбце должна равняться 15.
- $ E $ 2: $ E $ 4 = 15 — сумма значений в каждой строке должна равняться 15.
- $ B $ 7: $ B $ 8 = 15 — сумма обеих диагоналей должна равняться 15.
Наконец, нажмите кнопку Решить , и решение есть!
Excel Solver, пример 2 (задача линейного программирования)
Это пример простой задачи оптимизации транспортировки с линейной целью. Многие компании используют более сложные модели оптимизации такого типа, чтобы ежегодно экономить тысячи долларов.
Проблема : Вы хотите минимизировать стоимость доставки товаров с 2 разных складов 4 разным покупателям. На каждом складе есть ограниченное предложение, и у каждого покупателя есть определенный спрос.
Цель : Свести к минимуму общую стоимость доставки, не превышая количества, доступного на каждом складе, и удовлетворить потребности каждого клиента.
Исходные данные
Вот как выглядит наша задача по оптимизации перевозок:
Формулировка модели
Чтобы определить нашу задачу линейного программирования для Excel Solver, давайте ответим на 3 основных вопроса:
- Какие решения необходимо принять? Мы хотим рассчитать оптимальное количество товаров для доставки каждому покупателю с каждого склада.Это ячеек переменной (B7: E8).
- Какие ограничения? Запасы, имеющиеся на каждом складе (I7: I8), не могут быть превышены, и количество, заказанное каждым клиентом (B10: E10), должно быть доставлено. Это ограниченных ячеек.
- Какова цель? Минимальная общая стоимость доставки. А это наша ячейка Objective (C12).
Следующее, что вам нужно сделать, это вычислить общее количество, отгруженное с каждого склада (G7: G8), и общее количество товаров, полученных каждым клиентом (B9: E9).Вы можете сделать это с помощью простых формул Sum, показанных на скриншоте ниже. Кроме того, вставьте формулу СУММПРОИЗВ в C12, чтобы рассчитать общую стоимость доставки:
Чтобы упростить понимание нашей модели оптимизации транспортировки, создайте следующие именованные диапазоны:
| Название диапазона | Ячейки | Параметр решателя |
| Отгружено товаров | B7: E8 | Переменные ячейки |
| В наличии | I7: I8 | Ограничение |
| Всего отгружено | G7: G8 | Ограничение |
| Заказано | B10: E10 | Ограничение |
| Всего_получено | B9: E9 | Ограничение |
| Стоимость доставки | C12 | Объектив |
Последнее, что вам осталось сделать, это настроить параметры Excel Solver:
- Цель: Стоимость доставки установлена на Мин.
- Ячейки с переменными: Products_shipped
- Ограничения: Total_received = Заказано и Total_shipped <= Доступно
Обратите внимание, что в этом примере мы выбрали метод решения Simplex LP , потому что мы имеем дело с задачей линейного программирования.Если вы не уверены, что это за проблема, вы можете оставить метод решения GRG Nonlinear по умолчанию. Дополнительные сведения см. В разделе «Алгоритмы решения Excel».
Решение
Нажмите кнопку Solve внизу окна Solver Parameters , и вы получите свой ответ. В этом примере надстройка Excel Solver рассчитала оптимальное количество товаров для доставки каждому покупателю с каждого склада с минимальной общей стоимостью доставки:
Как сохранять и загружать сценарии Excel Solver
При решении определенной модели вы можете захотеть сохранить значения ячейки Variable в качестве сценария, который вы можете просмотреть или повторно использовать позже.
Например, при расчете минимальной стоимости услуги в самом первом примере, обсуждаемом в этом руководстве, вы можете попробовать разное количество прогнозируемых клиентов в месяц и посмотреть, как это повлияет на стоимость услуги. При этом вы можете сохранить наиболее вероятный сценарий, который вы уже рассчитали, и восстановить его в любой момент.
Сохранение сценария Excel Solver сводится к выбору диапазона ячеек для сохранения данных. Загрузка модели Solver — это просто вопрос предоставления Excel диапазона ячеек, в котором сохраняется ваша модель.Подробные инструкции приведены ниже.
Сохранение модели
Чтобы сохранить сценарий Excel Solver, выполните следующие действия:
- Откройте рабочий лист с рассчитанной моделью и запустите Excel Solver.
- В окне параметров решателя нажмите кнопку Загрузить / сохранить .
- Excel Solver сообщит вам, сколько ячеек необходимо для сохранения вашего сценария. Выделите столько пустых ячеек и нажмите Сохранить :
- Excel сохранит вашу текущую модель, которая может выглядеть примерно так:
В то же время появится окно Solver Parameters , где вы можете изменить свои ограничения и попробовать разные варианты «что, если».
Загрузка сохраненной модели
Когда вы решите восстановить сохраненный сценарий, сделайте следующее:
- В окне параметров решателя нажмите кнопку Загрузить / сохранить .
- На листе выберите диапазон ячеек, содержащих сохраненную модель, и щелкните Загрузить :
- В диалоговом окне Загрузить модель нажмите кнопку Заменить :
- Откроется главное окно Excel Solver с параметрами ранее сохраненной модели.Все, что вам нужно сделать, это нажать кнопку Решить , чтобы пересчитать его.
Алгоритмы решателя Excel
При определении проблемы для Excel Solver вы можете выбрать один из следующих методов в раскрывающемся списке Выберите метод решения :
- ГРГ Нелинейный. Обобщенный нелинейный алгоритм с редуцированным градиентом используется для задач, которые являются гладкими нелинейными, то есть в которых по крайней мере одно из ограничений является гладкой нелинейной функцией переменных решения.Более подробную информацию можно найти здесь.
- LP Simplex . Метод Simplex LP Solving основан на алгоритме Simplex, созданном американским ученым-математиком Джорджем Данцигом. Он используется для решения так называемых задач Linear Programming — математических моделей, требования которых характеризуются линейными отношениями, т.е. состоят из единственной цели, представленной линейным уравнением, которое должно быть максимизировано или минимизировано. Для получения дополнительной информации посетите эту страницу.
- Эволюционный . Он используется для негладких задач, которые являются наиболее сложным типом задач оптимизации для решения, поскольку некоторые функции негладкие или даже прерывистые, и поэтому трудно определить направление, в котором функция увеличивается или уменьшается. Для получения дополнительной информации посетите эту страницу.
Чтобы изменить способ поиска решения, нажмите кнопку Options в диалоговом окне Solver Parameters и настройте любые или все параметры на вкладках GRG Nonlinear , All Methods и Evolutionary .
Вот как вы можете использовать Solver в Excel, чтобы найти наилучшие решения для ваших проблем принятия решений. А теперь вы можете загрузить примеры решения Excel, обсуждаемые в этом руководстве, и перепроектировать их для лучшего понимания. Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе.

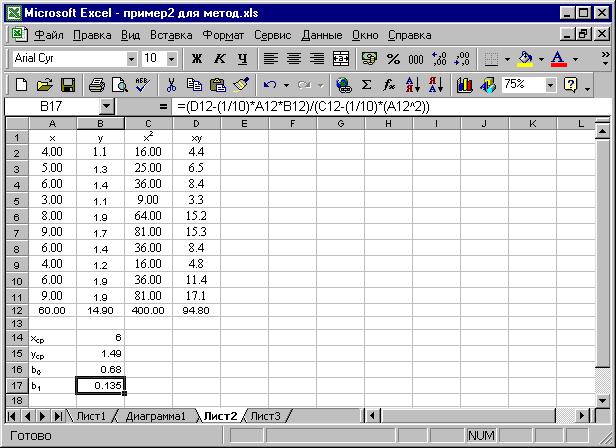

 -384с.
-384с. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СИМПЛЕКСНОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ Л.П.
Методичка, описание решения (скачать 2 документа Word в RAR-архиве — 50кб)
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СИМПЛЕКСНОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ Л.П.
Методичка, описание решения (скачать 2 документа Word в RAR-архиве — 50кб)