Сборник примеров подробных решений по симплекс-методу
Классификацию решения задач линейного программирования можно представить в виде следующей схемы.| Метод решения | Примечание | Целевая функция |
| 1. Графический метод | Используется при двух переменных (x1, x2) | max, min |
| 2. Симплексный метод | Формы записи: симплексная таблица, строчечная форма, строковая форма. Алгоритм решения: метод искусственного базиса (М-метод, двухфазный метод), правило прямоугольника, правило Креко | max, min |
| 3. Двойственный симплекс-метод | Формы записи: симплексная таблица, строчечная форма, строковая форма. Алгоритм решения: метод искусственного базиса (М-метод, двухфазный метод) | min |
| 4. Двойственная задача | Алгоритм решения: симплекс-метод, теоремы двойственности | max, min |
5. Метод Гомори Метод Гомори | Алгоритм решения: метод отсечений | max, min |
Прежде чем решать ЗЛП, необходимо ознакомится с материалом Как привести задачу линейного программирования к канонической форме и Как привести каноническую задачу линейного программирования к стандартной форме.
Ниже представлены примеры решения задач линейного программирования.
Линейное программирование. Решение задач графическим способом
- Как решать графическим способом. Применение графического способа при трех и более переменных
- Графический анализ чувствительности
- Анализ эффективности оптимального решения задачи графическим методом
Симплексный метод решения задач линейного программирования
- Метод искусственного базиса
- Задача оптимального производства продукции
- Пример решения симлекс-методом
Решить следующую задачу ЛП в неканонической форме симплекс-методом:
f(x) = x1 – x2 – 3x3 → min - М-метод.
 Решить задачу М-задачу.
Решить задачу М-задачу.
- Пример нахождения максимума функции симплексным методом
- Пример нахождения минимума функции симплексным методом
- Пример решения модифицированным симплекс-методом
- Пример решения симплекс-методом в столбцовой форме записи
- Симплекс-метод в строчечной форме записи. Пример решения
- Пример решения задачи симплексным методом в Excel
- Линейное программирование в Excel
Решение двойственной задачи линейного программирования
- Двойственная задача ЛП
Необходимо выполнить в указанном порядке следующие задания.
1. Найти оптимальный план прямой задачи:
а) графическим методом;
б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
- Двойственная задача в Excel
- Оценка целесообразности выпуска новой продукции
Двойственный симплекс-метод
- Алгоритм двойственного симплекс-метода. Подробный пример решения Р-методом
Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.
Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика, совмещаются с логически обоснованным пониманием сущности изучаемого явления.
Методом линейного программирования решается транспортная задача, т.е. задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.
см. также Решение задач по ЭММ
Лекции по линейному программированию
Симплекс-метод, примеры решения задач
Здесь приведено ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач симплекс-методом. Первая задача содержит знаки неравенства только » ≤ » (задача с начальным базисом), вторая может содержить знаки » ≥ «, » ≤ » или » = » (задача с искусственным базисом), они решаются по разному.
1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений » ≤ «).
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:
Эта система является
системой с базисом (базис s1,
s2,
s3,
каждая из них входит только в одно
уравнение системы с коэффициентом 1),
x1 и x2 — свободные переменные. Задачи, при
решении которых применяется симплекс-метод,
должны обладать следующими двумя
свойствами:
-система ограничений
должна быть системой уравнений с
базисом;
-свободные члены всех уравнений
в системе должны быть неотрицательны.
Задачи, при
решении которых применяется симплекс-метод,
должны обладать следующими двумя
свойствами:
-система ограничений
должна быть системой уравнений с
базисом;
-свободные члены всех уравнений
в системе должны быть неотрицательны.
Полученная система — система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0) для решения задачи на симплекс-метод, т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь «БП» означает столбец базисных переменных, «Решение» — столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.
симплекс-метод итерация 0
БП | x | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | -6 | 0 | 0 | 0 | 0 | — |
s1 | 2 | 1 | 1 | 0 | 0 | 64 | 64/1=64 |
s2 | 1 | 3 | 0 | 1 | 0 | 72 | 72/3=24 |
s3 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Для улучшения решения
перейдем к следующей итерации симплекс-метода,
получим следующую симплекс-таблицу.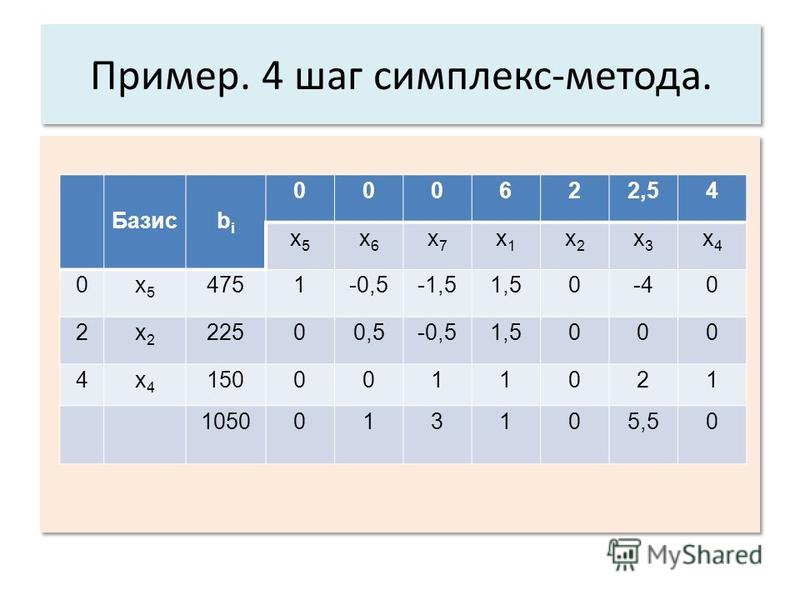 Для этого надо выбрать разрешающий
столбец, т.е.
переменную, которая войдет в базис на
следующей итерации симплекс-метода. Он
выбирается по наибольшему по модулю
отрицательному коэффициенту в z-строке
(в задаче на максимум) – в начальной
итерации симплекс-метода это столбец
x2 (коэффициент -6).
Для этого надо выбрать разрешающий
столбец, т.е.
переменную, которая войдет в базис на
следующей итерации симплекс-метода. Он
выбирается по наибольшему по модулю
отрицательному коэффициенту в z-строке
(в задаче на максимум) – в начальной
итерации симплекс-метода это столбец
x2 (коэффициент -6).
Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца «Решение» к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s 3 (коэффициент 20).
Разрешающий элемент находится на пересечении разрешающего
столбца и разрешающей строки, его ячейка
выделена цветом, он равен 1. Следовательно,
на следующей итерации симплекс-метода
переменная x2 заменит в базисе s1.
Заметим, что в z-строке отношение не
ищется, там ставится прочерк » — «.
В случае если есть одинаковые минимальные
отношения, то выбирается любое из них.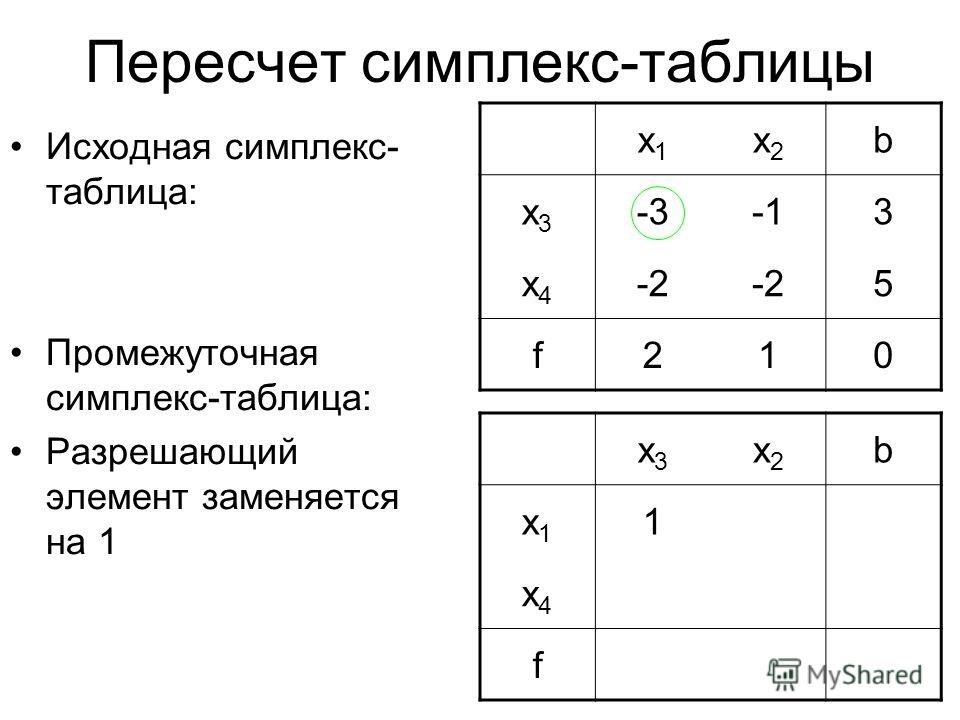 Если в разрешающем
столбце все коэффициенты меньше или
равны 0, то решение задачи бесконечно.
Если в разрешающем
столбце все коэффициенты меньше или
равны 0, то решение задачи бесконечно.
Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований — превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).
1)Вычисление строки х2
2) Вычисление z-строки
таблицы «Итерация 1». На месте -6
в первой строке (z-строке) в столбце х2 таблицы «Итерация 0» должен быть 0
в первой строке таблицы «Итерация
1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1
0 0 1 20 умножим на 6, получим 0 6
0 0 6 120 и сложим эту строку с первой строкой
(z — строкой) таблицы «Итерация 0» -4
-6
0 0 0 0, получим -4 0
0 0 6 120. В столбце x2 появился ноль
0, цель
достигнута. Элементы разрешающего
столбца х2 выделены красным цветом.
На месте -6
в первой строке (z-строке) в столбце х2 таблицы «Итерация 0» должен быть 0
в первой строке таблицы «Итерация
1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1
0 0 1 20 умножим на 6, получим 0 6
0 0 6 120 и сложим эту строку с первой строкой
(z — строкой) таблицы «Итерация 0» -4
-6
0 0 0 0, получим -4 0
0 0 6 120. В столбце x2 появился ноль
0, цель
достигнута. Элементы разрешающего
столбца х2 выделены красным цветом.
3) Вычисление строки s1 таблицы «Итерация 1». На месте 1 в s1 строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х2 получен необходимый 0.
4) Вычисление строки
s2 таблицы «Итерация 1». На месте 3
в s2 строке таблицы «Итерация 0» должен
быть 0 в таблице «Итерация 1». Для
этого все элементы строки х2 таблицы «Итерация 1» 0 1
0 0 1 20 умножим на -3, получим 0 -3
0 0 -3 -60 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 1 3 0
1 0 72, получим строку 1 0
0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице «Итерация 1» стал единичным,
он содержит одну 1 и остальные 0.
Для
этого все элементы строки х2 таблицы «Итерация 1» 0 1
0 0 1 20 умножим на -3, получим 0 -3
0 0 -3 -60 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 1 3 0
1 0 72, получим строку 1 0
0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице «Итерация 1» стал единичным,
он содержит одну 1 и остальные 0.
Строки таблицы «Итерация 1» получаем по следующему правилу:
Новая строка = Старая строка – (Коэффициент разрешающего столбца старой строки)*(Новая разрешающая строка).
Например для z-строки имеем:
Старая z-строка (-4 -6 0 0 0 0) -(-6)*Новая разрешающая строка -(0 -6 0 0 -6 -120) =Новая z-строка (-4 0 0 0 6 120).
Для следующих таблиц пересчет элементов таблицы делается аналогично, поэтому мы его опускаем.
симплекс-метод итерация 1
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | 0 | 0 | 0 | 6 | 120 | — |
s1 | 2 | 0 | 1 | 0 | -1 | 44 | 44/2=22 |
s2 | 1 | 0 | 0 | 1 | -3 | 12 | 12/1=12 |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | — |
Разрешающий столбец
х1,
разрешающая строка s2,
s2 выходит из базиса, х1 входит в базис. Совершенно аналогично
получим остальные симплекс-таблицы,
пока не будет получена таблица со всеми
положительными коэффициентами в
z-строке. Это признак оптимальной таблицы.
Совершенно аналогично
получим остальные симплекс-таблицы,
пока не будет получена таблица со всеми
положительными коэффициентами в
z-строке. Это признак оптимальной таблицы.
симплекс-метод итерация 2
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 0 | 4 | -6 | 168 | — |
s1 | 0 | 0 | 1 | -2 | 5 | 20 | 20/5=4 |
x1 | 1 | 0 | 0 | 1 | -3 | 12 | — |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Разрешающий столбец
s3,
разрешающая строка s1,
s1 выходит из базиса, s3 входит в базис.
симплекс-метод итерация 3
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 6/5 | 8/5 | 0 | 192 | — |
s3 | 0 | 0 | 1/5 | -2/5 | 1 | 4 | — |
x1 | 1 | 0 | 3/5 | -1/5 | 0 | 24 | — |
x2 | 0 | 1 | -1/5 | 2/5 | 0 | 16 | — |
В z-строке все
коэффициенты неотрицательны, следовательно,
получено оптимальное решение x1 = 24, x2 = 16, zmax = 192.
Пример стандартного симплексного метода
|
|
|
|
|
|
| См. шаги 3,4,5 из . СИМПЛЕКСНЫЙ МЕТОД как вы обращаетесь с ИНДИКАТОРАМИ, СООТНОШЕНИЯ и ПОВОРОТКИ. |
|
|
|
|
|
|   |
| Все индикаторы {0, 0, | 49 16 | , 0, | 1 16 | а также | 3 8 | } теперь равны нулю или больше («13» НЕ показатель). |
| Таким образом, как и в шаге 8 СИМПЛЕКСНОГО МЕТОДА, последняя таблица является ОКОНЧАТЕЛЬНОЙ ТАБЛИЦЕЙ. | ||||||
| Выполняются рядовые операции СИМПЛЕКСНОГО МЕТОДА. |
|
|
Пример симплексного метода, шаг за шагом
Пример 1. Решение задачи линейного программирования с использованием симплекс-метода.
Нахождение максимального значения функции
Это решение было сделано с помощью калькулятора, представленного на сайте.
Пример 2. Нахождение минимального значения функции
Пример 3. Нахождение максимального значения функции (искусственные переменные)
Пример 4. Нахождение минимального значения функции (искусственные переменные)
Нахождение минимального значения функции (искусственные переменные)
Пример 5. Решение не только один
Пример 6. Функция неограниченно возрастает
Пример 7. Функция неограниченно убывает
Пример 8. Область допустимых решений — пустое множество
Задача:
Найти максимальное значение функции
| F | = | 3 | x 1 | + | 4 | x 2 |
. 1
Решение:
1. Это необходимое условие решения задачи:
Это необходимое условие решения задачи:
числа в правых частях системы ограничений должны быть неотрицательны.
Это условие выполнено.
2. Это необходимое условие решения задачи:
все ограничения должны быть уравнениями.
| x 1 | + | x 2 | ≤ | 55 | ||||
| 2 | x 1 | + | 3 | x 2 | ≤ | 120 | ||
| 12 | x 1 | + | 30 | x 2 | ≤ | 960 |
| x 1 | + | x 2 | + | S 1 | = | 55 | |||||||||||
| 2 | x 1 | + | 3 | x 2 | + | S 2 | = | 120 | |||||||||
| 12 | x 1 | + | 30 | x 2 | + | S 3 | = | 960 |
S 1 ≥ 0, S 2 ≥ 0, S 3 ≥ 0. Введенные переменные S 1 , S 2 , S 3 называются резервными переменными.
Введенные переменные S 1 , S 2 , S 3 называются резервными переменными.
3. Нахождение начального базиса и значения функции F, соответствующего найденному начальному базису.
Что такое базис?
Переменная называется основной переменной уравнения, если она входит в это уравнение с коэффициентом, равным единице, и не входит в другую систему уравнений (при условии, что в правой части уравнения стоит неотрицательное число).
Если в каждом уравнении есть базисная переменная, то говорят, что система имеет базис.
Переменные, не являющиеся базовыми, называются небазовыми.
В чем суть симплекс-метода?
Каждому основанию соответствует одно значение функции. Одно из них является максимальным значением функции F.
Мы будем двигаться от одной базы к другой.
Следующий базис будет выбран таким образом, чтобы значение функции F было не меньше, чем мы имеем сейчас.
Очевидно, что количество возможных оснований для любой задачи не очень велико.
Так что рано или поздно ответ будет получен.
Как мы будем переходить от одного базиса к другому?
Решение удобнее записывать в виде таблиц. Каждая строка таблицы эквивалентна системному уравнению. Выделенная строка состоит из коэффициентов функции (см. таблицу ниже). Это позволяет нам не переписывать переменные каждый раз. Это экономит время.
В выделенной строке выбираем максимальный положительный коэффициент (мы можем выбрать любой положительный коэффициент).
Это необходимо для того, чтобы получить значение функции F не меньше, чем у нас.
Колонка выбрана.
Для положительных коэффициентов выбранного столбца считаем коэффициент Θ и выбираем минимальное значение.
Это необходимо для того, чтобы получить неотрицательные числа в правой части уравнений после перехода на другой базис.
Строка выбрана.
Найден элемент, который будет основным. Далее нам нужно будет произвести расчет.
Есть ли у нашей системы основа?
| x 1 | + | x 2 | + | S 1 | = | 55 | |||||||||||
| 2 | x 1 | + | 3 | x 2 | + | S 2 | = | 120 | |||||||||
| 12 | x 1 | + | 30 | х 2 | + | S 3 | = | 960 |
В нашей системе есть основа. Мы можем приступить к решению нашей проблемы.
Мы можем приступить к решению нашей проблемы.
| F | = | 3 | x 1 | + | 4 | x 2 |
non-basic ariables is zero. В уме мы можем найти значения основных переменных. (см. систему)
Функция F содержит только неосновные переменные. Поэтому значение функции F для этого базиса можно найти в уме.
| x 1 = 0 x 2 = 0 S 1 = 55 S 2 = 120 S 1 3 = 120 S 3 | => F = 0 |
Исходная база найдена. Найдено значение функции F, соответствующее исходному базису.
4. Нахождение максимального значения функции F.
Шаг 1
| х 1 | х 2 | S 1 | S 2 | S 3 | конст. | Θ |
| 1 | 1 | 1 | 0 | 0 | 55 | 55 : 1 = 55 |
| 2 | 3 | 0 | 1 | 0 | 120 | 120 : 2 = 60 |
| 12 | 30 | 0 | 0 | 1 | 960 | 960 : 12 = 80 |
| 3 | 4 | 0 | 0 | 0 | F — 0 | |
| 1 | 1 | 1 | 0 | 0 | 55 | |
| 0 | 1 | -2 | 1 | 0 | 10 | |
| 0 | 18 | |||||
| 0 | 18 | |||||
| 0 | 3 18||||||
| 0 | 3 180010-12 | 0 | 1 | 300 | ||
| 0 | 1 | -3 | 0 | 0 | F -165 | 0 | F -165 | 0 | F -165 |
 В уме мы можем найти значения основных переменных. (см. таблицу)
В уме мы можем найти значения основных переменных. (см. таблицу) Функция F содержит только неосновные переменные. Поэтому значение функции F для этого базиса можно найти в уме. (см. выделенную строку в таблице)
| x 2 = 0 S 1 = 0 x 1 = 55 S 2 = 10 S 3 930071 = 0 => F — 165 = 0 => F = 165 | |
Шаг 2
| x 1 | x 2 | S 1 | S 2 | S 3 | Const. | Θ | |||
| 1 | 1 | 1 | 0 | 0 | 55 | 55 : 1 = 55 | |||
| 0 | 1 | -2 | 1 | 0 | 10 | 10 : 1 = 10 | |||
| 0 | 18 | -12 | 0 | 1 | 300 | 300: 18 {0003 0 | 0 | F — 165 | |
| 1 | 0 | 3 | -1 | 0 | 45 | ||||
| 0 | 1 | -2 | 1 | 0 | 10 | ||||
| 0 | 0 | 24 | -18 | 1 | 120 | ||||
| 0 | 0 | 9001-19||||||||
| 0 | 0 | 9000 -1||||||||
| 0 | 0 | ||||||||
| 0 | 010 | -1 | 0 | F — 175 |
Неосновные переменные равны нулю.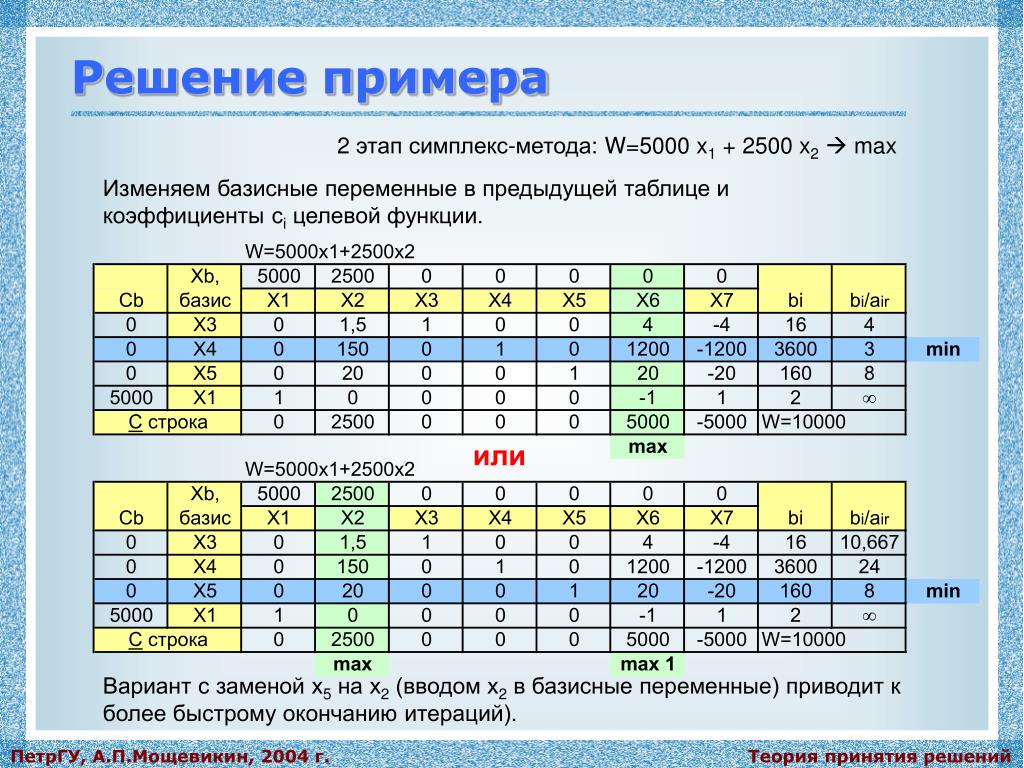

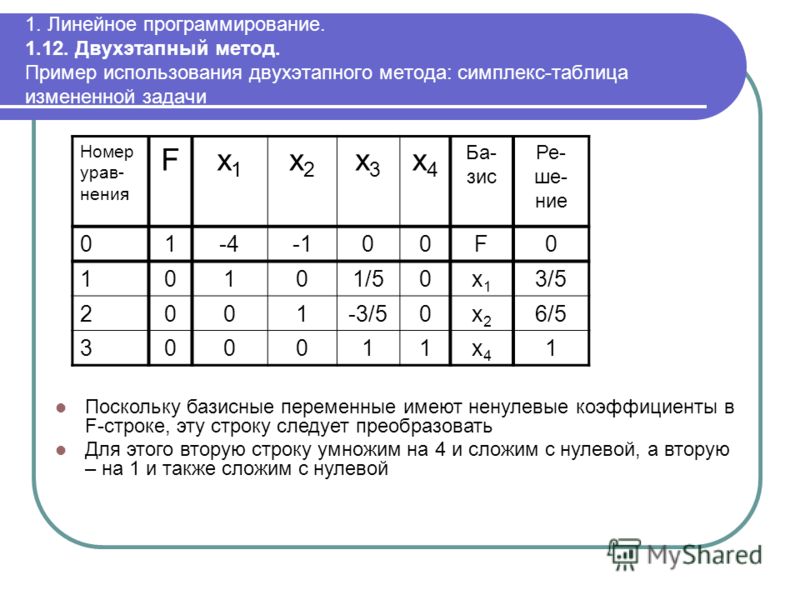 Решить задачу М-задачу.
Решить задачу М-задачу.
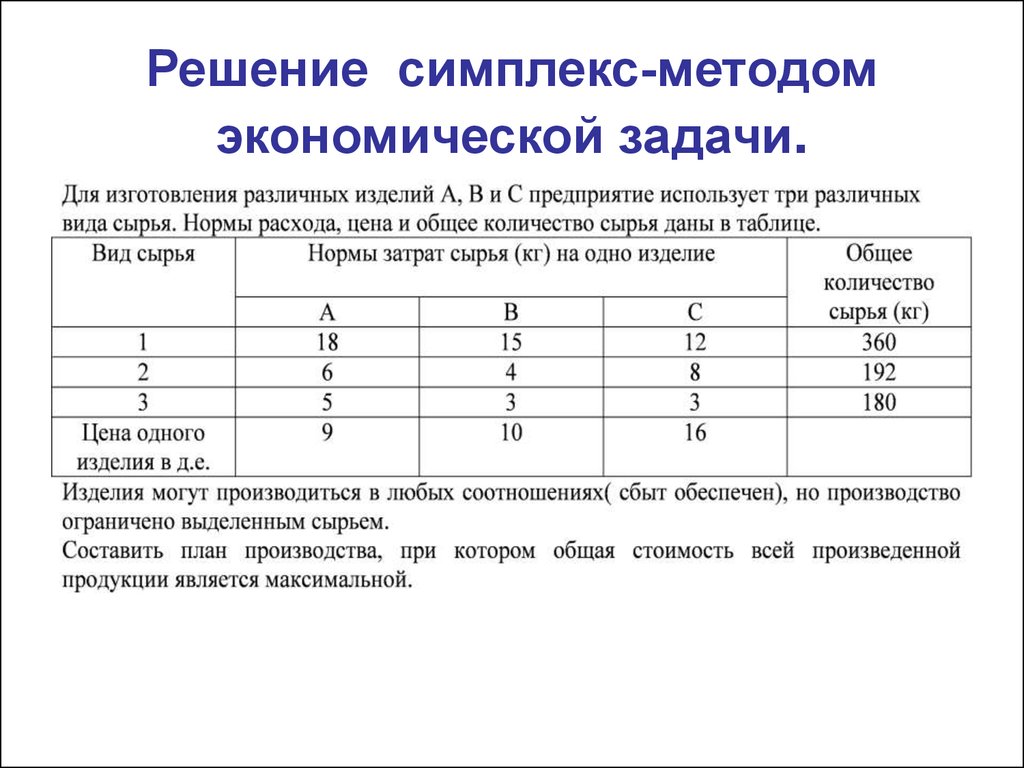

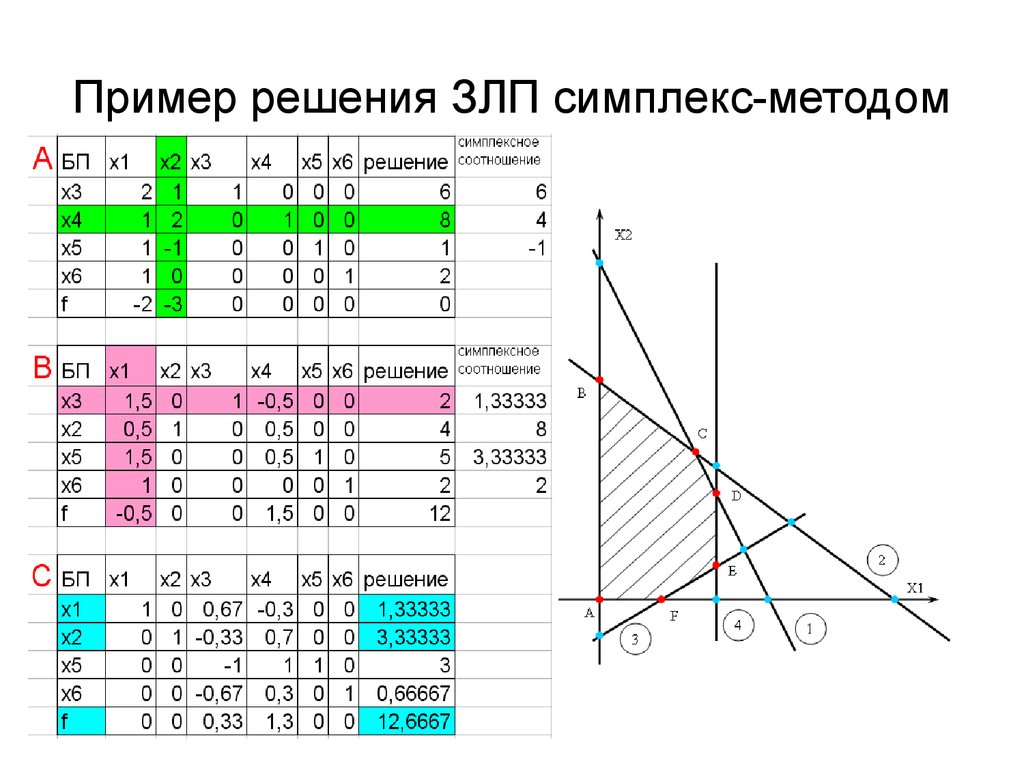 Справа — результат
заключительные 3 операции ряда. «ISM» выделено
Справа — результат
заключительные 3 операции ряда. «ISM» выделено Столбцы
финальной таблицы имеют переменные теги.
Столбцы
финальной таблицы имеют переменные теги.