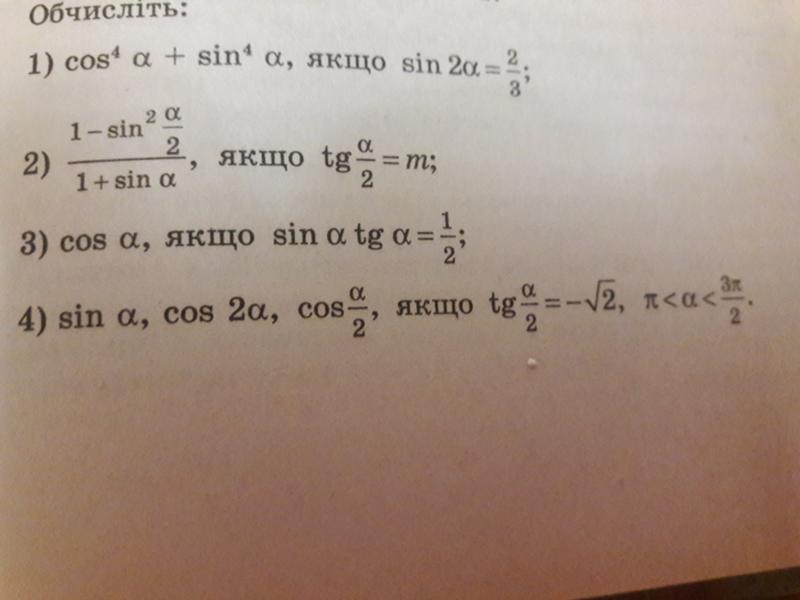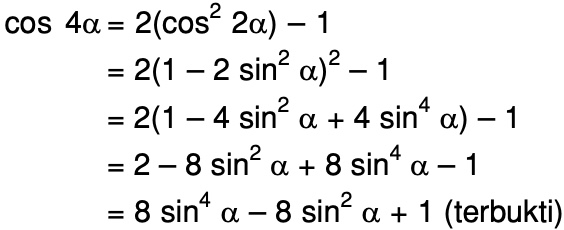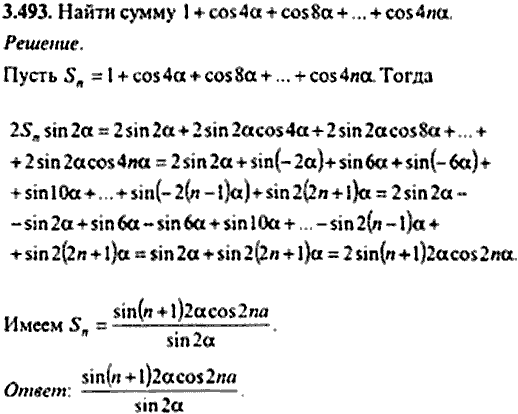| 1 | Найти точное значение | sin(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найти точное значение | sin(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти точное значение | sin(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найти точное значение | sin(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найти точное значение | tan(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найти точное значение | arcsin(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти точное значение | sin(pi/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | cos(pi/4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найти точное значение | sin(45 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти точное значение | sin(pi/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти точное значение | arctan(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найти точное значение | cos(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найти точное значение | cos(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найти точное значение | tan(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найти точное значение | csc(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | tan(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найти точное значение | sec(30 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найти точное значение | cos(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найти точное значение | cos(150) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найти точное значение | sin(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найти точное значение | cos(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти точное значение | tan(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найти точное значение | csc(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найти точное значение | sec(45 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найти точное значение | csc(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найти точное значение | sin(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найти точное значение | sin(120) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найти точное значение | cos(90) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Преобразовать из радианов в градусы | pi/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найти точное значение | tan(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Преобразовать из градусов в радианы | 45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | Найти точное значение | cos(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Преобразовать из радианов в градусы | pi/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найти точное значение | cot(30 град.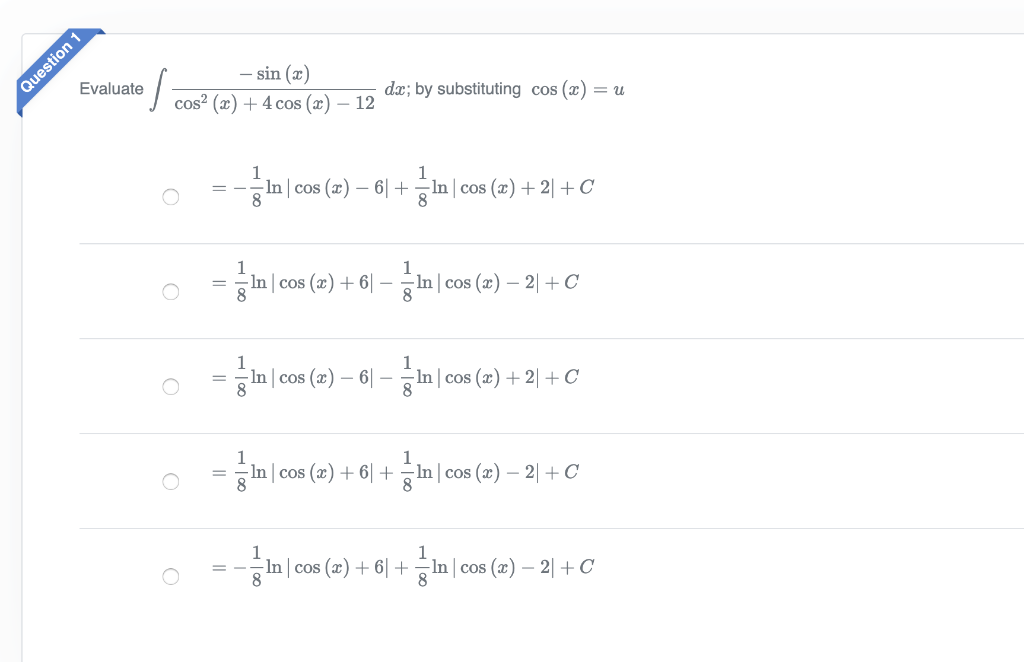 ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найти точное значение | arccos(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | arctan(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найти точное значение | cot(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразовать из градусов в радианы | 30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найти точное значение | sin((5pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найти точное значение | sin((3pi)/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Найти точное значение | tan(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найти точное значение | sin(300) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найти точное значение | cos(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найти точное значение | cos(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | Найти точное значение | cos(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | Найти точное значение | cos(135) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | Найти точное значение | cos((5pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | Найти точное значение | cos(210) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | Найти точное значение | sec(60 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | Найти точное значение | sin(300 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | Преобразовать из градусов в радианы | 135 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 | Преобразовать из градусов в радианы | 150 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | Преобразовать из градусов в радианы | 89 град. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | Преобразовать из градусов в радианы | 60 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найти точное значение | sin(135 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Найти точное значение | sin(150) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | Найти точное значение | sin(240 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | Найти точное значение | cot(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | Найти точное значение | sin(225) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Найти точное значение | sin(240) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | Найти точное значение | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Найти точное значение | tan(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Вычислить | sin(30 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Найти точное значение | sec(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Найти точное значение | cos((5pi)/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Найти точное значение | csc(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | Найти точное значение | tan((5pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | Найти точное значение | tan(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | Вычислить | sin(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | Найти точное значение | sin((7pi)/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Найти точное значение | arcsin(-1/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | Найти точное значение | sin((4pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | Найти точное значение | csc(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | Упростить | arctan( квадратный корень из 3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | Найти точное значение | sin(135) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найти точное значение | sin(105) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | Найти точное значение | sin(150 град.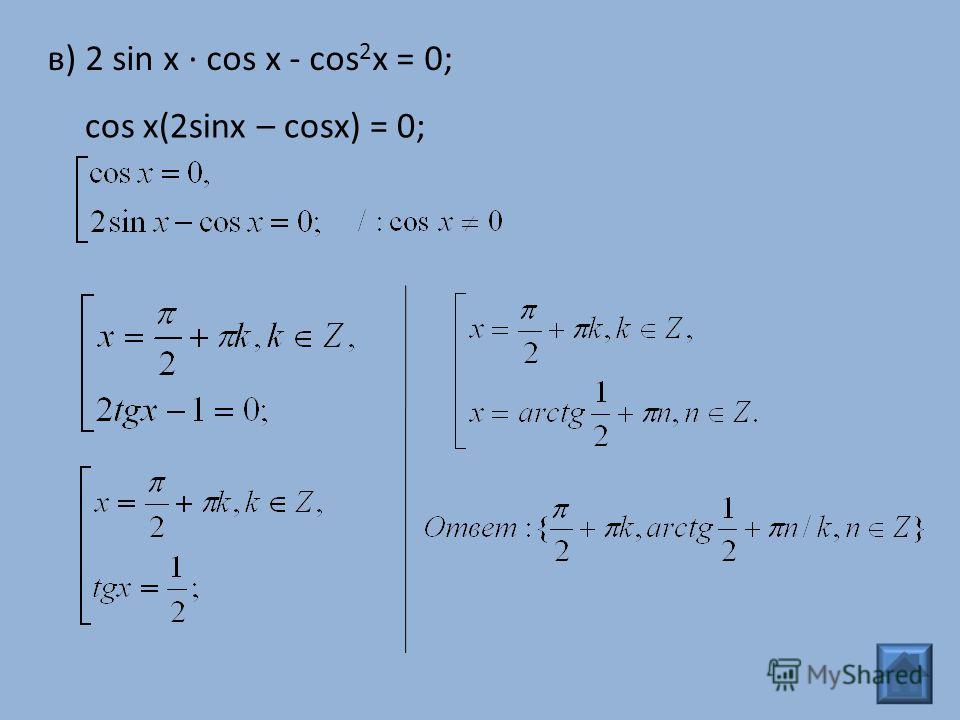 ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | Найти точное значение | sin((2pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | Найти точное значение | tan((2pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | Преобразовать из радианов в градусы | pi/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | Найти точное значение | sin(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | Найти точное значение | sec(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | Найти точное значение | cos((5pi)/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | Найти точное значение | cos((7pi)/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | Найти точное значение | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | Найти точное значение | sin(120 град. 4a+cos2a. … 4a+cos2a. … | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
2sin^2x+cos4x=0
помогите решить 5x^2+1=0
Русский язык, сохраняя свою уникальность и своеобразие на протяжении громадного пространства и длительного времени, вобрал в себя славянское
Построить график функции y=2x-2 и определить проходит ли график через точку:A(10;-20)
Решено
Точка движется в плоскости XOY. Вектор ŕ, модуль которого равен 1м, направлен под углом 30° к оси X. Чему равны проекции вектора ŕ на оси X и Y?
Помогите пожалуйста! Важно само решение, а не ответ.
Вектор ŕ, модуль которого равен 1м, направлен под углом 30° к оси X. Чему равны проекции вектора ŕ на оси X и Y?
Помогите пожалуйста! Важно само решение, а не ответ.
Пользуйтесь нашим приложением
Объясните существуют ли углы альфа и бета для которых tgb sin 4a cos 4a
Обновлено: 27.09.2022
1. У 1. Упростите выражение: 1)-u-(h-u)+(-h-u)-(-h)+h-u-(h-u)+(-h-u)-(-h)+h 2) v-(v-d)+(-d+v)-(-d)-dv-(v-d)+(-d+v)-(-d 2. Упростите сумму выражений: 1 … ) 5,6+d5,6+d и-0,3-d-0,3-d 2) 7,4-у7,4-уи у-5,1у-5,1
1)Произведение четырех и логарифма двадцати семи по основанию одна третья 2)Сумма логарифма нуля целых четырех десятых по основанию два и логарифма ну … ля целых пяти десятых по основанию два и логарифма ста шестидесяти по основанию два 3)Произведение минус единицы и логарифма тридцати двух по основанию нуль целых пять десятых 4)Произведение нуля целых пяти десятых и логарифма шестисот двадцати пяти по основанию нуль целых две десятых 5)Сумма произведения минус трех и логарифма девяти по основанию три и произведения десяти и логарифма тридцати двух по основанию два 6) Произведение двух и логарифма шестидесяти четырех по основанию одна четвертая 7) Разность произведения двух и логарифма восьми по основанию два и произведения четырех и логарифма двадцати пяти по основанию пять
Вы уже наверняка знаете, что тождественный — это равный.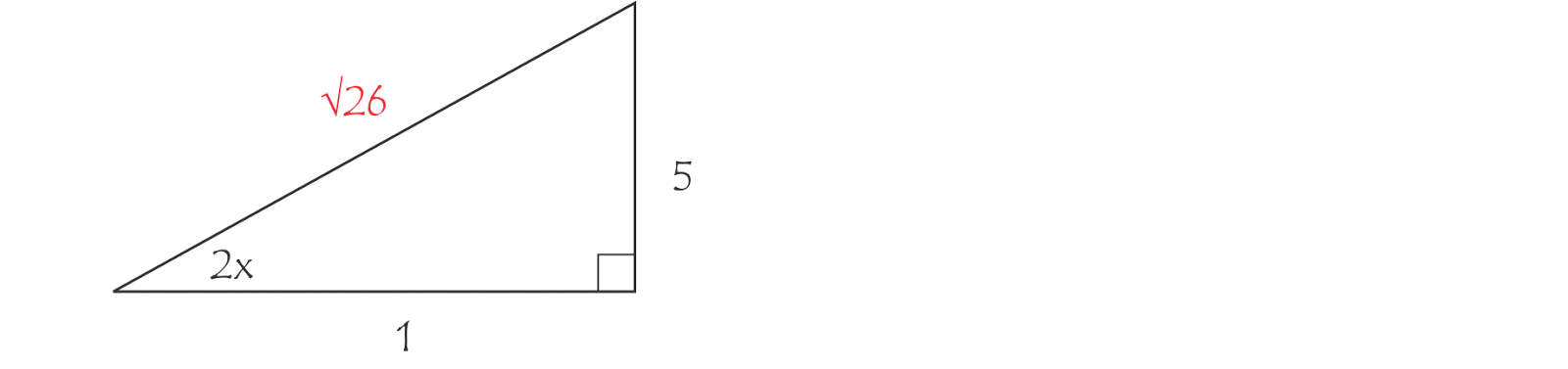
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Взаимно обратные числа — это два числа, произведение которых равно 1.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
- Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α = . - Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.

- А тригонометрическое тождество 1 + ctg 2 α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
-
Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Задачка 2.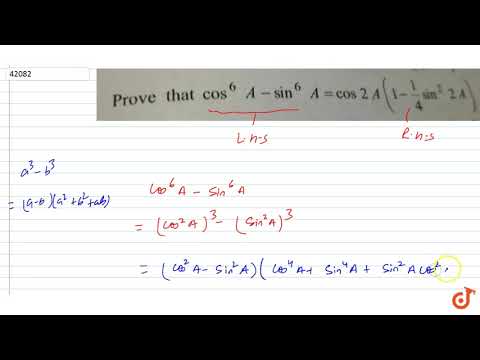 Найдите значение cos α,
Найдите значение cos α,
если:
-
Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.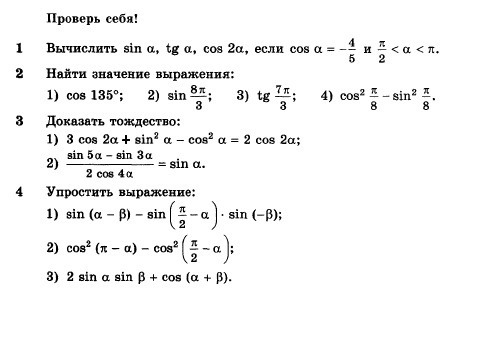
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.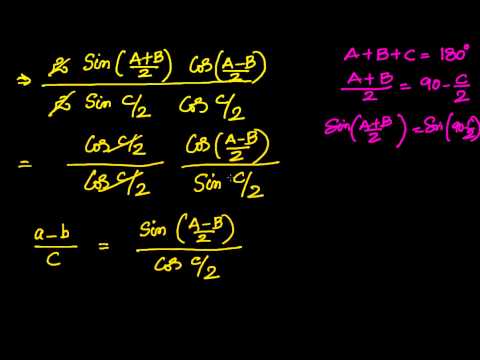
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.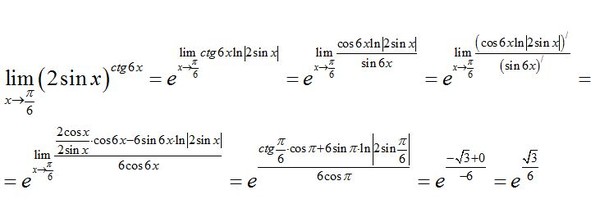
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Читайте также:
- Киберпанк перенесли на 22 апреля
- Какие раскраски работают без интернета
- Black desert mobile доспехи опустошения
- Dead by daylight красные символы
- Джин фразы лига легенд
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | 94(а))-sin(2π-a)+1 | Wyzant Спросите эксперта

 09.17
09.17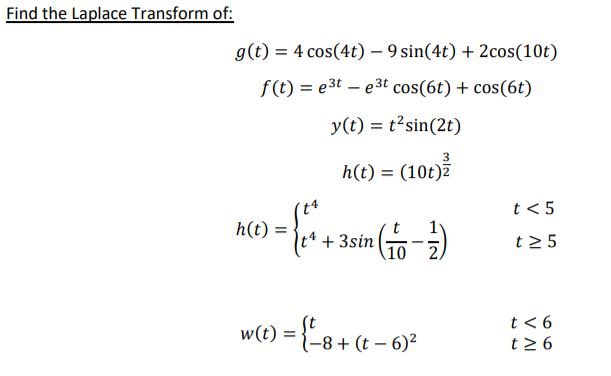 2a+cos2a = 19-cos2a+cos2a = 19 — ответ.
2a+cos2a = 19-cos2a+cos2a = 19 — ответ. 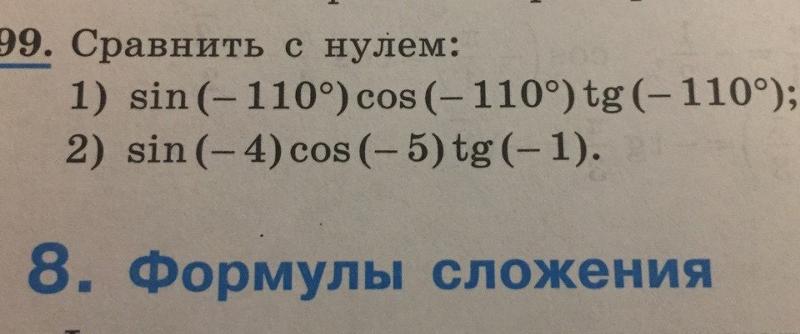
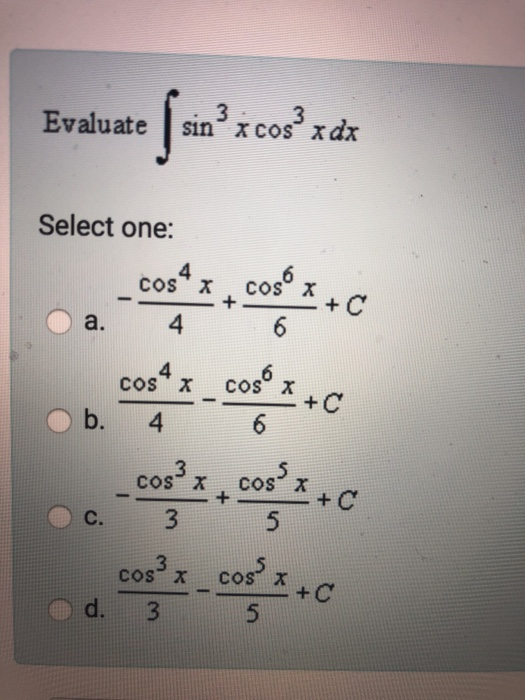


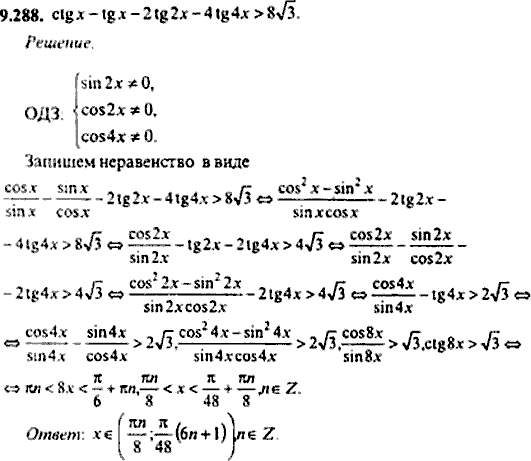 ответил 30.09.19
ответил 30.09.19
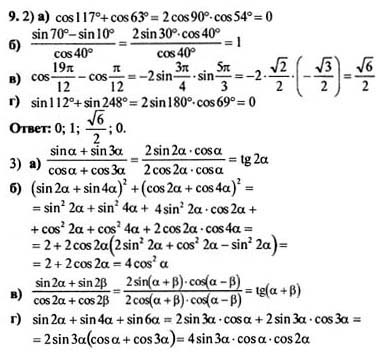
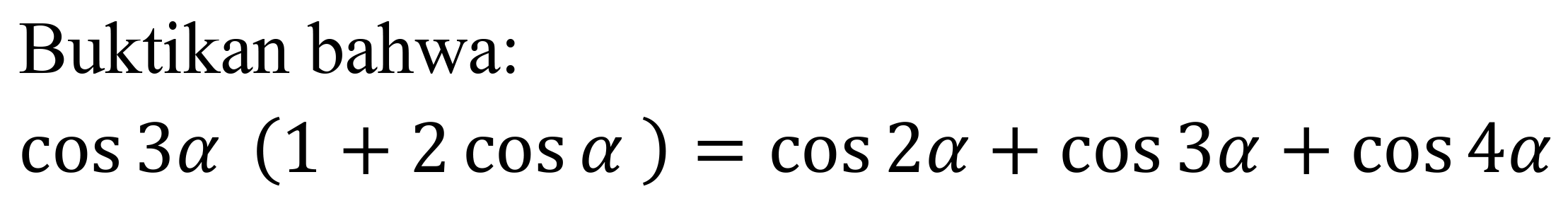 в ответах по тригонометрии
по
анонимный
| 596 просмотров
в ответах по тригонометрии
по
анонимный
| 596 просмотров в ответах по тригонометрии
по
Тевин
| 2,2 тыс. просмотров
в ответах по тригонометрии
по
Тевин
| 2,2 тыс. просмотров 2A в виде p √3 + q
2A в виде p √3 + q Синди, работавшая с ним, сказала, что sin 30 = x 2 . Они спросили госпожу Габриэль, кто был прав. Что она им ответила и почему?
Синди, работавшая с ним, сказала, что sin 30 = x 2 . Они спросили госпожу Габриэль, кто был прав. Что она им ответила и почему? sin4a−cos4a=cos2a
sin4a−cos4a=cos2a 13.2021
1,602
13.2021
1,602 Khi đó 3sinα−2cosα12sin3α+4cos3α có giá trị bằng:
Khi đó 3sinα−2cosα12sin3α+4cos3α có giá trị bằng: 13.2021
309
13.2021
309 13.2021
180
13.2021
180 09.2022
Ксем Джап ан
09.2022
Ксем Джап ан 09.2022
Ксем Джап
09.2022
Ксем Джап 09.2022
Ксем Джап
09.2022
Ксем Джап 09.2022
Ксем Джап
09.2022
Ксем Джап 09.2022
Ксем Джап ан
09.2022
Ксем Джап ан