Sin 5 радиан: SIN (функция SIN)

alexxlab / / Разное

Содержание

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )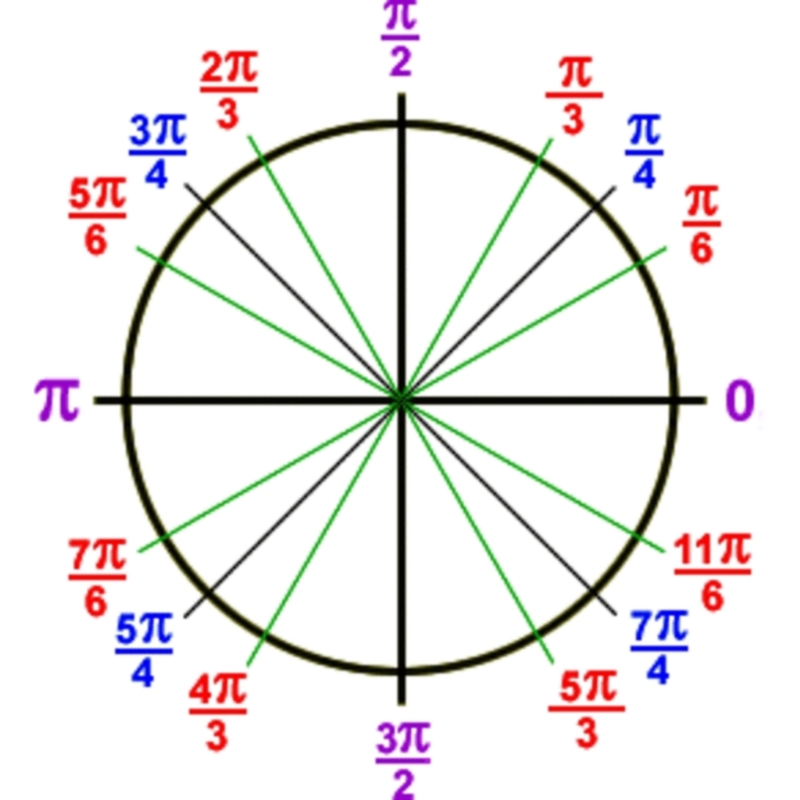
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )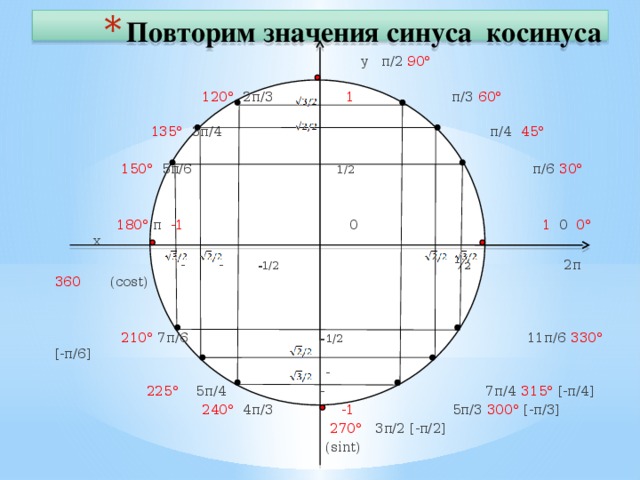
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Радианы и графики в тригонометрии . Магия математики [Как найти x и зачем это нужно]

До сих пор нам встречались углы, значения которых находились исключительно в диапазоне от 0 до 360

градусов. Но пристальный взгляд на единичную окружность невольно заставляет усомниться в обоснованности выбора числа 360.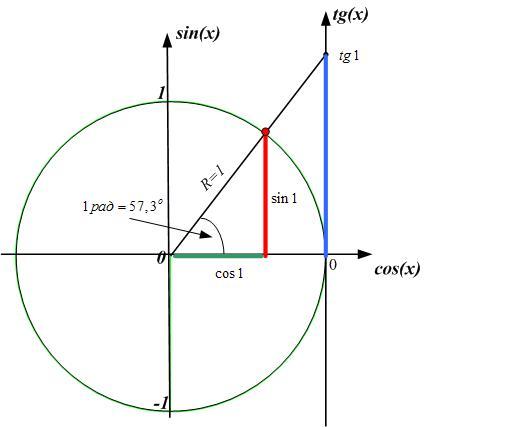 Сделан он был давным-давно, еще в древнем Вавилоне, где в обиходе была шестидесятеричная система счисления, использовавшаяся в том числе и в календаре (да-да, число 360 подозрительно напоминает количество дней в году). Альтернатива была предложена много позже, в XIX веке, когда в математике – а затем и в других науках – появилось понятие радиана, представляющего собой

2? рад = 360°

или, другими словами,

Для тауистов, почитающих число t как 2?,

В числовом же выражении 1 радиан примерно равен 57°.

Но зачем они нужны, спросите вы. И чем вдруг научному сообществу так не угодили привычные всем градусы?

В круге с радиусом r угол в 2? радианов охватывает длину окружности 2?r. Если взять часть этого большого угла, величина дуги, отделяемой этой частью, будет в 2?r раз больше получившейся дроби. Если говорить конкретнее, то 1 радиан «захватывает» дугу длиной 2?r(1/2?) = r, а m радианов – дугу длиной mr. В единичной окружности значение угла в радианах равно длине соответствующей ему дуги. Разве не удобно?

А вот единичный круг, поделенный на самые «популярные» углы – значения выражены как в градусах, так и в радианах.

Для сравнения – версия с t вместо ?.

На рисунках, кстати, очень хорошо заметно, насколько t удобнее ?. Для угла 90° (занимающего четверть окружности) представление в радианах выглядит как t/4; для угла 120° (треть окружности) – как t/3; для угла 60° (одна шестая окружности) – как t/6; t же есть, по сути, один полный оборот, то есть угол 360°.

Как нам еще предстоит убедиться, радианы позволяют значительно упростить формулы и уравнения подсчета тригонометрических функций. Формулы синуса и косинуса, например, можно превратить в «бесконечные ряды многочленов»:

sin x = x – x2/3! + x5/5! – x7/7! + x9/9! –…

cos x =1 – x2/2! + x4/4! – x6/6! + x8/8! –…

но только если x измеряется в радианах. Или при исчислении, например, мы увидим, что cos x есть производная функция sin x при том же условии. Так же и графики тригонометрических функций y = sin x и y = cos x строятся обычно на основании радианного представления x.

Графики эти будут повторяться с шагом 2? (тауисты, на старт!). Происходит это из-за того, что как синус, так и косинус берут свои начала в окружности, а угол x + 2? по своей природе ничем не отличается от угла x. Именно поэтому эти функции называются периодическими, а шаг 2? – периодом синуса и косинуса. Кстати, если сдвинуть график косинуса вправо на ?/2, он точь-в-точь совпадет с графиком синуса, потому что значение ?/2 в радианах соответствует углу 90°. Из всего этого следует, что

sin x = cos (?/2 – x) = cos (x – ?/2)

(например, sin 0 = 0 = cos (–?/2), а sin ?/2 = 1 = cos 0).

Тангенс, равный, как мы помним, sin x/cos x, так и останется неопределенным при cos x = 0 (что происходит всякий раз, когда линия графика проходит ровно посередине двух значений, кратных числу ?). Значит, период тангенса равен ?.

Синуса и косинуса, в принципе, достаточно, чтобы прийти к любой другой периодической тригонометрической функции. Именно благодаря такому своему уникальному свойству, как периодичность, они обрели огромную популярность для решения практических задач, в условиях которых заложена цикличность и «сезонность». Это и измерение температур, и анализ экономических данных, и многое другое. А еще с тригонометрическими функциями так или иначе связаны звуковые колебания, волны на воде, электричество и даже сердцебиение.

Ну и, по традиции, в завершение главы – самое интересное: между тригонометрией и числом ? существует удивительная, поистине волшебная связь. Хотите ее увидеть? Возьмите калькулятор и наберите на нем столько пятерок, сколько получится. У меня, например, на экране уместилось их целых 16 – 5 555 555 555 555 555. Теперь посчитайте величину, обратную этому числу; у меня получилось

1/5 555 555 555 555 555 = 1,8 ?10–16

Нажмите кнопку «sin» и посмотрите, что у вас получилось (вначале может идти несколько нолей – просто не обращайте на них внимания). Лично на меня с дисплея смотрело число

3,1415926535898 ? 10–18

которое (после отбрасывания 17 нолей, идущих за запятой) почти в точности повторяло первые 16 цифр числа ?! К тому же результату можно прийти, начав с любого числа, состоящего как минимум из пяти пятерок.

В этой главе мы выяснили, зачем нужна тригонометрия, и увидели, как она помогает нам лучше понять свойства треугольников и окружностей. Тригонометрические функции – не просто «вещи в себе», они взаимодействуют, вступая друг с другом в замысловатые, но прекрасные в своей стройности отношения. А еще мы проследили их связь с числом ?. Теперь черед за двумя другими важнейшими для математики величинами: иррациональной e = 2,71828… и мнимой i.

Zero To Hero

Совершенно очевидно, что в круге 360 градусов, не так ли?

А вот и нет. Большинство из нас совершенно не понимают, почему в круге 360 градусов. Мы запоминаем это магическое число как «размер окружности», а затем, изучая физику или высшую математику, удивляемся всем этим «радианам».

«Радианы делают математику проще!» — так говорят математики; вот бы они еще научились конкретнее объяснять, в чем заключается простота (чтобы и мы чувствовали себя в дискуссиях на тему рядов Тейлора, как рыба в воде). Сегодня мы откроем, что на самом деле представляют собой радианы, и поймем, почему именно они делают математику проще.

Откуда берутся градусы?

До чисел и языка слов у нас были звезды. Древние цивилизации использовали астрономию для определения времен года, предсказания будущего и задабривания богов (если уж приносить в жертву богам людей, то лучше делать это в правильное время).

И как всё это относится к углам? Попробуйте разгадать: не странно ли то, что в окружности 360 градусов, а в году 365 дней? И с чего это вдруг созвездия в течение года совершают оборот на небосклоне?

Спорим, вы не сможете определить время года по картине ночного неба? Вот созвездие Большой Медведицы, видимое в 2008 году из Нью-Йорка:

Созвездия каждую ночь немного продвигаются по кругу. Если Вы будете смотреть на небо в одно и то же время (например, в полночь), то заметите, что созвездия совершают полный круг по небу в течение года. Вот теория о возникновении градусов:

  • Люди заметили, что за год созвездия совершали полный круг
  • Каждый день они отодвигались совсем на немножно (это и есть «градус»)
  • Поскольку в году около 360 дней, то и в круге было 360 градусов.

Но, есть одно но… Почему бы не сделать 365 градусов в окружности?

Простим древним эту погрешность: они пользовались солнечными часами, и не знали, что за год должно было набежать ровно 365. 242199 градусов или дней, как вам теперь известно.

360 — достаточно точная цифра для тех времен. Она отлично согласуется с Вавилонской 60-ричной системой счисления, а также отлично делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 90… ну вы поняли).

Математические расчеты по Солнцу выглядят вполне уместными

Земле везет: ~360 — отличное количество дней в году. Но эта цифра выглядит довольно субъективно: на Марсе у нас было бы ~680 градусов в окружности, так как марсианский год длится дольше (и сам марсианский день также длится дольше, как вы понимаете). В некоторых странах Европы люди пользуются градами, при которых круг приходится делить на 400 частей.

Многие из объяснений сходятся к следующему: «Ну, градус — довольно субъективная мера, но нам нужно было выбрать какое-то число». Не сейчас: далее мы увидим, что же на самом деле скрывают градусы.

Радианы спорят с градусами

Градус — это то, насколько мне, стоя в центре стадиона, приходится повернуть голову, чтобы увидеть человека, бегущего по беговой дорожке.

Представьте, что вы заметили друга, бегущего по огромному кругу:
— Привет, как далеко ты добежал?
— Ну, пробежался я нехило, около 10 километров.
— Ты что, совсем? Как сильно я повернул свою голову, чтобы тебя увидеть?
— Что?
— Я поясню словами покороче для непонятливых. Я в центре круга. Ты бежал вокруг. Насколько… я… повернул… свою… голову?
— Придурок.

Эгоистично, не так ли? Вот как вся эта математика построена! Мы пишем уравнения по типу «Слушай, как сильно я повернул свою голову, чтобы увидеть движущуюся планету/маятник/колесо?» Я уверен, что вы никогда не думали о том, что чувствует, о чем мечтает и на что надеется маятник. Это эгоистичный подход. Не кажется ли вам, что уравнения должны быть простыми не только для зрителя, но и для самого бегуна?

Радианы: скажи эгоизму нет

Многие вещи из физики (да и из жизни!) заставляет нас вылезти из своей привычной системы координат и посмотреть на вещи с другой точки. Вместо того, чтобы вычислять поворот своей головы, задумайтесь, как далеко продвинулся бегун.

Градусы измеряют уголы по повороту головы. А радианы измеряют углы по пройденной дистанции.

Но само по себе расстояние не особо полезно, так как дистанция в 10 км может состоять из разного количества кругов, всё зависит от длины самого круга. Так что мы делим пройденную дистанцию на радиус круга, чтобы получить приведенный угол:

Вы часто будете встречать эту же формулу в таком виде:

угол в радианах (тета) — это длина дуги (s), поделенная на радиус (r).

Окружность описывает 360 градусов или 2π радиан — пройти весь круг будет 2*π* r / r. То есть, радиан — это примерно 360 /(2 * π) или 57.3 градусов.

Надеюсь, вы не будете думать, как я: «Ну вот, еще одна непонятная единица. 57.3 — такое странное число». Оно странное только потому, что вы всё еще думаете о себе!

Пройти 1 радиан (единицу) — вполне себе нормальная дистанция для путешествия.

Другими словами, наш «чистый, ровный угол в 90°» означает то же, что и непонятные π/2 единицы для пройденного бегуном пути. Подумайте об этом: «Эй, парень, а не пробежишь ли ты для меня еще 90°? Сколько это? А, ну да, для тебя это будет π/2 километра». Для бегуна дистанция в градусах выглядит также странно, как и поворот в радианах для зрителя.

Радианы в математике — это как бы поставить себя на место другого: передвинуть свою точку зрения с поворота головы на движение бегуна.

Что в имени тебе моем?

Радианы — это единица измерения движения по кругу, характеризуемого радиусом. Я думаю, слово «радиан» иллюстрирует как раз связь с радиусом движения.

По сути, радианы — это такие же числа, как 1.5 или 73, без каких либо единиц измерения (в формуле «радианы = пройденный путь / радиус» длина делится на длину, так что любые единицы измерения сокращаются).

Но, говоря практическим языком, мы не математические роботы, так что проще думать о радиане как о «пути», пройденному по единичной окружности.

Использование радиан

Я пока и сам привыкаю думать радианами. Но мы уже довольно близко подобрались к понятию «дистанции бегуна»:

  • Мы используем «вращений в минуту», а не «градусов в секунду» при измерении определенных угловых скоростей. Это ближе к точке зрения бегуна («Как много кругов он уже намотал?»)
  • Когда спутник движется вокруг Земли, мы понимаем его скорость как «километров в час», а не «градусов в час». Разделите эту скорость на расстояние от земли к спутнику, и вы получите орбитальную скорость в радианах в час.
  • Синус, эта замечательная функция, определяется в радианах, как:

Эта формула работает, только если х представлен в радианах! Почему? Синус непосредственно связан с пройденным путем, а не с поворотом головы. Но мы отложим эту беседу до следующего раза.

Пример 1: Колеса автобуса

Давайте попробуем разобрать реальный пример: у вас есть автобус с колесами, радиус которых 2 метра (это автобус в стиле монстр-трак). Я скажу, как быстро вращаются колеса, а вы мне скажете, как быстро едет автобус. Готовы? «Колеса вращаются со скоростью 2000 градусов в секунду». Вы думаете:

  • Хорошо, колеса вращаются на 2000 градусов в секунду. Это значит, они делают 2000/360 или 5 и 5/9 оборота в секунду. Длина окружности = 2*π*r, так что автобус движется со скоростью, эм, 2 * 3.14 * 5 и 5/9… где же мой калькулятор…

«Колеса проходят 6 радиан в секунду». Вы подумаете:

  • Радианы — это длина единичной окружности, мы просто масштабируем эту величину согласно реальному радиусу, чтобы рассчитать, как далеко мы уедем. 6 * 2 = 12 метров в секунду. Следующий вопрос.

Вау! Никаких сумасшедших формул, никакого π — просто умножаем, чтобы конвертировать угловую скорость в линейную. А всё потому, что радианы говорят на языке движущегося тела.

Обратное действие также простое. Предположим, что мы несёмся 30 метров в секунду по автостраде (108 км/ч) на 24-дюймовых колесах (радиус которых равен 30 см). Как быстро вращаются колеса?

Ну, 30 метров в секунду / 0.3 м радиуса = 100 радианов в секунду.

Это было просто.

Пример 2: sin(x)

Пришло время для примера помощнее. Выберите число градусов (х) и вычислите значение sin(x) в калькуляторе:

Когда вы берете х очень маленьким, вроде 0.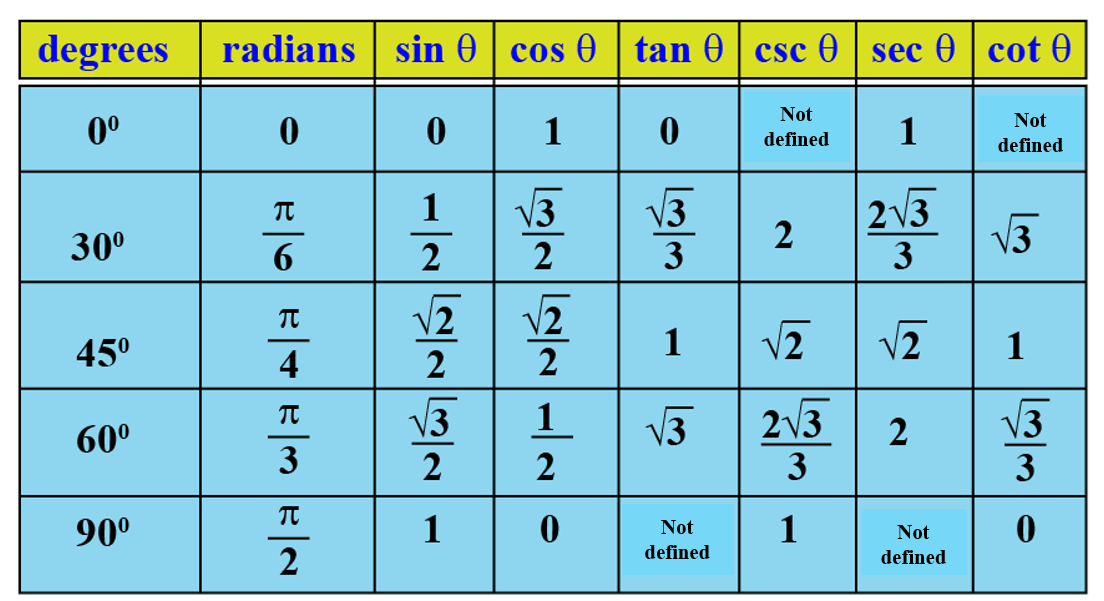 01, sin(x) тоже становится маленьким. И отношение sin(x)/x будет около 0.017 — что это означает? И еще страннее, что означает деление или умножение на градусы? Можно ли иметь квадратные или кубические градусы?

Радианы нас спасут. Зная, что они отвечают за пройденную дистанцию (это не просто пропорция!), мы можем интерпретировать уравнение таким образом:

  • х — это то, как далеко вы прошли по кругу
  • sin(x) — это то, как высоко вы взобрались по нему
  • Так что sin(x)/x — это отношение того, как высоко вы находитесь, к тому, как далеко вы прошли: количество энергии, которое ушло в направлении «вверх». Если вы двигались вертикально, то это отношение будет равно 100%. Если вы двигались горизонтально, то равенство будет давать 0%.

Когда что-то пододвигается на крошечное расстояние, как 0 или 1 градус с прежнего места, оно движется практически вверх. Если вы шагнете еще на меньшее расстояние, например с 0 до 0.00001 градуса, то вы действительно пройдете прямо вверх. Пройденное расстояние (х) очень близко к высоте (sin(x)).

Чем меньше х, тем ближе отношение к 100% — больше движения происходит вверх.

Радианы помогают увидеть, интуитивно, почему sin(x)/x стремится к 1 по мере уменьшения х. Мы просто топчемся на крошечном отрезке пути вверх. Между прочим, это также поясняет, почему sin(x) ~ x для маленьких чисел.

Конечно, вы можете точно доказать это с помощью калькулятора, но мышление радианами помогает вам это понять.

Запомните, эти связи работают только при измерении углов радианами. С градусами вы сравниваете высоты на окружности (sin(x)) с тем, насколько какой-то зритель поверную свою голову (х градусов).

Так в чем же смысл?

Градусы занимают свое место в нашей жизни. Нам ведь важно знать, насколько надо повернуть телескоп, развернуть сноуборд или покрутить рулем? По законам природы мы наблюдаем за тем, как движутся другие. И радианы больше подходят тем, кто движется, чем тем, кто за ними наблюдает. У меня ушло много лет на то, чтобы понять:

  • Градусы выбраны произвольно, так как они основываются на солнце (365 дней ~ 360 градусов), но они как бы идут от обратного, потому что описывают процессы с точки зрения наблюдателя.
  • Радианы описывают движение с точки зрения самих его участников, и поэтому «всё стает на свои места». Конвертировать угловую скорость в линейную довольно просто, и идеи вроде sin(x)/x приобретают смысл.

Даже углы можно рассматривать с более, чем одной точки зрения. Понимание радиан делают математические и физические формулы более осмысленными.

Приятных вычислений!

Перевод статьи «Intuitive Guide to Angles, Degrees and Radians»

Sin 5 градусов — найти значение Sin 5 градусов

LearnPracticeDownload

Значение sin 5 градусов равно 0,0871557. . . . Sin 5 градусов в радианах записывается как sin (5° × π/180°), т. е. sin (π/36) или sin (0,087266…). В этой статье мы обсудим способы нахождения значения sin 5 градусов на примерах.

  • Sin 5°: 0,0871557. . .
  • Sin (-5 градусов): -0,0871557. . .
  • Sin 5° в радианах: sin (π/36) или sin (0,0872664 . . . .)

Каково значение греха 5 градусов?

Значение sin 5 градусов в десятичном виде равно 0,087155742. . .. Sin 5 градусов также можно выразить с помощью эквивалента заданного угла (5 градусов) в радианах (0,08726 . . .).

Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 5 градусов = 5° × (π/180°) рад = π/36 или 0,0872. . .
∴ sin 5 ° = sin (0,0872) = 0,0871557. . .

Объяснение:

Для sin 5 градусов угол 5° лежит между 0° и 90° (первый квадрант). Поскольку функция синуса положительна в первом квадранте, значение sin 5° = 0,0871557. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 5° как sin 5 градусов = sin(5° + n × 360°), n ∈ Z.
⇒ sin 5° = sin 365° = sin 725° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-5°) = -sin(5°).

Методы нахождения значения Sin 5 градусов

Функция синуса положительна в 1-м квадранте. Значение sin 5° равно 0,08715. . .. Мы можем найти значение sin 5 градусов по:

  • Используя тригонометрические функции
  • Использование единичного круга

Sin 5° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить sin 5 градусов как:

  • ± √(1-cos²(5°))
  • ± тангенс 5°/√(1 + тангенс²(5°))
  • ± 1/√(1 + раскладушка²(5°))
  • ± √(сек²(5°) — 1)/сек 5°
  • 1/косек 5°

Примечание. Поскольку 5° лежит в 1-м квадранте, конечное значение sin 5° будет положительным.

Мы можем использовать тригонометрические тождества для представления sin 5° как

  • sin(180° — 5°) = sin 175°
  • -sin(180° + 5°) = -sin 185°
  • cos(90° — 5°) = cos 85°
  • -cos(90° + 5°) = -cos 95°

Sin 5 градусов с помощью единичной окружности

Чтобы найти значение sin 5 градусов с помощью единичной окружности:

  • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 5° с положительной осью x.
  • Грех в 5 градусов равен координате y (0,0872) точки пересечения (0,9962, 0,0872) единичной окружности и r.

Отсюда значение sin 5° = y = 0,0872 (приблизительно)

☛ Также проверьте:

  • sin 15 градусов
  • грех 180 градусов
  • грех 90 градусов
  • грех 750 градусов
  • грех 57 градусов
  • грех 71 градус

Примеры использования Sin 5 градусов

  1. Пример 1: Упростить: 2 (sin 5°/sin 365°)

    Решение:

    Мы знаем, что sin 5° = sin 365°
    ⇒ 2 sin 5°/sin 365° = 2(sin 5°/sin 5°)
    = 2(1) = 2

  2. Пример 2: Найдите значение 2 × (sin 2,5° cos 2,5°). [Подсказка: используйте sin 5° = 0,0872]

    Решение:

    Используя формулу sin 2a,
    2 sin 2,5° cos 2,5° = sin(2 × 2,5°) = sin 5°
    ∵ sin 5° = 0,0872
    ⇒ 2 × (sin 2,5° cos 2,5°) = 0,0872

  3. Пример 3. Найдите значение 5 sin(5°)/7 cos(85°).

    Решение:

    Используя тригонометрические тождества, мы знаем, что sin(5°) = cos(90° — 5°) = cos 85°.
    ⇒ sin(5°) = cos(85°)
    ⇒ Значение 5 sin(5°)/7 cos(85°) = 5/7

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Sin 5 Degrees

Что такое Sin 5 Degrees?

Sin 5 градусов — значение тригонометрической функции синуса для угла, равного 5 градусам. Значение sin 5° равно 0,0872 (приблизительно).

Как найти Sin 5° в терминах других тригонометрических функций?

Используя формулу тригонометрии, значение sin 5° может быть выражено через другие тригонометрические функции следующим образом:

  • ± √(1-cos²(5°))
  • ± тангенс 5°/√(1 + тангенс²(5°))
  • ± 1/√(1 + раскладушка²(5°))
  • ± √(сек²(5°) — 1)/сек 5°
  • 1/косек 5°

☛ Также проверьте: тригонометрическую таблицу

Каково точное значение sin 5 градусов?

Точное значение sin 5 градусов может быть задано с точностью до 8 знаков после запятой как 0,08715574.

Каково значение Sin 5 градусов в терминах Tan 5°?

Мы знаем, что, используя тригонометрические тождества, мы можем записать sin 5° как tan 5°/√(1 + tan²(5°)). Здесь значение тангенса 5° равно 0,087488.

Как найти значение греха 5 градусов?

Значение sin 5 градусов можно рассчитать, построив угол 5° с осью x и затем найдя координаты соответствующей точки (0,9962, 0,0872) на единичной окружности. Значение sin 5° равно координате y (0,0872). ∴ sin 5° = 0,0872.

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
наглядный учебный план

Калькулятор — sin(5) — Solumaths

Sin, расчет онлайн

Резюме:

Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.

sin online

Описание:

Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.

Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.

  1. Расчет синуса

    2. Вычисление синуса угла в радианах

    Калькулятор синуса позволяет через функцию sin вычислить онлайн синус синус угла в радианах, сначала нужно выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

    Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 50, введите sin(50), после вычисления, возвращается результат `sqrt(2)/2`.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

  2. Таблица специальных синусоидальных значений

    3. Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах.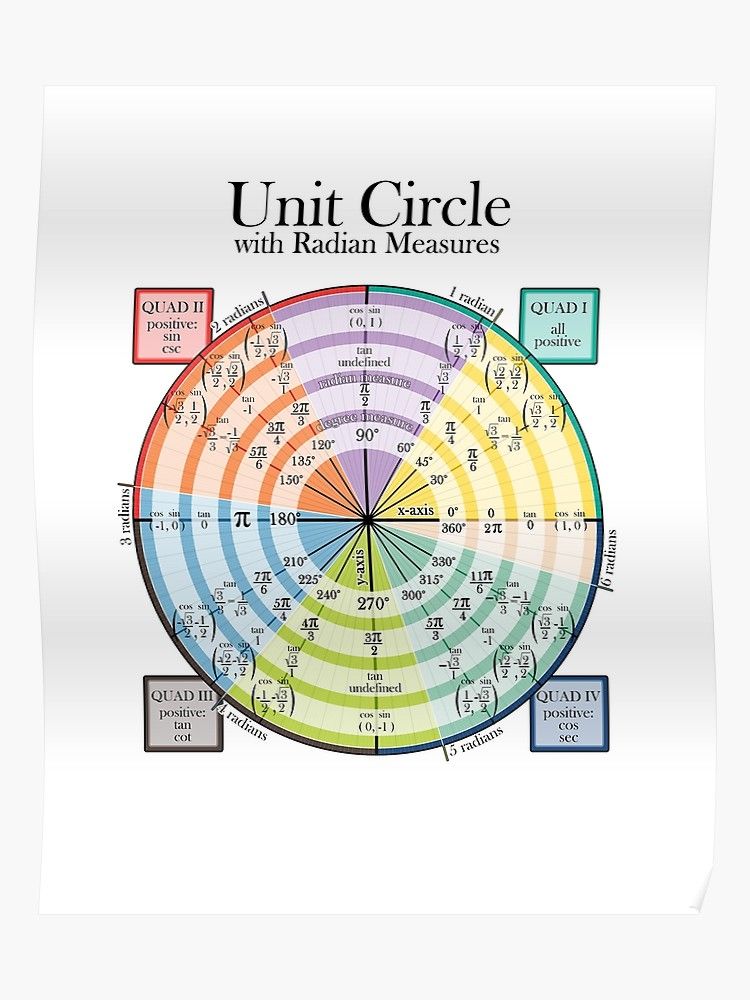 Вот таблица значений общего синуса :

    sin(`2*pi`) `0`
    sin(`pi`) `0`
    sin(`pi/90 `2` 30
    sin(`pi/4`) `sqrt(2)/2`
    sin(`pi/3`) `sqrt(3)/2`
    sin(`pi/6`) `1/2`
    sin(`2*pi/3`) `sqrt(3) /2`
    sin(`3*pi/4`) `sqrt(2)/2`
    sin(`5*pi/6`) `1/2`
    sin(`0`) `0`
    sin(`-2*pi`) `0`
    sin(`-pi`)
    0 sin(`pi/2`) `-1`
    sin(`-pi/4`) `-sqrt(2)/2`
    sin(`-pi/3`) `-sqrt(3)/2`
    sin(`-pi/6`) `-1/2`
    sin(`-2*pi/3`) `-sqrt(3)/2`
    sin( `-3*pi/4`) `-sqrt(2)/2`
    sin(`-5*pi/6`) `-1/2`

  3. Основные свойства

    4. `AA x в RR, k в ZZ`,

  • `sin(-x)= -sin(x)`
  • `sin(x+2*k*pi)=sin(x)`
  • `sin(pi-x)=sin(x)`
  • `sin(pi+x)=-sin(x)`
  • `sin(pi/2-x)=cos(x)`
  • `sin(pi/2+x)=cos(x)`

  • Производная синуса

    • Производная синуса равна cos(x).

  • Первообразная синуса

    • Первообразная синуса равна -cos(x).

  • Свойства функции синуса

    • Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.

  • Уравнение с синусом

    • Калькулятор имеет решатель, который позволяет решать уравнение с синусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.

    Синтаксис:

    sin(x), где x — мера угла в градусах, радианах или градах.

    Примеры:

    sin(`0`), возвращает 0

    Производный синус:

    можно использовать калькулятор производной, который позволяет вычислить производную функции синуса

    производная sin(x) является производной(`sin(x)`)=`cos(x)`

    Синус первообразной :

    Калькулятор первообразной позволяет вычислить первообразную функции синуса.

    Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`

    Предел синуса :

    Калькулятор предела позволяет вычислить пределы функции синуса.

    предел sin(x) is limit(`sin(x)`)

    Обратная функция синуса :

    обратная функция синуса представляет собой функцию арксинуса, обозначенную как arcsin.

    График синуса :

    Графический калькулятор может отображать синусоидальную функцию в заданном интервале.

    Свойство функции синуса:

    Функция синуса является нечетной функцией.

    Расчет онлайн с sin (синусом)

    См. также

    Список связанных калькуляторов:

    • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
    • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
    • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
    • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
    • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
    • Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
    • Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
    • Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
    • Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
    • Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Синус : грех. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
    • Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

    Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции

     

    Значение Sin(5) — Синус

    Дом Инструменты Темы Мобильная версия 903:00
    Дом >> Площадь
    903:00

    Расчет значений Sin, Cos, Tan, Cot, Cosec, Sec, SinH, CosH, TanH, CotH, CosecH, SecH, ASin, ACos, ATan, ACot, ACosec, ASec и других функций тригонометрии

    Значение Sin(5 градусов) = 0,08715574
    Also find for nearby Angle’s . ..
    ◄ 4.5 4.6 4.7 4.8 4.9 5 5.1 5.2 5.3 5,4 5,5 ►
       градус/радиан    Function    Angle / Value    
    (angle in degree)(angle in radian)   SinCosTanCotSecCosecSinHCosHTanHCosecHSecHCotHArc SinArc CosArc TanArc CosecArc SecArc Cot  ( )  знак равно

    Вместо этого использовать мастер?

    ». Найти ЗВЕЗДА
    Related . ..
    »   Angle Conversion
    »   Area Conversion
    »   Calculate Area of ​​different objects
    »   Calculate Surface Area of ​​different objects
    »   Калькулятор логарифмов
    »   Калькулятор квадратного и кубического корня
    »   Преобразование поверхностной плотности тока
    »Преобразование плотности поверхностного заряда
    » Преобразование поверхностного натяжения
    »
    »   Мировое время — Найдите время в разных местах
    »   Размер стран и океанов
    »Размер планет, лун, кометы и астероиды
    » Создатель календаря
    »Преобразование длины
    ». Весо
    3. Найти СВЕТИ3. Найти СВЕТИ3. Найти СВЕТИ3. Найти СВЕТИ3. Найти СВЕТИ3. Найти СТАРИЙ3. ИСПОЛЬЗОВАНИЕ

    9.RIND

    . Найти СТАРИНГ

    		3. Найти СВЕТ3. Найти СВЕТ3. 9029».
    »   Калькулятор ИМТ (индекс массы тела)
    »   Калькулятор жировых отложений
    »   Расчет калорий, сожженных при различных видах деятельности
    »Рассчитайте свой идеальный вес
    » )
    »   Методы контроля рождаемости
    »   Найти определение различных единиц
    »   Список различных единиц измерения
    Topic of Interest …
    Area Astrology Baby Names Banking Birth Control
    Chemistry Chinese Astrology City Info Electricity Finance
    Жидкости География Health Length Magnetism
    Pregnancy Radiation Scientific Speed ​​ Technology
    Telephone Temperature Time & Date Train Info Volume
    Вес Мировое время Зодиак Астрология Другое  

    Поддерживаемые типы преобразования . ..
    Acceleration Angle Angular Acceleration Angular Velocity
    Area Blood Sugar Clothing Size Computer Storage Unit
    Cooking Volume Cooking Weight Data Transfer Rate Дата
    Плотность Динамическая вязкость Электрическая емкость Электрический заряд
    Electric Conductance Electric Conductivity Electric Current Electric Field Strength
    Electric Potential Electric Resistance Electric Resistivity Energy
    Energy Density Energy Mass Euro Currency Концентрация жидкости
    Расход жидкости Массовый расход жидкости Сила Frequency
    Fuel Economy Heat Capacity Heat Density Heat Flux Density
    Heat Transfer Coefficient Illumination Image Resolution Inductance
    Kinematic Viscosity Length Luminance (Свет) Сила света
    Линейная плотность заряда Линейная плотность тока Напряженность магнитного поля Magnetic Flux
    Magnetic Flux Density Magnetomotive Force Mass Flux Density Molar Concentration
    Molar Flow Rate Moment of Inertia Number Permeability
    Power Prefix Давление Радиация
    Поглощение радиации Воздействие радиации Радиоактивность Shoe Size
    Sound Specific Volume Speed ​​ Surface Charge Density
    Surface Current Density Surface Tension Temperature Thermal Conductivity
    Thermal Expansion Thermal Resistance Время Крутящий момент
    Объем Объем Плотность заряда Вода Вязкость масла Вес
    .

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

    Карта сайта