Названия углов при параллельных прямых и секущей: Углы при пересечении двух прямых

Если прямые параллельны то они равны. Признаки и свойства параллельных прямых. Аксиома параллельных прямых

AB и С D пересечены третьей прямой MN , то образовавшиеся при этом углы получают попарно такие названия:

соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7;

внутренние накрест лежащие углы : 3 и 5, 4 и 6;

внешние накрест лежащие углы : 1 и 7, 2 и 8;

внутренние односторонние углы : 3 и 6, 4 и 5;

внешние односторонние углы : 1 и 8, 2 и 7.

Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.

Следовательно, ∠ 2 =∠ 8.

3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.

4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.

5. Сумма

внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам , как углы вертикальные .

Из выше доказанного обоснования получаем обратные теоремы.

Когда при пересечении двух прямых произвольной третьей прямой получим, что:

1. Внутренние накрест лежащие углы одинаковы;

или 2. Внешние накрест лежащие углы одинаковые;

или 3. Соответственные углы одинаковые;

или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;

или 5. Сумма внешних односторонних равна 2d = 180 0 ,

то первые две прямые параллельны.

Видеоурок «Признаки параллельности двух прямых» содержит доказательство теорем, которые описывают признаки, означающие параллельность прямых. При этом в видео описывается 1) теорема о параллельности прямых, при которых секущей созданы равные углы, 2) признак, означающий параллельность двух прямых — по равным образованным соответственным углам, 3) признак, означающий параллельность двух прямых в случае, когда при их пересечении секущей односторонние углы в сумме составляют 180°.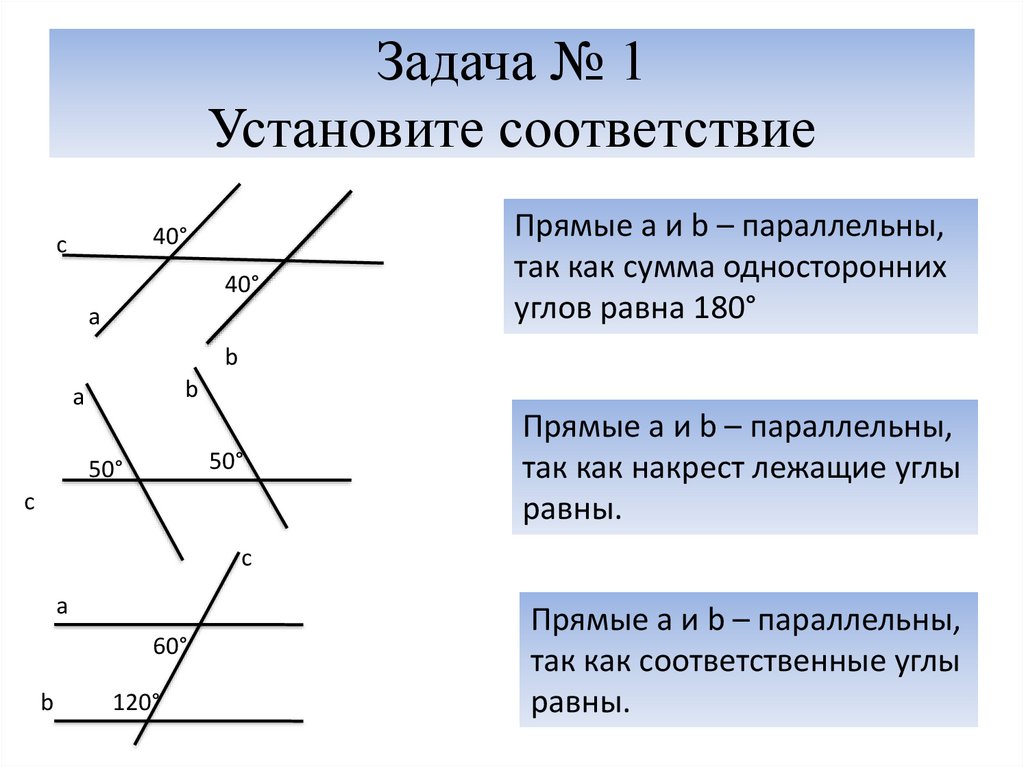

Задача данного видеоурока — ознакомить учеников с признаками, означающими параллельность двух прямых, знание которых необходимо для решения многих практических задач, наглядно представить доказательство данных теорем, формировать навыки в доказательстве геометрических утверждений.

Преимущества видеоурока связаны с тем, что при помощи анимации, голосового сопровождения, возможности выделения цветом, он обеспечивает высокую степень наглядности, может послужить заменой подачи стандартного блока нового учебного материала учителем.

Начинается видеоурок с выведения на экран названия. Перед описанием признаков параллельности прямых ученики знакомятся с понятием секущей. Дается определение секущей как прямой, которая пересекает другие прямые. На экране изображены две прямые a и b, которые пересекаются прямой с. Построенная прямая с выделена синим цветом, акцентируя внимание на том, что они является секущей данных прямых а и b. Для того чтобы рассматривать признаки параллельности прямых необходимо более детально ознакомиться с областью пересечения прямых.

Секущая в точках пересечения с прямыми образует 8 углов ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8, анализируя соотношения которых можно вывести признаки параллельности данных прямых. Отмечается, что углы ∠3 и ∠5, а также ∠2 и ∠4 называются накрест лежащими. Дается подробное объяснение при помощи анимации расположения накрест лежащих углов как углов, которые лежат между параллельными прямыми, и примыкают к прямым, располагаясь накрест. Затем дается понятие односторонних углов, в число которых входят пары ∠4 и ∠5, а также ∠3 и ∠6. Также указываются пары соответственных углов, которых на построенном изображении 4 пары — ∠1-∠5, ∠4-∠8, ∠2-∠6, ∠3-∠7.

В следующей части видеоурока рассматриваются три признака параллельности любых двух прямых. На экран выводится первое описание. Теорема утверждает, что при равенстве накрест лежащих углов, образуемых секущей, данные прямые будут параллельны. Утверждение сопровождается рисунком, на котором изображены две прямые а и b и секущая АВ. Отмечается, что образуемые накрест лежащие углы ∠1 и ∠2 равны между собой. Данное утверждение требует доказательства.

Наиболее просто доказываемый частный случай — когда данные образуемые накрест лежащие углы являются прямыми. Это означает, что секущая является перпендикуляром к прямым, а по уже доказанной теореме в этом случае прямые а и b не будут пересекаться, то есть являются параллельными. Доказательство для данного частного случая описывается на примере изображения, построенного рядом с первым рисунком, выделяя важные детали доказательства при помощи анимации.

Для доказательства в общем случае необходимо проведение дополнительного перпендикуляра из середины отрезка АВ на прямую а. Далее на прямой b откладывается отрезок ВН 1 , равный отрезку АН. Из полученной при этом точки Н 1 проводится отрезок, соединяющий точки О и Н 1 . Далее рассматриваются два треугольника ΔОНА и ΔОВН 1 , равенство которых доказывается по первому признаку равенства двух треугольников. Стороны ОА и ОВ равны по построению, так как точка О отмечалась как середина отрезка АВ. Стороны НА и Н 1 В также равны по построению, так как мы откладывали отрезок Н 1 В, равный НА. А углы ∠1=∠2 по условию задачи. Так как образованные треугольники равны между собой, то и соответствующие оставшиеся пары углов и сторон также равны между собой. Из этого следует, что и отрезок ОН 1 является продолжением отрезка ОН, составляя один отрезок НН 1 . При этом отмечается, что так как построенный отрезок ОН — перпендикуляр к прямой а, то соответственно и отрезок НН 1 является перпендикулярным к прямым а и b. Данный факт означает, используя теорему о параллельности прямых, к которым построен один перпендикуляр, что данные прямые а и b являются параллельными.

Следующая теорема, требующая доказательства — признак равенства параллельных прямых по равенству соответственных углов, образованных при пересечении секущей. Утверждение указанной теоремы выведено на экран и может быть предложено под запись учениками. Доказательство начинается с построения на экране двух параллельных прямых а и b, к которым построена секущая с. Выделенная на рисунке синим цветом. Секущей образованы соответственные углы ∠1 и ∠2, которые по условию равны между собой. Также отмечаются смежные углы ∠3 и ∠4. ∠2 по отношению к углу ∠3 является вертикальным углом. А вертикальные углы всегда равны. К тому же углы ∠1 и ∠3 являются накрест лежащими между собой — их равенство (по уже доказанному утверждению) означает, что прямые а и b параллельны. Теорема доказана.

Последняя часть видеоурока посвящена доказательству утверждения о том, что если сумма односторонних углов, которые образованы при пересечении двух некоторых прямых секущей прямой, будет равняться 180°, в этом случае данные прямые будут параллельны между собой. Доказательство демонстрируется, используя рисунок, на котором изображены прямые а и b, пересекающиеся с секущей с. Образованные пересечением углы отмечены аналогично предыдущему доказательству. По условию, сумма углов ∠1 и ∠4 равна 180°. При этом известно, что сумма углов ∠3 и ∠4 равна 180°, так как они являются смежными.

Это означает, что углы ∠1 и ∠3 равны между собой. Данный вывод дает право утверждать, что прямые а и b параллельны. Теорема доказана.

Видеоурок «Признаки параллельности двух прямых» может быть использован учителем в качестве самостоятельного блока, демонстрирующего доказательства названных теорем, заменяющего объяснение учителя или сопровождающего его. А подробное объяснение дает возможность использовать материал для самостоятельного изучения учениками и поможет в объяснении материала при дистанционном обучении.

Признаки параллельности двух прямых

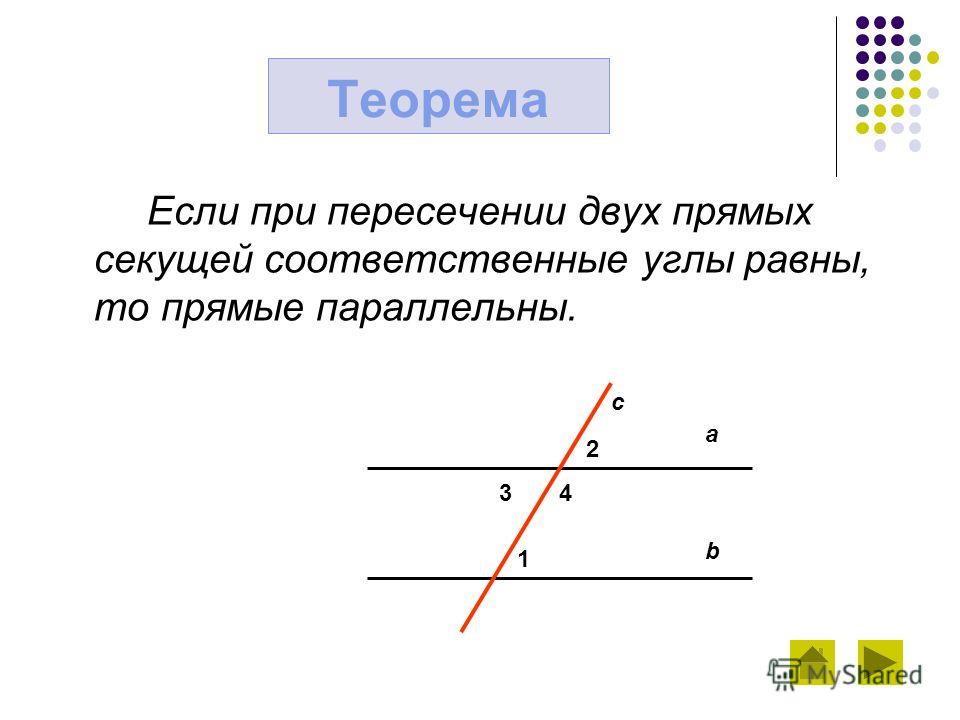
Теорема 1. Если при пересечении двух прямых секущей:

накрест лежащие углы равны, или

соответственные углы равны, или

сумма односторонних углов равна 180°, то

прямые параллельны (рис.1).

Доказательство. Ограничимся доказательством случая 1.

Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6.

Докажем, что а || b.

Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.

Следствие 1 . Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).

Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду).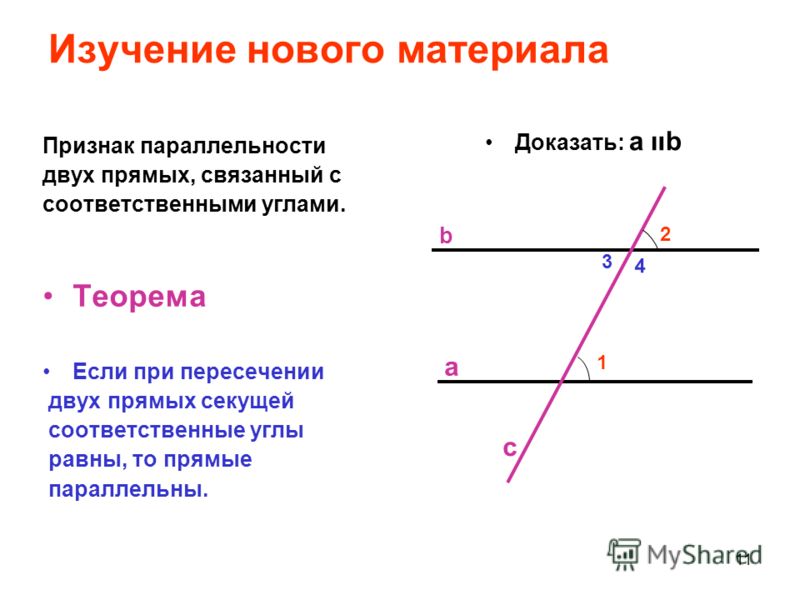

Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.

Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.

Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).

Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.

Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .

Основное свойство параллельных прямых состоит в следующем.

Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.

1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис. 4).

2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).

Справедлива и следующая теорема.

Теорема 2. Если две параллельные прямые пересечены секущей, то:

накрест лежащие углы равны;

соответственные углы равны;

сумма односторонних углов равна 180°.

Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).

Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.

Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно.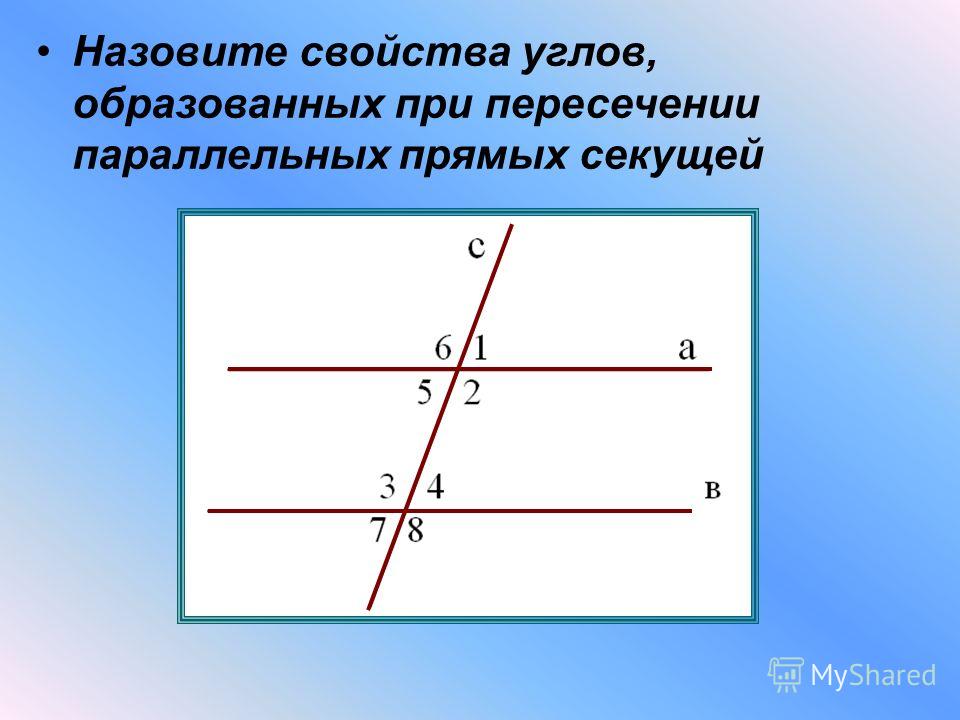 Два равных угла вовсе не обязаны быть вертикальными.

Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.

Решение. Пусть условию отвечает рисунок 6.

Сначала рассмотрим разницу между понятиями признак, свойство и аксиома.

Определение 1

Признаком называют некий факт, по которому можно определить истинность суждения об интересующем объекте.

Пример 1

Прямые являются параллельными, если их секущая образует равные накрест лежащие углы.

Определение 2

Свойство формулируется в том случае, когда есть уверенность в справедливости суждения.

Пример 2

При параллельных прямых их секущая образует равные накрест лежащие углы.

Определение 3

Аксиомой называют такое утверждение, которое не требует доказательства и принимается как истина без него.

Каждая наука имеет аксиомы, на которых строятся последующие суждения и их доказательства.

Аксиома параллельных прямых

Иногда аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.

Теорема 1

Через точку, которая не лежит на заданной прямой, на плоскости можно провести лишь одну прямую, которая будет параллельной заданной.

Аксиома доказательства не требует.

Свойства параллельных прямых

Теорема 2

Свойство1. Свойство транзитивности параллельности прямых:

Когда одна из двух параллельных прямых является параллельной третьей, то и вторая прямая будет ей параллельна.

Свойства требуют доказательств.

Доказательство:

Пусть имеются две параллельные прямые $a$ и $b$. Прямая $с$ параллельна прямой $а$. Проверим, будет ли в таком случае прямая $с$ параллельна и прямой $b$.

Для доказательства будем пользоваться противоположным суждением:

Представим, что возможен такой вариант, при котором прямая $c$ параллельна одной из прямых, например, прямой $a$, а другую – прямую $b$ – пересекает в некоторой точке $K$.

Получаем противоречие согласно аксиоме параллельных прямых. Получается ситуация, при которой в одной точке пересекаются две прямые, к тому же параллельные одной и той же прямой $a$. Такая ситуация невозможна, следовательно, прямые $b$ и $c$ пересекаться не могут.

Таким образом, доказано, что если одна из двух параллельных прямых является параллельной третьей прямой, то и вторая прямая параллельна третьей прямой.

Теорема 3

Свойство 2.

Если одна из двух параллельных прямых пересекается третьей, то ею будет пересекаться и вторая прямая.

Доказательство:

Пусть имеются две параллельные прямые $а$ и $b$. Также пусть имеется некоторая прямая $с$, которая пересекает одну из параллельных прямых, например, прямую $а$. Необходимо показать, что прямая $с$ пересекает и вторую прямую – прямую $b$.

Построим доказательство методом от противного.

Представим, что прямая $с$ не пересекает прямую $b$. Тогда через точку $К$ проходят две прямые $а$ и $с$, которые не пересекают прямую $b$, т. С D , что возможно. Прямая CE параллельна AB .

Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M . Тогда из точки M к прямой С D мы имели бы два различных перпендикуляра M D и MС , что невозможно. Значит, CE не может пересечься с AB , т.е. С E параллельна AB .

Следствие.

Два перпендикуляра (С E и DB ) к одной прямой (С D ) параллельны.

Аксиома параллельных линий.

Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.

Так, если прямая С D , проведенная через точку С параллельна прямой AB , то всякая другая прямая С E , проведенная через ту же точку С , не может быть параллельна AB , т.е. она при продолжении пересечется с AB .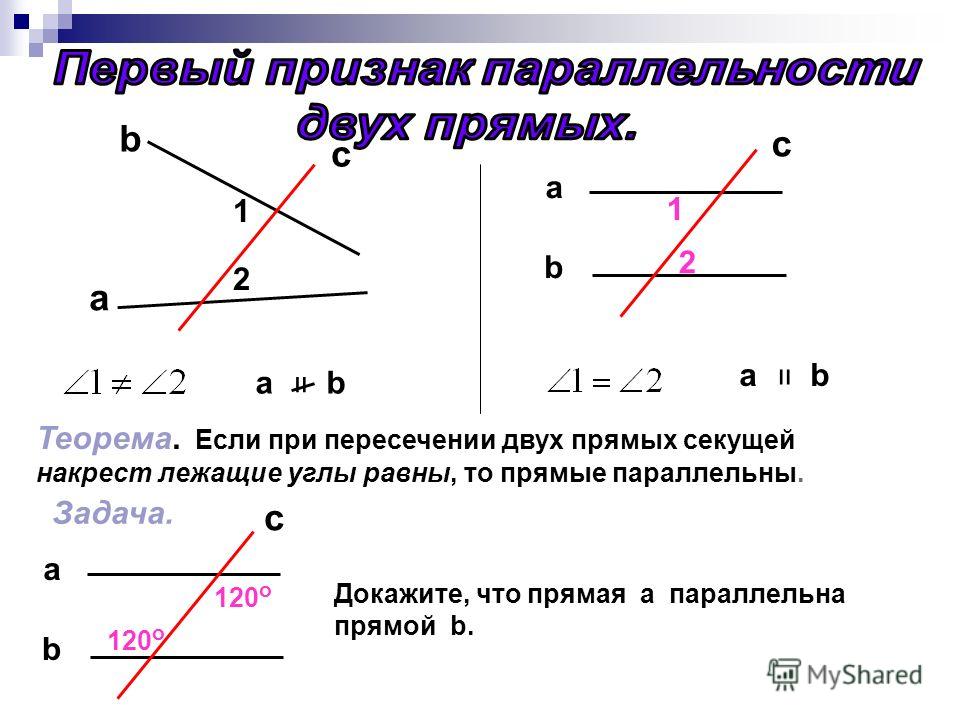

Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).

Следствия.

1. Если прямая (С E ) пересекается с одной из параллельных (СВ ), то она пересекается и с другой (AB ), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB , что невозможно.

2. Если каждая из двух прямых (A и B ) параллельны одной и той же третьей прямой (С ) , то они параллельны между собой.

Действительно, если предположить, что A и B пересекаются в некоторой точке M , то тогда через эту точку проходили бы две различные прямые, параллельные С , что невозможно.

Теорема .

Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной .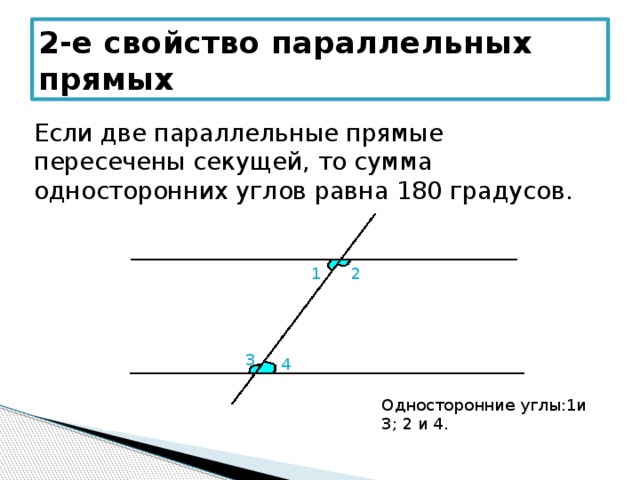 С D .

Перпендикуляр E F , пересекаясь с AB , непременно пересечет и С D . Пусть точка пересечения будет H .

Предположим теперь, что С D не перпендикулярна к EH . Тогда какая-нибудь другая прямая, например HK , будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB : одна С D , по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH .

Признаки параллельности двух прямых / Параллельные прямые / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Параллельные прямые
5. Признаки параллельности двух прямых

Рассмотрим две прямые и , которые пересекает в двух точках третья прямая (Рис. 1). Прямая называется секущей по отношению к прямым и .

При пересечении прямых и секущей образуется восемь углов, которые обозначены цифрами на Рис.2. 

Некоторые пары из этих углов имеют специальные названия:

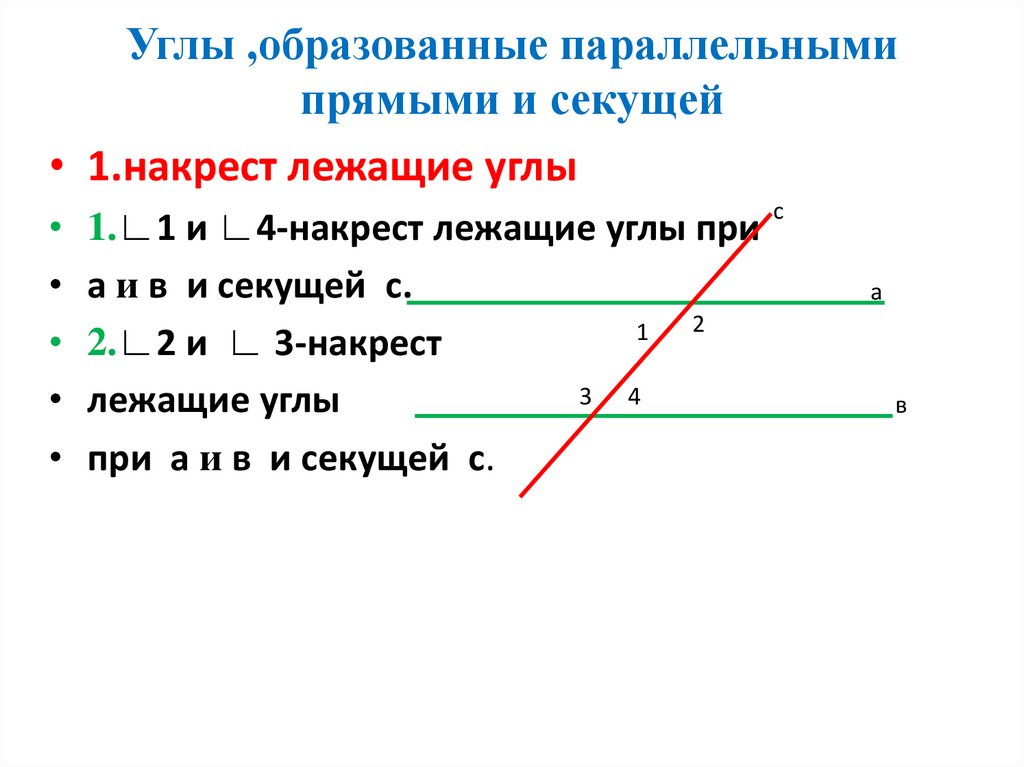
накрест лежащие углы: 3 и 5, 4 и 6;

односторонние углы: 4 и 5, 3 и 6;

соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Признаки параллельности двух прямых

1.

Теорема

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Дано: прямые и , АВ — секущая, 1 и 2 — накрест лежащие, 1 = 2 (Рис.3).

Доказать: .

Доказательство:

1 случай

Предположим, что 1 = 2 = 90⁰, т.е. эти углы прямые, получим АВ и АВ (Рис.4), следовательно, (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны).

2 случай

Предположим, что 1 и 2 — не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой и продолжим его до пересечения с прямой , точку пересечения ОН с прямой обозначим Н₁ (Рис. 5).

Получим ОНА = ОН₁В по 2 признаку равенства треугольников (углы 3 и 4 вертикальные, т.к. получены при пересечении двух прямых АВ и НН₁, а вертикальные углы равны друг другу, т.е. 3 = 4, АО = ОВ, т.к. О — середина АВ, 1 = 2 по условию), следовательно, 5 =6, значит, 6 — прямой, также как и 5 (т.к по построению ОН ).

Получаем, НН₁ и НН₁, значит  (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны). Что и требовалось доказать.

2.

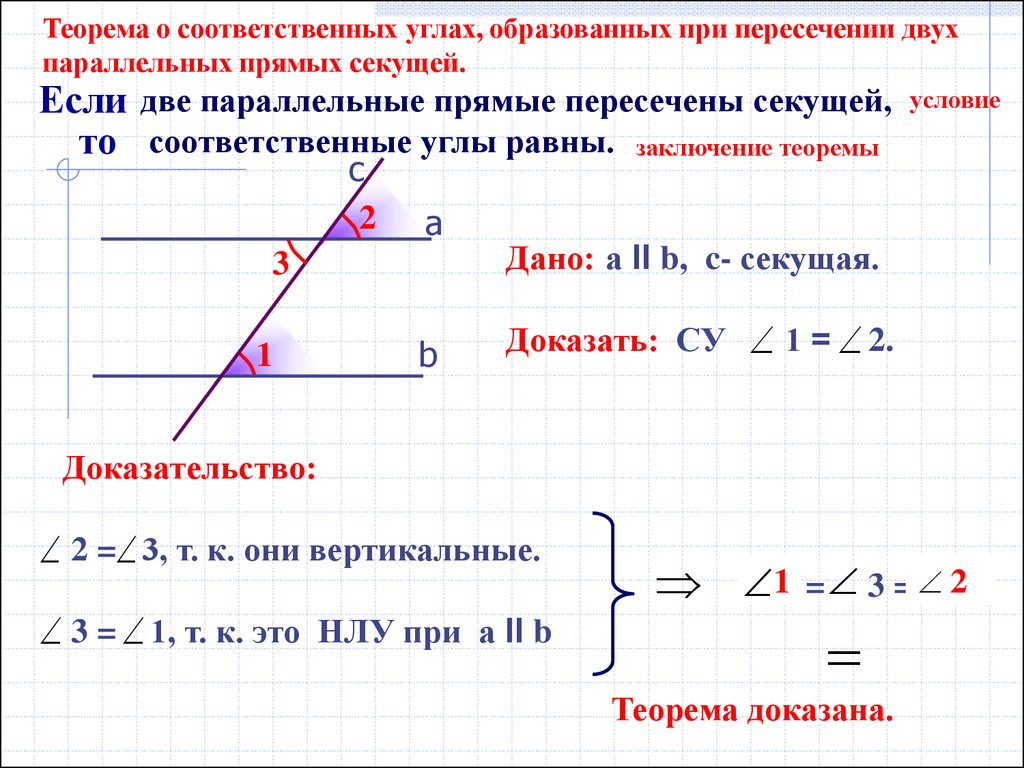
Теорема

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Дано: прямые и , АВ — секущая, 1 и 2 — соответственные, 1 = 2 (Рис.6).

Доказать: .

Доказательство:

По условию 1 = 2 и 2 = 3, т.к.они вертикальные, откуда 1 = 3, при этом углы 1 и 3 накрест лежащие, следовательно,  (см. теорему 1). Что и требовалось доказать.

3.

Теорема

Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.

Дано: прямые и , АВ — секущая, 1 и 2 — односторонние, 1 + 2 = 180⁰ (Рис.7).

Доказать: .

Доказательство:

Углы 3 и 2 — смежные, значит по свойству смежных углов 3 + 2 = 180⁰, откуда 3 = 180⁰ — 2, при этом 1 + 2 = 180⁰, откуда 1 = 180⁰ — 2, тогда 1 = 3, а углы 1 и 3 накрест лежащие, следовательно, (см.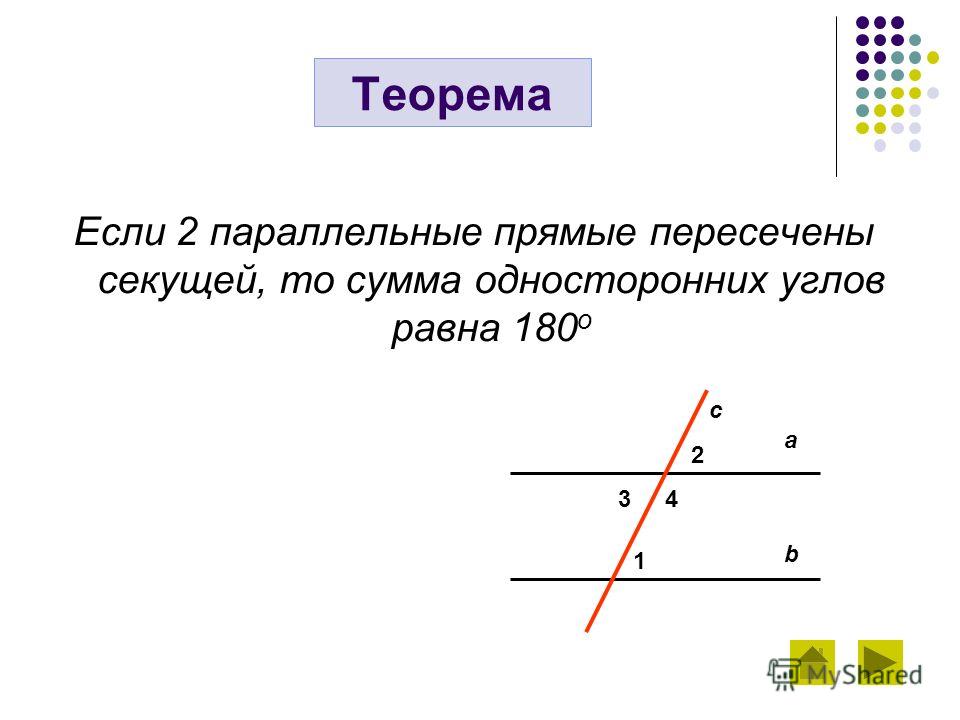 теорему 1). Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Параллельные прямые

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о накрест лежащих углах

Теорема о соответственных углах

Теорема об односторонних углах

Теорема об углах с соответственно параллельными сторонами

Теорема об углах с соответственно перпендикулярными сторонами

Параллельные прямые

Правило встречается в следующих упражнениях:

7 класс

Задание 188, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 202, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 206, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 588, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 628, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 795, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1296, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Параллельные прямые на плоскости.

Углы, возникающие при…

Привет, мой друг, тебе интересно узнать все про параллельные прямые, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое параллельные прямые, углы возникающие при пересечении прямых , настоятельно рекомендую прочитать все из категории Планометрия.

параллельные прямые (от греч. παράλληλος, буквально — «идущий рядом», «идущий вдоль другого») — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.

Две прямые называются параллельными, если они не пересекаются.
Для обозначения параллельности прямых используется символ ||.
a || b – прямая a параллельна прямой b.

Аксиома Через точку, не лежащую на данной прямой, можно провести на плоскости не боле одной прямой, параллельной данной.

Прямые BC и AD пересекаются прямой AB. Прямая AB по отношению к прямым BC и AD называется секущей.
Если точки С и D лежат в одной полуплоскости от секущей AB, то углы CBA и DAB называются внутренними односторонними.

Если точки K и M лежат в одной полуплоскости от секущей AB, то углы KBA и MAB называются внутренними накрест лежащими.

Если у пары внутренних накрест лежащих углов ( угол 1 и угол 2) один из углов заменить на вертикальный ему ( заменить угол 2 на угол 3), то полученные углы называются соответственными углами (угол 1 и угол 3) данных прямых с секущей.

В евклидовой геометрии

На чертежах параллельные линии выделяются одинаково направленными стрелками.

В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются^{. В другом варианте определения совпадающие прямые также считаются параллельными.}

Преимущество последнего определения состоит в том, что параллельность становится отношением эквивалентности^.

Параллельность прямых и обычно обозначается:

Свойства

• Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведет к геометрии Лобачевского (см. ниже).
• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
  • Соответственные углы равны (Рис.1).
  • Накрест лежащие углы равны (Рис.2).
  • Внутренние односторонние углы в сумме составляют 180° (Рис.3).

Рис. 1: Соответственные углы равны, .	Рис.2: Внутренние накрест лежащие углы равны, .	Рис.3: Односторонние углы являются дополнительными, .

• Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает все множество прямых на классы параллельных между собой прямых.
• Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от нее, есть прямая, параллельная данной.

Построение параллельных прямых

В стереометрии

В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.

В геометрии Лобачевского

Параллельные прямые в модели Пуанкаре: две зеленые прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к ней

---

---

геометрии Лобачевского в плоскости через точку вне данной прямой проходит бесконечное множество прямых, не пересекающих . Об этом говорит сайт https://intellect.icu . Прямая называется равнобежной прямой в направлении от к , если:

1. точки и лежат по одну сторону от прямой ;
2. прямая не пересекает прямую , но всякий луч, проходящий внутри угла , пересекает луч .

Аналогично определяется прямая, равнобежная в направлении от к .

Равнобежные прямые называются также асимптотически параллельными или просто параллельными. Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися^.

Свойства[править | править код]

Расходящиеся параллельные прямые имеют единственный общий перпендикуляр. Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.

Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.

В геометрии нельзя «на глазок» определить, параллельны прямые или нет. Это может быть либо дано, либо доказано. Вы уже знаете, что на плоскости справедлива теорема: «Две прямые, перпендикулярные третьей, параллельны между собой».

Есть еще три признака параллельности прямых, которые можно объединить в одну теорему, она так и называется: «Признаки параллельности прямых». Данные признаки связаны с углами, которые образуются при пересечении двух прямых третьей прямой. Это так называемые накрест лежащие углы, соответственные углы и односторонние углы.

Оказывается, что если накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые будут параллельны.

Справедливы и обратные утверждения. Если даны две заведомо параллельные прямые, которые пересечены третьей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°.

Ранее мы доказали, что через точку вне прямой можно провести единственную прямую, перпендикулярную данной. Можно также доказать, что через точку, не лежащую на прямой, можно провести прямую, параллельную данной. А вот доказать, что такая прямая — единственная, нельзя! Утверждение «Через точку, не лежащую на прямой, можно провести ЕДИНСТВЕННУЮ прямую, параллельную данной» называется аксиомой параллельных прямых. У Евклида эта аксиома называлась пятым постулатом.

На протяжении двух тысячелетий это утверждение вызывало захватывающие и драматичные споры между такими знаменитыми учеными, как Лобачевский, Гаусс и другие. Споры состояли в том, можно или нельзя доказать этот пятый постулат Евклида на основании уже известных теорем. В конце концов работы в этом направлении привели к полному пересмотру научных представлений о геометрии Вселенной.

При пересечении двух прямых третьей, которая называется секущей, образуется 4 пары накрест лежащих углов, 4 пары соответственных и 4 пары односторонних.

3 и 5; 4 и 6 — внутренние накрест лежащие углы;
1 и 7; 2 и 8 — внешние накрест лежащие углы;
1 и 5; 2 и 6; 4 и 8; 3 и 7 — соответственные углы;
3 и 6; 4 и 5 — внутренние односторонние углы;
2 и 7; 1 и 8 — внешние односторонние углы.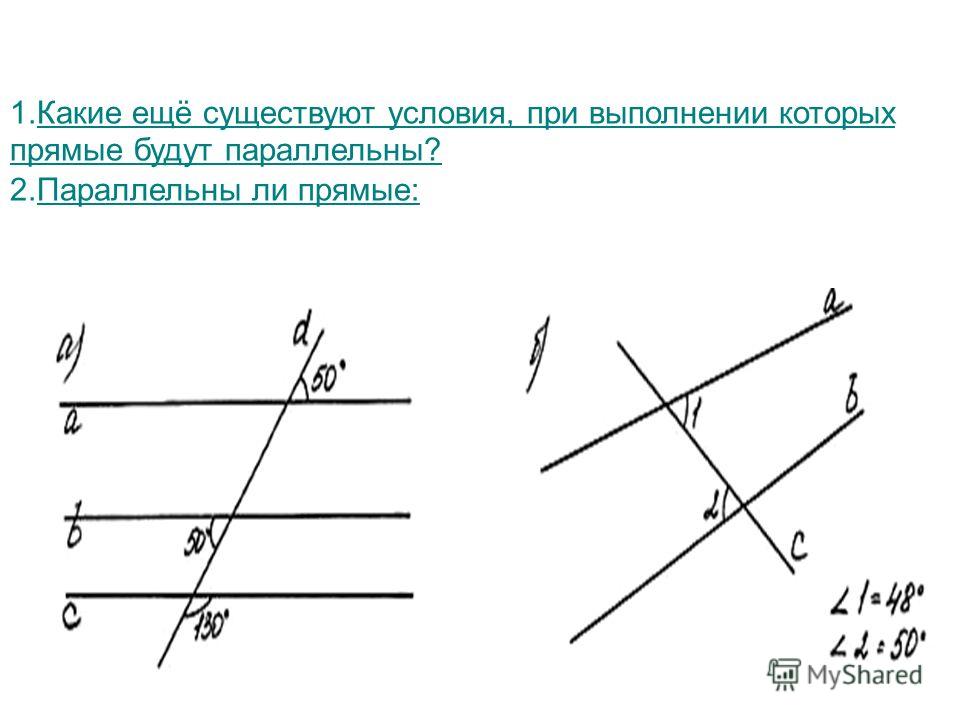

Признаки параллельности прямых. Если накрест лежащие углы равны, ши соответственные углы равны, ши сумма односторонних углов равна 180°, то прямые параллельны. В первую очередь нужно доказать, что если накрест лежащие углы равны, то прямые параллельны. Доказательство опирается на уже доказанное нами свойство: две прямые, перпендикулярные третьей, параллельны между собой. Из середины отрезка секущей опускают перпендикуляр на одну из параллельных прямых. Затем перпендикуляр продляют до пересечения со второй прямой. Из равенства полученных треугольников следует, что прямая, проходящая через перпендикуляр, будет перпендикулярна и второй прямой. Дальнейшее просто.

Через точку, не лежащую на данной прямой, МОЖНО провести прямую, параллельную данной. Опустив перпендикуляр из точки на прямую, а затем, восставив перпендикуляр к проведенной прямой, получим две прямые, перпендикулярные третьей, которые будут параллельны. А вот доказать, что такая прямая единственная, нельзя.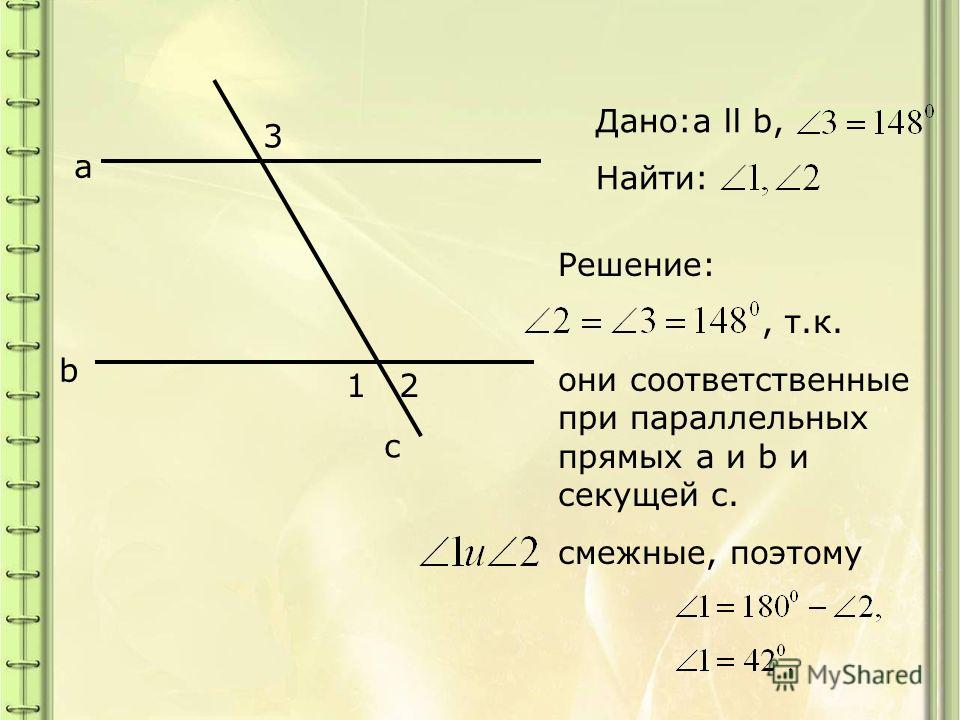 Поэтому справедлива АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: «Через точку, не лежащую на данной прямой, проходит ЕДИНСТВЕННАЯ прямая, параллельная данной».

Теорема о двух прямых, параллельных третьей. Две прямые, параллельные третьей, параллельны между собой. Если бы они пересекались, то через одну точку проходили бы две прямые, параллельные третьей.

Теорема о пересечении параллельных прямых. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Если бы эта прямая не пересекала вторую прямую, то она была бы ей параллельна. Но тогда через одну точку проходили бы две прямые, параллельные третьей. А это невозможно.

Свойства углов при параллельных прямых и секущей. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°. В первую очередь нужно доказать, что если прямые параллельны, то накрест лежащие углы равны. Пусть прямые параллельны, а накрест лежащие углы 1 и 2 не равны. Отложим угол, равный углу 2, как показано на рисунке. Получим еще одну прямую, параллельную нижней прямой (если накрест лежащие углы равны, то прямые параллельны). Но через точку нельзя провести две прямые, параллельные третьей. Значит, наше предположение неверно, и накрест лежащие углы равны. Остальное несложно.

Из указанных свойств параллельных прямых вытекает важное следствие: перпендикуляр к одной из параллельных прямых будет перпендикуляром и к другой. Доказательство следует из равенства соответственных углов.

Теорема об углах с соответственно параллельными сторонами. Углы с соответственно параллельными сторонами равны, если они одновременно острые ши одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Продлив стороны данных углов, получим две пары равных соответственных углов, откуда ∠1 = ∠2. Продлив сторону угла 1 за его вершину, получим доказательство второй части теоремы.

Теорема об углах с соответственно перпендикулярными сторонами. Углы с соответственно перпендикулярными сторонами равны, если они одновременно острые или одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Проведя перпендикулярные лучи из вершины угла 1, получим, что углы 2 и 3 равны и углы 3 и 1 дополняют один и тот же угол 4 до 90°. Значит, ∠1 = ∠3, ∠1 = ∠2. Продлив сторону угла 2 за его вершину, получим доказательство второй части теоремы.

Большинство людей убеждено, что в математике все понятия определяются и все утверждения доказываются. Но ведь каждое понятие определяют через другие понятия, а каждое утверждение доказывают, опираясь на другие утверждения. Самое интересное — что же знают и думают люди об аксиоме параллельных прямых. И все ли здесь на самом деле так просто, однозначно и очевидно, как кажется на первый взгляд?!

Что такое параллельные прямые, знают практически все. Практически все слышали про аксиому о параллельных прямых, ведь ее проходят в школе. Абсолютное большинство опрошенных нами взрослых и подростков отвечали так: аксиома о параллельных состоит в том, что параллельные прямые не пересекаются. Именно такая формулировка аксиомы о параллельных бытует в массовом сознании. Получив указанный выше ответ, следует немедленно задать следующий вопрос: а что такое параллельные прямые? Скорее всего, вам ответят, что параллельными называются такие прямые, которые не пересекаются. Многие сразу же осознают: тут что-то не так, ибо не может же аксиома заключаться в том, что непересекающиеся прямые не пересекаются. Многих из тех, кто не поймет этого сразу сам, удастся в этом убедить. Останется незначительное меньшинство, считающее, что аксиома о непересекаемости непересекающихся прямых имеет право на существование.

В традиционной Евклидовой геометрии аксиома на самом деле звучит так: «через точку, не лежащую на прямой, можно провести только одну прямую параллельную данной». А вот определение параллельных прямых: «Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются». А вот, к примеру, прямые, которые не пересекаются, но лежат в разных плоскостях, называются скрещивающимися. Но также существует много теорий, которые не сходятся и даже опровергают Евклидову (элементарную) геометрию. Одна из таких: «Геометрия Лобачевского».

7 февраля 1826 Лобачевский представил для напечатания в Записках физико-математического отделения сочинение: «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных». Но издание не осуществилось. Рукопись и отзывы не сохранились, однако само сочинение было включено Лобачевским в его труд «О началах геометрии» (1829—1830), напечатанный в журнале «Казанский вестник». Это сочинение стало первой в мировой литературе серьезной публикацией по неевклидовой геометрии, или геометрии Лобачевского.

Лобачевский считает аксиому параллельности Евклида произвольным ограничением. С его точки зрения, это требование слишком жесткое, ограничивающее возможности теории, описывающей свойства пространства. В качестве альтернативы предлагает другую аксиому: на плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную.

Вот модель этого дела:

Доказательством непротиворечивости какой-либо геометрии является построение модели. Одной из первых моделей, в которой «работает» геометрия Лобачевского, является круг. Неевклидовыми точками будут считаться те, которые расположены внутри него (заметим, в аксиоматики Лобачевского, аксиома параллельности заменена его личной аксиомой, остальные аксиомы Евклидовой геометрии остались). Точки, лежащие на окружности, исключаем из рассмотрения. Прямыми будем считать хорды данной окружности. Из точки A проведем хорду AB. Концы данной хорды лежат на окружности, следовательно, мы принять их не можем, все же точки, лежащие внутри круга и принадлежащие хорде AB являются неевклидовыми, и мы их можем принять во внимание, но какое бы малое расстояние мы не брали приближаясь к точке A, все равно будет существовать еще более маленькое, еще более близкое к точке A. Отсюда можно сделать вывод: хорда AB не имеет четко определенного начала и конца, следовательно, AB – прямая.
Пусть даны неевклидова прямая AB и точка C вне ее. Бесконечное множество прямых, проходящих через точку C, не пересекают хорду-прямую AB.

Но Лобачевский далеко не единственный разрабатывал подобные теории. Существуют модели, которые были как до, так и после открытия Лобачевского.

Над ними работали Э. Бельтрам (1868), Ф. Клейн (1871), А. Пуанкаре (1883), а также Фридрих Гаусс.

Вот представлены модели некоторых из них:

Модель Клейна

Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовем любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах.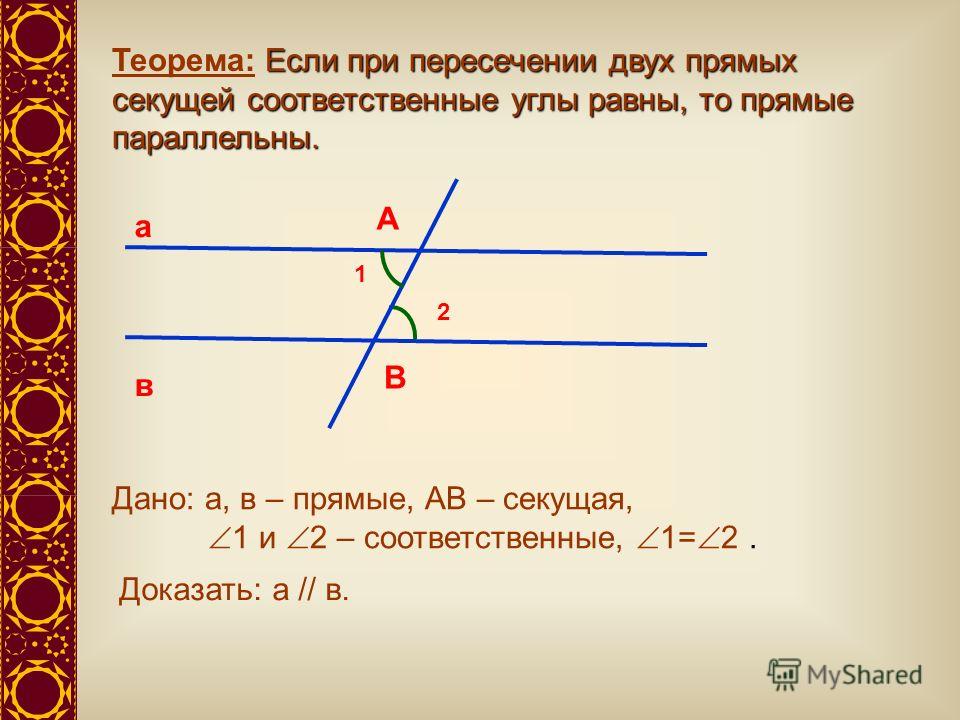

Модель Пуанкаре.

За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

Но напоминаю, что о параллельных прямых мы не только на геометрии слышим. Они встречаются в жизни везде, куда не посмотри! Параллельные грядки и ряды деревьев в посадках, рельсы и шпалы на железной дороге, параллельные эскалаторы в торговых центрах, поднимающие и опускающие нас с этажа на этаж, беговые дорожки параллельные брусья на стадионе, и даже цветы, растущие рядом, тянутся к солнцу параллельно…

Но вот еще интересная вещь: даже миры могут быть параллельными!

Команда ученых во главе с Дэвидом Deutsch Оксфорде сделали открытие в области математики. Параллельные миры действительно существуют.

Сама теория таких миров появилась еще в 1950 в США (автор — Хью Эверетт) и объяснила тайны квантовой механики, вызывавшие споры ученых. В Эвереттовской «многомирной» Вселенной каждое новое событие возможно и вызывает разделение Вселенной. Число возможных альтернативных исходов равно числу миров.

К примеру, водитель машины видит выскочившего на дорогу пешехода. В одной реальности он, избегая наезда, гибнет сам, в другой попадает в больницу и остается живым, в третьей гибнет пешеход. Число альтернативных сценариев бесконечно.

Теория была признана фантастической и забыта. Но неожиданно в Оксфорде в ходе математического исследования обнаружили, что Эверетт был на верном пути.

Согласно квантовой механике, до эксперимента про то, что внутри атома, нельзя сказать, что оно реально существует. До замеров частицы занимают неясную «суперпозицию», в которой они могут иметь одновременно верхний и нижний спин, или появляться в разных местах в одно и то же время. Наблюдение проводят для «проявления» конкретного состояния реальности, ведь и подброшенная монета приходит только в 1 положение «орел» или «решка», как только ее поймают.

Главный вывод из открытия состоит в следующем. Кустоподобные ветвящиеся структуры, возникающие при расщеплении Вселенной на параллельные версии ее самой, объясняют вероятностный характер результатов в квантовой механике. То есть неизбежно мы живем лишь в одном из множества параллельных миров, а не в единственном.

Физики Европейской организации ядерных исследований (ЦЕРН) приближаются к главному открытию XXI века, пытаясь доказать, что параллельные вселенные – это не выдумки фантастов, а реальный факт. Именно в 2013 году Большой адронный коллайдер будет выведен на рабочий максимум. Главным открытием этого момента станет создание модели рождения нашей Вселенной, а другие миры, в том числе и путешествия во времени, пока кажущихся выдумкой фантастов, по мнению ученых, приложатся. В октябрьском сообщении пресс-службы ЦЕРН поясняется, что до сих пор ученые не смогли найти доказательства существования параллельных вселенных лишь потому, что другие миры «спрятаны» в измерениях, куда не проникает свет.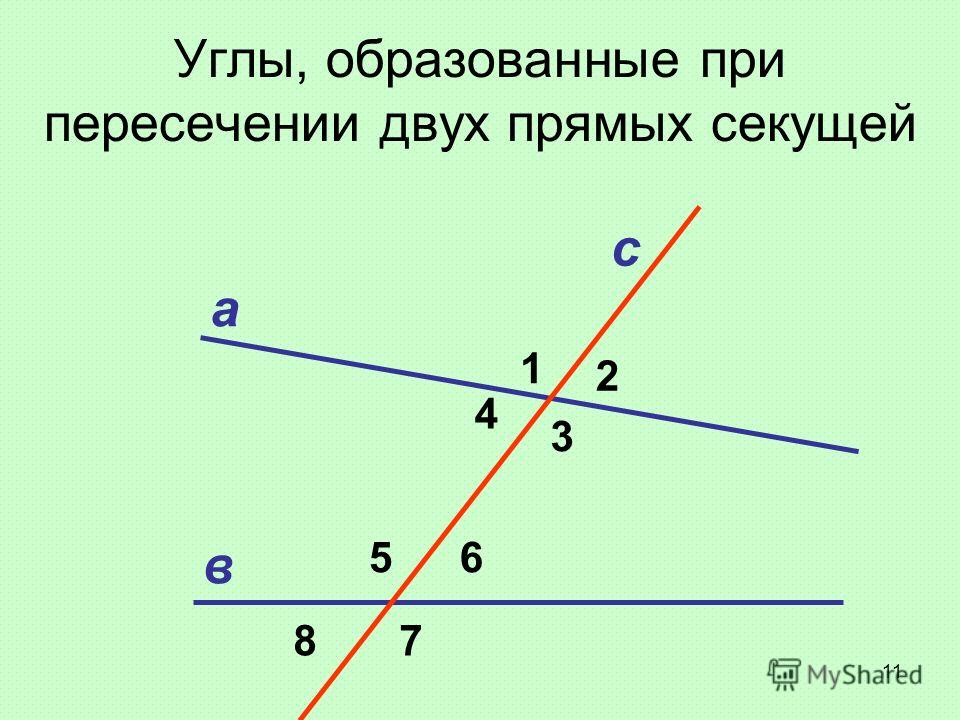 Однако воссоздание рождения Вселенной должно помочь исправить эту проблему. Несколько лет назад стало известно о сенсационной работе оксфордского теоретика Дэвида Дойча. Большой поклонник таланта Эверетта израильский физик Дойч создал математическую модель, согласно которой параллельные миры реальны. В этих вселенных не работают законы классической квантовой теории. При этом ученый верит и в возможность путешествий во времени. Пока же физики, работающие с коллайдером, опережают собственные графики.

Концепция существования иных миров, отличающихся от нашего, возникла в литературе 18 века. Пример — «Кандид» Вольтера, где один из персонажей, Панглос, заявляет ставшую крылатой фразу: «Все к лучшему в этом лучшем из миров».

В повести братьев Стругацких «Понедельник начинается в субботу» описаны путешествия персонажей в разные варианты описываемого фантастами будущего.

Также интересно описывает теорию параллельных миров Алексей Фомичев в своей серии книг «Пусть бог не вмешивается».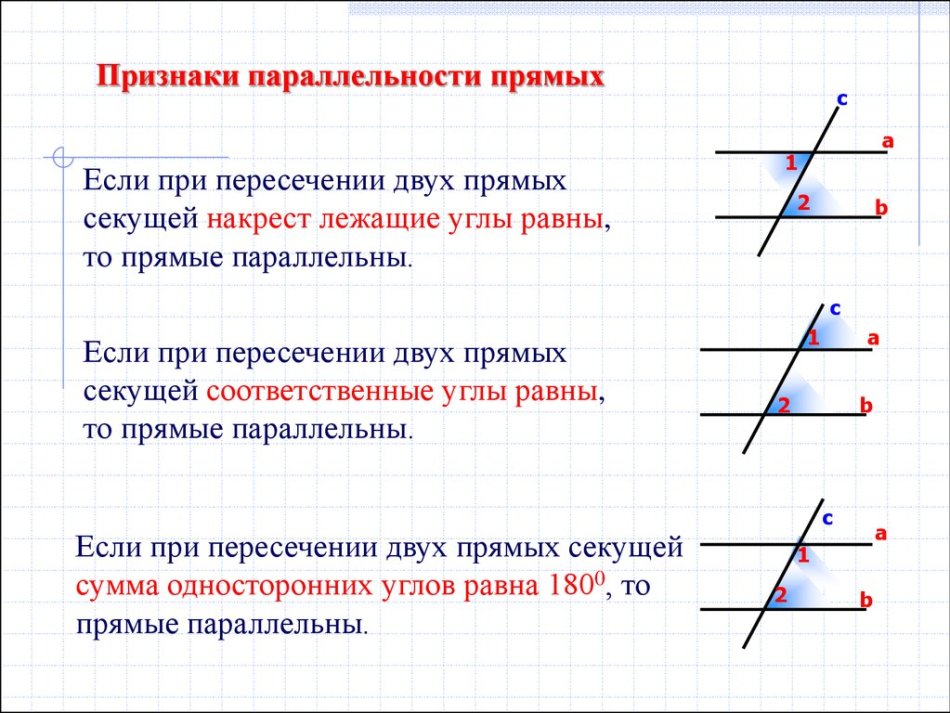

Параллельные прямые в жизни

См. также

• антипараллельность , антипараллельные прямые ,
• параллельные прямые в пространстве ,
• Параллельность плоскостей
• Параллельные плоскости
• Перпендикулярность
• Ортогональность
• Параллельная кривая ( Параллельные кривые )

Понравилась статья про параллельные прямые? Откомментируйте её Надеюсь, что теперь ты понял что такое параллельные прямые, углы возникающие при пересечении прямых и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия

Объяснение урока: Параллельные прямые и сечения: отношения углов

В этом объяснении мы узнаем, как называть и идентифицировать пары углов, образованные параллельными линии и секущие и распознавать их отношения, чтобы найти недостающий угол.

Прежде чем рассматривать ситуацию с двумя параллельными прямыми, пересекаемыми поперечной линией, пусть вспомним, что такое вертикально противоположные углы и некоторые свойства углов между двумя пересекающимися линиями.

Резюме: углы между пересекающимися линиями

Если две прямые пересекаются в одной точке, то мы называем пару углов, противоположных друг к другу «вертикально противоположными углами».

Любая пара вертикально противоположных углов конгруэнтна (имеют одинаковые мера).

Поскольку смежные углы образуют прямой угол, мы можем заметить, что сумма их мер должна быть 180∘.

Мы называем пару углов, сумма мер которых дает 180∘ дополнительные углы. Мы показали, что любые смежные углы в паре пересекающихся прямых равны дополнительные углы.

Мы можем распространить эти идеи и свойства на пересечение параллельных прямых. Напомним, что секущей параллельных прямых называется прямая, пересекающая обе прямые.

Мы видим, что 𝐿⫽𝐿 и 𝐿 является секущей этих прямых. Мы можем определить 4 пары вертикально противоположных углов, рассматривая углы вокруг точки пересечения между 𝐿 и 𝐿, и 𝐿 и 𝐿.

У нас есть 𝑎 и 𝑐, 𝑏 и 𝑑, 𝑒 и 𝑔, и 𝑓 и ℎ — пары вертикально противоположных углов. Это не единственное соотношение между этими углами. С 𝐿⫽𝐿, можно заметить, что углы, лежащие в одинаковое положение на пересечении между секущей и каждой прямой конгруэнтный. Они называются соответственными углами.

Определение: соответствующие углы

Углы, лежащие в одном и том же положении на пересечении поперечной а две прямые называются соответствующими углами.

Если пара прямых, соединенных секущей, параллельна, то соответствующие углы имеют равные меры.

Давайте теперь посмотрим на некоторые примеры использования сравнения соответствующих и вертикально противоположные углы, чтобы найти недостающие угловые меры на диаграммах.

Пример 1. Определение величины угла

На рисунке ниже найдите 𝑚∠𝐴𝐵𝐶.

Ответ

Прежде всего заметим, что нам даны два параллельных луча: 𝐴𝐷⫽𝐵𝐶.

Мы можем продолжить эти лучи, чтобы получить пару параллельных прямых и продолжить 𝐵𝐸 чтобы получить следующее.

У нас есть пара параллельных прямых, пересеченных секущей. Мы видим, что углы ∠𝐸𝐴𝐷 и ∠𝐴𝐵𝐶 занимают одинаковое положение на пересечениях между поперечные и параллельные прямые. Таким образом, эти углы равны соответствующие углы.

Напомним, что при пересечении пары параллельных прямых секущей любые соответствующие углы имеют равные меры. Следовательно, 𝑚∠𝐴𝐵𝐶=𝑚∠𝐸𝐴𝐷=65.∘

Поскольку вертикально противоположные углы и соответствующие углы имеют равные размеры когда пара линий параллельна, мы можем объединить эти два результата, чтобы увидеть несколько пар соответствующих углов.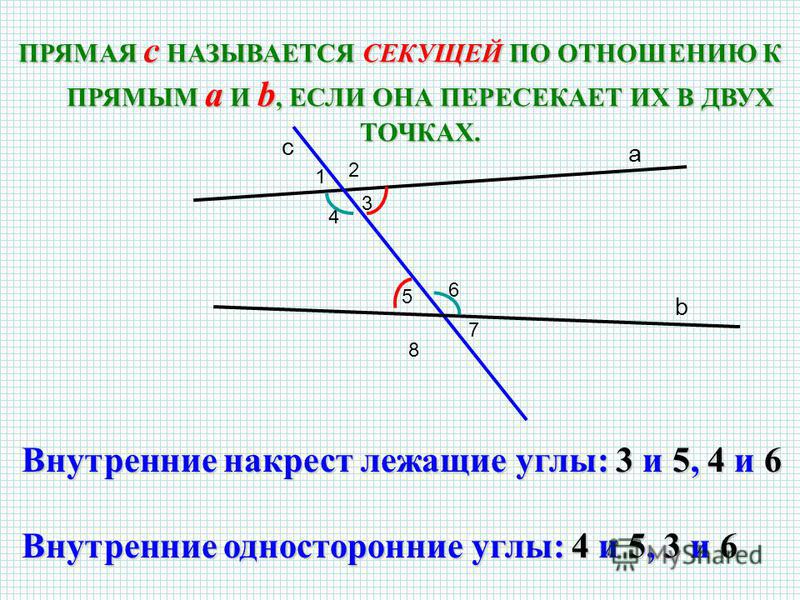

Таким образом, эти два угла имеют одинаковую меру.

Мы называем эти альтернативные внешние углы, поскольку они лежат на со стороны 𝐿 и с внешней стороны 𝐿 и 𝐿. Мы можем сформировать «альтернативные внутренние углы» таким же образом.

Таким образом, следующие углы имеют одинаковую меру.

Они называются «чередующимися внутренними углами», так как они лежат на со стороны 𝐿 и с внутренней стороны 𝐿 и 𝐿. Формально их можно определить следующим образом.

Определение: Альтернативные внутренние и внешние углы

Альтернативные внутренние углы представляют собой пары углов из любого набора из четырех углов образован поперечной линией 𝐿, пересекающей две (здесь параллельные) прямые 𝐿 и 𝐿, которые находятся по обе стороны от 𝐿 и внутри 𝐿 и 𝐿.

Альтернативные внешние углы представляют собой пары углов из любого набора из четырех углов образован поперечной линией 𝐿, пересекающей две (здесь параллельные) прямые 𝐿 и 𝐿, которые находятся по обе стороны от 𝐿 и вне 𝐿 и 𝐿.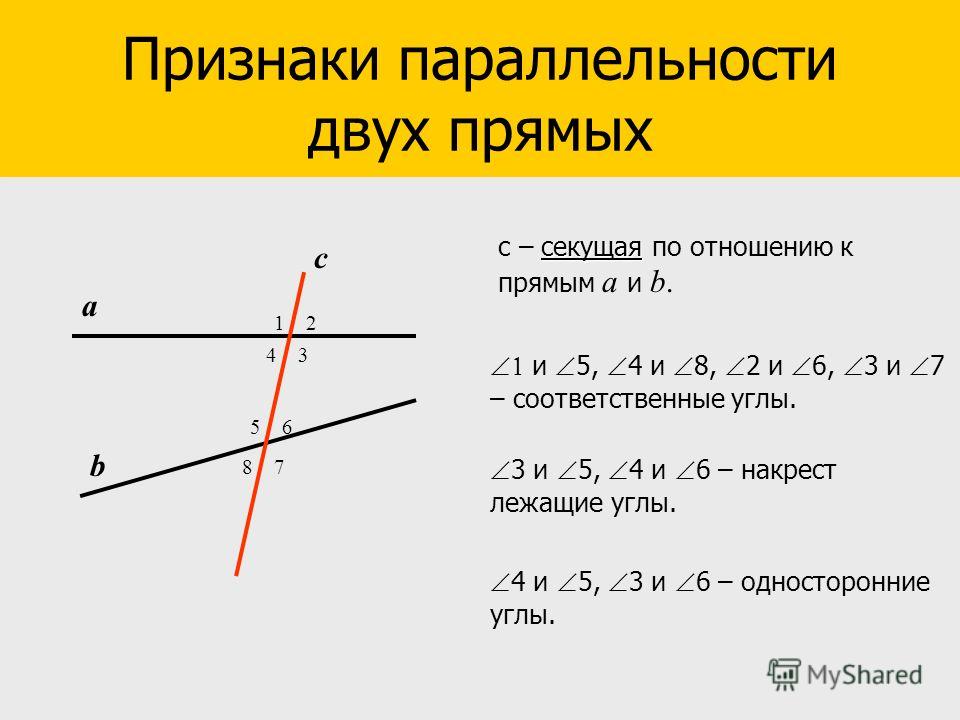

Если секущая пересекает пару параллельных прямых, то внутренние углы равны по мере. Точно так же, если секущая пересекает пару параллельных прямых, тогда противоположные внешние углы равны по размеру.

Все эти сравнения углов обычно называют теоремами о параллельных прямых.

Давайте теперь посмотрим на несколько примеров использования альтернативных внутренних и внешних углов. определить размеры углов, приведенных на чертеже.

Пример 2. Нахождение меры угла

Определите значение 𝑥 на рисунке.

Ответ

Начнем с того, что нам даны трансверсаль и пара параллельных линии. В частности, два приведенных угла являются альтернативными внутренними углами. так как они находятся внутри двух параллельных прямых (следовательно, они внутренние углов) и по обе стороны от поперечной линии.

Мы можем вспомнить, что чередующиеся внутренние углы пары параллельных прямых сечения секущей имеют одинаковую меру.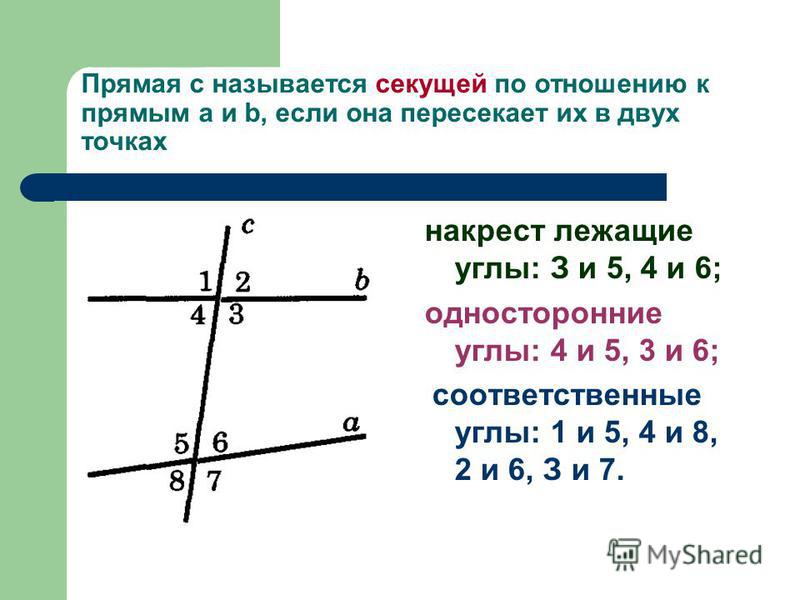 Следовательно, 𝑥=61.

Пример 3. Определение меры угла по диаграмме

Найдите значение 𝑥 на рисунке.

Ответ

Прежде всего заметим, что нам даны пара параллельных прямых и поперечная этих параллельных прямых. Мы также можем видеть, что два заданных угла лежат на по обе стороны от поперечных и вне параллельных прямых.

Подобные углы мы называем альтернативными внешними углами. В частности, мы можем Напомним, что любые альтернативные внешние углы в секущей параллельных прямых конгруэнтны.

Отсюда имеем 𝑥=124.

В нашем следующем примере мы определим отношение между двумя заданными углами которые не являются вертикально противоположными, соответствующими, альтернативными внутренними или альтернативными внешние углы.

Пример 4. Нахождение неизвестного угла в задачах с параллельными прямыми

Из информации на рисунке ниже, найти 𝑚∠𝐴𝐸𝐶.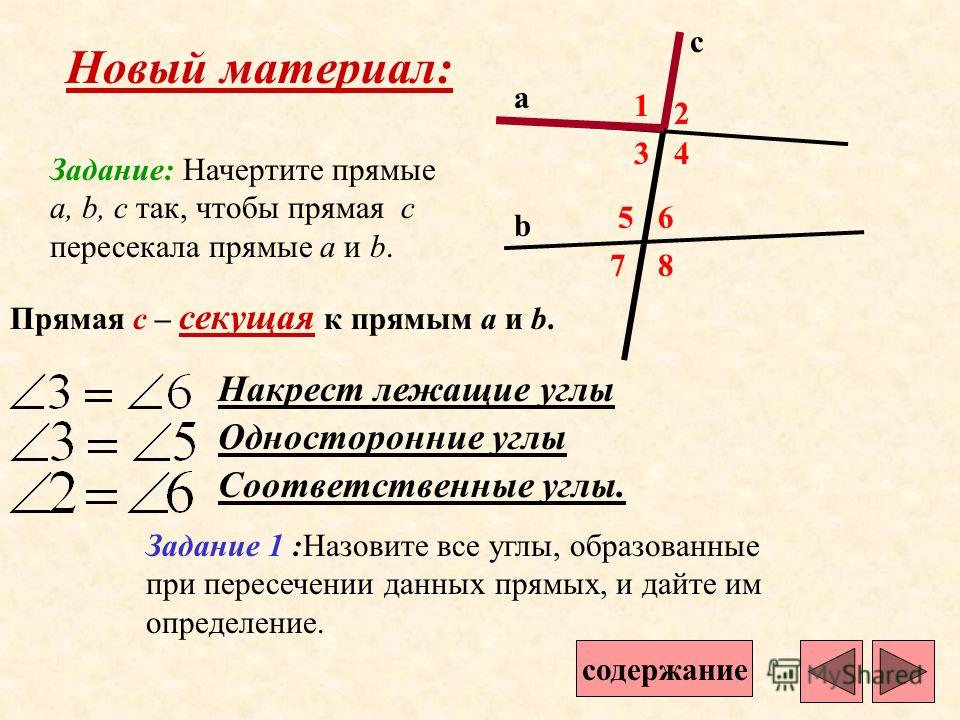

Ответ

Сначала заметим, что у нас есть три параллельные линии, каждая пара которых пересекается поперечная линия. Мы можем отметить ∠𝐴𝐸𝐶 на диаграмме, чтобы помочь нам визуализировать угол, меру которого мы пытаемся определить.

Мы видим, что ∠𝐴𝐸𝐶 состоит из двух углов ∠𝐴𝐸𝐹 и ∠𝐶𝐸𝐹. Следовательно, 𝑚∠𝐴𝐸𝐶=𝑚∠𝐴𝐸𝐹+𝑚∠𝐶𝐸𝐹.

Мы можем определить меры этих углов, используя параллельные линии. Мы видим что ∠𝐵𝐴𝐸 и ∠𝐴𝐸𝐹 — внутренние углы по разные стороны поперечный.

Мы можем вспомнить, что чередующиеся внутренние углы пары параллельных прямые, пересекаемые секущей, имеют одинаковую меру. Таким образом, 𝑚∠𝐴𝐸𝐹=𝑚∠𝐵𝐴𝐸=92.∘

Мы можем следовать аналогичному процессу для ∠𝐶𝐸𝐹. Начнем с разметки угла соответствующий ∠𝐶𝐸𝐹 на диаграмме.

Так как противоположные внутренние углы имеют одинаковую меру и меры углы на прямой складываются в 180∘, мы имеем 𝑚∠𝐶𝐸𝐹+131=180𝑚∠𝐶𝐸𝐹=180−131=49. ∘∘∘∘∘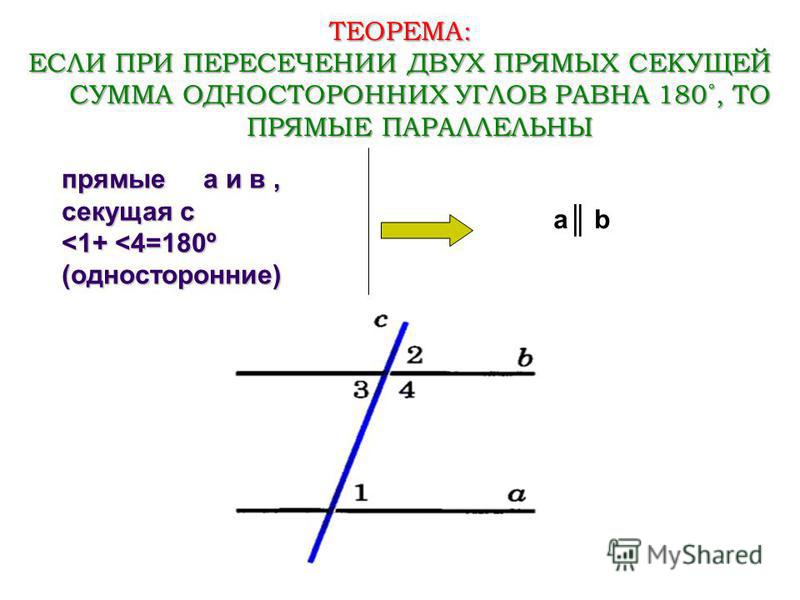

Теперь мы можем сложить вместе меры этих углов: 𝑚∠𝐴𝐸𝐶=𝑚∠𝐴𝐸𝐹+𝑚∠𝐶𝐸𝐹=92+49=141.∘∘∘

В нашем следующем примере мы найдем неизвестный угол, используя параллельные прямые теоремы.

Пример 5. Нахождение неизвестного угла в задачах с параллельными прямыми

На рисунке ⃖⃗𝐸𝑁 пересекает ⃖⃗𝐴𝐵 и ⃖⃗𝐶𝐷 в 𝑀 и 𝐹 соответственно. Находить 𝑚∠𝐸𝐹𝐶.

Ответ

Сначала заметим, что у нас есть две параллельные прямые, пересеченные поперечной линией. Однако, ∠𝐸𝑀𝐵 и ∠𝐸𝐹𝐶 не соответствуют друг другу, альтернативные внутренние или альтернативные внешние углы. Итак, нам нужен дополнительный шаг, чтобы позволить нам найти мера ∠𝐸𝐹𝐶. Мы можем отметить этот угол на схема, как показано.

Есть несколько методов, которые мы можем использовать, чтобы найти меру этого угла. Один заключается в том, чтобы заметить, что ∠𝐸𝑀𝐵 и ∠𝑁𝐹𝐶 находятся по обе стороны от поперечной и снаружи от параллельных прямых. Итак, они альтернативные внешние углы.

Тогда мы можем вспомнить, что чередующиеся внешние углы в поперечной параллели линии совпадают. Итак, 𝑚∠𝑁𝐹𝐶=84∘.

Теперь мы можем отметить, что ∠𝐸𝐹𝐶 и ∠𝑁𝐹𝐶 объединить, чтобы сделать прямой угол, поэтому они являются дополнительными углами. Таким образом, 𝑚∠𝐸𝐹𝐶+𝑚∠𝑁𝐹𝐶=180.∘

Мы знаем, что 𝑚∠𝑁𝐹𝐶=84∘, поэтому 84+𝑚∠𝐸𝐹𝐶=180.∘∘

Вычитание 84∘ с каждой стороны дает нам 𝑚∠𝐸𝐹𝐶=96.∘

Мы могли бы также рассмотреть любой другой угол, связанный с обоими ∠𝐸𝑀𝐵 и ∠𝐸𝐹𝐶, конгруэнтные одному из них, и тогда мы обнаружили бы, что оно дополняет другое.

В наших предыдущих двух примерах мы смогли показать, что некоторые углы в секущие параллельных прямых являются дополнительными. В общем, полезно Обратите внимание, что внутренние углы по одну сторону от секущей равны дополнительный.

Мы можем доказать этот результат, рассмотрев трансверсаль 𝐿 параллельных прямых 𝐿 и 𝐿 с угол измеряется, как показано. Мы также можем отметить конгруэнтные углы.

Мы знаем, что смежные углы дополнительные, поэтому 𝑎+𝑏=180.∘

Мы также знаем, что углы меры 𝑎 и 𝑒 являются соответствующими углами. Таким образом 𝑎=𝑒.

Мы можем подставить это в дополнительное уравнение, чтобы получить 𝑒+𝑏=180.∘

Мы можем использовать аналогичное доказательство, чтобы показать, что 𝑐+ℎ=180.∘

Мы также можем показать, что внешние углы по одну сторону от трансверсали также являются дополнительными. Мы доказали следующее.

Теорема: Совнутренние и ковнешние углы секущей параллельных прямых

Совнутренние углы (т. строки являются дополнительными: 𝑏+𝑒=180,𝑐+ℎ=180.∘∘

Совнешние углы по одну сторону от секущей параллельных прямых равны дополнительный: 𝑎+𝑓=180,𝑑+𝑔=180.∘∘

Теперь рассмотрим пример использования этого свойства для определения меры угол на заданной фигуре.

Пример 6. Нахождение неизвестного угла в задачах на параллельные прямые

Найти 𝑚∠𝐷.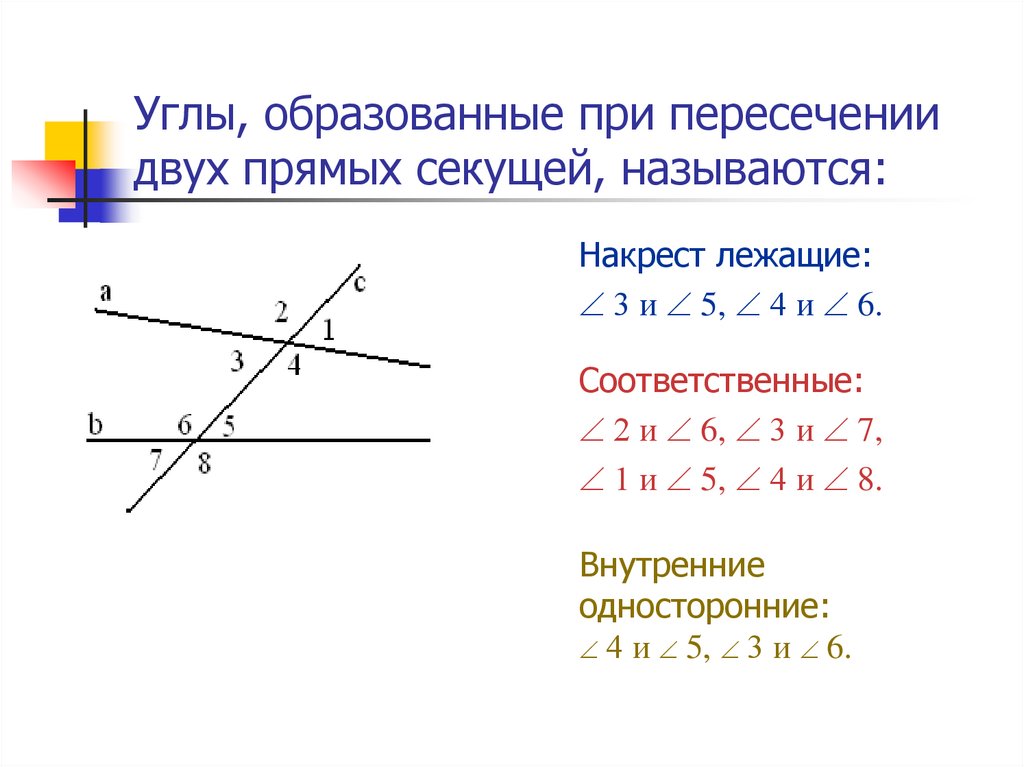

Ответ

Нам дана мера только одного угла, поэтому мы должны начать с попытки использовать этот угол вместе с параллельными прямыми и секущими, чтобы определить меры других углов на диаграмме. Мы можем отметить, что ∠𝐶 — альтернативный внутренний угол ∠𝐶𝐵𝐸.

Мы можем вспомнить, что чередующиеся внутренние углы на поперечной паре параллельные прямые имеют одинаковую меру, поэтому 𝑚∠𝐶𝐵𝐸=124∘.

Затем мы можем определить 𝑚∠𝐴𝐵𝐶, заметив, что это внутренний угол с ∠𝐶 так как они оба лежат внутри пары параллельных прямых на одной стороне поперечной.

Вспомним, что сумма мер внутренних углов равна 180∘, так что 124+𝑚∠𝐴𝐵𝐶=180𝑚∠𝐴𝐵𝐶=180−124=56.∘∘∘∘∘

На диаграмме нам сказано, что 𝐵𝐹 делит этот угол пополам, поэтому каждый из этих углы имеют меру 1242=62∘∘.

Затем мы можем определить 𝑚∠𝐴𝐵𝐶, вспомнив, что меры углов на прямой сумме равны 180∘. Таким образом, 180=𝑚∠𝐴𝐵𝐶+62+62.∘∘∘

Теперь у нас есть меры двух внутренних углов четырехугольника 𝐴𝐵𝐶𝐷. Мы можем определить меру ∠𝐷, найдя меру ∠𝐴 и используя сумму внутренних углов четырехугольника, 360∘.

Мы можем найти 𝑚∠𝐴, заметив, что ⃖⃗𝐴𝐷⫽⃖⃗𝐵𝐹 и ∠𝐴 — соответствующий угол 𝑚∠𝐸𝐵𝐹.

Следовательно, они оба имеют меру 62∘.

Теперь мы можем найти 𝑚∠𝐷, используя сумму внутренних углов в 𝐴𝐵𝐶𝐷. У нас есть 𝑚∠𝐴+𝑚∠𝐵+𝑚∠𝐶+𝑚∠𝐷=36062+56+124+𝑚∠𝐷=360𝑚∠𝐷=360−62−56−124=118.∘∘∘∘∘∘∘

Мы показали ряд соотношений, включающих углы в поперечной плоскости. параллельные линии. Однако мы можем рассмотреть и обратное. Например, если поперечная имеет конгруэнтные соответствующие углы с парой прямых, будут ли эти прямые параллельны? Возьмем, к примеру, пересечение двух прямых. 𝐿 и 𝐿 с конгруэнтными соответствующими углы.

Кажется, что 𝐿 и 𝐿 параллельны; однако этого недостаточно для доказательства утверждения. Мы можем доказать это, вместо этого при условии, что прямые не параллельны. Поскольку мы предполагаем, что они не параллельны, они должны пересекаться в точке, которую мы будем называть 𝐶. Если обозначить точки пересечение между прямыми и секущими 𝐴 и 𝐵, то 𝐴𝐵𝐶 является треугольник.

Мы можем определить меры двух из этих углов, используя дополнительные углов и вертикально противоположных углов.

Мы видим, что углы внутри параллельных прямых имеют меры, которые сумма 180∘. С сумма внутренних углов треугольника должна быть равна 180∘, у нас не может быть двух дополнительные углы как два внутренних угла треугольника. Это означает не может быть точки одновременно на 𝐿 и 𝐿, поэтому строки параллельны. Мы показали, что любые две прямые с конгруэнтными соответствующими углы параллельны.

То же верно, если они имеют конгруэнтные чередующиеся внутренние или внешние углы или если внутренние углы дополнительные. Мы можем следовать тому же доказательству или показать, что в любом случае прямые будут иметь конгруэнтные соответствующие углы. Мы показали следующий результат.

Свойство: соответствие соответствующих углов двух прямых другой прямой Подразумевается, что они параллельны

Если две линии имеют конгруэнтное соответствие, альтернативную внутреннюю или альтернативную внешнюю сторону углы с одной линией, то они должны быть параллельны.

Если две линии имеют дополнительные внутренние или внешние углы, то они должны быть параллельным.

В нашем последнем примере мы будем использовать это свойство, чтобы определить, что две строки параллельно.

Пример 7. Определение того, что две линии параллельны, поскольку чередующиеся Внутренние углы конгруэнтны

Заполните пропуск: Из диаграммы можно сделать вывод, что 𝐿 является 𝐿.

Ответ

Мы видим, что 𝐿 и 𝐿 — трансверсали из двух строк 𝐿 и 𝐿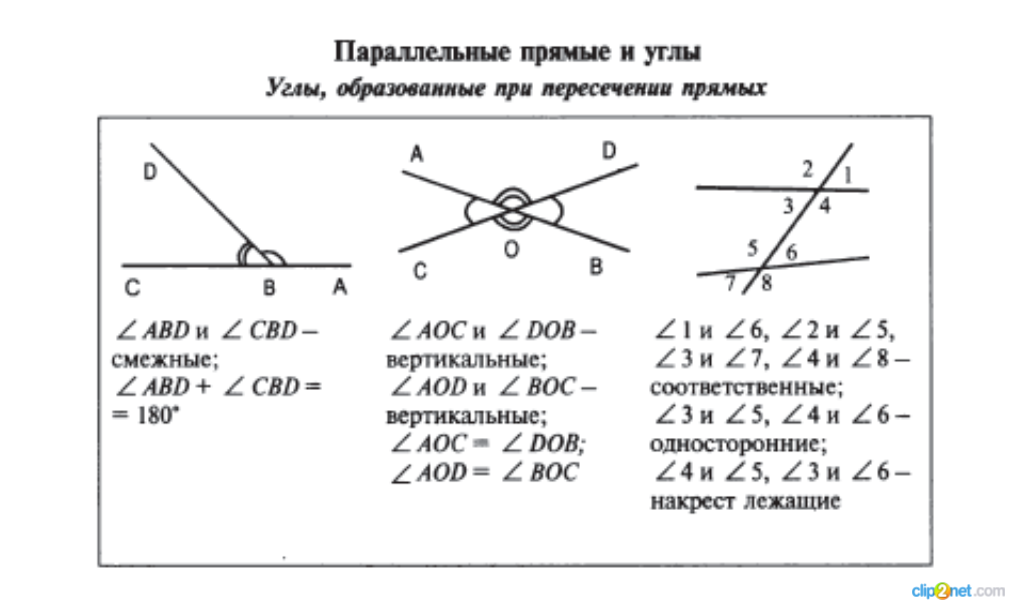. Мы можем найти несколько углов меры с использованием заданных углов. Например, мы можем определить меру угла, альтернативного внутреннему углу измерения 30∘ следующим образом.

Мы знаем, что сумма углов на прямой равна 180∘, поэтому следующее угол имеет меру 50∘.

Сумма внутренних углов треугольника равна 180∘, так что финал угол в треугольнике имеет меру 30∘.

Теперь мы видим, что у нас есть конгруэнтные альтернативные внутренние углы поперечной 𝐿 строк 𝐿 и 𝐿.

Тогда мы можем вспомнить, что если две прямые имеют конгруэнтные чередующиеся внутренние углы с секущей, то они должны быть параллельны.

Следовательно, 𝐿⫽𝐿.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые точки

• Углы, лежащие в одном и том же положении на пересечении секущей а две прямые называются соответствующими углами.
• Соответствующие углы в секущей параллельных прямых равны.
• Альтернативные внутренние углы представляют собой пары углов из любого набора из четырех углов образован поперечной линией, пересекающей две линии 𝐿 и 𝐿 по обе стороны от трансверсали и на внутри 𝐿 и 𝐿.
• Альтернативные внешние углы представляют собой пары углов из любого набора из четырех углов образован поперечной линией, пересекающей две линии 𝐿 и 𝐿 по обе стороны от трансверсали и на снаружи 𝐿 и 𝐿.
• Если секущая пересекает пару параллельных прямых, то внутренние углы равны по мере. Точно так же, если секущая пересекает пару параллельных прямых, тогда противоположные внешние углы равны по размеру.
• Если поперечная пересекает пару параллельных прямых, то внутренние углы на те же стороны трансверсали являются дополнительными.
• Верно обратное утверждение теоремы: если соответствующие углы чередуются внутренние углы или чередующиеся внешние углы, образованные поперечной разрезкой две прямые равны, то прямые, пересеченные поперечной, параллельны.

Теорема о

параллельных прямых: значение, примеры и типы

Изучая геометрию, мы узнали о концепции линий. Эта фундаментальная концепция также встречается повсюду в повседневной жизни, например, на сторонах дверей и окон или на любой плоской поверхности с прямым краем. Часто мы видим две одинаковые параллельные линии, такие как пешеходный переход, рельсы или лестницы.

Параллельные прямые являются важной частью изучения четырехугольников, таких как, например, параллелограммы, которые представляют собой четырехсторонние фигуры с параллельными противоположными сторонами. В этой статье мы изучим теоремы и постулаты о параллельных прямых. Но сначала давайте определим параллельные линии.

Копланарные прямые, равноудаленные друг от друга и никогда не пересекающиеся ни в одной точке, известны как параллельных прямых.

Параллельные прямые, StudySmarter Originals

Теоремы об углах и параллельных прямых

Мы можем делать утверждения относительно параллельных прямых на основе углов, которые они образуют. Другими словами, мы можем доказать, что прямые параллельны, основываясь на углах, и наоборот, мы также можем доказать конгруэнтность углов, основываясь на существовании параллельных прямых. Прежде чем двигаться дальше, давайте рассмотрим некоторые основные определения и понятия, касающиеся параллельных линий. Во-первых, как отличить параллельные прямые от непараллельных?

Непараллельные линии — это две или более линий, которые не находятся на одинаковом расстоянии и пересекаются в некоторой точке или которые пересекутся в некоторой точке.

Непараллельные линии, StudySmarter Originals

Вам может быть интересно, как параллельные линии соотносятся с углами, если они никогда не пересекаются? Ответ: трансверсали: поперечные линии играют важную роль в определении углов, связанных с параллельными линиями.

Прямая, проходящая через две прямые в разных точках одной плоскости, называется поперечная линия .

Transversal, Studysmarter Originals

Конгруэнтность углов на основе параллельных прямых

Сначала мы рассмотрим важные утверждения, демонстрирующие конгруэнтность углов на основе параллельных прямых.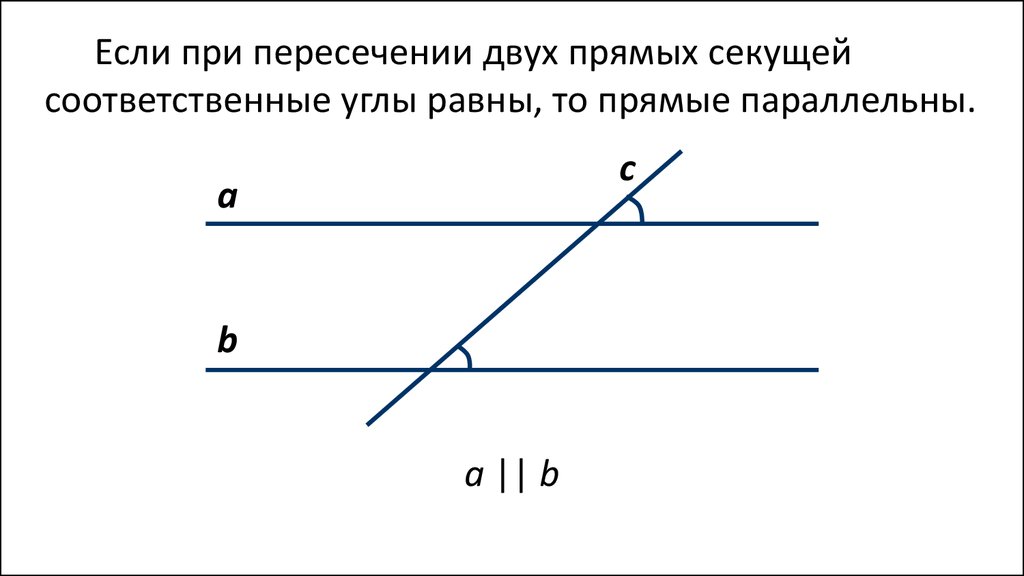

Теорема 1 : Альтернативный внутренний угол

Если две параллельные прямые на плоскости пересечены секущей, то образующиеся альтернативные внутренние углы конгруэнтны (одинаковы). Обратите внимание, что внутренние углы — это те, которые находятся внутри параллельных прямых.

Альтернативные внутренние углы, StudySmarter Originals

Углы, образованные на противоположной стороне поперечной и находящиеся на внутренней стороне параллельных линий, называются альтернативными углами.

Теорема 2 : Альтернативный внешний угол

Если две параллельные прямые на плоскости пересечены секущей, то образованные внешние углы равны. Обратите внимание, что внешние углы — это те, которые находятся внутри параллельных прямых.

Альтернативные внешние углы, StudySmarter Originals

Теорема 3 : Смежные внутренние углы

Если две параллельные прямые на плоскости пересечены секущей, то последовательные внутренние углы, образованные на одной стороне, являются дополнительными.

Последовательные внутренние углы, StudySmarter Originals

Два угла являются дополнительными, если сумма величин обоих углов составляет 180°.

Теорема 4 : Последовательные внешние углы

Если две параллельные прямые на плоскости пересечены секущей, то последовательные внешние углы, образованные на одной стороне, являются дополнительными. 9Теорема 5

Соответствующие углы, StudySmarter Originals

Углы, образованные на совпадающих углах параллельных прямых, образованных секущими, называются соответствующими углами.

Доказательство параллельности прямых на основе углов

Теперь обратимся к обратной части вышеупомянутых теорем.

Теорема 6 : Альтернативные внутренние углы обратные

Если две прямые на плоскости пересечены секущей так, что образующиеся чередующиеся внутренние углы конгруэнтны, то эти две прямые параллельны.

Параллельные прямые с чередующимися внутренними углами, StudySmarter Originals

Теорема 7 : Противоположные чередующиеся внешние углы

Если две прямые на плоскости пересечены секущей так, что образующиеся противоположные внешние углы равны, то эти две прямые параллельны. Теорема 8. две линии параллельны.

Параллельные линии с последовательными внутренними углами, StudySmarter Originals

Теорема 9 : Последовательные внешние углы обратны

Если две прямые на плоскости пересечены секущей так, что сумма последовательных внешних углов равна 180°, то эти две прямые параллельны.

Параллельные прямые с последовательными внешними углами, StudySmarter Originals

Теорема 10 : Соответствующие углы обратные .

Параллельные прямые с соответствующими углами, StudySmarter Originals

Углы и параллельные прямые: Решенные примеры

Здесь мы рассмотрим некоторые примеры, касающиеся вышеупомянутых теорем.

На данном рисунке p∥q и m∥n. И m∠3=102°.

Найдите (a) m∠5 (b) m∠6 (c) m∠14

Параллельные прямые с двумя секущими, StudySmarter Originals

Решение : (a) Здесь m∥n и прямая p работают как трансверсальные для прямых m и n. Теперь, применяя теорему о чередующихся внутренних углах, мы получаем ∠3≅∠5.

⇒∠3=∠5⇒∠5=102°

(b) Аналогично (a), p является секущей параллельных прямых m и n. Воспользуемся теоремой о последовательном внутреннем угле. Таким образом, ∠3 и ∠6 являются дополнительными.

⇒∠3+∠6=180°⇒∠6=180°-∠3⇒∠6=180°-102°∴∠6=78°

(c) Мы будем использовать ∠6 для расчета ∠14 так как оба лежат на одной линии n . Здесь ∠6 и ∠14 лежат на параллельных прямых p и q соответственно, а прямая n служит секущей для обеих прямых. Таким образом, ∠6 и ∠14 образуют соответствующие углы.

Итак, из теоремы о соответствующих углах оба угла равны.

⇒∠6≅∠14∴∠14=78°

Теперь давайте разберемся с некоторыми дополнительными важными теоремами о параллельных прямых и взглянем на их доказательства.

Теорема о перпендикулярных поперечных для параллельных прямых

Следующее утверждение представляет связь между перпендикулярными поперечными и параллельными прямыми.

Теорема 11 : Теорема о перпендикулярной поперечной

Если две прямые на плоскости пересекаются перпендикулярной секущей, то обе прямые параллельны.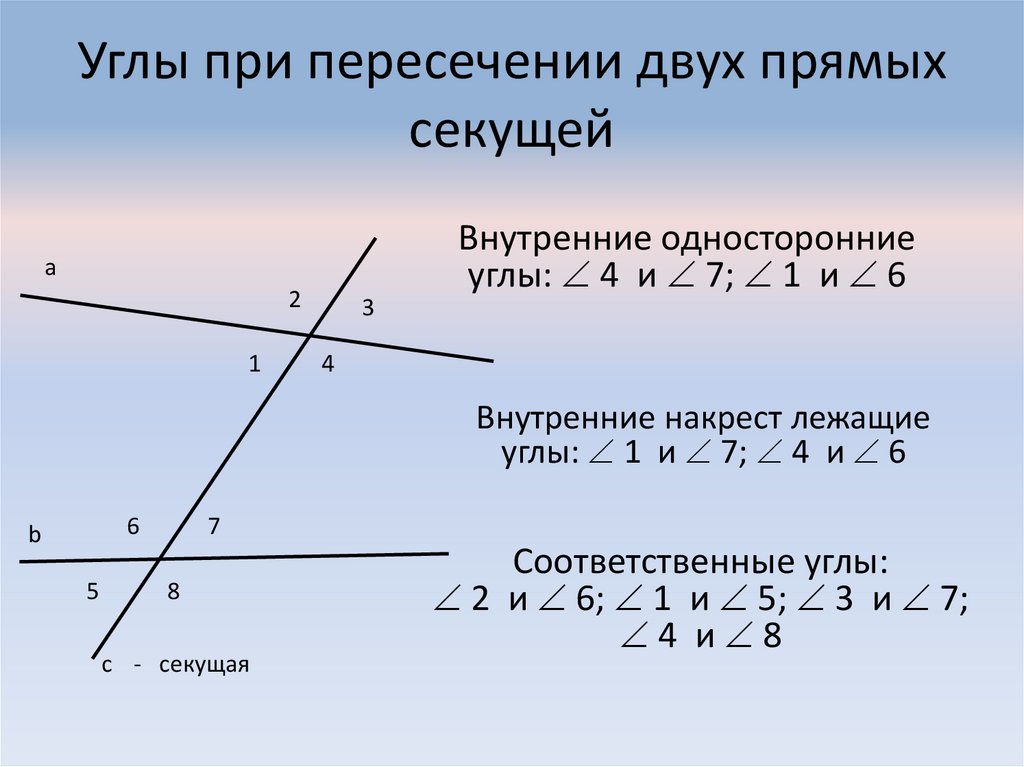

Параллельные прямые с перпендикулярными секущими, StudySmarter Originals

Доказательство : Здесь трансверсаль t перпендикулярна как прямой p, так и прямой q, т. е. t⊥p,t⊥q

Теперь нам нужно доказать, что p и q параллельны. Поскольку трансверсаль t перпендикулярна p, отсюда следует, что m∠1=90°. Точно так же, поскольку трансверсаль t перпендикулярна q, мы получаем m∠2=90°.

⇒m∠1= m∠2

Теперь, используя определение конгруэнтности, которое гласит, что если мера двух углов равна, то оба угла конгруэнтны друг другу, мы получаем ∠1≅∠2.

Из рисунка ясно видно, что оба угла являются соответствующими углами. Таким образом, используя теорему 10, теорему об обращении соответствующих углов, мы можем прямо сказать, что p∥q. То есть и прямая p, и прямая q параллельны друг другу. Следовательно, теорема доказана.

Теорема о транзитивности параллельных прямых

Одно из других важных утверждений о параллельных прямых использует отношение транзитивности.

Теорема 11 : Транзитивность параллельных прямых

Если две прямые на плоскости параллельны одной и той же прямой, то все прямые параллельны друг другу.

Транзитивное свойство параллельных прямых, StudySmarter Originals

Доказательство : Теперь давайте докажем, что прямая, общая с другими параллельными прямыми, параллельна. То есть p∥q,q∥r.

Тогда, без ограничения общности, мы можем сказать, что прямая q лежит между прямой p и прямой r.

Теперь нам нужно доказать, что прямая p и r параллельны. т. е. p∥r

Здесь мы воспользуемся методом противоречия , чтобы доказать этот результат, который показывает, что утверждение истинно, просто доказывая, что оно не может быть ложным. Следовательно, чтобы доказать, что прямая p и r параллельны, мы сначала предположим, что прямая p и r являются , а не параллельными прямыми (противоречие). Это означает, что линия p и линия r должны пересекаться друг с другом, исходя из определения непараллельных линий. Теперь, поскольку линия q лежит между линиями p и r, при пересечении этих линий линия p или линия r также должны были бы пересечься с линией q. Однако, поскольку линия q параллельна как линии p, так и линии r, это невозможно. Следовательно, наше предположение о том, что прямая p и r не параллельны, неверно. Методом от противного прямые p и прямые r параллельны друг другу. Итак, мы доказали, что если p∥q и q∥r, то p∥r.

Рассмотрим теорему о пропорциональности между тремя параллельными прямыми.

Теорема 12 : Теорема о трех параллельных прямых

Если три параллельные прямые пересечены двумя секущими, то отрезки, образованные на этой секущей, имеют равные пропорции.

Три параллельные прямые, StudySmarter Originals

Доказательство : Здесь прямые p, q и r параллельны друг другу. И эти прямые пересекаются двумя секущими t и s в точках A, B, C и D, E и F соответственно.

Теперь нам нужно показать, что ABBC=DEEF.

Чтобы доказать это, воспользуемся теоремой о пересечении. Нам дано, что прямые p, q и r параллельны. Затем из точки A строим прямую AH, параллельную DF.

Три параллельные линии с третьей поперечной, StudySmarter Originals

Мы можем заметить, что левая часть рисунка точно соответствует теореме о пересечении. Итак, из теоремы о пересечении мы получаем:

ABBC=AGGH

Поскольку мы построили параллельную прямую AH, мы знаем, что AH∥DF.

Нам также известно, что прямые p, q и r параллельны. Таким образом, по определению параллелограмма ADEG и EFHG являются параллелограммами. Теперь из свойств параллелограмма мы знаем, что противоположные стороны равны.

⇒AG=DE,GH=EF

Используя свойство транзитивности, мы можем напрямую подставить и получить следующий результат.

ABBC=AGGH=DEEF

⇒ABBC=DEEF

Следовательно, можно сказать, что отрезки, образованные на обеих трансверсалях, находятся в равных пропорциях.

Решенные примеры с теоремами о параллельных прямых

Применим приведенные выше теоремы о параллельных прямых к некоторым примерам.

Каждая линия параллельна следующей непосредственной линии на рисунке ниже. Затем покажите, что K1∥K4.

Пример свойства транзитивности с четырьмя параллельными прямыми

Решение : Дано, что K1∥K2 и K2∥K3. Затем, применяя теорему о транзитивности параллельных прямых, мы получаем, что K1∥K3. Теперь также дано, что K3∥K4, и мы уже нашли K1∥K3. Итак, снова применяя транзитивность теоремы о параллельных прямых, мы знаем, что K1 ∥К4.

На следующем рисунке две линии a и c перпендикулярны линии s. Также дано, что a∥b. Затем докажите, что b∥c.

Пример параллельных прямых, StudySmarter Originals

Решение : Здесь дано, что прямая s пересекает прямые a и c перпендикулярно. Таким образом, применяя теорему о перпендикулярных трансверсалях, мы получаем a∥c. Нам дано a∥b, и мы уже нашли, что a∥c. Тогда из теоремы о транзитивности параллельных прямых немедленно доказывается, что b∥c.

Теорема о параллельных прямых. Ключевые выводы

• Если две параллельные прямые пересечены секущей, то внутренние углы равны. И наоборот, если две прямые пересечены секущей так, что смежные внутренние углы равны, то эти две прямые параллельны.
• Если две параллельные прямые пересечены секущей, то внешние углы равны. Наоборот, если две прямые пересечены секущей так, что противоположные внешние углы равны, то прямые параллельны.
• Если две параллельные прямые пересечены секущей, то последовательные внутренние углы и последовательные внешние углы на одной стороне являются дополнительными. Обратное этому тоже существует.
• Две прямые на плоскости, пересеченной секущими, параллельны тогда и только тогда, когда соответствующие углы равны.
• Если две прямые на плоскости пересечены перпендикулярной секущей, то обе прямые параллельны.
• Если две прямые на плоскости параллельны одной и той же прямой, то все прямые параллельны друг другу.
• Если три параллельные прямые пересечь двумя секущими, то отрезки, образованные секущими, имеют равные пропорции.

Parallel Lines and Transversal Lines

To do 3 min read 8 min video

Parallel Lines and Transversal Lines

Contents

• Parallel Lines and Transversal Lines
• Example
  • Question
  • Use the properties of parallel lines найти все равные углы на чертеже
  • Определить неизвестные углы
  • Определить, являются ли \(EF\параллельными CG\)

Две прямые пересекаются, если они пересекаются в одной точке. Например, на транспортной развязке пересекаются две или более улиц; середина перекрестка является общей точкой между улицами.

Параллельные линии всегда находятся на одинаковом расстоянии друг от друга и обозначаются символами со стрелками, как показано ниже.

В письме мы используем две вертикальные линии, чтобы указать, что две линии параллельны:

\[AB \parallel CD \text{ и } MN \parallel OP\]

Поперечная прямая пересекает две или более параллельных прямых. На приведенной ниже диаграмме \(AB\параллельно CD\) и \(EF\) — это поперечная линия.

Свойства углов, сформированных этими пересекающими линиями, суммированы в следующей таблице:

Наименование угла	. Разработка	.0244	Примечания
Внутренние углы	Углы, лежащие между параллельными линиями.	\(\шляпа{а}\), \(\шляпа{b}\), \(\шляпа{с}\) и \(\шляпа{d}\) — внутренние углы.	Интерьер означает внутри.
Внешние углы	Углы, лежащие вне параллельных прямых.	\(\шляпа{e}\), \(\шляпа{f}\), \(\шляпа{g}\) и \(\шляпа{h}\) — внешние углы.	Внешний означает снаружи.
Соответствующие углы	Углы по одну сторону от прямых и по одну сторону от поперечной. Если прямые параллельны, то соответствующие углы будут равны.	\(\шляпа{а}\) и \(\шляпа{е}\), \(\шляпа{b}\) и \(\шляпа{е}\), \(\шляпа{с }\) и \(\шляпа{g}\), \(\шляпа{d}\) и \(\шляпа{h}\) — пары соответствующих углов. \(\шляпа{а}=\шляпа{е}\), \(\шляпа{b}=\шляпа{f}\), \(\шляпа{с}=\шляпа{г}\) и \( \шляпа{д}=\шляпа{ч}\).
Внутренние углы	Углы, лежащие между прямыми и по одну сторону от поперечной. Если прямые параллельны, то углы смежные.	\(\шляпа{а}\) и \(\шляпа{d}\), \(\шляпа{b}\) и \(\шляпа{с}\) — пары внутренних углов . \(\шляпа{а}+\шляпа{d}= 180°\), \(\шляпа{b}+\шляпа{с}=180°\).
Альтернативные внутренние углы	Равные внутренние углы, лежащие внутри прямых и по разные стороны от секущей. Если прямые параллельны, то внутренние углы будут равны.	\(\шляпа{а}\) и \(\шляпа{с}\), \(\шляпа{b}\) и \(\шляпа{d}\) являются парами чередующихся внутренних углов. \(\шляпа{а}=\шляпа{с}\), \(\шляпа{b}=\шляпа{d}\)

В этом видео представлен краткий обзор некоторых ракурсов образованы пересекающимися линиями.

Если две прямые пересекаются такой секущей, что:

• соответствующие углы равны; или

• альтернативные внутренние углы равны; или

• внутренние углы являются дополнительными

, то две прямые параллельны.

Факт:

Когда мы говорим о линиях, мы можем написать \(EF\) для обозначения линии, проходящей через точки \(E\) и \(F\), или \(\overline{EF}\) для обозначения отрезок прямой от точки \(E\) до точки \(F\).

Пример

Вопрос

Найдите все неизвестные углы. Является ли \(EF\параллельный CG\)? Поясните свой ответ.

Используйте свойства параллельных линий, чтобы найти все равные углы на диаграмме

Перерисуйте диаграмму и отметьте все равные углы.

Определить неизвестные углы

\[\begin{array}{rll} AB& \parallel CD & \text{(дан)} \\ \следовательно \hat{x} & = 60° & \text{( alt }\angle \text{s; } AB \parallel CD \text{)}\\ \hat{y} + 160° & = 180° & \text{(co-int }\angle \text{s; } AB \parallel CD \text{)}\\ \следовательно \hat{y} & = 20° & \\ \hat{p}& = \hat{y} & \text{(vert opp }\angle \text{ s } = \text{)}\\ \следовательно \шляпа{p}& = 20° & \\ \шляпа{r}& = 160° & \text{(соответствует }\угол \text{s; } AB \ параллельный CD \text{)} \\ \hat{s} + \hat{x} + 90° & = 180° & \text{(}\angle \text{s на линии str)}\\ \hat{s} + 60° & = 90°& \\ \следовательно \hat{s} & = 30° & \end{array}\]

Определить, будет ли \(EF\parallel CG\)

Если \(EF\parallel CG\), то \(\hat{p}\) будет равен соответствующему углу \ (\шляпа{s}\), но \(\шляпа{р}= 20°\) и \(\шляпа{s}= 30°\).

No related posts.