| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | tan(45) | ||
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Доказать, что sin…Упр 599 параграф 34 Алгебра Алимов 10-11 класс – Рамблер/класс
Доказать, что sin…Упр 599 параграф 34 Алгебра Алимов 10-11 класс – Рамблер/класс Интересные вопросыШкола
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Привет! Скиньте решение вот этого задания:
Доказать, что sin (arcsin а) = а при —1 ≤ а ≤ 1.
Я над ним уже битый час сижу(((
ответы
Лови) не майся)
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)
..)
ГДЗ11 классКолмогоров А.Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
9. Определите ряд, в котором в обоих словах пропущена одна и та же буква. ЕГЭ-2017 Русский язык Цыбулько И. П. ГДЗ. Вариант 12.
9.
Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите
эти слова, вставив пропущенную букву. (Подробнее…)
ГДЗРусский языкЕГЭЦыбулько И.П.
10. Выпишите слово, в котором на месте пропуска пишется буква Е. Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 12.
10.
Выпишите слово, в котором на месте пропуска пишется буква Е.
подчёркивать (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Калькулятор — arcsin(10) — Solumaths
Arcsin, расчет онлайн
Резюме:
Функция арксинуса позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
Функция arcsin является обратной функцией функции синуса.
арксинус онлайн
Описание:
Функция арксинус является обратной функцией синусоидальная функция, это позволяет вычисляет арксинус числа онлайн .
Число, к которому вы хотите применить функцию арксинуса, должно принадлежать диапазону [-1,1].
- Расчет арксинуса
- Таблица замечательных значений
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус: арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: тангенс. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
- Исправленные упражнения на числовые функции
- Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
- Научитесь считать с помощью обычных математических функций
- Что такое арксинус?
- График арксинуса x
- Арксинус, тригонометрические функции и другие взаимосвязи
- Пример использования калькулятора арксинуса твоя проблема. Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно помнить, это ограниченный домен арксинуса (-1 ≤ синуса ≤ 1). Если вам интересно что такое арксинус или как выглядит график арксинуса x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинуса, таких как отношение между интегралом арксинуса и производной. И так, чего же ты ждешь?
💡 Если вы понятия не имеете, что такое тригонометрия, рекомендуем вам сначала взглянуть на калькулятор тригонометрических функций Omni и, в частности, на калькулятор грехов.

Что такое арксинус?
Арксинус является обратной функцией синуса. Другими словами, это помогает найти угол треугольника, для которого известно значение синуса:
arcsin(x) = y тогда и только тогда, когда x = sin(y) .
Так как кодовая область синуса для действительных чисел равна [−1, 1] , мы можем вычислить арксинус только для чисел в этом интервале. Это означает, что область определения дуги в (для реальных результатов) равна -1 ≤ x ≤ 1. У нас есть
Однако, как вы могли бы (и должны!) помнить, синус является периодической функцией, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin(0) = 0, но также sin(π) = 0, sin(2π) = 0, sin(-π) = 0 и sin(-326π) = 0. Следовательно, если кто-то хочет вычислить arcsin( 0), ответ может быть 0, 2π (360°) или -π (-180°), чтобы назвать несколько вариантов! Все они верны, но обычно мы даем только одно число, называемое 9.0016 основная стоимость .

💡 Обычный диапазон обычных главных значений составляет -π/2 ≤ y ≤ π/2
радиан, то есть -90° ≤ y ≤ 90°.Arcsin(x) является наиболее распространенным обозначением, так как sin -1 x может привести к путанице (поскольку sin -1 x ≠ 1/sin(x) ). Аббревиатура asin(x) обычно используется в языках компьютерного программирования.
График арксинуса x
Поскольку базовая функция синуса не является однозначной, ее область определения должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π/2 ≤ y ≤ π/2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции арксинуса составляет [−π/2,π/2], а область арксинуса находится между [−1,1]. Ниже вы можете найти график арксинуса (x), а также некоторые часто используемые значения арксинуса:
x
arcsin(x)
deg
rad
-1
-90°
-π/2
-√3 / 2
-60°
-π/3
-√2 / 2
-45°
-π/4
-1/2
-30°
-π/6
0
0°
0
1/2
30°
π/6
√2 / 2
45°
π/4
√ 3 / 2
60°
π/3
1
90°
π/2
And here’s how the graph of arcsin x looks like:
Geek3 , CC BY-SA 4. 0 через Wikimedia Commons
0 через Wikimedia CommonsХотите знать, откуда взялся этот график? Его можно найти, отразив график sin(x) между диапазоном [-π/2 π/2] через линию y = x:
Jaro.p CC BY-SA 3.0, через Wikimedia CommonsInverse синус, тригонометрические функции и другие соотношения
Связь между тригонометрическими функциями и арксинусом может помочь вам лучше понять тему. Хорошей отправной точкой является прямоугольный треугольник с гипотенузой длиной 1.
Небольшое напоминание: для прямоугольного треугольника функция синуса принимает угол θ и возвращает отношение противоположности к гипотенузе, которое равно x в нашем примерном треугольнике. Функция обратного синуса, арксинус, принимает отношение противоположности к гипотенузе (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin(x) = θ, мы также можем написать, что:
- Синус:
sin(arcsin(x)) = x - Косинус:
cos(arcsin(x)) = √(1-x²) - Тангенс:
tan(arcsin(x)) = x / √(1-x²)
Другие полезные соотношения с арксинусом:
-
arcsin(x) = π/2 - arccos(x) -
арксинус(-х) = -арксинус(х)
Иногда также необходимы интеграл и производная от arcsin:
- интеграл от arcsin:
∫arcsin(x) dx = x arcsin(x) + √(1 - x²) + C - производная от arcsin:
d/dx arcsin(x) = 1 / √(1 - x²), где x ≠ -1, 1
Пример использования калькулятора арксинуса
Арксинус — полезная функция, например, при нахождении угла прямоугольного треугольника.
 Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, известная теорема Пифагора не будет столь полезной. Нахождение углов прямоугольного треугольника требует применения арксинуса:
Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, известная теорема Пифагора не будет столь полезной. Нахождение углов прямоугольного треугольника требует применения арксинуса:- для α:
sin(α) = a/c, поэтому α = arcsin(a/c) - для β:
sin(β) = b/c, поэтому β = arcsin(b/c)
Итак, давайте предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α:
- Введите значение, которое вы хотите найти арксинус . В нашем случае это 6/10. Итак, вы можете ввести значение как 0,6, но подойдет и форма 6/10 . Просто помните, что значение должно быть между −1 и 1,9.0030
- И… все! Калькулятор арксинуса сделал свое дело, и вы нашли арксинус вашего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 ° .
🙋 Учитель, я буду использовать это в реальной жизни? На этот раз да! А может и нет, надеюсь.

- Синус:
Чтобы вычислить арксинус числа, просто введите число и примените функция arcsin . Таким образом, для при вычислении арксинус числа следующего за 0.4, необходимо ввести арксинус(`0.4`) или сразу 0.4, если кнопка arcsin уже появляется, возвращается результат 0.411516846067. 92)`.
| arcsin(`-1`) | `-pi/2` | ||
| arcsin(`-sqrt(3)/2`) | `-pi/3` | arcsin(5 угловых дюймов) sqrt(2)/2`) | `-pi/4` |
| arcsin(`-1/2`) | `-pi/6` | ||
| arcsin(`0`) | ``-pi/6` 0` | ||
| arcsin(`1/2`) | `pi/6` | ||
| arcsin(`sqrt(2)/2`) | `pi/4` | ||
| arcsin(`sqrt(3)/2`) | `pi/3` | ||
| arcsin(`1`) | 10 9`pi/5` | 109`pi/2` | `pi/3`Синтаксис: arcsin(x), где x — число. Иногда используются другие обозначения: asin Примеры:arcsin(`0`) возвращает 0 Производная арксинуса :Чтобы дифференцировать функцию арксинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арксинуса 92)` Предел арксинуса :Калькулятор предела позволяет вычислить пределы функции арксинуса. предел арксинуса (x) is limit(`»arcsin»(x)`) Обратная функция арксинуса :обратная функция арксинуса представляет собой синусоидальную функцию, отмеченную как sin. Графический арксинус :Графический калькулятор может отображать функцию арксинуса в заданном интервале. Свойство функции арксинуса: Функция арксинуса является нечетной функцией. Расчет онлайн с арксинусом (арксинусом) См. также Список связанных калькуляторов: Прочие ресурсы
Калькулятор арксинуса. Обратная функция синуса. Обратная функция синуса.Автор: Ханна Памула, доктор философии Рецензию сделали Богна Шик и Джек Боуотер Последнее обновление: 3 ноября 2022 г. Содержание: |



 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.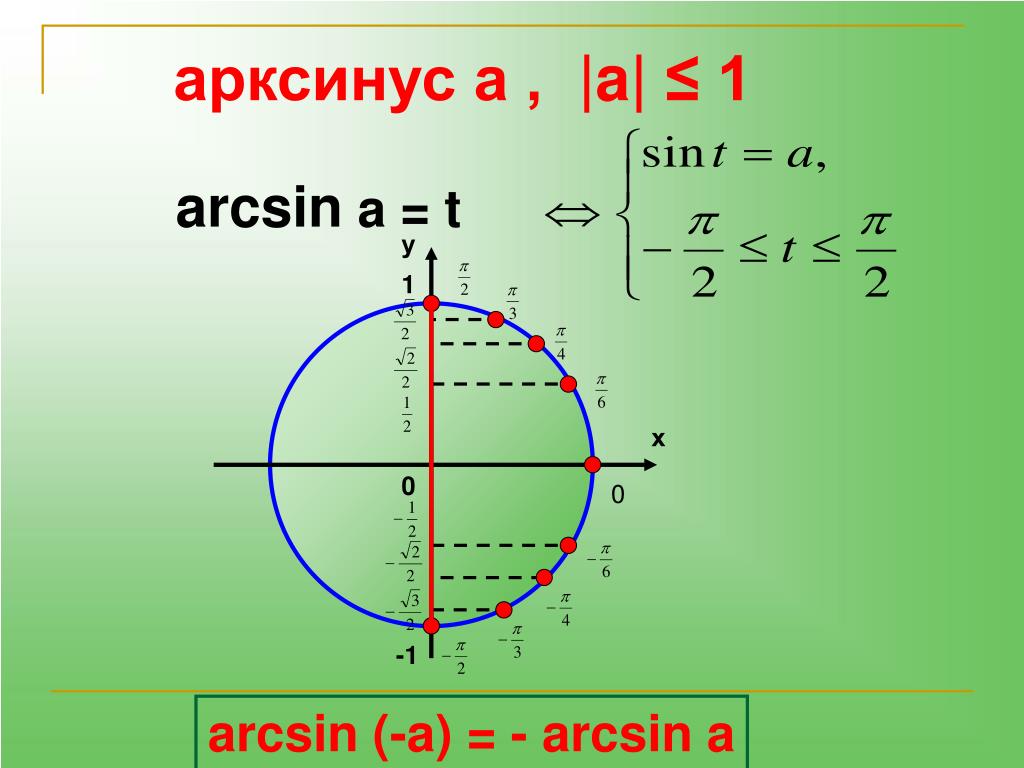 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.

 0 через Wikimedia Commons
0 через Wikimedia Commons Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, известная теорема Пифагора не будет столь полезной. Нахождение углов прямоугольного треугольника требует применения арксинуса:
Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, известная теорема Пифагора не будет столь полезной. Нахождение углов прямоугольного треугольника требует применения арксинуса: