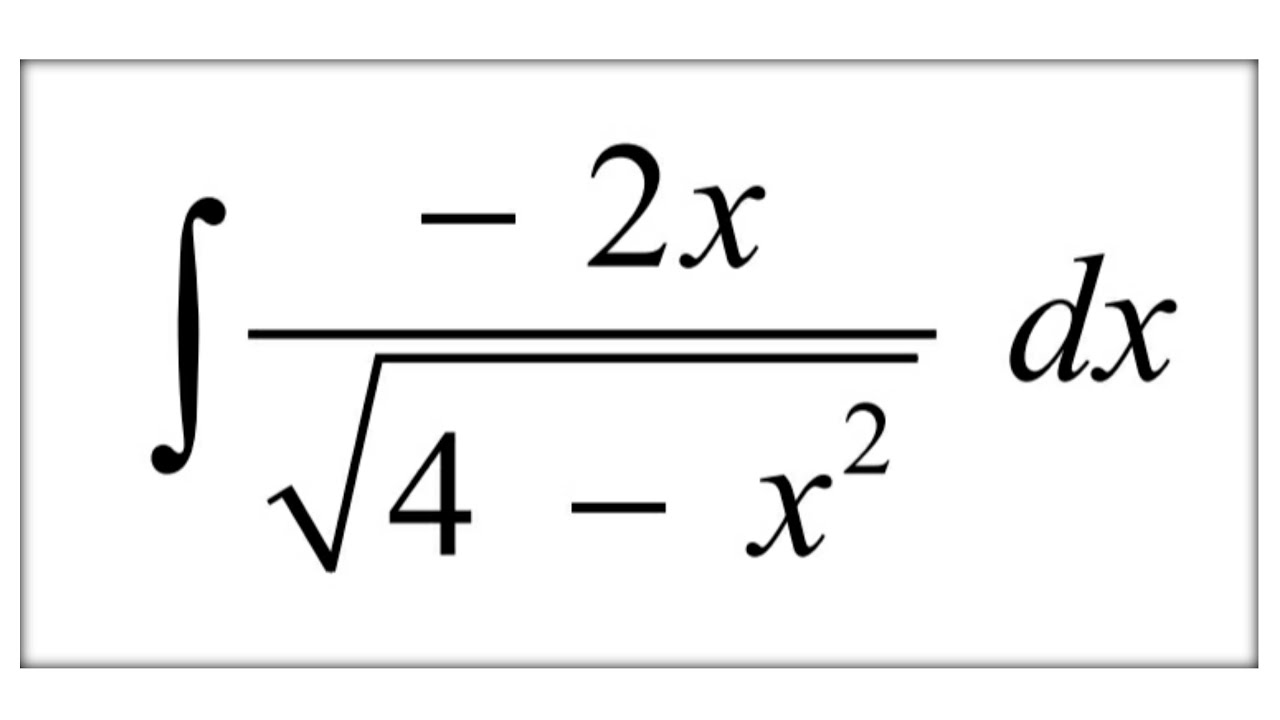Sqrt x 2 x: Решите неравенство sqrt(x-2)>=x (квадратный корень из (х минус 2) больше или равно х)

23-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Предварительное вычисление алгебры — Как решить $\sqrt{x+2}\geq x$?

Во-первых, предположим, что ¹ $x$ — действительное число, поскольку поле комплексных чисел не имеет порядка с обычными операциями сложения и умножения. Например, если $i<2i$, то $0 2 $0<-1$. С другой стороны, если $i>2i$, то $0>i$ или, что то же самое, $-i>0$, но возведение в квадрат дает то же противоречие. Это означает, что $\sqrt{x+2}\ge x$ естественно не имеет смысла, когда $\Im x\ne0$ или $\Im\sqrt{x+2}\ne0$. Обратите внимание, что существуют и другие порядки, такие как $a\preceq b$ тогда и только тогда, когда $\Re a\le\Re b$ и $\Im a\le\Im b$, но поскольку они несовместимы с операциями, управляющими полем, мы не занимайтесь этим здесь. 92$ и $x\ge0$;

$\sqrt{x+2}\ge x$ и $x\le0$.

Однако второй случай всегда верен, поскольку квадратный корень должен быть неотрицательным, как обсуждалось в первом абзаце. Таким образом, это зависит только от интервала, на котором определено $\sqrt{x+2}$, который равен $x+2\ge0\iff x\ge-2$, и поэтому мы имеем решение $x\in[-2 ,0]$ в этом случае.

Первый случай можно решить несколькими способами. 2\le9{-3/2}/4<0.$$ Аналогично, решая $f'(x)>0$ и $f'(x)<0$, мы находим, что $f$ строго возрастает на $(- 2,-7/4)$ и строго убывает на $(-7/4,+\infty)$. Поскольку $f(-2)=2$ и $f(2)=0$ (по наблюдению ⁷ ), мы можем заключить, что $f(x)\ge0$ и, следовательно, $\sqrt{x+ 2}\ge x$ только при $x\in[-2,2]$.

---

¹ Мы любим принимать вещи. Гипотеза Римана, кто-нибудь?

² Требуется ссылка. На самом деле доказать это очень непросто: действительно, очень и очень долгое время люди не понимали, что такое отрицательные числа. Таким образом, можно утверждать, что вопрос о том, верно ли $0<-1$, оставался открытой проблемой в течение миллионов лет.

³ Расширение для интереса: квадратные корни кватерниона.

⁴ Вот визуальное решение.

⁵ Один из способов устранить это неудобство состоит в том, чтобы предположить , что $x\ge0$.