Sin калькулятор онлайн: Инженерный калькулятор онлайн, Научный калькулятор

Тангенс и котангенс. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти тангенсы и котангенсы угла, представленных как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Тангенс и котангенс − теория, примеры и решения

Определение 1. Число, равное отношению

называется тангенсом угла α и обозначается

Определение 2. Число, равное отношению

называется котангенсом угла α и обозначается

Подробнее о синусах и косинусах посмотрите на странице Синус и косинус. Онлайн калькулятор.

Свойство A1. Область определения функции тангенс −это все действительные числа α, удовлетворяющие выражению

где Z множество целых чисел.

Действительно. Из равенства (1) следует, что cos α должен быть отличным от нуля. А это в свою очередь показывает справедливость равенства (3).

Свойство A2. Область определения функции котангенс −это все действительные числа α, удовлетворяющие выражению

где Z множество целых чисел.

Действительно. Из равенства (2) следует, что sin α должен быть отличным от нуля. А это в свою очередь показывает справедливость равенства (4).

Свойство 1. tg α и сtg α нечетные функции, т.е. для любого допустимого значения α справедливы равенства

Доказательство. Воспользуемся равенствами и (cм. на странице Синус и косинус. Онлайн калькулятор). Тогда имеем:

 

Свойство 2. tg α и сtg α периодичные функции с основным периодом π (180°), т.е. для любого допустимого значения α справедливы равенства

или в градусах:

Доказательство. Воспользуемся тем, что или (cм. на странице Синус и косинус. Онлайн калькулятор):

или в градусах:

И вообще

или в градусах:

Использем таблицы синусов и косинусов, и построим таблицу тангенсов и котангенсов некоторых углов, учитывая уравнение (1):

Пример 1. Найти тангенс и котангенс угла равного 420°(или радиан).

Воспользуемся уравнениями (11)− (14):

или :

или :

Пример 2. Найти тангенс и котангенс угла равного -225°(или радиан).

Воспользуемся уравнениями (11)− (14):

или :

или :

Как мы уже знаем из определения синуса и косинуса sin α=y₂, cos α=x₂ (Рис.1). Покажем, что tg α=AN, ctg α=KP

Построим каноническое уравнение прямой, проходящей через точки и (см. статью на странице Каноническое уравнение прямой на плоскости):

Тогда учитывая, что , имеем:

или

Поскольку , , тогда

При x=1 имеем y=tg α. Т.е. tg α − это ординат точки пересечения прямых ON и NA

Выразим в (15) x через y:

Подставляя , , получим:

Взяв y=1, получим x=ctg α. Таким образом ctg α − это абсцисс точки пересечения прямых ON и KP.

Так как для функциий привычнее запись y=f(x), то вместо записей u=tg α и u=сtg α мы будем использовать записи y=tg x и y=сtg x.

График функции тангенс (

y=tg x)

Построим график функции тангенс на интервале . Выберем контрольные точки:

Отметим эти точки на координатной плоскости XOY и проведем через них плавную кривую (Рис. 2)

Учитывая свойство 1 построим симметричную к этой кривой относительно начала координат (Рис.3)

Функция тангенс периодичная (свойство 2) с основным периодом π. Тогда на графике функции тангенс, ветвь на рисунке Рис.2 повторяется бесконечное число раз от -∞ до ∞:

В точках функция имеет разрыв. Каждая прямая вида является вертикальной асимптотой графика функции.

График функции котангенс (

y=сtg x)

Построим график функции котангенс на интервале [0; π). Выберем контрольные точки:

Взяв π≈3, высислим значения x, отметим эти точки на координатной плоскости XOY и проведем через них плавную кривую (Рис. 5)

Функция котангенс периодичная (свойство 2) с основным периодом π. Тогда на графике функции котангенс, ветвь на рисунке Рис.5 повторяется бесконечное число раз от -∞ до ∞:

В точках функция имеет разрыв. Каждая прямая вида является вертикальной асимптотой графика функции котангенс.

Калькулятор угла наклона крыши — расчет уклона кровли онлайн и расчет односкатной крыши

Калькулятор угла наклона крыши используется для расчета как угла уклона кровли, так и недостающих данных о кровле — проекции, высоты, длины и угла наклона ската кровли. Визуально где и какие величины можно увидеть на чертеже калькулятора, находящимся под формой расчета.

Для расчета угла наклона крыши или данных достаточно указать только две известные величины, а остальные величины (если они есть) можно использовать для проверки.

Единица измерений:

Метрическая система

Длина проекции (W):

Высота (H):

Длина ската кровли (L):

Угол наклона (α):

Градус

Формулы угла наклона крыши и длины ската

На картинке: a — угол ската, S — длина ската кровли, H — высота кровли в верхней части, L — длина проекции ската кровли

Соответственно все величины можно найти:

• a = arctg(H/L) или a = arcsin(H/S)
• H = L * tg a
• S = H / sin a

Выше приведенные формулы позволяют рассчитать любое требуемое значение (если Вам почему-то не подошел наш калькулятор)

Расчет углов уклона кровель по типам

Расчет угла наклона односкатной крыши

Односкатная кровля является одной из самых популярных и, одновременно, одной из самых легких для расчета. Фактически — наш калькулятор рассчитывет именно ее, так как более сложные кровли (например, угол наклона двускатной крыши) требуют разбивки элементов кровли на отдельные скаты и просчета каждого из них.

При расчете наклона односкатной кровли и расчете длины и угла ската крыши обязательно учитывайте свесы! Посчитать их можно задавая данные не самого ската, а высоту и проекцию кровли именно вместе со свесами.

Материалы и углы для односкатных кровель

• крыша из рубероида – 5-10 градусов
• из профнастила – от 8 до 20 градусов
• из металлочерепицы – 20-30 градусов
• из шифера – 20-35 градусов
• для фальцевой кровли необходим наклон 18-30 градусов

Расчет угла наклона двускатной крыши

Посчитать двускатную кровлю уже сложнее, чем посчитать угол наклона односкатной кровли. В случае для двух скатов необходимо рассчитывать на нашем калькуляторе уже каждый из скатов индивидуально, а для расчета материала лучше применить калькулятор кровли, т. к. расположение материала и его размеры могут быть не точными.

Расчет угла наклона вальмовой кровли

В свою очередь расчет вальмовой кровли еще сложнее чем расчет угла двускатной кровли. Вам необходимо не просто разбить и считать угол каждого ската отдельно, но и учитывать что углы для вальмовой кровли различаются.

Для вальмовой кровли так же особенно нужно учесть гуляющие размеры обрешетки, поэтому при расчете Вашей реальной кровли углы вальмовой кровли пусть немного, но будут различаться!

Виды кровли в зависимости от угла уклона крыши

Существует 4 основных типа крыш в зависимости от угла наклона:

• 3-10° — плоские
• 10-30° — пологие
• 30-45° — скатные
• 45-60° — высокие

грех(х) | функция синуса

sin(x) | функция синуса

Главная›Математика›Тригонометрия› Функция синуса

sin(x), функция синуса.

• Определение синуса
• График синуса
• Правила синусов
• Функция обратного синуса
• Таблица синусов
• Синус калькулятор

Определение синуса

В прямоугольном треугольнике ABC синус α, sin(α) определяется как отношение между стороной, противоположной углу α, и сторона, противоположная прямому углу (гипотенуза):

sin α = a / c

Пример

a = 3 дюйма

c = 5″

sin α = a / c = 3 / 5 = 0,6

График синуса

TBD

Правила синуса

Название правила	Правило
Симметрия	sin(- θ ) = -sin θ
Симметрия	sin(90° — θ ) = cos θ
Пифагорейское тождество	грех 2 α + cos 2 α = 1
	sin θ = cos θ × тангенс θ
	sin θ = 1 / csc θ
Двойной уголок	sin 2 θ = 2 sin θ cos θ
Сумма углов	sin( α+β ) = sin α cos β + cos α sin β
Разница углов	sin( α-β ) = sin α  cos β — cos α sin β
Сумма к произведению	sin α + sin β = 2 sin [( α+β )/2] cos [( α — β )/2]
Отличие от продукта	sin α — sin β = 2 sin [( α-β )/2] cos [( α+β )/2]
Закон синусов	a / sin α = b / sin β = c / sin γ
Производная	sin’ x = cos x
Интеграл	∫ грех х d х = — cos х + С
Формула Эйлера	sin x = ( e ix — e — ix ) / 2 i

Функция обратного синуса

Арксинус x определяется как функция обратного синуса x, когда -1≤x≤1.

Когда синус y равен x:

sin y = x

Тогда арксинус x равен функции обратного синуса x, который равен y:

arcsin x = sin ^-1 ( x ) = y

См.: Функция Arcsin

Таблица синусов

90 057

x (°)	x (рад)	грех х
-90°	-π/2	-1
-60°	-π/3	-√3/2
-45°	-π/4	-√2/2
-30°	-π/6	-1/2
0°	0	0
30°	№/6	1/2
45°	№/4	√2/2
60°	№/3	√3/2
90°	№/2	1

 

---

См. также

• Функция арксинуса
• Калькулятор синуса
• Функция косинуса
• Перевод градусов в радианы

Напишите, как улучшить эту страницу

ТРИГОНОМЕТРИЯ

• Функция Arccos
• Функция арксинуса
• Функция арктангенса
• Функция косинуса
• Синусоидальная функция
• Касательная функция

RAPID TABLES

• Рекомендовать сайт
• Отправить отзыв
• О

Калькулятор греха — MathCracker.

com

Инструкции: Используйте этот калькулятор греха для вычисления любой операции, включающей грех. Если это числовое выражение с синусом, калькулятор упростит это, и если это функция греха, он отобразит ее на графике. Пожалуйста, введите выражение греха, с которым вы хотите работать.

Об этом калькуляторе грехов

Этот калькулятор sin выполнит следующие действия: вы можете указать числовое выражение, например sin(pi/4), и в этом случае калькулятор упростит его и при необходимости даст приблизительное числовое значение. Кроме того, если вы предоставляете функцию греха, например sin(3x+1), калькулятор отобразит это на графике.

Затем процесс прост: после того, как вы ввели выражение sin , которое хотите рассчитать, вы просто нажимаете кнопку «Рассчитать», которая находится под формой, чтобы получить шаги. решения.

Синус, наряду с косинусом, являются двумя краеугольными камнями тригонометрии. Вы увидите синус и косинус вокруг например, при решении треугольников, а также в таких областях, как физика.

Как вычислить грех?

Грех является одним из основных строительных блоков в геометрии и тригонометрии. Sin — это величина, которую можно вычислить для углов в контексте прямоугольного треугольника. Когда у тебя есть один из углов прямоугольного треугольника, не равный 90 _o один, вы можете найти противоположную сторону и соседнюю сторону .

Тогда формула греха будет

\[\sin \theta = \frac{\text{Противоположная сторона}} }{\text{Гипотенуза}}\]

Чему равен грех?

Sin – это безразмерная величина, которая измеряет величину наклона угла относительно горизонтальной точки отсчета, где находится соседняя сторона.

Когда sin равен нулю, угол равен нулю, поэтому отверстия нет. Максимальное раскрытие угла происходит, когда sin = 1, что происходит при 90 _или .

Что такое sin 1?

Этот вопрос может показаться невинным, но он часто приводит к путанице. В формальной математике все тригонометрические функции по умолчанию измеряются в радианах. Но по какой-то причине радианы малоизвестны или слишком популярны среди студентов, которые предпочитают использовать в качестве меры градусы, потому что они просто более привычны.

Учащиеся хорошо знают известные углы в градусах, такие как 90 _o прямой угол и 360 _или — полный круг. Вы можете использовать это градус радиан калькулятор для перемещения между двумя системами.

Таким образом, правильный ответ на вопрос, что такое sin(1), состоит в том, что sin(1) приблизительно равен 0,841471, если предположить, что угол 1 выражается в радианах. Теперь sin(1) приблизительно равен 0,017452, когда Предполагается, что 1 выражается в градусах. Поэтому при работе с углами следует проявлять крайнюю осторожность.

Чему равен синус минус 1?

Еще один вопрос, на который формально есть простой ответ, но иногда он зависит от используемого соглашения. Синус к отрицательной 1 необходимо уточнить, так как синус функция. Таким образом, вы можете сделать sin(1), и это число, а sin(1) к отрицательной 1 просто взять обратное число sin(1), так что у вас есть 1/sin(1), что является число. 9{-1}(х)\).

Могу ли я использовать научный калькулятор для расчета греха

Конечно, можно, но одним из преимуществ использования этого калькулятора греха является то, что вы получите показанные шаги вместе с результатом. Большинство калькуляторов покажет только окончательный ответ.

Как пользоваться калькулятором грехов?

Основная идея калькулятора греха состоит в том, чтобы вычислять введенные вами выражения греха. Вот некоторые известные углы, обычно кратные или доли \(\pi\), которые являются простыми, целые или дробные результаты при вычислении их греха, поэтому рекомендуется использовать калькулятор выражения греха, чтобы помочь вам в этом.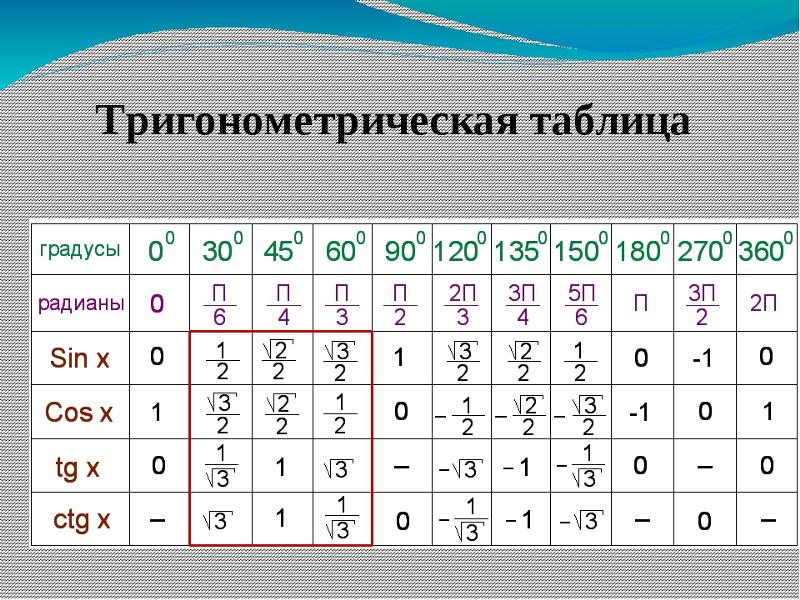

Нелегко запомнить все расчеты греха для ВСЕХ заметных углов, и в итоге вы будете работать с треугольником, пытаясь получить ответ вручную, и калькулятором пригодится, чтобы дважды проверить, что вы получаете вручную.

Кроме того, вместо этого вы можете ввести в калькулятор функцию sin, например, sin(pi x), и вместо оценки нескольких точек этот калькулятор выдаст вам соответствующую graph

Каковы шаги по использованию калькулятора грехов?

• Шаг 1: Определите выражение sin, которое вы хотите вычислить
• Шаг 2: Введите выражение в соответствующее поле. Вам не нужно предварительно упрощать, калькулятор сделает это за вас
• Шаг 3: Калькулятор проверит, можно ли вычислить выражение, и в этом случае оно уменьшится до простейших выражений
• Шаг 4: Если sin все еще присутствует в выражении, потому что его нельзя упростить дальше, например, sin(3/4), калькулятор выдаст вам приблизительное числовое значение. значение
• Шаг 5: Если вместо этого предоставляется функция sin, будет предоставлен график

Мы не можем не подчеркнуть важность правильного вычисления операций с синусоидами, так как они будут встречаться буквально везде.

формула синуса и косинуса

Синус и косинус — два очень близких родственника, если не сестры. Между ними существует тесная связь, выраженная в следующей формуле:

\[\ displaystyle \ sin \ left (\ frac {\ pi} {2} — x \ right) = \ cos (x) \] 92(х) = 1 \]

Почему грех так важен?

Синусы важны, потому что наряду с косинусами находятся в центре и ядре построения круга. И тогда круги таят в себе много других построений, как треугольники и так далее.

Следовательно, синус и косинус переплетаются в каждой геометрической конструкции.

Пример: калькулятор Sin

Вычислите следующее выражение sin: \(\sin\left(\frac{\pi}{3}\right)\)

Решение: Для расчета было предоставлено следующее тригонометрическое выражение:

\[\sin\left(\frac{\pi}{3}\right)\]

Изучив данное тригонометрическое выражение, мы можем найти один заметный угол, который равен \(\sin\left(\frac{\pi{}}{3}\right)\).

▹ Для угла \(\frac{\pi{}}{3}\) графически получаем:

Приведенное тригонометрическое выражение можно упростить следующим образом:

\( \displaystyle \sin\left(\frac{\pi{}}{3}\right)\)

Вычисляя тригонометрическое выражение при заметном угле \(\displaystyle\frac{\pi{}}{3}\), мы получаем, что: \(\displaystyle \sin\left(\frac{\pi{}}{3}\ справа) = \frac{1}{2}\sqrt{3}\)

«=»

\(\displaystyle \frac{1}{2}\sqrt{3}\)

Вывод: Мы заключаем, что \(\displaystyle \sin\left(\frac{\pi}{3}\right) = \frac{1}{2}\sqrt{3} \приблизительно 0,866\).

Пример: больше вычислений синуса

Вычислите следующее: \( \sin\left(\frac{5}{4}\right) \)

Решение: Для расчета было предоставлено следующее тригонометрическое выражение:

\[ \sin\left(\frac{5}{4}\right)\]

, но данное тригонометрическое выражение не может быть далее упрощено.

Вывод: Переданная функция не может быть упрощена, и мы получаем, что примерно \(\displaystyle \sin\left(\frac{5}{4}\right) \ приблизительно 0,949\).

Пример: функция Sin

Вычислить \( \sin(3x + 1) \).

Решение: Нам нужно работать со следующей тригонометрической функцией

\[f(x) = \sin\left(3x+1\right)\]

На основе переданного аргумента тригонометрической функции частота и период вычисляются следующим образом:

\[ \begin{array}{ccl} \text{Точка} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \приблизительно & 2.0944 \конец{массив}\]

, а также

\[ \begin{array}{ccl} \text{Частота} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \ приблизительно & 0,4775 \end{массив}\]

На основе предоставленной тригонометрической функции \(f(x) = \sin\left(3x+1\right)\) мы получаем, что:

» Амплитуда в этом случае равна \(A = 1\) .