I семестр / Математический Анализ — ответы — 21-31 билеты / вопрос 22
22 Критерий Коши сходимости последовательности.
Определение: Последовательность {xn} называется фундаментальной, если > 0 N, n >N и натурального p: xn+p—xn < .
Так как m = n+p — тоже произвольное число >N, то определение фундаментальности можно сформулировать следующим образом: > 0 N, n >N и m > N:xm—xn < .
Геометрически
фундаментальность последовательности
{xn}
означает, что для любого сколь угодно
малого
существует такой номер N,
что любые два члена последовательности
с большим, чем N,
номерами, отстоят друг от друга не более,
чем на .
(здесь рисунок)
Пример: Докажем, что последовательность =1, ,, … — фундаментальная. Зададим произвольное > 0, возьмем N > . Тогда > , и n >N и натурального p: xn+p—xn = =-< << . Это и означает, что последовательность — фундаментальная.
Лемма 2. Фундаментальная последовательность ограничена.
Доказательство:
Пусть {xn}
— фундаментальная последовательность.
Возьмем какое-нибудь положительное ,
например,
= 1. По определению фундаментальности,
N,
n >N и m > N:xm—xn
< 1. Зафиксируем какое-нибудь m0 > N,
тогда
<
1 при n >N,
или
—
1 < xn <
+
1 при n >N.
Таким образом, все члены последовательности
с номерами n >N лежат в интервале (-
1,
+
1), вне этого интервала лежит только
конечное число членов последовательности.
Лемма доказана.
Теорема 6.4 (критерий Коши сходимости последовательности) Для того, чтобы числовая последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство.
Необходимость. Дано: Последовательность {xn} сходится. Требуется доказать, что последовательность {xn} — фундаментальная. Пусть =a. Зададим произв. > 0.
По определению предела, N, n > N:xn—a < , и m > N:xm—a < . Если n > N, m > N, то x
Это и означает по
определению, что последовательность
{xn}
— фундаментальная.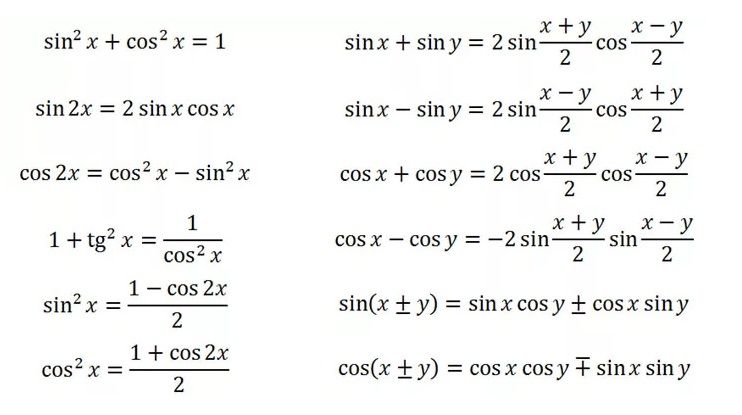
Необходимость доказана.
Достаточность. Дано: Последовательность {xn} — фундаментальная. Требуется доказать: {xn} сходится. По лемме 2, последовательность {xn} ограничена, следовательно, можно выделить сходящуюся подпоследовательность . Пусть = a. Докажем, что = a. Зададим произвольное > 0. Так как подпоследовательность сходится к a, начиная с некоторого номера N1 все члены {- окрестности точки a}, а так как последовательность {x
n} — фундаментальная, то начиная с некоторого номера N2 все члены xn отстоят от членов меньше, чем на . Следовательно, начиная с номера N = max (N1, N2) все члены последовательности xn {- окрестности точки a}, а это и означает, что = a, что и требовалось доказать.
Теорема доказана.
Теорема доказана.[12] Сформулировать определение нефундаментальной последовательности.
Пример: Рассмотрим последовательность {sin n}. Докажем, что эта последовательность расходится. Для этого достаточно доказать, что она не является фундаментальной. Предположим противное: допустим, что {sin n} — фундаментальная. Тогда если > 0
sin(n+2) — sin n< 2sin 1cos(n+1)< .
> 0 N, n >N: cos(n+1)< .
=> {cos n} — бесконечно малая, то есть cos n 0 при n .
cos(n+1)
= cos ncos
1- sin nsin
1.
sin n = ( cos ncos 1 — cos(n+1)) 0 при n .
cos n и sin n 0 при n . Но это противоречит тому, что cos2n + sin2n =1.
Полученное противоречие доказывает, что последовательность {sin n} расходится.
Попробуйте исследовать вопрос, сколько предельных точек у последовательности {sin n}.
исчисление — показывает, что $a_n=\sin(n)$ не сходится
Задать вопрос
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 9к раз
$\begingroup$
Показать, что $a_n=\sin(n)$ не сходится
Моя идея:
Возьмем две подпоследовательности: $a_{n_k}=\sin(\frac {\pi k} 2)$ , $a_{n_l}=\sin(\frac {2\pi l} 3 )$
Итак: $\forall n$ : $\lim_{n\to\infty} a_{n_k}=1$, $\lim_{n\to\infty} a_{n_l}=-1$
Таким образом, две бесконечные подпоследовательности сходятся к разным пределам, поэтому последовательность $a_n$ не сходится.
Верно?
Редактировать:
Противоположное определение предела последовательности:
$\exists\epsilon>0 : \forall n\in N : \exists n>N \Rightarrow |x_n-L|>\epsilon$
Возьмем $\epsilon =1$ и мы знаем, что $\sin( n)$ ограничен, поэтому возьмем его супермуму: 1
$|1-1|>\epsilon=1\Rightarrow 0>1 \Rightarrow$ Противоречие.
- исчисление
- последовательности-и-ряды
- пределы
- проверка-проверка
$\endgroup$
13
$\begingroup$
Ваш аргумент неверен, так как вы вычисляете в нем значения $\sin{k\pi\over 2}$, которые не являются значениями исходной последовательности.
Вот доказательство, не использующее аргументы плотности:
Предположим, что $\lim_{n\to\infty}\sin n=\sigma\in{\mathbb R}$. Затем
$$2\cos n\>\sin 1=\sin(n+1)-\sin(n-1)\to 0\qquad(n\to\infty)\ ,$$
откуда следует $\lim_{n\to\infty}\cos n=0$, откуда $\sigma\in\{-1,1\}$.
Впуск $n\to\infty$ в
$$\sin(n+1)=\sin n\>\cos 1+\cos n\>\sin 1$$
тогда будет означать $\cos 1=1$, что явно неверно.
$\endgroup$
2
$\begingroup$
Здесь нужен более глубокий результат. Обозначим через $\{x\}$ дробную часть $x$. По теореме Кронекера множество $\left\{ \{\frac{n}{2\pi}\}:n\in\Bbb{N}\right\}$ является плотным подмножеством $[0,1] $, (поскольку $\pi$ иррационально.) Итак, существуют две последовательности целых чисел $(n_k)_k$ и $(m_k)_k$ такие, что
$$
\lim_{k\to\infty}\left\{\frac{n_k}{2\pi}\right\}=0,\quad\hbox{and}\quad\lim_{k\to\infty}\left \{\ frac {m_k} {2 \ pi} \ right \} = \ frac {1} {4}
$$
Эквивалентно
$$
\lim_{k\to\infty}\left(n_k-2\pi\left\lfloor\frac{n_k}{2\pi}\right\rfloor\right)=0,\quad\hbox{and}\quad \lim_{к\к\infty}
\left(m_k-2\pi\left\lfloor\frac{m_k}{2\pi}\right\rfloor\right)=\frac{\pi}{2}
$$
Это $\lim\limits_{k\to\infty}\sin(n_k)=0$ и $\lim\limits_{k\to\infty}\sin(m_k)=1$.
Таким образом, последовательность $(\sin(n))_n$ не сходится. 9n}n$$сходится?
(Задача поставлена 22.06.2017 аспирантами Центра им. Г. Штейнхауса Вроцлавской политехники. Обещанный приз за решение — «butelka miodu pitnego», см. стр. 37 тома 1 Львовской шотландской книги. Чтобы получить приз, напишите на адрес электронной почты: [email protected]).
- nt.теория чисел
- реальный анализ
- последовательности-и-ряды
- диофантовое приближение
$\endgroup$
17
$\begingroup$
Обратите внимание, что если бы $\pi$ было рациональным (с четным числителем), то $\sin(n)$ периодически равнялось бы $1$, поэтому ряд расходился бы. Аналогично, если бы $\pi$ было достаточно сильным числом Лиувилля. Таким образом, для установления сходимости необходимо использовать некоторую количественную меру иррациональности $\pi$.